Abstract
Oxygen is in many ways a unique element: It is the only known diatomic molecular magnet, and it exhibits an unusual O8 cluster in its high-pressure solid phase. Pressure-induced molecular dissociation as one of the fundamental problems in physical sciences has been reported from theoretical or experimental studies of diatomic solids H2, N2, F2, Cl2, Br2, and I2 but remains elusive for molecular oxygen. We report here the prediction of the dissociation of molecular oxygen into a polymeric spiral chain O4 structure (space group I41/acd, θ-O4) above 1.92-TPa pressure using the particle-swarm search method. The θ-O4 phase has a similar structure as the high-pressure phase III of sulfur. The molecular bonding in the insulating ε-O8 phase or the isostructural superconducting ζ-O8 phase remains remarkably stable over a large pressure range of 0.008–1.92 TPa. The pressure-induced softening of a transverse acoustic phonon mode at the zone boundary V point of O8 phase might be the ultimate driving force for the formation of θ-O4. Stabilization of θ-O4 turns oxygen from a superconductor into an insulator by opening a wide band gap (approximately 5.9 eV) that originates from the sp3-like hybridized orbitals of oxygen and the localization of valence electrons.
Keywords: solid oxygen, spiral chain structure
As a long-standing problem in physics and chemistry, as well as earth and planetary sciences, high-pressure dissociation of diatomic molecules, such as H2, N2, O2, F2, Cl2, Br2, and I2, has attracted a lot of attention. Among these molecular systems, solid oxygen is a system of particular interest and exhibits many unusual physical properties by virtue of its molecular spin and the resultant spin-spin interactions, which make the system a critical test case for condensed-matter theory (1, 2). Oxygen is also the third most abundant element in the Solar System, and its behavior under extreme pressures provides important insight into the oxygen-related systems for a better understanding of the physics and chemistry of planetary interiors.
Oxygen exhibits a rich polymorphism with seven unambiguously established crystalline phases. Upon cooling at ambient pressure, oxygen is in turn solidified to the paramagnetic γ-phase, the magnetically disordered (short-range ordered) β-phase (3, 4), and ultimately the antiferromagnetic α-phase (5). Upon compressing to approximately 6 GPa, the α-phase transforms into the antiferromagnetic δ-phase (6–8). Under a higher pressure of approximately 8 GPa, the magnetic order of oxygen is destroyed, which leads to the ε-O8 phase consisting of O8 clusters (9, 10). The ε-O8 phase displays the bonding characteristics of a closed-shell system, in which the intermolecular interactions primarily involve the half-filled 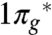 orbital of O2 (11). Above 96 GPa, ε-O8 has been observed to transform into a metallic ζ-phase (12, 13) and intriguingly exhibits superconductivity with a transition temperature of 0.6 K (14). This superconducting ζ-phase has been predicted by theory (15) and subsequently confirmed by experiment (16) to be isostructural with ε-O8, except that the ζ-O8 phase has a shorter O-O distance between O8 clusters than between O2 pairs within an O8 cluster. These studies have explored the high-pressure phase diagrams of solid oxygen up to the maximum pressure of 500 GPa (15). At such pressures, other diatomic molecules (17–21) readily exhibit molecular dissociations, whereas the O2 molecules remain intact.
orbital of O2 (11). Above 96 GPa, ε-O8 has been observed to transform into a metallic ζ-phase (12, 13) and intriguingly exhibits superconductivity with a transition temperature of 0.6 K (14). This superconducting ζ-phase has been predicted by theory (15) and subsequently confirmed by experiment (16) to be isostructural with ε-O8, except that the ζ-O8 phase has a shorter O-O distance between O8 clusters than between O2 pairs within an O8 cluster. These studies have explored the high-pressure phase diagrams of solid oxygen up to the maximum pressure of 500 GPa (15). At such pressures, other diatomic molecules (17–21) readily exhibit molecular dissociations, whereas the O2 molecules remain intact.
In this work, we have extensively explored the high-pressure crystal structures of solid oxygen up to 2 TPa by using the first-principles method of crystal structure prediction (22), which was designed to perform global minimization of free energy surfaces. This analysis was conducted by merging ab initio total-energy calculations via the CALYPSO (crystal structure analysis by particle-swarm optimization) method (22). Our CALYPSO method has been implemented in the CALYPSO code and successfully benchmarked on a number of known systems (22). Several predictions of high-pressure structures of dense Li, Mg, Bi2Te3, and water ice (23–26) were successfully made, and predictions of the high-pressure insulating Aba2-40 (Pearson symbol oC40) structure of Li and the two low-pressure monoclinic structures of Bi2Te3 were confirmed by independent experiments (25, 27).
Results and Discussion
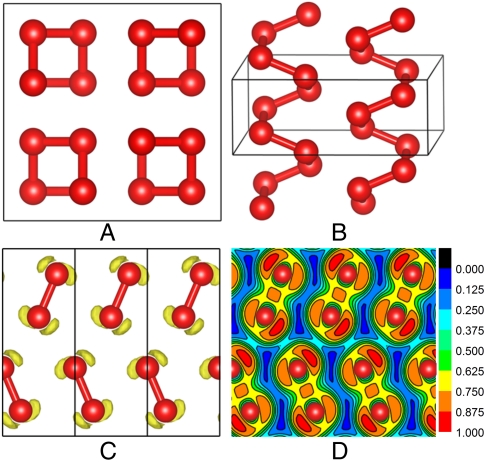
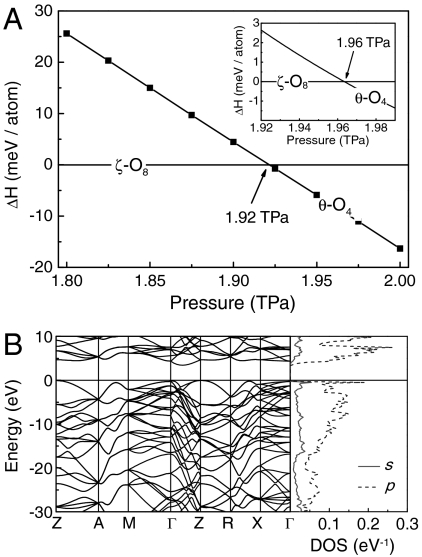
Our structure searches using the CALYPSO code with system sizes that were up to 24 atoms per simulation cell were performed at pressures of 0.02–2 TPa. The structural simulations at 0.02 TPa were able to successfully predict the experimentally observed ε-O8 structure, whereas at 0.1–1.5 TPa, ζ-O8 was predicted to be stable, which is in agreement with an earlier prediction (15) and experimental observation (16). At 2 TPa, we surprisingly discovered an energetically most stable tetragonal I41/acd structure (named θ-O4, 16 atoms per cell, Fig. 1A), which is slightly denser (approximately 1.3%) than ζ-O8. Remarkably, the molecular feature is no longer preserved in the θ-O4 structure; instead, squared chains with four atoms per turn are formed. In this configuration, each oxygen atom has two identical nearest neighbors with a nearest O-O distance of 1.153 Å at 2 TPa, which is considerably larger than the intramolecular distances (e.g., 1.036 Å at 1.8 TPa) in ζ-O8. The chains are formed along the c axis with an O-O-O bond angle of 98.79°. The nearest-neighbor O-O distance between chains is 1.552 Å, which is approximately 35% longer than the intrachain O-O distance. Calculating the enthalpy curve (Fig. 2A) at a higher level of accuracy for θ-O4 confirms its energetic stability relative to ζ-O8. Phonon calculations (SI Text) establish the dynamical stability of the θ-O4 structure because we do not find any imaginary phonon within the Brillouin zone.
Fig. 1.
(A and B) The predicted θ-O4 structure viewed along the c and a axes, respectively. The optimized lattice parameters at 2 TPa are a = 5.651 Å and c = 1.803 Å with oxygen occupying 16f (0.1359, 0.3859, 0.125) positions. (C) The calculated ELF isosurface of the θ-O4 structure with ELF = 0.8. (D) ELF plots in the (100) section.
Fig. 2.
(A) Calculated enthalpy per atom as a function of pressure with respect to ζ-O8. For confirmation, the Inset in A shows the enthalpy of θ-O4 relative to that of ζ-O8 that was obtained by a full-potential all-electron calculation using WIEN2K code. The all-electron method finds basically the same result on the transition pressure with a < 2% difference, which confirms the validity of the PAW potential adopted here at such high pressures. B shows the band structure (Left) and partial electronic density of states (DOS, Right) for θ-O4 at 2 TPa.
Oxygen is the lightest element in group VI of the periodic table, with sulfur being the next heavier family member. Previous theoretical studies assumed that the molecular ring structure of S8 (S-I) in sulfur might be one of the candidates for the high-pressure phases of solid oxygen (28). However, calculations suggested that oxygen in the S8 structure was energetically very unfavorable when compared with other known oxygen phases. Interestingly, we found that θ-O4 shares the same structure type as the high-pressure S4 phase (S-III) of sulfur (29). The reasons why atomic oxygen is unable to adopt the lower pressure phases (S-I and the trigonal chain S-II) of sulfur might stem from the fact that oxygen has a very small 1s core (the 1s orbital radius of oxygen is 0.068 Å) which is capable of forming very short bonds. This small 1s core in oxygen is apparently in contrast to the much larger 2p core in sulfur (the 2p orbital radius of sulfur is 0.169 Å).
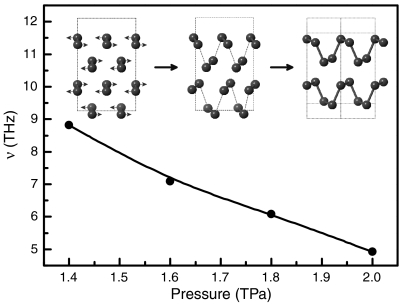
To understand the driving force for the formation of polymeric θ-O4 structure, we calculated the phonon dispersion curves of ζ-O8 at elevated pressures. A transverse acoustic (TA) phonon mode at the zone boundary V point was found to soften linearly with increasing pressure (Fig. 3). It is well established that imaginary phonons (i.e., phonon frequencies having negative values) lead to the lattice instability and thus induce phase transitions (30, 31). Notably, even though at the phase transition pressure of 1.92 TPa the TA(V) phonon frequency in ζ-O8 does not soften to zero or become imaginary, it can still initiate the phase transition. This transition mechanism is similar to those observed in SiO2 (32) and MgH2 (33), where the rutile → CaCl2 phase transition is driven by the softened nonzero optical mode at the zone center (33). We have plotted the eigenvectors of this TA(V) phonon mode (Fig. 3, Inset), where the arrows represent the directions of atomic vibrations. It is clearly seen that this softening phonon mode is involved in the planar rotation of oxygen molecules around the a axis. The role of this rotation is to effectively shorten the intermolecular O-O distance and lengthen the intramolecular bond, which ultimately leads to the stabilization of the squared chains in the θ-O4.
Fig. 3.
Phonon frequencies of the softened transverse acoustic phonon mode at the zone boundary V point versus pressure in ζ-O8. The Inset shows the phase transition mechanism of ζ-O8→ θ-O4. Arrows indicate the eigenvector of this softened mode.
The metallization of ζ-O8 is attributed to the creation of nearly free electrons by the pressure-induced band overlap (15). As a result, a very low electronic density of states is achieved at the Fermi level in close correlation with the observed low superconducting transition temperature (0.6 K) (14). As the atomic θ-O4 phase forms, solid oxygen remarkably turns to an insulator as suggested by the simulated band structure and partial electronic density of states at 2 TPa (Fig. 2B). The calculated band gap is approximately 3.2 eV, although it should be much larger because the density functional calculation is known to significantly underestimate the band gap. A Heyd-Scuseria-Ernzerhof (HSE) hybrid function was adopted to correct the underestimation problem and to derive a better band gap estimation of approximately 5.9 eV. To probe the physical mechanism of this insulation, we have performed a chemical bonding analysis of θ-O4 through calculations of the electron localization function (ELF) as shown in Fig. 1 C and D. In these figures, the calculated ELF isosurface clearly indicates two lone pairs and two O-O covalent bondings for each oxygen atom. This result allows us to identify the peculiar sp3-like bonding orbitals of oxygen in θ-O4. Consequently, a full localization of valence electrons is found, and this system creates a wide gap insulator. The intriguing bonding behavior of oxygen in θ-O4 is not completely unexpected because it somewhat resembles the chemistry of oxygen in water ice, which forms two O-H single bonds. What makes it unique, however, is that the sp3 orbitals of oxygen in θ-O4 are distributed along infinite chains, unlike the perfect localization in isolated water molecules. Notably, the O-O-O bond angle is 98.79° in θ-O4, which is evidently smaller than the ideal tetrahedral angle of 109°. This angle deviation is a result of Coulomb repulsive interaction between the lone pairs.
The insulating feature in θ-O4 stands in contrast to the metallicity of the high-pressure atomic phases predicted for hydrogen (17) and established for halogens (18, 19). This contrast originates from the fact that hydrogen and halogen elements, having one and seven electrons in their outer shells, respectively, are unable to form the perfect saturation bonding in atomic structures favorable to the metallicity. This insulation in θ-O4 seemingly resembles polymeric nitrogen (21, 34) in which five valence electrons of each N atom form three covalent bonds and one lone pair, which results in the complete localization of the valence electrons. However, creation of the insulating θ-O4 from the compression of a metallic (and superconducting) solid clearly goes against the conventional wisdom that high pressure metallizes materials. The predicted formation of θ-O4 in dense oxygen provided another case on the metal-insulator transition as previously exemplified in dense lithium (24, 35) and sodium (36) and represents a significant step forward in understanding the behavior of solid oxygen and other oxygen-related materials at extreme conditions, such as in the interiors of giant planets.
Methods
The underlying ab initio structural relaxations and electronic calculations were performed in the framework of density functional theory within the Perdew-Burke-Ernzerhof (PBE) theory, as implemented in the Vienna Ab Initio Simulation Package code (37). We also applied the HSE hybrid functions (38, 39) to correct the band gap error of the PBE functional. The all-electron projector augmented wave (PAW) (40, 41) method was adopted, with the PAW potential treating 1s2 as the core. The cutoff energy (910 eV) for the expansion of the wave function into plane waves and Monkhorst-Pack k (42) meshes were chosen to ensure that all of the enthalpy calculations are well converged to better than 1 meV per atom. The phonon calculations were carried out by using a supercell approach (43) as implemented in the phonopy code (44). The validity of the used PAW potential for the currently studied high-pressure (≤ 2 TPa) scenarios was carefully verified by comparing it with the full-potential all-electron calculation using the WIEN2K code (45). In the full-potential calculations, the muffin-tin radii were chosen to be 0.97 a.u. for O. The plane-wave cutoff was defined as KmaxRMT = 7, where RMT represents the muffin-tin radius and Kmax denotes the maximum size of the reciprocal-lattice vectors. Convergence tests resulted in the choices of 1,000 k points for both the ζ-O8 and the θ-O4 phases in the electronic integration of the Brillouin zone.
Supplementary Material
Acknowledgments.
The authors acknowledge the High Performance Computing Center of Jilin University for supercomputer time and for funding from the National Natural Science Foundation of China under Grants 11025418 and 91022029, and the China 973 Program under Grant 2011CB808200. H.M. was supported by the EFree grant, which is an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under Award DE-SC0001057.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1119375109/-/DCSupplemental.
References
- 1.Freiman YA, Jodl HJ. Solid oxygen. Phys Rep. 2004;401:1–228. [Google Scholar]
- 2.Young DA. Phase Diagrams of the Elements. Berkeley: University of California Press; 1991. [Google Scholar]
- 3.Horl E. Structure and structure imperfections of solid β-oxygen. Acta Crystallogr. 1962;15:845–850. [Google Scholar]
- 4.LeSar R, Etters RD. Character of the α—β phase transition in solid oxygen. Phys Rev B. 1988;37:5364–5370. doi: 10.1103/physrevb.37.5364. [DOI] [PubMed] [Google Scholar]
- 5.Meier RJ, Helmholdt RB. Neutron-diffraction study of α- and β-oxygen. Phys Rev B. 1984;29:1387–1393. [Google Scholar]
-
6.Schiferl D, Cromer DT, Schwalbe LA, Mills RL. Structure of “orange”
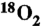 at 9.6 GPa and 297 K. Acta Crystallogr B. 1983;39:153–157. [Google Scholar]
at 9.6 GPa and 297 K. Acta Crystallogr B. 1983;39:153–157. [Google Scholar] - 7.Gorelli FA, Santoro M, Ulivi L, Hanfland M. Crystal structure of solid oxygen at high pressure and low temperature. Phys Rev B. 2002;65:172106. [Google Scholar]
- 8.Goncharenko IN, Makarova OL, Ulivi L. Direct determination of the magnetic structure of the delta phase of oxygen. Phys Rev Lett. 2004;93:055502. doi: 10.1103/PhysRevLett.93.055502. [DOI] [PubMed] [Google Scholar]
- 9.Fujihisa H, et al. O8 cluster structure of the epsilon phase of solid oxygen. Phys Rev Lett. 2006;97:085503. doi: 10.1103/PhysRevLett.97.085503. [DOI] [PubMed] [Google Scholar]
- 10.Lundegaard LF, Weck G, McMahon MI, Desgreniers S, Loubeyre P. Observation of an O8 molecular lattice in the ε phase of solid oxygen. Nature. 2006;443:201–204. doi: 10.1038/nature05174. [DOI] [PubMed] [Google Scholar]
- 11.Meng Y, et al. Inelastic x-ray scattering of dense solid oxygen: Evidence for intermolecular bonding. Proc Natl Acad Sci USA. 2008;105:11640–11644. doi: 10.1073/pnas.0805601105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Desgreniers S, Vohra YK, Ruoff AL. Optical response of very high density solid oxygen to 132 GPa. J Phys Chem. 1990;94:1117–1122. [Google Scholar]
- 13.Akahama Y, et al. New high-pressure structural transition of oxygen at 96 GPa associated with metallization in a molecular solid. Phys Rev Lett. 1995;74:4690–4693. doi: 10.1103/PhysRevLett.74.4690. [DOI] [PubMed] [Google Scholar]
- 14.Shimizu K, Suhara K, Ikumo M, Eremets MI, Amaya K. Superconductivity in oxygen. Nature. 1998;393:767–769. [Google Scholar]
- 15.Ma Y, Oganov AR, Glass CW. Structure of the metallic zeta -phase of oxygen and isosymmetric nature of the ε-ζ phase transition: Ab initio simulations. Phys Rev B. 2007;76:064101. [Google Scholar]
- 16.Weck G, Desgreniers S, Loubeyre P, Mezouar M. Single-crystal structural characterization of the metallic phase of oxygen. Phys Rev Lett. 2009;102:255503. doi: 10.1103/PhysRevLett.102.255503. [DOI] [PubMed] [Google Scholar]
- 17.Pickard CJ, Needs RJ. Structure of phase III of solid hydrogen. Nat Phys. 2007;3:473–476. [Google Scholar]
- 18.Fujii Y, et al. Evidence for molecular dissociation in bromine near 80 GPa. Phys Rev Lett. 1989;63:536–539. doi: 10.1103/PhysRevLett.63.536. [DOI] [PubMed] [Google Scholar]
- 19.Takemura K, Minomura S, Shimomura O, Fujii Y. Observation of molecular dissociation of iodine at high pressure by x-ray diffraction. Phys Rev Lett. 1980;45:1881–1884. [Google Scholar]
- 20.Eremets MI, Hemley RJ, Mao H-k, Gregoryanz E. Semiconducting non-molecular nitrogen up to 240 GPa and its low-pressure stability. Nature. 2001;411:170–174. doi: 10.1038/35075531. [DOI] [PubMed] [Google Scholar]
- 21.Ma Y, Oganov AR, Li Z, Xie Y, Kotakoski J. Novel high pressure structures of polymeric nitrogen. Phys Rev Lett. 2009;102:065501. doi: 10.1103/PhysRevLett.102.065501. [DOI] [PubMed] [Google Scholar]
- 22.Wang Y, Lv J, Zhu L, Ma Y. Crystal structure prediction via particle-swarm optimization. Phys Rev B. 2010;82:094116. [Google Scholar]
- 23.Li P, Gao G, Wang Y, Ma Y. Crystal structures and exotic behavior of magnesium under pressure. J Phys Chem C. 2010;114:21745–21749. [Google Scholar]
- 24.Lv J, Wang Y, Zhu L, Ma Y. Predicted novel high-pressure phases of lithium. Phys Rev Lett. 2011;106:015503. doi: 10.1103/PhysRevLett.106.015503. [DOI] [PubMed] [Google Scholar]
- 25.Zhu L, et al. Substitutional alloy of Bi and Te at high pressure. Phys Rev Lett. 2011;106:145501. doi: 10.1103/PhysRevLett.106.145501. [DOI] [PubMed] [Google Scholar]
- 26.Wang Y, et al. High pressure partially ionic phase of water ice. Nat Commun. 2011;2:563. doi: 10.1038/ncomms1566. [DOI] [PubMed] [Google Scholar]
- 27.Guillaume CL, et al. Cold melting and solid structures of dense lithium. Nat Phys. 2011;7:211–214. [Google Scholar]
- 28.Kim KS, Jang JH, Kim S, Mhin B-J, Schaefer HF. Potential new high energy density materials: Cyclooctaoxygen O8, including comparisons with the well-known cyclo-S8 molecule. J Chem Phys. 1990;92:1887–1892. [Google Scholar]
- 29.Degtyareva O, et al. Novel chain structures in group VI elements. Nat Mater. 2005;4:152–155. doi: 10.1038/nmat1294. [DOI] [PubMed] [Google Scholar]
- 30.Li Y, et al. Phonon instabilities in rocksalt AgCl and AgBr under pressure studied within density functional theory. Phys Rev B. 2006;74:054102. [Google Scholar]
- 31.Xie Y, et al. Electronic and phonon instabilities in face-centered-cubic alkali metals under pressure studied using ab initio calculations. Phys Rev B. 2007;75:064102. [Google Scholar]
- 32.Choudhury N, Chaplot SL. Ab initio studies of phonon softening and high-pressure phase transitions of α-quartz SiO2. Phys Rev B. 2006;73:094304. [Google Scholar]
- 33.Zhang L, et al. CaCl2-type high-pressure phase of magnesium hydride predicted by ab initio phonon calculations. Phys Rev B. 2007;75:144109. [Google Scholar]
- 34.Pickard CJ, Needs RJ. High-pressure phases of nitrogen. Phys Rev Lett. 2009;102:125702. doi: 10.1103/PhysRevLett.102.125702. [DOI] [PubMed] [Google Scholar]
- 35.Guillaume CL, et al. Cold melting and solid structures of dense lithium. Nat Phys. 2011;7:211–214. [Google Scholar]
- 36.Ma Y, et al. Transparent dense sodium. Nature. 2009;458:182–185. doi: 10.1038/nature07786. [DOI] [PubMed] [Google Scholar]
- 37.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B. 1996;54:11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
- 38.Heyd J, Scuseria GE, Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J Chem Phys. 2003;118:8207–8215. [Google Scholar]
- 39.Paier J, et al. Screened hybrid density functionals applied to solids. J Chem Phys. 2006;124:154709. doi: 10.1063/1.2187006. [DOI] [PubMed] [Google Scholar]
- 40.Blochl PE. Projector augmented-wave method. Phys Rev B. 1994;50:17953–17979. doi: 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
- 41.Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B. 1999;59:1758–1775. [Google Scholar]
- 42.Monkhorst HJ, Pack JD. Special points for Brillouin-zone integrations. Phys Rev B. 1976;13:5188–5192. [Google Scholar]
- 43.Parlinski K, Li ZQ, Kawazoe Y. First-principles determination of the soft mode in cubic ZrO2. Phys Rev Lett. 1997;78:4063–4066. [Google Scholar]
- 44.Togo A, Oba F, Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2 -type SiO2 at high pressures. Phys Rev B. 2008;78:134106. [Google Scholar]
- 45.Blaha P, Schwarz K, Madsen GKH, Kvasnicka D, Luitz J. WIEN2K—An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties. Wien, Austria: Technische Universität Wien; 2001. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.