Coupling between internal dynamics and rotational diffusion in the presence of exchange between discrete molecular conformations

Abstract

We present a general formalism for the computation of orientation correlation functions involving a molecular system undergoing rotational diffusion in the presence of transitions between discrete conformational states. In this formalism, there are no proscriptions on the time scales of conformational rearrangement relative to that for rotational diffusion, and the rotational diffusion tensors of the different states can be completely arbitrary. Although closed-form results are limited to the frequency domain, this is generally useful for many spectroscopic observables as the result allows the computation of the spectral density function. We specialize the results for the computation of the frequency-domain correlation function associated with the NMR relaxation.

INTRODUCTION

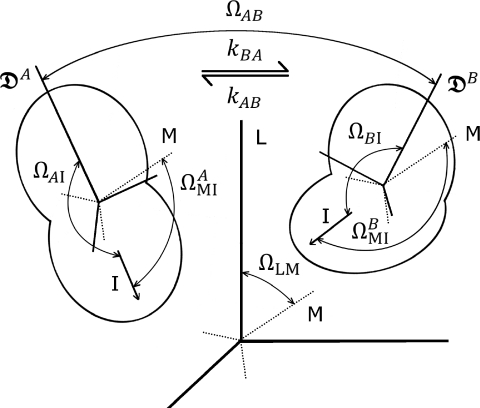
The interdependence of rotational diffusion and conformational transitions is of fundamental importance in understanding many molecular processes. When conformational exchange and rotational diffusion of the whole molecule occur on significantly different time scales, one can neglect coupling between the two processes so that experimental observables are readily interpreted. However, when these processes occur on similar time scales simple decoupling is no longer possible, and a more general description is required. An example of a system for which rotational diffusion and conformational exchange occur on similar time scales is a protein undergoing large-scale inter-domain motions (see Fig. 1).

Figure 1.

Schematic of a molecular system undergoing inter-conversion between two conformations A and B with rate constants k_BA and k_AB for the forward and backward processes, respectively. L denotes a laboratory-fixed reference frame, M a reference frame rotating with diffusional tumbling, and I the frame of a vector of interest giving rise to an observable signal. Ω_LM specifies the orientation of the tumbling molecular frame relative to the laboratory-fixed frame. ${\mathfrak{D}}^{\epsilon }$ denotes the diffusion tensor of conformation ε, while Ω_εI specifies the orientation of the vector of interest relative to the associated principal axes, and Ω_AB specifies the rotation required to transform between the principal axis frames of states A and B. The orientation of the vector of interest in state ε relative to the molecular frame is given by ${\Omega }_{\text{MI}}^{\epsilon }$. Note that the resulting vector autocorrelation function depends only on ${\mathfrak{D}}^{\epsilon }$, Ω_AB, Ω_εI, and the rate constants for inter-conversion between the states.

In previous work, it was shown that fast local internal dynamics are decoupled from much slower overall rotation (whose time scale is at least two orders of magnitude slower for proteins) and can be described by the “model-free” approach.^{1, 2} Subsequently, an “extended model-free” approach³ was developed to treat internal motions with two (or more) distinct time scales, where the slower motion is still an order of magnitude faster than the rotational correlation time so that the decoupling approximation is still valid. This approach was successfully applied to the analysis of slower modes of local internal protein dynamics ranging in time scales from 100 ps to 1 ns.⁴ Later, the extended model-free approach was also applied to large-scale domain reorientations^{5, 6, 7, 8} where time scale separation with overall rotation is less clear cut such that the decoupling approximation may be less apt and no longer appropriate. The special case of protein domain motion on time scales similar to the rotational correlation time, but not involving any significant change in overall molecular shape was considered in Refs. ^{9, 10}. Finally, internal rearrangements in the presence of rotational diffusion in the slow exchange limit were treated in Ref. 11.

Most approaches for treating the relationship between rotational diffusion dynamics and internal protein mobility use a diffusion tensor to describe interactions between a solute molecule and its solvent environment. Implicit in this description is the assumption that conformation changes of a solute molecule do not change the state of its solvent environment. An alternate description of solute-solvent interactions posits that changes in solute conformations influence the solvent in the form of a “slowly relaxing local structure” model^{12, 13} in which a solute molecule reorients within a molecular cage constructed from solvent molecules. In general, this approach is only solvable numerically using many body Fokker-Planck-Kramers equations,¹⁴ with closed-form solutions available only in those asymptotic cases corresponding to the extended model free results.

In the current work, we adopt an approach¹⁵ in which overall molecular tumbling is coupled to internal motions described as instantaneous inter-conversions between discrete molecular states with rates which can be arbitrary relative to the time scale of rotational diffusion. Wong et al.¹⁶ specified this approach to protein NMR applications in which the rotational diffusion tensor is axially symmetric. Previous work^{15, 16} contained a serious limitation in that diffusion tensors for the different conformational states were not allowed to be truly independent: the principal axes of the diffusion tensors in the different states were not allowed to change direction, only the magnitudes of these components could vary. In the present work, we generalize these results such that each conformational state can have a unique rotational diffusion tensor whose principal axes take arbitrary, but fixed orientations relative to those of diffusion tensors of the other states. The resulting expression for the time correlation function in the frequency domain can be used to obtain expressions for spectroscopic observables with applications in fields as diverse as dielectric spectroscopy, light scattering, and NMR relaxation. We specialize our result to the case of NMR relaxation in the presence of inter-conversion between two states with differing diffusion tensors (see Fig. 1).

THEORY

Many experimental observables can be related to time correlation functions. In this work, we concern ourselves with molecular systems undergoing rotational diffusion in the presence of internal motions that result in a change in molecular shape (see Fig. 1). In the current treatment, fast local internal motions are ignored, since for proteins they occur on time scales that are several orders of magnitude shorter than the rotational correlation time.

The orientational time correlation function is the dot product of a unit vector of interest n(t) at time t with initial value n(0) given by

$$C\left(t\right)=⟨P_l[\mathbf{n}\left(t\right)·\mathbf{n}\left(0\right)]⟩,$$ (1)

where the angle brackets denote ensemble averaging. P_l is the Legendre polynomial appropriate for the desired experimental observable. For example, P₂ is the appropriate function for dipole-dipole interactions involved in NMR relaxation or light scattering experiments, while P₁ is relevant for dielectric spectroscopy. Many spectroscopic observables are expressed in terms of the spectral density J(ω), which is the Fourier transform of C(t). The spherical harmonic addition theorem provides an alternate representation of a Legendre polynomial

$$P_l[\mathbf{n}\left(t\right)·\mathbf{n}\left(0\right)]=\frac{4\pi }{2l+1}\sum _{m=-1}^l{Y}_l^m\left({\Omega }_{\text{LI}}\right)Y_l^{m*}\left({\Omega }_{\text{LI}}^0\right),$$ (2)

where $Y_l^m$ are spherical harmonics, Ω_LI represents the time-varying orientation of the vector n(t) in the fixed laboratory reference frame, with initial value ${\Omega }_{\text{LI}}^0$, and the star denotes the complex conjugation. Further, we represent the spherical harmonics in terms of Wigner rotation matrices $D_{mn}^l\left(\Omega \right)$,¹⁷

$$Y_l^m\left(\Omega \right)=\sqrt{\frac{2l+1}{4\pi }}{D}_{m0}^{l*}\left(\Omega \right).$$ (3)

The Wigner rotation matrices are particularly convenient when describing rigid body rotations. [Note that the orientation dependence of the Wigner rotation matrices corresponds to the rotation of an arbitrary rigid body and, thus, consists of three degrees of freedom, while only two degrees of freedom are required to arbitrarily orient a vector in space. For consistency, we consider Ω to comprise a general 3 degree of freedom rotation throughout this work with zero rotation about the vector axis where appropriate, as in Eq. 2.]

To separate out overall molecular tumbling from internal molecular motion, we represent the orientation of the internal vector of interest in the rotating molecular frame as Ω_MI, while the tumbling molecular frame is represented as Ω_LM in the fixed laboratory frame. The closure property of the Wigner rotation matrices allow us to rewrite Eq. 1 as

$$\begin{array}{c}\hfill C\left(t\right)\\ & & ={\displaystyle 〈\sum _{m,k,k^{\prime }=-l}^l{D}_{mk}^{l*}\left({\Omega }_{\text{LM}}\right)D_{k0}^{l*}\left({\Omega }_{\text{MI}}\right)D_{m{k}^{\prime }}^l\left({\Omega }_{\text{LM}}^0\right)D_{k^{\prime }0}^l\left({\Omega }_{\text{MI}}^0\right)〉.}\hfill \\ & \end{array}$$ (4)

Now, we posit that the molecule changes shape by instantaneously jumping between N_c discrete states with arbitrarily different diffusion tensors. In each state, the vector of interest occupies a distinct orientation ${\Omega }_{\text{MI}}^{\epsilon }$ relative to the tumbling molecular frame. We assume that internal molecular rearrangements are independent of tumbling. The conditional probability density function of being in state ε at time t with orientation Ω_LM, having started in state η at t = 0 with orientation ${\Omega }_{\text{LM}}^0$, is $p^{\epsilon \eta }({\Omega }_{\text{LM}},t|{\Omega }_{\text{LM}}^0,0)$. If the system is in equilibrium, the correlation function can be written as

$$\begin{array}{ccc}\hfill C\left(t\right)& =& \sum _{\epsilon ,\eta }\int d{\Omega }_{\text{LM}}^0\int d{\Omega }_{\text{LM}}{p}^{\epsilon \eta }\left({\Omega }_{\text{LM}},t|{\Omega }_{\text{LM}}^0,0\right)p_{\text{eq}}^{\eta }\left({\Omega }_{\text{LM}}^0\right)\hfill \\ & & \times \sum _{m,k,k^{\prime }}{D}_{mk}^{l*}\left({\Omega }_{\text{LM}}\right)D_{m{k}^{\prime }}^l\left({\Omega }_{\text{LM}}^0\right)D_{k0}^{l*}\left({\Omega }_{\text{MI}}\right)D_{k^{\prime }0}^l\left({\Omega }_{\text{MI}}\right),\hfill \end{array}$$ (5)

where the indices ε and η run over all possible states. $p_{\text{eq}}^{\eta }\left(\Omega \right)$ is the equilibrium probability density of being in state η with orientation Ω, and if we confine ourselves to isotropic solution, this probability density is

$$p_{\text{eq}}^{\eta }\left(\Omega \right)=\frac{1}{8{\pi }^2}{P}_{\text{eq}}\left(\eta \right),$$ (6)

where P_eq(η) is the equilibrium orientation-independent probability of being in state η. P_eq(η) is normalized such that ∑_ηP_eq(η) = 1.

The rate of transitions from state η to state ε is given by k_εη. Summing over all states ε gives the total rate of outflow of probability from state η to all other states, k^η = ∑_{ε ≠ η}k_εη. At equilibrium, the populations are at a steady state such that the outflow of probability is equal to the inflow,

$$\begin{array}{c}\hfill P_{\text{eq}}\left(\eta \right)k^{\eta }=\sum _{\epsilon \ne \eta }{P}_{\text{eq}}\left(\epsilon \right)k_{\eta \epsilon }.\end{array}$$ (7)

For given values of k_ηε, one obtains equilibrium populations from Eq. 7.

In the rotational diffusion regime, the evolution of $p^{\epsilon \eta }({\Omega }_{\text{LM}},t|{\Omega }_{\text{LM}}^0,0)$ is governed by the diffusion tensor, neglecting inertial aspects. In molecular conformation state ε, the probability density evolves via the diffusion equation written using the second-order differential operator ${\sum }_{ij}{\widehat{L}}_i{\mathfrak{D}}_{ij}^{\epsilon }{\widehat{L}}_j$, where ${\widehat{L}}_i$ is the angular momentum operator along axis i in the molecule-fixed frame and ${\mathfrak{D}}_{ij}^{\epsilon }$ are elements of the rotational diffusion tensor of state ε.^{18, 19, 20, 21} If we write ${\widehat{L}}^T$ as the row vector $\{{\widehat{L}}_x,{\widehat{L}}_y,{\widehat{L}}_z\},$ then the Liouville operator for conformation ε in the absence of transitions becomes ${\widehat{L}}^T{\mathfrak{D}}^{\epsilon }\widehat{L}$.

In Ref. 15, the time-dependence of the conditional probability $p^{\epsilon \eta }({\Omega }_{\text{LM}},t|{\Omega }_{\text{LM}}^0,0)$ has been shown to obey

$$\begin{array}{ccc}& & \frac{\partial p^{\epsilon \eta }\left({\Omega }_{\text{LM}},t|{\Omega }_{\text{LM}}^0,0\right)}{\partial t}\hfill \\ & & =-[{\widehat{L}}^T{\mathfrak{D}}^{\epsilon }\widehat{L}+k^{\epsilon }]p^{\epsilon \eta }\left({\Omega }_{\text{LM}},t|{\Omega }_{\text{LM}}^0,0\right)\hfill \\ & & +\sum _{\mu \ne \epsilon }{k}_{\epsilon \mu }{p}^{\mu \eta }\left({\Omega }_{\text{LM}},t|{\Omega }_{\text{LM}}^0,0\right)\hfill \end{array}$$ (8)

with initial conditions

$$\begin{array}{c}\hfill {\left.p^{\epsilon \eta }\left({\Omega }_{\text{LM}},t|{\Omega }_{\text{LM}}^0,0\right)\right|}_{t=+0}={\delta }_{\epsilon \eta }\delta \left({\Omega }_{\text{LM}}-{\Omega }_{\text{LM}}^0\right),\end{array}$$ (9)

where δ_εη is the Kronecker delta and δ(Ω − Ω⁰) is a Dirac delta function in rotation space.

Next, we choose the complete orthogonal basis of Wigner rotation matrices in Ω_LM to expand the conditional probability

$$\begin{array}{c}\hfill p^{\epsilon \eta }\left({\Omega }_{\text{LM}},t|{\Omega }_{\text{LM}}^0,0\right)=\sum _{J=0}^{\infty }\sum _{g,q=-J}^J{c}_{J,gq}^{\epsilon \eta }\left(t\right)D_{gq}^J\left({\Omega }_{\text{LM}}\right),\end{array}$$ (10)

where the dependence on the initial orientation is obtained by the initial boundary conditions [Eq. 9]. Inserting Eq. 10 into Eq. 8 yields the coupled differential equations for the coefficients $c_{J,gq}^{\epsilon \eta }\left(t\right)$,

$$\begin{array}{c}\hfill \sum _{J,g,q}\frac{\partial c_{J,gq}^{\epsilon \eta }\left(t\right)D_{gq}^J\left({\Omega }_{\text{LM}}\right)}{\partial t}\end{array}$$ (11)

$$\begin{array}{ccc}& & =-[{\widehat{L}}^T{\mathfrak{D}}^{\epsilon }\widehat{L}+k^{\epsilon }]\sum _{J,g,q}{c}_{J,gq}^{\epsilon \eta }\left(t\right)D_{gq}^J\left({\Omega }_{\text{LM}}\right)\hfill \\ & & +\sum _{\mu \ne \epsilon ,J,g,q}{k}_{\epsilon \mu }{c}_{J,gq}^{\mu \eta }\left(t\right)D_{gq}^J\left({\Omega }_{\text{LM}}\right).\hfill \end{array}$$ (12)

While the sum in Eq. 10 is over all possible values of J, the orthogonality properties¹⁷ of the Wigner rotation matrices pick out a single value of J = l when all indices are summed over and both Ω_LM and ${\Omega }_{\text{LM}}^0$ are integrated over as in Eq. 5. Thus, we only consider J = l below.

The eigenvalues and eigenfunctions of the free diffusion Liouville operator ${\widehat{L}}^T{\mathfrak{D}}^{\epsilon }\widehat{L}$ are known in closed form²⁰ for l ⩽ 2, such that it is convenient to express the operation of this Liouville operator on the Wigner rotation matrices in terms of these eigenfunctions. For state ε, we write ${\widehat{L}}^T{\mathfrak{D}}^{\epsilon }\widehat{L}{\psi }_{mn}^{\epsilon ,l}\left(\Omega \right)={\Lambda }_n^{\epsilon ,l}{\psi }_{mn}^{\epsilon ,l}\left(\Omega \right)$, where ${\Lambda }_n^{\epsilon ,l}$ is the eigenvalue corresponding to the normalized eigenfunction ${\psi }_{mn}^{\epsilon ,l}\left(\Omega \right)$ for m, n = −2l + 1, …, 2l + 1. We collect the (2l + 1)-dimensional set of ${\psi }_{mn}^{\epsilon ,l}\left(\Omega \right)$ which have the same eigenvalue ${\Lambda }_n^{\epsilon ,l}$ and form a eigenvector${\psi }_n^{\epsilon ,l^T}\left(\Omega \right)=\{{\psi }_{-ln}^{\epsilon ,l}\left(\Omega \right),...,{\psi }_{ln}^{\epsilon ,l}\left(\Omega \right)\}$. The vectors ${\psi }_n^{\epsilon ,l^T}\left(\Omega \right)$, for all n, and also the vectors $D_n^{l^T}\left(\Omega \right)=\{D_{-ln}^l\left(\Omega \right),...,D_{ln}^l\left(\Omega \right)\}$ form complete orthogonal bases, such that one can convert between basis sets using the unitary matrix U^{ε, l} and write $D_{mn}^l\left(\Omega \right)={\sum }_s{U}_{ms}^{\epsilon ,l}{\psi }_{sn}^{\epsilon ,l}\left(\Omega \right)$ and ${\psi }_{mn}^{\epsilon ,l}\left(\Omega \right)={\sum }_s{U}_{ms}^{\epsilon ,l^{†}}{D}_{sn}^l\left(\Omega \right)$, where U^{ε, l} has matrix elements

$$\begin{array}{c}\hfill {\mathbf{U}}_{s^{\prime }s}^{\epsilon ,l}=\sum _{n=-l}^l{D}_{n{s}^{\prime }}^{l*}\left(\Omega \right){\psi }_{ns}^{\epsilon ,l}\left(\Omega \right).\end{array}$$ (13)

The unitarity condition implies ${\mathbf{U}}^{\epsilon ,l^{†}}{\mathbf{U}}^{\epsilon ,l}={\mathbf{I}}_{2l+1}$, where † denotes Hermitian conjugation and I_{2l + 1} is a (2l + 1)-dimensional unit matrix. One can then write the operation of the free diffusion Liouville operator on the Wigner rotation matrix as

$$\begin{array}{c}\hfill {\widehat{L}}^T{\mathfrak{D}}^{\epsilon }\widehat{L}{D}_{gq}^l\left(\Omega \right)=\sum _{s,s^{\prime }=-l}^l{D}_{g{s}^{\prime }}^l\left(\Omega \right)U_{s^{\prime }s}^{\epsilon ,l}{\Lambda }_s^{\epsilon ,l}{U}_{sq}^{\epsilon ,l^{†}}.\end{array}$$ (14)

Substituting Eq. 14 into Eq. 12, multiplying by $D_{gq}^{l*}\left({\Omega }_{\text{LM}}\right)$, integrating over Ω_LM, and using the orthogonality properties of the Wigner rotation matrices yields the following differential equation for coefficients $c_{l,mn}^{\epsilon \eta }\left(t\right)$:

$$\begin{array}{ccc}\hfill \frac{\partial c_{l,mn}^{\epsilon \eta }\left(t\right)}{\partial t}& =& -\sum _{s,q=-l}^l{c}_{l,mq}^{\epsilon \eta }\left(t\right)U_{ns}^{\epsilon ,l}{\Lambda }_s^{\epsilon ,l}{U}_{sq}^{\epsilon ,l^{†}}\hfill \\ & & -k^{\epsilon }{c}_{l,mn}^{\epsilon \eta }\left(t\right)+\sum _{\mu \ne \epsilon }{k}_{\epsilon \mu }{c}_{l,mn}^{\mu \eta }\left(t\right),\hfill \end{array}$$ (15)

with the initial conditions

$$c_{l,mn}^{\epsilon \eta }\left(t\right){|}_{t=+0}=\frac{2l+1}{8{\pi }^2}{D}_{mn}^{l*}\left({\Omega }_{\text{LM}}^0\right){\delta }_{\epsilon \eta }.$$ (16)

A key feature of Eq. 15 is that the coefficients $c_{l,mn}^{\epsilon \eta }$ with different values of the first index m are not mixed. This feature is a consequence of the fact that the exchange kinetics are independent of the orientation of the molecular reference frame M, and that the molecular system tumbles isotropically.

Equation 15 can be written in block vector form as

$$\begin{array}{c}\hfill \frac{\partial {\mathbf{c}}_m^{\eta }\left(t\right)}{\partial t}=\mathbf{M}{\mathbf{c}}_m^{\eta }\left(t\right),\end{array}$$ (17)

where the expansion coefficients of the Wigner rotation matrices are contained in a column vector ${\mathbf{c}}_m^{\eta }$ with N_c blocks, with the elements of block ε given by

$${\left[{\mathbf{c}}_m^{\eta }\right]}_{\epsilon }=\left(\begin{array}{c}{c}_{m,-l}^{\epsilon \eta }\\ ⋮\\ c_{m,l}^{\epsilon \eta }\end{array}\right),$$ (18)

and M is a matrix consisting of N_c × N_c blocks each defined as

$${\mathbf{M}}_{\epsilon ,\eta }=\left\{\begin{array}{cc}\hfill {\mathbf{U}}^{\epsilon ,\mathit{l}}{\mathit{\Lambda }}^{\epsilon }{\mathbf{U}}^{{\epsilon ,\mathit{l}}^{†}}-k^{\epsilon }{\mathbf{I}}_{2l+1}& \hfill \text{for}\epsilon =\eta \\ \hfill k_{\epsilon \eta }{\mathbf{I}}_{2l+1}& \hfill \text{otherwise}\end{array},\right.$$ (19)

where the diagonal matrices Λ^ε contain elements which are the 2l + 1 eigenvalues ${\Lambda }_n^{\epsilon ,l}$ of the appropriate ${\widehat{L}}^T{\mathfrak{D}}^{\epsilon }\widehat{L}$ operator.

To solve the differential equation given by Eq. 17, we convert the expression into the frequency domain via a Laplace transform L (Ref. ²²) to obtain

$$\begin{array}{c}\hfill {\tilde{\mathbf{c}}}_m^{\eta }\left(\sigma \right)={\left(\sigma {\mathbf{I}}_{N_c(2l+1)}-\mathbf{M}\right)}^{-1}{\left.{\mathbf{c}}_m^{\eta }\left(t\right)\right|}_{t=+0},\end{array}$$ (20)

where ${\tilde{\mathbf{c}}}_m^{\eta }\left(\sigma \right)$ are the Laplace-transformed coefficients ${\mathbf{c}}_m^{\eta }\left(t\right)$, and ${\left.{\mathbf{c}}_m^{\eta }\left(t\right)\right|}_{t=+0}$ are the initial conditions. The frequency domain is most relevant for spectroscopic observables: NMR relaxation rates are expressed in terms of the spectral density function J(ω) which can be simply evaluated from the real part of the Laplace-transformed correlation function $\tilde{C}\left(\sigma \right)$ for imaginary σ:²³$J\left(\omega \right)=\text{Re}\left[\tilde{C}\left(i\omega \right)\right]$. Moreover, as Eq. 20 is algebraic in form, it allows us to solve for the frequency-domain correlation function in closed form. The time-domain expression for the coefficients [Eq. 17] is solvable by numeric integration, but its solution in closed form typically involves eigenvalue decomposition of a N_c(2l + 1) × N_c(2l + 1) matrix, and determination of the roots of the associated characteristic polynomial is not generally possible even for N_c = 2, if l ⩾ 1.

NMR relaxation in the presence of exchange between two states

For NMR relaxation, l = 2 is the relevant value and the simplest case which requires the current formulation corresponds to exchange between two states labeled A and B (see Fig. 1). In this case, Eq. 20 reads

$$\begin{array}{c}\hfill {\tilde{\mathbf{c}}}_m^{\eta }\left(\sigma \right)={\left(\begin{array}{cc}\hfill {\mathbf{U}}^A{\mathbf{Q}}^A{\mathbf{U}}^{A^{†}}& \hfill -k_{AB}{\mathbf{I}}_5\\ \hfill -k_{BA}{\mathbf{I}}_5& \hfill {\mathbf{U}}^B{\mathbf{Q}}^B{\mathbf{U}}^{B^{†}}\end{array}\right)}^{-1}{\left.{\mathbf{c}}_m^{\eta }\left(t\right)\right|}_{t=+0},\end{array}$$ (21)

with Q^ε = Λ^ε + (k^ε + σ)I₅. Substituting the expression for the coefficients in Eq. 21 into Eqs. 10, 5 results in the final expression for the correlation function in the frequency domain $\tilde{C}\left(\sigma \right)$,

$$\begin{array}{c}\hfill \tilde{C}\left(\sigma \right)=\frac{4\pi }{5}\sum _{\epsilon ,\eta =A,B}{\mathbf{Y}}_2^T\left({\Omega }_{\epsilon \text{I}}\right){\mathbf{A}}^{{\epsilon }^{†}}{\mathbf{R}}^{\epsilon \eta }{\mathbf{A}}^{\eta }{\mathbf{Y}}_2^{*}\left({\Omega }_{\eta \text{I}}\right)P_{\text{eq}}\left(\eta \right),\end{array}$$ (22)

where ${\mathbf{Y}}_2^T=\{Y_2^{-l},...,Y_2^l\}$ is a row vector consisting of spherical harmonics, Ω_εI specifies the orientation of the vector of interest relative to the principal axes of ${\mathfrak{D}}^{\epsilon }$, and A^η is a matrix of decomposition coefficients which defines ${\psi }_{nm}^{\epsilon ,l}\left(\Omega \right)$ in terms of Wigner rotation matrices $D_{nk}^l\left(\Omega \right)$ and whose elements depend on the principal values of ${\mathfrak{D}}^{\epsilon }$. The coefficients of the A^η matrix are defined and discussed in the supplementary material.²⁴ The matrix ${\mathbf{U}}^{\epsilon \eta }={\mathbf{U}}^{\epsilon ,2^{†}}{\mathbf{U}}^{\eta ,2}$ is a unitary transformation from the five-dimensional eigenvectors of ${\widehat{L}}^T{\mathfrak{D}}^{\eta }\widehat{L}$ to those of ${\widehat{L}}^T{\mathfrak{D}}^{\epsilon }\widehat{L}$, while the rate matrices R^εη are defined as

$$\begin{array}{c}\hfill {\mathbf{R}}^{\text{AA}}={\mathbf{U}}^{AB}{\mathbf{Q}}^B{\left({\mathbf{Q}}^A{\mathbf{U}}^{AB}{\mathbf{Q}}^B-k_{AB}{k}_{BA}{\mathbf{U}}^{AB}\right)}^{-1},\end{array}$$ (23a)

$$\begin{array}{c}\hfill {\mathbf{R}}^{\text{BA}}=k_{BA}{\left({\mathbf{Q}}^A{\mathbf{U}}^{AB}{\mathbf{Q}}^B-k_{AB}{k}_{BA}{\mathbf{U}}^{AB}\right)}^{-1},\end{array}$$ (23b)

$$\begin{array}{c}\hfill {\mathbf{R}}^{\text{AB}}=k_{AB}{\left({\mathbf{Q}}^B{\mathbf{U}}^{BA}{\mathbf{Q}}^A-k_{AB}{k}_{BA}{\mathbf{U}}^{BA}\right)}^{-1},\end{array}$$ (23c)

$$\begin{array}{c}\hfill {\mathbf{R}}^{\text{BB}}={\mathbf{U}}^{BA}{\mathbf{Q}}^A{\left({\mathbf{Q}}^B{\mathbf{U}}^{BA}{\mathbf{Q}}^A-k_{AB}{k}_{BA}{\mathbf{U}}^{BA}\right)}^{-1}.\end{array}$$ (23d)

All dependence of the Laplace-transformed correlation function on imaginary frequency σ comes via the diagonal Q^ε matrices in Eqs. 23a, 23b, 23c, 23d. In the supplementary material,²⁴ we provide explicit expressions for the eigenvalues ${\Lambda }_n^{\epsilon ,l}$ and the U^εη transformations both for systems with axially symmetric and fully anisotropic diffusion tensors, and discuss the relationship between the results in the limiting case where the two results become equivalent.

As originally stipulated, the resulting correlation function in Eq. 22 is independent of orientation in the lab frame. Equation 22 is also independent of the arbitrary rotating frame M, a property we confirm explicitly in the supplementary material²⁴ for systems with both axially symmetric and fully anisotropic diffusion tensors. Finally, it is evident from Eqs. 23 that the rate matrices R^εη are independent of bond vector orientation, such that all bond-vector orientation dependence comes from the projections of the spherical harmonics in Eq. 22.

References 15, 16 examined this two-state problem for the special case where the eigenvectors of the two states are the same, and only the eigenvalues change. In this case, U^{A, 2} = U^{B, 2} = U^AB = U^BA = I₅, and Eq. 22 reduces to the expression in Ref. 15, if one ignores the effect of translational diffusion which are not of interest in the current work, and to the time-domain analog in Ref. 16. To validate our results for the general two-state case in which the diffusion tensors have different principal axes, we numerically inverted the Laplace-transformed Eq. 22 and compared the results with the Monte Carlo calculations of diffusion propagation in the time domain. This comparison shows complete agreement within machine precision and is described in the supplementary material.²⁴

CONCLUDING REMARKS

We have obtained an expression for the frequency-domain correlation function [Eq. 22] of a rotating molecular system undergoing inter-conversion between internal states, the diffusion tensors of which can have arbitrarily different orientations and shapes (see Fig. 1). For such systems, this solution allows us to conveniently evaluate spectroscopic observables, such as NMR relaxation rates.²³

This closed-form solution is advantageous in that it allows rapid calculation of spectroscopic observables, thus facilitating analysis of the experimental data. Closed-form derivatives of Eq. 22 are readily evaluated allowing applications such as molecular structure determination from relaxation data. Such a form also allows greater understanding of the influence on observables of different inputs such as inter-conversion rates, diffusion tensor parameters, and bond vector orientation.

One might use the NMR relaxation data to test hypotheses about the nature of candidate conformational states, their relative orientations, and inter-conversion rates. Diffusion tensors can be calculated directly from molecular structures,²⁵ and then Eq. 22 can be combined with expressions for relaxation rates²³ to back-calculate values to be directly compared with experiment. Example calculations of NMR transverse to longitudinal relaxation rate ratios for a hypothetical conversion between open and closed forms of a protein are shown in the supplementary material.²⁴ Alternatively, the inverse problem can be attempted: given relaxation data, k_BA, k_AB, and Ω_AB (five parameters) can be determined if the structures of the conformational states are known. Finally, given enough relaxation data of high enough quality, one could attempt to simultaneously determine the diffusion tensors of the two states along with inter-conversion rates and relative orientation (15 parameters).

While the frequency-domain correlation function in Eq. 22 includes only two conformational states, Eq. 20 can be solved for any number of states and likewise combined to obtain a correlation function. Molecular conformations often exist not in discrete states but as a continuum with transitions taking a finite amount of time. In circumstances where intermediate conformations become important, one approach would be to include additional intermediate states. Alternatively, one might consider a formalism which would allow continuous transitions between states.