A novel technique to enable experimental validation of deformable dose accumulation

Abstract

Purpose: To propose a novel technique to experimentally validate deformable dose algorithms by measuring 3D dose distributions under the condition of deformation using deformable gel dosimeters produced by a novel gel fabrication method.

Method: Five gel dosimeters, two rigid control gels and three deformable gels, were manufactured and treated with the same conformal plan that prescribed 400 cGy to the isocenter. The control gels were treated statically; the deformable gels were treated while being compressed by an actuation device to simulate breathing motion (amplitude of compression = 1, 1.5, and 2 cm, respectively; frequency = 16 rpm). Comparison between the dose measured by the control gels and the corresponding static dose distribution calculated in the treatment planning system (TPS) has determined the intrinsic dose measurement uncertainty of the gel dosimeters. Doses accumulated using MORFEUS, a biomechanical model-based deformable registration and dose accumulation algorithm, were compared with the doses measured by the deformable gel dosimeters to verify the accuracy of MORFEUS using dose differences at each voxel as well as the gamma index test. Flexible plastic wraps were used to contain and protect the deformable gels from oxygen infiltration, which inhibits the gels’ dose sensitizing ability. Since the wraps were imperfect oxygen barrier, dose comparison between MORFEUS and the deformable gels was performed only in the central region with a received dose of 200 cGy or above to exclude the peripheral region where oxygen penetration had likely affected dose measurements.

Results: Dose measured with the control gels showed that the intrinsic dose measurement uncertainty of the gel dosimeters was 11.8 cGy or 4.7% compared to the TPS. The absolute mean voxel-by-voxel dose difference between the accumulated dose and the dose measured with the deformable gels was 4.7 cGy (SD = 36.0 cGy) or 1.5% (SD = 13.4%) for the three deformable gels. The absolute mean vector distance between the 250, 300, 350, and 400 cGy isodose surfaces on the accumulated and measured distributions was 1.2 mm (SD < 1.5 mm). The gamma index test that used the dose measurement precision of the control gels as the dose difference criterion and 2 mm as the distance criterion was performed, and the average pass rate of the accumulated dose distributions for all three deformable gels was 92.7%. When the distance criterion was relaxed to 3 mm, the average pass rate increased to 96.9%.

Conclusion: This study has proposed a novel technique to manufacture deformable volumetric gel dosimeters. By comparing the doses accumulated in MORFEUS and the doses measured with the dosimeters under the condition of deformation, the study has also demonstrated the potential of using deformable gel dosimetry to experimentally validate algorithms that include deformations into dose computation. Since dose less than 200 cGy was not evaluated in this study, future investigations will focus more on low dose regions by either using bigger gel dosimeters or prescribing a lower dose to provide a more complete experimental validation of MORFEUS across a wider dose range.

INTRODUCTION

Intrafractional organ movements and deformations, especially those related to respiration, can result in geometric and dosimetric uncertainties in the planning and delivery of radiotherapy.^{1, 2} When not accounted for, respiratory motion can also reduce the dose to the targeting volume and increase the dose to the surrounding normal tissues.^{3, 4} This uncertainty is even more important with high-precision radiotherapy techniques, such as stereotactic body radiation therapy (SBRT), where doses up to 20 Gy per fraction are delivered while the patient is breathing freely.^{5, 6} Therefore, intrafractional organ motion and deformation induced by respiration should be incorporated into dose calculations.

A number of algorithms and models have been developed to investigate the dosimetric influences of respiratory motions. For example, Zhong and Slebers used a Monte Carlo-based energy and mass congruent mapping (EMCM) technique to compute the dose received by deforming organs.⁷ Flampouri et al. used a Monte Carlo method to calculate dose distributions at different phases of a breathing cycle and summed the distributions using deformation maps derived from 4D CT data to morph each breathing phase to end-of-exhale.⁸ Rosu et al. convolved the static dose distribution with a patient-specific probability function that describes breathing motion.² Brock et al. has developed a 3D dose accumulation algorithm based on MORFEUS, a biomechanics-based multimodality deformable image registration platform that utilizes finite element modeling (FEM) techniques.^{9, 10, 11} The MORFEUS algorithm combines the static dose distribution calculated in the treatment planning system with the deformation profile of an organ through a particular motion.¹⁰

Several studies have also experimentally investigated the effects of motion on dose distribution and could potentially provide means to experimentally validate the deformable dose calculation algorithms mentioned above. For example, Ceberg et al. used a robot that simulates the respiratory motion of the thoracic region to move 3D gel dosimeters in and out of a radiation beam.¹² Oliver et al. inserted radiographic films in a motion phantom, which followed a sinusoidal motion pattern during treatment delivery.¹³ These studies simulated respiratory motions as rigid bodies without considering deformation and, therefore, are not ideal experimental validations of deformable dose accumulation algorithms. Vinogradskiy et al. incorporated deformation by using a deformable insert to mimic one lung in an anthropomorphic thoracic phantom and measured point doses and 2D doses with thermoluminescent dosimeters (TLD) and films, respectively.¹⁴ However, to the authors’ knowledge, an experimental method to measure spatially continuous 3D dose under deforming conditions is yet unavailable.

The purpose of this work is to propose a novel technique to experimentally validate deformable dose algorithms using polymer-based gel dosimeters to achieve 3D dose distribution measurements under the condition of deformation. Polymer-based gel dosimeters undergo polymerization reaction upon exposure to ionizing radiation. Since the polymer product increases the local transverse magnetic relaxation constant (R₂) by affecting the mobility of surrounding water molecules, dose can be read out using magnetic resonance imaging (MRI).¹⁵ The radiation properties of polymer-based gel dosimeters have been well studied,^{15, 16, 17, 18} and they have been used for 3D dose verification in intensity modulated radiotherapy.^{19, 20} In this study, an actuation device applied sinusoidal compressions to the gel dosimeters during irradiation to investigate the effects of deformation on received dose. Since oxygen inhibits the polymerization reaction, gel dosimeters are conventionally concealed in rigid, air-tight containers that prevent any deformation to be applied to the gels.^{15, 16, 17, 18} Therefore, the first step in this work was to develop a technique that provides the gels flexible oxygen barriers. The dose measurement accuracy of the gel dosimeters was verified by comparing the dose measured by gels under static conditions with the dose calculated in the treatment planning system (STATIC), which was regarded as the gold standard in this study. The MORFEUS deformable dose accumulation algorithm was then validated by comparing the accumulated dose with the dose measured by deformable gel dosimeters that underwent the same deformation pattern.

METHODS AND MATERIALS

Gel dosimeter fabrication

Polymer-based gel dosimeters were chosen in this study because of their tissue equivalency¹⁷ and their ability to preserve spatial dose distribution information over time.¹⁶ Five gel dosimeters were produced in the same batch and were divided into two groups: group I, the control group, which consisted of two static gels, was used to determine the dose measurement accuracy of the gels; group II consisted of three deformable gels, which were to be irradiated under the condition of deformation to evaluate the MORFEUS dose accumulation algorithm.

The gels’ dose measurement accuracy was determined by comparing the dose measured by the control gels in group I under static conditions with the dose calculated in the treatment planning system (Pinnacle, v7.6, Philips Medical Systems, Madison, WI), which is regarded as the “gold standard” in this study. Ion chamber tests have shown that the dose calculation accuracy of the treatment planning system (TPS) is within 2%.²¹

The gels in group II were irradiated under the condition of deformation to assess the MORFEUS dose accumulation algorithm. Conventionally, polymer-based gels are fabricated and stored in rigid, airtight containers, which would prohibit deformation. To generate deformable gel dosimeters, a new fabrication technique that uses low-density polyethylene (LDPE) wrap as a flexible oxygen barrier to protect the gels has been developed.

The gel composition used in this study is listed in Table TABLE I.. A lower gelatin concentration of 6 (w/w) % was tried in a preliminary experiment, and the gels produced were too sloppy to hold shape against their own weight. Therefore, gelatin concentration was raised to 8 (w/w) % to make gels of sufficient rigidity. The gelatin powder was thoroughly soaked in 90% of the water for 60 min. The solution was then heated to 50°C while being stirred for 45−60 min to completely dissolve the gelatin. Methacrylic acid (MAA) and tetrakis (hydroxymethyl) phosphonium chloride (THP) were mixed in the remaining 10% of the water while the temperature of the gelatin solution was lowered to 35°C. The two solutions were combined and stirred for another 2 min. To make the control gels in group I, the mixture was poured into rigid, airtight high-density polyethylene (HDPE) cylindrical jars (diameter = 73 mm, height = 76 mm). To make the deformable gels in group II, the mixture was poured into paper coffee cups (bottom diameter = 52 mm, top diameter = 68 mm, height = 74 mm), which were in turn inserted in the HDPE jars. All gels were kept at 4°C in a refrigerator for 8 h to set.

TABLE I.

Composition of the gel dosimeters.

Compound	Function	Quantity
Gelatin (300 Bloom, Type A, Sigma)	Forms the bulk of the gel dosimeter	8 (w/w) %
Methacrylic acid or MAA (99%, Aldrich)	Radiation sensitizing monomer	5 (w/w) %
Tetrakis (hydroxymethyl) phosphonium chloride or THP (80% H2O solution, Aldrich)	Oxygen scavenger	50 mM
De-ionized water		87 (w/w) %

After solidification, three external markers were attached on the jar surface of each control gel (group I) for position reproducibility during imaging and irradiation. Paper cups were peeled off the deformable gels (group II), and three gold seeds used for image-guided prostate cancer radiotherapy²² were implanted in each gel using brachytherapy needles to later verify the accuracy of motion characterization. To avoid seed movements within the gel, the needles were inserted radially, perpendicular to the direction of compression applied to the gel during irradiation. The deformable gels were then immediately enclosed using LDPE wraps carefully to minimize contact with the ambient oxygen while ensuring that the wraps would not constrain the deformation and motion of the gel during irradiation. In addition to the five gels, four small cubic gels with the dimension of approximately 3 × 3 × 1 cm³ were produced from the same batch to measure the gels’ Young’s modulus using a commercially available elastometer.²³ Young’s modulus is an important material property used by MORFEUS to perform deformable image registration. Since the flexible wraps did not contain the gels in a motion-constraining way, they should not generate any significant effect on the elastic properties of the gels.

Treatment plan generation

Gels were not CT imaged in this experiment to avoid nontreatment irradiation. A 12-field conformal plan (Conf) with a prescription of 400 cGy was generated on the previously acquired CT images of a gel fabricated in an earlier experiment using the same method described in Sec. II A. All five gels were to be treated by the same plan but under different conditions: The two control gels were to be irradiated without any motion, and the three deformable gels were to be irradiated while being deformed by the amplitudes of 1, 1.5, and 2 cm, respectively. The frequency of the applied motion was set to be 16 rpm, mimicking natural breathing frequency. The treatment design for the five gels is summarized in Table TABLE II..

TABLE II.

Summary of the designed treatment for the five gel dosimeters fabricated in this study, including the purpose they serve, the magnitude of deformation applied to them, the treatment plan, and the number of gold seeds implanted to serve as internal fiducials.

GelPurpose	Conf1, Conf2Control gels	Conf3, Conf 4, Conf5 Measure dose with applied deformation
Magnitude of applied deformation	No deformation applied	1, 1.5, and 2 cm, respectively
# of gold seeds implanted	0	3
Treatment plan	12-beam conformal plan with a prescription of 400 cGy

Actuation device

An actuation device, adapted from the apparatus described by Samani et al.,²⁴ was constructed to apply sinusoidal compressions to the deformable gel dosimeters during irradiation (Fig. 1). This portable device, made with Plexiglass, is 120 cm in length and 22 cm in height. It can be conveniently set up on a treatment couch. A nonmagnetic ultrasonic motor (model USR60-E3N, Shinsei Corporation, Japan) was selected to drive the actuation device. An external control circuit for the motor was constructed to adjust the frequency of the output motion from 15 to 150 rpm. An eccentric disc drilled with holes at various distances (1, 1.5, and 2 cm) from the disc center is fixed on the motor shaft. The compression piston that applies deformation to the gel dosimeters is in turn attached to the disc. The amplitude of the applied motion can be adjusted by changing the hole to which the piston is attached.

Figure 1.

Pictures of the actuation device used to apply breath-mimicking sinusoidal motions to deform gel dosimeters during irradiation. In particular, the sample chamber and the motor unit are illustrated in more details.

Irradiation

All gels were irradiated by 6 MV photon beams at the dose rate of 600 MU/min on a clinical linear accelerator (Elekta Synergy, Elekta Oncology Systems, Crawley, United Kingdom) 34 h after gel fabrication to allow the oxygen scavenger to remove the oxygen molecules in the gels. Each control gel was set up on the treatment couch by aligning the external markers with the three in-room orthogonal laser beams. A kilovolt cone-beam CT (CBCT) image was acquired immediately before treatment to perform a rigid online registration with the planning image. Any translational positioning errors were corrected for via couch shifts. The control gel was then treated statically.

Each deformable gel was set up in the sample chamber of the actuation device and was positioned so that the compression applied by the actuation device would be in the superior-inferior (SI) direction. The motor was turned on to deliver the desired compression to the gel while a 4D CBCT imaging was performed to capture the motion, and the acquired CBCT images were registered with the planning image. The gel was then irradiated while the motion continued.

MR imaging and R₂ map generation

Dose measurements were read out using a birdcage transceiver head coil on a clinical MR simulator (GE Signa 1.5 T) 24 h after irradiation to allow the polymerization process to occur and stabilize.¹⁶ A magnetization-prepared spiral imaging method, termed T₂-prep,^{25, 26, 27} was used to measure the T₂ values of the gel. It is a time-efficient volumetric imaging method, yet T₂ contrast development is robust to the characteristic uniformities of both the radio frequency (RF) and static fields at 1.5 T.

The T₂-prep sequence consisted of three segment modules. The first module segment is a magnetization preparation interval to develop T₂ contrast robustly. The second segment is the imaging interval during which spectral-spatial excitation pulse and spiral gradient waveforms are applied repetitively for spatial encoding of multiple slices within a single repetition time (TR). The third segment is the longitudinal recovery interval, which is approximately TR less the combined duration of the echo time and imaging interval to ensure a constant period of longitudinal recovery despite the variable echo time (TE).^{25, 26, 27} The imaging parameters used were as follows: TE = 3.2, 61.8, 120.4, 237.7, and 472.2 ms; TR = 6000 ms; NEX = 10; image resolution = 2 × 2 × 2 mm³; k-space trajectory = 6 × 1900 spiral interleaves; field-of-view (FOV) = 160 × 160 mm²; and total image acquisition time = 30 min. The TEs were strategically selected to cover the possible range of T₂ values throughout the irradiated gels based on previous experience. The long TR allowed more time for longitudinal magnetization recovery, and the high NEX improved the signal-to-noise ratio (SNR) for more precise T₂ estimation.

At each axial position for each gel, the five echo times generated a set of five images with decreasing voxel intensities due to T₂ decay. The T₂ value at a voxel was determined by fitting the grayscale intensities at that voxel in the set of five images to a monoexponential decay function:

$$I(t)=I_O\exp (-\frac{t}{T_2}),$$ (1)

where t is the time after the excitation pulse, I(t) is the pixel intensity at time t, and I_O is the signal intensity immediately after the excitation pulse. Once the T₂ map was generated, the R₂ map for each gel could be easily obtained by calculating the reciprocal of T₂. R₂ measurement uncertainty from static field inhomogeneities depends on the refocusing train design rather than on a specific echo time. The T₂-prep optimization of the refocusing train used in this study provides R₂ accuracy within 5% at 1.5 T over typical ranges of RF and static field inhomogeneities and refocusing intervals.

Static dose grids

Each control gel was manually contoured in the TPS on the CBCT images representing the treated position. The gel density was overridden with a constant value of 1.03 g/cm³, which was obtained from the CT images of gels with the same composition manufactured in earlier experiments. The remaining space on the CBCT images was regarded as air and assigned a density of 0 g/cm³. The same conformal plan was calculated on the density-overridden CBCT images by the TPS to give the delivered dose.

For each deformable gel, CBCT images were first sorted into motion-correlated phases (4D CBCT).²⁸ Two static image sets representing the gel at its undeformed state (primary) and fully deformed state (secondary) were extracted. The gel, the sample chamber containing the gel, and the piston of the actuation device were then contoured on both the primary and secondary image sets in the TPS. The density of the gels was overridden with a constant value of 1.03 g/cm³; the density of the sample chamber and the piston was overridden with a constant value of 1.08 g/cm³; the remaining space was regarded as air with a constant density of 0 g/cm³. The primary and secondary static dose distributions for each deformable gel were then calculated based on the density-overridden primary and secondary CBCT images, respectively, with the conformal plan. The resolution of all dose grids is 2 × 2 × 2 mm³.

The dose delivered by the CBCT, which is in the order of milligray, is considered negligible comparing to the prescribed dose of 4 Gy. In addition, all gel dosimeters, including the calibration gels and the deformable gels, were all imaged with CBCT prior to treatment. Assuming a linear R₂-dose relationship, dose contribution from CBCT would be accounted for by the constant term in the R₂-dose equation, thus would not affect the dose readout translated from the R₂ values.

R₂-dose calibration

Since gel dosimetry is a relative dose measurement method, a calibration curve needs to be generated to translate R₂ values to doses.¹⁹ The two control gels, Conf1 and Conf2, were used to generate the R₂-dose calibration curve. The R₂ maps of the two gels were first imported into the TPS and rigidly aligned with their respective CBCT images and static CBCT-based dose grids. Fourteen regions of interest (ROIs) were selected within homogenously irradiated volumes on the dose grid for each gel. The mean ROI volume was 37 mm³ (range: 35.5−38 mm³). The mean and the standard deviation of the dose values in each ROI were calculated. The same set of ROIs was propagated onto the R₂ map of each gel to obtain the mean and standard deviation of R₂ values in each ROI. In this way, the mean dose and R₂ values in each ROI generated one point on the calibration curve. The mathematical R₂-dose relationship was then obtained by fitting the data points to a linear relation and was used to convert the R₂ maps of all five gels into dose distributions. Although the control gels were concealed in rigid HDPE containers while the deformable gels in flexible LDPE wraps, they were all manufactured in the same batch and had identical chemical compositions, which would dictate the gels to respond to radiation in the same manner. In addition, since all gels were irradiated and imaged with MRI at the same time and in the same environment, it was deemed appropriate to transfer the R₂-dose relationship obtained using the control gels to the deformable gels.

Motion characterization in MORFEUS

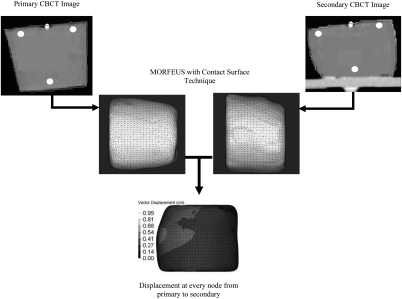
Dose accumulation on the deformable gels requires a quantitative characterization of the motion the gels had experienced during irradiation. This was accomplished by using the MORFEUS deformable image registration method, which utilizes a commercially available FEM pre- and postprocesses software product (HyperMesh v9.0, Altair Engineering, Troy, MI) and a finite element analysis (FEA) software package (ABAQUS, ABAQUS Inc, Pawtucket, RI) for model creation and analysis, respectively. The contours of each deformable gel on the primary 4D CBCT image set were converted into a binary mask, which was in turn converted into a surface mesh consisting of 3.5 mm triangular elements using the IDL software (ITT, Boulder, CO) to represent the gel at its undeformed state. The volume enclosed by the surface mesh was filled with 3.5 mm tetrahedral elements to construct a volume mesh of the gel. Another surface of the gel was also generated from the contours on the secondary 4D CBCT images to represent the maximally compressed gel position. To accurately model the compression applied onto each gel, the contact surface technique recently implemented in MORFEUS to model lung motions²⁹ was used to simulate the interaction between the piston and the gel. The deformation at each node in the volume mesh was calculated based on the material properties of the gel, including Young’s modulus (6.5 kPa) and Poisson’s ratio (0.45). The motion characterization process is depicted in Fig. 2.

Figure 2.

An illustration of the motion characterization process in morfeus. The primary and secondary CBCT images were extracted from the 4D CBCT images acquired at the time of treatment to represent the gel at the undeformed and fully deformed states, respectively. The locations of the three seeds implanted in each deformable gel are indicated as white circles on the CBCT images. Gel contours on the primary and secondary CBCT images were converted into meshes, and the displacement profile at every node was then calculated using the contact surface technique in MORFEUS.

To verify the accuracy of motion characterization, the displacements of the three gold seeds (also shown in Fig. 2) implanted in each deformable gel were measured by identifying the seeds on the primary and secondary 4D CBCT image sets. The measured seed displacements were then compared with the displacements predicted by MORFEUS.

MORFEUS deformable dose accumulation algorithm

The deformation maps were subsequently used by MORFEUS to accumulate the dose to each deformable gel through the motion cycle applied during irradiation. The displacement at each node in the finite element model was divided into six uniform increments to simulate phases of the motion cycle: Phase 0 corresponds to the undeformed position of the gel and phase 5 corresponds to the fully deformed position.¹⁰ The primary dose grid, which describes the static dose distribution at the gel’s undeformed position, is denoted as D_p; and the secondary dose grid, describing the distribution at the fully deformed gel position, is denoted as D_s. The dose distribution at each intermediate phase was determined by a combined linear interpolation from both D_p and D_s, multiplied by the time weighting factor, which indicates the time fraction the gel spent in each phase.¹⁰ The dose at a point (x, y, z) accumulated through one cycle of motion is described by the following equation:

$$D(x,y,z)=\sum _{\phi =0}^5{\tau }_{\phi }[D_S(x,y,z)\frac{\phi }{5}+D_P(x,y,z)\frac{(5-\phi )}{5}]$$ (2)

In the above equation, ф is the index of the motion phase (ф = 0 refers to the undeformed position; ф = 1−4 refer to the intermediate phases; and ф = 5 refers to the fully deformed position), and τ is the time weighting factor. In the present study, the motion was sinusoidal with respect to time and the corresponding values of τ are shown in Table TABLE III..

TABLE III.

The six phases (ф) into which the motion applied to the deformable gels was divided and the time weighting factor (τ_ф) associated with each phase used in the MORFEUS dose accumulation computation.

Ф	Time weighting factor (τф)
0 (Undeformed state)	0.27
1	0.12
2	0.11
3	0.11
4	0.12
5 (Fully deformed state)	0.27

Comparison between the dose measured by control gels and the static dose calculated in the TPS

The accuracy of the gel dosimeters was calculated by comparing the dose measured by the two control gels, Conf1 and Conf2, with the corresponding static dose calculated in the TPS (STATIC). Various quantitative dose comparison tools exist, and each has its unique advantages and limitations. To achieve a more comprehensive comparison between the two dose distributions, three different metrics were used.

First, after rigidly registering each gel-measured dose map with the STATIC distribution, dose differences, in terms of both dose levels (centigray) and percentage (%) of the STATIC dose, were calculated on a voxel-by-voxel basis. The mean voxel-by-voxel difference between the control gel dose and the STATIC dose reflected the accuracy of the gels in measuring radiation dose, while the standard deviation of the voxel-by-voxel dose difference determined the dose measurement uncertainty (δ) of the gels.

The voxel-by-voxel comparison can be overly sensitive, especially in regions with a steep dose gradient, to noise and small spatial errors in gel positioning or registration.³⁰ The second dose comparison metric, which is considered to be complementary to the voxel-by-voxel metric,³⁰ calculated the spatial correspondence of selected isodose surfaces. The isodose surfaces at 250, 300, 350, and 400 cGy were delineated on each gel dose grid and the corresponding STATIC dose grid and were converted into triangular-element surface meshes. The distance between each pair of corresponding isodose surfaces was computed at each node of the surface mesh in MORFEUS using the guided surface projection method.¹¹

The third dose comparison method was the gamma index test described by Low and Dempsey, which simultaneously considers both dose difference and distance-to-agreement (DTA), which is analogous to isodose surface distances.³⁰ The 2%/2 mm and 3%/3 mm are commonly seen criteria and were both used to evaluate the dose measured by each control gel against the STATIC dose. All dose analyses were restricted to regions receiving a dose of 200 cGy or more for the reasons described in Sec. II K.

Verification of MORFEUS dose accumulation algorithm

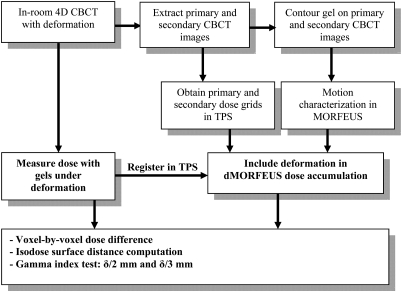
After the dose measurement uncertainty of the gel dosimeters has been determined from the control gels, the deformable gels were used as a reference to evaluate the dose accumulated in MORFEUS. This was conducted using a voxel-by-voxel dose comparison, an isodose surface position comparison, and a gamma index test. For the gamma index test, the allowable dose discrepancy between the accumulated and the measured doses was the dose measurement uncertainty (δ) of the gel dosimeters, which had been determined by the standard deviation of the voxel-by-voxel dose difference in both centigray and percentage, between the control gel and STATIC doses. Therefore, instead of using 2%/2 mm and 3%/3 mm, δ/2 mm and δ/3 mm were used as the criteria of the gamma index test. The experiment procedure and dose analysis methods to evaluate the MORFEUS dose accumulation algorithm using deformable gel dosimeters are summarized in Fig. 3.

Figure 3.

A flowchart summarizing the experiment procedure and the dose analysis methods to compare the dose accumulated in MORFEUS with the dose measured by the deformable gels under the same deformation.

The flexible wraps provide the deformable gels a less effective oxygen barrier than conventional rigid containers, thus allowing some oxygen penetration to occur at the gel peripheries (from gel surface to approximately 1−1.5 cm beneath), which could inhibit the gels’ radiation detection ability, interfering with dose measurement in the peripheral regions. Dose readout accuracy in the peripheral regions may be further affected by the magnetic field inhomogeneities caused by the gel-air interfaces during the MR imaging process. All dose analyses for the deformable gels were, therefore, performed only in regions receiving a dose of 200 cGy or more, around the center of each gel. This restriction was also applied to the control gels described in Sec. 2J to maintain consistency in dose comparison procedures.

RESULTS

R₂-dose calibration curve

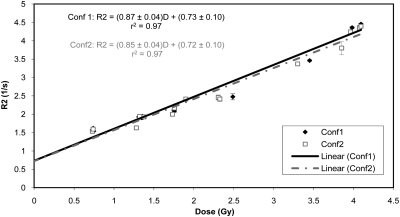
The R₂-dose calibration curves obtained from Conf1 and Conf2 are shown in Fig. 4 along with the equations describing the R₂-dose relationship. The error bars reflect the standard deviations of R₂ values. The bigger error bars at two points is attributed to the fact that slightly less uniformly distributed regions were selected to generate these data points. Coefficients of determination (r²) of 0.97 suggest a strong linear R₂-dose relationship for both gels. The average of the two linear fits is

$${\mathrm{R}}_2=0.86\mathrm{Dose}+0.725.$$ (3)

This calibration equation was used to convert the R₂ maps of all gels into dose distributions.

Figure 4.

R₂-dose calibration curves obtained from Conf1 and Conf2. The linear fit equations and the coefficients of determinants (r²) are also displayed.

Accuracy of motion characterization in MORFEUS

Since the gold seeds served as markers against which the accuracy of motion characterization was checked, the reproducibility of seed positions in each deformable gel across at least three motion cycles was verified first by examining the 4D CBCT images acquired immediately prior to irradiation. The absolute average change in seed positions from cycle to cycle is 0.4, 0.3, and 0.5 mm in left-right (LR), anterior-posterior (AP), and SI directions, respectively, with all seed position changes in any direction less than 1.0 mm, showing stability in seed positions through repeated motion cycles.

MORFEUS with the contact surface technique was used to generate a deformation map for each deformable gel to quantitatively describe the motion applied to the gel during irradiation. The differences between the measured seed displacements and the seed displacements estimated by MORFEUS in LR, AP, and SI directions are summarized in Table TABLE IV.. For all three deformable gels, the mean vector error of MORFEUS at the locations of the three seeds implanted in each gel is less than the CBCT image resolution of 2 mm, and the standard deviation of the absolute vector error for each gel is less than 1 mm. The overall absolute average vector magnitude accuracy (mean ± SD) of the MORFEUS motion characterization across all three deformable gels is 1.1 ± 0.5 mm.

TABLE IV.

Summary of the absolute accuracy of the deformation map calculated by the MORFEUS deformable image registration method with the contact surface technique integrated. For each deformable gel, accuracy was assessed by comparing the displacements of the three implanted gold seeds estimated by MORFEUS with the seed displacements measured from the sorted 4D CBCT images of that gel. The mean and standard deviation of the absolute vector errors and the absolute errors in the LR, AP, and SI direction are shown, as well as the magnitude of deformation applied to each gel.

		Absolute error (mm)
Gel (maximum magnitude of motion)		LR	AP	SI	Vector
Conf3 (1 cm)	Mean	0.3	0.6	0.7	1.1
	SD	0.1	0.7	0.4	0.4
Conf4 (1.5 cm)	Mean	0.8	0.3	0.7	1.2
	SD	0.2	0.1	0.5	0.2
Conf5 (2 cm)	Mean	0.7	0.4	0.7	1.1
	SD	0.5	0.3	0.7	0.9

Comparison between the dose measured by control gels and the static dose calculated in the TPS

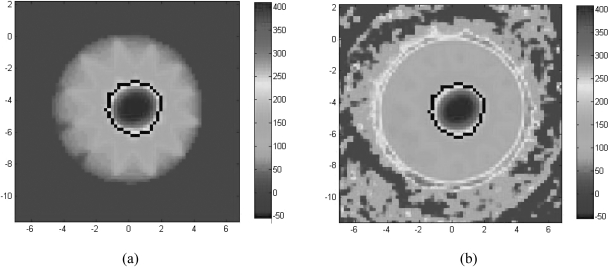
An axial snapshot of the gel dose and the STATIC dose for Conf1 are shown in Fig. 5 to illustrate the ROI in which dose comparison was performed. For both control gels, the mean and standard deviation of the voxel-by-voxel dose differences between the gel and the STATIC distributions in both dose levels (centigray) and percentage (%) are summarized in Table TABLE V.. The results shows that the control gels agreed well with the STATIC dose distributions with a mean absolute voxel-by-voxel dose difference of less than 4 cGy or 1.5% for both gels. The standard deviation of the dose differences is on average 11.8 cGy or 4.7%, which is regarded to represent the inherent dose measurement uncertainties (δ) of the gel dosimeters used in this study.

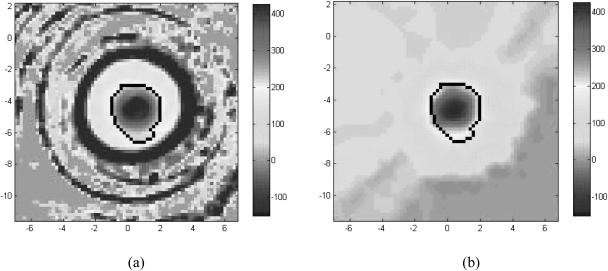
Figure 5.

An axial snapshot of the STATIC dose for Conf1 (c) and the dose measured by Conf1 (d). The dose comparisons between the STATIC distribution and the distribution measured by the control gels were performed in the volume enclosed by the 200 cGy isodose surface on the STATIC dose map, which is outlined in black in (a) and (b).

TABLE V.

The mean and standard deviation of the voxel-by-voxel dose differences between the dose measured by each control gel and the corresponding STATIC distribution calculated in the TPS. Dose difference is reported in terms of both dose level (cGy) and as a percentage (%) of the STATIC dose, which was the benchmark distribution against which the dose measured by the gel was compared.

Voxel-by-voxel dose difference	Conf1	Conf2
Mean (SD) (cGy)	−3.8 (13.7)	−0.8 (9.8)
Mean (SD) (%)	−1.4 (5.4)	−0.2 (4.0)

The 250, 300, 350, and 400 cGy isodose surfaces were delineated on the gel-measured and the STATIC dose maps for Conf1 and Conf2. The vector distance and the distance in the LR, AP, and SI directions between each pair of corresponding isodose surfaces were calculated and displayed in Table TABLE VI., showing good agreement. At all isodose levels investigated, the average distance is less than 0.5 mm in all three directions and the vector distance is less than 1 mm, below the dose grid resolution of 2 mm, for both gels. The standard deviation of isodose surface distances is less than 0.5 mm in all cases. The gamma index test showed a 76−79% pass rate for 2%/2 mm and a 93−96% agreement for 3%/3 mm, as shown in Table TABLE VII..

TABLE VI.

The mean and standard deviation of the distances between corresponding isodose surfaces on the dose distribution measured by the control gels (Conf1 and Conf2) and on the STATIC distribution calculated in the TPS.

		LR	AP	SI	Vector
Gel	Isodose Surface (cGy)	Mean (SD)(mm)	Mean (SD)(mm)	Mean (SD)(mm)	Mean (SD)(mm)
Conf1	250	0.2 (0.3)	0.0 (0.3)	−0.1 (0.2)	0.4 (0.4)
	300	0.2 (0.2)	0.0 (0.3)	−0.1 (0.2)	0.4 (0.3)
	350	0.2 (0.3)	0.0 (0.2)	−0.1 (0.3)	0.4 (0.4)
	400	0.3 (0.5)	0.3 (0.4)	0.0 (0.4)	0.8 (0.4)
Conf2	250	0.1 (0.3)	0.0 (0.3)	0.0 (0.2)	0.4 (0.3)
	300	0.1 (0.1)	0.0 (0.2)	0.0 (0.2)	0.2 (0.2)
	350	0.0 (0.3)	0.0 (0.3)	−0.2 (0.3)	0.4 (0.4)
	400	0.1 (0.5)	0.1 (0.5)	0.0 (0.3)	0.7 (0.4)

TABLE VII.

The percentage of the voxels of the dose distribution measured by each control gel that have passed the gamma index test using the 2%/2 mm and 3%/3 mm criteria.

Criterion	Conf1(%)	Conf2(%)
2%/2 mm	75.8	79.0
3%/3 mm	93.4	95.7

Verification of MORFEUS dose accumulation algorithm

The doses accumulated in MORFEUS and measured by the deformable gels were compared. An axial snapshot of the measured and accumulated doses for Conf3 are shown in Fig. 6 as examples to illustrate the ROI in which dose comparison was performed. For all three deformable gels, the mean and standard deviation of the voxel-by-voxel dose difference in terms of dose levels (centigray) and percentage (%) of the gel dose are summarized in Table Table VIII.. The absolute mean voxel-by-voxel difference is less than 10 cGy or 3% for all deformable gels and the standard deviation is relatively consistent for all gels, ranging from 33.2 cGy (13.0%) for Conf3 to 37.7 cGy (13.8%) for Conf5. For comparison, the maximum dose difference between the compressed and uncompressed state was 374 cGy.

Figure 6.

An axial snapshot of the dose measured by Conf3 (a) and the dose accumulated by MORFEUS for Conf3 (b). The dose comparisons between the dose measured by the deformable gels and the accumulated dose were performed in the volume enclosed by the 200 cGy isodose surface on the gel dose map, which is outlined in black in (a) and (b).

Table VIII.

The mean and standard deviation of the voxel-by-voxel differences between the dose measured by each deformable gel and the dose accumulated in MORFEUS for the same gel. Dose difference is reported in terms of both dose level (cGy) and as a percentage (%) of the gel-measured dose, which was the benchmark distribution against which the accumulated dose was compared. The magnitude of deformation applied to each gel during irradiation is also included.

Voxel-by-voxel dose difference	Conf3(1 cm)	Conf4(1.5 cm)	Conf5(2 cm)
Mean (SD) (cGy)	−4.8 (33.2)	−1.3 (37.2)	−7.9 (37.7)
Mean (SD) (%)	−1.4 (13.0)	−0.3 (13.5)	−2.8 (13.8)

The isodose surfaces at 250, 300, 350, and 400 cGy were delineated on the measured and accumulated dose maps. The vector distance and the distance in the LR, AP, and SI directions between each pair of corresponding isodose surfaces were calculated and displayed in Table TABLE IX., which shows that the mean absolute isodose surface distances are less than 2 mm in all three directions and at all isodose levels investigated, with most mean distances (34 of 36) less than 1 mm. The average vector distance is also less than 2 mm except for Conf5, for which the average vector distance between the 400 cGy isodose surfaces is 2.1 mm. The average vector distance across all four pairs of isodose surfaces is 0.9, 1.2, and 1.6 mm for Conf3, Conf4, and Conf5, respectively. The standard deviation of the vector distances is less than 1.5 mm in all cases.

TABLE IX.

The mean and standard deviation of the distances between corresponding isodose surfaces on the dose distribution measured by each deformable gel (Conf3, Conf4, and Conf5) and on the dose accumulated in MORFEUS for the same gel.

		LR	AP	SI	Vector
Gel	Isodose surface (cGy)	Mean (SD)(mm)	Mean (SD)(mm)	Mean (SD)(mm)	Mean (SD)(mm)
Conf3	250	0.4 (0.6)	−0.3 (0.7)	0.0 (0.4)	0.9 (0.7)
	300	0.5 (0.6)	−0.3 (0.8)	0.0 (0.3)	0.9 (0.8)
	350	0.5 (0.6)	0.0 (0.5)	0.0 (0.3)	0.8 (0.6)
	400	0.4 (0.7)	0.6 (0.7)	−0.1 (0.4)	1.1 (0.7)
Conf4	250	−0.3 (0.8)	0.1 (0.6)	0.1 (0.5)	0.9 (0.7)
	300	−0.5 (0.9)	0.2 (0.6)	0.2 (0.5)	1.1 (0.8)
	350	−0.4 (0.7)	0.3 (1.1)	0.2 (0.6)	1.2 (1.0)
	400	0.8 (1.4)	−1.1 (1.1)	−0.3 (0.8)	1.7 (1.6)
Conf5	250	−0.5 (0.7)	−0.3 (0.8)	−0.2 (0.7)	1.1 (0.8)
	300	−0.5 (0.8)	−0.3 (0.7)	−0.2 (1.0)	1.3 (0.9)
	350	−0.8 (1.1)	−0.2 (0.7)	−0.1 (0.3)	1.3 (0.9)
	400	−1.7 (0.8)	0.1 (0.7)	−0.2 (0.7)	2.1 (0.6)

The gels’ inherent dose measurement uncertainties have been determined using the control gels and were set to be the acceptable dose difference errors in the gamma index test to evaluate the dose distributions accumulated in MORFEUS, thus making the gamma test criteria 11.8 cGy/2 mm (3 mm) and 4.7%/2 mm (3 mm). Under the same DTA criterion (i.e., 2 or 3 mm), the pass rate of the accumulated dose voxels for each dose difference criterion, as well as the total pass rate, which includes all voxels that passed either dose difference criterion, were calculated and shown in Table TABLE X.. With the DTA criterion of 2 mm, the average total pass rates of the accumulated dose voxels is 92.7%, with similar pass rates (range: 90.8% for Conf5 to 94.4% for Conf4) seen across the accumulated doses for all three deformable gels. When the DTA criterion is relaxed to 3 mm, the average total pass rate of the accumulated doses for all three deformable gels has increased to above 96.9% (range: 94.9% for Conf5 to 99.3% for Conf4).

TABLE X.

The percentage of the voxels of the accumulated doses for the deformable gels (Conf3, Conf4, and Conf5) that have passed the gamma index test using the 11.8 cGy/2 mm (3 mm) and 4.7%/2 mm (3 mm) criteria. The dose difference criteria of 11.8 cGy and 4.7% reflect the gel dosimeters’ dose measurement precision of the conformal plan and were determined from the results of the voxel-by-voxel comparison between the control gels and the corresponding STATIC distributions.

Criterion	Conf3(%)	Conf4(%)	Conf5(%)	Criterion	Conf3(%)	Conf4(%)	Conf5(%)
11.8 cGy/2 mm	90.9	91.8	88.6	11.8 cGy/3 mm	96.2	98.9	94.8
4.7%/2 mm	92.1	93.9	89.7	4.7%/3 mm	96.2	99.3	93.6
Total pass rate	92.8	94.4	90.8	Total pass rate	96.5	99.3	94.9

DISCUSSION

This research has proposed a novel technique, which uses polymer-based gel dosimeters to measure volumetric dose distributions under the condition of deformation. A deformable gel dosimeter was developed by using LDPE wraps to provide flexible oxygen barriers, and an actuation device was designed and built to apply sinusoidal compressions to the gels during irradiation. This work has also applied this technique in an attempt to experimentally validate the deformable dose accumulation algorithm derived from the FEM-based deformable image registration platform MORFEUS.

Since the result of the dose accumulation algorithm greatly depends on the deformation quantitatively characterized in MORFEUS, the accuracy of motion characterization was verified prior to dose calculation. By measuring the displacements of the three gold seeds implanted in each deformable gel on the time-resolved 4D CBCT images, it was shown that, for all three deformable gels, MORFEUS had an average absolute vector error of less than 2 mm, the isotropic resolution of the CBCT images, regardless of the magnitude of the applied deformation. The standard deviation of the average error for each gel is always less than 1 mm, suggesting that MORFEUS achieved consistent accuracy at all three seed locations in each gel. The CBCT images were also used to verify that the seeds did not slide within the gels and that the seed positions were stable through repeated compression cycles. Therefore, the seeds were considered as reliable fiducial markers.

Doses measured by the gel dosimeters were read out by MRI. A number of previously published studies have reported that dose accuracy in gel dosimetry is greatly affected by the SNR in MR images, which in turn depends on the MR imaging parameters.32 The imaging parameters used in this study were selected empirically to optimize the SNR. Assuming that the transverse magnetization follows a monoexponential decay, mathematically, two TEs shall be sufficient to derive the T₂ value. However, five TEs were used to provide a more accurate T₂ estimation. To precisely measure T₂, the distribution of the TEs was also carefully selected to correspond to the range of T₂ values (200–500 ms) throughout the gel volume in which dose analyses were carried out. A long TR of 6000 ms was chosen to ensure complete longitudinal spin recovery. SNR was further improved by using an NEX of 10. This set of imaging parameters has generated an SNR of 200 on the echo images. A number of published studies have also documented how RF and static field inhomogeneities can bias T₂, and T₂ prep is optimized to minimize such biases at 1.5 T.^{25, 26, 27, 28}

The dose measurement accuracy of the gel dosimeters was verified by comparing the dose measured by the two control gels, Conf1 and Conf2, under static conditions with the STATIC dose, which was calculated in the TPS and considered the gold standard. Doses were compared through three methods: voxel-by-voxel dose difference, isodose surface distance, and gamma index. The absolute average voxel-by-voxel difference between the STATIC dose and the dose measured by the two control gels is small (<4 cGy). The standard deviation of the dose differences is on average 11.8 cGy or 4.7%, mainly due to the dose measurement uncertainties intrinsic to the gels (e.g., polymerization could occur in un- or less-irradiated regions due to radical diffusion) and small positioning errors. The mean vector distances between 250, 300, 350, and 400 cGy isodose surfaces are less than 1 mm, with standard deviations of ≤0.5 mm, as shown in Table TABLE VI.. The gamma index test looks at both dose difference and isodose surface distance. Using the 2%/2 mm criterion, the pass rates for Conf1 and Conf2 in the gamma index test are 75.8% and 79.0%, respectively. The voxels that have failed the test are expected to congregate in regions with the steepest dose gradients, where small spatial offsets between the measured distribution and the STATIC distribution could reduce the pass rate. With the more relaxed 3%/3 mm criterion, the pass rates for Conf1 and Conf2 have increased to 93.4% and 95.7%, respectively. The results of all three dose comparison methods have demonstrated that using the STATIC distribution as the benchmark, the gels could provide accurate static volumetric dose distribution measurement.

To validate the MORFEUS deformable dose accumulation algorithm, three deformable gels were used to measure dose under conditions of deformation. Doses calculated in MORFEUS were then compared with the measured doses using the same three methods described above. The results of the voxel-by-voxel comparison show that the absolute values of the mean dose differences are below 10 cGy, but the standard deviations of the dose differences are above 30 cGy for all deformable gels, much larger than the standard deviations (∼10 cGy) of the dose differences between the STATIC distribution and the distribution measured by the control gels. This can be attributed to a number of uncertainties introduced mainly by the deformability of the gels and the incorporation of motion during irradiation. As previously mentioned, the soft gels could be deformed due to gravity. In addition, because they were not perfectly elastic, the compressions, especially the one with 2 cm amplitude, applied during irradiation could permanently deform the gels. The gel geometry could, therefore, change from the CBCT images to the MR images, making precise registration between the two image sets challenging. The shape of the dose distribution in the gel could also be affected. The possible sources of errors in the MORFEUS dose accumulation process include the errors in deformation modeling and the fact that dose was accumulated in six discrete steps instead of continuously. Furthermore, the gel dosimeters are not perfect that they have intrinsic dose measurement uncertainties, which can be seen from the comparison between the STATIC dose and the dose measured by the control gels. All these factors could contribute to the more widely distributed discrepancy between the accumulated dose and the dose measured with the deformable gels.

The isodose surface distances between the dose measured by each deformable gel and the corresponding MORFEUS dose range from 0.4 to 1.4 mm, larger than the isodose surface distances between the STATIC dose and the dose measured by the control gels. This result is expected since the spatial uncertainties associated with the deformable gels would be larger than those associated with the rigid control gels. The average vector distances between the four isodose surface pairs increase with the magnitude of compression applied to the gels during irradiation. This observation is consistent with the speculation that larger deformations are more likely to cause permanent change in gel geometry and the shape of the spatial dose distribution. Overall, the average absolute isodose surface distances are equal to or less than the CBCT voxel size and the standard deviation of the isodose surface distances is less than 1.5 mm for all three gels and all isodose surfaces, showing a good agreement between MORFEUS and the gels on the spatial dose distribution of the conformal plan delivered under conditions of deformation.

The gamma index test provided a more comprehensive assessment of the MORFEUS dose distributions. Comparing with the gamma test to evaluate the control gels, the dose difference criteria have changed from 2% and 3% to the dose measurement uncertainties (δ) of the control gels, which represented the best dose measurement precision attainable by using gel dosimeters in this study. The distance criteria of 2 and 3 mm remained the same to compensate for small spatial errors when registering the MR images with the CBCT images. The pass rates of the voxels in the dose grids accumulated in MORFEUS are summarized in Table TABLE X.. Under the distance criterion of 2 mm, the average total pass rate of the accumulated distributions for the three deformable gels is 92.7%, 15.3% higher than the average pass rate of the dose distributions measured by the two control gels (77.4%), indicating that the less strict dose difference criteria (11.8 cGy and 4.7%, comparing with the 2% criterion for the control gels) applied to the accumulated doses have compensated for the increase in dose uncertainties associated with the deformable gels. When the distance criterion is loosened to 3 mm, the total pass rates of all accumulated doses have increased to above 94%, with an average of 96.9%, demonstrating a good agreement between the doses accumulated in MORFEUS and the corresponding doses measured by the deformable gels. For all three dose comparison methods used, no strong correlations between the MORFEUS -gel agreement and the magnitude of the applied deformation have been observed.

By developing a deformable volumetric dosimeter and using it to validate the MORFEUS dose accumulation algorithm, this study has demonstrated the feasibility of using such dosimeters to experimentally validate algorithms that include organ deformations into dose calculations. Comparing to the methods used in other experimental studies that have investigated the effect of respiration related organ deformations on dose distributions, deformable gel dosimeters can provide a continuous volumetric dose measurement instead of dose measurements at specific points or planes. The gels can also be deformed at controlled frequency and amplitude to better simulate organ motions than linearly moving a phantom as a rigid body. However, several limitations of the gel dosimetry method have also been found. Oxygen inhibition in combination with the nonperfect oxygen barrier provided by the LDPE wraps has reduced the dose detection ability in the peripheral region of the deformable gels. As a result, dose comparison was limited to the central region with a received dose of 200 cGy or above in this study. Consequently, the accuracy of the MORFEUS dose accumulation algorithm in the low dose (<200 cGy) regions could not be examined, making the validation of MORFEUS incomplete in this investigation. Deformations applied during irradiation could permanently deform the gels, which in turn, alters the shape of the measured dose distribution and introduces additional uncertainties in spatial dose information.

Future investigations will focus more on lower doses by utilizing bigger gels to include a wider dose range in the central region unaffected by oxygen inhabitation. Alternatively, a lower dose can be prescribed to the gel centre. Also, the reproducibility of gel deformation through multiple compression cycles during irradiation will be examined more thoroughly in future studies by implanting more gold seeds and acquiring 4D CBCT images for a longer period of time while deformation is being applied. Further work will also address increasing the complexity of the phantom to include changes in electron density between the compressed and uncompressed state.