Using RNA sample titrations to assess microarray platform performance and normalization techniques

Abstract

We have assessed the utility of RNA titration samples for evaluating microarray platform performance and the impact of different normalization methods on the results obtained. As part of the MicroArray Quality Control project, we investigated the performance of five commercial microarray platforms using two independent RNA samples and two titration mixtures of these samples. Focusing on 12,091 genes common across all platforms, we determined the ability of each platform to detect the correct titration response across the samples. Global deviations from the response predicted by the titration ratios were observed. These differences could be explained by variations in relative amounts of messenger RNA as a fraction of total RNA between the two independent samples. Overall, both the qualitative and quantitative correspondence across platforms was high. In summary, titration samples may be regarded as a valuable tool, not only for assessing microarray platform performance and different analysis methods, but also for determining some underlying biological features of the samples.

Microarrays are widely used to simultaneously measure the levels of thousands of RNA targets in a biological sample. Despite their widespread use, many in the community are concerned with the comparability of the results obtained using different microarray platforms and thus the biological relevance of the qualitative and quantitative results obtained. Microarray platform performance has been evaluated before on the criteria of sensitivity, specificity, dynamic range, precision and accuracy^1–12. As part of the MicroArray Quality Control (MAQC) project, similar assessments have also been reported^13,14. Other studies have used defined mixtures of RNA samples (titration samples) for interplatform^2,15 and interlaboratory¹⁵ comparisons. Here we have investigated an alternative performance metric: the abilities of different microarray platforms to accurately detect a signal trend produced by mixing samples (titration trend) and the effects of normalization and other data analysis practices on this performance characteristic. Gene-expression levels were measured for two pure samples and two mixtures using five different commercial whole-genome platforms at three different test sites per platform. The five commercially available whole-genome platforms tested were Applied Biosystems (ABI), Affymetrix (AFX), Agilent Technologies (AG1), GE Healthcare (GEH) and Illumina (ILM). The level of accurate titration response was quantified by determining the number of probes for which the average signal response in the titration samples was consistent with the response in the independent, reference RNA samples. We analyzed every platform at each site, and here we present comparisons of the various platforms using various data processing and normalization techniques.

To assess the titration response of as many genes as possible, an a priori expectation of differential expression of many transcripts was necessary. On the basis of results from pilot titration studies (data not shown), we elected to use two independent samples (A, Stratagene Universal RNA, and B, Ambion Human Brain RNA) that showed large, statistically significant differences in expression for a large number of transcripts to generate the two titration samples (C and D, consisting of 3:1 and 1:3 ratios of A to B, respectively; see Fig. 1). We defined the series of mean signals generated by a gene on a microarray platform across these samples as its titration response. For these analyses, we assumed that the expression measurement of a transcript in a titration sample follows a linear titration relationship: the signal of any given transcript in the two titration samples should be a linear combination of the signals produced by the two independent samples. From the signal intensities in the microarray titration experiments, we obtained the percentage of genes on each platform that showed a monotonic titration response and analyzed that percentage as a function of the magnitude of differential expression between A and B or as a function of the signal intensity.

Figure 1.

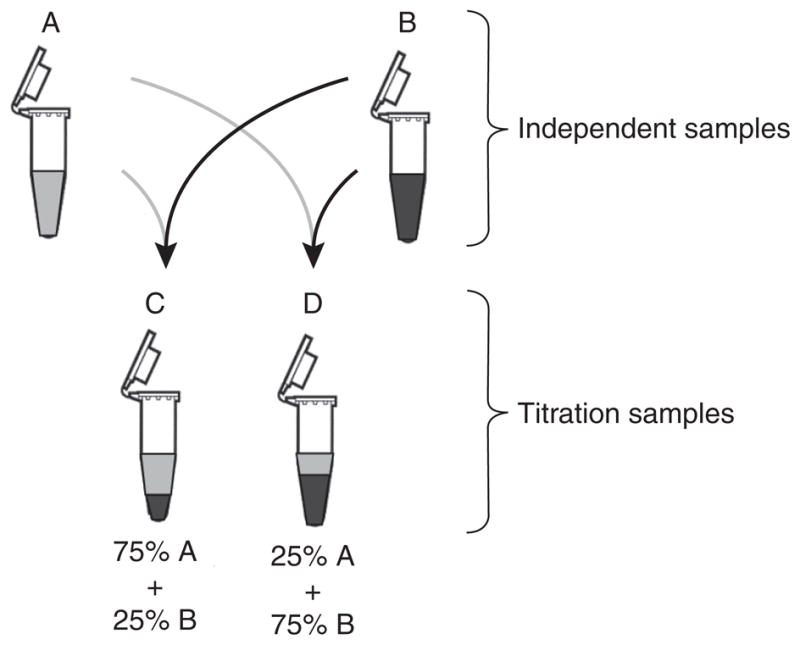
RNA samples. We used expression measurements from two independent total RNA samples, A and B, and mixtures of these two samples at defined ratios of 3:1 (C) and 1:3 (D). The titration mixtures were generated once for all experiments, with samples A and B at equal total RNA concentrations as determined by A₂₆₀.

Many normalization methods have been developed that are commonly used for different microarray platforms^16–24, including those methods that have been recommended by the array manufacturers for the MAQC project¹³ (see Methods). Differences in these methods significantly influence several aspects of microarray performance, including precision and sensitivity^{9,16–20,23,24}. However, no clear consensus exists in the microarray community as to which method is best under a given set of circumstances. The optimal normalization or scaling methods for a given dataset may depend both on the experiment and on many attributes of that microarray dataset, including signal distribution and noise characteristics²⁵. The experimental design used here is valuable for assessing the influence of different data processing techniques on the self-consistency of microarray data with regard to titration response. In addition, the different data processing techniques were also analyzed with respect to their impact on the statistical power of these platforms to distinguish between the independent and titration samples. The titration analysis presented here was applied to all commercial whole-genome microarray platforms tested in the MAQC project¹³, using various data processing techniques, to evaluate the self-consistency and statistical power of the resulting data.

When assessing accuracy in experimental systems, the goal is to compare observed results to the expected ‘true’ values of the system. For most experiments measuring gene expression, the ‘true’ values are either unknown or difficult to measure independently. However, the titration response results presented here can provide some quantitative information about the relative accuracy of measurements of differential gene expression. Monotonicity in the titration response indicates a self-consistent relationship among the expression measurements from the four samples. Because many inferences drawn from microarray experiments depend as much or more on the direction of expression changes as on their magnitudes, the consistency with which microarray assays determine direction of change is an important performance characteristic. The main advantages of our method are that titration responses can be assessed on a large scale, independent of a designated reference platform, and that it does not require substantial assumptions to be made about the data^2,25.

RESULTS

The experimental design of the main MAQC study is described in detail elsewhere¹³. Briefly, two independent RNA samples were chosen for study and used to generate two titration samples. The gene-expression profiles of these samples, all split from a single pool, were measured on ten gene-expression measurement platforms. For each of the five whole-genome microarray platforms examined in this study, the samples were analyzed at three different test sites, each with ≤5 replicate assays per sample, for a total of 293 microarray hybridizations at 15 different sites. Data from all platforms were then processed using the recommended method from each array manufacturer, as represented in the main MAQC paper¹³, as well as one or more alternative normalization methods.

Using probe sequence information, we identified 12,091 genes that were uniquely targeted by at least one probe for all five commercial whole-genome microarray platforms. For each platform, only the probe closest to the 3′ end of the gene was considered¹³. We chose to exclude genes that were not detected across all samples and focused on genes whose signals were above the noise level and therefore more reliable¹⁰. Each manufacturer provided quantitative detection calls characterizing the probability that a gene was detected in a given replicate¹³. For most analyses, only genes detected in at least three replicates for a given sample and site were considered. This detection-call protocol is the same as described in the main MAQC paper¹³.

Measuring titration response as a function of fold change

The chief advantage of an experiment that evaluates gene expression in a series of known mixtures of two samples is that the rank order of measured expression levels of any given gene across the series can be predicted from the relative expression levels in the two original samples. For the series described in this paper, if the true expression level (A_i) of any gene i in sample A is greater than the true expression level (B_i) of the same gene i in sample B, then A_i > C_i > D_i > B_i, where C_i and D_i are the true expression levels of gene i in samples C and D. If B_i > A_i, then B_i > D_i > C_i > A_i. In our case, if we postulate A_i > B_i on the basis of the observed sample mean of $A_i(\overline{A_i})$ being significantly larger (P < 0.001) than the observed sample mean of $B_i(\overline{B_i})$, then we expect $\overline{A_i}>\overline{C_i}>\overline{D_i}>\overline{B_i}$. Finally, if A_i ≈ B_i, then the order of observed means will be nearly random.

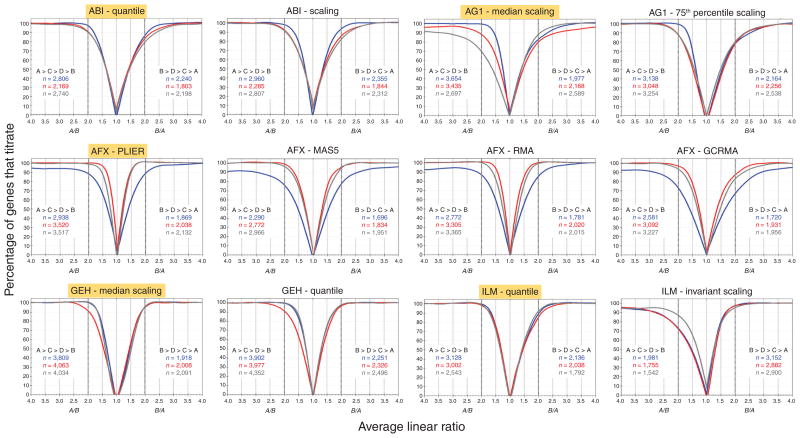
In Figure 2, the percentage of genes in a 100-gene moving window that produce the expected titration response for each site and platform is plotted as a function of the average $\overline{A_i}/\overline{B_i}$ ratio of those 100 genes, when $\overline{A_i}>\overline{B_i}$ (left side of graph), or of the $\overline{B_i}/\overline{A_i}$ ratio, when $\overline{B_i}>\overline{A_i}$ (right side of graph). The x-axis origin of these graphs is at $\overline{A_i}/\overline{B_i}=\overline{B_i}/\overline{A_i}=1$, the ratio at which the titration response changes direction. The overall shapes of all of the curves are similar: as expected from theory, they rise from a value near zero at $\overline{A_i}/\overline{B_i}=\overline{B_i}/\overline{A_i}=1$ to an asymptote of 100% at larger values of $\overline{A_i}/\overline{B_i}$ or $\overline{B_i}/\overline{A_i}$. Figure 2 also illustrates how alternative normalization methods (for AFX, alternative data reduction methods of the individual features) affect the quantitative outcome. For example, the data from the different test sites for AG1 show distinct behaviors under the standard normalization, but exhibit much more similar titration behaviors when normalized using the alternative method. In addition, for the AFX data, GCRMA processing²⁶ (a modified version of robust multichip analysis (RMA) processing that models intensity of probe level data as a function of GC content) results in titration curves with a broader spread than those produced by probe logarithmic intensity error (PLIER)²¹ or RMA¹⁸. It should be noted that the different data processing techniques also yield different numbers of genes showing significant deviations in expression values between samples A and B (Fig. 2 and Table 1), which can also influence titration performance. The most striking differences resulting from normalization techniques are seen with the ILM data, where the alternative method, invariant scaling, resulted in many fewer significant genes on the left side of the panel as well as lower percentages of genes that titrate at lower-fold changes.

Figure 2.

Percentage of genes showing the monotonic titration responses $\overline{A_i}>\overline{C_i}>\overline{D_i}>\overline{B_i}$ and $\overline{B_i}>\overline{D_i}>\overline{C_i}>\overline{A_i}$ plotted against the linear $\overline{A_i}/\overline{B_i}$ and $\overline{B_i}/\overline{A_i}$ ratios, respectively, for each commercial whole-genome microarray platform, using various normalization methods. All graphs were generated from the set of 12,091 genes common across whole-genome platforms, with outlier arrays excluded per manufacturer’s recommendations¹³. Genes detected across all four samples per site that were also significantly differentially expressed (P < 0.001) in independent samples A and B were used in the calculations (Table 1, rows 4 and 5). A two-sample t-test, with equal variance, was performed within each site on log₂ expression values. For each platform, a 100-probe moving window, based on sorted $\overline{A_i}/\overline{B_i}$ ratios (left side of plot) or $\overline{B_i}/\overline{A_i}$ ratios (right side of plot), was used to calculate the percentage of self-consistent monotonic titration response genes (y-axis) as a function of the corresponding moving average of $\overline{A_i}/\overline{B_i}$ or $\overline{B_i}/\overline{A_i}$ ratios (x-axis) within each site. Graphs are plotted with a scale break between −1 and 1, with reassignment of the x-axis for clarity. Each graph contains six series of data points (three sites in two monotonic directions), which were smoothed using a distance-weighted least-squares method. Blue, site 1; red, site 2; gray, site 3. Total number of genes showing the monotonic trend for each site are indicated in each graph, for both directions ( $\overline{A_i}>\overline{C_i}>\overline{D_i}>\overline{B_i}$ for $\overline{A_i}/\overline{B_i}$ ratios >1 and $\overline{B_i}>\overline{D_i}>\overline{C_i}>\overline{A_i}$ for $\overline{B_i}/\overline{A_i}$ ratios >1), and are also listed in Table 1 (rows 4 and 5). The normalization methods highlighted in yellow for each platform represent the manufacturer’s recommended method used in the MAQC main paper¹³.

Table 1.

Gene counts for AFX and ABI (top) and AG1, GEH and ILM (bottom) for each normalization method

Row	Condition	Quantile			Scaling			PLIER			MAS 5.0			RMA			GCRMA
		ABI_1	ABI_2	ABI_3	ABI_1	ABI_2	ABI_3	AFX_1	AFX_2	AFX_3	AFX_1	AFX_2	AFX_3	AFX_1	AFX_2	AFX_3	AFX_1	AFX_2	AFX_3
1	Detected in A · B · C · D	8,049	7,863	8,550	8,049	7,863	8,550	7,359	7,006	7,424	7,359	7,006	7,424	7,359	7,006	7,424	7,359	7,006	7,424
2	A > B	4,284	4,191	4,509	4,308	4,219	4,424	4,423	4,291	4,557	4,244	4,040	4,267	4,414	4,192	4,440	4,356	4,125	4,376
3	B > A	3,765	3,672	4,041	3,741	3,644	4,126	2,936	2,715	2,867	3,115	2,966	3,157	2,945	2,814	2,984	3,003	2,881	3,048
4	A > B and P < 0.001	3,144	2,298	3,046	3,143	2,376	3,037	3,723	3,632	3,848	2,982	2,934	3,168	3,559	3,491	3,670	3,420	3,273	3,490
5	B > A and P < 0.001	2,572	1,886	2,436	2,571	1,930	2,494	2,356	2,176	2,306	2,074	1,999	2,182	2,272	2,274	2,372	2,224	2,172	2,303
6	A > C > D > B	3,063	2,924	3,159	3,296	3,104	3,256	3,042	3,751	3,616	2,493	3,111	3,258	2,862	3,462	3,479	2,708	3,297	3,407
7	B > D > C > A	2,471	2,424	2,622	2,670	2,487	2,772	1,924	2,154	2,222	1,873	2,089	2,170	1,858	2,100	2,087	1,829	2,071	2,075
8	A > C > D > B and P < 0.001	2,806	2,169	2,740	2,960	2,285	2,807	2,938	3,520	3,517	2,290	2,772	2,966	2,772	3,305	3,365	2,581	3,092	3,227
9	B > D > C > A and P < 0.001	2,240	1,803	2,198	2,355	1,844	2,312	1,869	2,038	2,132	1,696	1,834	1,951	1,781	2,020	2,015	1,720	1,931	1,956
10	(A > C > D > B)/(A > B)	0.71	0.70	0.70	0.77	0.74	0.74	0.69	0.87	0.79	0.59	0.77	0.76	0.65	0.83	0.78	0.62	0.80	0.78
11	(B > D > C > A)/(B > A)	0.66	0.66	0.65	0.71	0.68	0.67	0.66	0.79	0.78	0.60	0.70	0.69	0.63	0.75	0.70	0.61	0.72	0.68
12	50% titrate when A/B =	1.35	1.35	1.36	1.28	1.32	1.32	1.30	1.13	1.20	1.52	1.28	1.30	1.40	1.18	1.25	1.60	1.28	1.32
13	75% titrate when A/B =	1.58	1.65	1.65	1.45	1.60	1.60	1.65	1.20	1.30	1.98	1.45	1.50	1.70	1.32	1.42	2.05	1.47	1.58
14	90% titrate when A/B =	1.80	1.98	1.99	1.68	1.90	1.94	2.10	1.30	1.52	3.00	1.67	1.78	2.10	1.42	1.61	2.80	1.68	1.85
15	50% titrate when B/A =	1.43	1.42	1.45	1.34	1.35	1.40	1.39	1.20	1.22	1.53	1.30	1.36	1.44	1.22	1.30	1.63	1.35	1.47
16	75% titrate when B/A =	1.77	1.80	1.88	1.60	1.75	1.83	1.68	1.37	1.38	1.82	1.45	1.52	1.75	1.40	1.50	2.22	1.65	1.80
17	90% titrate when B/A =	2.08	2.23	2.40	1.85	2.12	2.30	2.05	1.49	1.50	2.50	1.75	1.87	2.15	1.58	1.68	2.90	2.10	2.30
18	A/B > 2.00	1,794	1,664	1,830	1,813	1,718	1,808	1,703	1,602	1,832	1,759	1,548	1,756	1,693	1,468	1,702	2,178	2,062	2,255
19	B/A > 2.00	1,636	1,562	1,745	1,634	1,548	1,793	1,171	1,028	1,136	1,360	1,202	1,346	1,172	1,017	1,141	1,462	1,378	1,501
20	A/B > 2.00 (P < 0.001)	1,772	1,558	1,802	1,793	1,626	1,782	1,703	1,602	1,832	1,732	1,542	1,748	1,693	1,468	1,700	2,168	2,049	2,233
21	B/A > 2.00 (P < 0.001)	1,613	1,423	1,672	1,612	1,435	1,716	1,171	1,028	1,136	1,350	1,195	1,335	1,171	1,017	1,141	1,447	1,365	1,487

Row	Condition	Median scaling			75th % scaling			Median scaling			Quantile			Quantile			Invariant scaling
		AG1_1	AG1_2	AG1_3	AG1_1	AG1_2	AG1_3	GEH_1	GEH_2	GEH_3	GEH_1	GEH_2	GEH_3	ILM_1	ILM_2	ILM_3	ILM_1	ILM_2	ILM_3
1	Detected in A · B · C · D	8,322	8,468	9,121	8,322	8,468	9,121	10,416	10,505	10,289	10,416	10,505	10,289	7,995	7,761	7,555	7,995	7,761	7,555
2	A > B	5,046	4,922	5,051	4,624	4,705	5,027	6,324	6,537	6,161	6,173	6,275	6,123	4,505	4,349	4,221	3,670	3,512	3,009
3	B > A	3,276	3,546	4,070	3,698	3,763	4,094	4,092	3,968	4,128	4,243	4,230	4,166	3,490	3,412	3,334	4,325	4,249	4,546
4	A > B and P < 0.001	3,711	3,763	3,710	3,443	3,624	3,807	3,998	4,753	4,393	4,042	4,582	4,512	3,657	3,289	2,808	2,868	2,479	1,769
5	B > A and P < 0.001	2,057	2,439	2,839	2,447	2,707	2,958	2,238	2,352	2,632	2,409	2,586	2,772	2,713	2,473	2,051	3,384	3,068	2,960
6	A > C > D > B	4,249	3,714	2,923	3,430	3,218	3,460	4,413	4,314	4,381	4,637	4,308	4,917	3,204	3,170	2,924	2,097	1,945	1,989
7	B > D > C > A	2,304	2,357	2,848	2,384	2,377	2,703	2,167	2,230	2,258	2,718	2,653	2,833	2,198	2,153	2,059	3,426	3,221	3,697
8	A > C > D > B and P < 0.001	3,654	3,435	2,697	3,138	3,048	3,254	3,809	4,063	4,034	3,902	3,977	4,352	3,128	3,002	2,543	1,981	1,755	1,542
9	B > D > C > A and P < 0.001	1,977	2,168	2,589	2,164	2,256	2,538	1,918	2,008	2,091	2,251	2,326	2,496	2,136	2,038	1,792	3,152	2,882	2,900
10	(A > C > D > B)/(A > B)	0.84	0.75	0.58	0.74	0.68	0.69	0.70	0.66	0.71	0.75	0.69	0.80	0.71	0.73	0.69	0.57	0.55	0.66
11	(B > D > C > A)/(B > A)	0.70	0.66	0.70	0.64	0.63	0.66	0.53	0.56	0.55	0.64	0.63	0.68	0.63	0.63	0.62	0.79	0.76	0.81
12	50% titrate when A/B =	1.24	1.35	1.60	1.38	1.48	1.43	1.34	1.45	1.40	1.25	1.38	1.25	1.32	1.30	1.34	1.52	1.55	1.32
13	75% titrate when A/B =	1.39	1.66	2.15	1.53	1.75	1.70	1.50	1.70	1.53	1.40	1.62	1.38	1.50	1.49	1.54	2.08	2.08	1.65
14	90% titrate when A/B =	1.55	2.09	3.20	1.68	2.02	2.02	1.65	1.95	1.66	1.60	1.95	1.55	1.65	1.70	1.72	2.72	2.80	2.15
15	50% titrate when B/A =	1.39	1.45	1.40	1.52	1.57	1.48	1.46	1.44	1.51	1.30	1.35	1.30	1.44	1.45	1.41	1.26	1.30	1.25
16	75% titrate when B/A =	1.76	1.87	1.70	1.90	1.92	1.87	1.65	1.65	1.70	1.50	1.58	1.50	1.74	1.81	1.69	1.42	1.47	1.47
17	90% titrate when B/A =	2.30	2.60	2.05	2.50	2.35	2.33	1.87	1.85	1.88	1.72	1.80	1.72	2.00	2.14	1.93	1.65	1.70	1.75
18	A/B > 2.00	2,570	2,435	2,284	2,179	2,236	2,262	2,363	2,772	2,640	2,216	2,522	2,570	1,620	1,602	1,446	1,377	1,298	1,063
19	B/A > 2.00	1,556	1,714	1,901	1,790	1,843	1,916	1,351	1,351	1,453	1,373	1,432	1,451	1,382	1,371	1,254	2,008	1,969	2,227
20	A/B > 2.00 (P < 0.001)	2,504	2,393	2,249	2,136	2,197	2,227	2,339	2,757	2,616	2,200	2,508	2,545	1,620	1,602	1,430	1,377	1,290	1,045
21	B/A > 2.00 (P < 0.001)	1,458	1,673	1,883	1,672	1,802	1,901	1,340	1,347	1,443	1,356	1,427	1,437	1,382	1,365	1,238	2,004	1,942	2,146

Row 1 lists the number of genes detected in all four samples for each platform, separated by site. Rows 2 and 3 represent the number of concordantly detected genes for Ā > B̄ and B̄ > Ā, respectively. The sum of rows 2 and 3 for each column is identical to the gene count in row 1. Rows 4 and 5 represent the number of concordantly detected, statistically significant (P < 0.001) genes for Ā > B̄ and B̄ > Ā. Rows 6 and 7 represent the number of detected genes that show the monotonic titration trends Ā > C̄ > D̄ >B̄ and B̄> D̄ > C̄ > Ā. Rows 8 and 9 represent the number of statistically significant (P < 0.001), concordantly detected genes that show the monotonic titration trends Ā > C̄ > D̄ >B̄ and B̄> D̄ > C̄ > Ā. The statistical test used was a two-sample t-test, using equal variance, calculated within each site and comparing log₂ expression values between the independent samples A and B. The gene counts in rows 8 and 9 are also indicated in Figure 2 for each monotonic direction. Rows 10 and 11 translate the previous rows into percentages of genes showing the monotonic titration trend. Rows 12–17 summarize Figure 2 for three specific y-axis values (50%, 75% and 90% of genes titrate at the listed average fold changes). Rows 18 and 19 show the numbers of genes for which Ā/B̄> 2 and B̄/Ā > 2. Rows 20 and 21 show the numbers of statistically significant (P < 0.001) genes used to create the box plots in Figure 4. Columns highlighted in blue, for each platform, represent the manufacturer’s recommended normalization methods used in the main MAQC paper¹³. More detailed gene counts with cross-site intersections can be found in Supplementary Table 1 online.

The quantitative differences between the various curves shown in Figure 2 are listed in Table 1, which presents the ratios at which 50%, 75% or 90% of the detected genes show a monotonic titration response. The performances observed for different sites and platforms were similar but not identical (Table 1). Many different platforms and sites identified the correct ordering of the titration samples for more than 90% of genes with twofold difference between A and B (Table 1, rows 14 and 17), which suggests that the DNA microarrays can reliably distinguish very small-fold differences in the mixture samples. The differences resulting from alternative normalization techniques are also apparent in the results presented in Figure 2 and Table 1.

Measuring titration response as a function of signal intensity

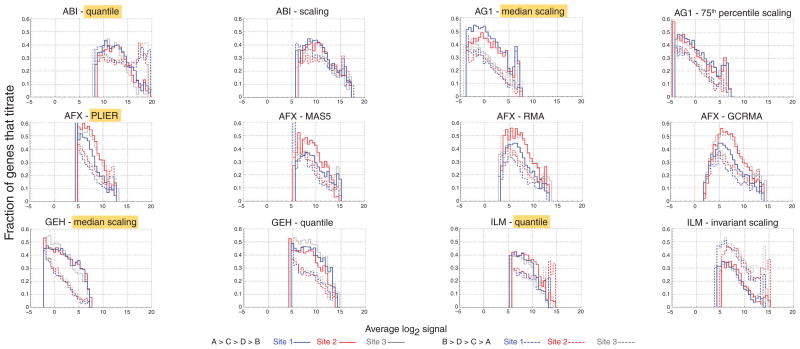
To further explore the impact of different normalization techniques, we assessed titration response as a function of signal intensity. In Figure 3, we plot the fraction of genes that titrate relative to the total number of genes in the given intensity range, as a function of the lowest signal in the monotonic titration trend. That is, for the monotonic trend $\overline{A_i}>\overline{C_i}>\overline{D_i}>\overline{B_i}$, we plotted this fraction against the signal intensity $\overline{B_i}$ (solid lines), whereas for the opposite trend $\overline{B_i}>\overline{D_i}>\overline{C_i}>\overline{A_i}$, we used the intensity $\overline{A_i}$ (dashed lines). We observed that, in general, the fraction of genes that titrate is inversely proportional to the signal intensity. The signal plotted on the x-axis is the lowest signal in the series; therefore, when this signal is low, the probes are more likely to show the expected titration response, as the fold differences will tend to be larger. When the magnitude of this lowest signal increases, the possible fold difference between A and B will decrease.

Figure 3.

Impact of normalization on the distributions of titrating genes as a function of signal intensity. Fractions of genes showing the monotonic titration responses $\overline{A_i}>\overline{C_i}>\overline{D_i}>\overline{B_i}$ and $\overline{B_i}>\overline{D_i}>\overline{C_i}>\overline{A_i}$ are plotted against $\overline{B_i}$ (solid line) and $\overline{A_i}$ (dashed line), respectively. Histograms in each panel represent data from a different platform and normalization technique, separated by site and direction. Normalization methods highlighted in yellow for each platform are the manufacturer’s recommended method used in the MAQC study. Blue, site 1; red, site 2; gray, site 3. The data for these graphs were generated from the set of 12,091 genes common across the platforms that were significantly differentially expressed (P < 0.001) in samples A and B and detected in all four samples (Table 1, rows 4 and 5). All data are plotted on the same scale: the x-axis is normalized signal in log₂ units and the y-axis shows the fraction of titrating probes relative to the total number of probes in the given intensity range. Bin centers are 0.5 apart on the log₂ scale. To avoid spurious oscillations in the lowest and highest signal intensities, we plotted only bins with more than ten genes. Differences between normalization techniques are demonstrated by the differing signal ranges within a platform for the monotonic titration response. The normalization methods highlighted in yellow for each platform represent the manufacturer’s recommended method used in the MAQC main paper¹³.

Differences in distribution among platforms and normalization methods are evident. For ABI, the fraction of genes that titrate follows the same trend as for the other platforms when A > B (Fig. 3, solid lines), but when B > A (dotted lines), these data show a sudden increase in that fraction at high intensity. This effect, although still present, is much less distinct for the scaled than for the quantile-normalized data. We saw improved reproducibility among sites and concordance between the two titration trends in the AG1 75th percentile scaling relative to the median scaling. For the AFX-PLIER data, the signal range across which a titration response is elicited is smaller than for the other platforms and normalization methods, possibly owing to the variance stabilization used in the PLIER method. In all cases, the AFX data show lower percentages for site 1, as in Figure 2. For the GEH data, median normalization results in a very clear distinction between the two different titration patterns; this distinction is moderated by quantile normalization. The data for the ILM rank invariant scaling indicate a larger number of genes showing the titration response $\overline{B_i}>\overline{D_i}>\overline{C_i}>\overline{A_i}$ than showing the opposite trend, a result not seen for any other platform or normalization method. Unlike in Figure 2, the percentage of titrating genes never reaches 100% because, at all signal ranges, some genes show only very small differences in expression across the samples and are more likely to yield a near-random ordering in their titration responses.

Analysis of titration mixtures

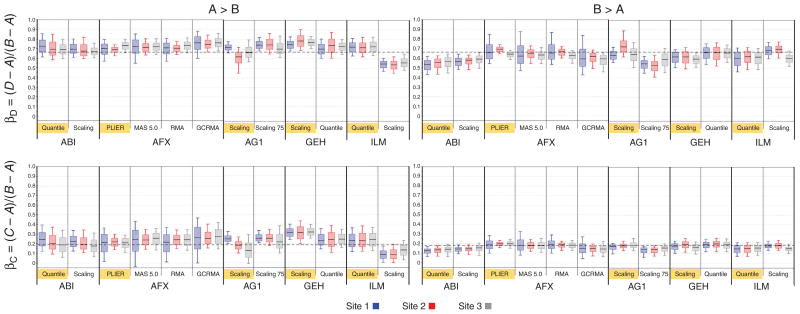
An underlying assumption for this study was that the proportions of each mRNA in the mixture samples (C and D) from each of the original samples (A and B) are equivalent to the mixing proportions of the total RNA. For this assumption to be true, the fractions of each mRNA in the total RNA samples A and B had to be the same and had to be processed by the various biochemical systems with equal efficiencies. Using mathematical modeling, we investigated whether we could derive the relative mRNA contents of the two independent samples using the microarray data from the independent and titration samples (see Methods). Such modeling defines the true fractions of mRNA derived from sample A in titration samples C and D as α_C and α_D, and the true fractions of mRNA derived from sample B in titration samples C and D as β_C and β_D (see Box 1 and Supplementary Fig. 5). Figure 4 shows the results of this modeling for all the platforms and normalization methods, with the y-axes representing the estimates of β_C (bottom) and β_D (top). The lower charts show median values of β_C centered on 0.18 but usually larger for $\overline{A_i}>\overline{B_i}$ (left) than for $\overline{B_i}>\overline{A_i}$ (right), and the upper charts show median values of β_D centered on 0.67. These deviations from the expected values of 0.25 and 0.75 based on the 3:1 mixtures of total RNA suggest that the mRNA concentrations of the A and B samples were not identical. From these results, we estimate the mRNA concentration in the B sample to be approximately two-thirds of the concentration in the A sample (see Box 1). An empirical evaluation of mRNA content in samples A and B is consistent with our estimates of 3% and 2%, respectively (see Methods).

Box 1. Modeling of titration mixtures.

Ideally, the mRNA expression levels of each gene in samples C and D may be mathematically expressed as

$$C={\alpha }_{\text{C}}A+{\beta }_{\text{C}}B\text{and}D={\alpha }_{\text{D}}A+{\beta }_{\text{D}}B,$$

where A and B are the measured mRNA abundances of the gene in samples A and B, respectively, and α_C, β_C, α_D and β_D are the mixture coefficients. If we impose the requirement that

$${\alpha }_{\text{C}}+{\beta }_{\text{C}}=1$$

and

$${\alpha }_{\text{D}}+{\beta }_{\text{D}}=1(\text{if}A=B,\text{then}C=A=B=D),$$

then elementary algebra can be used to derive simple formulas for β_C and β_D:

$${\beta }_{\text{C}}=(C-A)/(B-A)$$

and

$${\beta }_{\text{D}}=(D-A)/(B-A).$$

If the mRNA fractions in samples A and B are identical and the normalization of samples A, B, C and D exactly the same, then the measured fraction should be centered on the ideal mixture fractions of β_C = 0.25 and β_D = 0.75 (implying α_C = 0.75 and α_D = 0.25). However, different mRNA concentrations in the A and B samples and differences in the normalization of the four samples for different platforms, sites and normalization methods can lead to deviations from these expected values (Fig. 4). For example, if the mRNA fractions for the A and B samples (termed a and b, respectively) are unequal (a ≠ b), then

$$C=((0.75a)A+(0.25b)B)/(0.75a+0.25b)$$

and

$$D=((0.25a)A+(0.75b)B)/(0.25a+0.75b).$$

We can express the true ratios of the B to A mRNA fractions,

$$b/a=3{\beta }_{\text{C}}/(1-{\beta }_{\text{C}})={\beta }_{\text{D}}/3(1-{\beta }_{\text{D}})$$

(see Supplementary Fig. 5). Using the empirical measurements of β_C and β_D, we can then estimate these true mRNA fractions. For example, if the B fraction of sample C is β_C ≈ 0.18, as indicated by microarray median values in Figure 4 (bottom), then we can deduce that the true ratio of mRNA fractions b/a is approximately 2:3. Moreover, these results predict that

$${\beta }_{\text{D}}=9{\beta }_{\text{C}}/(1+8{\beta }_{\text{C}})\approx 0.67,$$

which is consistent with the empirical microarray results in Figure 4 (top).

Figure 4.

Titration-response concordance for each commercial whole-genome microarray platform, using different normalization methods, with data from each platform separated by site and fold-change direction. Data shown are from the 12,091 genes common across whole-genome platforms. Box plots were generated in cases where a gene was detected across all samples per site and had a statistically significant (P < 0.001) A/B ratio >2 in the direction indicated. A two-sample t-test, with equal variance, was performed within each site on log₂ expression values. Data for each site were split by direction of fold change: left, genes where A/B > 2; right, genes where B/A > 2 (all differences significant, P < 0.001, for both directions). Number of genes used for each box plot is indicated by individual site counts in Table 1 (rows 20 and 21). Each box represents the interquartile range, with median marked by a horizontal black line and 10th and 90th percentiles marked by the outer whiskers. Blue, site 1; red, site 2; gray, site 3. The horizontal dashed black lines represent expected values assuming 3% and 2% mRNA abundance levels for samples A and B, respectively. In other words, when the mRNA/total RNA fraction in A is equal to 3% and in B is equal to 2%, then β_C = (C − A)/(B − A) = 0.18 (bottom two charts) and β_D = (D − A)/(B − A) = 0.67 (top two charts). Refer to Box 1 for further details. Normalization methods highlighted in yellow for each platform represent the manufacturer’s recommended method used in the MAQC main paper¹³.

The values calculated from the different platforms and normalization methods are generally similar, with two clear exceptions. For ILM, invariant scaling results in much lower estimates for β_C and β_D than the other platforms and normalization methods when A > B (left side) but not when B > A. This difference is consistent with the results noted for the titration response (Figs. 2 and 3). For ABI, the estimates of β_C and β_D are consistent with the other platforms when A > B but lower than the other platforms when B > A. This result was seen with both normalization methods, although to different extents, and may be related to the differences noted in Figure 3. The deviations for β_C and β_D are particularly noteworthy because of the relatively small errors of the ABI data in this analysis.

The individual microarray measurements for the titration coefficients shown in Figure 4 indicate that normalization and data-processing differences are not the primary cause for the deviations from the theoretical values. Differences in mRNA abundance contribute to these deviations and may not be circumvented with normalization alone. Additionally, further analysis of microarray measurements from these titration mixtures may provide greater-resolution observations of the global tendency (Fig. 4) of estimates of β_C and β_D to be larger for A > B than for B > A (see Supplementary Fig. 1 online).

Effects of outlier data

During execution and analysis of the MAQC study, the consortium identified one outlier site and multiple outlier arrays on the basis of objective criteria of data quality¹³. In some cases, we evaluated the effects of not censoring such data from the analysis. The results (data not shown) were as expected: inclusion of low-quality data degraded both intra- and intermethod reproducibility. This result, although predictable, is nonetheless noteworthy because microarray experiments are expensive and are sometimes used to analyze samples that are available in very limited quantities. Low-quality microarray data are discarded with great pain. It is therefore important that the community develop shared standards of microarray data quality to allow use and interpretation of less-than-perfect data while preventing overinterpretation. The well-characterized RNA samples and all of the data (including outliers) produced by the MAQC study are a good start on the road to such data-quality standards. In particular, the titration experimental design used in this work may prove to be an important tool for developing such standards, as the experiments can be interpreted using a small number of plausible assumptions.

DISCUSSION

The MAQC titration study was conceived as an experiment that could be implemented across several platforms, with a minimum of assumptions. One of the initial goals of the titration study was to assess relative accuracy by comparing observed expression in the titration samples with the expression expected on the basis of the known mixing ratios of the two independent samples. This analysis proved to be more complex than originally anticipated, largely owing to the effects of different mRNA fractions in the two independent samples. However, the qualitative expectation of a particular signal ordering is still valid and provides a sensitive tool for differentiating microarray platform performance and normalization methods. As the measurement of titration response illustrates, different platforms and data analysis methods have slightly different performance optima: design and processing choices that increase the number of detected genes also tend to increase noise in the titration series. In addition to differences in the number of genes analyzed, the variations seen in Figure 2 and Table 1 can also result from differences in expression-ratio compression (leading to different ratios observed for any given gene) as well as levels of noise in each measurement. In general, the behaviors of various sites and platforms are quite similar.

The analysis of the titration mixtures reveals some interesting observations about the data. These results show asymmetry in the titration responses (Figs. 2 and 3) and the estimates of the true fractions of mRNA in the titration samples (Fig. 4). This asymmetry may be caused in part by additional differences in the normalization of the A and B samples (Supplementary Fig. 1), may relate to more difficulty in distinguishing A and C at low signal or may be a consequence of nonlinearity in the signal response relative to the concentration amounts (Supplementary Fig. 2 online). In addition, the results presented here demonstrate that the mRNA content of the two independent samples is not equal. This conclusion is supported by additional lines of evidence. First, an apparent power analysis^27–30 (Supplementary Figs. 3 and 4 online) is asymmetric between the sample pairings (A, C) and (B, D). This asymmetry is probably the result of the A sample being more similar to C than B is to D. Second, the slopes of the linear trends for the titration sample/independent sample ratios (Supplementary Fig. 1) suggest that the ratio of sample A to B in sample C differs from the expected value from the total RNA ratios. Third, external spike-in RNA controls were included for several platforms; these controls were amplified and labeled along with the sample RNA and indicate that the A sample contains a higher percentage of mRNA relative to the B sample³¹. Finally, a preliminary empirical analysis of mRNA content in the A and B samples (see Methods) confirmed that the mRNA content differs between the samples.

The discovery of a difference in the mRNA content of samples A and B has important implications for the future use of these commercially available samples in method calibration, proficiency testing and other activities requiring well-characterized, complex RNA. As a result of the MAQC study, these samples are probably the best-characterized complex RNA preparations available. The RNA-measurement community should complete the characterization of these samples by more accurately measuring the fraction of mRNA in each preparation, so that the scientific community can make better use of this resource.

The utility of the titration samples for assessing normalization and data preprocessing methods can be seen throughout the analyses presented here. Notably, for all platforms except AFX and ILM, the performance of the MAQC ‘standard’ normalization or data preprocessing method was slightly inferior to that of the secondary method, especially in the apparent power analysis (Supplementary Fig. 3). This result highlights the observation noted throughout this study that data processing methods determined to be optimal under one set of circumstances may not always prove appropriate under all conditions, particularly if primary assumptions underlying those data processing methods are violated.

A great strength of the design presented here is that, despite the added complexities of varying mRNA content, the qualitative expectation of a particular signal ordering is still valid, provided that the different data sets are properly scaled relative to one another. Therefore, this design is very valuable for assessing microarray performance. Specifically, as we have shown here, the titration response can be used to distinguish between normalization methods that are sensitive to changes in mRNA fraction and methods that are robust despite such changes. One observation of this study is that the robustness of a normalization method depends in part on the subset of data used to determine the scaling constant or function. Our results indicate a path toward objective optimization of this normalization set. The differences in gene expression among samples may be greater and the variability across replicates may be smaller in this study than in typical biological experiments; nonetheless, the lessons learned regarding the use of titration mixtures to evaluate the performance and normalization of large-scale gene-expression measurements may have widespread application in more realistic settings. In addition, the wide range of gene expression in these samples probably served to amplify data processing–derived differences that would have been more difficult to detect in analyses of more closely matched samples.

Finally, it should be noted that the majority of genes considered here yielded very similar behavior across all platforms, in spite of the complications noted in this manuscript. Therefore, these results should be considered a testament to the underlying strength of all of the methods examined. Improvement of mRNA quantification methods remains an important objective, and the MAQC study has produced samples and data that will aid the community in making such improvements. The concordance of data presented here demonstrate that the methods used are sound and, when properly implemented and interpreted, can be used to measure expression levels of thousands of RNA targets simultaneously.

METHODS

Preparation of the RNA sample titrations

RNA samples are described in detail in the main MAQC paper¹³. Briefly, two commercially available total RNA solutions and 3:1 and 1:3 mixtures were chosen at the outset by the members of the MAQC project. For simplicity, these samples were designated as A, B, C and D. A and B are independent total RNA samples. A is derived from a collection of ten human cell lines and B from human brain tissue. Sample A is sold commercially under the name Universal Human Reference RNA (Catalog number 740000, Stratagene). Sample B is sold commercially under the name FirstChoice Human Brain Reference RNA (Catalog number 6050, Ambion).

RNA titration samples were generated once for all MAQC experiments (Fig. 1), with samples A and B at equal concentrations as measured by A₂₆₀. Sample C was made by mixing sample A with sample B at a volumetric ratio of 75:25, and sample D was made by mixing sample A with sample B at a volumetric ratio of 25:75.

Normalization methods used in this study

For ABI, we used quantile normalization¹⁷ independently for each test site and 90% trim mean scaling. For trim mean scaling, the signals for highest 5% and lowest 5% are removed, and the remaining 90% of signals are used to calculate the mean. The mean of each array is scaled to the same level, and the scaling factor for each array is used to scale the signals. The trim mean scaling was calculated independently for each test site.

For AG1, the data were transformed so that signal values below 5 were set to 5. After this transformation, each measurement was divided by the median of all detected measurements in that sample (for median scaling) or by the 75th percentile of all measurements in that sample (for 75^th percentile scaling).

For AFX data, we used PLIER²¹, MAS 5.0, RMA¹⁸ and GCRMA²⁷ for data preprocessing and normalization. The PLIER method produces a summary value for a probe set by accounting for experimentally observed patterns in feature behavior and handling error appropriately at low and high abundance. PLIER accounts for the systematic differences between features by means of parameters termed feature responses, using one such parameter per feature (or pair of features, when using mismatch (MM) probes to estimate cross-hybridization signal intensities for background). Feature responses represent the relative differences in intensity between features hybridizing to a common target. PLIER produces a probe-set signal by using these feature responses to interpret intensity data, applying dynamic weighting by empirical feature performance and handling error appropriately across low and high abundances. Feature responses are calculated using experimental data across multiple arrays. PLIER also uses an error model that assumes error is proportional to the observed intensity rather than to the background-subtracted intensity. This ensures that the error model can adjust appropriately for relatively low and high abundances of target nucleic acids. Here, PLIER was run with the default options (quantile normalization and PM-MM) with the addition of a 16 offset to each expression value¹³.

The AFX MAS 5.0 algorithm is a method for calculating probe-set signal values. The MAS 5.0 algorithm is implemented on a chip-by-chip basis and is not applied across an entire set of chips. The signal value is calculated from the background-adjusted PM and MM values of the probes in the set using a robust biweight estimator. Here, MAS 5.0 is implemented with default options, and global scaling (96% trim mean) is used for normalization.

RMA¹⁸ fits a robust linear model to the probe-level data and conducts a multichip analysis. The algorithm includes a model-based background correction, quantile normalization and an iterative median polishing procedure to generate a single expression value for each probe set. GCRMA substantially refines the RMA algorithm by replacing the model for background correction with a more sophisticated computation that uses each probe’s sequence information to adjust the measured intensity for the effects of nonspecific binding, according to the different bond strengths of the two types of base pairs. It also takes into account the optical noise present in data acquisition. Both RMA and GCRMA were implemented using the ArrayAssist Lite package with default settings (Affymetrix; http://www.affymetrix.com/products/software/specific/arrayassist_lite.affx).

For GEH data, we compared median scaling and quantile normalization. For the median-scaling approach, each measurement was divided by the median of all measurements within each array. Therefore, the median signal is scaled to 1 for each array. The quantile normalization approach¹⁶ was applied to log₂-transformed expression values across all samples and replicates within each site.

For ILM data, we compared quantile normalization¹⁶ with the addition of 15 counts of offset to each probe signal¹³ and normalization by a robust least-squares fit of rank-invariant genes. For the latter normalization method, array data corresponding to sample A were averaged and used as a reference on each site independently. Signals from each array in the experiment were compared to the reference, and probes with relative rank changes of less than 5% (only probes ranked between the 50th and 90th percentiles were included) were considered to be rank invariant. Normalization coefficients were computed with iteratively reweighted linear least squares using the Tukey bisquare weight function. Background signal, estimated as the mean signal of negative controls, was subtracted before normalization. Each ILM array contains approximately 1,600 negative control probes, which are thermodynamically equivalent to regular probes but do not have specific targets in the transcriptome. Gene signals were ranked relative to signals of negative controls, and the detection flag was set to present if gene signal exceeded 99% of signals of negative controls.

Purification of mRNA to empirically determine abundance in samples A and B

In a follow-up experiment, mRNA was isolated from 100 μg of samples A and B total RNA in duplicate using the Absolutely mRNA purification kit (Stratagene) according to the manufacturer’s protocol. Briefly, 50 μl of mRNA oligo (dT) magnetic particles were combined with 100 μl of total RNA and washed four times, and mRNA was eluted with 100 μl elution buffer. mRNA quantity and quality were evaluated by ND-1000 NanoDrop spectrophotometer (NanoDrop Technologies) and Agilent 2100 Bioanalyzer with RNA 6000 Nano LabChip Kit (Agilent Technologies). This empirical evaluation of mRNA content in each 100 ng of total RNA produced an average yield of 2.870 ± 0.095 ng for sample A and 2.003 ± 0.124 ng for sample B (mean ± s.d.).