Abstract
The diversity of experimental designs that can be used with functional magnetic resonance imaging (fMRI) has played a key role in its widespread application to studies of human cognition. This flexibility is possible because the fMRI response to external stimuli is remarkably well approximated as the response of a linear time variant system. The experimental demonstration of this property provided the foundation for the development of event-related designs, in which the fMRI response is modeled as the linear summation of the hemodynamic response to discrete events. Building upon prior work from the fields of engineering, neuroscience, and statistics, researchers in the field have created a rich collection of event-related designs and developed a rigorous theoretical framework for characterizing and optimizing the performance of designs. Ongoing challenges include the optimization of designs in the presence of experimental constraints and the development of more time-efficient optimization algorithms.
Keywords: fMRI, experimental design, efficiency, event related
INTRODUCTION
Event-related designs are now a standard part of the fMRI experimental repertoire. The paper by Scott Huettel in this issue provides an excellent discussion of the importance of event-related designs for cognitive neuroscience. In this paper, I will review the technical development of designs for event-related fMRI. In the spirit of this special issue of NeuroImage, in addition to describing the overall arc of the technical development of experimental designs for fMRI, I will also provide a bit of personal perspective on some of the challenges faced and insights gained along the path.
One can trace the birth of event-related fMRI design to the work of (Blamire et al., 1992), which appeared in the same year that the first papers demonstrating human fMRI were published. This work showed that one could measure the fMRI response to brief stimuli that were widely spaced and provided an early example of what is now commonly referred to as the hemodynamic response function. It was also the first example of a slow event related design in which the wide spacing between stimuli allowed the experimenter to isolate the responses to individual stimuli. Such designs have been used to measure the brain response to isolated events (McCarthy et al., 1997), and have also been a standard tool for basic studies of the dynamics of the hemodynamic response (Behzadi and Liu, 2006; Huettel et al., 2001).
One of the key advances needed for the progression to more complex designs was the introduction of the convolution model for fMRI analysis by (Friston et al., 1994). This framework was subsequently extended to the analysis of slow event related fMRI experiments (Josephs et al., 1997). A key assumption of these studies was that the fMRI signal could be modeled as the output of a linear time invariant system. The seminal work of (Boynton et al., 1996) provided the field with the experimental data showing that the assumption of linear time variance was reasonable. Additional support for this assumption was subsequently provided by (Dale and Buckner, 1997).
Selective averaging and rapid presentation rates
The demonstration of linearity gave researchers in the field the confidence to explore fast event related designs in which the hemodynamic responses from different stimuli could overlap. The initial step was taken by (Dale and Buckner, 1997), who demonstrated the ability to obtain robust activation maps when using left and right-hemifield visual checkerboard stimulus presented in a random order and spaced as little as 2 seconds apart. Adopting a key concept from prior work on selective averaging of event-related potentials, the authors counter-balanced the presentation of the stimuli so that in forming the average BOLD response for a desired trial type (e.g. left hemifield stimulus) the contributions from all other trial types (e.g. right hemifield stimulus) would average out. (Clark et al., 1998) used a similar approach to show that experiments with rapid presentation rates (2 second spacing) could be used to distinguish responses in higher-order cortical areas for a study of face perception and memory. Building upon this prior work, (Burock et al., 1998) obtained convincing visual BOLD responses using randomly ordered stimuli spaced only 500 ms apart. In their work, they made use of “non-events”, which were defined as periods in the stimulus sequence that contained a fixation condition, such as a blank screen with a small central fixation cross (Buckner et al., 1998). The estimate of the hemodynamic response for a stimulus was obtained by subtracting the event-related average of the non-event trials from the average of the event types of interest. These non-events have also been referred to as null events, which is the terminology that has been more widely adopted (Friston et al., 1999).
Optimizing Design Performance
The promising results obtained with randomized event-related designs led researchers in the field to ask what type of design was optimal. Was it a design with randomized rapid presentation of events or a periodic single trial design in which the spacing between stimuli was fixed and on the order of the length of the hemodynamic response? How did these event-related designs compare to the more traditional blocked design? In 1999, three related efforts used the framework of the general linear model to provide some initial answers to these questions (Dale, 1999; Friston et al., 1999; Josephs and Henson, 1999). The performance of a design was defined as its statistical efficiency, which is inversely proportional to the variance of the experimental contrasts of interest. This definition of efficiency was equivalent to the A-optimal definition of efficiency that had long been used in the statistical literature (Seber, 1977).
With the introduction of this formal measure of efficiency into the fMRI literature, a firm basis was established for the rigorous comparison of various experimental designs. And yet the papers published in 1999 seemed to differ on what constituted an optimal design. The work of (Dale, 1999) concluded that efficiency was maximized with designs in which the stimuli were presented in a randomized manner, with efficiency increasing as the spacing between stimuli was decreased. In contrast, while (Friston et al., 1999) also found that the efficiency of a randomized design increased with decreased stimulus spacing, they concluded that the most efficient design was obtained with a conventional block design.
This apparent contradiction was addressed in an abstract that Buxton and colleagues presented at the Human Brain Mapping meeting in San Antonio in June of 2000 (Buxton et al., 2000). They pointed out that the efficiency for detecting an activation when the shape of the hemodynamic response is known was distinctly different from the efficiency for estimating the shape of an unknown response. Now it should be noted that (Friston et al., 1999) had already mentioned this range of potential knowledge with regards to the hemodynamic response and advocated the use of temporal basis functions to gracefully model varying assumptions about the shape of the response. However, the examples in their paper focused on modeling the hemodynamic response with either one or two basis functions, which corresponded to assuming a great deal of knowledge about the shape of the response. In contrast, (Dale, 1999) had used an finite impulse response model of the hemodynamic response in which the basis functions are the Kronecker delta functions (e.g. unit impulse functions) and the number of basis functions is equal to the number of points in the estimated response. The use of this model corresponded to making no assumptions about the response shape, other than assuming the length of the response.
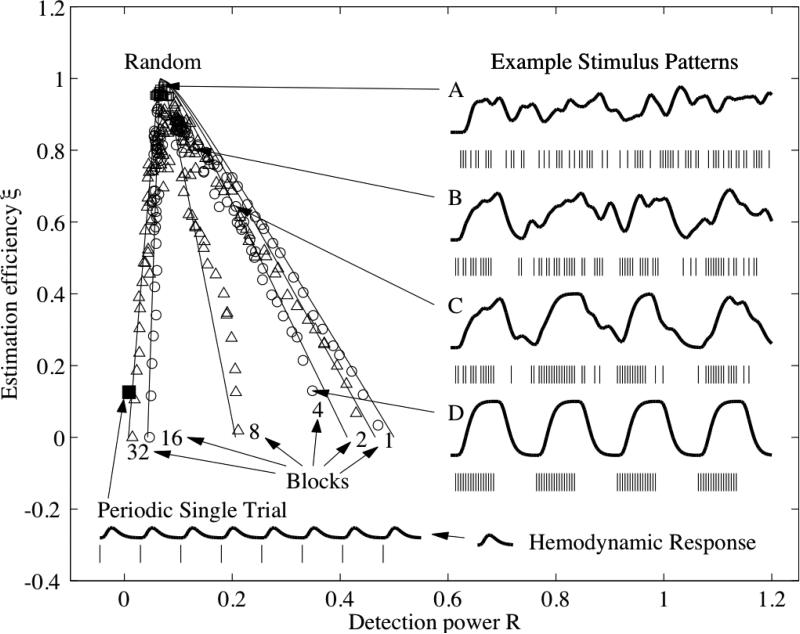
After pointing out the distinction between the two types of efficiency, Buxton et al. went on to demonstrate the trade-off between these two types of efficiency using a plot similar to that shown in Figure 1. In the plot the efficiency for detecting an activation with an assumed shape for the hemodynamic response is referred to as detection power, while the efficiency for estimating an unknown shape is referred to as estimation efficiency. Because the lines demonstrating the trade-offs resembled tentacles dangling from a central point, these types of plots were referred to as “jellyfish” plots by members of the UCSD MRI Physics group, which included Rick Buxton and myself at the time. When Rick first showed me his preliminary results in early 2000, I was struck by the geometric structure of the jellyfish and thought it would be interesting to look for a mathematical explanation for the structure.
Figure 1.
The fundamental trade-off between estimation efficiency and detection power. Each of the symbols indicates the estimation efficiency and detection power for a particular design. The solid lines are based on the theory developed in (Liu et al., 2001), where this figure was first presented. Example stimuli and responses based on permutations of a 4-block design are shown on the right-hand side. A is a random design, B and C are semi-random, and D is the block design. The performance and stimulus pattern for a periodic single trial experiment are shown in the lower left-hand corner.
In searching for a suitable framework, I relied heavily on prior knowledge in the areas of estimation efficiency from the statistical literature (Seber, 1977), sub-space based approaches to signal estimation and detection from the electrical engineering literature (Scharf and Friedlander, 1994) and quadratic forms and the Rayleigh quotient from my undergraduate linear algebra textbook (Strang, 1980). Integrating these concepts with the intuition provided by the jellyfish plots led to the understanding that the observed trade-off between detection power and estimation efficiency was indeed fundamental. In addition, this trade-off could be modeled by varying the spread of the eigenvalues of the Fisher information matrix XTX formed from the design matrix X used in the general linear model (Liu et al., 2001). An equal spread of eigenvalues provides optimal efficiency when one wants to estimate the shape of the hemodynamic response, while concentrating a design's energy into one dominant eigenvalue is optimal when one wants to detect an activation with an assumed hemodynamic response shape. These two limits correspond to randomized and block designs, respectively. In between these two limits, there is a wide range of other possible designs that offer various trade-offs between detection power and estimation efficiency, such as the dynamic stochastic designs proposed by (Friston et al., 1999), the semi-random and mixed designs in (Liu et al., 2001), the varying stimulus duration designs of (Birn et al., 2002), and the probability distribution based designs of (Hagberg et al., 2001). A geometric interpretation of the fundamental trade-off is provided below.
Extension to Multiple Trial Types and the Importance of m-sequences
Once the fundamental trade-off between detection power and estimation efficiency had been demonstrated for experimental designs containing one trial type plus a null event (e.g. a simple design with visual flicker as the trial type and a fixation cross as null event), the next logical step was to see if this trade-off held for designs with multiple trial types. Although preliminary simulations indicated that the trade-off observed for designs with multiple trial types was similar to that found for single trial types, it wasn't clear how to demonstrate this from a mathematical viewpoint. After several brief attempts in 2000 and 2001, I finally decided in the summer of 2002 to make a concerned effort towards extending the mathematical framework to handle multiple trial types. It turned out that a key step was to approximate the Fisher information matrix as the Kronecker product of two matrices -- one matrix representing the average auto-correlation (across trial types) of the experimental designs and the other matrix containing information about the cross-correlation between designs from different trial types (Liu and Frank, 2004). With this approximation, it could be shown that the theoretical trade-off between detection power and estimation efficiency was independent of the number of trial types. Thus, the basic framework that had been developed for single trial type designs could be readily extended to multiple trial type designs. An unexpected bonus of the extension of the framework to handle multiple trial types was the ability to derive an expression for the optimal frequency of occurrence for presentation of stimuli. This expression showed that the optimal frequency depended on the relative importance assigned to estimation of individual events versus pair-wise contrasts and provided a rigorous justification for the inclusion of null events.
An important difference between single trial type and multiple trial type designs was pointed out by Giedrius Buracas who was experimenting with m-sequences at the Salk Institute. He found that event-related designs based upon m-sequences could generally provide greater estimation efficiency as compared to designs based upon random search (Buracas and Boynton, 2002). For single trial type designs, the advantage offered by m-sequences is not typically that great since a random search can usually return a design that offers nearly optimal estimation efficiency (Liu et al., 2001). However, as the number of trial types grows, the space of possible designs expands rapidly and it becomes increasing unlikely that a random search can find a design that is even close to optimal (Liu, 2004). To make this point clear, consider going from a design with 1 trial type to a design with 4 trial types. Assuming a null trial type is included in each design and that each design has 100 timepoints, then there are approximately 1040 times more possibilities for the 4 trial type design. In contrast to designs based on random search, m-sequences can come very close to achieving the theoretical upper bound on estimation efficiency because of their nearly optimal autocorrelation properties (Liu, 2004). The advantageous properties of m-sequences have also made them a good starting point for designs that attempt to achieve flexible tradeoffs between estimation efficiency and detection power, such as the clustered m-sequence designs of (Liu, 2004) and the genetic algorithm based designs discussed below.
Modeling assumptions with basis functions
A deeper understanding of the trade-offs inherent in fMRI design can be gained by revisiting the work of (Friston et al., 1999), who pointed out that the use of basis functions allows us to flexibly describe our assumptions about the shape of the hemodynamic response. If we assume that the shape is completely known, then there is just one basis function that is equal to the assumed shape. The main drawback to making this assumption is that the shape of the hemodyanmic response can vary greatly between subjects (Aguirre et al., 1998) and can be altered by modulation of the baseline vascular state due to factors such as age, disease, or medication (Cohen et al., 2002; D'Esposito et al., 2003). As a result, a design that is optimized for one assumed shape can perform quite poorly if the actual response differs significantly from what is assumed (Liu et al., 2001).
On the other hand, if we assume no knowledge of the response shape, then as discussed above, the basis functions are simply the Kronecker delta functions (i.e. unit impulses), with one basis function for each point in the response. However, this is an overly conservative assumption, since there is quite a lot of prior knowledge about the shape of the hemodynamic response. For example, the vast majority of hemodynamic responses that have been observed over the past twenty years are smooth functions that rise and fall with transitions lasting several seconds or more. This prior knowledge can be captured through the use of a set of smooth basis functions, such as the gamma density function and its temporal derivatives (Friston et al., 1999). All possible hemodynamic responses are then assumed to live within the space spanned by these basis functions. By choosing a limited number of basis functions, one can achieve a significant gain in estimation efficiency, since the number of parameters that needs to be estimated is greatly reduced. When it is assumed that the response may be represented by smooth basis functions, the optimal design lies somewhere between the block design that is optimal when there is just one basis function and the fully randomized design that is optimal when the basis functions are unit impulses (Liu, 2004).
Despite the advantages of using basis functions and the availability of sophisticated processing approaches (Woolrich et al., 2004), their adoption for estimating response shapes in event-related fMRI has been limited. I believe this is partly due to concern about the bias introduced by potential misspecification of the basis functions. This bias occurs when the shape that one wants to estimate does not lie within the space spanned by the basis functions. Although hemodynamic responses are generally smooth functions, they can exhibit interesting features that may not be captured by a limited set of basis functions.
The Geometry of fMRI Designs
As the mathematics underlying fMRI design can sometimes be a bit daunting, I have found it helpful over the years to use geometric arguments to understand the basic principles. To develop a geometric picture, we start with the general linear model y = Xh + n where y is the observed fMRI time series, X is the design matrix that contains the stimulus timing information, h is the hemodynamic response function, and n represents additive noise. For any given level of additive noise, the optimal design will be the one that maximizes the energy of the desired signal component Xh. In the case where we assume full knowledge of h, we simply need to find the design matrix that maximizes Xh. However, in the cases where there is either no knowledge or only partial knowledge about the hemodynamic response, there will be a range of possible values for Xh and our goal is to find the design matrix that maximizes the minimum value. To achieve this goal, it is helpful to first review what a matrix does.
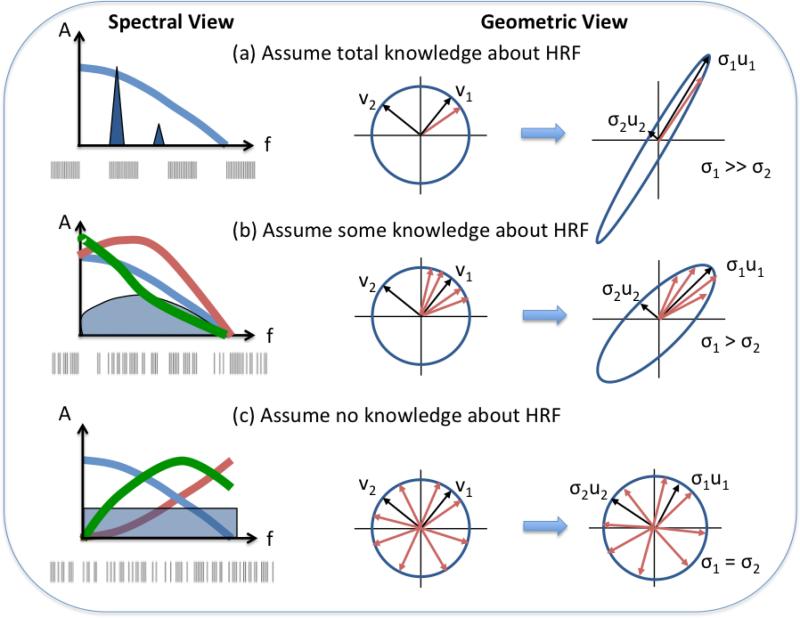
As discussed in detail in (Trefethen and Bau, 1997), we can think of any m × n matrix X as an operator that stretches a unit sphere within an n-dimensional space into a hyper-ellipse within an m-dimensional space. In two dimensions, the unit sphere is a unit circle and the hyper-ellipse is an ellipse. As shown in middle column of Figure 2, the principal semi-axes of the unit circle are given by the right singular vectors vi of the matrix X. These semi-axes are transformed by the matrix into the principal semi-axes of the ellipse, where the length of each semi-axis is given by the corresponding singular value σi. In mathematical notation, multiplying each right singular vector by the matrix produces the scaled vector σiui = Xvi where ui denotes the ith left singular vector. Essentially, the matrix stretches the unit circle into the ellipse, where the amount of stretching along each axis is specified by the singular values. Note that the singular values are simply the square roots of the eigenvalues of the Fisher information matrix presented in a previous section.
Figure 2.
Geometric and spectral views demonstrating the principles underlying optimal fMRI design. (a) When full knowledge of the shape of hemodynamic response function (HRF) is assumed , then the HRF is represented by the single red vector in the unit sphere. The optimal design will maximally amplify this vector, while minimizing the gain in other directions. This transforms the unit circle into a narrow ellipse. In the spectral domain, the HRF spectrum is fully specified (blue line), and the optimal design will place a spectral peak near the maximum of the spectrum. This is typically achieved with a block design , similar to the example design shown below the spectrum. (b) When some knowledge of the HRF shape is assumed (e.g. with the use of a limited set of basis functions), then the possible HRF vectors span a sector within the unit circle. The optimal design will focus on amplifying vectors within the sector, transforming the unit circle into an ellipse. In the spectral domain, there is a range of similar HRF spectral shapes, and the optimal design will tend to have a broadband spectrum (blue shaded area) that has relatively more energy where the average HRF spectra overlap. This is achieved with a semi-random design. An example design is shown below the spectrum. (c) When no knowledge of the HRF shape is assumed, then the possible HRF vectors span the entire unit circle. The optimal design must equally amplify all directions, such that the unit circle is transformed into another unit circle. In the spectral domain, there can be widely varying HRF spectral shapes, and the optimal design must therefore place equal energy at each frequency. This is achieved with a random or m-sequence design, as shown below the spectrum.
To apply this understanding to fMRI experimental design, we first have to consider how our assumptions about the hemodynamic response map onto the unit circle. Under the assumption of perfect knowledge of the hemodynamic response, the response is represented by a single vector h with a specific orientation within the unit circle (shown by the red vector in the middle column of Figure 2a). The response Xh will be maximized when the right singular vector v1 closest to h has the largest singular value σ1, so that the portion of the unit circle in this direction is maximally “stretched”. At the same time all other singular values are minimized, resulting in a design matrix that takes the unit circle into a very skinny ellipse. In contrast, when there is no knowledge about the shape of the response, then the response can be represented by any vector terminating on the surface of the unit circle (shown as red vectors in the middle column of Figure 2c). Because there is no preferred orientation, we should stretch all right singular vectors equally, such that the unit circle is simply transformed to another unit circle. This equal stretching of directions occurs when all the singular values are the same. When basis functions are used to express some knowledge about the shape of the response, then the vector h lies within a subset of the unit circle (shown as vectors spanning a sector of the circle in the middle column of Figure 2b). The optimal design will amplify vectors within the subset and lies between a design with one dominant singular value and a design with equal valued singular values.
Spectral Interpretation
Because the spread of the singular values is related to the shape of the power spectrum of the design (Haykin, 1996), there is a corresponding spectral interpretation of fMRI designs (see lefthand column of Figure 2). A design with a dominant singular value, such as a block design, will have a dominant peak in its power spectrum which allows it to concentrate most of its energy at a single frequency. On the other hand, a design with equally spread eigenvalues corresponds to a flat power spectrum. Under the assumption that we know nothing about either the shape or spectrum of the hemodynamic response, this design is optimal because it spreads the energy equally across all frequencies. When basis functions are used, the spread of the singular values results in a power spectrum that lies between a perfectly flat spectrum and a spectrum with a few dominant peaks (see Figure 2b). Such a design will attempt to place the majority of its energy in a band of frequencies where there is the greatest overlap of the spectra of the expected hemodynamic responses. Although beyond the scope of this paper, the spectral and geometric interpretations of optimal design can also be extended to aid in the understanding of the effects of correlated noise (Liu and Frank, 2004).
Genetic Algorithms
The mathematical framework that has been developed for fMRI design tell us what levels of performance are achievable, but except for a few limiting cases (such as m-sequences and block designs), can only provide general guidance on how to generate additional designs (e.g. clustered m-sequences). These designs can achieve various trade-offs between efficiency and power, but are not guaranteed to find optimal points within the large search space. In addition, the basic framework does not provide predictions of how the performance may be affected by key experimental factors, such as non-linearities in the BOLD response or the inclusion of additional constraints on the experimental design. As an example of the latter factor, in many event-related experiments, there exists a constraint on the order of the different trial types - e.g. a probe event is always be followed by a distractor event, which is then followed by a decision event. This constraint limits the space of possible designs. An extension of the currently available framework to predict the optimal performance in the presence of the constraints would be useful.
A practical approach to finding optimal fMRI designs is the genetic algorithm design method first proposed by (Wager and Nichols, 2003). This method allows the experimenter to specify all of their assumptions and constraints as well as their desired performance criteria, which can include multiple objectives. The performance of the genetic algorithm method has been recently improved by (Kao et al., 2009), and the improved algorithm has been applied to generate designs that are optimal for linear estimation in the presence of uncertainty in the noise autocorrelation structure (Maus et al., 2010) and for nonlinear estimation of hemodynamic response parameters (Maus et al., 2011). The genetic algorithm approach can take advantage of known good designs, such as block designs and m-sequences, as starting points. The resultant designs will typically perform better than those found through random search, especially when the search space is large, as is the case for multiple trial type designs. A disadvantage of this approach has been the long time required to search for optimal designs, but recent work indicates that significant reductions in search time may be possible with improved algorithms (Kao and Mittelmann, 2011).
The Future of fMRI Design
Although the basic trade-offs involved in fMRI design are now generally well known by the community, the actual design of experiments has not necessarily benefited from the latest technical developments in the field. Many researchers still use routines provided in open source fMRI software packages to randomly generate and evaluate designs, even though m-sequences or genetic algorithms would provide better performance in many cases. Of course, even a random search is preferred to arbitrarily picking a design without first evaluating its performance. The continued development of intelligent search approaches, such as the genetic algorithm based method, will be beneficial to the field. For these advanced approaches to be more widely adopted, the software implementation will need to be robust and easy to use. In addition, further theoretical work that takes into account the effect of practical design constraints (such as the ordering of trials) on efficiency would complement the computer-based design approaches by providing bounds on performance and general guidelines for design under such constraints.
Although much of the prior work has focused on efficiency in the context of detecting or estimating hemodynamic responses, there is growing interest in optimizing designs to estimate more subtle aspects of neural activity, such as adaption and habituation (Aguirre et al., 2011). In addition, as more sophisticated analysis methods, such as multi-voxel pattern analysis (Norman et al., 2006) and dynamic causal modeling (Friston et al., 2003), become more widely adopted, there will be a need to develop designs that optimize estimates obtained with these approaches. Researchers who take up this challenge may very well discover the next class of optimal designs for fMRI.
Acknowledgements
This work was supported in part by NIH grants R01NS015661 and R01MH084796.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aguirre GK, Mattar MG, Magis-Weinberg L. de Bruijn cycles for neural decoding. NeuroImage. 2011;56:1293–1300. doi: 10.1016/j.neuroimage.2011.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aguirre GK, Zarahn E, D'Esposito M. The variability of human, BOLD hemodynamic responses. NeuroImage. 1998;8:360–369. doi: 10.1006/nimg.1998.0369. [DOI] [PubMed] [Google Scholar]
- Behzadi Y, Liu TT. Caffeine reduces the initial dip in the visual BOLD response at 3 Tesla. NeuroImage. 2006;32:9–15. doi: 10.1016/j.neuroimage.2006.03.005. [DOI] [PubMed] [Google Scholar]
- Birn RM, Cox RW, Bandettini PA. Detection versus Estimation in Event-Related fMRI: Choosing the Optimal Stimulus Timing. NeuroImage. 2002;15:252–264. doi: 10.1006/nimg.2001.0964. [DOI] [PubMed] [Google Scholar]
- Blamire AM, Ogawa S, Ugurbil K, Rothman D, McCarthy G, Ellermann JM, Hyder F, Rattner Z, Shulman RG. Dynamic mapping of the human visual cortex by high-speed magnetic resonance imaging. Proc. Natl. Acad. Sci. USA. 1992;89:11069–11073. doi: 10.1073/pnas.89.22.11069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boynton GM, Engel SA, Glover GH, Heeger DJ. Linear systems analysis of functional magnetic resonance imaging in human V1. J. Neuroscience. 1996;16:4207–4221. doi: 10.1523/JNEUROSCI.16-13-04207.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Goodman J, Burock M, Rotte M, Koutstaal W, Schacter D, Rosen B, Dale AM. Functional-anatomic correlates of object priming in humans revealed by rapid presentation event-related fMRI. Neuron. 1998;20:285–296. doi: 10.1016/s0896-6273(00)80456-0. [DOI] [PubMed] [Google Scholar]
- Buracas GT, Boynton GM. Efficient Design of Event-Related fMRI Experiments Using M-Sequences. NeuroImage. 2002;16:801–813. doi: 10.1006/nimg.2002.1116. [DOI] [PubMed] [Google Scholar]
- Burock MA, Buckner RL, Woldorff MG, Rosen BR, Dale AM. Randomized event-related experimental designs allow for extremely rapid presentation rates using functional MRI. NeuroReport. 1998;9:3735–3739. doi: 10.1097/00001756-199811160-00030. [DOI] [PubMed] [Google Scholar]
- Buxton RB, Liu TT, Martinez A, Frank LR, Luh W-M, Wong EC. Sorting out event-related paradigms in fMRI: The distinction between detecting an activation and estimating the hemodynamic response. NeuroImage. 2000;11:S457. [Google Scholar]
- Clark VP, Maisog JM, Haxby JV. fMRI study of face perception and memory using random stimulus sequences. J. Neurophysiol. 1998;79:3257–3265. doi: 10.1152/jn.1998.79.6.3257. [DOI] [PubMed] [Google Scholar]
- Cohen ER, Ugurbil K, Kim SG. Effect of basal conditions on the magnitude and dynamics of the blood oxygenation level-dependent fMRI response. J Cereb Blood Flow Metab. 2002;22:1042–1053. doi: 10.1097/00004647-200209000-00002. [DOI] [PubMed] [Google Scholar]
- D'Esposito M, Deouell LY, Gazzaley A. Alterations in the BOLD fMRI signal with ageing and disease: a challenge for neuroimaging. Nat Rev Neurosci. 2003;4:863–872. doi: 10.1038/nrn1246. [DOI] [PubMed] [Google Scholar]
- Dale AM. Optimal experimental design for event-related fMRI. Hum. Brain Mapp. 1999;8:109–114. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<109::AID-HBM7>3.0.CO;2-W. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM, Buckner RL. Selective averaging of rapidly presented individual trials using fMRI. Hum. Brain Mapp. 1997;5:329–340. doi: 10.1002/(SICI)1097-0193(1997)5:5<329::AID-HBM1>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Harrison L, Penny W. Dynamic causal modelling. NeuroImage. 2003;19:1273–1302. doi: 10.1016/s1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Jezzard P, Turner R. Analysis of functional MRI time-series. Human Brain Mapping. 1994;1:153–171. [Google Scholar]
- Friston KJ, Zarahn E, Josephs O, Henson RNA, Dale AM. Stochastic designs in event-related fMRI. NeuroImage. 1999;10:607–619. doi: 10.1006/nimg.1999.0498. [DOI] [PubMed] [Google Scholar]
- Hagberg GE, Zito G, Patria F, Sanes JN. Improved detection of event-related functional MRI signals using probability functions. NeuroImage. 2001;14:1193–1205. doi: 10.1006/nimg.2001.0880. [DOI] [PubMed] [Google Scholar]
- Haykin S. Adaptive Filter Theory. Prentic Hall; Upper Saddle River, NJ: 1996. [Google Scholar]
- Huettel SA, Singerman JD, McCarthy G. The effects of aging upon the hemodynamic response measured by functional MRI. NeuroImage. 2001;13:161–175. doi: 10.1006/nimg.2000.0675. [DOI] [PubMed] [Google Scholar]
- Josephs O, Henson RNA. Event-related functional magnetic resonance imaging: modelling, inference and optimization. Phil. Trans. R. Soc. Lond. B. 1999;354:1215–1228. doi: 10.1098/rstb.1999.0475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Josephs O, Turner R, Friston KJ. Event-related fMRI. Hum. Brain Mapp. 1997;5:243–248. doi: 10.1002/(SICI)1097-0193(1997)5:4<243::AID-HBM7>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]
- Kao M, Mittelmann HD. A Fast Algorithm for Constructing Efficient Event-Related fMRI Designs. Computational Statistics and Data Analysis. 2011 (In Review) [Google Scholar]
- Kao M-H, Mandal A, Lazar N, Stufken J. Multi-objective optimal experimental designs for event-related fMRI studies. NeuroImage. 2009;44:849–856. doi: 10.1016/j.neuroimage.2008.09.025. [DOI] [PubMed] [Google Scholar]
- Liu TT. Efficiency, power, and entropy in event-related fMRI with multiple trial types. Part II: design of experiments. NeuroImage. 2004;21:401–413. doi: 10.1016/j.neuroimage.2003.09.031. [DOI] [PubMed] [Google Scholar]
- Liu TT, Frank LR. Efficiency, power, and entropy in event-related FMRI with multiple trial types. Part I: theory. NeuroImage. 2004;21:387–400. doi: 10.1016/j.neuroimage.2003.09.030. [DOI] [PubMed] [Google Scholar]
- Liu TT, Frank LR, Wong EC, Buxton RB. Detection power, estimation efficiency, and predictability in event-related fMRI. NeuroImage. 2001;13:759–773. doi: 10.1006/nimg.2000.0728. [DOI] [PubMed] [Google Scholar]
- Maus B, van Breukelen GJP, Goebel R, Berger MPF. Robustness of optimal design of fMRI experiments with application of a genetic algorithm. NeuroImage. 2010;49:2433–2443. doi: 10.1016/j.neuroimage.2009.10.004. [DOI] [PubMed] [Google Scholar]
- Maus B, van Breukelen GJP, Goebel R, Berger MPF. Optimal design for nonlinear estimation of the hemodynamic response function. Hum. Brain Mapp. 2011 doi: 10.1002/hbm.21289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy G, Luby M, Gore J, Goldman-Rakic P. Infrequent events transiently activate human prefrontal and parietal cortex as measured by functional MRI. J Neurophysiol. 1997;77:1630–1634. doi: 10.1152/jn.1997.77.3.1630. [DOI] [PubMed] [Google Scholar]
- Norman KA, Polyn SM, Detre GJ, Haxby JV. Beyond mind-reading: multi-voxel pattern analysis of fMRI data. Trends Cogn Sci (Regul Ed) 2006;10:424–430. doi: 10.1016/j.tics.2006.07.005. [DOI] [PubMed] [Google Scholar]
- Scharf LL, Friedlander B. Matched subspace detectors. IEEE Trans. Sig. Proc. 1994;42:2146–2157. [Google Scholar]
- Seber GAF. Linear Regression Analysis. 1st ed. John Wiley & Sons; New York: 1977. [Google Scholar]
- Strang G. Linear Algebra and Its Applications. 2nd ed. Harcourt Brace Jovanovich; San Diego: 1980. [Google Scholar]
- Trefethen LN, Bau D. Numerical Linear Algebra. SIAM; Philadelphia: 1997. [Google Scholar]
- Wager TD, Nichols TE. Optimization of Experimental Design in fMRI: A General Framework Using a Genetic Algorithm. NeuroImage. 2003;18:293–309. doi: 10.1016/s1053-8119(02)00046-0. [DOI] [PubMed] [Google Scholar]
- Woolrich MW, Behrens TE, Smith SM. Constrained linear basis sets for HRF modelling using Variational Bayes. NeuroImage. 2004;21:1748–1761. doi: 10.1016/j.neuroimage.2003.12.024. [DOI] [PubMed] [Google Scholar]