Impact of pulmonary vascular stiffness and vasodilator treatment in pediatric pulmonary hypertension: 21 patient-specific fluid-structure interaction studies

Abstract

Recent clinical studies of pulmonary arterial hypertension (PAH) have found correlations between increased pulmonary vascular stiffness (PVS) and poorer disease outcomes. However, mechanistic questions remain about the relationships amongst PVS, RV power, and vascular hemodynamics in the setting of progressive PAH that are difficult or impossible to answer using direct measurements. Clinically-validated patient-specific computational modeling may allow exploration of these issues through perturbation-based predictive testing.

Here we use a simple patient-specific model to answer four questions: how do hemodynamics change as PAH worsens? How does increasing PVS impact hemodynamics and RV power? For a patient with moderate PAH, what are the consequences if the pressures increase modestly yet sufficiently to engage collagen in those vessels? What impact does pressure-reducing vasodilator treatment have on hemodynamics?

Twenty-one sets of model-predicted impedance and mean PA pressure (mPAP) show good agreement with clinical measurements, thereby validating the model. Worsening was modeled using data from three PAH outcomes groups; these show not only the expected increase in mPAP, but also an increase in pressure pulsatility. Interestingly, chronically increasing mPAP decreased WSS, suggesting that increased PA cross-sectional area affected WSS greater than increased PVS. For a patient with moderately high PVR (12.7 WU) with elastin-based upstream vascular remodeling, moving from elastin-dominant vessel behavior to collagen-dominant behavior caused substantial increases in mPAP, pressure and WSS pulsatility. For the same patient, reducing PVR through a simulated vasodilator to a value equivalent to mild PAH did not decrease pressure pulsatility and dramatically increased WSS pulsatility.

Overall, these results suggest a close association between PVS and hemodynamics and that hemodynamics may play an important role in progressing PAH. These support the hypothesis that treatments should target decreasing or reversing upstream vascular remodeling in addition to decreasing mean pressures.

Introduction

Pulmonary arterial hypertension (PAH) is a complex disease, associated with a progressive increase of pulmonary vascular resistance (PVR) [1] and sustained elevation of mean pulmonary artery pressure (mPAP), which together contribute to right heart dysfunction. PAH is primarily considered to be a small vessel disease, and distal vessel vasculopathy is generally considered a major contributor to its progression [2-5]. Recent research has focused on changes in upstream pulmonary arteries as well. In patients with PAH, proximal arterial wall remodeling can result in increased pulmonary vascular stiffness (PVS) [6, 7], which decouples the upstream vasculature from the right ventricle (RV) and increases RV loading. In systemic vessels, studies have shown that upstream vascular stiffness is prognostic of disease outcomes [8], and this idea is beginning to be evaluated in the pulmonary circulation as well [9-11]. These early studies suggest that vascular stiffening plays an important role in the development and progression of PAH; however, very little is known about how increasing PVS impacts the pulmonary circulation and its role in progressing the disease.

Collagen and elastin are extracellular matrix components that bear the vast majority of arterial wall stress and determine the passive stiffness of the conduit pulmonary arteries. Recent studies of hypoxia-induced pulmonary hypertensive calves [12] indicate that adaptations of the continuum and geometric properties of elastin, in response to PAH, elevate the circumferential stiffness of proximal pulmonary arterial tissue while maintaining some degree of vascular elasticity. Thus, elastin remodeling of upstream pulmonary vessels may be an adaptation that maintains the vascular Windkessel and preserves RV-vascular coupling. Studies have also shown that vascular collagen accumulation occurs under severely hypertensive conditions [13]. Collagen remodeling may be an adaptation to preserve pulmonary vascular integrity at very high pressures; however, collagen due to its stretch-locking function would cause a loss to Windkessel function and decouple the RV from the upstream pulmonary vasculature [12]. These ideas continue to be explored in basic research studies.

The effects of upstream vascular remodeling on clinical status have yet to be determined. In particular, the question of how increasing PVS affects RV performance and pulmonary vascular hemodynamics remains open. Recent studies have shown that changes in hemodynamics, especially wall shear stress (WSS), can cause marked changes in endothelial and smooth muscle activity within the vasculature. For example, Li et al [14] showed that increasing WSS pulsatility caused distal pulmonary vascular cells to release vasoconstrictive and proliferative factors. Further, given the significant half-life of elastin [15], vasodilator infusion, the most common clinical treatment of PAH, may not alleviate chronic increases in stiffness due to elastin remodeling, while collagen-induced stiffening due to moderate worsening could strongly affect a patient's overall hemodynamic state.

In this paper, we explore the above questions and investigate the relationships amongst vascular stiffness, patient outcomes, and hemodynamics using a patient-specific, two dimensional (2D) numerical model meant to represent the conduit pulmonary arteries. Patient-specific model parameters of cardiac output, PVR, and main pulmonary artery diameter are obtained from standard clinical measurements, while pulmonary vascular stiffness is estimated with a new, validated echo-based method. The modeling technique is first validated through comparison of 21 patient-specific models with clinically measured mean pulmonary artery pressure (mPAP) and input impedance (Z) [11, 16]. The impacts of resistance and stiffness on power and global hemodynamics are related to previously defined pediatric PAH outcomes [11] with predictive models based on averaged clinical parameters from 30 patients grouped into three outcomes categories [11]. Finally, two predictive models examine our hypothesis regarding the importance of vascular stiffness in two clinical scenarios, vasodilator treatment and acute moderate vasoconstriction leading to collagen engagement.

Methods

Numerical Analysis/Study Types

We approach the modeling problem by investigating three analysis/study groups. The first consists of fully patient-specific models, with input parameters obtained or derived from clinical data as described in the next section, with model output (results) compared on a patent-specific basis to additional clinical values. This first validation study is performed to insure that the models reasonably reproduce specific clinical outputs given specific inputs. The next two studies predict overall hemodynamics in a specific hypothetical patient. The first of these predictive (but not prognostic) studies examines mean hemodynamic values as a function of the hypothetical patient's 1-year soft outcome (OC) category, while the second set of models predict hemodynamic changes due to the patient undergoing known processes typical in disease progression or treatment.

Numerical Model

Our group and others have developed a variety of numerical models to simulate and predict cardiovascular hemodynamics; these range from extremely complex models that include three-dimensionality, non-linearity in material properties and fluid rheology, and fully bi-directional fluid-solid coupling, to simple one-dimensional models that simulate bulk flow. Although each type of model has advantages and disadvantages, we believe that two factors are critical to moving such techniques from research to clinic: developing a unique model for each patient that is validated using that patient's data; and achieving reasonable solution times to allow the model to be used on many patients. Here we take a compromise approach by reducing the complexity of the model to allow reasonable solution times yet answer the questions posed, but maintaining patient-specificity and validation over a larger number of patients.

Since our primary intent was to evaluate the relationship between upstream pulmonary vascular stiffness and hemodynamics, we lumped upstream vessels into a single elastic tube, modeled in two dimensional (2D) axisymmetric coordinates. Figure 1 shows the schematic of the tube model with diameter D, and a total length of 0.2 m.

Fig. 1.

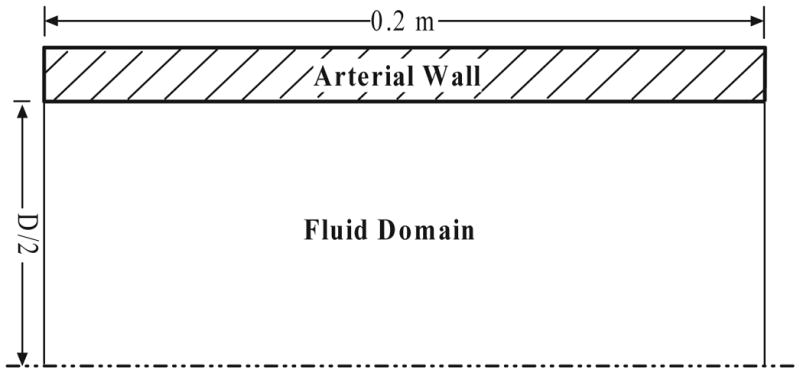
The schematic of the two dimensional symmetric pulmonary artery model.

Fluid Domain

Blood is modeled as an incompressible, laminar, Newtonian fluid with a viscosity 3.5 mPa·s and density 1050 kg/m³. Prior to model initialization, no transmural pressure exists with zero flow; thus no additional dynamic external fluid loading is considered. The stress vector is continuous across the fluid structure boundary, where the non-slip condition is applied to the fluid velocity vector. The inlet flow rate is transient, with pulse shape obtained from clinical measurements as described below. The outlet boundary condition of the flow domain is specified as a resistance boundary condition [17]

$$R=P/Q$$ (1)

in which P and Q are the mean pressure (mm Hg) and flow rate (L/min) at the outlet boundary and R is the pulmonary vascular resistance (PVR), defined as PVR = (mPAP-PCWP)/CO [18] where PWCP is pulmonary capillary wedge pressure. This boundary condition is implemented by transiently changing the outlet pressure based on the current flow condition and constant resistance. For validation the model is scaled to each patient size and we used PVR instead of PVRI (PVRI = PVR×BSA) as an exit condition. Our predictive models, which are not patient specific, are sized for patients with a BSA≈1 m²; more detail regarding model scaling is below (“Use of Clinical Data in the Model”)

Solid Domain

The pulmonary artery wall is considered as an incompressible isotropic linear elastic solid with density 1200 kg/m³ and Poison's ratio 0.48; its incremental elastic modulus is specified from clinical measurements on a patient-specific basis and will be discussed further below. The artery wall is constrained to move only radially at each end, while exterior and interior boundary surfaces are loaded with constant uniform pressure and fluid pressure/shear stress, respectively.

Solution Procedure

The CFD-ACE multiphysics package (CFD Research Corporation, CA, USA) is used to perform mesh generation, develop the numerical model, and to solve the governing equations for fluid flow and structural motion with the finite volume and element methods, respectively. A rectangular mesh is generated for the axisymmetric geometry containing 4221 fluid nodes and 804 solid nodes, with 201 nodes on the fluid-structure boundary. Mesh validation was carried out by taking a 1.5× refined mesh (9331 fluid nodes, 1206 solid nodes); comparisons displayed a maximum of 1% difference in pressure and velocity in the fluid domain. Time integration utilized a first order Euler approach with a time step of 2 ms. Time convergence was verified by halving the time step (1 ms). We compared the fluid pressure and velocity at the end of simulations (typical 6 cadiac cycles) with and without this refined time step, and found less than a 1% change in fluid pressure or velocity at nine different locations (a 3×3 array of points defined in the axial direction at the inlet, midpoint, and outlet and along the radial direction at the axis of symmetry, halfway between the axis and the wall, and at the arterial wall). Each model is run for 6 cardiac cycles to insure that the simulations are convergent in the transient inlet condition: the resistance boundary condition coupled with wall stiffness allows for fluid storage, which can take several cardiac cycles to become periodic. The details about the solution of fluid and structural equations can be referred to our previous work [19-21]. In the solution procedure, we use the CFD-ACE algebraic multigrid solver for the fluid equations and a direct (linear) solver for the structural equations.

Clinical Data Acquisition

After institutional review board approval and informed consent and assent had been obtained, data were obtained from 30 patients during routine cardiac catheterization as part of the regular evaluation and treatment of these subjects at the Children's Hospital in Denver, CO. Pressure measurements were made with standard fluid-filled catheters (Transpac IV, Abbot Critical Care Systems) within the main pulmonary artery (MPA). Two echocardiographic measurements (Vivid 5, GE Medical Systems) were used: 1) PW Doppler velocity measurements were taken within the midsection of the MPA with a commercial ultrasound scanner from a parasternal short-axis window; and 2) right pulmonary arterial (RPA) diameter was obtained from Color M-Mode Tissue Doppler Images (CMM-TDI) of the RPA wall from the suprasternal short-axis view. More detail regarding echo data acquisition may be found elsewhere [11, 16]. Cardiac output (CO), here defined as the mean flow from the right ventricle to the main pulmonary artery, was measured by Fick's method with measured oxygen consumption in cases where intracardiac shunts were in place and by thermodilution otherwise. Two derived measures were calculated from the measured data according to previously published methods: pulmonary vascular input impedance (Z) was computed from pressure and PW Doppler [16], while an estimate of vascular elastic modulus was obtained from pressure and RPA diameter [22]. The pulmonary vascular resistance (PVR) was calculated from mPAP, PCWP, and CO as described above.

All patients included in this study were hypertensive and were grouped according to a “soft” outcome based on the change in their world health organization (WHO) functional status [1, 11] from initial disease assessment to one-year follow up. The WHO functional status consists of four classes (I, II, III and IV) associated with increasing symptoms of disease. The three outcome categories generally indicate 1) improvement, taken as a change of ≥1 functional class for the better, such as moving from class II →I; III →II, I; IV →I, II, III; 2) slight worsening, corresponding moving from class I →II or II →III; and 3) significantly worsening or death, the former indicated by an increase of > 2 functional classes, such as I →III, IV; or II →IV. Patients who maintained functional class were categorized according to severity: constant class 1 denoted an outcome of 1; constant class 2 or 3 denoted an outcome of 2; and constant class 4 yielded an outcome of 3.

Use of Clinical Data in the Model

The model input parameters are cardiac output, elastic modulus, PVR, MPA diameter, arterial wall thickness, and transient flow profile. The first three of these are directly obtained or estimated on a patient-specific basis from clinical data, whereas the last three are approximated from clinical data either on a patient specific basis or use a single source as explained in more detail in the three subsections below. Additionally we describe our method for modeling the stiffening process, which incorporates clinical stiffness measurements and observations from animal studies.

Model Diameter

The model diameter should correspond to MPA diameter, given that our input flow condition corresponds to the total pulmonary flow; however we were unable to obtain its dimensions from our existing ultrasound dataset. MPA diameter is thus estimated from the measured RPA diameter (using CMM-TDI as noted above) by using an average MPA/RPA diameter ratio of 1.58 in diastole [23, 24]. For validation, each model has a patient-specific MPA diameter estimated from direct measurements of the RPA, while the predictive models were sized for a simulated patient with a BSA of ≈ 1.0m². To obtain the proper size for these models we found the average diameter (2cm), flow (4L/min), and heart rate (100Hz) of ten patients (5 in OC1, 4 in OC2 and 1 in OC3) with BSA in the range 0.9∼1.1 m². We note that only 5 patients of these 10 patients are listed in Table 1; the other 5 patients were missing a single parameter (such as CO, etc) rendering them unusable in our validation study.

Table 1. Parameters from clinical measurements to develop patient-specific numerical models.

Patient	MPA Diameter (mm)	HR (bpm)	CO (L/min)	Elastic Modulus (kPa)	PVRI (mm Hg/(L/min))	mPAP (mm Hg)	BSA (m2)
PHT48	16.7	97	3.5	29	6.57	23	0.92
PHT49	13.6	97	2.1	236	21.0	44	0.73
PHT50	17.1	94	3.6	194	10.2	37	0.67
PHT52	12.2	69	2.0	110	9.13	18	0.47
PHT53	30.3	92	4.3	322	14.6	62	1.33
PHT55	8.85	130	1.4	144	24.5	34	0.30
PHT58	11.2	112	5.2	238	15.4	80	1.20
PHT59	5.06	120	2.1	74	12.2	28	0.28
PHT61	24.2	75	3.8	80	12.8	55	1.35
PHT62	8.06	107	2.2	57	15.5	34	0.51
PHT63	12.4	110	2.3	34	7.73	18	0.53
PHT65	5.69	150	0.9	128	10.8	24	0.28
PHT66	19.1	114	3.9	133	4.64	23	1.10
PHT78	17.4	100	1.5	59	13.1	19	1.10
PHT80	17.2	126	2.2	290	25.0	56	0.82
PHT83	17.2	78	6.1	100	4.40	27	1.30
PHT84	9.10	135	1.1	95	16.7	20	0.24
PHT85	13.1	77	4.5	184	5.48	18	0.91
PHT86	19.7	50	3.0	75	10.6	32	1.76
PHT87	13.1	89	4.2	85	4.80	20	0.94
PHT90	11.3	76	2.0	113	13.3	27	0.56
IPAH			3
FPAH			0
Associate PAH			18
Congenital Heart Disease			Repaired/Unrepaired
Ventricular Septal Defect			2/3
Atrial Septal Defect			5/2
Patent Ductus Arteriosus			3/0
Total Anom. Pul. Ven. Return			1/0
Pulmonary Atresia			1/0
Omphalocele			1
High Alti Pulmonary Adema			1

Model Thickness

Because the pulmonary artery wall thickness, for children is within the uncertainty of trans-thoracic ultrasound (i.e., 1-3 mm) it is difficult to directly measure from the clinical images. Again, we obtain a reasonable estimate from reported thickness values for different arteries and the associated artery wall thickness-to-diameter ratios [25-29], which ranged from 0.08 to 0.11. We used 0.10, an average of these ratios, for the main pulmonary artery in our calculations, as we did in previous computational work [21]. Use of an average thickness was shown to provide an acceptable estimate of elastic modulus in a validation study of the CMM-TDI method [22]. Note that elastic modulus is estimated on a patient specific basis using the methods outlined in this work [22].

Inlet Flow Condition

Inlet flow velocity is assumed to be spatially constant, with magnitude determined from patient-specific or generic flow time histories and current inlet cross-sectional area. We did not use a parabolic profile here because we did not expect he pulsatile flow exiting the right ventricle to be fully developed (i.e. parabolic) within the MPA, given its high Wormersley number (>10). For the validation models, flow time histories were obtained by combining mean flow measurement (i.e. cardiac output) with MPA midsection blood velocity (obtained from PW Doppler as noted above); this procedure corresponds to our previous methods for approximating transient flow from velocity using an area correction factor [11, 16, 30]. Because only a single profile per patient is used here (unlike previous work, which examined multiple cardiac cycles independently), PW Doppler velocity histories in five consecutive cardiac cycles were taken from each patient set, averaged ( $\overline{u_t}={\sum }_{n=1}^5{u}_{t,n}/5$, u is the measured velocity, t indicates at the same time in five cardiac cycles), and scaled to the known mean cardiac output with the area correction factor to obtain a final flow time history. For the three predictive models, a single flow time history was obtained from spatial and temporal velocity fields measured by phase-contrast magnetic resonance imaging (PC-MRI) [31] in a single, healthy patient with BSA=1.0. Preliminary work has shown that with preserved cardiac function, this temporal waveform, and thus flow, is similar between patients at different states of disease [31].

Modeling of the Stiffening Process

As noted in the introduction, our recent animal model study of vascular stiffening [12] suggests there are two stages of the process: elastin remodeling and collagen engagement. The first of these approximately doubles the (roughly) linear elastic Young's modulus of the artery wall at smaller stretch ratios. The latter is a nonlinear effect that occurs due to the engagement of vascular collagen at higher stretch, and yields a substantial increase (>10× in some cases) in the incremental material modulus. According to recent mechanical studies of the pulmonary arteries [12, 32], this stiffening occurs when the artery is deformed above what is known as the engagement stretch (≈1.5 for normal and hypertensive animals), indicative of collagen carrying the pressure load. Each change is modeled as a single linear incremental modulus as measured clinically as noted above. For example, to simulate collagen engagement, we set the wall modulus to the highest value suggested by our clinical data, obtained from the sickest patients; similarly, elastin remodeling is simulated by setting the wall modulus to an intermediate clinically value, obtained from moderately sick individuals. Here the stretch ratio is defined as ratio of instantaneous lumen diameter to initial lumen diameter.

Post Numerical Data Processing

We first validate our models by comparing mean main pulmonary arterial pressure (mPAP) and first harmonic of impedance measured for each patient against mPAP and impedance produced by the model for that patient using previously described methods [16]. For our predictive and reactivity studies, we investigate inter-model changes in pressure, flow, impedance, wall stretch ratio (computed directly from model results) and wall shear stress (WSS). WSS is calculated by fitting the velocity data with a polynomial function [33] at the middle point between inlet and outlet boundaries; we note that our result is significantly different than what would be computed simply from flow or velocity data using the parabolic assumption for pulsatile and unsteady flow in large artery [34]. Additionally, RV power (the rate of ventricular work), which comprises potential energy and kinetic energy is compared in our predictive and reactivity models. Kinetic energy has been shown to account for a small fraction of the total ventricular power and is neglected here [35, 36]. The mean power (mean energy per unit time) was calculated as W_M = P₀ · Q₀, where P₀ and Q₀ are the zero-frequency components of the pressure and flow moduli, respectively. The oscillatory power (pulsatile energy per unit time) was calculated as

$$W_o=\frac{1}{2}\sum _{n=1}^3{\left|Q_n\right|}^2\left|Z_n\right|cos{\varphi }_n$$ (2)

here n represents the harmonic of the fundamental frequency. Finally, total RV power was calculated as

$$W_T=W_M+W_O$$ (3)

Results

Numerical Model Validation

To validate the artery model, 21 patient-specific simulations (age range 4 months-17 years, median age 6 years, 11 females) were performed, and the computed first harmonic modulus of input impedance (Z₁) and computed mPAP were compared to clinical measurements. Nine patients (PHT57, 65, 70, 79, 89, 92, 93, 74 and 97) were excluded from the validation models due to missing parameters required for validation, including but not limited to mPAP, CO or impedance, which precluded comparisons between these clinical results with our numerical results. Table 1 provides the patient-specific parameters that determined model geometry, main arterial lumen diameter and estimated wall thickness which is 0.1 of the local lumen diameter, inlet rate (heart rate (HR) and cardiac output (CO)) material properties (in-vivo elastic modulus) and exit conditions (PVR).

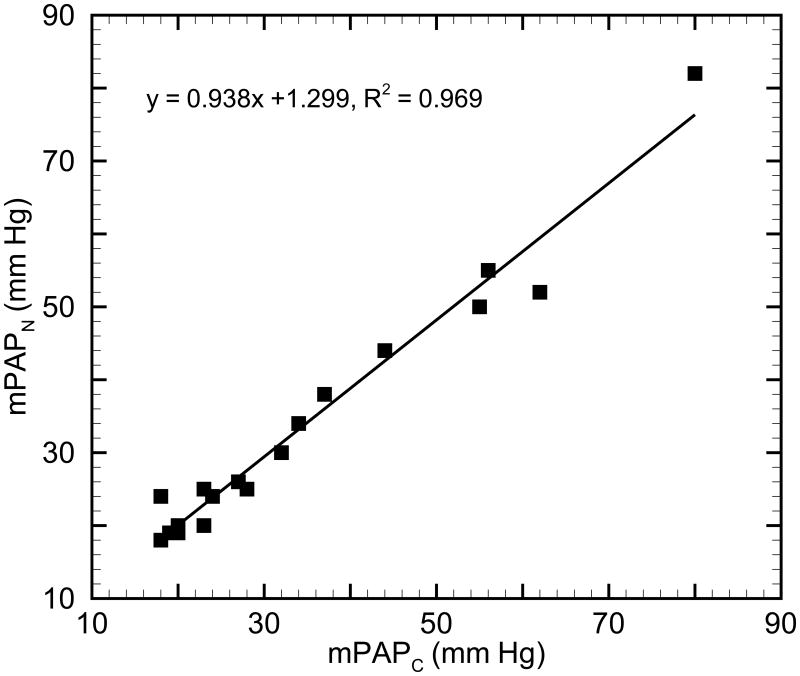
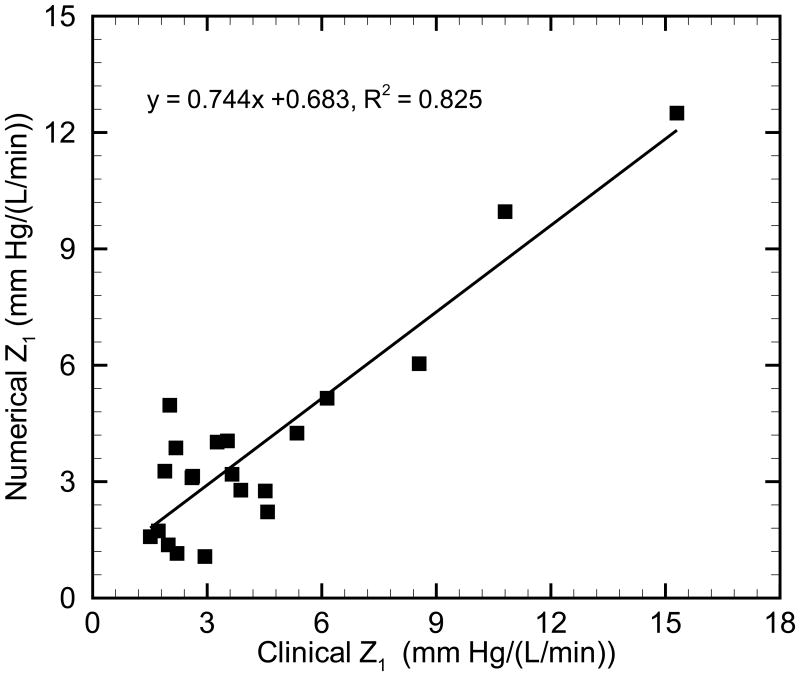
Comparison of the numerical mPAP_N results to clinical mPAP_C measurements is shown in Figure 2. A linear regression between the clinical and numerical results yields y = 0.938 x + 1.299, R² = 0.969 (p < 0.05), which suggests that measures are in good agreement. Comparison of numerical and clinical input impedance moduli (Z₁) for all patients is shown in Figure 3. Good agreement is seen in the linear regression between clinical and numerical Z₁: y = 0.744 x + 0.683, R² = 0.825 (p < 0.05). The numerical Z₁ are smaller than the clinical Z₁ in most cases (18 of 21 cases), which we believe is due to limitation of the linear constitutive model in use; when a linear model is used instead of the more realistic nonlinear model, any collagen engagement is ignored and an incremental measure of stiffness is potentially lower in the hypertensive condition. As a result, numerical Z₁ is smaller than that obtained from clinical measurements.

Fig. 2.

Comparison of the mean main pulmonary arterial pressure between numerical (mPAP_N) and clinical (mPAP_C) results.

Fig. 3.

Comparison of the input impedance modulus Z₁ in pulmonary normotensive and hypertensive states.

Given these comparisons of mPAP and input impedance modulus Z₁ between the numerical simulation and clinical measurements, the model appears to reasonably represent global hemodynamics through the use of patient-specific model parameters.

Outcomes-Specific Models

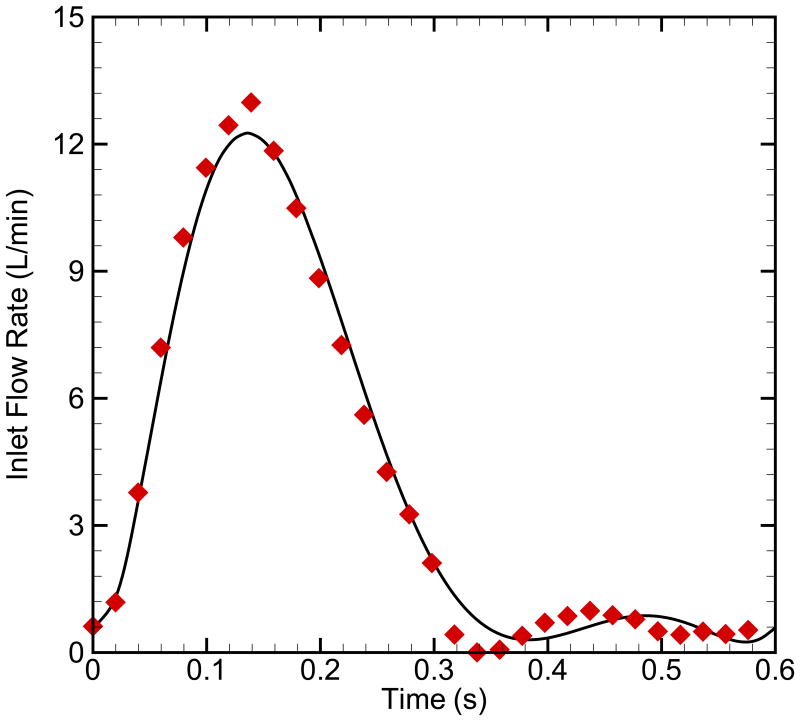
Three outcomes-specific models, referred to as “OC1”, “OC2” and “OC3” for outcome 1 through 3 respectively, were created with group-averaged clinical data to examine general changes in the global hemodynamic between the outcomes categories. For this set of simulations, 30 patients who were previously divided into the three outcome categories were used to construct the models (Table 2). Model OC1 has an elastic modulus of 90 kPa and pulmonary vascular resistance index (PVRI) [11] of 7.3 mm Hg/(L/min) (n=17); model OC2 has averaged elastic modulus of 150 kPa and PVRI of 12.7 mm Hg/(L/min) (n=10); and model OC3 has averaged elastic modulus of 270 kPa and PVRI of 25 mm Hg/(L/min) (n=3). Figure 4 shows the inlet flow rate from the clinical MRI data before and after polynomial data fitting. The parameter of MPA diameter, CO, HR, elastic modulus and PVRI based on the clinical measurements of 30 patients are used as input variables to develop outcome-specific numerical models for three groups. To assist in the comparison amongst the outcomes models and remove any size effect, we simulated a single hypothetical patient with BSA≈1 m². The diameter, HR, and CO for this model were averaged amongst 10 patients (5 in OC1, 4 in OC2, and 1 in OC3) with BSA≈1 m² and were constant across the three outcome groups; notably, these did not show high variance amongst the groups. Table 2 provides the group-varying parameters of modulus and PVRI for different outcomes, as well as the MPA diameter (2cm), CO (4L/min) and HR (120 bpm) are the same for the three outcomes.

Table 2. Comparisons of flow rate, wall pressure and power for three outcomes states in PAH.

	Category	OC1	OC2	OC3
Input	Elastic modulus (kPa)	90	150	270
	PVR (mm Hg/(L/min))	7.30	12.7	25.0
Output	Mean/Pulse flow rate (L/min)	4.00/2.52	4.00/2.42	4.00/2.18
	Mean/Pulse wall pressure (mm Hg)	28.7/17.2	49.8/29.6	98.4/50.5
	Mean/Oscillatory power (mW)	253/46.8	441/82.8	873/158
	Ventricular power (mW)	300	524	1031

Fig. 4.

The inlet flow rate from the clinical data before and after polynomial data fitting.

Figure 5 shows the comparison of the blood outflow, stretch ratio, wall pressure and WSS as a function of time during one cardiac cycle for the three outcome-specific models. Here wall pressure is obtained at the middle point between inlet and outlet boundaries, the same location of WSS. Although the pulse outflow rates are almost the same, the stretch ratio of the arterial wall, arterial mean pressure and pulse pressure increase from category 1 to 3. Stiffness has clear and direct effects on the pulsatility in the pulmonary circulation. When the elastic modulus increases 167 % (OC1 →OC2) and 300 % (OC1 →OC3) the pulse pressure similarly undergoes increases of 172% and 294 % respectively.

Fig. 5.

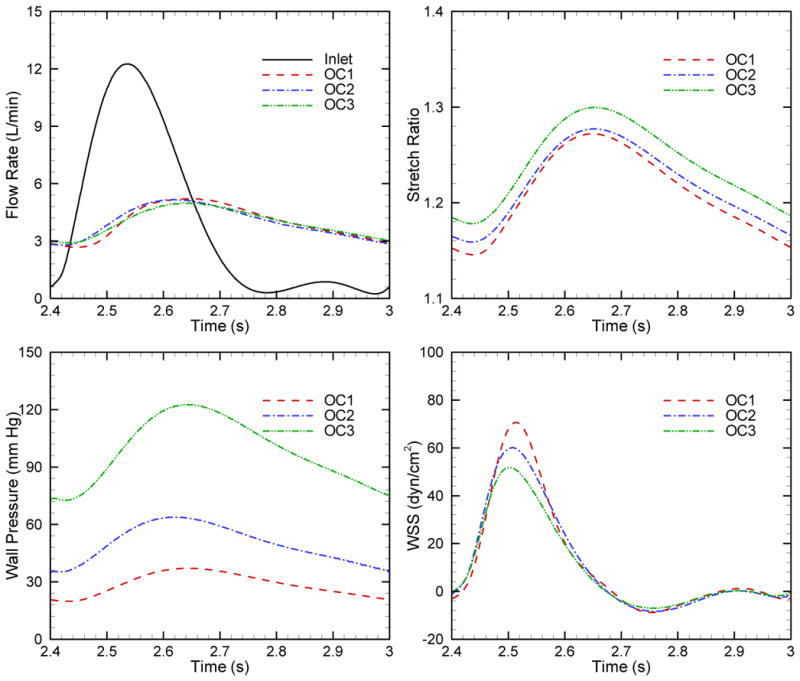
Comparison of the blood outflow, stretch ratio, wall pressure and WSS as a function of time during one cardiac cycle for three outcome categories in PAH.

Table 2 lists the flow rate, wall pressure and power for three outcomes models. Here elastic modulus and PVR for three categories are implemented in numerical models as input variables; as well flow rate, pressure and powers are obtained from numerical simulations. We see that the ratio of oscillatory to total power is relatively constant for the three categories; generally these W_O/ W_T values are higher than clinical measurements in the PAH conditions for children [16], but are lower than those reported for adults [36]. It has been proposed that the W_O/ W_T is not only determined by the PVS and PVR, but also affected by the heart rate [36] and thus the higher heart frequency in children (∼1.7 Hz) leads to an overall decrease in W_O/W_T compared to adults (∼1Hz) [35].

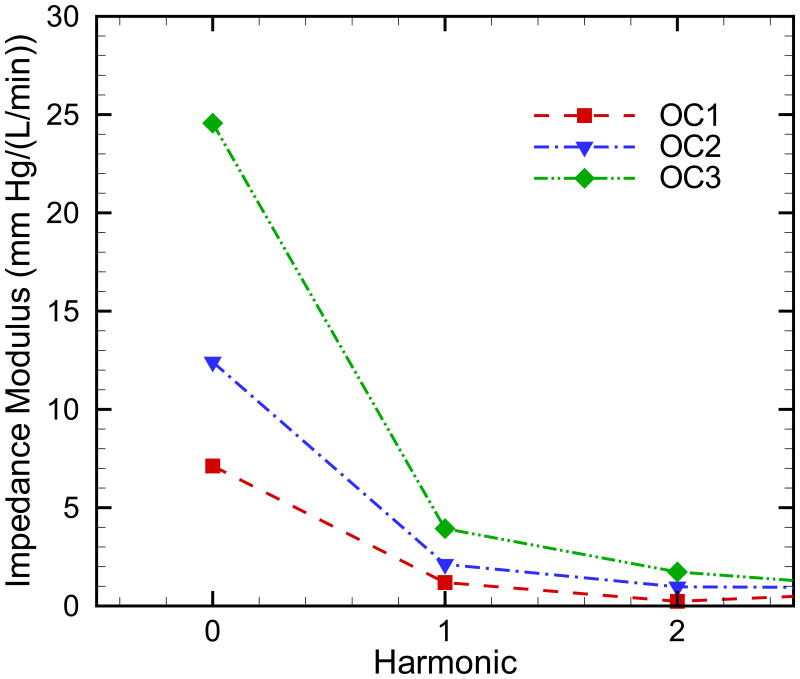
Figure 6 shows the comparison of the input impedance modulus for the three outcomes models. It is well known that identification of the input impedance moduli in higher harmonic is problematic, as noise on pressure and flow signals affects higher harmonics [37]. The input impedance modulus Z₀ corresponds exactly to the resistance applied as the outflow boundary condition, while Z₁ and Z₂ increase as the elastic modulus increases.

Fig. 6.

Comparison of the input impedance modulus for three outcome categories in PAH.

Effect of Collagen Engagement on Category 2 Patient

Our averaged outcomes parameters for OC2 and OC3 displayed a clear difference in their elastic moduli. Given that collagen engagement is a passive change associated with increasing pressures, the potential exists for moderate increases in OC2 pressures that result in passive stiffening; here we test the hemodynamic consequences of a moderate acute increase in PVR causing an increase in collagen ECM engagement in, and significant stiffening of, the conduit arteries. Starting with the OC2 scenario, we model a moderate 20% increase in resistance increase and a change in elastic modulus to the OC3 value of 270 kPa, to determine the potential hemodynamic and work requirements associated with this change (Table 3).

Table 3. Comparisons of flow rate, wall pressure and power for OC2, collagen engagement and vasodilator of OC2.

	Category	OC2	Collagen engagement	Vasodilator treatment
Input	Elastic modulus (kPa)	150	270	150
	PVR (mm Hg/(L/min))	12.7	15.2	7.3
Output	Mean/Pulse flow rate (L/min)	4.00/2.42	4.00/3.54	4.00/4.16
	Mean/Pulse wall pressure (mm Hg)	49.8/29.6	60.2/51.6	28.7/28.7
	Mean/Oscillatory power (mW)	441/82.8	534/124	254/76.8
	Ventricular power (mW)	524	658	331

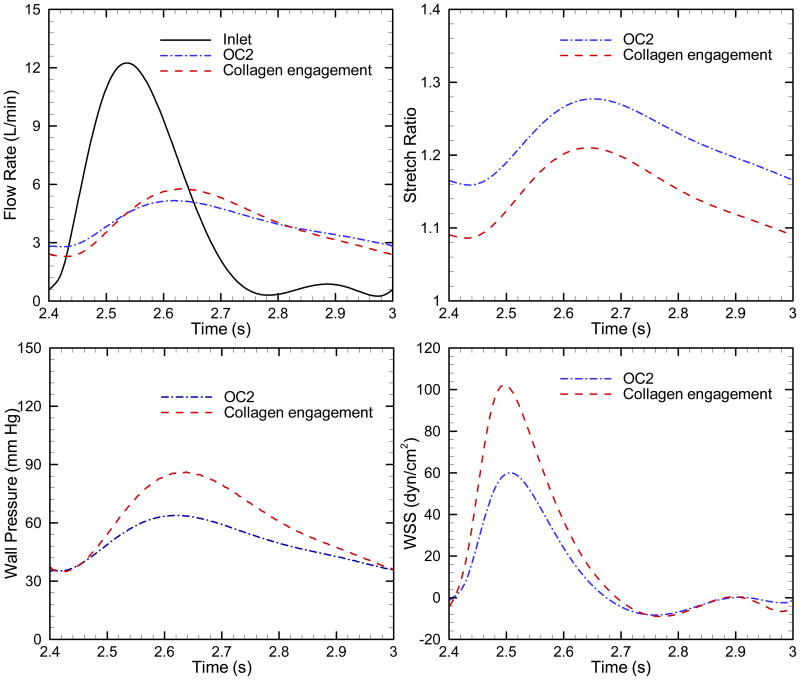
Figure 7 compares the blood outflow, stretch ratio, wall pressure and WSS as a function of time during one cardiac cycle for OC2 and collagen engagement; clearly the latter is associated with increased pulmonary arterial pulsatility in the flow rate, stretch ratio, wall pressure and WSS. Table 3 lists flow rate, wall pressure and power for OC2 and collagen engagement of OC2. Elastic modulus and pulse pressure increase by approximately 180%, while similarly PVR and mPAP increase approximately 120%, again displaying the clear association between the parameters and their respective pressures. The mean and oscillatory powers are increased 121% and 150% respectively with the collagen effect. Thus this significant increase in stiffness yields moderate impacts on the total power, but significantly alters pulsatility.

Fig. 7.

Comparison of the blood outflow, stretch ratio, wall pressure and WSS as a function of time during one cardiac cycle for OC 2 and collagen engagement.

Effect of Vasodilator Treatment on Category 2 Patient

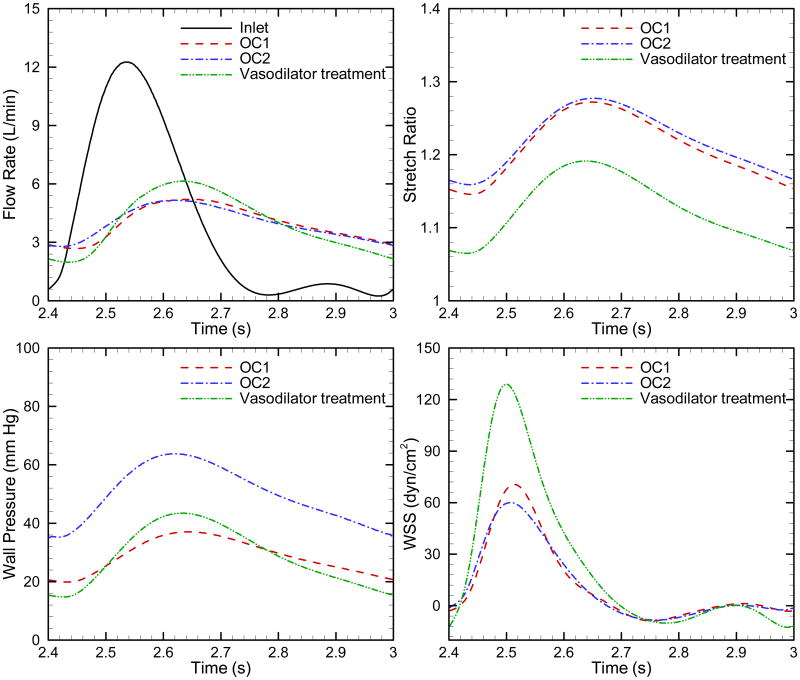
The objective of PAH treatment is to decrease the pulmonary arterial pressure, which in turn is associated with lower RV afterload and power. Vasodilator treatment can reduce distal resistance in some patients; however if such patients have undergone elastin-based proximal vascular remodeling as seen in prior studies of the hypoxic calf [12], their afterload would retain high-stiffness characteristics. To examine this situation we modeled a condition with elastic modulus of 150 kPa and a PVR of 7.3 mm Hg/L/min corresponding to an outcome 2 patient who strongly responded to vasodilator treatment (Table 3).

Figure 8 displays blood outflow, stretch ratio, wall pressure and WSS as a function of time during one cardiac cycle for OC2, OC2 with vasodilator treatment and OC1. After the vasodilator treatment, decreased distal resistance yields reductions in mean power to nearly the level of OC1, while oscillatory power is nearly the same as that of OC2 (Table 3). The latter represents moderate component of the total power, which is substantially reduced and the apparent objective of vasodilator therapy is achieved. Although the modeled OC2 vasodilator treatment reduces the mean pressure and wall deformation, its hemodynamic state clearly does not match the OC1 state, with the former exhibiting higher flow, pressure and WSS pulsatility.

Fig. 8.

Comparison of the blood outflow, stretch ratio, wall pressure and WSS as a function of time during one cardiac cycle for OC1, OC2 and vasodilator treatment of OC2.

Discussion

Results from the outcomes-specific models show that percentage increases in pulse pressure move in lockstep with percentage increases in the elastic modulus. This corresponds to our expectations that increasing PVR is associated with increased mPAP while increasing stiffness increases pressure pulsatility. In contrast, WSS pulsatility tends to decrease in the stiffer condition, and is likely due to the fact that the vessel is more greatly distended in the severe condition (i.e. greater stretch ratio), resulting in a greater cross sectional area for the same flow and thus, an overall reduction in velocity and WSS. Interestingly, these observations of reduced WSS have also recently been made in clinical MRI of PAH patients [38]; [31]. This reduced WSS is reminiscent of flow conditions in atherosclerotic arteries [39], suggesting that mechanotransduction in these proximal vessels could possibly play a role in disease progression [40].

Previous work has shown that the proximal stiffness is an important contributor to ventricular power [36] in adults with PAH, while for children, Weinberg et al. [16] observed the effect of proximal stiffness on the total RV power is lower (<10%); our results lie between these clinical observations. Although the majority of the RV power requirement is due to mean power and thus PVR, these results confirm the idea that the neglect of oscillatory power can significantly (20-30%) underestimate the total power. Improving the power estimate appears to have the greatest importance in evaluating disease treatment and progression; for example, in both OC2 perturbation studies (vasodilator and collagen engagement), oscillatory power increased as a total percentage of the total power.

Impedance has previously been shown to be a useful prognostic, but it has previously required invasive measurement of pressure and flow. Our model's ability to predict impedance, pulsatility, and general shear conditions from only a handful of common clinical parameters, both on individual (in the validation above) and grouped bases may make it useful in the future as a screening tool, if such parameters can be estimated on a non-invasive basis [11, 41, 42]. Additionally, to confirm greatest clinical applicability the model must be validated not only on diagnostic parameters as was done here, but must further be shown to be predictive of prognosis; this is a future modeling goal.

The collagen engagement and vasodilator treatment perturbation model results suggest that focusing only on elevations or reductions in PVR neglect more significant hemodynamic changes. The modeled vasodilator treatment result highlights the ineffectiveness of mPAP-reducing vasodilator therapy to reduce hemodynamic pulsatility in the setting of permanently remodeled upstream pulmonary vessels, although under current clinical guidelines such a patient would be seen as having highly reactive pulmonary vessels. Similarly, the collagen model posits that changes in pulsatility and mean-to-pulsatile power ratio are possible even with relatively minor increases in resistance. If these simulated results are representative, and stiffening plays a significant role in outcomes and thus, disease progression, these models suggest it two mechanisms: through changes in flow and pressure pulsatility, and through increasing required RV power. Given recent findings relating changes in flow pulsatility to changes in pulmonary endothelial cell signaling [14, 43], this appears a reasonable hypothesis, and places equal importance of stiffening on power and hemodynamic derangement.

Limitations

While we believe this simple 2D axisymmetric numerical model represents a reasonable advance in patient-specific models that are applied to larger numbers of subjects, several limitations remain. The two dimensional axisymmetric numerical model ignores 3D effects and complex geometry. An additional flow assumption is the use of resistance boundary condition, which simplifies the complex flow impedance presented by the distal vasculature to merely a resistance condition and precludes the existence of diastolic flow. Such simplification appears reasonable for these single branch models, but impedance-based outlet boundary conditions would be more realistic. The inlet boundary condition is applied with the same cardiac output for all cases, in which the effect of decreasing CO in more severe PAH condition is ignored. All these simplifications, however, yield a model that has substantially reduced construction time and runtime, and thus may be more easily implemented clinically. Finally, we note that our predictive models are intended to explore our hypothesized changes in hemodynamics due to vascular stiffening; additional work is required to determine if they possess patient-specific prognostic capabilities.

Conclusion

In this paper, the effect of vascular stiffness on pulmonary flow in progressing PAH is examined using a patient-specific and patient-validated 2D numerical model. Comparison of 21 model runs to their corresponding clinical data show good agreement between model predictions of impedance and mean PA pressures and clinical measurements, thereby validating the model. PAH worsening was modeled using data from three PAH outcomes groups; these show not only the expected increase in mean PA pressures, but suggest an increase in pressure pulsatility as well. Interestingly, chronically increasing PA pressures decreased WSS, in agreement with clinical data that the impact of increased PA areas on WSS was greater than the impact of increased PVS. For a patient having moderate PAH with elastin-based upstream vascular remodeling, the model suggested that moving from elastin-dominant upstream vessel behavior to collagen-dominant behavior caused substantial increases in pressure, pressure pulsatility and WSS pulsatility. For the same patient, reducing PVR through a simulated vasodilator to a value equivalent to mild PAH did not decrease pressure pulsatility and in fact increased WSS pulsatility dramatically. Overall, these results suggest a close association between PVS and hemodynamics and those treatments should target decreasing or reversing upstream vascular remodeling in addition to decreasing mean pressures.