Directed Graph Based Image Registration

Abstract

In this paper, a novel image registration method is proposed to achieve accurate registration between images having large shape differences with the help of a set of appropriate intermediate templates. We first demonstrate that directionality is a key factor in both pairwise image registration and groupwise registration, which is defined in this paper to describe the influence of the registration direction and paths on the registration performance. In our solution, the intermediate template selection and intermediate template guided registration are two coherent steps with directionality being considered. To take advantage of the directionality, a directed graph is built based on the asymmetric distance defined on all ordered image pairs in the image population, which is fundamentally different from the undirected graph with symmetric distance metrics in all previous methods, and the shortest distance between template and subject on the directed graph is calculated. The allocated directed path can be thus utilized to better guide the registration by successively registering the subject through the intermediate templates one by one on the path towards the template. The proposed directed graph based solution can also be used in groupwise registration. Specifically, by building a minimum spanning arborescence (MSA) on the directed graph, the population center, i.e., a selected template, as well as the directed registration paths from all the rest of images to the population center, is determined simultaneously. The performance of directed graph based registration algorithm is demonstrated by the spatial normalization on both synthetic dataset and real brain MR images. It is shown that our method can achieve more accurate registration results than both the undirected graph based solution and the direct pairwise registration.

1. Introduction

Non-rigid image registration is one of the most important techniques in medical image analysis [1–5]. A large number of registration methods have been developed for pairwise image registration [6–10], where the subject is registered directly towards the template with the estimated spatial transformation by maximizing a certain similarity measure between the warped subject and the template. Although many pairwise registration methods have been proposed in the literature, such as landmark-based methods [11–13], intensity-based methods [7, 8, 14–17] and feature-based methods [6, 18–20], the accurate and consistent registration is still challenging due to the difficulties in establishing precise and consistent correspondences and optimizing the highly non-linear function.

The pairwise registration methods could face two major challenges. First, in practice, it is often the case that a group of images need to be registered toward a common space together to facilitate the subsequent group analysis. However, it is a non-trivial task to identify an appropriate template by which the whole population under study can be well represented. On one hand, if the template is pre-defined out of the population, the template may not be able to characterize the whole population under study. On the other hand, selecting an image within the population could also be problematic if it differs significantly from some images in the population. Second, it is generally difficult to achieve a reliable registration by simply registering each image to the template directly, especially when anatomical variations are significant across images within the population. The considerable anatomical variation in structures also limits the application of pairwise registration on a large dataset. Since only those subjects that are close to the template could be accurately registered while others far-away from the template may not achieve a good registration, the overall registration accuracy could be compromised.

For the first challenge, several algorithms have been proposed in the literature on selecting an appropriate template from the population. For example, in [21], the image which is the closest to the geometrical mean of the population is selected as the template. The geometrical center on the image space is obtained by applying Multi-Dimensional Scaling (MDS) [22] and all other images are then registered to the selected template. A similar method was proposed in [23] with the pairwise distance defined on the log-Euclidean space. However, the limitation of these single-template-selection approaches is that the sub-optimal performance is often achieved on the subjects which are distant from the template.

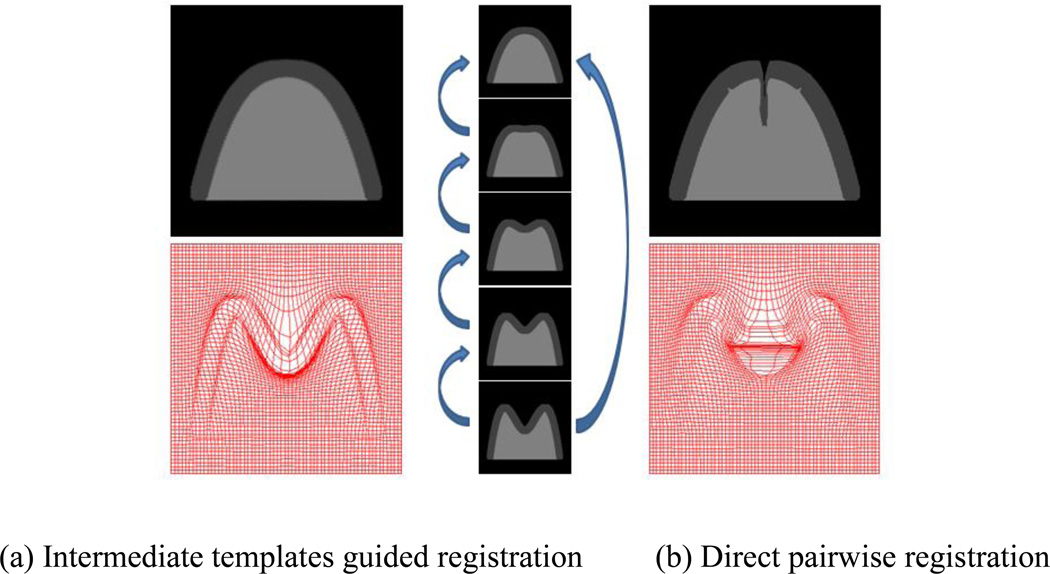
Many algorithms have also been proposed in the literature to alleviate the second challenge by getting other images involved into the registration between images with significant anatomical variations [24–33]. These images, often called intermediate templates (IT), can be used to better guide the registration from the subject to the template. To illustrate the advantage of the intermediate templates guided registration, an example is given in Fig. 1. Two registration strategies from a subject to a template are compared, i.e., direct pairwise registration (Fig. 1 (b)) and intermediate templates guided registration (Fig. 1 (a)). A sequence of five synthetic images (changing from double-peak to single-peak) is shown in the middle column of Fig. 1, with the template, three intermediate templates, and the subject from top to bottom, respectively. It can be seen that the intermediate templates guided approach (Fig. 1 (a)) performs more accurate registration than the direct pairwise registration (Fig. 1 (b)). Especially, at the center of the warped image by the pairwise registration, there exists a deep fissure with the similar depth of the valley as in the original subject image, which is caused by the inconsistent warping of different image parts and the incorrect computation on correspondences mapping. This example shows that the use of appropriate intermediate templates can guide more accurate registration.

Fig. 1.

The illustration of the benefit in using intermediate templates to guide the registration of images with large shape difference. Among the five images in the middle column, three images between the template (top one) and the subject (bottom one) are the selected intermediate templates. The registration results from the subject to the template by the intermediate templates guided registration (a) and the direct pairwise registration (b) are compared on both warped images and deformation fields. It shows that the intermediate templates guided registration can give more reasonable and accurate results.

The intermediate templates guided registration methods can be classified into two categories, intermediate template generation [25–28] and intermediate template selection [29, 31, 32], based on how to formulate the intermediate templates.

The intermediate template generation algorithms try to construct the intermediate templates using the statistical deformation models learned from a training dataset [27, 28]. In [27], a set of sample deformation fields are simulated by varying the deformation coefficients which are learned from a set of training deformation fields using Principal Component Analysis (PCA). Then the intermediate templates are generated by warping the original template with the simulated deformation fields. During the registration, the intermediate template closest to the subject is determined by comparing the image similarity. Since the transformation between the intermediate template and the original template is already known, only the residual deformation between the subject and the intermediate template needs to be estimated, which can be done much faster and more reliably by refining the known transformation. Nevertheless, the intermediate templates in this method are still limited on representing the real brain population, largely due to the insufficient sampling on the space of deformation fields and the dependency on the single selected template. To solve this problem, a Support Vector Regression (SVR) model has been proposed to correlate the statistical deformation and image appearance model based on a number of training deformation fields and images [28]. With the learned correlation by the regression model, for a new subject, its initial deformation field towards the template can be immediately predicted based on its image appearance. Albeit these methods demonstrate to have better performance compared to the direct pairwise registration, its overall performance is still limited by the training deformation fields estimated by the certain direct pairwise registration algorithm.

On the other hand, instead of generating new images as the intermediate templates, another category of methods aims to select the intermediate templates from real images, to bridge between subject and template [31, 32]. In general, the intermediate templates are selected from the same dataset. It is worth noting that the number of intermediate templates used to guide the registration is no longer limited to be one, which differs from the intermediate template generation method described above. Thus, the possible large deformation between the subject and the template can be decomposed into several mild ones along the respective path, which can be estimated with high reliability. After successfully concatenating the deformations of all segments, only a fast and efficient refinement step is necessary to achieve the final result. In [31], after learning the intrinsic manifold from the whole dataset, the pseudo-geodesic median image is determined as the template since it minimizes the total path length from each image to the template. The corresponding geodesic paths between each individual image and the template are computed to construct a tree to characterize the shape distribution of the population. The registration error could be reduced since only the nearby similar images need to be registered. Another way to implement this idea [32] is to build a Minimum Spanning Tree (MST) [34], where each node corresponds to one image and each edge is weighted by the distance between two connected images. The root node of the MST can be determined by selecting a node that has the minimal edge length to all other nodes on the MST or a node with the most children nodes, and the corresponding image is then utilized as the template for the image population. The major difference between these two methods is on the order of tree construction step and root/template selection step. In MST-based method [32], the tree is first built without specifying the root node by minimizing the total edge length between neighboring nodes on the tree. The root node is then selected on the built tree under a different criterion as introduced above. Since the edge length is directly related to the registration accuracy, the main goal in this framework is to minimize the overall registration error. On the contrary, in the pseudo-geodesics based registration method [31], the root image is determined before the path allocation to emphasize the significance of the template’s representativeness. Although these two methods may perform well on the registration of a group of images to one image, they do not provide an efficient way to solve the registration between arbitrary image pair in the dataset. Since the compositional path may not be the optimal registration path between the image pair, the registration accuracy could be undermined as the result of sub-optimal path allocation. For example, there may be registration paths bypassing the root node, which can be shorter, thus providing more efficient guidance to the underlying registration.

The success of intermediate templates selection based registration relies on the following two factors: the similarity definition between images and the registration path allocation. First, the similarity measurement has to characterize the essential difference between images and be consistent with the pairwise registration scheme adopted, which thus can sort all intermediate images properly with respect to the subject image. The inconsistency between the inter-subject similarity and the optimization criteria within the pairwise registration, e.g., intensity based intermediate template selection and mutual information based pairwise registration scheme, may compromise the overall performance. Second, as we can see in Section 2, the intermediate templates guided registration is essentially a directed process. The intermediate templates are allocated to be a singly-linked list, and thus the distance measure from one image to the next on the registration path should be directed to comply with the registration direction. We introduce a new term, directionality, to describe all registration path/direction related effects. Hence, a more intrinsic and consistent distance measurement can facilitate the selection of more appropriate intermediate templates to better guide the registration.

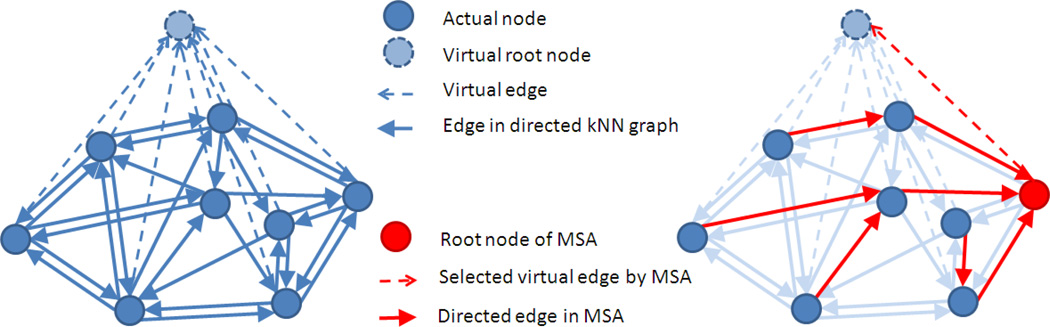
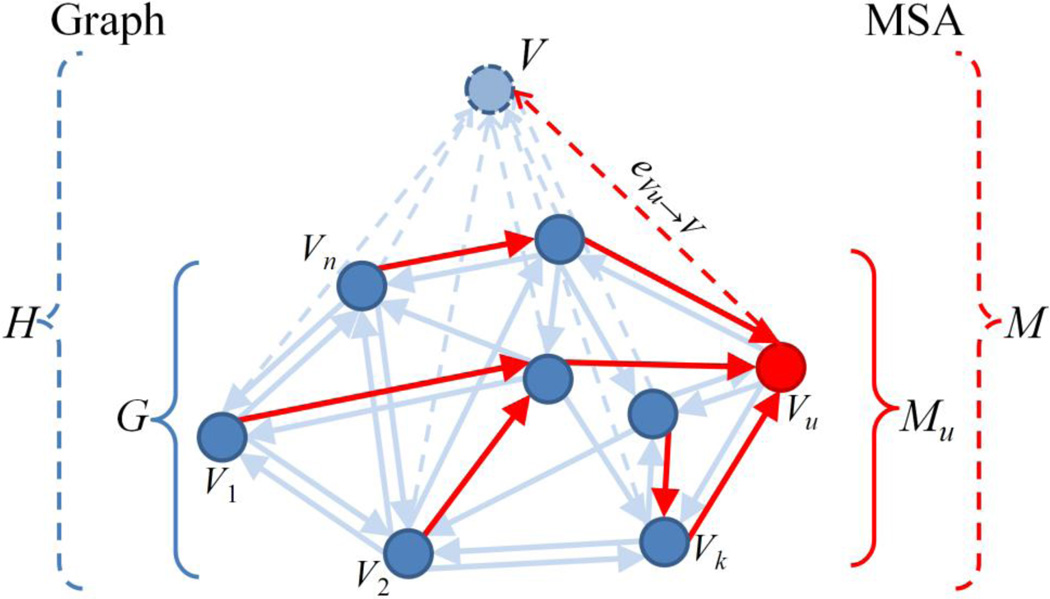
In this paper, a novel directed graph based image registration method is proposed, in which the registration is guided by the selected intermediate templates in the population. We define an asymmetric similarity measure on the ordered image pairs and construct a fully connected directed graph. To learn the local data structure, the directed k-Nearest-Neighbor (kNN) graph is then extracted and the optimal paths from one image to another via intermediate templates are identified. For the pairwise registration between subject and template among a group of images, it can be done by registering the subject image to the template along the allocated path. For the groupwise registration on an image population, the Minimum Spanning Arborescence (MSA) algorithm [35, 36] is applied to build a tree with the root node determined simultaneously. One example of the MSA extracted from a directed kNN graph is illustrated in Fig. 2 to demonstrate the framework of the proposed registration algorithm. Compared with other tree-based registration [31, 32], the proposed method takes both the template’s representativeness and the overall registration error into consideration together by solving the path allocation and template selection simultaneously. As our experimental results on both synthetic and real brain MR images will show, the proposed algorithm can choose better paths between images and could achieve more consistent and robust registration results than other methods, e.g., the undirected graph based method and the direct pairwise registration. Our directed graph based registration framework with intermediate templates can not only aid the groupwise registration from multiple subjects to one fixed template, but also benefit the pairwise registration between any image pairs.

Fig. 2.

Example for demonstrating the proposed directed graph based image registration framework. (a) The directed kNN graph built on the asymmetric similarity measures between ordered image pairs, and (b) its corresponding MSA extracted with the root template determined simultaneously. The registration is performed by deforming each image to the template along its respective path.

Some previous works took into consideration the order of the floating subject and the fixed template in pairwise registration, e.g., the symmetric diffeomorphic registration [37] which warps two images simultaneously to an implicit template in-between, and the asymmetric image-template registration [38] which introduces a correction factor to the symmetric cost function. However, in these methods, only the direction-related effect between two images was discussed without taking into consideration any other images, i.e., intermediate templates used in this paper. It is worth noting that the effect by directionality has been studied in the context of image interpolation and image segmentation [39, 40], but the directionality on the registration of whole image population has not been investigated in the literature yet, according to our best knowledge.

The rest of this paper is organized as follows. The concept of directionality and its existence in the registration is explored in Section 2. In Section 3, the proposed image registration framework based on the intermediate templates selection with directed graph is described in detail, with its applications in both pairwise and groupwise registration. In Section 4, extensive experiments on both synthetic and real datasets, as well as the comparison with other registration methods, are provided to demonstrate the performance of the proposed registration framework. We conclude and discuss the future work in Section 5.

2. Directionality in registration

In this section, a new concept, directionality in registration, is introduced, which is inspired by the inconsistency between the registration direction and the undirected similarity measurement of images. It is worth noting that the difference between two directional registration results of two images has been studied before, e.g., in [37, 41]. However, the directionality discussed here is a more general concept which is not limited within pairwise registration, and we have extended the application of this concept to intermediate template guided groupwise registration. Then we explore the existence of directionality in the real image registration and demonstrate with experimental results that the directionality is an essential factor to the success of registration. We further investigate the improvement of the registration accuracy and robustness by considering the directionality, which becomes the basis for the proposed directed graph based method.

Given a moving image S and a fixed target T in the image population I, the goal of the intermediate templates guided registration is to warp S towards T with the help of a subset of images in I, i.e., the intermediate templates, denoted as T_S→T = {T₁, T₂,…, T_m} ⊆ I, where m is the total number of intermediate templates. The registration path starts from S and follows all T_i as bridges until reaching T, by deforming S w.r.t. each intermediate template one by one, i.e., S → T₁ → T₂ → ⋯ → T_m → T. The registration R_S→T from S to T along the path takes less risk of being trapped in local minima than directly registering S to T (one example is given in Fig. 1).

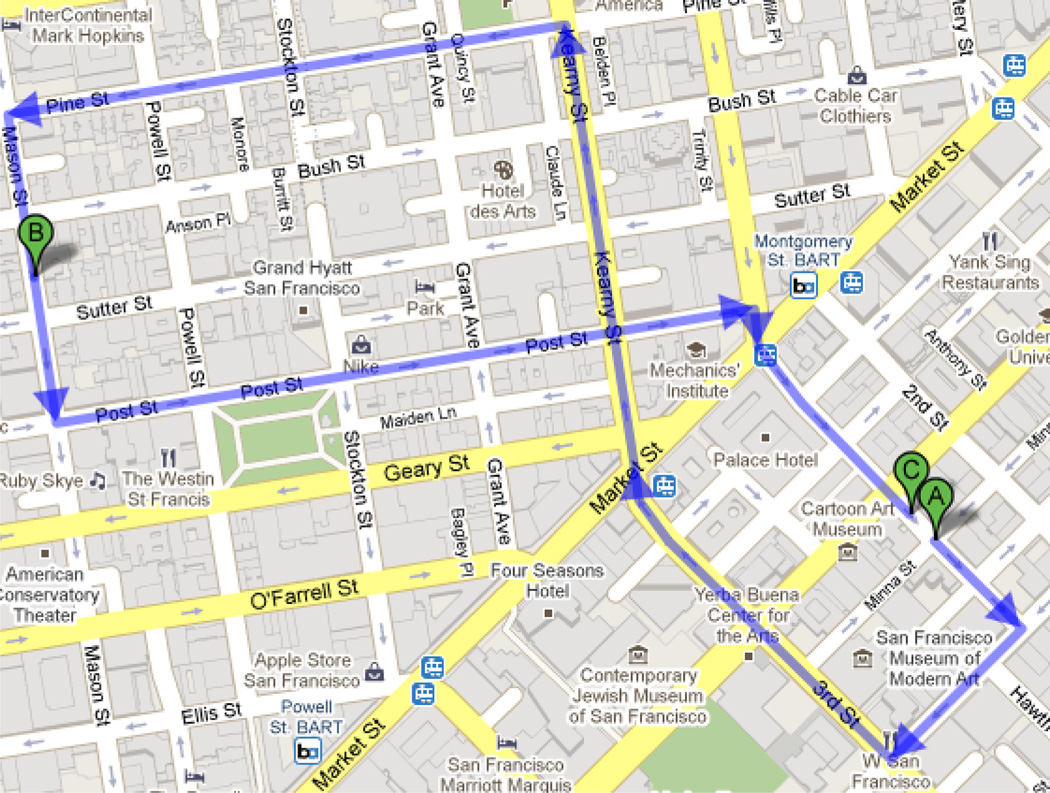
A potential inconsistency of image registration exists in the methods discussed above and it may compromise the registration performance. Since the intermediate template set T consists of an ordered image sequence, the registration from S to T is a directed process. In other words, only the forward registrations, i.e., R_S→T1, R_Ti→Ti+1 (i = 1,2,…, m−1) and R_Tm→T, are directly related to the final registration result, while the registration between all other image pairs and the backward registrations (e.g., R_T1→S) are irrelevant to the results. Therefore, the order among these images becomes important to affect the registration, and different orders will give different results. However, most distance measures defined in the literature are symmetric, or undirected. For example, the symmetric Euclidean distance on the intensity space, i.e., d_e(S,T) = ∫_Φ|S − T|² dx defined between two unaligned images in the image domain Φ, may not characterize the essential difference between images. For example, two images which appear to be quite different could be registered together very well, and thus they are almost equivalent to each other in the sense of spatial transformation. More advanced metric has been defined based on the transformation between images, e.g., a distance metric defined as the average between the measures on two directed pairwise registration results [32]. This undirected distance, however, is intrinsically inconsistent to the directed registration process from the moving subject to the fixed template, which has been largely overseen in the literatures. In other words, the measurements on the result of the forward registration R_S→T, e.g., the intensity difference between the template and the warped subject, is generally different from that of the backward registration R_T→S, even after taking interpolation errors into consideration. This is still true even when the forward and backward registrations are estimated to be invertible [8] as there are no explicit constraints to enforce a similar registration accuracy for two different directions. For the clarity of describing the existence and importance of the directionality, we here provide a simple real world example, where different directions could result in different consequences. In the routing example as shown in Fig. 3, the minimum distance between two locations of different direction is 1.2 miles from A to B and 0.7 mile from B to A (or C), respectively, due to the one-way constraints. Such a difference is considerably large, and thus it is not appropriate to describe the driving distance between A and B on the map with an average distance of 0.95 mile.

Fig. 3.

A real world example of directionality (from Google Map). The minimum driving distance between two locations is 1.2 miles (from A to B) and 0.7 mile (from B to C (or A)), respectively.

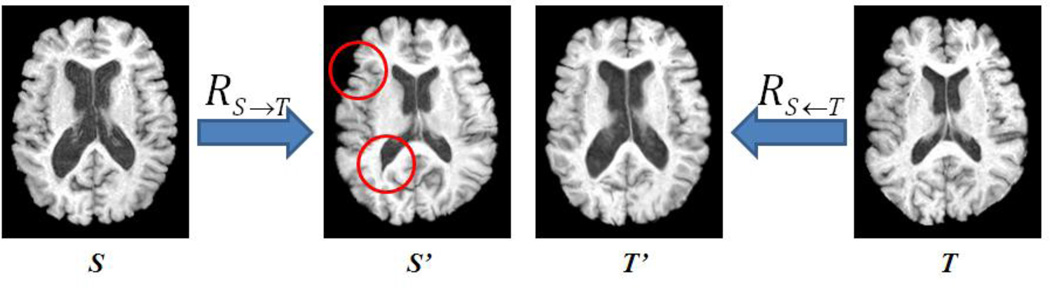
In this paper, we introduce the directionality to the registration, by considering the effect related to the registration direction or the path between two images. We first explore the directionality by visual examination on the pairwise registration results. On one hand, different registration directions may generate visually different results. In Fig. 4, two brain MR images from two elderly subjects with large shape difference are registered to each other by the diffeomorphic demons [7, 42] with same parameters. The warped subject image S’ by the forward registration cannot align subject S (with large ventricles) to T (with regular ventricles) very well, e.g., the regions indicated by the red circles in Fig. 4. However, the result T’ for R_T→S is more satisfactory as the difference between S and T’ is much smaller. On the other hand, we have seen that, in Fig. 1, the registration following different paths can result in completely different registered image.

Fig. 4.

Visual inspection of pairwise registration results by different directions. It shows that the registration quality varies according to the different registration directions. With the forward registration R_S→T, some regions in the warped image S’ are not aligned to T very well (as indicated by the red circles). While the registration result of R_T→S is more satisfactory, as the difference between S and T’ is much smaller.

Note that for an ideal registration solution which gives perfect alignment between subject and template, the registration performance is independent of the order of the images in registration or different registration paths, and thus the effect of directionality vanishes. However, such a perfect solution for the non-rigid registration does not exist in general, due to the intrinsic high non-linearity of the problem and the difficulty to establish a perfect one-to-one mapping between the anatomies of two images with different shapes (and most of the time, such a mapping does not exist at all).

The directionality exists not only in the pairwise registration but also in the groupwise registration. As we have discussed in Section 1, in the MST based groupwise registration [32] or the pseudo-geodesics based registration [31], the root templates (to determine final direction) and intermediate templates (to determine registration paths) are proved to be pivotal factors to the final registration performance. To be consistent with the essentially directed registration step and obtain a better result, the directionality should be taken into consideration in the tree-building step, e.g., constructing a directed graph with different weights assigned to the edges from S to T and from T to S. However, the metric defined in [32] is still symmetric when building an undirected graph. Such a non-negligible inconsistency between the undirected distance measures and the directed registration may undermine the registration performance. The distance between two images in [31] is defined only based on a single directed registration, which may cause troubles in performing registration on the opposite direction. Therefore, the registration based on the directionality requires a directed intermediate templates selection step.

To further quantitatively analyze the directionality, the general registration procedures between two images are discussed. To register two images S and T together, either of them can serve as the fixed template and the floating subject, and this may result in different registration performance. We first define a directed distance on an ordered image pair (S,T) based on the result of R_S→T. In non-rigid image registration, the performance is usually evaluated based on two coupled aspects of the registration result with respect to the estimated deformation field f_S→T(x): the dissimilarity between the fixed image T and the warped image S(f_S→T), i.e., d(S(f_S→T),T); and the measurement of the deformation degree of f_S→T, i.e., r(f_S→T). These two measurements are complementary to each other to balance the registration performance and both of them are essentially directional. Specifically, to quantify the registration result from S to T, two directed measurements are defined on the result of R_S→T: one is the intensity difference between the registered image and the template, d(S(f_S→T), T) = ∫_Φ|S(f_S→T(x))−T(x)|² dx, to measure the inherent appearance difference in the intensity space; and the other is the smoothness measure on f, r(f_S→T) = ∫_Φ‖∇² f_S→T(x)‖dx, where Φ is the image domain and ∇² is the Laplacian operator. The combined directed difference can be calculated as a weighted average, i.e.,

$$g(S,T)=\alpha ·d(S(f_{S\to T}),T)+(1-\alpha )·r(f_{S\to T}),\alpha \in [0,1].$$ (1)

The two measurements are normalized into the same range ([0, 1]) divided by the respective maximum value before being used in Eq. 1 based on the calculation results over the underlying dataset. The directed difference g defines an asymmetric measurement between two images in our algorithm, and it is different from a true metric which has to be symmetric. To quantitatively measure the directionality of a directed metric, we define the relative difference between two directed measurements as the directionality significance. For the directed measurement of d as defined above, its directionality significance on the image pair (S, T) is defined as

$${\mathit{\text{sig}}}_d(S,T)=\frac{|d(S,T)-d(T,S)|}{\text{min}(d(S,T),d(T,S))}\times 100\%.$$ (2)

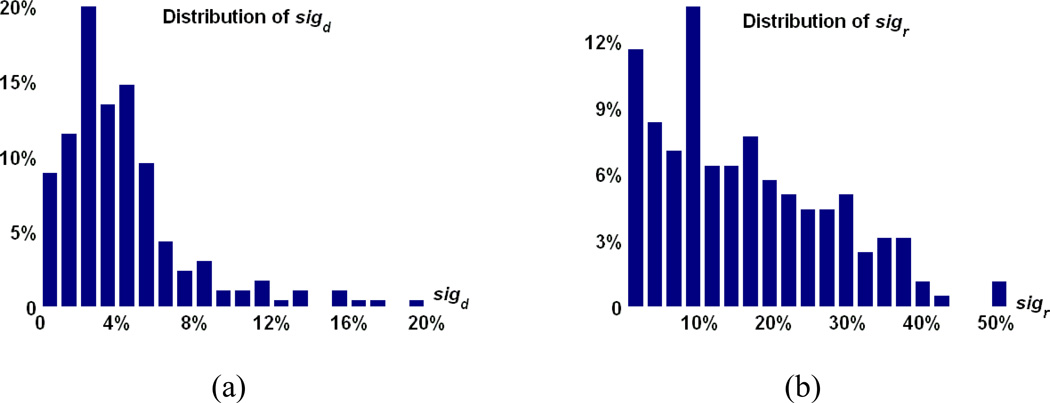
We can also define the directionality significance sig_r on the directed measurement of r in a similar way. For illustration, the directionality significances sig_d and sig_r are calculated for all image pairs in a dataset of 18 elderly brains with large shape difference [43]. The distribution of the directionality significance is shown in Fig. 5. We can see that the relative difference between the measurement on the forward and backward registration results can be reaching up to 20% and 50% on sig_d and sig_r, respectively, implying that the ignorance of the directionality in image registration may lead to a sub-optimal solution.

Fig. 5.

The distribution of the directionality significance defined on (a) the intensity difference between the registered image and the template (sig_d, left) and (b) the smoothness of the estimated deformation field (sig_r, right) on a set of 18 real brain images. In these plots, x-axis shows the value of directionality significance and y-axis shows the distribution of different values of directionality significance in percentage.

In the undirected graph based intermediate template selection [32], the edge connecting two images is assigned with a weight of the average value of two directed measurements. However, this similarity cannot reflect the results of any registration direction if the difference between the results of two directions is large. If such edges are finally selected, the resulting registration path could be far away from what it is expected in the tree-building step, and thus the registration performance is no longer optimal. Based on these observations, we further point out that the directionality could be a key factor that affects the selection of the ordered intermediate template set T and the registration accuracy greatly. This assertion is confirmed in our experiments, especially for the registration between images with large shape difference. It is worth noting that the proposed method does not aim to pursue an invertible image registration but rather to help allocate better registration path with intermediate templates, which has not been discussed in the literature to our best knowledge. In the following, the directionality will be utilized to find better paths for guiding both pairwise and groupwise registration.

3. Methods

In this section, a novel image registration framework based on directed graph is introduced. Within the framework, the pairwise registration between any two images is achieved with the help of intermediate templates selected from the same dataset, by the optimal directed registration path allocation (Section 3.1). To accomplish the simultaneous registration over the whole group, the minimum spanning arborescence (MSA) algorithm is applied to select the template and find the paths from other subject images to the template on the directed graph (Section 3.2). It is worth noting that the registration path in the generated MSA is exactly the same as the direction of the registration. Moreover, the order inside the selected intermediate template set is also consistent with the order of registration, which is inherently different from the undirected graph based methods as in [31, 32]. The overall proposed registration framework is summarized in Section 3.3 with discussions.

3.1. Directed graph based pairwise registration

In this section, the algorithm of intermediate templates guided pairwise registration is described. Given an image population I, the goal of pairwise registration is to accurately align the moving subject S towards the fixed target T with the help of a selected subset of images, i.e., intermediate templates. The image population is denoted as I = {I_i|i = 1,2,…, N}, where N is the number of images within the dataset. After assigning the directed dissimilarity measurement g to all ordered image pairs (I_i, I_j) in the dataset I, we can build a directed graph by considering each subject as a node and weighting each directed edge e_i→j with the corresponding path length g(I_i, I_j). To further learn the underlying structure, we construct a directed kNN graph (as shown in Fig. 2) and then approximate the directed distance on the image space by the shortest directed path from I_i to I_j on the kNN graph. The located shortest path is called the pseudo directed geodesics on the image space.

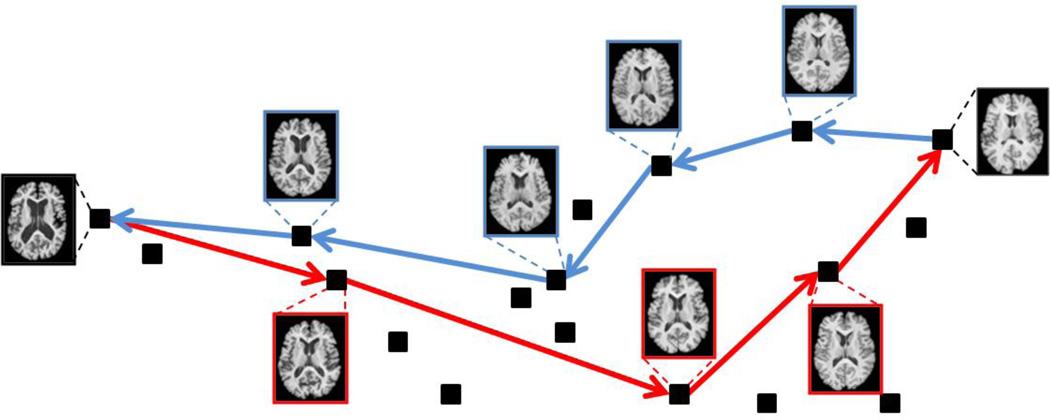
The construction process of the directed kNN graph is similar to that of the undirected kNN graph [44], while the only difference is that, in the directed kNN graph, two types of the nearest neighbors need to be considered, i.e., k-out-NN and k-in-NN, based on the edge direction. For each subject I_i, we first sort all other subjects I_u(u ≠ i, 1 ≤ u ≤ N) according to their distances g(I_i,I_u). Then, the nearest k neighbors with the shortest distances are selected as the k-out-NN since the direction of such edges is from I_i to I_u. Another set of k-in-NN (the direction of edge is from I_u to I_i) is also selected in a similar way. For each subject I_i, only those directed edges from the k-in-NN to the subject I_i and those from the subject I_i to the k-out-NN are kept in the directed kNN graph. One example of the resulting directed kNN graph is illustrated in Fig. 2a. If the resulting graph is not fully connected, we can increase k and repeat the above procedure till the directed kNN graph becomes a connected graph. The minimum k to guarantee a connected kNN graph is [N/2]. However, if k is set to be [N/2], the kNN graph can hardly characterize the local data structure and thus compromise the performance of the following steps, i.e., tree construction and intermediate template based registration. In this paper, we set k = 3 which has already assured a connected kNN graph in all of our experiments. Next, we adopt the Floyd–Warshall algorithm to find the shortest paths between any ordered image pair on this directed kNN graph. For the given image pair (I_s, I_t), the registration can be implemented by following the determined pseudo directed geodesics on the image space. It should be noted that the shortest directed path from I_s to I_t may be different from that in opposite direction, due to the characteristics of the directionality. For example, with an 18-elderly-brain dataset, we have detected totally 153 pairs of directed paths. Among them, only 40 pairs (26.1%) share exactly the same intermediate templates with each other, and all others (113 pairs, 73.9%) have different intermediate templates to guide the respective directed registration. This shows the existence of the directionality in the pairwise registration problem of real images. Such an example on the elderly brain image set is given in Fig. 6, which shows the different registration paths allocated between two images.

Fig. 6.

Different registration paths are determined by the directed graph based method for the forward and backward registrations between two images. Two such paths are shown by the red and blue arrows, respectively. Only the images on the path are displayed.

3.2. MSA based groupwise registration

To solve the groupwise registration in a population, both the final template and the intermediate templates for each subject need to be determined. With the assigned asymmetric weights on the directed edges, the minimum spanning tree (MST) algorithm is no longer applicable on the directed kNN graph since it is only defined on an undirected graph. Instead, we propose to build an MSA on the dataset. Note that in other tree-based groupwise registration [29, 31, 32], the global template selection and respective registration paths allocation are two separated steps based on different criteria by focusing on either the importance of the final template representativeness or the overall registration error. For the optimal solution to satisfy two different criteria, we build MSA and solve the combinative optimization problem by simultaneously determining the template and finding the path to the template for each subject.

In graph theory, the MSA algorithm is first proposed by Zhu and Liu [35] and Edmonds [36] independently to solve the directed-graph-based tree-building problem by minimizing the total length of the directed edges along the direction from root to other nodes. In the proposed MSA algorithm [35], an iterative strategy is applied to remove the unnecessary edges until the final tree is determined. First, for each node, the inward edge with the minimum weight is selected and all such edges form an interim graph. If there is a circle in the graph, a new node is added to replace the circle and update the corresponding edge weights, which is called shrinking, and the above steps are iterated on the new graph after shrinking. If there is no circle, we can expand those shrunk circles to recover the original nodes and finally build the MSA. Note that the original MSA method can only construct a tree with a pre-specified root with O(N²) complexity. However, if the template is pre-defined to guide the path allocation, we can only obtain a sub-optimal solution. To obtain the global optimal solution of MSA, we have to set each of the subjects as the potential root and build totally N trees, and then choose the tree giving the shortest total path length as the final solution. Thus the computational complexity increases to O(N³). Here, for saving computation time, we take another strategy to find the global optimal solution in one run by adding a virtual node (in the left of Fig. 7), which is designated as the fixed root in the extended graph. The N extra directed edges from all existing N nodes to the virtual node are added with the same weight, which is assigned to be larger than the summation of all edge lengths in the original graph. First, MSA is built on the extended graph, with a fixed root (the virtual node) and red (both solid and dashed) edges. Then, the global optimal MSA on the original graph can be obtained by removing the virtual node from the extended tree, as shown by the solid red edges with the red node as root (in the right of Fig. 7). The reason to account for the mathematical equivalence between these two methods is that all directed edges connecting the virtual node have the same weight, and there is one and only one such edge can be selected in the extended tree due to the minimum total length requirement. The computational complexity of this new solution is O((N+1)²), i.e., at the same level as in the case of building MSA with a pre-defined root node. Please refer to the appendix for the proof. The introduction of virtual node can not only significantly reduce the computing complexity when formulating MSA, but also help automatically determine the optimal template, which makes it possible to take into consideration simultaneously both the proper representativeness of the root template and the global optimal intermediate template selection.

Fig. 7.

One example to show the fast MSA algorithm without a pre-defined template. By adding the virtual node (indicated by the dashed circle) and assigning each virtual edge with a specific weight (the left plot), MSA with the virtual node as the pre-defined template on the extended graph can be used to determine the optimal MSA without a pre-defined root (the tree with solid red edges) on the original graph.

3.3. Summary and discussion

The proposed image registration framework with directed graph based intermediate template selection can be summarized as follows:

1. For the image population, do fast pairwise registration on each ordered image pair and their directed distance is calculated based on Eq. 1.

2. Build a fully connected directed graph with the asymmetric distance and further extract the directed kNN graph.

3. If the image pair of fixed template and floating subject is pre-determined, go to Step 4 (i.e., pairwise registration); otherwise go to Step 5 (i.e., groupwise registration).

4. For pairwise registration: find the shortest directed path by applying the Floyd-Warshall algorithm and the registration to the template can be completed by warping the subject to the intermediate templates on the path one by one.

5. For groupwise registration: build MSA on the directed kNN graph to simultaneously determine the optimal template and the corresponding registration path from each subject to the template. The groupwise registration can be achieved by warping each subject to the template along the respective registration path.

The proposed directed graph based registration has two major advantages compared with other methods. First, the intermediate templates selection step and the registration step are inherently consistent by considering the directionality in the framework. This is also the most important benefit achieved in the proposed algorithm. Second, the template in population registration is determined automatically, and the registration paths from all other images to the template are allocated at the same time. Other methods, e.g., the undirected graph based method [31] and [32], solve the tree building and root selection in two separate steps without any coherent criteria. That means the proposed method can take both the importance of the final template and the overall registration error into consideration within a single framework.

Note that the computational complexity of the proposed algorithm is the same as other tree-based algorithms. We need O(N²) times of fast registrations for the graph construction and O(N) times of elaborated registrations for the final registration by sequentially compositing the deformation fields at each node along the path. The MSA algorithm can be performed very fast compared to the running time of image registration. In our experiments, the directed kNN graph built on the results of the elaborated registration is quite similar to that based on the fast registration, but the computing time is about 3~4 times longer.

4. Experiments

To demonstrate the advantages of the proposed directed graph based registration method, we evaluate it on both synthetic data set and real brain MR images. The results from two related pairwise registration methods, namely the undirected graph based registration and the direct pairwise registration, are provided for comparison. For undirected graph based methods, the edge weight is assigned to be the average value of two directed measurements in Eq. 1. Two groupwise registration methods, the group mean method [45] and the congealing method [46–48], are also compared with the proposed algorithm on real image data set. Throughout this paper, the diffeomorphic demons [7] is used as basic pairwise registration method. It is worth noting that other pairwise registration algorithms can be adapted in the proposed framework as the basic computing unit, e.g., the symmetric log-diffeomorphic demons [42] and the consistent image registration [8]. They show a similar improvement on the registration accuracy in the proposed framework compared to the results of undirected graph based registration. For the concatenation of a series of intermediate deformation fields, the deformation field composition method is applied [7]. The experimental results demonstrate that the registration results of the proposed method are more consistent and accurate.

4.1. Synthetic dataset

We first evaluate the performance of the proposed method on a synthetic dataset with 56 synthetic 2D shapes with the size of 140×140 simulating different structures of gyri and sulci in brain (some samples are shown in the first row of Fig. 8). The regions of gray matter (GM) and white matter (WM) are represented by the pixels with intensity of 128 and 255, respectively, and the background regions are filled with pixels of intensity 0. This selection is to maximize the contrast among different regions, i.e., the background, WM and GM, and thus help to amplify the misalignment related effects, especially for the regions with small registration errors.

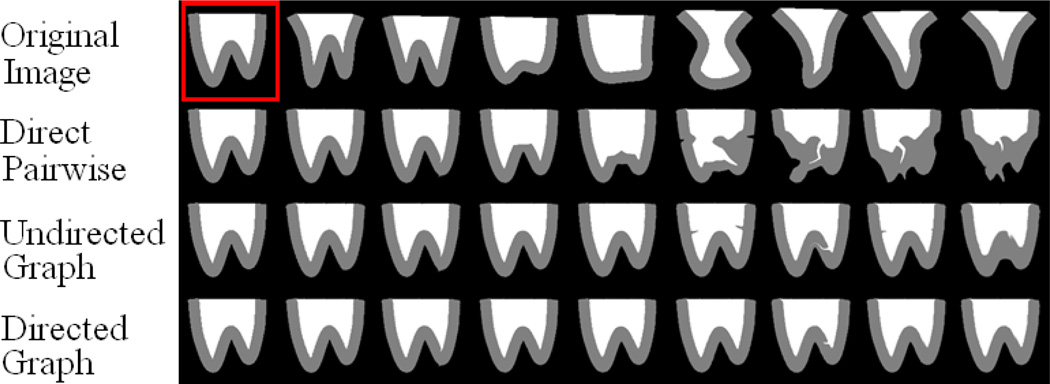
Fig. 8.

Different registration results on a synthetic dataset to illustrate the importance of identifying a proper registration path formed by intermediate templates. All images on the first row are registered to the template (the top-left one within the red box) along the path given by three different methods, i.e., direct pairwise, undirected graph based registration and directed graph based registration, with the results shown in the second to the fourth rows, respectively.

The performance for the intermediate templates based pairwise registration of the proposed algorithm is demonstrated in Fig. 8. In Fig. 8, the top-left image (highlighted by the red box) is selected as the template and all other images are registered to the template by following the paths given by three different methods. The template is specifically selected to be the one that is far away from the population center as illustrated in Fig. 9, to test the performance on registering images with significant differences. As shown in Fig. 8, the registration results on different images within the synthetic dataset vary dramatically by following different registration paths. Several images even fail to be registered to the template by the direct pairwise registration (the 2^nd row in Fig. 8). On the contrary, the intermediate templates based registration can provide a much better guidance than the pairwise registration. Comparing the results in the 3^rd and 4^th row, it can be seen that all images are roughly warped onto the template space, although the results of undirected graph based method are not very satisfactory for some cases where the shape difference is considerably large. The proposed method can find more suitable paths with smoother changes between intermediate templates, thus successfully guiding the registration for each subject. The registration results in this experiment clearly show that even both with the guidance from the intermediate templates, the results by the directed graph based method (which takes advantage of the directionality) are better than those by its undirected counterpart.

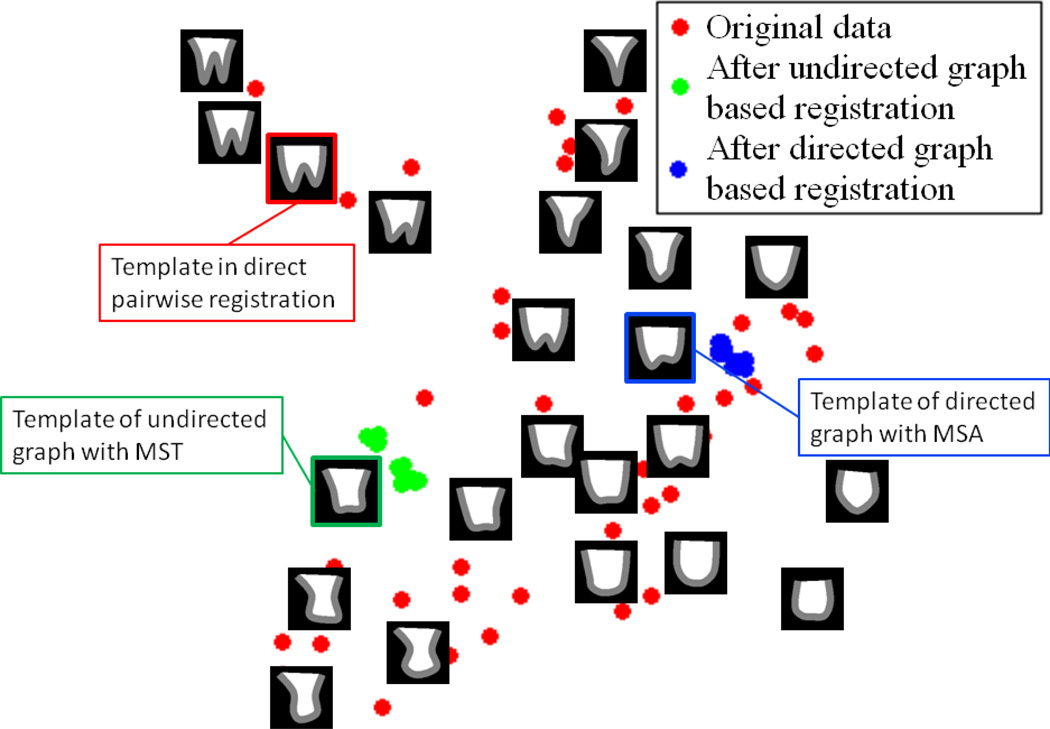
Fig. 9.

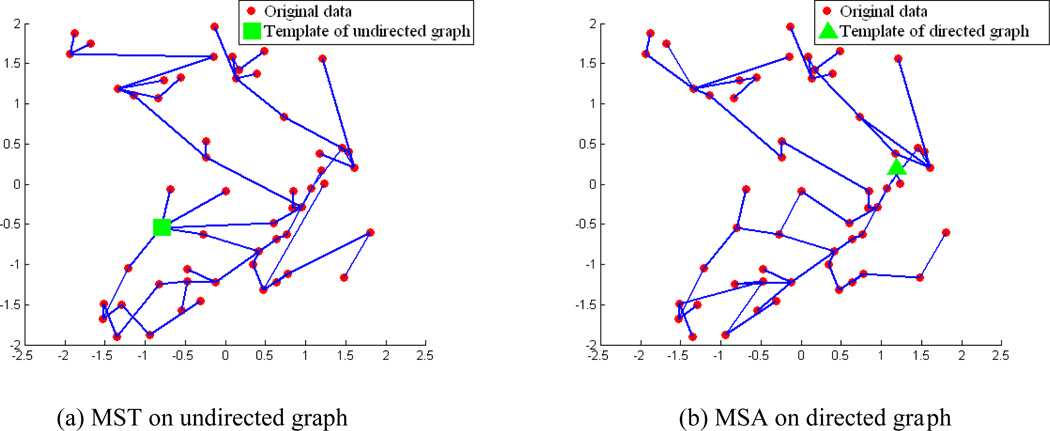
The illustration of the data distribution on the 2D PCA space of the synthetic dataset. The original dataset is projected onto the 2D PCA space, along with the selected templates of direct pairwise, undirected graph with MST and directed graph with MSA method. To clearly demonstrate the relative positions of the different templates in the data space, some images are also displayed at their corresponding locations. It can be seen that the template determined by directed graph with MSA is much closer to the geometric center than that by undirected graph with MST. The registered image sets of both methods are also projected onto the same 2D space. The warped images are much closer to each other by the method of directed graph with MSA than that by the undirected graph method as it is relatively easy for all images to be registered to the geometric center.

To validate the influences of the directionality in intermediate templates guided groupwise registration, two methods based on undirected graph with MST and directed graph with MSA are applied on the synthetic dataset, respectively. The root in MST is selected to be the node with the shortest total length along the registration path on the tree. Each original image is projected onto a 2D space which is spanned by the two eigen-vectors corresponding to the largest two eigen-values after applying PCA on the original dataset before any registration processing (as illustrated in Fig. 9). In Fig. 9, the template utilized in the direct pairwise registration, and two templates selected by MST and MSA, respectively, are all marked in the data space. The template used in the direct pairwise registration is selected to be distant to the population center, and the template of MSA is much closer to the population center than that of MST. Some original images are overlaid on the 2D PCA space to demonstrate the relative locations and the shape changes from different directions to the population center. The registered image set of different methods is also projected onto the same 2D space to visualize the registration results in the data space. It can be seen that the registration results of directed graph based method are much denser around the geometric center of the underlying space. The built MST on the undirected graph and the MSA on directed graph are illustrated in Fig. 10.

Fig. 10.

The built MST on undirected graph and the MSA on directed graph are illustrated.

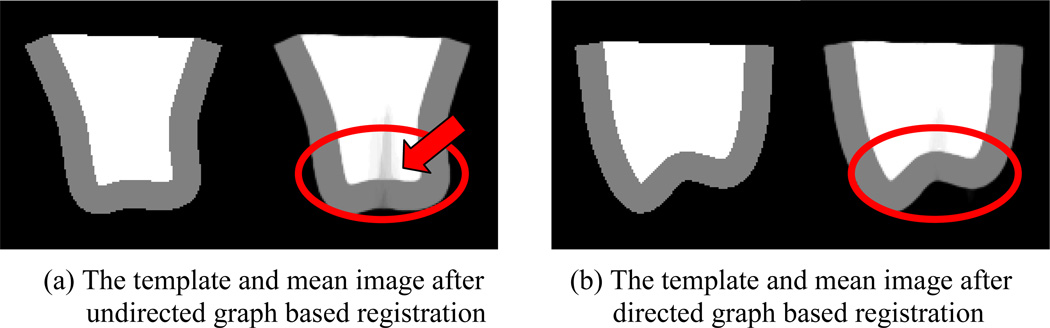
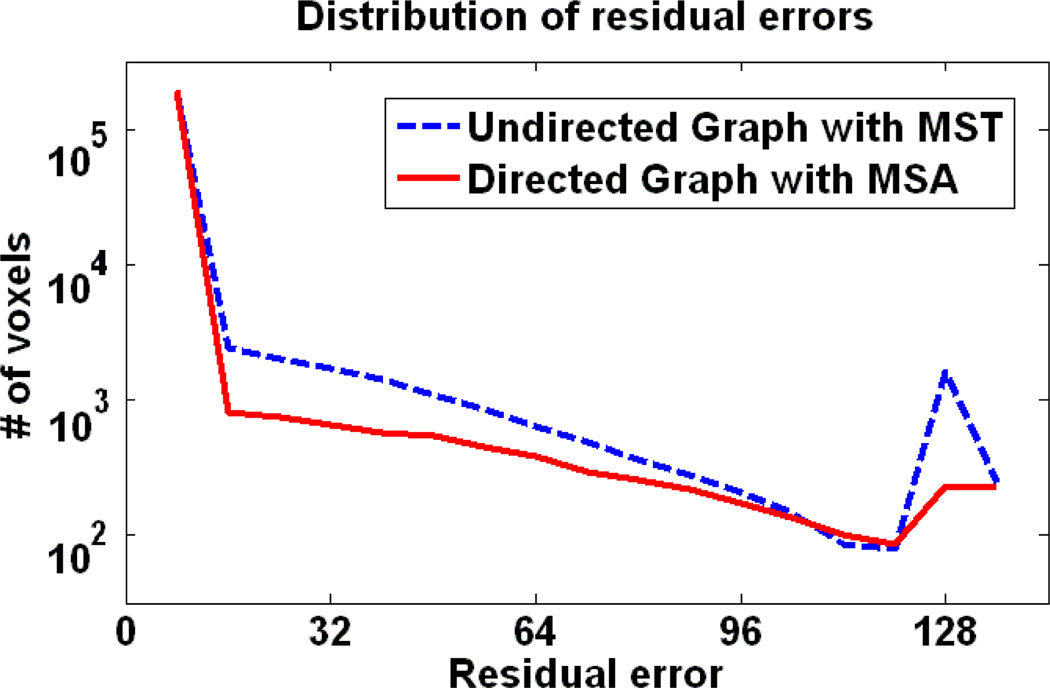
The mean aligned images by two different registration methods are shown together with the template in Fig. 11 (a) and (b), respectively. The undirected method fails to register images precisely in more cases thus giving a mean image with a much larger shaded area in the center (as indicated by the arrow). On the other hand, the proposed method can achieve more consistent registration. Note that different methods detect different templates in this case and their relative locations can be seen in Fig. 9. Here we choose the same weighting factor α = 0.5 in Eq. 1. To emphasize the registration accuracy and consistency of the proposed algorithm, we provide the distribution of the voxelwise residual errors in Fig. 12. The residual errors of directed graph based method are more concentrated around zero and with much less voxels having the largest value. It should be noted that the largest residual error is around 128, which is equal to the intensity difference between two adjacent areas.

Fig. 11.

The template and the mean aligned image of the synthetic dataset by (a) undirected graph with MST and (b) directed graph with MSA.

Fig. 12.

The distribution of the voxelwise residual errors between the registered images and the template. It can be seen that the proposed directed graph based registration method can achieve much smaller errors than its undirected counterpart.

We also provide the quantitative comparisons in Table 1 on the mean/max of all the pairwise distances between registered images (dist_p), the average overlap rate (overlap) and the average entropy (entropy) on different tissues in the region defined by the red circle in Fig. 11(a) and (b). Here, we use the Jaccard coefficient metric [49] to measure the overlap rate between two registered images of the same region. For two registered regions U and V, the Jaccard Coefficient is defined as J(U,V) = |U∩V|/|U∪V|, where | · | defines the area of region under consideration.

Table 1.

The quantitative comparisons on average distance on all registered image pairs, average overlap rate and entropy are listed for undirected graph and directed graph based registration.

	mean(distp)	max(distp)	overlap	entropy
Before registration	67.7	104.1	66.0%	0.330
Undirected graph based registration	15.8	43.2	96.1%	0.032
Directed graph based registration	13.5	30.0	97.8%	0.025

To demonstrate the overlap rate of the registered images in a group, tissue labels of each voxel on each ROI from all warped images first vote to obtain a common atlas. This is done by assigning each voxel with a tissue label that is the majority of all tissue labels at the same location from all the aligned images. Then, the Jaccard Coefficient between each of the registered images and the common atlas is calculated, with the average score listed in Table 1. The average entropy is calculated in a similar way between the registered tissue-segmented images and the common atlas, which is another measurement of the registration accuracy based on the anatomical structures. We can see that the proposed method consistently outperforms the undirected graph based method. The paired t-test on the pairwise distances between registered images shows that the directed graph based method can generate a much more compact registered image set (with p < 10⁻⁵). We can also draw the similar conclusions based on the paired t-test on the overlap rate and entropy with p < 10⁻³.

4.2. ADNI dataset

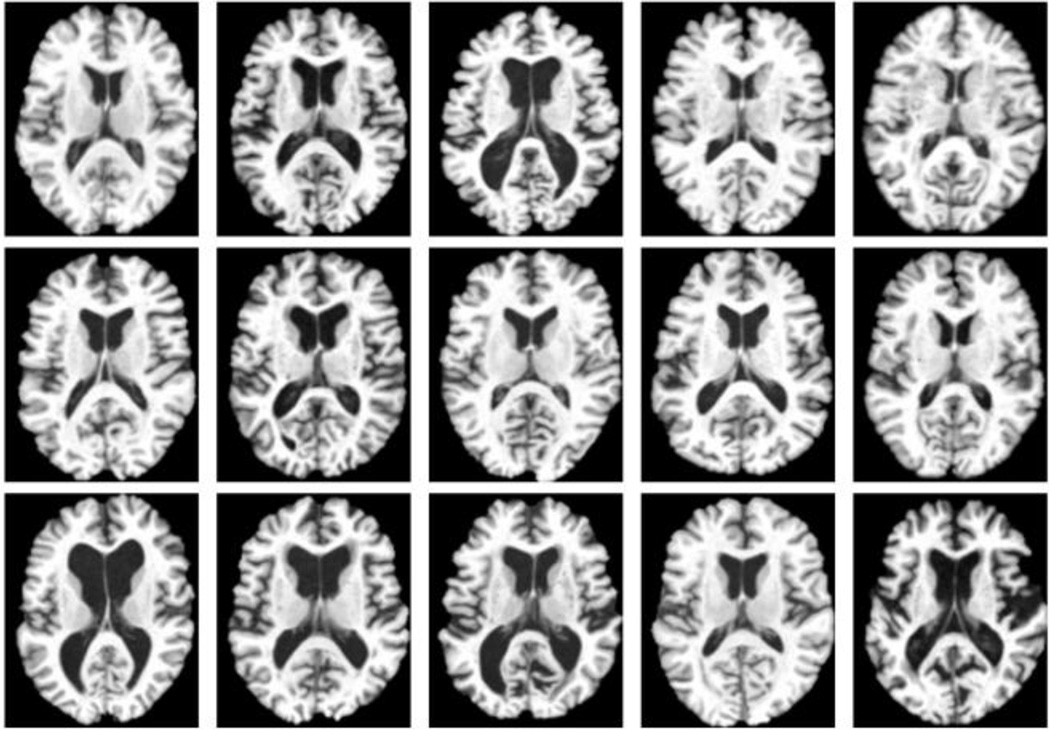
We apply the proposed algorithm on the ADNI dataset [50] to further test it on the large dataset with real images by groupwise registration. 60 brain MR images in total are selected from ADNI dataset with 20 from each category of normal control, MCI and AD. All images are pre-processed in the following way. First, we do AC (anterior commissure) − PC (posterior commissure) corrections [51] on all images and then resample them to 256×256×256. We then use N3 algorithm [52] to correct the intensity inhomogeneity followed by skull stripping. Here we take advantage of two popular methods, Brain Surface Extractor (BSE) [53] and Brain Extraction Tool (BET) [54], facilitated with further manual editing, to obtain clean skull stripping results. We finally apply FAST in FSL [55] to segment brains into three different tissues (i.e., GM, WM and CSF) and FLIRT for affine registration to remove global shape differences (translation, rotation, scaling, etc.). Some examples after affine registration are shown in Fig. 13, from which we can see the significant brain anatomical differences in the dataset.

Fig. 13.

Examples from ADNI dataset with large anatomical difference in brain MR images.

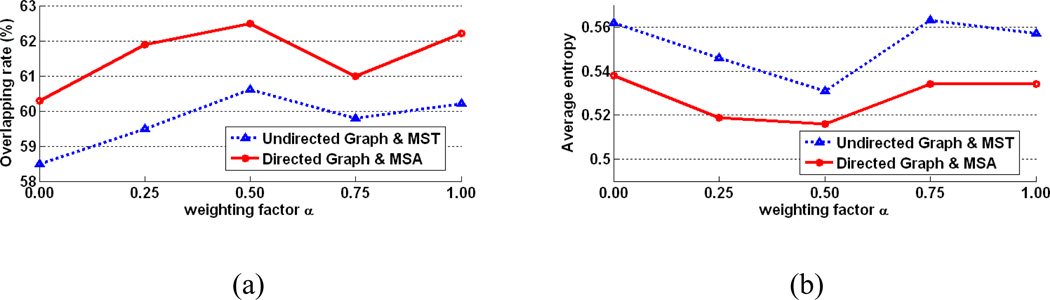
To show the influence of weighting factor in Eq. 1, the directed/undirected graph based algorithms are implemented with α = 0.0, 0.25, 0.5, 0.75 and 1.0, respectively. From Fig. 14, we can see that the registration accuracy measured by the overall overlap rate and the average entropy on all registered tissue-segmented images by the proposed method is consistently better than the undirected graph based method. Since both methods select the same image as the template when using α = 0.5, we can make fair comparison on the registration accuracy between two methods for this case. The quantitative comparison on tissue overlap rate and average entropy clearly shows the advantages of the proposed method in determining the registration paths. Our method gives 62.5% on the average tissue overlap rate over GM, WM, and CSF, which is higher than 60.5% given by the undirected graph based registration and 57.5% by the direct pairwise registration to the same template (with all the standard deviations less than 0.8%). This result is also significantly higher than results of the group mean method (58.7%) and the congealing method (47.2%).

Fig. 14.

The average overlap rate (a) and average entropy (b) on the ADNI dataset are plotted after alignment by the undirected graph based registration method and the directed graph based registration method, with different weighting factors α∈ [0, 1].

We also measure the average overlap rate and entropy on different tissues (GM, WM and CSF) on the ADNI dataset in Table 2. Our method achieved the highest overlap rates on all three tissues. The average entropy for our method on the aligned segmentation images is 0.52, which also tops all other methods.

Table 2.

The overlap rate and average entropy of the registered segmentation images by four different methods on ADNI dataset.

	Overlap rate			Entropy
	GM	WM	CSF
	Before registration	40.1%	54.5%		28.8%	0.85
Direct pairwise	54.7%	70.4%	47.4%	0.58
Undirected graph with MST	57.3%	73.2%	50.8%	0.54
Directed graph with MSA	59.6%	74.8%	52.9%	0.52
Group mean	54.1%	73.4%	48.5%	0.55
Congealing	42.9%	59.5%	39.2%	0.59

4.3. LPBA40 dataset

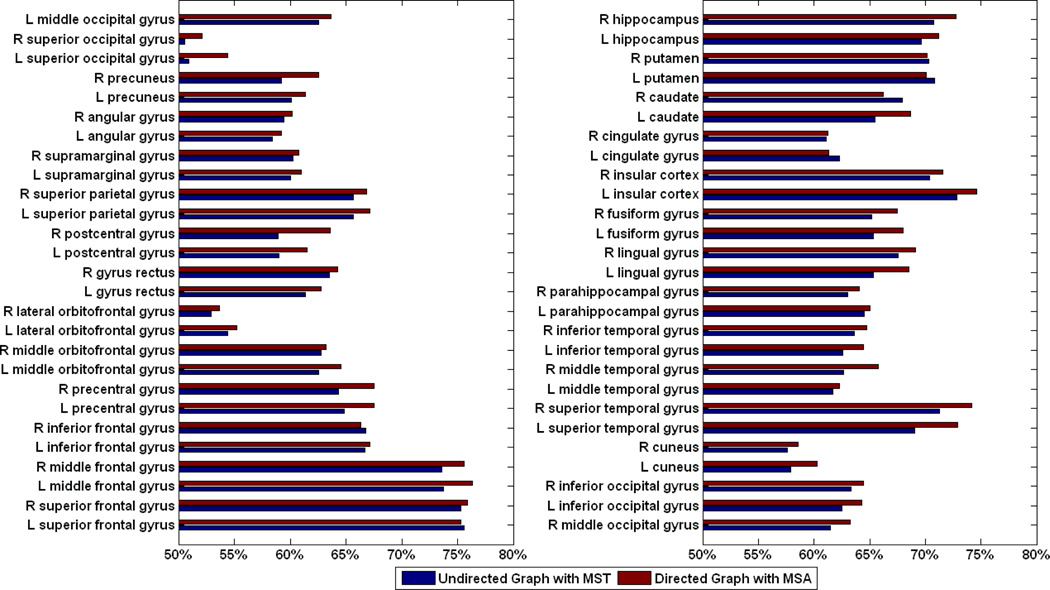
We here evaluate the proposed registration framework on LONI LPBA40 dataset [56], which has 40 brain images with 54 manually labeled ROIs. In this section, we set the weighting factor α = 0.5 in Eq. 1 for all experiments. The proposed registration method with directed graph based intermediate templates selection can increase the mean overlap rate of the registered images to 68.22%, which is higher than that given by the undirected graph based method (66.32%). It is worth noting that the built tree from the directed graph has a height of 5, which is smaller than that of the undirected graph (i.e., 7). It means that for those images far away from the population center, the proposed algorithm can achieve a better registration performance by allocating less but more appropriate intermediate templates. We plot the overlap rates of all 54 ROIs in Fig. 15, which shows the proposed method is better for most of ROIs (48 out of all 54 ROIs). The paired t-test of the overlap rates on all ROIs shows that the proposed method can achieve consistently higher overlap rates than undirected graph based method (with p<0.001).

Fig. 15.

The overlap rates of 54 ROIs on the registered LONI LPBA40 dataset by the undirected graph based registration method and the proposed directed graph based registration method.

Since each registration method identifies different subject image as the respective final template, it thus may not be a fair comparison of the registration results based on different templates. To fairly compare the performance of different registration methods, we therefore apply one common template to all three registration methods, i.e., the direct pairwise registration, the undirected graph based and the directed graph based registration methods. Specifically, the template determined by MSA and MST in the proposed algorithm, T_MSA and T_MST, are used as the common template, respectively. For the direct pairwise registration, all other images will be registered towards this common template directly. For the MST-based tree building algorithm, the weight on each undirected edge is assigned to be the average value of the measures on two directions, and then the common template is selected as a root node for building the tree. Thus, based on the same template determined by the MSA algorithm, the average overlap rate given by the direct pairwise registration method and the undirected graph based method is 64.79% and 66.68%, respectively. It can be seen that on the same template T_MSA, the directed graph based method can still achieve better registration performance (68.22%) compared to the undirected graph based method (66.68%) as shown in the 6^th and 5^th row of Table 3. One possible reason is that, for a fixed template, MSA can find better registration paths than the undirected MST based solutions with the directionality being considered. We can also make comparison between the results by undirected graph based registration with different templates, to demonstrate the importance of selecting an appropriate template in registration. As shown in the 2^nd and 5^th rows of Table 3, we can see that even with the same undirected graph based tree building algorithm, the performance of the registration with the template selected by MSA is slightly better (0.36%) than that of the registration with the template selected by MST. But if we compare the results on the five ROIs with smallest volume (usually with lower overlap rates), the average improvement becomes 1.51%, and this value goes up to 2.78% comparing between methods in the 2^nd and 6^th rows (and the overall increase is 1.90%), which means that the small ROIs can gain larger improvement. It is also interesting to see that the registration results T_MSA are consistently better than that with T_MST. This also implies the better representativeness of the template selected by the directed graph based method. The registration accuracy measured by the tissue overlap rate and average entropy for the group mean and congealing method is also given in 7^th and 8^th rows of Table 3.

Table 3.

Comparison of different registration methods and effect of template in undirected graph based method. T_MSA and T_MST are the templates selected by the original MSA and MST, respectively on LPBA40 dataset.

	Tree-building algorithm	Selected template	Overlap rate	Entropy
Direct pairwise	Direct path	TMST	63.90%	0.468
Undirected graph with MST	MST	TMST	66.32%	0.448
Directed graph with a different template	MSA	TMST	66.85%	0.446
Direct pairwise	Direct path	TMSA	64.79%	0.462
Undirected graph with MST (with a different template)	MST	TMSA	66.68%	0.445
Directed graph with MSA	MSA	TMSA	68.22%	0.431
Group mean method	-	-	66.36%	0.450
Congealing method	-	-	66.80%	0.449

5. Conclusions

Accurate spatial alignment between images with large shape differences is not only clinically important but also technically challenging. In this paper, a new image registration framework is proposed by taking advantages of the directionality in image registration. Moreover, a large deformation between the images to-be-registered is decomposed into several gentle ones by selecting intermediate templates. Since each small deformation can be easily estimated with higher precision, the registration accuracy could be improved compared to the direct pairwise registration methods. In the proposed framework, the pairwise registration is guided along the shortest path on the directed graph defined with asymmetric distance measures. On the other hand, the groupwise registration is achieved by building an MSA on the directed kNN graph with the automatically selected template. Compared with direct pairwise registration and undirected graph based registration, the proposed algorithm can determine a set of more appropriate intermediate templates to facilitate more accurate registration. Our future work includes applying our directed graph based registration method to the general groupwise registration of large clinical dataset, e.g., for detecting disease related brain abnormalities.

Appendix I

Proof for the mathematical equivalence of the MSA without a specified root on a directed graph and the MSA with a virtual node as the fixed root on the extended graph.

Problem: A directed graph G is given with n node, V₁, V₂, …, V_n, some of which are connected by the directed edges, e.g., e_Vi→Vj (see Fig. 16). The total edge length on graph G is denoted by L(G). For each node V_i, i=1,2,…,n, the MSA on G with V_i as the root is denoted as M_i, and the total edge length on M_i is L(M_i). Among all M_i, M_u gives the minimum total length, i.e., L(M_u) < L(M_i), i ≠ u. One virtual node V and n virtual directed edges are added to G and result in an extended directed graph H, assigning the same weight w = 2×L(G) to each directed virtual edge e_Vi→V, i=1,2,…,n. On the extended graph H, the MSA with the fixed root V is denoted as M. Now we need to prove M = M_u ∪ e_Vu→V.

Fig. 16.

The mathematical equivalence of the MSA without a specified root on a directed graph G and the MSA with a virtual node as the fixed root on the extended graph H.

Lemma 1: There is one and only one virtual edge in M.

Proof of Lemma 1:

First, there is at least one virtual edge in M. If there is no virtual edge in M, M has two separated part, graph G and node V, and thus it is not an MSA since it is not a connected graph with.

Second, if there is more than one virtual edge in M, since L(M_u) < 2×L(G), we have L(M)> 2×(2×L(G))>2×L(G)+L(M_u) = L(M_u ∪ e_Vu→v).

As M_u ∪ e_Vu→V is a spanning tree on H, which means M is not a tree with the minimum total length, it is contradictory to the definition of MSA on H.

Proof:

From Lemma 1, we know that there is one and only one virtual edge in M, and this edge is denoted as e_Vk→V, where V_k is the node bridging between the original graph G and virtual node V.

First, we will prove that M = M_k ∪ e_Vk→V. Since M_k is the MSA on the original graph G with a fixed root at V_k, any other tree (T) with V_k as the root thus has larger total edge length than L(M_k), which means L(M_k ∪ e_Vk→V) < L(T ∪ e_Vk→V). So M = M_k ∪ e_Vk→V is the MSA on the extended graph H with the fixed root V.

Second, we are going to prove that the node V_k is V_u, and thus it makes M consists of M_u and e_Vu→V.

$$\begin{array}{ccc}\text{If }k\ne u,\text{we have }L(M)=\hfill & L(M_k\cup e_{\mathit{\text{Vk}}\to V})\hfill & \hfill \\ \hfill & =L(M_k)+L(e_{\mathit{\text{Vk}}\to V})\hfill & \hfill \\ \hfill & >L(M_u)+L(e_{\mathit{\text{Vk}}\to V})\hfill & (L(M_u)\text{ is smaller than any tree length on }G)\hfill \\ \hfill & =L(M_u)+L(e_{\mathit{\text{Vu}}\to V})\hfill & (L(e_{\mathit{\text{Vk}}\to V})=L(e_{\mathit{\text{Vu}}\to V})=2\times L(G))\hfill \\ \hfill & =L(M_u\cup e_{\mathit{\text{Vu}}\to V}),\hfill & \hfill \end{array}$$

which is contradicting to the definition of MSA.

Till now, we have proven that M = M_u ∪ e_Vu→V, which means we can remove the virtual edge from the MSA with virtual node as fixed root on the extended graph to get the MSA without a specified root on the original graph.