The Energetics of CNS White Matter

Abstract

The energetics of CNS white matter are poorly understood. We derive a signaling energy budget for the white matter (based on data from the rodent optic nerve and corpus callosum) which can be compared with previous energy budgets for the gray matter regions of the brain, perform a cost-benefit analysis of the energetics of myelination, and assess mechanisms for energy production and glucose supply in myelinated axons. We show that white matter synapses consume ≤0.5% of the energy of gray matter synapses and that this, rather than more energy-efficient action potentials, is the main reason why CNS white matter uses less energy than gray matter. Surprisingly, while the energetic cost of building myelin could be repaid within months by the reduced ATP cost of neuronal action potentials, the energetic cost of maintaining the oligodendrocyte resting potential usually outweighs the saving on action potentials. Thus, although it dramatically speeds action potential propagation, myelination need not save energy. Finally, we show that mitochondria in optic nerve axons could sustain measured firing rates with a plausible density of glucose transporters in the nodal membrane, without the need for energy transfer from oligodendrocytes.

Introduction

The brain is only 2% of the body's mass, but requires 20% of its resting energy consumption (Sokoloff, 1960), reflecting the high metabolic demand of neural processing (Attwell and Laughlin, 2001). The brain reduces conduction delays and energy use by dividing local and global connections into distinct gray and white matter regions (Wen and Chklovskii, 2005). While the energetics of information processing have been analyzed for the gray matter (Attwell and Laughlin, 2001; Lennie, 2003; Nawroth et al., 2007; Alle et al., 2009; Howarth et al., 2010; Sengupta et al., 2010), much less is known about white matter energetics. This is surprising because: (1) the white matter is half of the human brain, (2) energy supply is a constraint on neuronal information processing (Laughlin and Sejnowski, 2003; Niven and Laughlin, 2008), (3) plasticity of the white matter is increasingly being invoked as a mechanism for learning (Ullén, 2009; Fields, 2010), and (4) a disrupted energy supply to the white matter can cause vascular dementia (Englund, 2002; Patel and Markus, 2011). We address several key principles of CNS white matter energetics, as follows.

First, while it is traditionally assumed that synapses are absent in white matter, it has recently been found that, during development, unmyelinated axons make glutamatergic (Kukley et al., 2007; Ziskin et al., 2007) and GABAergic (Káradóttir et al., 2008) synapses onto oligodendrocyte precursor cells (OPCs). Similar synapses may also be present after myelination is complete (Royeck et al., 2010). Synapses account for the major proportion of energy use in the gray matter [from the studies by Attwell and Laughlin (2001) and Howarth et al. (2010), corrected for new data showing that the Na⁺ influx underlying action potentials is threefold less than was previously believed: Alle et al. (2009); Carter and Bean (2009); Sengupta et al. (2010)], but it is not known whether the axon-OPC synapses in the white matter account for a comparable proportion of white matter energy use. Second, while the long-term energetic benefit of myelin in terms of action potential cost reduction is well described (Hartline and Colman, 2007), little is known about how this compares to the size of the initial energetic investment for building myelin during development, or to the cost of maintaining the myelinating oligodendrocytes. Finally, once myelinated, most of the volume of the axon is spatially remote from the extracellular space, prompting the suggestion that myelinated axons must receive metabolic support from ensheathing glia (Nave, 2010), but it is not known whether this is really necessary.

Here, we investigate these three aspects of energy use and supply in CNS white matter by (1) deriving a signaling energy budget for the white matter that can be compared with similar energy budgets for the gray matter regions of the cerebral cortex (Attwell and Laughlin, 2001; Lennie, 2003), olfactory glomerulus (Nawroth et al., 2007), and cerebellar cortex (Howarth et al., 2010); (2) performing a cost-benefit analysis of the energetics of myelination; and (3) assessing mechanisms for energy production and glucose supply in myelinated axons.

Materials and Methods

This section provides the detailed calculations that are used to reach the conclusions presented in Results. On a first reading this section can be omitted without loss of continuity. For convenience, many of the parameters used are collected in Table 1.

Table 1.

Assumed values for the calculations, listed in order of appearance in Materials and Methods

Energy budget for the white matter
No. axons in optic nerve	100,000		Lam et al. (1982)
Percentage axons myelinated at P12	10	%	Foster et al. (1982)
Mean diameter of myelinated axon in rat	0.77	μm	Foster et al. (1982)
Mean diameter of myelinated axon in guinea pig	0.89	μm	Koch et al. (2006)
Mean diameter of unmyelinated axon	0.3	μm	Foster et al. (1982)
Optic nerve length at P12	5.5	mm	Matheson (1970)
Mean firing rate of axons	4.34	Hz	Koch et al. (2006), Perge et al. (2009)
Voltage change for action potential	100	mV	Attwell and Laughlin (2001)
Internode length	240	μm	Ransom et al. (1991)
Node length	0.8	μm	Ishibashi et al. (2002)
Membrane capacitance	1	μF/cm2
g ratio	0.81		Guy et al. (1989)
Myelin wrap periodicity	15.6	nm	Agrawal et al. (2009)
Space between axon and myelin	4	nm	Halter and Clark (1991)
Node capacitance	0.019	pF	Calculated
Internode capacitance	0.49	pF	Calculated
Action potential Na+ entry scaling factor	1.3		Alle et al. (2009)
Optic nerve cross-sectional area at P12	0.13	mm2	Matheson (1970)
OPC EPSC charge transfer	366	fC	Kukley et al. (2007)
No. OPCs in P12 rat optic nerve	45,400		Barres et al. (1992)
No. axons contacting 1 OPC	141	axons	Kukley et al. (2007)
Vesicles released onto 1 OPC/axon/action potential	0.34	vesicles	Kukley et al. (2007)
Release cost/vesicle	23,400	ATPs	Attwell and Laughlin (2001)
Nernst potential Na	50	mV	Assumed
Nernst potential K	−100	mV	Assumed
No. oligodendrocytes in P12 optic nerve	38,100		Barres et al. (1992)
No. astrocytes in P12 optic nerve	15,650		Barres et al. (1992)
Astrocyte resting potential	−80	mV	Assumed
All other cells' resting potential	−70	mV	Bakiri et al. (2011), or assumed
Axon resistance for unit area	7.35	Ω.m2	Alle and Geiger (2006)
Axon internal resistivity	1.5	Ω.m	D'Angelo et al. (1997)
Oligodendrocyte input resistance	200	MΩ	Karadottir et al. (2005)
OPC input resistance	800	MΩ	Clarke and Attwell, unpublished
Astrocyte input resistance	560	MΩ	Clark and Mobbs (1994)
ATP use on nonsignaling processes	25	%	Attwell and Laughlin (2001)
Optic nerve cross-sectional area in adult	0.494	mm2	Phillips et al. (1991)
Cortex: no. synapses/neuron	8000		Braitenberg and Schuz (1998)
Cortex: neuron density	9.20×1013	/m3	Braitenberg and Schuz (1998)
Energetic costs and benefits of myelination
Fraction of myelin that is protein	0.25		Jahn et al. (2009)
Fraction of myelin that is lipid	0.75		Jahn et al. (2009)
Density of myelin	1.1	g/cm3	Inouye and Kirschner (1988)
Mean firing rate d = 0.76 μm	3	Hz	Perge et al. (2009)
Mean firing rate d = 0.86 μm	4	Hz	Perge et al. (2009)
Mean firing rate d = 1.06 μm	6	Hz	Perge et al. (2009)
Mean firing rate d = 1.26 μm	8	Hz	Perge et al. (2009)
O2 use by muscle mitochondria	5.8	ml O2/min/ml	Schwerzmann et al. (1989)
ATPs generated per glucose molecule	30	ATP	Stryer (1995)
Energy supply and production in myelinated axons
O2 molecules consumed per glucose molecule	6	O2	Stryer (1995)
Turnover rate of GLUT3	6500	/s	Maher et al. (1991)
GLUT3 Km for glucose	1	mm	Nualart et al. (2009)

An energy budget for the CNS white matter

The major energy requirement for neural signaling is the cost of reversing cellular sodium ion influx (Siesjo, 1978; Attwell and Laughlin, 2001). For the developing optic nerve, we therefore estimated the energy requirement for reversing the sodium ion entry producing action potentials in axons, producing synaptic potentials in postsynaptic OPCs, and occurring at the resting potential in the neurons and glial cells present. We mainly used values for the P12 rat optic nerve and corpus callosum, when the myelination process is under way (Foster et al., 1982) and synaptic communication between axons and OPCs is relatively high (Kukley et al., 2007; Ziskin et al., 2007), thus providing a likely upper limit for the energy consumption of synapses in the white matter. For simplicity in this calculation we assumed that all myelinated axons had the same diameter, the mean diameter measured in the adult rat optic nerve. Later sections will investigate how myelinated fibers of different diameters have different properties.

Energy required for action potentials.

The rodent optic nerve contains ∼100,000 axons (Lam et al., 1982; Koch et al., 2006). To model a white matter tract with mature myelinated axons of large diameter and smaller unmyelinated axons coexisting, for example as occurs in the corpus callosum (Wang et al., 2008), we considered the nerve at P12, when 10% of the axons have become myelinated and have a mean diameter inside the myelin of 0.77 μm (in rat), while 90% are unmyelinated with a mean diameter of 0.3 μm (Foster et al., 1982), and the nerve is 5.5 mm long (Matheson, 1970). For simplicity, the diameter of myelinated axons was assumed to be the same at the node as in the internode (0.77 μm), although in fact the nodal diameter is about half that in the internode (Fabricius et al., 1993; Sánchez et al., 1996): the node and internode capacitance values derived below imply that this will increase the ATP calculated to be used on the action potential by <2%. In addition, myelination was assumed to occur at the same time to different physiologically defined classes of ganglion cell (i.e., we assume that at P12 10% of all classes of ganglion cell axon are myelinated), and was assumed not to affect the mean rate of action potential firing (which will be set by the intraretinal information processing driving firing of the ganglion cell somata). The analysis was then extended to the adult optic nerve to characterize a situation where all axons were myelinated (see below).

The mean axonal firing rate was estimated by averaging the action potential frequency (produced by natural visual scenes) over all the classes of ganglion cell studied in guinea pig retina by Koch et al. [(2006) their Table 1] weighted by frequency of occurrence (their Table S2). Since Koch et al. (2006) did not state a mean firing rate for “sluggish cells” that could not be classified, we assigned those cells a mean firing rate of 3 Hz, equal to that seen for the lowest firing rate of the classified cells (i.e., the ON-direction cells). The resulting mean firing rate was 4.34 Hz, similar to that reported in the study by Perge et al. (2009), their Figure 6.

The minimum Na⁺ entry generating each axonal action potential was calculated as the charge entry needed to change the voltage across the axon capacitance by the action potential amplitude. This amplitude was set to 100 mV following Attwell and Laughlin (2001), which is the standard textbook value and is between the value of 80 mV recorded in retinal ganglion cell axons by Massey and Miller (1988) and the value of 120 mV recorded in hippocampal neurons by Alle et al. (2009). Computer simulations of the action potential in myelinated axons (Bakiri et al., 2011) show that its amplitude in the internode is essentially identical to that at the node, being only 2% lower at the center of the internode; this difference was ignored. For each unmyelinated axon the capacitance (52 pF for the whole length of the nerve) was calculated from the axon diameter and length, and the standard specific biological membrane capacitance of C_A = 1 μF/cm². For each myelinated axon, the total 5.5 mm length of the optic nerve was occupied by 23 internodes of mean length 240 μm (Ransom et al., 1991) and nodes of length 0.8 μm (Ishibashi et al., 2002). These experimentally determined internode length and axon diameter values give a higher internode:diameter ratio (310:1) than is often quoted based largely on measurements from myelinated peripheral nerves [100:1 (Rushton (1951)]. The total effective axon capacitance was the sum of the capacitance of the nodes and of the internodes. For each node the capacitance was calculated from the node diameter and length, and the standard specific biological membrane capacitance per unit area of C_A = 1 μF/cm², to be 0.019 pF. For the internode, an axon diameter of 0.77 μm and the CNS g ratio of 0.81 (Guy et al., 1989; Chomiak and Hu, 2009) predict an outer myelin diameter of 0.95 μm and, for a myelin wrap periodicity of 15.6 nm (Agrawal et al., 2009) starting after a 4 nm extracellular space around the axon (Halter and Clark, 1991), 6 myelin wraps (each consisting of two membranes with a center to center separation of 7.8 nm). The capacitance of each membrane was calculated (using a specific capacitance per membrane of 1 μF/cm²) from its 240 μm length and its radius, starting with the axon (radius 0.77/2 μm), then the inner membrane of the first myelin wrap (radius 0.77/2 + 0.004 μm), the outer membrane of the first myelin wrap (radius 0.77/2 + 0.004 + 0.0078 μm), the inner membrane of the second myelin wrap (radius 0.77/2 + 0.004 + 2 × 0.0078 μm) etc. These capacitances were then summed as capacitors in series to obtain an effective capacitance of 0.49 pF for a single internode of length 240 μm.

The minimal sodium ion entry, calculated as above, was then multiplied by a factor of f = 1.3 to take account of overlap of the voltage-gated Na⁺ and K⁺ currents [from the study by Alle et al. (2009) for hippocampal neurons; Carter and Bean (2009) found f = 1.24 for cortical neurons], and converted to ATP use using the fact that the Na⁺/K⁺-ATPase consumes one ATP per three Na⁺ extruded. Per action potential, each myelinated axon was predicted to use 23% of the ATP consumed by each (smaller) unmyelinated axon. The ATP use per action potential was then multiplied by the mean firing rate of 4.3 Hz, and summed over all axons to give the total ATP used per second on action potentials in the optic nerve. The result was 5.48 × 10¹² ATP/s on unmyelinated axons and 1.38 × 10¹¹ ATP/s on myelinated axons, giving a total of 5.62 × 10¹² ATP/s for the whole nerve. For a nerve of length 5.5 mm and cross-section 0.13 mm² (Matheson, 1970), this gives an ATP consumption of 7.86 × 10²¹ ATP/ m³/s.

Action potential costs in the gray matter of the cerebral cortex were based on the calculations in the study by Attwell and Laughlin (2001). The ATP costs for action potentials were adjusted downward by a factor of 3.08, according to the smaller factor for the Na⁺ entry needed to produce the action potential that was recently reported for mammalian axons [f = 1.3 times the minimum needed to charge the membrane capacitance (Alle et al., 2009), replacing the original factor of f = 4.0 used by Attwell and Laughlin (2001) and Howarth et al. (2010), which was derived from the less energetically efficient squid giant axon (Hodgkin, 1975)].

Energy required for synaptic transmission.

There is no evidence for axo-axonal synapses in the optic nerve, and thus the only synapses considered were those between axons and OPCs. Kukley et al. (2007) characterized the electrophysiological, pharmacological, and biophysical properties of these synapses in the optic nerve as being identical to those found in the developing rat corpus callosum, so we used their more extensive analysis of corpus callosum axon-OPC synapses to assess the postsynaptic and presynaptic energy usage at these synapses.

Postsynaptic energy use was estimated from the fact that Kukley et al. (2007) showed that, when all presynaptic axons are stimulated, the postsynaptic current in a single corpus callosum OPC generates an average charge transfer of 366 fC. This value, along with the number of OPCs in the P12 rat optic nerve [45400: Barres et al. (1992)], allowed us to calculate the total postsynaptic charge entry in the nerve when all presynaptic axons are excited (assuming the same number of inputs to OPCs in the optic nerve and corpus callosum). Converting this to Na⁺ entry and thus ATP use, and multiplying by the mean action potential frequency of 4.3 Hz, gave us an estimate of the total energy needed for postsynaptic processes in the optic nerve (1.5 × 10¹¹ ATP/nerve/s).

To calculate the energy needed for presynaptic processes in the optic nerve, we used the estimate of Kukley et al. (2007) that each OPC receives input from 141 axons, each of which releases 0.34 vesicles per action potential. From these values and the number of OPCs in the P12 rat optic nerve (above), it follows that 2.2 × 10⁶ vesicles will be released when every axon in the optic nerve is excited. Since 23,400 ATP are consumed per vesicle released on presynaptic calcium flux, vesicle cycling, and neurotransmitter recycling (Attwell and Laughlin, 2001), the total energy needed for presynaptic processes in the optic nerve with axons firing at a mean rate of 4.3 Hz is 2.21 × 10¹¹ ATP/nerve/s.

Summing these presynaptic and postsynaptic costs gave the total ATP used on synaptic processes as 3.71 × 10¹¹ ATP/nerve/s, or 5.19 × 10²⁰ATP/m³/s.

Energy required for the resting potential.

Equation 4 of Attwell and Laughlin (2001) gives the ATP needed to pump out the resting Na⁺ influx and thus maintain the resting potential of a cell of membrane resistance R_m and resting potential V_rp, as follows:

moles/s, where V_Na (+50mV) and V_K (−100mV) are the Nernst potentials for Na⁺ and K⁺, and F is the Faraday constant. In the P12 rat optic nerve, apart from 90,000 unmyelinated axons and 10,000 myelinated axons (Lam et al., 1982), there are also 38,100 oligodendrocytes, 45,400 OPCs, and 15,650 astrocytes [Barres et al. (1992), their Fig. 6]. We assumed a resting potential of −80 mV for the astrocytes and −70 mV for all the other cells. The resting membrane resistance, R_m, of the axons was calculated as follows. Using the measured 700 μm space constant of 0.4 μm diameter hippocampal mossy fiber axons (Alle and Geiger, 2006), and an assumed internal resistivity of 1.5 Ωm (D'Angelo et al., 1997), we calculated the specific resistance of a CNS axon membrane to be 7.35 Ωm². The total axon membrane resistance (for the 5.5 mm long nerve) was then calculated as 1.42 GΩ for an unmyelinated axon of 0.3 μm diameter and 0.55 GΩ for a myelinated axon of 0.77 μm diameter. The input resistance of oligodendrocytes was set to 200 MΩ (Káradóttir et al., 2005), that of OPCs to 800 MΩ (as measured by L. Clarke and D. Attwell, unpublished, in white matter OPCs in P30 cerebellar white matter), and that of single astrocytes (when not gap-junctionally coupled to other astrocytes) to 560 MΩ [as measured in the ganglion cell axon layer of the retina: Clark and Mobbs (1994)]. Calculating the ATP used to maintain the resting potential in each cell type, and multiplying by the number of cells present, gave the total ATP usage on resting potentials as 2.38 × 10¹³ ATP/nerve/s or 3.33 × 10²² ATP/m³/s.

ATP used on housekeeping mechanisms.

Nonsignaling related ATP consumption was assumed to be 1/4 of the total energy use in the gray matter of the cerebral cortex (Attwell and Laughlin, 2001), both in the gray and in the white matter, i.e., 6.88 × 10²² ATP molecules/m³/s.

Extending the analysis to the adult optic nerve with all axons myelinated.

To assess the ATP consumption in a purely myelinated white matter tract, we assumed that in the adult rat optic nerve the same number of astrocytes and OPCs (with the same input resistance) were present per unit length of nerve (in fact the number of OPCs in the adult optic nerve may be less than in the developing nerve, so this assumption will, if anything, overestimate the energy used on synapses in the adult white matter). We also assumed that the number of oligodendrocytes per unit length of the nerve (with the same input resistance) was increased tenfold (to provide the extra myelin sheaths needed), and that instead of 10% of axons being myelinated and of 0.77 μm diameter with the remaining 90% being unmyelinated and of 0.3 μm diameter, all the axons were myelinated and of 0.77 μm diameter [as a result of which the cross-sectional area of the optic nerve increases by a factor of 3.8 on going from P12 to adulthood: Phillips et al. (1991)]. These changes decrease the ATP use on action potentials (from 7.86 × 10²¹ to 5.08 × 10²⁰ ATP/m³/s), but increase the ATP used to maintain resting potentials (from 3.33 × 10²² to 5.42 × 10²² ATP/m³/s) because of the larger diameter of myelinated axons and the larger number of oligodendrocytes. OPCs have been reported to still receive synaptic input from axons in the adult white matter (Ziskin et al., 2007; Royeck et al., 2010). The energy used on synaptic transmission to each OPC was, for simplicity, assumed to be the same as in the developing optic nerve, as was the housekeeping energy (6.88 × 10²² ATP molecules/m³/s).

Comparing synapse density between white and gray matter regions.

We calculated synapse density in the optic nerve (8.95 × 10¹⁵ synapses/m³) by dividing the total number of synapses in the P12 rat optic nerve (calculated from the known number of OPCs and their known number of synaptic inputs, see above) by the total volume of the P12 rat optic nerve [calculated from the known cross-sectional area and length: Matheson (1970)]. To calculate synapse density in the rat cerebral cortex (7.36 × 10¹⁷ synapses/m³), the number of synapses/neuron [8000: Braitenberg and Schuz (1998)] was multiplied by the density of neurons [9.2 × 10¹³ neurons/m³: Braitenberg and Schuz (1998)]. We then calculated the ATP cost per synapse per second in the optic nerve and cortex by dividing the total synaptic energy cost per cubic meter per second for each region by that region's synaptic density.

The energetic costs and benefits of myelination

Energetic and metabolic substrates can be obtained from food, or from fat, protein, or glycogen reserves previously laid down in the body. Investment of resources in myelination requires either more food intake, or the use of internal reserves that later need to be replenished (which may be allowed by the reduction of energy expenditure on action potentials that myelination confers). We compared the local energetic cost of synthesizing the myelin of one internode with the ATP saving made on subsequent action potentials propagated along that internode, and then investigated whether the ATP saving made per unit time on action potentials outweighed the extra ATP use on maintaining the resting potential of the myelinating oligodendrocyte. Wherever possible, we used values specific to the adult guinea pig optic nerve, where the morphological and physiological features of retinal ganglion cell axons are well defined.

For an internode of length L_internode around an axon of radius r, the energetic cost of constructing the myelin for one internode is given by the cost of synthesizing the mass of protein and lipid making up the myelin, i.e., as follows:

where F_protein = 0.25 and F_lipid = 0.75 (Jahn et al., 2009) are the fractions of myelin by weight that are protein and lipid respectively, C_protein and C_lipid are the cost in ATP molecules per gram of protein or lipid synthesized (estimated below), and ρ.π.r².[(1/g²) − 1].L_internode is the mass of the myelin in one internode, where ρ is the density of myelin [1.1 g/cm³: Inouye and Kirschner (1988)], and g (the ratio of the axon diameter to outer diameter of the myelin) is 0.81 (Guy et al., 1989; Chomiak and Hu, 2009). The number of ATP molecules saved by propagating N_APs action potentials along this myelinated internode, instead of along an unmyelinated axon of the same diameter is given by the following:

where C_A is the capacitance per unit area of the unmyelinated axon (1μF/cm²), C_L is the capacitance per unit length of the myelinated axon (estimated below), ΔV is the voltage excursion of the action potential [100 mV; simulations by Bakiri et al. (2011) found that the action potential amplitude in the internode is essentially identical to that at the node, being only 2% lower at the center of the internode], e is the elementary charge that is used to convert Na⁺ influx in moles to number of ions, f = 1.3 is the factor by which the theoretical minimum charge entry needed to polarize the axon by ΔV must be multiplied (because of overlap of the voltage-gated Na⁺ and K⁺ currents) to estimate the true Na⁺ entry occurring (Alle et al., 2009), and the factor 3 is present because the Na⁺/K⁺ pump extrudes 3 Na⁺ per ATP hydrolyzed. From Equations 2 and 3, the number of action potentials that need to pass in order for the energy saved to outweigh the cost of synthesizing the myelin is given by the following:

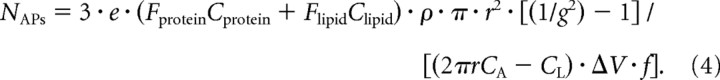We will show below that C_L is much smaller than 2πrC_A (by a factor approximately equal to the number of cell membranes comprising the myelin sheath), so it follows that the number of action potentials required to pay back the cost of myelination rises approximately in proportion to the axon radius. The parameters in this equation were estimated as follows.

The energetic cost of building myelin.

If myelination did not occur, then ATP use and consumption of constituent molecules (such as amino acids) would be reduced, allowing the ATP and other molecules to be used for other purposes within the same cell, or by other cells in the body, or allowing the animal to eat less. We estimated the energetic cost of synthesizing the lipids and proteins present in one internode of myelin by carrying out an analysis at the cellular level and assuming that all of the basic components were available locally (therefore not including the energetic costs of global tasks such as hunting for food, digestion, or molecule transportation from the gut). For simplicity, we also ignore any ATP cost of wrapping the oligodendrocyte process around the axon.

The ATP cost of synthesizing the proteins in myelin.

We assume that amino acids are used primarily for protein production rather than entry into the citric acid cycle, so that use of amino acids to make myelin protein does not involve a loss of ATP production. (If a significant fraction of the amino acids used for myelin protein production could theoretically be diverted to the liver to provide ATP by gluconeogenesis, then this would imply that the ATP cost of making myelin is even higher than we calculate below). New methods have recently led to a reassessment of the relative abundance of different proteins in myelin (Jahn et al., 2009). We therefore assumed that the relative abundance of the proteins by weight was PLP 16%, DM20 1% [Jahn et al. (2009) give the combined abundance of PLP-derived proteins as 17% and this 16:1 split of PLP and DM20 proteins derived from the PLP gene was estimated from a Western blot for adult rat [Siegel et al. (2006), their Fig. 4.12], MBP 8% [assumed to be split equally between 18.5 kDa and 14 kDa isoforms: Siegel et al. (2006), their Fig. 4.12], CNP 4%, and other proteins with a mean molecular weight of ∼50 kDa (Jahn et al., 2009) 71%. (Although these relative abundances are only approximate, the exact values have little effect on the final calculated ATP used to synthesize the proteins, since this is determined solely by the total number of peptide bonds present.) Using these proportions and the molecular weights of the proteins, we calculated the number of molecules of each protein present in each gram of myelin [taking into account the fact that only 25% of the myelin is protein: Jahn et al. (2009)]. From the number of amino acids in each protein, we then calculated the number of peptide bonds present, which was then multiplied by the energetic cost to form one peptide bond [5 ATPs including the ATP needed for amino acid uptake, but ignoring ATP expended on initiating the polypeptide chain, or on acylating or glycosylating it after it is synthesized as occurs for some myelin proteins: (Lehninger, 1975; Hawkins, 1991)]. We thus obtained the total ATP cost to synthesize the protein present in one gram of myelin as F_proteinC_protein = 6.84 × 10²¹ ATP/g myelin.

Figure 4.

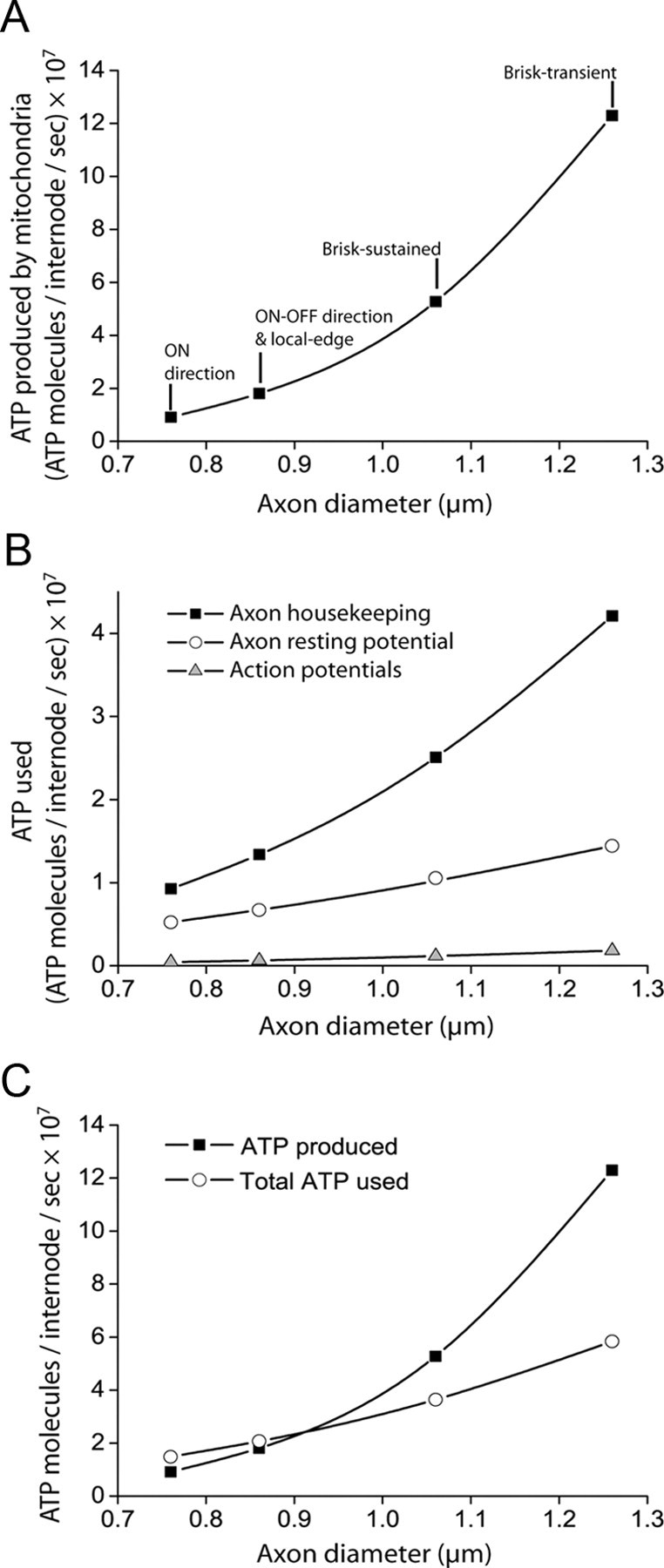
ATP supply and consumption in myelinated axons. A, ATP production by axonal mitochondria increases nonlinearly with axon diameter. B, ATP use on housekeeping, resting potentials, and action potentials all increase with axon diameter. ATP use on presynaptic processes was considered negligible. C, For axons larger than 0.9 μm in diameter, the ATP produced by axonal mitochondria can comfortably sustain the observed action potential firing rate, resting potential, and housekeeping processes. For smaller axons, there is up to a 38% deficit in the ATP available.

The ATP cost of synthesizing the lipids in myelin.

Although essential fatty acids must be obtained from the diet, myelin lipids are formed, at least in part, not from recently taken up fatty acids but from acetyl CoA, which is provided to oligodendrocytes by glycolysis and in the form of N-acetylaspartate (Burri et al., 1991; Chakraborty et al., 2001). Inhibiting the provision of acetyl CoA in the form of N-acetylaspartate dramatically inhibits myelination (Madhavarao et al., 2005; Traka et al., 2008). To estimate the ATP used to synthesize the lipids present in myelin, we therefore assumed that the majority of the lipids had to be synthesized from substrates such as acetyl CoA, and we took into account the fact that acetyl CoA (and hence glucose or N-acetylaspartate) can be used either to provide carbon skeletons for lipid synthesis or as a substrate for ATP generation by the TCA cycle and oxidative phosphorylation. Including the ATP cost of diverting acetyl CoA from entering the TCA cycle produces a much larger effective ATP cost for lipid synthesis than is obtained by simply counting the ATP molecules used directly in the synthetic reactions [for instance, Ames (1992) concluded that 8 ATP were consumed per lipid molecule formed].

Myelin comprises a diverse set of lipids (Chrast et al., 2011), and some simplifications are needed to estimate the energy needed to synthesize them. For adult rat brain myelin we consider three main classes of lipid present, which occur in the following molar ratios: phospholipids (including plasmalogens) 42%, cholesterol 38%, and galactolipids 20% [Norton and Poduslo (1973), their Table 2]. The relative occurrence of the different lipid classes, and estimates of the mean molecular weight of the molecules in each class [788, 387, and 756, respectively, obtained by averaging the molecular weights of the different subspecies in each class, as listed in the Human Metabolome Database (www.hmdb.ca)] were used to calculate the number of molecules of each lipid type present in 1 g of myelin lipid. These were then multiplied by our estimates of the ATP needed to synthesize each molecule (given below), and then by 0.75 [since lipids provide 75% of the weight of myelin: (Jahn et al., 2009)] to obtain the total ATP used to synthesize the lipid present in 1 g of myelin.

Table 2.

Sensitivity analysis for key parameters in each section of the calculations

Parameter increased by 10%	Percentage change		To result for
Energy budget for the white matter	P12	Adult
Voltage change for action potential	10.0	10.0	Total ATP use on APs (ATP/m3/s)
Internode length	−0.01	−0.31	Total ATP use on APs (ATP/m3/s)
Node length	0.01	0.34	Total ATP use on APs (ATP/m3/s)
g ratio	1.80	73.4	Total ATP use on APs (ATP/m3/s)
Action potential Na+ entry scaling factor	10.0	10.0	Total ATP use on APs (ATP/m3/s)
Mean firing rate	10.0	10.0	Total ATP use on APs (ATP/m3/s)
Mean firing rate	10.0	10.0	Total ATP use on synapses (ATP/m3/s)
No. OPCs in P12 rat optic nerve	10.0	10.0	Total ATP use on synapses (ATP/m3/s)
No. synapses/OPC (and hence charge entry)	10.0	10.0	Total ATP use on synapses (ATP/m3/s)
Vesicle release probability (and hence charge entry)	10.0	10.0	Total ATP use on synapses (ATP/m3/s)
Resistance per area of axon under myelin	−0.5	−0.8	Total ATP use on RPs (ATP/m3/s)
Oligodendrocyte resting potential	−17.1	−17.1	ATP on oligodendrocyte RP
ATP use on nonsignaling processes	6.20	5.55	Total white matter/grey matter ATP use
Energetic costs and benefits of myelination
Mean firing rate		−9.09	Days to pay back myelin assembly cost
Oligodendrocyte resting potential		−17.1	Energy saving firing rate
Oligodendrocyte input resistance		−9.1	Energy saving firing rate
Energy supply and production in myelinated axons
O2 use by muscle mitochondria		10.0	GLUT3 density at node (GLUT3/μm2)
Turnover rate of GLUT3		−9.1	GLUT3 density at node (GLUT3/μm2)

AP, Action potential; RP, resting potential.

Literature estimates for the ATP needed to make the different lipids vary significantly depending on the assumptions made, so we reevaluated these ATP costs noting that if ATP, acetyl CoA, NADH, or NADPH are consumed to make lipid, then any of these would deprive the cell of glucose-derived ATP that could be used for other purposes.

Phospholipids.

As a representative example of a phospholipid we chose phosphatidyl-ethanolamine [the commonest myelin phospholipid: Norton and Poduslo (1973), their Table 2], with one C(18:0) and one C(18:1) fatty acid group [these are the commonest fatty acids in myelin: Chrast et al. (2011), their Fig. 2]. Synthesis of the fatty acids starts with synthesis of palmitic acid, the overall reaction for which is:

[the end product is actually palmitoyl-acyl carrier protein, which can react to add palmitate to further molecules as described below; this and the following reaction details are taken from Lehninger (1975) and Stryer (1995)]. Since entry of two acetyl CoA molecules (derived from one glucose) into the citric acid cycle ultimately generates 28 ATP by oxidative phosphorylation, diversion of 8 acetyl CoA to make palmitic acid costs 112 ATP (i.e., 112 ATP are not made that otherwise could have been made). In addition, the 8 acetyl CoA need to be moved (in the form of acetyl residues) from the mitochondrion (where they are formed) to the cytoplasm (where palmitate is made), which costs 2 ATP per acetyl CoA transferred, thus removing another 16 ATP. The 7 ATP in the reaction above are consumed in elongating the fatty acid chain. Finally, of the 14 NADPH, 8 are generated without an extra ATP cost when acetyl CoA is moved from mitochondria into the cytoplasm, but 6 are generated from 3 glucose molecules in the pentose phosphate shunt. This diverts glucose from the process of generating its normal 30 ATP by glycolysis and oxidative phosphorylation at the glucose-6-phosphate stage where one ATP has been expended to add a phosphate to the glucose, the end result thus being that 3 × 31 = 93 ATP are removed from the cell. Summing all these contributions, 112 + 16 + 7 + 93 = 228 ATP are effectively removed from the cell to make one palmitate molecule. To extend this (in the endoplasmic reticulum) to form C(18:0), another cytoplasmic acetyl CoA (costing 14 + 2 = 16 ATP as above), 1 ATP, and 2 NADPH are needed, costing a total of 32.5 ATP (one NADPH is generated during movement of the acetyl CoA to the cytosol, but one must be generated from 0.5 glucose in the pentose phosphate shunt, which effectively removes another 15.5 ATP, as described above). Thus, the synthesis of C(18:0) costs a total of 260.5 ATP. To add a double bond to form C(18:1), one cytoplasmic NADH is required, which could otherwise be used to form 1.5 ATP by oxidative phosphorylation, so synthesis of C(18:1) costs 262 ATP. These fatty acids become attached to glycerol-3-phosphate that can be synthesized from glucose via the glycolytic intermediate dihydroxyacetone phosphate at the expense of one cytoplasmic NADH [equivalent to 1.5 ATP: Nguyen et al. (2007)]. Removal of this glycolytic product also effectively deprives the cell of 15 ATP (14 ATP that would otherwise be generated by glycolysis and oxidative phosphorylation, and 1 of the 2 ATP that were consumed earlier in glycolysis to convert glucose into 2 molecules of dihydroxyacetone phosphate). The resulting diacylglycerol 3-phosphate can then react with cytidine diphosphoethanolamine, which is formed from dietary ethanolamine at the expense of 2 ATP (in fact 1 ATP and 1 CTP), to form phosphatidylethanolamine. Uptake of the ethanolamine into the cell is via a Na⁺-dependent transporter (Yorek et al., 1985) the operation of which will require ∼1 ATP for maintenance of the transmembrane [Na⁺] and voltage gradients. Thus, the total ATP expenditure for the synthesis of phosphatidylethanolamine is 260.5 + 262 + 1.5 + 15 + 2 + 1 ATP = 542 ATP, equivalent to the ATP that would be generated by glycolysis plus oxidative phosphorylation from 18 glucose molecules.

Figure 2.

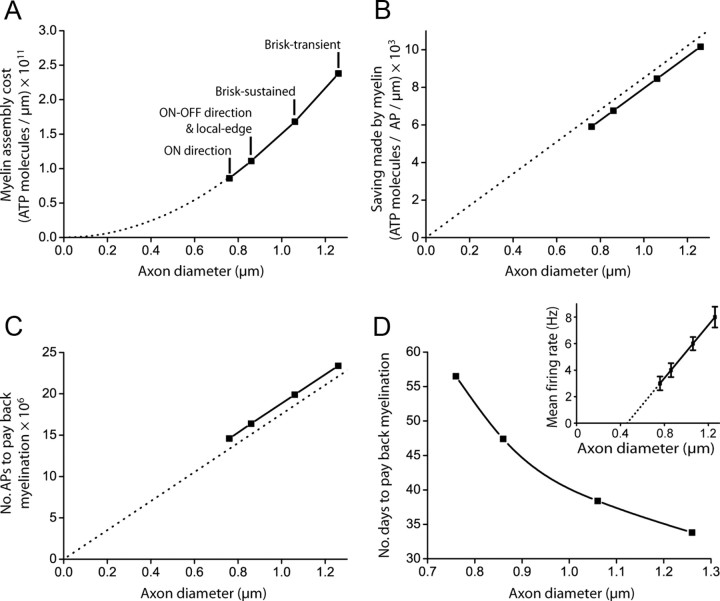
The energetic cost of making myelin and the ATP saved on axonal action potentials in the guinea pig optic nerve. A, The ATP cost, per length of internode, for assembling myelin from local lipid and protein resources increases quadratically with axon diameter (Eq. 2 of the Materials and Methods). Data points are labeled with the ganglion cell type(s) of each diameter [from the study by Perge et al. (2009)]. B, The ATP saving per action potential, per length of internode, conferred by myelin increases approximately linearly with axon diameter (dashed straight line has slope predicted from Eq. 3 of the Materials and Methods when C_L is set to zero). C, The number of action potentials required to pay back the cost of myelination increases approximately linearly with axon diameter (dashed straight line has slope predicted from Eq. 4 of the Materials and Methods when C_L is set to zero). D, Taking into account mean firing rates [inset: experimental data from which a linear axon diameter-firing rate relationship was derived in the study by Perge et al. (2009)], the time taken to pay back myelination decreases with axon diameter.

Cholesterol.

The overall reaction for cholesterol synthesis is

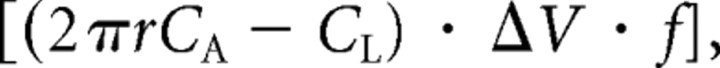The reactions take place in the cytosol. As outlined above, each acetyl CoA transferred from the mitochondrion to the cytoplasm costs 2 ATP for the transfer, and deprives the cell of 14 ATP that could otherwise be made by oxidative phosphorylation. Thus, the 18 acetyl CoA used to synthesize cholesterol cost 288 ATP molecules. To this must be added the 18 ATP in the reaction above, but the NADPH in the reaction costs no ATP because 1 NADPH is made for each acetyl CoA transferred to the cytoplasm. Thus the total energy cost per cholesterol synthesized is 288 + 18 ATP = 306 ATP.

Galactolipids.

As a representative galactolipid we took galactosyl cerebroside, the dominant glycolipid in myelin (Norton and Poduslo, 1973; Chrast et al., 2011). The synthesis of this molecule is similar to that of the phospholipids. After palmitoyl-acyl carrier protein is formed (costing 228 ATP, see above), it reacts with serine to form dehydrosphingosine, which then is converted to sphingosine consuming 1 NADPH and generating 1 FADH₂. As detailed above, each NADPH costs 15.5 ATP, but 1 FADH₂ could be used to generate 1.5 ATP in oxidative phosphorylation, so this step has a net ATP cost of 14 ATP. Then, C(18:1)-acyl carrier protein (made at the cost of 262 ATP, see above) can react with sphingosine to form ceramide, which reacts with UDP-galactose (formed from dietary galactose at the expense of 1 ATP to phosphorylate it, plus 30 ATP because the galactose could otherwise be used to make ATP from glycolysis and oxidative phosphorylation), thus forming galactosyl cerebroside at a total cost of 228 + 14 + 262 + 1 + 30 ATP = 535 ATP.

Having estimated the ATP needed to synthesize each class of lipid, we then used the relative abundance of these lipid classes (given above) to calculate the total ATP needed to synthesize 1 g of myelin lipid and thus, using the fact that 75% of myelin by weight is lipid (Jahn et al., 2009), obtained the total ATP used to synthesize the lipid present in 1 g of myelin as F_lipidC_lipid = 3.24 × 10²³ ATP/g myelin.

The relative cost of synthesizing myelin lipids and proteins.

From the calculations above, the cost of synthesizing the lipids in myelin is 48 times that of synthesizing the proteins. This difference occurs for the following main reasons: (1) there is three times more (by mass) lipid as protein present; (2) protein synthesis requires ∼5 ATP per amino acid, i.e., ∼1 ATP/carbon, while fatty acid synthesis requires 1 cytoplasmic acetyl CoA (= 16 ATP) + 1 ATP, for each 2 carbons added, as well as ∼5 ATP per carbon added for NADPH synthesis, i.e., in total ∼ 13.5 ATP/carbon.

The number of action potentials needed to repay the cost of myelination.

From the estimates above, the total number of ATP molecules needed to synthesize 1 g of myelin is F_proteinC_protein + F_lipidC_lipid = 3.30 × 10²³ ATP. The number of action potentials needed to repay the cost of myelination is given by Equation 4 as follows:

for which all the parameters have been given above apart from C_L.

We estimated above, in the section on Energy required for action potentials, that the capacitance of a 240-μm-long internode (with a 0.77 μm diameter axon) was 0.49 pF, implying that C_L = 2.06 × 10⁻⁹ F/m. This will also be the capacitance per unit length for an internode on an axon of any other size, provided that the g ratio remains constant. This is because, when the axon radius is increased, the outer radius of the myelin will scale up accordingly, and the thickness of the sheath will increase in proportion to the radius, so that the number of myelin wraps will increase in proportion to the radius. Consequently, because the capacitance of each membrane of the sheath increases with the radius, but the number of membranes in series increases in proportion, the total capacitance across the sheath remains constant. This can also be seen from the classical formula for the capacitance per unit length of a cylindrical volume (between the axon radius and the myelin radius) filled with dielectric of permittivity ε, which is (1/2πε).ln(myelin radius/axon radius) or (1/2πε).ln(1/g), which depends on the g ratio but not on the axon radius. Note that in the equation above, for a 0.77 μm diameter axon, 2πrC_A (2.42 × 10⁻⁸ F/m) is >10-fold greater than C_L (2.06 × 10⁻⁹ F/m).

Using the values from above in the equation we obtain the number of action potentials needed to repay the cost of myelination as being the following:

with r in meters. For a 1 μm diameter axon (r = 0.5 μm), this implies that N_APs = 1.9 × 10⁷ action potentials must pass to repay the cost of myelination. For larger diameters this number will be approximately proportional to the radius, because in the denominator the second term is <10% of the first term (i.e., 2πrC_A ≪ C_L in Eq. 3).

In this calculation, for simplicity, the radius of the unmyelinated axon was assumed to be the same as that of the myelinated axon it becomes, while in the rat optic nerve 0.3 μm diameter unmyelinated axons turn into 0.77 μm diameter myelinated axons (Foster et al., 1982). To include this change in the calculation, in Equations 4 and 5 the r in the numerator becomes r_myel, the radius of the axon when myelinated, and the r in the denominator becomes r_unmyel, the radius of the unmyelinated axon, so Equation 4 becomes as follows:

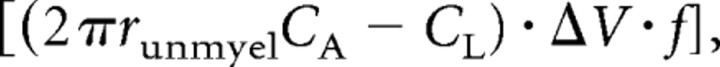and N_APs is approximately increased by the ratio r_myel / r_unmyel (because 2πr_unmyelC_A ≫ C_L) or ∼2.6. For simplicity, in what follows we use Equations 4 and 5 with both r values set to the value for myelinated axons.

Applying these formulae to the different size axons in the optic nerve.

The optic nerve comprises axons of different diameter transmitting different types of information and with different mean firing rates (Perge et al., 2009). We estimated the diameter of each axon class from the linear dependence on firing rate provided by Perge et al. (2009) and calculated the number of action potentials that would need to pass along each class of myelinated fiber to pay back the initial cost of myelination. This was then divided by the mean firing rate of the neuron, to evaluate the time needed for the payback to occur.

The cost of maintaining the oligodendrocyte membrane potential.

The analysis so far has considered only ATP used to make myelin and saved in the axon, but adding a myelin sheath to an axon implies a constant added ATP cost per unit time for maintaining the oligodendrocyte resting potential. For all the sheaths made by an oligodendrocyte of input resistance R_oligo (assumed to be independent of the diameter of the axons myelinated) and resting potential V_rp, this cost is (from Eq. 1) as follows:

moles/s, where V_Na (+50 mV) and V_K (−100 mV) are the Nernst potentials for Na⁺ and K⁺, and F is the Faraday constant. Assuming that each oligodendrocyte makes N_sheath sheaths, the ATP cost per unit time per sheath will thus be as follows:

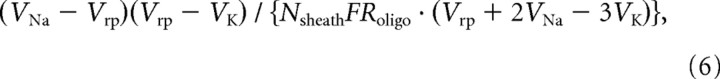while the ATP saved on action potentials by myelination, per unit time per internode, is (from Eq. 3, converted from molecules/s to moles/s) as follows:

where F_APs is the frequency of action potentials. Combining Equations 6 and 7, we see that for myelination to confer a reduction in energy expenditure in the long term (i.e., ignoring the ATP cost of making the myelin), requires that:

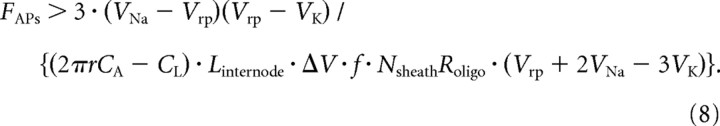Taking R_m = 200 MΩ (Káradóttir et al., 2005), V_rp = −70 mV (Bakiri et al., 2011), and N_sheath = 14 (Ransom et al., 1991), with the other parameters as above for guinea pig myelinated axons of mean diameter 0.89 μm [calculated from the diameters of the different classes of ganglion cell considered in Koch et al. (2006) and Perge et al. (2009) weighted by their frequency of occurrence] and with the internode length set as described in the following paragraph, we find that myelination only confers a net energy saving if the firing rate is >12.4 Hz, yet the mean firing rate of guinea pig optic nerve axons (estimated above) is 4.3 Hz. Some papers have reported a more positive or negative resting potential and a lower input resistance for oligodendrocytes [e.g., −58 mV and 58 MΩ (De Biase et al., 2010) or −83 mV and 23 MΩ (Kukley et al., 2010)]. Using these values would not alter the conclusion of the calculation: the firing rate would then need to be >52 or 71 Hz respectively for a net saving of energy in the long term, i.e., much higher than the mean firing rate of 4.3 Hz.

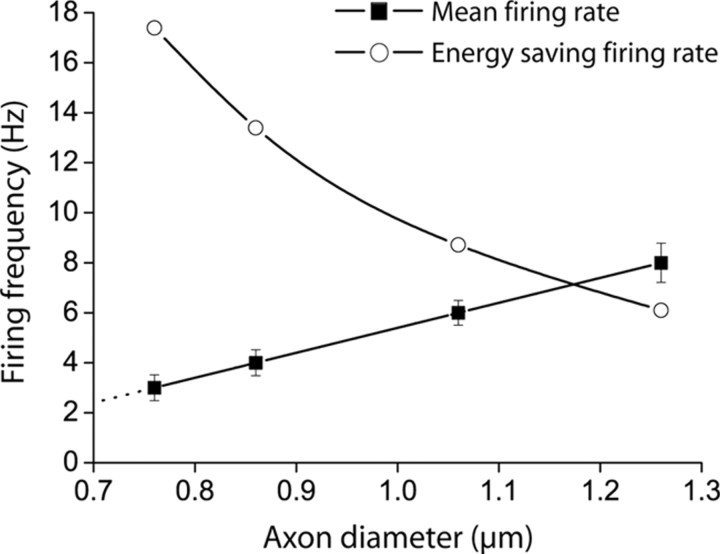
We then did the same analysis for each class of myelinated fiber in the guinea pig optic nerve, assuming that the input resistance is the same for the oligodendrocytes myelinating these different diameter fibers, and assuming that the internode length is proportional to the axon diameter (Rushton, 1951; Berthold, 1978), with a proportionality constant equal to the mean internode length of 240 μm in rat optic nerve (Ransom et al., 1991) divided by the mean axon diameter of 0.77 μm measured in the same preparation (Foster et al., 1982). The resulting firing rates needed for myelination to produce an energy saving are shown in Figure 3. Because 2πrC_A≫C_L (see above) and L_internode is proportional to r, Equation 8 predicts that the critical firing rate for myelination to reduce ATP consumption decreases approximately as the inverse of the square of the radius. For comparison, Figure 3 also shows the mean firing rate measured experimentally for each class of axon. For all except the largest fibers, the mean firing rate is below that needed for the ATP saved on action potentials to outweigh that used on the oligodendrocyte resting potential.

Figure 3.

The action potential firing rate needed for myelination to save energy in the long term. Open circles show, as a function of axon diameter, the critical firing rate above which myelination produces a larger saving of ATP on action potentials than is expended on the oligodendrocyte resting potential (from Eq. 8 of the Materials and Methods). Black squares show the measured mean firing rate for optic nerve axons of different classes (Perge et al., 2009).

Energy supply and production in myelinated axons

We calculated the maximum ATP that could be produced through oxidative phosphorylation by the mitochondria present in the two half internodes surrounding each node of a myelinated axon in the optic nerve, to determine whether this was sufficient to support physiological action potential firing rates and maintenance of the resting potential of the axon. We then assessed whether sufficient glucose could be imported from the extracellular space at the node of Ranvier or whether it was necessary to posit metabolic support from myelin to provide sufficient substrate for this level of ATP production.

Mitochondrial ATP-generating capacity in myelinated axons.

The maximum possible ATP generated by a mitochondrion is proportional to its membrane surface area (across which the proton gradient critical for the electron transport chain is set up) and is proportional to the total mitochondrial volume (Hoppeler et al., 1987; Perge et al., 2009). We used a formula (Hoppeler et al., 1987; Perge et al., 2009) to calculate, for the five major axon types in the optic nerve (Koch et al., 2006), the total mitochondrial volume of the axoplasm given the diameter of the myelinated axon: P_m = 0.0044(d − 0.46)[(d − 0.46) + 4.7], where P_m is the proportion of axoplasmic volume that is taken up by mitochondria and d is the diameter of the axon (inside the myelin) in micrometers. The value of d for each axon class was calculated from the linear dependence of diameter on firing rate provided by Perge et al. (2009). We assumed that mitochondria are evenly distributed along the axon, with no increase or decrease of density at the node (see Results). The ATP-generating capacity of mitochondria can be calculated from the estimated O₂ usage for physiological conditions of 5.8 ml O₂/min/ml of muscle mitochondria (Schwerzmann et al., 1989). Assuming that 30 ATP are produced per glucose and 6 O₂ molecules consumed (Stryer, 1995), this value predicts that 1.29 × 10⁷ molecules of ATP can be made per second per cubic micron of mitochondria.

The volume of mitochondria in the node and half internodes on each side of one node was then estimated for optic nerve axons of different diameter by assuming that the internode length is proportional to the axon diameter (Rushton, 1951; Berthold, 1978), with a proportionality constant equal to the mean internode length of 240 μm in rat optic nerve (Ransom et al., 1991) divided by the mean axon diameter of 0.77 μm measured in the same preparation (Foster et al., 1982). This was then multiplied by the volume fraction that was occupied by mitochondria for axons of different diameter (given by the formula for P_m above). Multiplying the resulting mitochondrial volume by the value derived above for ATP production (1.30 × 10⁷ molecules of ATP/μm³/s) gave the maximum possible rate of ATP production in the five major axon types of different diameter in the optic nerve (Koch et al., 2006), i.e., the ATP production per node and associated half internodes (see Fig. 4A).

ATP needed for action potential firing at physiological rate.

The rate of ATP use per action potential by each node and associated half internodes is given, by analogy with Equation 3, as follows:

where C_A is the capacitance per unit area of the nodal membrane (10⁻² F/m²), L_node is the length of the node [0.8 μm: Ishibashi et al. (2002)], C_L is the capacitance per unit length of internode (2.06 × 10⁻⁹ F/m, see above), L_internode is the internode length, ΔV = 100 mV, f = 1.3, and e is the elementary charge. This was calculated for each of the five major axon types of different diameter in the optic nerve (Koch et al., 2006). Multiplying Equation 9 by the observed mean firing rate for each class of axon [F_APs: Koch et al. (2006)] gives the rate of ATP use per second as follows:

This ranged from 4.1 × 10⁵ ATP/s for 0.76 μm diameter axons (“On direction” cells, F_APs = 3 Hz) to 1.8 × 10⁶ ATP/s for 1.26 μm diameter axons (“brisk transient” cells, F_APs = 8 Hz).

ATP needed for the resting potential.

The ATP consumption on the resting potential was calculated for a single node and associated half internodes, as described in An energy budget for the white matter, for the axon classes of different diameters considered by Koch et al. (2006). The calculated membrane resistance per node and associated half internodes ranged between 13 GΩ for 0.76 μm diameter axons and 4.7 GΩ for 1.26 μm diameter axons, and the resulting ATP use/s ranged from 5.2 to 14.4 × 10⁶ molecules per second (i.e., 1.27 to eightfold more than is used on action potentials).

Housekeeping energy.

The bulk tissue value for housekeeping energy use of 6.88 × 10²² ATP molecules/m³/ sec (from An energy budget for the white matter) was scaled up (by a factor of 1/0.8), to allow for the fact that no housekeeping ATP use occurs in the extracellular space [occupying 20% of the volume: Lehmenkühler et al. (1993)], and the amount for one node and associated half internodes was calculated by multiplying this number by the volume of the axon. The resulting ATP use per node and associated half-internodes ranged from 9.25 × 10⁶ molecules/s for 0.76 μm diameter axons to 4.21 × 10⁷ molecules/s for 1.26 μm diameter axons, and thus was larger than the ATP consumption on action potentials and the resting potential.

Total ATP consumption per node and associated half internodes.

The total ATP consumption per second was calculated by summing the values obtained in the sections above on action potentials, the resting potential, and housekeeping (see Fig. 4B), and was then compared with the ATP production rate calculated from the volume of mitochondria present as above (see Fig. 4C).

A general equation for the ATP used by an axon of radius r.

Collating the expressions used to evaluate (for one node and its associated half internodes) the ATP use on action potentials, on the resting potential, and on housekeeping energy, we obtain the following:

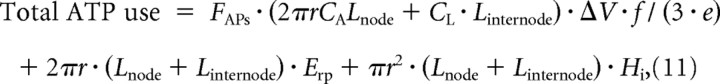where: E_rp is the ATP used to maintain the resting potential in unit area of axonal membrane and H_i is the intracellular housekeeping energy use per unit volume (estimated as 6.88 × 10²²/0.8 ATP molecules/s/m³ above). Of these terms, the first (action potential) term increases with axon radius through the dependence of mean firing rate on r [this is approximately proportional to r at large values of r: Perge et al. (2009)], and through the proportionality of node capacitance and internode length to r (the combination being approximately proportional to r² at large r); the resting potential term increases approximately with r² since L_internode is proportional to r; and the housekeeping term increases approximately in proportion to r³ (because L_internode is proportional to r). This implies that for axons larger than the largest that we have considered, the increased mitochondrial volume in the larger axon will result in increased ATP production that will more than compensate for the increased energy use on action potentials, on the resting potential, and on housekeeping [particularly since the mitochondrial volume fraction increases with axon diameter: Perge et al. (2009)].

Glucose delivery to the axon.

We first calculated how much glucose would need to be supplied to one node and its associated half internodes to allow ATP production at the maximum possible rate by the mitochondria that are present within this volume. This was deduced from the maximum O₂ usage of the mitochondria present, calculated as the product of the volume of mitochondria (calculated as above) and the value for the maximum O₂ consumption per unit volume of mitochondria [5.8 ml O₂/min/ml of mitochondria: Schwerzmann et al. (1989)]. This O₂ usage was converted to the necessary glucose supply by assuming that 6 O₂ molecules are needed for each glucose molecule, which gave values between 3.1 × 10⁵ glucose molecules/s for the smallest fibers and 4.1 × 10⁶ molecules/s for the largest (see Fig. 5A). Assuming that the main glucose transporter in myelinated axons is GLUT3, which has a turnover rate of 6500 glucose molecules/s (Maher et al., 1991; Simpson et al., 2008) and a K_m for glucose of ∼1 mm (Nualart et al., 2009), and also assuming an extracellular glucose concentration of 1 mm (McNay and Gold, 1999) so the transporters run at half their maximal rate, we calculated how many transporters would need to be present in one node and associated half internodes to achieve this import of glucose molecules, by dividing the glucose import rate needed by 3250/s. Assuming that all these transporters are present in the node, dividing by the nodal area, which was calculated assuming a nodal length of 0.8 μm [Ishibashi et al. (2002); node length does not vary significantly with axon diameter: Rydmark and Berthold (1983)], gave the predicted density of transporters at the node (see Fig. 5C), which ranged from ∼50 − 400 transporters/μm².

Figure 5.

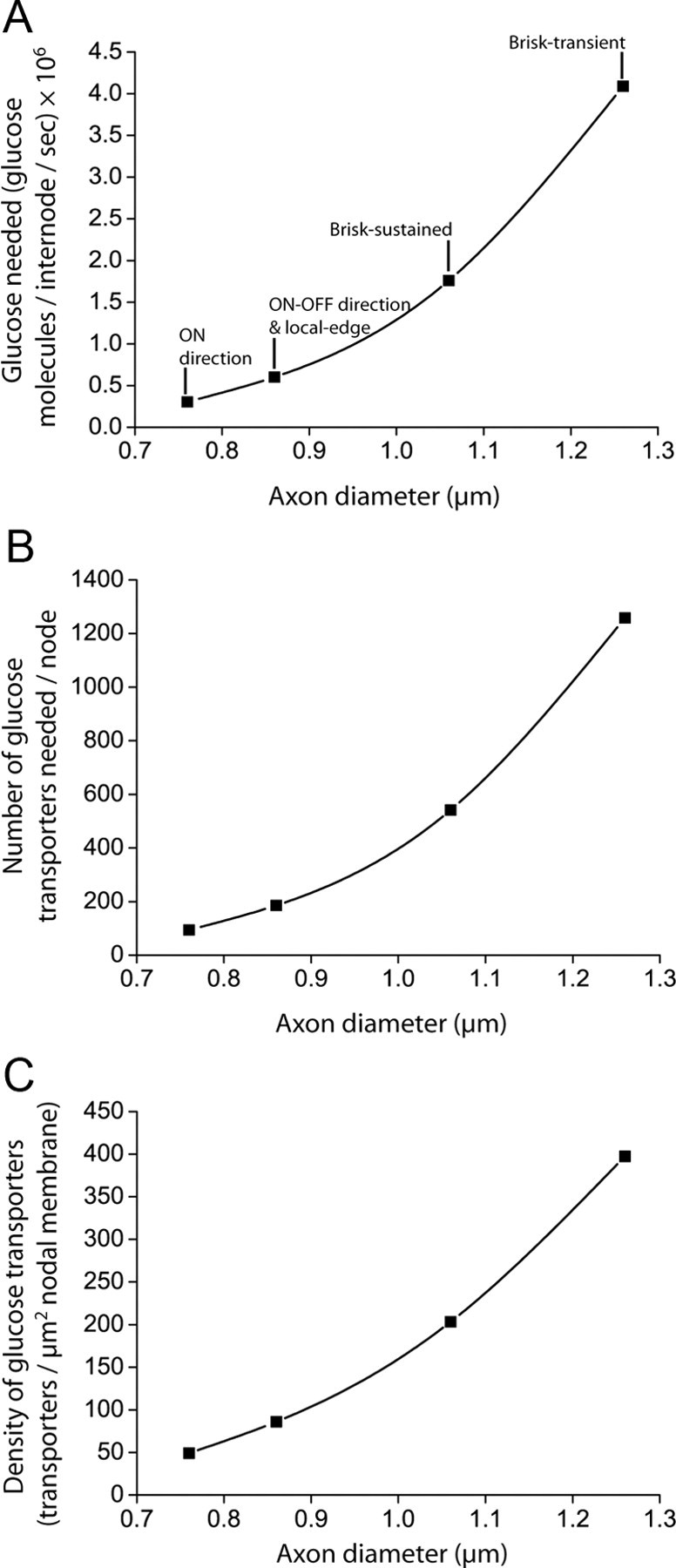
Glucose supply to CNS internodes. A, B, The amount of glucose required by mitochondria in the internode (A), and therefore the number of glucose transporters required at the node (B) increases with axon diameter. C, Assuming a constant node length, the density of glucose transporters required in the nodal membrane increases with axon diameter, but remains below the density observed in other neurons [800/μm²: Li et al. (1994)].

Results

Full details of the calculations are given in the Materials and Methods.

An energy budget for the white matter

Central white matter consumes approximately one third of the energy of gray matter [measured as glucose uptake: Sokoloff et al. (1977)]. Apart from the greater energetic efficiency of myelinated action potentials, another factor that this reduced energy consumption might be attributed to is an absence of synapses in the white matter, since synapses account for a large proportion of the signaling energy use in gray matter: 59% in the cortex and 30% in the cerebellum [recalculated from the numbers in Attwell and Laughlin (2001) and Howarth et al. (2010)—all estimates of action potential energy use given in this study, whether calculated here or taken from the previous literature, are adjusted for the lower sodium influx per action potential now known to occur, as described by Alle et al. (2009), Carter and Bean (2009), and Sengupta et al. (2010)]. However, synapses from unmyelinated (and possibly from myelinated) axons onto OPCs have recently been discovered in the developing and mature white matter (Kukley et al., 2007; Ziskin et al., 2007; Káradóttir et al., 2008; Royeck et al., 2010). We used data from the developing rodent optic nerve and corpus callosum to produce an energy budget for white matter tracts containing both myelinated and unmyelinated axons, and also for a tract such as the adult optic nerve where all the axons are myelinated. These CNS areas were chosen because: (1) the P12 rat optic nerve provides the most comprehensive data for the diameters of myelinated and unmyelinated axons, (2) the properties of synapses made onto OPCs have been extensively studied in rat and mouse corpus callosum and optic nerve, and (3) there are extensive data from the guinea pig optic nerve on the physiological firing rates of different ganglion cell types. The aim of this analysis was to assess the energetic cost of the synapses onto OPCs relative to the energetic cost of action potentials and of maintaining the resting potentials of cells in the white matter. This distribution of energy use could then be compared with the distribution of energy used on the same processes in the gray matter.

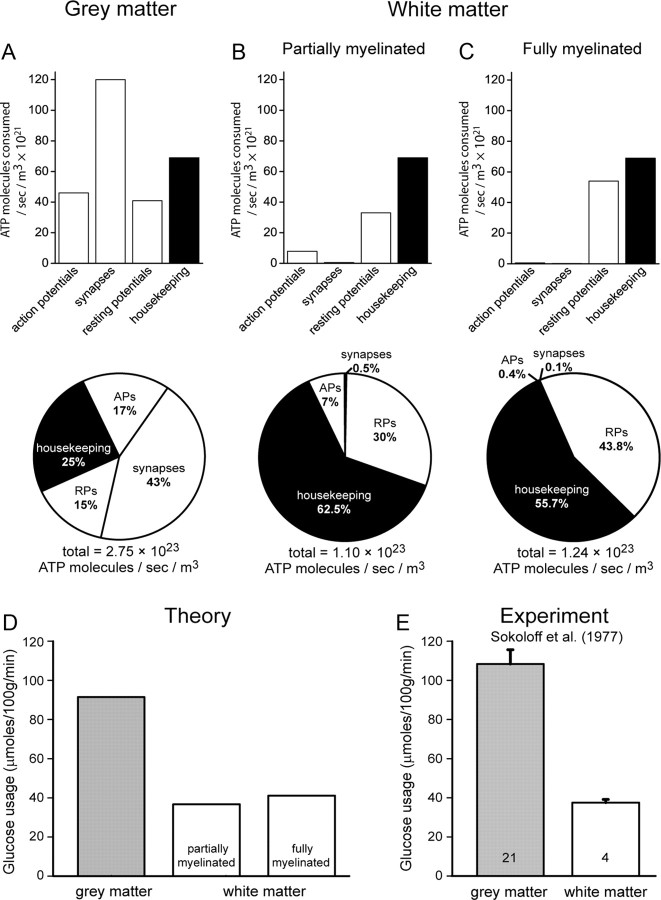
We used experimentally derived values from the literature to estimate the energy used on reversing the ion movements associated with action potential firing, synaptic transmission, and maintaining resting potentials in the partially myelinated P12 rat optic nerve, with all axons firing at the mean physiological rate [4.3 Hz, see Materials and Methods, similar to the 4 Hz estimated for excitatory neurons in rat cortex (Attwell and Laughlin, 2001)]. The predicted distribution of signaling energy consumption across the different mechanisms, expressed as ATP consumption per cubic meter per second, is compared with the values derived by Attwell and Laughlin (2001) for the gray matter of the cortex (adjusted as described above) in Figure 1A,B. Synaptic energy use was defined to include ATP use on postsynaptic currents, presynaptic Ca²⁺ entry, and transmitter and vesicle cycling.

Figure 1.

Comparing gray and white matter energy consumption. A–C, Top (bar graphs), Calculated absolute energy use on different cellular processes in the cortex [A; adapted from Attwell and Laughlin (2001)], and the partially (B) and fully (C) myelinated optic nerve. Bottom (pie charts), Distribution of ATP usage on signaling and housekeeping processes in the cortex (A), and the partially (B) and fully (C) myelinated optic nerve. D, Theoretically estimated rates of glucose usage in gray and white matter regions. E, Experimentally estimated rates of glucose uptake [obtained from 2-deoxyglucose uptake (Sokoloff et al., 1977)] in gray and white matter regions (1 μmole/100 g/min equals 1.67 × 10⁻⁷ moles/kg/s).

The predicted energy use on action potentials and synaptic transmission (7.86 × 10²¹ and 5.19 × 10²⁰ ATPs/m³/s, respectively) in the developing (P12) optic nerve (i.e., with 10% of axons myelinated, Fig. 1B, top) was found to be considerably smaller than the energy use on the same two processes in the gray matter of the neocortex [4.6 × 10²² and 1.2 × 10²³ ATPs/m³/s from the study by Attwell and Laughlin (2001)] (Fig. 1A, top). In contrast, the ATP use on maintaining resting potentials in the developing white matter (3.33 × 10²² ATP/m³/s; Fig. 1B, top) dominates the signaling energy consumption, and is similar to that in the gray matter of the neocortex (4.08 × 10²² ATP/m³/s; Fig. 1A, top) [for an extensive discussion of the importance of resting costs in neuronal energy consumption, see Niven et al. (2007)].

Assuming that “housekeeping” ATP use (e.g., on protein and lipid synthesis, and intracellular trafficking of molecules and organelles) uses 1/4 of the total energy in the gray matter (Attwell and Laughlin, 2001) (Fig. 1A), and that housekeeping ATP use is the same per unit volume in the white matter (Fig. 1A,B), then the numbers derived above predict the percentage distribution of energy use over all processes that is shown in Figure 1B (bottom). They also predict that the total ATP use (per m³/s) in the partially myelinated developing white matter should be 40% of that in the gray matter (Fig. 1D, second bar), similar to the ratio found experimentally by Sokoloff et al. (1977), who reported that on average rat white matter areas had 35% of the glucose consumption of gray matter areas (Fig. 1E).

The most dramatic difference in energy consumption between gray and white matter regions is the energy used on synapses, which is 230 times smaller in the developing optic nerve than in the neocortical gray matter, while the action potential cost is only ∼6 times smaller in the developing optic nerve than in the neocortex. Thus, although the decrease in action potential energy use conferred by myelination contributes to the lower energy use of the white matter, by far the dominant factor is the low energy consumption on synaptic processes. Indeed, there is a major difference in the distribution of energy use on signaling processes between the gray matter and the white matter: of the total energy used for each region (including the resting potential and housekeeping energy), 43% goes on synaptic transmission in the cortex but just 0.5% goes on synaptic transmission in the developing optic nerve, while 17% and 7%, respectively, go on action potentials (Fig. 1A, bottom; B, bottom).

We then applied the same analysis to the adult optic nerve, with all the axons myelinated [which decreases ATP expenditure on action potentials but increases the ATP expended on maintaining the resting potential in the larger myelinated axons, while energy on synapses to OPCs was assumed to be unchanged (see Materials and Methods)]. The ATP use on synaptic transmission fell to just 0.1% of the total (1.37 × 10²⁰ ATP/m³/s) and that on action potentials fell to 0.4% (5.08 × 10²⁰ ATP/m³/s, Fig. 1C), while the total energy used by the white matter was predicted to be 45% of that used by the gray matter (Fig. 1D, third bar).

Thus, in the gray matter, much more energy (2.6-fold more) is used on synapses than on action potentials, while the reverse is true for the white matter, with 15-fold (in the developing optic nerve) or 3.7-fold (in the mature optic nerve) more energy going on action potentials than on synapses. Is this smaller synaptic energy cost in white matter due to a lower density of synapses in the optic nerve, or due to a reduced energy cost for each synapse in the optic nerve? We found (see Materials and Methods) that the density of synapses in the white matter is 82-fold less than in the gray matter (8.95 × 10¹⁵ synapses/m³ of P12 optic nerve vs 7.36 × 10¹⁷ synapses/m³ in the cerebral cortex), while the energy consumption per individual synapse per second was 2.8-fold lower in the P12 optic nerve (5.8 × 10⁴ ATP/s with synapses activated by action potentials occurring at 4.3 Hz, see above) than in the cerebral cortex [1.6 × 10⁵ ATP/s, with action potentials occurring at 4 Hz: Attwell and Laughlin (2001)]. Thus, the reduced energetic cost of synapses in the white matter can be largely accounted for by the far smaller number of synapses present, but also partly reflects a smaller cost per individual synapse.

The good agreement of the total predicted energy use for the white matter with the experimentally measured values (Fig. 1D,E) suggests that, as for the gray matter (Attwell and Laughlin, 2001; Lennie, 2003; Nawroth et al., 2007; Alle et al., 2009; Howarth et al., 2010), it is feasible to construct an energy budget for this tissue from the bottom up, by estimating the ATP needed to reverse the ion fluxes mediating signaling.

The energetic costs and benefits of myelination

Myelination, by reducing axon capacitance and hence the sodium influx required to change the membrane potential, reduces the amount of energy required to restore the resting ion concentrations after each action potential. However, in developing white matter, myelination is a costly process, as enough lipid and protein must be generated to wrap many membranes around each axon. It is not clear how this initial energetic investment, which may require more food intake or deplete fat, protein, or glycogen reserves previously laid down in the body, compares to the long-term energetic saving as a result of each action potential subsequently costing less ATP. We therefore assessed the cost-benefit ratio for myelination by estimating the number of action potentials (using less energy) that would need to be propagated along a myelinated axon to pay back the energy invested in myelinating the axon.

We estimated the minimum energetic cost of myelin synthesis (3.30 × 10²³ ATP molecules/g) by assuming that all of the basic components for lipid and protein assembly were available locally, therefore not including the energetic costs of global tasks such as hunting for food, digestion, or molecule transportation from the gut, and ignoring the energetic cost of wrapping the oligodendrocyte process around the axon. Thus, the cost was calculated (Fig. 2A) for assembling the lipid and protein needed for one internode from locally available acetyl CoA, amino acids, and other substrates [allowing some lipid manufacture directly from dietary fatty acids, as occurs for the essential fatty acids that are a small component of the sheath (Chrast et al., 2011) would reduce the cost, while requiring some amino acids to be locally synthesized would increase it]. This could then be compared directly with the local energy saved per subsequent action potential, which was estimated as the difference between the cost of propagating one action potential along one internode of a fully myelinated axon and the cost of propagating one action potential along the same length of unmyelinated axon (Fig. 2B). The unmyelinated axon was assumed to have the same diameter as the myelinated axon has inside the myelin sheath, i.e., we ignore the fact that unmyelinated axons are smaller than the myelinated fibers they become (Fabricius et al., 1993; Sánchez et al., 1996), which would reduce the energy saved (so this calculation provides a minimum value for the time needed for repayment of the cost of myelination: see Materials and Methods).

Equation 4 of the Materials and Methods shows that the number of action potentials (of reduced ATP cost) that need to pass along a myelinated axon to repay the cost of myelination is given by N_APs=3·e·(F_proteinC_protein+F_lipidC_lipid)·ρ·π·r²·[(1 / g²)−1] / [(2πrC_A − C_L)·ΔV·f], where: e is the elementary charge; F_protein = 0.25 and F_lipid = 0.75 are the fractions of myelin by weight that are protein and lipid respectively; C_protein and C_lipid are the cost in ATP molecules per gram of protein or lipid synthesized; ρ is the density of myelin; r is axon radius; g is the ratio of the axon diameter to the outer diameter of the myelin; C_A is the capacitance per unit area of a biological membrane; C_L is the capacitance per unit length of the internode; ΔV is the voltage change of the action potential; and f is the factor (1.3) by which the actual charge entry generating the action potential is in excess of the absolute minimum needed due to temporal overlap of the voltage-gated Na⁺ and K⁺ currents (Alle et al., 2009). From the parameters collected in the Materials and Methods (Table 1), for CNS axons with a g ratio of 0.81 this simplifies to Equation 5 of the Materials and Methods (where r is in meters): N_APs=2.21×10¹² · r² / (2πr10⁻²−2.06×10⁻⁹).

We applied this formula to the five major retinal ganglion cell types in the optic nerve that have different diameters, transmit different types of information, and have different mean firing rates (Perge et al., 2009). We calculated the number of action potentials that would need to pass along each class of myelinated fiber to pay back the initial cost of myelination. This was then divided by the mean firing rate of the cell type, to evaluate the time needed for the payback to occur. Depending on the size of axon, between 15 and 23 million action potentials have to pass to pay back the cost of myelinating one axon (Fig. 2C), which, at the cells' mean firing rates, takes 34–57 d (Fig. 2D). The number of action potentials needed increases approximately in proportion to diameter but, because the smaller diameter axons have disproportionately lower mean firing rates, the time needed to repay the myelination cost is actually longer for smaller axons. For axons in the peripheral nervous system, where the g ratio is 0.7 instead of 0.81 (Arbuthnott et al., 1980), the number of action potentials needed would be larger by a factor of 1.99, all other factors being equal.

This analysis has assumed that the energetic saving on action potentials will eventually repay the cost of myelination. However, we need to also take into account the ongoing cost of maintaining the resting potential of the oligodendrocytes that make the myelin sheath. If this is larger than the energy saving on action potentials then myelination does not save energy for the combined assembly of myelinated axons and oligodendrocytes. Equation 8 of the Materials and Methods shows that, ignoring the ATP used to make the sheath in the first place, a net energy saving is produced by myelination only if the firing rate of action potentials, F_APs, is larger than a certain value:

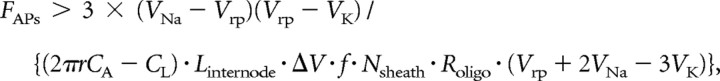where V_Na and V_K are the Nernst potentials for Na⁺ and K⁺, V_rp is the resting potential, L_internode is the length of the internode, and N_sheath is the number of myelin sheaths (internodes) made by each oligodendrocyte of input resistance R_oligo. For the average diameter of myelinated axons in the guinea pig optic nerve, this gives F_APs > 12.4 Hz (see Materials and Methods), i.e., threefold higher than the 4.3 Hz mean firing rate of optic nerve axons. When examined as a function of axon diameter, the firing rate needed for myelination to confer a net energy benefit falls approximately with the inverse square of the diameter (Fig. 3) and, furthermore, this critical value of firing rate is higher than the mean firing rate measured for most of the different classes of axon in the optic nerve (Fig. 3). Thus, surprisingly, myelination does not in general confer a reduction in energy use on axon tracts.

This conclusion would be further reinforced if energy use were included on any turnover that may occur of the lipid and protein content of the myelin sheath. These considerations suggest that myelin may have evolved primarily to allow faster nerve conduction. This would facilitate rapid escape reflexes, and perhaps more efficient hunting of prey, allowing the occupation of new ecological niches. As brain size increased with evolution of larger primates, the faster conduction conferred by myelination would also promote more rapid information processing and greater cognitive power.

Energy supply and production in myelinated axons

Myelin provides a massive benefit by speeding action potential propagation, but also results in most of the axon volume being remote from the extracellular space. It is unknown whether sufficient nutrients for axonal activity can be imported at the node of Ranvier, prompting the suggestion that myelinated axons may receive energy by collaborating metabolically with oligodendrocytes or (in the peripheral nervous system) Schwann cells (Nave, 2010). To investigate whether this is necessary, we first assessed whether oxidative phosphorylation by mitochondria—thought to be the main method of ATP production in neurons (Malonek and Grinvald, 1996; Thompson, 2003; Kasischke et al., 2004; Lin et al., 2010) and adult myelinated axons (Hamner et al., 2011)—can produce enough ATP to support experimentally observed axonal firing rates in the optic nerve. We then calculated whether the glucose required for this level of ATP production by oxidative phosphorylation could theoretically be provided at the nodes along the axon, or whether it is necessary to posit some sort of metabolic supply from ensheathing oligodendrocytes.

When action potentials occur in mammalian myelinated fibers, Na⁺ enters at the nodes and K⁺ leaves at the juxtaparanodes (Chiu et al., 1979; Chiu and Ritchie, 1980; Röper and Schwarz, 1989; Wang et al., 1993; Rasband et al., 1999a,b). Intracellular Na⁺ and extra-axonal K⁺ will then spread along the internode (although some K⁺ may diffuse to the extracellular space at the node), ultimately being pumped back across the membrane by axonal membrane Na⁺/K⁺ pumps, which are located all along the internode (Mata et al., 1991; Young et al., 2008; but see Ariyasu et al., 1985). Since the initial ion fluxes are located at the nodes, it might be thought most efficient to position mitochondria near the nodes, but the utility of this depends on the time scale over which ion gradients are reversed: if pumping occurs over a long period then diffusion will result in concentration changes occurring along a significant stretch of internode and ATP will need to be provided over all of this region. Experimentally, in the CNS, mitochondria are distributed fairly spatially uniformly along internodes, with only small (one to threefold) increases or small (one to twofold) decreases in density at the node of Ranvier (Fabricius et al., 1993; Edgar et al., 2008; Perge et al., 2009; Ohno et al., 2011). Interestingly, in the PNS, mitochondria are more concentrated at nodes (Berthold, 1978): in the dorsal and ventral roots of the spinal cord mitochondria are present at a 24- and tenfold, respectively, higher density at the nodes than in the internodes, but even here (because of the short length of the node) 91% and 96%, respectively, of all mitochondria are located in the internodes [Fabricius et al. (1993), their Table 3; Berthold et al. (1993)]. For simplicity we assumed a uniform density of mitochondria along the axon.

Using measurements of mitochondrial density for optic nerve axons of different diameter (Perge et al., 2009), together with a value for the O₂ usage (and hence the ATP produced) per unit volume of mitochondria (Schwerzmann et al., 1989), we calculated the amount of ATP that could be provided by mitochondria within each node and its two associated half internodes, for the five main classes of myelinated axon (of different diameter) that are present in the optic nerve (Koch et al., 2006). The resulting values are shown in Figure 4A as a function of axon diameter.

For each of these axon classes we also calculated the ATP needed for each node and its associated half internodes to pump out the Na⁺ that enters with each action potential. Using the mean physiological firing rate for each axon class (Koch et al., 2006), these values were used to calculate the ATP needed per second for action potentials in each fiber class. For all axon classes, the resulting values, shown in Figure 4B, are substantially less than the maximum estimated ATP production from mitochondria in each node and associated internode, by a factor which ranges from 22 for the smallest fibers to 68 for the largest fibers. However, as expected from the energy budgets for the white matter presented in Figure 1, the ATP consumption needed to maintain the resting potential of the axon and for housekeeping tasks is much larger than that needed for action potentials (Fig. 4B). Summing the ATP needed for action potentials, the resting potential, and housekeeping, and comparing this total ATP need with the ATP that can be produced within each node and associated half internodes (Fig. 4C), shows that the ATP production by mitochondria is approximately matched to the predicted average ATP consumption. For the largest fibers, mitochondria are predicted to be able to make 2.1-fold more ATP than is used on average, while for the smallest fibers there is an apparent 38% shortfall in ATP production compared with ATP use. The significance of this shortfall is considered in Discussion.

Whether the mitochondria can in fact provide the level of ATP that we have calculated above depends critically on the availability of one of the major metabolic substrates, glucose, which must be taken up by the axon either directly at the node or across the myelin sheath. We calculated how much glucose would be needed to generate the maximum amount of ATP that could theoretically be produced by the mitochondria present in one node and associated half internodes, which ranged from 3.1 × 10⁵ to 4.1 × 10⁶ glucose molecules per second depending on the axon size (Fig. 5A). We then considered how this may be delivered to the axon. The main glucose transporter in neuronal membranes is GLUT3, a facilitative glucose transporter with a maximum turnover rate of 6500 glucose molecules/s (Maher et al., 1991; Simpson et al., 2008). Assuming that GLUT3 works at ∼50% of its maximum turnover rate, since its K_m for glucose is ∼1 mm (Nualart et al., 2009) while the extracellular glucose concentration in the CNS is ∼1 mm (McNay and Gold, 1999), we found that enough glucose could be supplied if between ∼95 and 1300 (depending on axon size) GLUT3 molecules are present in each node (Fig. 5B), corresponding to a density of 50–400 transporters/μm² of nodal membrane (Fig. 5C) or approximately twice this if nodal constriction of the axon is taken into account (Fabricius et al., 1993; Sánchez et al., 1996). Glucose transporters have been found at higher densities than this in sensory neurons [800/μm²combined GLUT1 and GLUT3 density in the rod outer segment (Li et al., 1994)], and GLUT3 has been found preferentially localized at paranodal regions of the axolemma in peripheral axons (Magnani et al., 1996), i.e., regions that are probably in much better diffusive contact with the extracellular space at the node than the membrane further into the internode would be. Furthermore, even with a density of 400 transporters/μm² along with 1300 Na⁺ channels/μm² (Chiu, 2011), the mean separation of proteins would be 24 nm, leaving adequate space for the proteins and associated lipid [the diameters of the transporters and channel proteins are ∼ 4 and 10 nm respectively: Dornmair et al. (1985), Sato et al. (2001)]. Thus, it seems plausible that direct glucose transport at nodes or paranodes is a sufficient strategy for providing the metabolic substrates needed for oxidative phosphorylation in myelinated axons of the optic nerve, without the need for metabolic support from the myelin sheath.

Sensitivity of the results to the parameter values chosen

In the calculations presented above, we have used the best estimates of the different parameter values that are available from the literature. The parameters that have been measured experimentally are likely to be accurate to within 10% of their stated value for the brain area they have been measured in (care should be taken in applying the results of the calculations to other regions where the parameters may have different values). However, parameters that have not been measured experimentally could be significantly less accurate. The most uncertain parameters are those determining the energy expended on the resting potential of the myelinated axon and on housekeeping tasks, and it is possible that these could be in error by significantly >10%. To provide a quantitative estimate of the sensitivity of the calculations to variations in parameter values, in Table 2 we show the effect on some key final results (the ATP usage on action potentials and synapses, the ratio of white matter to gray matter energy use, the time needed to pay back the ATP cost of myelination, the rate at which axons have to fire for myelination to save energy, and the glucose transporter density at the node) of altering each of a range of parameters by 10%. Since many of the calculations involve the product of (typically) five variables, it is of course the case that if each variable were underestimated by 10% then the final product would be underestimated by a factor of 1.1⁵-1, or 61%. However, in general, errors in different parameters will tend to cancel out, and it is reassuring that there is reasonable agreement between the predicted total energy use for the gray and white matter and the experimentally measured values (Fig. 1D,E).

The analysis in Table 2 shows that a 10% change of a parameter leads, for most parameters, to no more than a 10% change in the result derived from that parameter. In particular, altering by 10% the values of the two most uncertain parameters, the resistivity of the axon under the myelin and the fraction of energy use expended on housekeeping tasks, leads to changes in total ATP consumption on resting potentials and by the white matter, respectively, which are <10%. However there are two exceptions where 10% changes of parameters lead to larger changes of ATP usage, as follows. First, a 10% increase in the g ratio leads to a 73% increase in the energy used on action potentials in the adult optic nerve. This is because, for a fixed axon radius, a 10% increase in g ratio leads to a halving of the number of myelin wraps, and thus to a near doubling of the Na⁺ entry needed (if, instead, we decrease the myelin thickness by 10%, then the energy use on action potentials increases by <10%). It is of interest that, even at a fixed axon radius, the g ratio can vary by 10% about its mean value (Brinkmann et al., 2008), implying large differences in energy use by myelinated axons of the same diameter. Second, a 10% increase of the oligodendrocyte resting potential (from −70 mV to −77 mV) decreases the ATP used on the oligodendrocyte resting potential by 17.1%, and thus lowers by 17.1% the rate at which axons must fire for the energy saved on action potentials by myelination to outweigh the energy used on the oligodendrocyte resting potential. This reduction of energy use occurs because the more negative resting potential implies less Na⁺ permeability to the oligodendrocyte membrane, and thus less ATP expended on pumping Na⁺ out. However, even with this 17.1% decrease, for most axons in the optic nerve, the physiological firing rate would still be lower than that needed to offset the ATP use on the oligodendrocyte resting potential.

The mean firing rate of 4.3 Hz assumed for the energy budget calculations is the mean value measured for optic nerve axons in response to natural visual stimuli, and is similar to the mean value of 4 Hz estimated for excitatory neurons in the cortex (Attwell and Laughlin, 2001). Inhibitory interneurons (and some excitatory neurons) can fire at substantially higher rates, for example Purkinje cells (which have myelinated axons) fire at a mean rate of 41 Hz in vivo (LeDoux and Lorden, 2002). Although this suggests caution in extrapolating our conclusions to the myelinated axons of interneurons, even a tenfold increase in the energy expended on action and synaptic potentials in a fully myelinated white matter tract would still leave resting potentials and housekeeping tasks as the dominant mechanisms consuming energy (Fig. 1C). Thus, although our calculations were based on data taken mainly from the optic nerve and corpus callosum, they should extrapolate to other white matter regions in the brain with similar size axons, given that the total ATP use predicted by our energy budget closely matches that measured experimentally (as glucose usage) in the corpus callosum, the internal capsule, and the cerebellar white matter (Sokoloff et al., 1977).

Discussion

Our calculations provide new insight into several aspects of white matter energetics. First, we have shown that the main reason that the white matter uses less energy than the gray matter is due to its relative paucity of synapses and not the increased energetic efficiency of action potentials provided by myelinated axons. Second, comparing the energy needed to myelinate an axon with the energy that myelination saves on action potentials revealed that the initial cost could be repaid in a few months (for the optic nerve). However, because of the ATP needed to maintain the oligodendrocyte resting potential, myelination need not confer a net energy saving on the combination of the myelinated axon plus associated oligodendrocyte. Finally, considering how much ATP is made by axonal mitochondria and the glucose needed to sustain this production indicates that glucose transporters present at a plausible density at the node could sustain action potential firing at the physiological rate (in the optic nerve) without needing oligodendrocytes to provide metabolic support to axons. We will now consider these themes in detail.

An energy budget for the CNS white matter

Our energy budget for the white matter (Fig. 1) assesses the relative energy costs of action potentials, synaptic currents in OPCs, resting potentials in all cells, and housekeeping tasks. This shows that the white matter uses less energy than the gray matter mainly because the density of synapses is ∼80-fold lower than in the gray matter. Together with ∼3-fold less energy use per synapse, this results in synaptic energy use being 230 times smaller in the developing optic nerve, and 875 times smaller in the mature optic nerve, than in the neocortical gray matter. In contrast, the energetic cost of action potentials is only ∼6 times smaller in the developing optic nerve, and ∼90 times smaller in the mature optic nerve, than in the neocortex. Thus, the density of synapses is too low for them to dominate the energy use of the white matter as they do in the gray matter.

The assumptions used to derive these conclusions are fairly robust. We used action potential firing rates in the guinea pig optic nerve, for axons with dimensions taken from rat optic nerve, but an error in the firing rates would not alter the relative magnitudes of the energy used on synapses and on action potentials (because both are proportional to firing rate: see Table 2). We also assumed that the number of synapses on corpus callosal OPCs could be applied to OPCs in the optic nerve. This number is unlikely to be sufficiently in error to significantly alter the conclusion that synapses use a very small fraction of the energy in the white matter.

Most ATP use in the white matter is predicted to be on resting potentials and housekeeping energy. However, the assumptions needed to calculate the absolute magnitudes of these ATP consumptions are more debatable than those needed to calculate action potential and synaptic ATP usage. For myelinated axons, there are no reliable measurements of the properties of the axonal membrane under the myelin sheath, where most ATP is used on maintaining the resting potential. Accordingly, we have assumed that the membrane will have the same properties per area as unmyelinated axons do. Furthermore, the ATP used on housekeeping tasks such as axoplasmic transport and molecule synthesis was assumed to be the same as that for the gray matter, but the white matter lacks neuronal somata and dendrites, which may have a different housekeeping energy demand to the neuronal axons and glia present in the white matter. Inaccuracies in these assumptions may account for the fact that we predict the total energy use of the white matter to be 40–45% of that in the gray matter, slightly higher than the 35% measured in rat white matter (Sokoloff et al., 1977).

The energetic cost and benefit of myelin

We estimated the ATP needed to construct the myelin sheath (Fig. 2), by considering the reactions needed to synthesize the most important protein and lipid molecules in the sheath. Because we consider the diversion of metabolites from energy-producing reactions to incur an ATP cost, our estimates of the ATP needed to make the lipid components of the sheath are significantly higher than if one simply counts the ATP molecules explicitly involved in the synthesis reactions (Ames, 1992). Importantly, we assumed that lipids were assembled from acetyl CoA available locally, rather than from preexisting fatty acids, and the cost of the sheath would decrease significantly if fatty acids were available locally.

Comparing the ATP thus used, with the ATP saved by the reduction in action potential costs, we concluded that 15–23 million action potentials (depending on axon size) must pass to repay the cost of making the sheath, and that this will take 1–2 months in the optic nerve (Fig. 2). Conceivably, energy expenditure on myelination occurs at a time in the animal's life when food supplies are abundant (e.g., in spring/summer), while the subsequent decreased expenditure on action potentials will last throughout its lifetime, including periods of poor food abundance. Nevertheless, considering the energy needed to maintain the myelin sheath makes it clear that energy consumption is not the main selective advantage driving the evolution of myelin (action potential speed is more important), for the following reasons.

The total energy use of a myelinated axon and its associated oligodendrocyte includes a contribution for maintaining the oligodendrocyte resting potential. We found that, because of this, myelination may not, in fact, confer a net decrease in energy expenditure on axon tracts. For most ganglion cell axons in the optic nerve, the ATP expenditure per second on the resting potential of the ensheathing oligodendrocyte is larger than that saved by reducing the Na⁺ entry per action potential (Fig. 3). This contradicts the common assumption that myelination saves energy. However, whether myelination can be said to be energy saving or not depends on the assumptions one starts with. To produce unmyelinated axons of the same conduction speed as myelinated axons would require much larger diameter axons with a far higher ATP usage, so ATP is saved by myelination if one considers conduction speed as the prime constraint, despite the fact that if one fixes axon diameter as the constraint then myelination increases energy use.

Energy production and supply in myelinated axons

By using data on mitochondrial density in optic nerve axons of different sizes (Perge et al., 2009), we assessed how much ATP can be produced per node and its associated half internodes on each side. Comparing this with the predicted ATP consumption in that same volume of axon, we found that for axon diameters larger than ∼0.9 μm, the mitochondria could comfortably produce enough ATP to sustain the observed action potential firing rate, resting potential, and housekeeping processes (Fig. 4). However, for axon diameters smaller than 0.9 μm, the calculated ATP synthesis rate was somewhat smaller than the calculated consumption (38% smaller for 0.76 μm axons). Nevertheless, this apparent mismatch depends critically on our estimates of ATP production and of the ATP consumption on the resting potential and housekeeping tasks. The latter, as noted above, are the values most likely to be in error, and if the housekeeping energy in the white matter were 38% of that in the gray matter, or if mitochondrial ATP production were 61% higher than what we derived from the properties of muscle mitochondria, then the mismatch would disappear.

Converting the ATP consumption to a value for glucose usage (assuming ATP is produced by glycolysis followed by oxidative phosphorylation), we then deduced how many glucose transporters would be needed at the Ranvier node to import glucose to sustain the activity of the myelinated axon (Fig. 5). The result (50–400 transporters/μm²) was lower than what has been found in other cells [800/μm²: Li et al. (1994)], and much lower than the density of sodium channels at the node [∼1300/μm²: Chiu (2011)]. On this basis, the function of CNS-myelinated axons could theoretically be sustained by mitochondrial oxidative phosphorylation based on glucose influx at the node of Ranvier, without the need to posit metabolic support from the myelin sheath. However, we do not exclude the possibility that some ATP production is driven by metabolic collaboration with ensheathing glia, and this may be useful to cope with sudden increases in ATP consumption triggered by abrupt rises in firing rate. We have focused on CNS axons with an internode length of ∼240 μm, for which the diffusion time for glucose to move from the node to the middle of the sheath (or for ATP made by mitochondria in the middle of the internode to diffuse to Na/K pumps near the node) is ∼60 s. In peripheral myelinated axons, for which the internode can be 1360 μm long (Nilsson and Berthold, 1988), the diffusion time for glucose from the node to the center of the internode becomes ∼32 min, and rapid provision of a mitochondrial substrate from the sheath could indeed be beneficial (Nave, 2010).