Digital image analysis of radial shrinkage of fresh spruce (Picea abies L.) wood

Abstract

Contact-free digital image analysis was performed of the radial shrinkage of fresh, fully saturated small spruce wood beams. An experimental test set-up was developed to ensure constant distance from the charge-coupled device camera to the sample surface as well as constant climate and light conditions during the whole experiment. Dimensional changes were observed immediately after the drying process began. An unexpected distinct effect could be observed which could not be explained by drying surface layers only. After a fast initial radial shrinkage a slowing down of the dimensional changes occurred at high mean moisture contents. A complete interruption of any dimensional changes followed. Finally, a recovery from shrinkage was even observed. It is assumed that strong negative pressure occurred in the fully saturated capillaries owing to dehydration which led to additional dimensional changes. As a consequence, the break of the water column and aeration in these capillaries finally resulted in a recovery period in the shrinkage rate due to the pressure release. After this effect, the dehydration was characterized by a phase of fast and almost linear shrinkage due to drying surface layers. Finally, the shrinkage slowed down to zero when reaching equilibrium moisture content.

Introduction

A lot of work has been published regarding the drying of wood and the associated dimensional changes. To avoid these dimensional changes and the associated defects, such as warping, cupping, checking and splitting during the final use of timber as a furniture or construction material, the sawn wood has to be dried to an average in-use moisture content. This is the main motivation for timber drying (e.g. Perré & Olek, 2007), besides other reasons such as preventing biological attacks or preconditioning for further processing, such as planing and gluing. Consequently, drying is a key operation that is essential in the chain of wood processing and the associated dimensional changes are key aspects of all dehydration phenomena (Katekawa & Silva, 2006). The dimensional changes during drying are termed shrinkage in almost all of the literature available concerning drying of wood.

It has further been generally accepted that shrinkage does not occur until a definite stage in the drying has been reached, namely the fibre saturation value of a given wood species (e.g. Stevens, 1938; Stamm 1964; Trübswetter 2006). The fibre saturation point of wood, which is the minimum moisture content in equilibrium with a saturated atmosphere (e.g. Barkas, 1935; Kollmann, 1951) or at which the cell walls are fully saturated with water but the lumina no longer contain free water (e.g. Stevens, 1938; Stamm, 1971; Skaar, 1972), is well known; so too are the hysteresis of shrinking and swelling and their dependencies on influencing factors such as temperature or initial moisture content (e.g. Barkas, 1932, 1935; Kollmann, 1951; Siau, 1984; Keey et al., 2000). A more differentiated look on the subject is to distinguish between the dimensional changes due to drying of the whole wood and the cell wall (e.g. Siau, 1984), but in the majority of cases only a small range of moisture content is analysed, namely in the hygroscopic range from zero to the fibre saturation point or slightly above. Consequently, quite often it is postulated without any closer definition that no dimensional changes occur at all during drying above fibre saturation (e.g. Simpson, 1999; Sakagami et al., 2007, 2009).

In fact, dimensional changes of wood above fibre saturation due to drying were already being published by the 1930s in the field of wood science (Barkas, 1935; Stevens, 1938, 1963; Kollmann, 1951; Stamm, 1964), where it was excluded that the observed dimensional changes were due only to dried surface layers, while the bulk of the material was still well above fibre saturation. In general, it was concluded that the extraction of moisture from the cell cavities resulting in negative pressure might be the reason. Similar observations were recently presented by Perré (2007) and Almeida et al. (2008), analysing the shrinkage of microsamples during drying. The observed dimensional changes in all these studies start at a moisture content of approximately 50% during the initial drying and are mainly drawn back to material accessible to collapse due to capillary pressure (Sandland & Gjerdrum, 2007). However, only a few studies show the drying behaviour of wood from the fully saturated state to the end of all shrinkage processes. Therefore, it was the aim of this study to analyse any dimensional changes along the whole moisture range.

Materials and methods

Thirty small beams with a size of 6 mm tangential, 6 mm radial and 100 mm longitudinal were prepared from fresh, never-dried sapwood of Norway spruce [Picea abies (L.) Karst.] from Austrian and Swedish sites. During all preparation steps the samples were kept wet; they were then soaked in distilled water under a partial vacuum (10 kPa) for 48 h to refill any embolized tracheids and to ensure the fully saturated state of the samples (Hietz et al., 2008). Finally, the samples were stored in degassed water until the experiments began. Consequently, the same starting position (fully saturated) could be guaranteed for all samples.

Changes in the radial direction during drying at 25°C and 60% relative humidity were monitored using a video extensometer (ME46; Messphysik, Fürstenfeld, Austria) equipped with a black and white high-resolution charge-coupled device (CCD) video camera (OS-65D; Mintron Enterprise Co., Taipei, Taiwan). An experimental test set-up was developed to ensure a constant distance from CCD camera to the sample surface. This system could measure distances with a resolution of 1 μm with the chosen set-up. Climate and light conditions were kept constant during the whole experiment (Figure 1). The sample holder was placed on a balance (resolution 10⁻³ g, ATL-623; Acculab, Göttingen, Germany) to monitor the weight loss due to drying. The sample was taken from the water storage, swabbed briefly with a tissue to remove adherent water from the sample surface, then mounted immediately in the sample holder. In this way, monitoring of dimensional changes began immediately after the drying process started.

Figure 1.

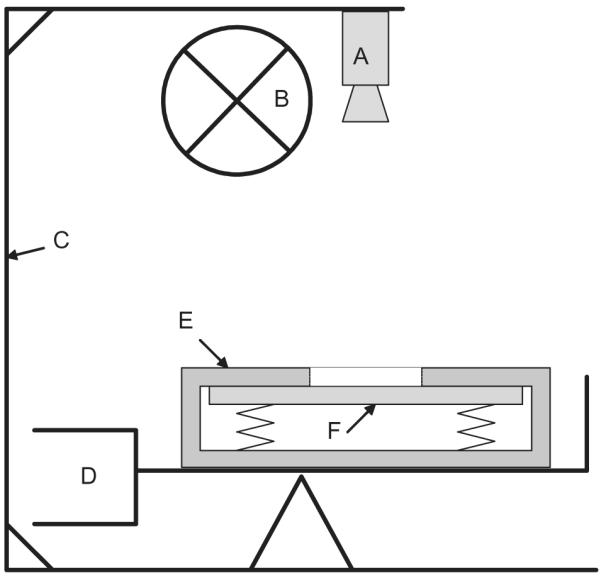
Schemata of the experimental test set-up: black and white high-resolution CCD camera (A) and cold light source (B) mounted on a stable frame (C). Balance (D). Special aluminium sample holder (E) with an aperture in the middle of the upper frame to which the wood sample (F) is pressed by means of compression springs.

Water loss and radial dimension were logged every 10 s, and a picture was taken by the CCD camera every minute. After the experiment, the oven-dry mass of the sample was determined by dying at 103°C to calculate the moisture content according to EN 13183-1 (CEN, 2002).

Results and discussion

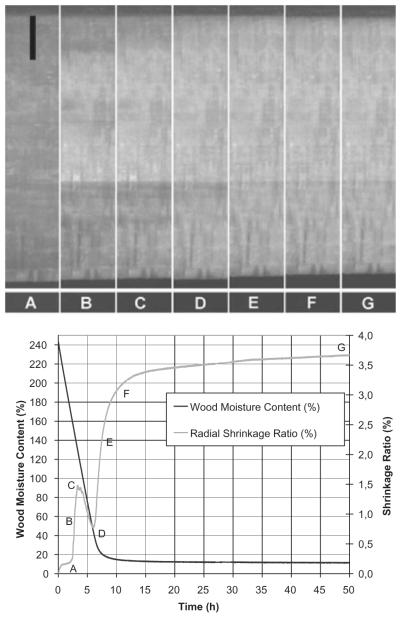
Figure 2 shows a typical example of the observations made during the drying experiments over the whole range of moisture content. Graphs showing the same behaviour with mean values and standard deviations can be found in Rosner et al. (2009, 2010). The high initial moisture content of 243% of the specimen with a quite low basic density of 322 kg m⁻³ represents well the fully saturated state of the specimen at the start of the experiment and is consistent with the possible maximum moisture content of wood (e.g. Bernhart, 1965; Skaar, 1972; Keey et al., 2000).

Figure 2.

Moisture content (%) and radial shrinkage (%) during the whole drying duration from the fully saturated state to equilibrium moisture content of approximately 11%. The letters (A–G) indicate different dehydration stages at which the corresponding seven photographs were taken. Scale bar = 1 mm.

As seen in Figure 2 (which shows original single values and not smoothed curves), the drying process started immediately, resulting in an almost linear, non-interrupted moisture loss until a moisture content of approximately 40% was reached. At this point fibre saturation was reached during this initial desorption, in contrast to a fibre saturation of around 30% during later adsorption or desorption processes for Norway spruce. (Kollmann, 1951; Bernhart, 1965; Stone & Scallan, 1967; Stamm, 1971; Wagenführ, 1996; Keey et al., 2000). Subsequently, the drying rate (seen as the slope of the curve) constantly slowed down to zero when reaching an equilibrium moisture content of approximately 11% in the given climate.

Dimensional changes were observed immediately after the drying process started. While an undefined part of the observed dimensional changes could be attributed to drying surface layers, an unexpected distinct effect was observed at very high moisture content which could not be explained by drying surface layers only (reaching point C in Figure 2). Very fast drying of the outermost layers is known to occur during drying of saturated wood, summarized as the dry shell concept (Salin, 2007). However, it is also known that this dry shell remains very thin during the early stages of drying (Tremblay et al., 2000; Salin, 2007) and could therefore not explain the observed fast and strong initial dimensional changes in radial direction (Figure 2, A–C).

Consequently, it is concluded that the observed dimensional changes are due to the negative water pressure in the cell lumina/capillaries, which is known to occur in the sapwood of living stems (Offenthaler et al., 2001; Perämäki et al., 2001; Ueda & Shibata, 2001; Zweifel et al., 2001; Gall et al., 2002) and also in other wood tissues as the first step in cell collapse (Barkas, 1935; Stevens, 1938, 1963; Kollmann, 1951; Siau, 1984; Perré, 2007). However, in the latter case the observed dimensional changes are reported to start at moisture contents of around 50%, whereas the observed changes in this study occurred at a higher mean moisture content, in the range of 170–130%. Dimensional changes at moisture contents above fibre saturation are caused by a decrease in the diameter of tracheids which contain free water (e.g. Offenthaler et al., 2001; Perré, 2007). Hydrostatic tension forces acting perpendicular to the cell walls try to draw the walls inwards (Rosner et al., 2010).

After a fast initial radial shrinkage a slowing down of the dimensional changes occurred at high mean moisture contents when the bigger part of the samples was well above fibre saturation. A complete interruption of any dimensional changes followed (Figure 2, point C). Finally, a recovery from shrinkage was even observed, which is also visible on the photographs (Figure 2, point D). It is therefore assumed that the strong capillary action that caused the observed dimensional changes suddenly disappeared as a result of aeration (Offenthaler et al., 2001; Hölttä et al., 2005; Rosner et al., 2009). Subsequently, this pressure release results in a recovery period leading to an increase in the radial dimension.

This partial recovery of the rapid and strong dimensional changes observed during the early stage of drying at high mean moisture contents additionally confirms that the observed effect was not induced by shrinkage and swelling effects of a dried and rewetted shell, as the moisture contents near the specimen surface of Norway spruce wood do not increase again during drying (Tarmian et al., 2009). However, 100% recovery from the pressure-induced dimensional changes could not be observed because it is masked by increasing cell-wall shrinkage due to further drying.

After this effect, the dehydration was characterized by a phase of fast and almost linear shrinkage (Figure 2, E) that is characteristic of drying due to bound water loss (Stamm, 1964; Skaar, 1972; Perré, 2007; Almeida et al., 2008). This phase corresponds well with the observed changes in moisture content and starts at approximately 40% moisture content (Figure 2, point D). Finally, the shrinkage slowed down to zero when reaching equilibrium moisture content (Figure 2, F and G).

Digital image analysis is well suited to analysing any dimensional changes of wood along the whole moisture range and the experiment set-up is simple. With this method, previous findings about the radial shrinkage of fresh spruce wood using a more sophisticated method (Rosner et al., 2009) could be confirmed.

In conclusion, digital image analysis of dimensional changes in the radial direction of fresh, never-dried Norway spruce samples showed that dimensional changes occur from the very beginning of the drying process. The method offers high accuracy and high repeatability. The observations could not be explained by drying surface layers alone, but also by strong capillary forces occurring far above fibre saturation. These findings are consistent with other studies but show that these dimensional changes can occur at higher moisture contents than reported by others and do not necessarily result in collapse. A recovery from diminished radial dimensions can even be observed owing to cavitation during further drying. The possible initiation of microcracks during this stage of drying, and consequently a practical impact on commercial timber drying, should be analysed in detail.