Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Feb 6;2:248. doi: 10.1038/srep00248

Energy gaps in Bi2Sr2CaCu2O8+δ cuprate superconductors

J K Ren 1, X B Zhu 1, H F Yu 1, Ye Tian 1, H F Yang 1, C Z Gu 1, N L Wang 1, Y F Ren 1, S P Zhao 1,a
PMCID: PMC3272663  PMID: 22355760

Abstract

The relationship between the cuprate pseudogap (Δp) and superconducting gap (Δs) remains an unsolved mystery. Here, we present a temperature- and doping-dependent tunneling study of submicron Bi2Sr2CaCu2O8+δ intrinsic Josephson junctions, which provides a clear evidence that Δs closes at a temperature Tc0 well above the superconducting transition temperature Tc but far below the pseudogap opening temperature T*. We show that the superconducting pairing first occurs predominantly on a limited Fermi surface near the node below Tc0, accompanied by a Fermi arc due to the lifetime effects of quasiparticles and Cooper pairs. The arc length has a linear temperature dependence, and as temperature decreases below Tc it reduces to zero while pairing spreads to the antinodal region of the pseudogap leading to a d-wave superconducting gap on the entire Fermi surface at lower temperatures.

The properties of the pseudogap and its relation to the superconducting gap are among the central issues in the search for the cuprate pairing mechanism. A number of spectroscopic studies such as scanning tunneling microscopy (STM) and angle-resolved photoemission spectroscopy (ARPES) have been reported1,2,3,4,5,6,7,8,9,10,11,12,13,14. Some experiments indicate that the pseudogap may arise fully from precursor superconductivity (single-gap picture)1,2,3,4,5, while others suggest an origin that is unrelated to superconductivity (two-gap picture)6,7,8,9,10,11,12,13,14. In the latter case, uncertainty exists as precursor pairing in certain temperature range above the superconducting transition temperature Tc is reported in some experiments8,13,14, which contrast with other experiments in which the superconducting gap Δs is found to close at Tc6,9,10,12. In this paper, we address the issue using the temperature- and doping-dependent tunneling spectroscopy of submicron Bi2Sr2CaCu2O8+δ intrinsic Josephson junctions.

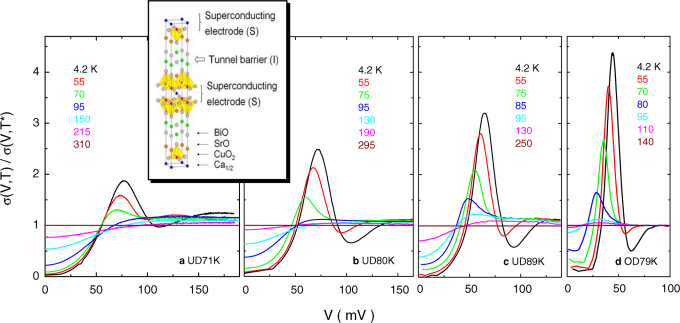
For conventional Bardeen-Cooper-Schrieffer (BCS) superconductors, Giaever's planar-type tunnel junctions15 provided decisive measurements of the superconducting gap, the electronic density of states (DOS), the quasiparticle scattering rate, and the effective spectrum of phonons that mediate pairing16,18,17. Bi2Sr2CaCu2O8+δ intrinsic Josephson junctions19 are the similar planar-type junctions with the best quality one may have for cuprate superconductors. As is shown in the inset of Fig. 1, these junctions are formed within the crystal with CuO2 double-layers as superconducting electrodes and BiO/SrO interlayers as the tunnel barrier. Such superconductor-insulator-superconductor (SIS) junctions avoid all kinds of extrinsic uncertainties during experiment and can offer stable and reproducible temperature-dependent measurements. Earlier spectroscopic studies using these junctions suffered from sample's self-heating that severely distorts the tunneling spectra and many efforts were made to solve the problem20,21,22,23,24,25,26,27. One effort involved optimizing the surface-layer contact and reducing the junction size well below 1 μm, which are shown to suppress heating sufficiently in the case of near optimally doped samples23,24,25,26. The data presented below were based on these works and extended to samples with different doping strength.

Figure 1. Temperature and doping dependence of intrinsic tunneling spectra of Bi2Sr2CaCu2O8+δ superconductors.

Figure 1

Open in a new tab

(a–d) doping strength increasing from underdoped (UD) to overdoped (OD) with Tc = 71, 80, 89 and 79 K, respectively. The spectra are presented with V corresponding to the voltage per junction and in each case are normalized to the respective ones at the pseudogap opening temperature T* = 310, 280, 230 and 140 K. Inset displays a crystal unit cell, showing that electron tunneling occurs between CuO2 double layers, which form planar-type superconductor-insulator-superconductor (SIS) tunnel junctions.

The present work demonstrates that the superconducting gap Δs closes at a temperature Tc0 well above Tc but far below the pseudogap opening temperature T*, which supports a two-gap picture with superconducting pairing persisting up to Tc0. The pairing is found to occur first on a limited Fermi surface near the node below Tc0, accompanied by a Fermi arc due to finite quasiparticle scattering rate and pair decay rate. The arc length has a linear temperature dependence, and as temperature decreases below Tc it reduces to zero while pairing spreads to the antinodal region of the pseudogap leading to a d-wave superconducting gap on the entire Fermi surface at lower temperatures.

Results

Experimental spectra

In Fig. 1, we show the tunneling conductance σ(V, T) at typical temperatures for four samples from underdoped (UD) to overdoped (OD) with Tc = 71, 80, 89 and 79 K, respectively (see Methods and Supplementary Information for details). The data are normalized to σ(V, T*) with T* = 310, 280, 230 and 140 K, above which the spectra become gapless. At low temperatures they exhibit the familiar peak-dip-hump structure with the superconducting coherence peak height and position, the peak-dip separation all evolving systematically with the doping strength. The dip feature, caused possibly by electron coupling to a Boson spectrum with energy linked to the peak-dip separation28, disappears gradually as temperature approaches Tc.

In Fig. 2 a-d, we plot half the conductance peak position in meV versus temperature (squares), which represents Δs approximately at low temperatures. We see that for all samples the value decreases slightly with increasing temperature toward Tc, similar to the BCS gap versus temperature dependence. Near and above Tc, however, it differs substantially for different doping samples, which should result from the increasing roles played by the pseudogap and by the lifetime effects of the quasiparticles and Cooper pairs.

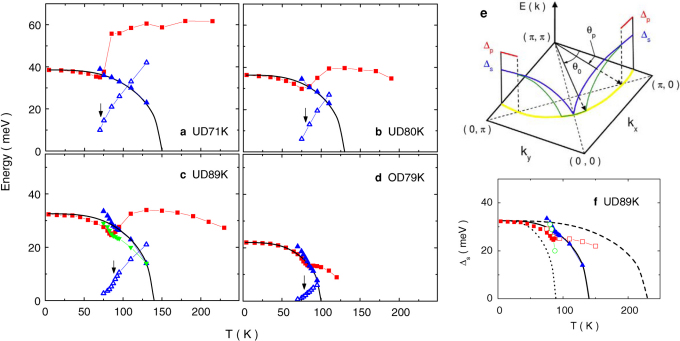
Figure 2. Measured and fitted quantities showing that the superconducting gap Δs closes at Tc0 (Tc < Tc0 < T*), above which a pseudogap already exists.

Figure 2

Open in a new tab

(a–d) squares: half the conductance peak position in meV; up-triangles: superconducting gap Δs (solid) and lifetime parameter γs (open) obtained by fitting the normalized spectra σ(V, T)/σ(V, Tc0) using Ns(θ, ω) excluding the pseudogap-dominant region from 0 to θp on the Fermi surface. Above Tc (indicated by arrows), Δs is seen to follow nicely the BCS d-wave gap (lines) closing at Tc0 = 150, 130, 140, 100 K, respectively. In (c) Δs obtained from fit considering the entire Fermi surface is plotted as down-triangles for comparison. (e) symbols and schematic gap profiles on the Fermi surface (yellow) in the temperature ranges of well below Tc (blue) and from Tc0 to T* (red). From near Tc to Tc0, half the peak separation of A(kF, ω) is shown (green) with a Fermi arc as observed in ARPES experiment. (f) Δs of the UD89K sample obtained from fits to the normalized σ(V, T)/σ(V, T*) (open squares) and σ(V, T)/σ(V, Tc) (circles) tunneling spectra. Both deviate considerably from the BCS gap closing at respective temperatures (dashed and dotted lines), as compared to the result from fit to σ(V, T)/σ(V, Tc0) (up-triangles, also in c) that shows a good agreement with the BCS prediction (solid line) above Tc (see text for more details).

Temperature dependence of the superconducting gap

A key feature one expects for superconductors is that Δs follows the BCS-like gap equation and closes at a temperature, possibly higher than Tc29, where Cooper pairs vanish. To clarify the situation, we fitted our experimental spectra with a DOS that is widely used in tunneling experiment for both BCS superconductors18,30 and cuprates1,26,31:

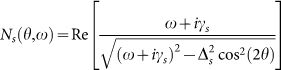graphic file with name srep00248-m13.jpg

where a d-wave gap is considered and the subscript s denotes the superconducting part. θ and γs are the angle of in-plane momentum measured from (π,0) (see Fig. 2e) and the parameter characterizing the lifetime effects, respectively. The DOS was first proposed by Dynes et al.30 and recently shown26 to be related to a phenomenological self-energy developed for the pseudogap discussion in which Δs extends to the precursor pairing regime above Tc32. Taking the UD89K data as an example, we replot half the peak position below Tc in Fig. 2f, in which lines are the BCS d-wave gap that closes at T* (dashed), Tc (dotted) and Tc0 = 140 K to be discussed below (solid). In the single-gap picture with pairing starting at T*, Δs should vary along the dashed line near and above Tc if the lifetime effects are taken into account. Δs obtained from fit to the normalized spectra σ(V, T)/σ(V, T*) using Ns(θ, ω) over the whole Fermi surface26 is shown in Fig. 2f as open squares (γs not shown for clarity). It is seen that the result deviates significantly from the dashed line, which means that the single-gap picture does not lead to an appropriate description.

In an STM experiment on Bi2Sr2CuO6+δ superconductors, Boyer et al.6 found that when seemingly irregular experimental spectra are normalized to the one slightly above Tc, they reveal a homogeneous superconducting gap that closes at Tc. This treatment eliminates the effect of the pseudogap that already exists above Tc. (Such treatment was also applied for Bi2Sr2CaCu2O8+δ SIS-type junctions28 and BCS SIS-type junctions where effects unrelated to superconductivity are successfully removed16). In the related two-gap picture, one may view the two phases as coexisting and being anticorrelated on the Fermi surface with different spectral weights, and there is a boundary θp below and above which they dominate respectively11. Fig. 2e shows a simple cut-off presentation as used in STM experiments7,8. In the present work, we fitted the normalized spectra σ(V, T)/σ(V, Tc), considering consistently Ns(θ, ω) for θ > θp only on the Fermi surface so the pseudogap-dominant region was excluded in the tunneling current calculation (see Methods). The resulting Δs taking θp = 12°, a value close to the STM observation7, is shown as open circles in Fig. 2f for the UD89K sample. It can be seen that the fit is again unsatisfactory when compared to the BCS curve (dotted line).

A satisfactory fit was nevertheless obtained when it was performed with respect to σ(V, T)/σ(V, Tc0) where Tc < Tc0 < T*, for which pair formation starting at Tc0 should be assumed. Precursor pairing above Tc has been suggested previously in some experiments8,13,14,33,34. We note that the half peak position in Fig. 2c (squares) shows an obvious turning near 140 K. In Fig. 2f (also in c), Δs from the fit considering Tc0 = 140 K and excluding the pseudogap region of θ < θp = 12° is shown as solid up-triangles. We see that Δs follows nicely the BCS curve (solid line) above Tc in this case. As temperature decreases below Tc, however, it deviates increasingly with decreasing temperature. To understand this behavior, we also plot Δs obtained with θp = 0 as down-triangles in Fig. 2c, which shows a clear tendency of approaching the BCS solid line below Tc. These two results can be naturally explained if, as temperature decreases below Tc, the superconducting pairing gradually spreads to the antinode on the Fermi surface with θ < θp, which is predominantly occupied by the pseudogap phase above Tc.

Similar results were obtained for other samples and they are displayed in Fig. 2a-d together with the fitted γs shown as open up-triangles. Tc0 from the best fit for the four samples is 150, 130, 140 and 100 K, respectively. For the more underdoped UD71K sample, pair spreading into the antinodal region is seen in a more limited temperature range below Tc since a tunneling dip quickly develops, which is beyond the simple description using Ns(θ, ω)28. On the other hand, all the data above Tc show a compelling evidence that the superconducting gap Δs closes at Tc0. They demonstrate that the superconducting phase grows out from the pseudogap phase with Tc0 as the Cooper pair formation temperature, which supports a two-gap picture with precursor pairing extending from above Tc up to Tc0.

Temperature dependence of the zero-bias conductance

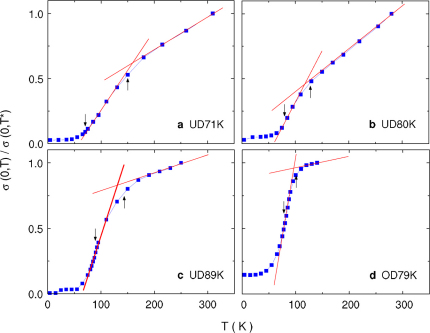
Additional evidence that the superconducting gap Δs closes (or opens if we look with decreasing temperature) at Tc0 came from the direct experimental data of the zero-bias conductance σ(0, T), which should be largely related to the density of states near the Fermi level and thus is sensitive to the formation of an energy gap. In Fig. 3, we plot the measured σ(0, T)/σ(0, T*) for the four samples in the temperature range from 4.2 K to T*. The up and down arrows indicate Tc0 and Tc, respectively. It can be seen that with lowering temperature an accelerated decrease occurs starting from Tc0 for all samples, which corresponds to the fast decrease of the density of states resulting from the opening of the superconducting gap Δs. Also, such a decrease is seen to continue farther below Tc for higher doping samples. This can be explained considering that for higher doping samples, Tc is closer to Tc0 so Δs will increase more below Tc before reaching the low-temperature value (see Fig. 2), which leads to the further reduction of σ(0, T).

Figure 3. Temperature dependence of the zero-bias conductance.

Figure 3

Open in a new tab

The data are presented from 4.2 K up to the pseudogap opening temperature T* and are normalized to those at T*. Arrows pointing upward and downward indicate Tc0 and Tc, respectively. Solid lines are guides to the eye.

Parameters of the superconducting and pseudogap phases

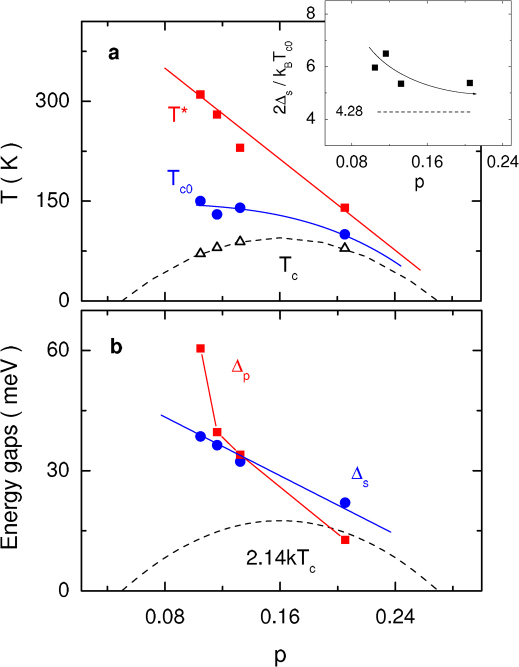
We emphasize that our fit based on σ(V, T)/σ(V, Tc0) assumes a temperature-independent pseudogap. As is discussed by Boyer et al.6 this should be a reasonable approximation. In many experiments such as STM1 the pseudogap peak position is found nearly temperature independent and it disappears by “filling-up” as temperature approaches T*. If we take the half peak position at Tc0 in Fig. 2 a-d to characterize the pseudogap Δp, it shows a distinct doping dependence as that of Δs. In Fig. 4a, we plot T*, Tc0 and Tc against the doping level p, while Δs and Δp are shown in Fig. 4b and the resulting 2Δs/kTc0 in the inset. In Fig. 4b, Δp is seen to have a fast increase as p reduces to the more underdoped level, as observed in ARPES experiments35. On the overdoped side, it continues to decrease to a value below Δs.

Figure 4. Doping dependence of superconducting and pseudogap phases parameters.

Figure 4

Open in a new tab

(a) Tc , Tc0 and T*. (b) Δs and Δp. Inset shows 2Δs/kBTc0. Hole concentration p is obtained from the relation Tc/Tc,max = 1–82.6(p − 0.16)2 with Tc,max = 95 K. Solid lines are guides to the eye.

Fermi arcs derived from lifetime parameters

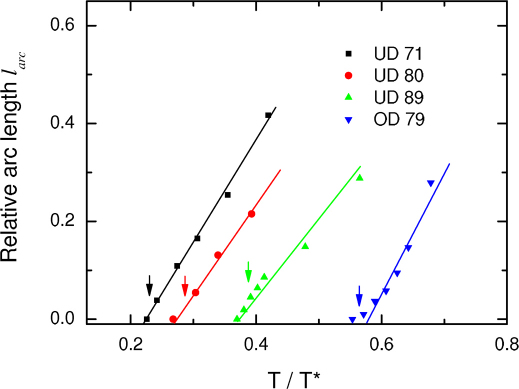
The lifetime effects play an important role in the precursor pairing regime from around Tc up to Tc0 due to increasing γs. One of the consequences is the appearance of a Fermi arc near the node with θ > θ0 (see Fig. 2e), which is defined through the peak separation of the spectral function A(k, ω) around Fermi surface in ARPES experiments36,37. The above-mentioned self-energy model32, from which Ns(θ, ω) can be derived26, contains three parameters: the quasiparticle scattering rate Γ, the pair decay rate ΓΔ, and Δs, with γs = (Γ + ΓΔ)/2. Assuming a linear temperature dependence of Γ, we inferred both Γ and ΓΔ from the fitted parameters γs in Fig. 2a-d. With known Δs, Γ and ΓΔ, A(kF, ω) was determined and the arc length larc = 1− (4/π)θ0 was calculated26,36,37 (see Methods). In Fig. 5, we show the calculated larc versus temperature for the four samples. The results display an approximate linear temperature dependence, which is quite general as discussed in the ARPES data analysis using the same self-energy in a simplified situation of Γ = ΓΔ36,37.

Figure 5. Temperature dependence of relative arc length larc calculated from fitted Δs, Γ and ΓΔ parameters.

Figure 5

Open in a new tab

Arrows indicate Tc. Solid lines are guides to the eye showing approximately the linear temperature dependence.

Discussion

We have shown that for the four Bi2Sr2CaCu2O8+δ crystals with different doping levels the superconducting gap Δs closes at a temperature Tc0 well above the superconducting transition temperature Tc but far below the pseudogap opening temperature T* thus an extensive precursor pairing regime between Tc and Tc0 is demonstrated. In the Methods section, we present an alternative fitting procedure considering both the superconducting part (Δs, γs) and the pseudogap part (Δp, γp), which leads to the same conclusion as using the conventional approach of normalizing out the pseudogap contribution described above. It is shown that Δp is nearly constant from slightly below Tc up to T* while γp experiences a continuous increase, which is consistent with the filling-up character of the pseudogap as temperature approaches T* from below.

So far the STM and ARPES results supporting the two-gap scenario alone for the Bi2Sr2CaCu2O8+δ materials are still diverse and controversial. Some results suggest that below Tc the superconducting gap would coexist with the pseudogap at the antinode12,13 while others indicate that they reside at the nodal and antinodal regions separately7. Above Tc, precursor pairing is demonstrated in some experiments8,13 whereas a superconducting gap closing at Tc is also observed9. The present tunneling results clearly support the precursor pairing view in the temperature range from Tc to Tc0, which is similar to the results in Refs. 8 and 13. In this temperature range, the superconducting gap and the pseudogap locate predominantly at the node and the antinode, respectively. We note that both the results of Δs presented as solid up- and down-triangles in Fig. 2c are obtained by fitting to the spectra that are normalized to the one at Tc0. In this case, the pseudogap contribution is not considered in the fits but it still exists. Therefore the result that the superconducting pairing spreads into the antinodal region below Tc means that the two components coexist at the antinode. Since all the data of Δs in Fig. 2a–d (solid up-triangles) show similar upturns as temperature decreases below Tc, we believe the coexisting nature to be true for all samples. On the other hand, for the UD71K sample we see from Fig. 2a (squares) that the pseudogap spectral peak quickly diminishes and switches to the superconducting peak below Tc. This may indicate that the spectral weight of the pseudogap becomes small compared to that of the superconducting gap below Tc for this sample which is still not deep enough into underdoping, or the pseudogap structure is obscured by the growth of the dip structure in the tunneling spectra. For higher doping samples, uncertainty arises from the fact that the superconducting gap and pseudogap scales becomes similar (see Fig. 2).

Fermi arcs in the ARPES experiments often show a relatively large size just above Tc, which collapse as temperature decreases below Tc3,9,38. In the two-gap scenario, the collapse results from the opening of the superconducting gap on the arc at Tc9. Our results are similar to those in a sense that Tc0 is in the place of Tc and the arc region is defined from θp to π/2 - θp in Fig. 2e in the pseudogap state. As mentioned above, the lifetime effects in the superconducting state can be successfully used to explain the linear temperature dependence of the arc length larc36,37. It is interesting to note that in the single-gap picture larc will exhibit a faster rise as temperature increases across Tc and therefore has a larger value compared to those in Fig. 5 just above Tc26, which is consistent with the results observed in ARPES experiments3,38. On the other hand, our present results, including the development of the superconducting gap at Tc0 > Tc on an arc spanned in the pseudogap state and the temperature dependence of the arc resulting from the lifetime effects in the superconducting state, as depicted in Fig. 5, bear a close resemblance to the STM observations8,29. The differences and similarities in these ARPES and tunneling experiments remain to be explained in the future.

Open questions that are of further interest are the nature of the pseudogap and whether the superconducting and pseudogap phases are formed from the same underlying physics. Recent experiments suggest that the pseudogap phase can result from various densitywave and other states, which may compete11 or have an intimate relationship with the superconducting state14. Our results indicate that the pseudogap Δp has a distinct temperature and doping dependence compared to Δs, which may not be in favor of the view that they have a common microscopic origin. In the classical BCS superconductors, the strong Coulomb and phonon interactions between electrons in the normal state lead to an average correlation energy in the order of eV, which is much larger than the pair-binding energy of meV. The strong interactions are later removed in Landau's Fermi-liquid theory with quasiparticles replacing the bare electrons. Consideration of the interaction neglected in Landau's approximation leads to the coupling between quasiparticles and formation of Cooper pairs17. In the present case of cuprate superconductors, however, the situation is different and is more complicated as we see that the pseudogap size can be larger, comparable, and smaller than the superconducting gap when doping increases.

Methods

Experimental details

Mesa-type intrinsic Josephson junctions (IJJs)19,20,21,22,23,24,25,26,27 were used in this work with their geometry shown schematically in Fig. S1. Details of the sample fabrication have been described elsewhere23,24. To reduce samples self-heating, a notorious problem in IJJs studies, we took special care to reduce the contact resistance between Au films and Bi2Sr2CaCu2O8+δ crystals which results in the surface layers with good properties23,25. In addition, mesa sizes were reduced well below 1 μm as it was demonstrated that heating can be largely neglected in this case24. Other methods to reduce heating include using IJJs made of HgBr2 intercalated Bi2Sr2CaCu2O8+δ crystals20,27 and adopting short-pulse measurements21, which are discussed extensively recently27. These studies demonstrate tunneling spectra with moderate sharpness of the conductance peak and clear presence of the dip feature after the reduction of heating, as achieved in the present experiment shown in Fig. 1. (See Supplementary Information for further details.)

Spectra fit separating the pseudogap contribution

The I-V characteristics of a superconductor-insulator-superconductor (SIS) junction can be calculated from18:

graphic file with name srep00248-m1.jpg

where RN is junction's normal-state resistance, n(ω) is the DOS of two identical S-electrodes and f(ω) is the Fermi function. Our results were obtained by fitting the normalized experimental spectra using σ = dI/dV from equation (1) with the following normalized DOS for n(ω):

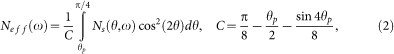graphic file with name srep00248-m2.jpg

where cos2(2θ) comes from the directional tunneling matrix element, which is found to improve the description for the intrinsic tunneling process within Bi2Sr2CaCu2O8+δ crystals26,27,28. In equation (2), integration is performed from θp to π/4 with θp ≥ 0 due to symmetry. If the superconducting phase is considered on the entire Fermi surface, we have θp = 0. As discussed in the paper, our central results in Fig. 2a–d were obtained from fitting σ(V,T)/σ(V, Tc0) with a nonzero θp to exclude the pseudogap-dominant region on the Fermi surface.

The θp parameters obtained from fits to the four samples used in this work are listed in Table SI. For samples from UD89K to OD79K, θp decreases from 12° to 10°. This trend is consistent with the STM observations7. However, for UD80K and UD71K samples, θp is 10° and 11°. The slight inconsistency could be caused by the fact that the UD80K and UD71K samples were yttrium doped, which were different from the oxygen doped UD89K and OD79K samples and might have altered crystalline arrangement resulting in reduced pseudogap expansion in momentum space. The satisfactoriness of our fit using these parameters can be seen in Fig. S4.

Using normalized spectra to get rid of the effects unrelated to superconductivity is a common practice in tunneling experiments for both BCS superconductors16,18 and cuprates6,28 in both SIN (N being a normal metal)6,18 and SIS16,28 type tunnel junctions. For example, McMillan and Rowell studied the SIS type Pb junctions16. By normalizing the data below Tc to the one above Tc, additional structures in the measured spectra resulting from tunnel barrier phonons are successfully removed. The phonon spectra extracted from the data are exactly the same as those obtained from the SIN type Pb junctions. Below we further justify this approach for the present experiment by considering both the superconducting and pseudogap contributions in the fitting procedure.

According to the two-gap scenario, from Tc0 up to T* there is only the pseudogap phase located predominantly near the antinode with θ < θp and one has Ns(θ, ω) = 1 for θ > θp. Below Tc0 down to at least Tc the superconducting and pseudogap phases exist predominantly above and below θp, respectively (see Fig. 2e). If we use the same form of d-wave DOS to model the pseudogap phase that may come from various density-wave states, now denoted by Np(θ, ω) with two parameters Δp and γp, we can write the following DOS for n(ω) in equation (1) for T > Tc0:

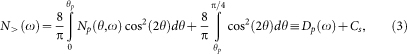graphic file with name srep00248-m3.jpg

where CS is a constant from the ungapped part on the Fermi surface. For T < Tc0 we have

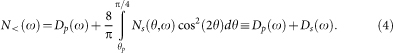graphic file with name srep00248-m4.jpg

The I-V curve can be calculated above Tc0 from

graphic file with name srep00248-m5.jpg

and below Tc0 from

graphic file with name srep00248-m6.jpg

In Fig. S5, we show the results from fits using I>(V) and I<(V) to the normalized experimental spectra σ(V, T)/σ(V, T*) (note that T* is used as normalization temperature instead of Tc0), taking also the UD89K IJJs as the example. Up-triangles are replotted Δs and γs from Fig. 2c and 2f. Above Tc0, only the pseudogap is concerned, the parameters Δp and γp are thus directly determined using I>(V), which are shown as down-triangles above Tc0. The down-triangles shown in the figure below Tc0 are obtained using I<(V) and the replotted Δs and γs parameters. In other words, if these Δp and γp are used, the two fitting approaches would produce the same Δs and γs. For comparison, squares in Fig. S5 show the Δs and γs when Δp and γp values at 150 K are used for temperatures below Tc0. These data show nearly the same Δs but slightly different γs.

These results confirm our central conclusion that the superconducting gap Δs closes at Tc0. We note that Δp in Fig. S5 is nearly constant while γp increases with increasing temperature all the way up to T*, which demonstrate that the pseudogap disappears by “filling-up” as temperature approaches T*. Since a continuing decrease of γp down to Tc seems reasonable, both Δs and γs parameters obtained from the simple fitting approach using σ(V, T)/σ(V, Tc0) and equations (1) and (2) should be a good approximation.

Fermi arc calculation

For the discussion of the cuprate pseudogap in ARPES experiments, Norman et al. proposed a phenomenological self-energy taking account of the lifetime effects32:

graphic file with name srep00248-m7.jpg

where k is the energy of bare electrons relative to the value at the Fermi surface. From equation (7) it can be shown that the Green's function G(k, ω) = 1/[ω − k − Σ(k, ω)] has the form

graphic file with name srep00248-m8.jpg

The spectral function on the Fermi surface A(kF, ω) = −(1/π)ImG(kF, ω), assuming Δk = Δs cos(2θ), is given by26

graphic file with name srep00248-m9.jpg

In the ARPES experiments, it is considered to be gapped if A(kF, ω) has maxima at ω = ±ωp ≠ 0, while Fermi arc appears at places where A(kF, ω) has maximum only at ω = 0. Thus ωp can be found by setting the first derivative of equation (9) to zero:

graphic file with name srep00248-m10.jpg

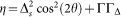where Inline graphic. By setting the second derivative to zero, the angle θ0 at which the arc starts is found to be

graphic file with name srep00248-m11.jpg

The relative arc length larc is defined by

graphic file with name srep00248-m12.jpg

In the present work, the quasiparticle scattering rate Γ and pair decay rate ΓΔ were estimated from the experimentally fitted parameter γs in Fig. 2a–d via the relation γs = (Γ + ΓΔ)/226. We assumed a linear temperature dependence of Γ and considered that Γ is larger than ΓΔ, which should be reasonable from the basic physical considerations. In Fig. S6 the results of Γ and ΓΔ for the four samples are shown, which were determined considering that ΓΔ = 0 near Tc and the slope of Γ set close to that of γs. The corresponding larc versus T calculated are plotted in Fig. 5.

Author Contributions

J.K.R., X.B.Z., Y.F.R., H.F.Yang and C.Z.G. prepared the mesa samples. J.K.R., X.B.Z., H.F.Yu and Ye T. did the measurement. J.K.R. and S.P.Z. performed the data analysis. N.L.W. provided and prepared single crystals for the UD71K, UD80K and OD79K samples. S.P.Z. designed the experiment and wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary information

srep00248-s1.pdf (350.6KB, pdf)

Acknowledgments

We thank N. P. Ong, Siyuan Han, X. J. Zhou and Z. Y. Weng for helpful discussions. This work was supported by the National Natural Science Foundation of China (Grant Nos. 10974242 and 50825206) and the Ministry of Science and Technology of China (Grant No. 2011CBA00106).

References

  1. Fischer ø., Kugler M., Maggio-Aprile I., Berthod C. & Renner C. Scanning tunneling spectroscopy of high-temperature superconductors. Rev. Mod. Phys. 79, 353–419 (2007). [Google Scholar]
  2. Shi M. et al. Coherent d-wave superconducting gap in underdoped La2–xSrxCuO4 by Angle-Resolved Photoemission Spectroscopy Phys. Rev. Lett. 101, 047002 (2008). [DOI] [PubMed] [Google Scholar]
  3. Nakayama K. et al. Evolution of a pairing-induced pseudogap from the superconducting state gap of (Bi,Pb)2Sr2CuO6. Phys. Rev. Lett. 102, 227006 (2009). [DOI] [PubMed] [Google Scholar]
  4. Meng J. et al. Monotonic d-wave superconducting gap of the optimally doped Bi2Sr1.6La0.4CuO6 superconductor by laser-based angle-resolved photoemission spectroscopy. Phys. Rev. B 79, 024514 (2009). [Google Scholar]
  5. Chatterjee U. et al. Observation of a d-wave nodal liquid in highly underdoped Bi2Sr2CaCu2O8+δ. Nat. Phys. 6, 99–103 (2010). [Google Scholar]
  6. Boyer M. C. et al. Imaging the two gaps of the high-temperature superconductor Bi2Sr2CuO6+δ. Nat. Phys. 3, 802–806 (2007). [Google Scholar]
  7. Kohsaka Y. et al. How Cooper pairs vanish approaching the Mott insulator in Bi2Sr2CaCu2O8+δ. Nature 454, 1072–1078 (2008). [DOI] [PubMed] [Google Scholar]
  8. Lee J. et al. Spectroscopic fingerprint of phase-incoherent superconductivity in the underdoped Bi2Sr2CaCu2O8+δ. Science 325, 1099–1103 (2009). [DOI] [PubMed] [Google Scholar]
  9. Lee W. S. et al. Abrupt onset of a second energy gap at the superconducting transition of underdoped Bi2212. Nature 450, 81–84 (2007). [DOI] [PubMed] [Google Scholar]
  10. Ma J.-H. et al. Coexistence of competing orders with two energy gaps in real and momentum space in the high temperature superconductor Bi2Sr2–xLaxCuO6+δ. Phys. Rev. Lett. 101, 207002 (2008). [DOI] [PubMed] [Google Scholar]
  11. Kondo T. et al. Competition between the pseudogap and superconductivity in the high-Tc copper oxides. Nature 457, 296–300 (2009). [DOI] [PubMed] [Google Scholar]
  12. Vishik I. M. et al. ARPES studies of cuprate Fermiology: superconductivity, pseudogap and quasiparticle dynamics. New J. Phys. 12, 105008 (2010). [Google Scholar]
  13. Kondo T. et al. Disentangling Cooper-pair formation above the transition temperature from the pseudogap state in the cuprates. Nat. Phys. 7, 21–25 (2011). [Google Scholar]
  14. Rui-Hua et al. From a single-band metal to a high-temperature superconductor via two thermal phase transitions. Science 331, 1579–1583 (2011). [DOI] [PubMed] [Google Scholar]
  15. Giaever I. Energy gap in superconductors measured by electron tunneling. Phys. Rev. Lett. 5, 147 (1960). [Google Scholar]
  16. McMillan W. L. & Rowell J. M. Tunneling and strong-coupling superconductivity, in Superconductivity, edited by R. D. Parks (Marcel Dekker, New York, 1969).
  17. Schrieffer J. R. Theory of Superconductivity, (Benjamin, New York, 1964). [Google Scholar]
  18. Wolf E. L. Principles of Electron Tunneling Spectroscopy, (Oxford University Press, New York, 1985). [Google Scholar]
  19. Kleiner R. et al. Intrinsic Josephson effects in Bi2Sr2CaCu2O8 single crystals. Phys. Rev. Lett. 68, 2394 (1992). [DOI] [PubMed] [Google Scholar]
  20. Yurgens A. et al. Pseudo-gap features of intrinsic tunneling in (HgBr2)-Bi2212 single crystals. Int. J. Mod. Phys. B 13, 3758–3763 (1999). [Google Scholar]
  21. Anagawa K. et al. 60 ns time scale short pulse interlayer tunneling spectroscopy for Bi2Sr2CaCu2O8+δ. Appl. Phys. Lett. 83, 2381–2383 (2003). [Google Scholar]
  22. Krasnov V. M., Sandberg M. & Zogaj I. In situ measurement of self-heating in intrinsic tunneling spectroscopy. Phys. Rev. Lett. 94, 077003 (2005). [DOI] [PubMed] [Google Scholar]
  23. Zhao S. P. et al. Bi2Sr2CaCu2O8+δ intrinsic Josephson junctions: Surface layer characterization and control. Phys. Rev. B 72, 184511 (2005). [Google Scholar]
  24. Zhu X. B. et al. Intrinsic tunneling spectroscopy of Bi2Sr2CaCu2O8+δ: The junctionsize dependence of self-heating. Phys. Rev. B 73, 224501 (2006). [Google Scholar]
  25. Li S. X. et al. Observation of macroscopic quantum tunneling in a single Bi2Sr2CaCu2O8+δ surface intrinsic Josephson junction. Phys. Rev. Lett. 99, 037002 (2007). [DOI] [PubMed] [Google Scholar]
  26. Zhao S. P., Zhu X. B. & Tang H. Tunneling spectra of submicron Bi2Sr2CaCu2O8+δ intrinsic Josephson junctions: evolution from superconducting gap to pseudogap. Eur. Phys. J. B 71, 195–201 (2009). [Google Scholar]
  27. Kurter C. et al. Counterintuitive consequence of heating in strongly-driven intrinsic junctions of Bi2Sr2CaCu2O8+δ mesas. Phys. Rev. B 81, 224518 (2010). [Google Scholar]
  28. Zasadzinski J. F. et al. Persistence of strong electron coupling to a narrow boson spectrum in overdoped Bi2Sr2CaCu2O8+δ tunneling data. Phys. Rev. Lett. 96, 017004 (2006). [DOI] [PubMed] [Google Scholar]
  29. Pasupathy A. N. et al. Electronic origin of the inhomogeneous pairing interaction in the high-Tc superconductor Bi2Sr2CaCu2O8+δ. Science 320, 196–201 (2008). [DOI] [PubMed] [Google Scholar]
  30. Dynes R. C., Narayanamurti V. & Garno J. P. Direct measurement of quasiparticlelifetime broadening in a strong-coupled superconductor. Phys. Rev. Lett. 41, 1509 (1978). [Google Scholar]
  31. Miyakawa N. et al. Strong dependence of the superconducting gap on oxygen doping from tunneling measurements on Bi2Sr2CaCu2O8–δ. Phys. Rev. Lett. 80, 157 (1998). [Google Scholar]
  32. Norman M. R. et al. Phenomenology of the low-energy spectral function in high-Tc superconductors. Phys. Rev. B 57, R11093 (1998). [Google Scholar]
  33. Wang Y. et al. Field-enhanced diamagnetism in the pseudogap state of the cuprate Bi2Sr2CaCu2O8+δ superconductor in an intense magnetic field. Phys. Rev. Lett. 95, 247002 (2005). [DOI] [PubMed] [Google Scholar]
  34. Wen H. H. et al. Specific-heat measurement of a residual superconducting state in the normal state of underdoped Bi2Sr2–xLaxCuO6+δ cuprate superconductors. Phys. Rev. Lett. 103, 067002 (2009). [DOI] [PubMed] [Google Scholar]
  35. Ideta S. et al. Enhanced superconducting gaps in the trilayer high-temperature Bi2Sr2Ca2Cu3O10+δ cuprate superconductor. Phys. Rev. Lett. 104, 227001 (2010). [DOI] [PubMed] [Google Scholar]
  36. Norman M. R. et al. Modeling the Fermi arc in underdoped cuprates. Phys. Rev. B 76, 174501 (2007). [Google Scholar]
  37. Chubukov A. V. et al. Gapless pairing and the Fermi arc in the cuprates. Phys. Rev. B 76, R180501 (2007). [Google Scholar]
  38. Kanigel A. et al. Protected nodes and the collapse of Fermi arcs in high-Tc cuprate superconductors. Phys. Rev. Lett. 99, 157001 (2007). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary information

srep00248-s1.pdf (350.6KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES