Penalized classification using Fisher’s linear discriminant

Summary

We consider the supervised classification setting, in which the data consist of p features measured on n observations, each of which belongs to one of K classes. Linear discriminant analysis (LDA) is a classical method for this problem. However, in the high-dimensional setting where p ≫ n, LDA is not appropriate for two reasons. First, the standard estimate for the within-class covariance matrix is singular, and so the usual discriminant rule cannot be applied. Second, when p is large, it is difficult to interpret the classification rule obtained from LDA, since it involves all p features. We propose penalized LDA, a general approach for penalizing the discriminant vectors in Fisher’s discriminant problem in a way that leads to greater interpretability. The discriminant problem is not convex, so we use a minorization-maximization approach in order to efficiently optimize it when convex penalties are applied to the discriminant vectors. In particular, we consider the use of L₁ and fused lasso penalties. Our proposal is equivalent to recasting Fisher’s discriminant problem as a biconvex problem. We evaluate the performances of the resulting methods on a simulation study, and on three gene expression data sets. We also survey past methods for extending LDA to the high-dimensional setting, and explore their relationships with our proposal.

1. Introduction

In this paper, we consider the classification setting. The data consist of a n × p matrix X with p features measured on n observations, each of which belongs to one of K classes. Linear discriminant analysis (LDA) is a well-known method for this problem in the classical setting where n > p. However, in high dimensions (when the number of features is large relative to the number of observations) LDA faces two problems:

1. The maximum likelihood estimate of the within-class covariance matrix is approximately singular (if p is almost as large as n) or singular (if p > n). Even if the estimate is not singular, the resulting classifer can suffer from high variance, resulting in poor performance.

2. When p is large, the resulting classifier is difficult to interpret, since the classification rule involves a linear combination of all p features.

The LDA classifier can be derived in three different ways, which we will refer to as the normal model, the optimal scoring problem, and Fisher’s discriminant problem (see e.g. Mardia et al. 1979, Hastie et al. 2009). In recent years, a number of papers have extended LDA to the high-dimensional setting in such a way that the resulting classifier involves a sparse linear combination of the features (see e.g. Tibshirani et al. 2002, 2003, Grosenick et al. 2008, Leng 2008, Clemmensen et al. 2011). These methods involve regularizing or penalizing the log likelihood for the normal model, or the optimal scoring problem, by applying an L₁ or lasso penalty (Tibshirani 1996).

In this paper, we instead approach the problem through Fisher’s discriminant framework, which is in our opinion the most natural of the three problems that result in LDA. The resulting problem is nonconvex. We overcome this difficulty using a minorization-maximization approach (see e.g. Lange et al. 2000, Hunter & Lange 2004, Lange 2004), which allows us to solve the problem efficiently when convex penalties are applied to the discriminant vectors. This is equivalent to recasting Fisher’s discriminant problem as a biconvex problem that can be optimized using a simple iterative algorithm, and is closely related to the sparse principal components analysis proposal of Witten et al. (2009).

To our knowledge, our approach to penalized LDA is novel. Clemmensen et al. (2011) state the same criterion that we use, but then go on to solve instead a closely related optimal scoring problem. Trendafilov & Jolliffe (2007) consider a closely related problem, but they propose a specialized algorithm that can be applied only in the case of L₁ penalties on the discriminant vectors; moreover, they do not consider the high-dimensional setting. In this paper, we take a more general approach that has a number of attractive features:

1. It results from a natural criterion for which a simple optimization strategy is provided.

2. A reduced rank solution can be obtained.

3. It provides a natural way to enforce a diagonal estimate for the within-class covariance matrix, which has been shown to yield good results in the high-dimensional setting (see e.g. Dudoit et al. 2001, Tibshirani et al. 2003, Bickel & Levina 2004).

4. It yields interpretable discriminant vectors, where the concept of interpretability can be chosen based on the problem at hand. Interpretability is achieved via application of convex penalties to the discriminant vectors. For instance, if L₁ penalties are used, then the resulting discriminant vectors are sparse.

This paper is organized as follows. We review Fisher’s discriminant problem in Section 2, we review the principle behind minorization-maximization algorithms in Section 3, and we propose our approach for penalized classification using Fisher’s linear discriminant in Section 4. A simulation study and applications to gene expression data are presented in Section 5. Since many proposals have been made for sparse LDA, we review past work and discuss the relationships between various approaches in Section 6. In Section 7, we discuss connections between our proposal and past work. Section 8 contains the Discussion.

2. Fisher’s discriminant problem

2.1. Fisher’s discriminant problem with full rank within-class covariance

Let X be a n × p matrix with observations on the rows and features on the columns. We assume that the features are centered to have mean zero, and we let X_j denote feature/column j and x_i denote observation/row i. C_k ⊂ {1, …, n} contains the indices of the observations in class k, and n_k = |C_k|, ${\sum }_{k=1}^K{n}_k=n$. The standard estimate for the within-class covariance matrix Σ_w is given by

$${\widehat{\mathbf{\sum }}}_w=\frac{1}{n}\sum _{k=1}^K\sum _{i\in C_k}({\mathbf{x}}_i-{\widehat{\mathit{\mu }}}_k){({\mathbf{x}}_i-{\widehat{\mathit{\mu }}}_k)}^T$$ (1)

where μ̂_k is the sample mean vector for class k. In this section, we assume that Σ̂_w is non-singular. Furthermore, the standard estimate for the between-class covariance matrix Σ_b is given by

$${\widehat{\mathbf{\sum }}}_b=\frac{1}{n}{\mathbf{X}}^T\mathbf{X}-{\widehat{\mathbf{\sum }}}_w=\frac{1}{n}\sum _{k=1}^K{n}_k{\widehat{\mathit{\mu }}}_k{\widehat{\mathit{\mu }}}_k^T.$$ (2)

In later sections, we will make use of the fact that ${\widehat{\mathbf{\sum }}}_b=\frac{1}{n}{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-1}{\mathbf{Y}}^T\mathbf{X}$, where Y is a n × K matrix with Y_ik an indicator of whether observation i is in class k.

Fisher’s discriminant problem seeks a low-dimensional projection of the observations such that the between-class variance is large relative to the within-class variance. That is, we sequentially solve

$${\text{maximize}}_{{\mathit{\beta }}_k\in {\mathbb{R}}^p}\{{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}_k\}\text{subject}\text{to}{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_w{\mathit{\beta }}_k\le 1,{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_w{\mathit{\beta }}_i=0\forall i<k.$$ (3)

Note that the problem (3) is generally written with the inequality constraint replaced with an equality constraint, but the two are equivalent if Σ̂_w has full rank, as is shown in the Appendix. We will refer to the solution β̂_k to (3) as the kth discriminant vector. In general, there are K − 1 nontrivial discriminant vectors.

A classification rule is obtained by computing Xβ̂₁, …, Xβ̂_{K − 1} and assigning each observation to its nearest centroid in this transformed space. Alternatively, one can transform the observations using only the first k < K − 1 discriminant vectors in order to perform reduced rank classification. LDA derives its name from the fact that the classification rule involves a linear combination of the features.

One can solve (3) by substituting ${\stackrel{\sim }{\mathit{\beta }}}_k={\widehat{\mathbf{\sum }}}_w^{\frac{1}{2}}{\mathit{\beta }}_k$, where ${\widehat{\mathbf{\sum }}}_w^{\frac{1}{2}}$ is the symmetric matrix square root of Σ̂_w. Then, Fisher’s discriminant problem is reduced to a standard eigenproblem. In fact, from (2), it is clear that Fisher’s discriminant problem is closely related to principal components analysis on the class centroid matrix.

2.2. Existing methods for extending Fisher’s discriminant problem to the p > n setting

In high dimensions, there are two reasons that problem (3) does not lead to a suitable classifier:

1. Σ̂_w is singular. Any discriminant vector that is in the null space of Σ̂_w but not in the null space of Σ̂_b can result in an arbitrarily large value of the objective.

2. The resulting classifier is not interpretable when p is very large, because the discriminant vectors contain p elements that have no particular structure.

A number of modifications to Fisher’s discriminant problem have been proposed to address the singularity problem. Krzanowski et al. (1995) consider modifying (3) by instead seeking a unit vector β that maximizes β^TΣ̂_bβ subject to β^TΣ̂_wβ = 0, and Tebbens & Schlesinger (2007) further require that the solution does not lie in the null space of Σ̂_b. Others have proposed modifying (3) by using a positive definite estimate of Σ_w. For instance, Friedman (1989), Dudoit et al. (2001), and Bickel & Levina (2004) consider the use of the diagonal estimate

$$\text{diag}({\widehat{\sigma }}_1^2,\dots ,{\widehat{\sigma }}_p^2),$$ (4)

where ${\widehat{\sigma }}_j^2$ is the jth diagonal element of Σ̂_w (1). Other positive definite estimates for Σ_w are suggested in Krzanowski et al. (1995) and Xu et al. (2009). The resulting criterion is

$${\text{maximize}}_{{\mathit{\beta }}_k\in {\mathbb{R}}^p}\{{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}_k\}\text{subject}\text{to}{\mathit{\beta }}_k^T{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}_k\le 1,{\mathit{\beta }}_k^T{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}_i=0\forall i<k.$$ (5)

where Σ̃_w is a positive definite estimate for Σ_w. The criterion (5) addresses the singularity issue, but not the interpretability issue.

In this paper, we extend (5) so that the resulting discriminant vectors are interpretable. We will make use of the following proposition, which provides a reformulation of (5) that results in the same solution:

Proposition 1

The solution β̂_k to (5) also solves the problem

$${\text{maximize}}_{{\mathit{\beta }}_k}\{{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k\}\text{subject}\text{to}{\mathit{\beta }}_k^T{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}_k\le 1$$ (6)

where

$${\widehat{\mathbf{\sum }}}_b^k=\frac{1}{n}{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{P}}_k^{\perp }{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{Y}}^T\mathbf{X}.$$ (7)

${\mathbf{P}}_k^{\perp }$ is defined as follows: ${\mathbf{P}}_1^{\perp }=\mathbf{I}$, and for k > 1, ${\mathbf{P}}_k^{\perp }$ is an orthogonal projection matrix into the space that is orthogonal to ${({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{Y}}^T\mathbf{X}{\widehat{\mathit{\beta }}}_i$ for all i < k.

Throughout this paper, Σ̂_w will always refer to the standard maximum likelihood estimate of Σ_w (1), whereas Σ̃_w will refer to some positive definite estimate of Σ_w for which the specific form will depend on the context.

3. A brief review of minorization algorithms

In this paper, we will make use of a minorization-maximization (or simply minorization) algorithm, as described for instance in Lange et al. (2000), Hunter & Lange (2004), and Lange (2004). Consider the problem

$${\text{maximize}}_{\mathit{\beta }}\{f(\mathit{\beta })\}.$$ (8)

If f is a concave function, then standard tools from convex optimization (see e.g. Boyd & Vandenberghe 2004) can be used to solve (8). If not, solving (8) can be dificult. (We note here that minimization of a convex function is a convex problem, as is maximization of a concave function. Hence, (8) is a convex problem if f(β) is concave in β. For non-concave f(β) – for instance if f(β) is convex – (8) is not a convex problem.)

Minorization refers to a general strategy for maximizing non-concave functions. The function g(β|β ^(m)) is said to minorize the function f(β) at the point β ^(m) if

$$f({\mathit{\beta }}^{(m)})=g({\mathit{\beta }}^{(m)}\mid {\mathit{\beta }}^{(m)}),f(\mathit{\beta })\ge g(\mathit{\beta }\mid {\mathit{\beta }}^{(m)})\forall \mathit{\beta }.$$ (9)

A minorization algorithm for solving (8) initializes β ⁽⁰⁾, and then iterates:

$${\mathit{\beta }}^{(m+1)}={\text{argmax}}_{\mathit{\beta }}\{g(\mathit{\beta }\mid {\mathit{\beta }}^{(m)})\}.$$ (10)

Then by (9),

$$f({\mathit{\beta }}^{(m+1)})\ge g({\mathit{\beta }}^{(m+1)}\mid {\mathit{\beta }}^{(m)})\ge g({\mathit{\beta }}^{(m)}\mid {\mathit{\beta }}^{(m)})=f({\mathit{\beta }}^{(m)}).$$ (11)

This means that in each iteration the objective is nondecreasing. However, in general we do not expect to arrive at the global optimum of (8) using a minorization approach: global optima for non-convex problems are very hard to obtain, and a local optimum is the best we can hope for except in specific special cases. Different initial values for β ⁽⁰⁾ can be tried and the solution resulting in the largest objective value can be chosen. A good minorization function is one for which (10) is easily solved. For instance, if g(β|β ^(m)) is concave in β then standard convex optimization tools can be applied.

In the next section, we use a minorization approach to develop an algorithm for our proposal for penalized LDA.

4. The penalized LDA proposal

4.1. The general form of penalized LDA

We would like to modify the problem (5) by imposing penalty functions on the discriminant vectors. We define the first penalized discriminant vector β̂₁ to be the solution to the problem

$${{\text{maximize}}_{\mathit{\beta }}}_1\{{\mathit{\beta }}_1^T{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}_1-P_1({\mathit{\beta }}_1)\}\text{subject}\text{to}{\mathit{\beta }}_1^T{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}_1\le 1,$$ (12)

where Σ̃_w is a positive definite estimate for Σ_w and where P₁ is a convex penalty function. In this paper, we will be most interested in the case where Σ̃_w is the diagonal estimate (4), since it has been shown that using a diagonal estimate for Σ_w can lead to good classification results when p ≫ n (see e.g. Tibshirani et al. 2002, Bickel & Levina 2004). Note that (12) is closely related to penalized principal components analysis, as described for instance in Jolliffe et al. (2003) and Witten et al. (2009) – in fact, it would be exactly penalized principal components analysis if Σ̃_w were the identity.

To obtain multiple discriminant vectors, rather than requiring that subsequent discriminant vectors be orthogonal with respect to Σ̃_w - a difficult task for a general convex penalty function - we instead make use of Proposition 1. We define the kth penalized discriminant vector β̂_k to be the solution to

$${\text{maximize}}_{{\mathit{\beta }}_k}\{{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k-P_k({\mathit{\beta }}_k)\}\text{subject}\text{to}{\mathit{\beta }}_k^T{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}_k\le 1,$$ (13)

where ${\widehat{\mathbf{\sum }}}_b^k$ is given by (7), with ${\mathbf{P}}_k^{\perp }$ an orthogonal projection matrix into the space that is orthogonal to ${({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{Y}}^T\mathbf{X}{\widehat{\mathit{\beta }}}_i$ for all i < k, and ${\mathbf{P}}_1^{\perp }=\mathbf{I}$. Here P_k is a convex penalty function on the kth discriminant vector. Note that (12) follows from (13) with k = 1.

In general, the problem (13) cannot be solved using tools from convex optimization, because it involves maximizing an objective function that is not concave. We apply a minorization algorithm to solve it. For any positive semidefinite matrix A, f(β) = β^TAβ is convex in β. Thus, for a fixed value of β ^(m),

$$f(\mathit{\beta })\ge f({\mathit{\beta }}^{(m)})+{(\mathit{\beta }-{\mathit{\beta }}^{(m)})}^T\nabla f({\mathit{\beta }}^{(m)})=2{\mathit{\beta }}^T\mathbf{A}{\mathit{\beta }}^{(m)}-{\mathit{\beta }}^{{(m)}^T}\mathbf{A}{\mathit{\beta }}^{(m)}$$ (14)

for any β, and equality holds when β = β ^(m). Therefore,

$$g({\mathit{\beta }}_k\mid {\mathit{\beta }}^{(m)})=2{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}^{(m)}-{\mathit{\beta }}^{{(m)}^T}{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}^{(m)}-P_k({\mathit{\beta }}_k)$$ (15)

minorizes the objective of (13) at β ^(m). Moreover, since P_k is a convex function, g(β_k|β^(m)) is concave in β_k and hence can be maximized using convex optimization tools. We can use (15) as the basis for a minorization algorithm to find the kth penalized discriminant vector. The algorithm assumes that the first k − 1 penalized discriminant vectors have already been computed.

Algorithm 1: Obtaining the kth penalized discriminant vector

1. If k > 1, define an orthogonal projection matrix ${\mathbf{P}}_k^{\perp }$ that projects onto the space that is orthogonal to ${({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{Y}}^T\mathbf{X}{\widehat{\mathit{\beta }}}_i$ for all i < k. Let ${\mathbf{P}}_1^{\perp }=\mathbf{I}$.

2. Let ${\widehat{\mathbf{\sum }}}_b^k=\frac{1}{n}{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{P}}_k^{\perp }{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{Y}}^T\mathbf{X}$. Note that ${\widehat{\mathbf{\sum }}}_b^1={\widehat{\mathbf{\sum }}}_b$.

3. Let ${\mathit{\beta }}_k^{(0)}$ be the first eigenvector of ${\mathbf{\sum }^{\sim }}_w^{-1}{\widehat{\mathbf{\sum }}}_b^k$.

4. For m = 1, 2, … until convergence: let ${\mathit{\beta }}_k^{(m)}$ be the solution to

   $${\text{maximize}}_{{\mathit{\beta }}_k}\{2{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k^{(m-1)}-P_k({\mathit{\beta }}_k)\}\text{subject}\text{to}{\mathit{\beta }}_k^T{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}_k\le 1.$$ (16)

   Let β̂_k denote the solution at convergence.

Of course, the solution to (16) will depend on the form of the convex function P_k. In the next section, we will consider two specific forms for P_k.

Once the penalized discriminant vectors have been computed, classification is straightforward: as in the case of classical LDA, we compute Xβ̂₁, …, Xβ̂_{K − 1} and assign each observation to its nearest centroid in this transformed space. To perform reduced rank classification, we transform the observations using only the first k < K − 1 penalized discriminant vectors.

4.2. Penalized LDA-L₁ and penalized LDA-FL

4.2.1. Penalized LDA-L₁

We define penalized LDA-L₁ to be the solution to (13) with an L₁ penalty,

$${\text{maximize}}_{{\mathit{\beta }}_k}\{{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k-{\lambda }_k\sum _{j=1}^p\mid {\widehat{\sigma }}_j{\beta }_{kj}\mid \}\text{subject}\text{to}{\mathit{\beta }}_k^T{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}_k\le 1.$$ (17)

When the tuning parameter λ_k is large, some elements of the solution β̂_k will be exactly equal to zero. In (17), σ̂_j is the within-class standard deviation for feature j; the inclusion of σ̂_j in the penalty has the effect that features that vary more within each class undergo greater penalization. Penalized LDA-L₁ is appropriate if we want to obtain a sparse classifier - that is, a classifier for which the decision rule involves only a subset of the features. In particular, the resulting discriminant vectors are sparse, so penalized LDA-L₁ amounts to projecting the data onto a low-dimensional subspace that involves only a subset of the features.

To solve (17), we use the minorization approach outlined in Algorithm 1. Step (d) can be written as

$${\text{maximize}}_{{\mathit{\beta }}_k}\{2{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k^{(m-1)}-{\lambda }_k\sum _{j=1}^p\mid {\widehat{\sigma }}_j{\beta }_{kj}\mid \}\text{subject}\text{to}{\mathit{\beta }}_k^T{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}_k\le 1.$$ (18)

The solution to (18) is given in Proposition 2 in Section 4.2.3.

4.2.2. Penalized LDA-FL

We define penalized LDA-FL to be the solution to the problem (13) with a fused lasso penalty (Tibshirani et al. 2005):

$${\text{maximize}}_{{\mathit{\beta }}_k}\{{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k-{\lambda }_k\sum _{j=1}^p\mid {\widehat{\sigma }}_j{\beta }_{kj}\mid -{\gamma }_k\sum _{j=2}^p\mid {\widehat{\sigma }}_j{\beta }_{kj}-{\widehat{\sigma }}_{j-1}{\beta }_{k,j-1}\mid \}\text{subject}\text{to}{\mathit{\beta }}_k^T{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}_k\le 1.$$ (19)

When the nonnegative tuning parameter λ_k is large then the resulting discriminant vector will be sparse in the features, and when the nonnegative tuning parameter γ_k is large then the discriminant vector will be piecewise constant. This classifier is appropriate if the features are ordered on a line, and one believes that the true underlying signal is sparse and piecewise constant.

To solve (13), we again apply Algorithm 1. Step (d) can be written as

$${\text{maximize}}_{{\mathit{\beta }}_k}\{2{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k^{(m-1)}-{\lambda }_k\sum _{j=1}^p\mid {\widehat{\sigma }}_j{\beta }_{kj}\mid -{\gamma }_k\sum _{j=2}^p\mid {\widehat{\sigma }}_j{\beta }_{kj}-{\widehat{\sigma }}_{j-1}{\beta }_{k,j-1}\mid \}\text{subject}\text{to}{\mathit{\beta }}_k^T{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}_k\le 1.$$ (20)

Proposition 2 in Section 4.2.3 provides the solution to (20).

4.2.3. The minorization step for penalized LDA-L₁ and penalized LDA-FL

Now we present Proposition 2, which provides a solution to (18) and (20). In other words, Proposition 2 provides details for performing Step (d) in Algorithm 1 for penalized LDA-L₁ and penalized LDA-FL.

Proposition 2

1. To solve (18), we first solve the problem

   $${\text{minimize}}_{\mathbf{d}\in {\mathbb{R}}^p}\{{\mathbf{d}}^T{\mathbf{\sum }^{\sim }}_w\mathbf{d}-2{\mathbf{d}}^T{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k^{(m-1)}+{\lambda }_k\sum _j\mid {\widehat{\sigma }}_j{d}_j\mid \}.$$ (21)

   If d̂ = 0 then β̂_k = 0. Otherwise, ${\widehat{\mathit{\beta }}}_k=\widehat{\mathbf{d}}/\sqrt{{\widehat{\mathbf{d}}}^T{\mathbf{\sum }^{\sim }}_w\widehat{\mathbf{d}}}$.

2. To solve (20), we first solve the problem

   $${\text{minimize}}_{\mathbf{d}\in {\mathbb{R}}^p}\{{\mathbf{d}}^T{\mathbf{\sum }^{\sim }}_w\mathbf{d}-2{\mathbf{d}}^T{\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k^{(m-1)}+{\lambda }_k\sum _{j=1}^p\mid {\widehat{\sigma }}_j{d}_j\mid +{\gamma }_k\sum _{j=2}^p\mid {\widehat{\sigma }}_j{d}_j-{\widehat{\sigma }}_{j-1}{d}_{j-1}\mid \}.$$ (22)

   If d̂= 0 then β̂_k = 0. Otherwise, ${\widehat{\mathit{\beta }}}_k=\widehat{\mathbf{d}}/\sqrt{{\widehat{\mathbf{d}}}^T{\mathbf{\sum }^{\sim }}_w\widehat{\mathbf{d}}}$.

The proof is given in the Appendix. Some comments on Proposition 2 are as follows:

• If Σ̃_w is the diagonal estimate (4), then the solution to (21) is

  $${\widehat{d}}_j=\frac{1}{{\widehat{\sigma }}_j^2}S({({\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k^{(m-1)})}_j,{\lambda }_k{\widehat{\sigma }}_j/2)$$ (23)
  where S is the soft-thresholding operator, defined as

  $$S(x,a)=\text{sign}(x){(\mid x\mid -a)}_{+}$$ (24)
  and applied component wise. To see why, note that differentiating (21) with respect to d_j indicates that the solution will satisfy

  $$2{\widehat{\sigma }}_j^2{d}_j=2{({\widehat{\mathbf{\sum }}}_b^k{\mathit{\beta }}_k^{(m-1)})}_j-{\lambda }_k{\widehat{\sigma }}_j{\mathrm{\Gamma }}_j,$$ (25)
  where Γ_j is the subgradient of |d_j|, defined as

  $${\mathrm{\Gamma }}_j=\{\begin{array}{ll}1\hfill & \text{if}{d}_j>0\hfill \\ -1\hfill & \text{if}{d}_j<0\hfill \\ a\hfill & \text{if}{d}_j=0\hfill \end{array}$$ (26)

  where a is some number between 1 and −1. Then (23) follows from (25).

• On the other hand, if Σ̃_w is a non-diagonal positive definite estimate of Σ_w, then one can solve (21) by coordinate descent (see e.g. Friedman et al. 2007). (21) is in that case closely related to the lasso, but may involve more demanding computations. This is due to the fact that when p ≫ n the standard lasso can be implemented by storing the n × p matrix X rather than the entire p × p matrix X^TX. But if Σ̃_w is a p × p matrix without special structure then one must store it in full in order to solve (21).

• If Σ̃_w is a diagonal estimate for Σ_w then (22) is a diagonal fused lasso problem, for which fast algorithms have been proposed (see e.g. Hoefling 2009, Johnson 2010).

4.2.4. Comments on tuning parameter selection

We now consider the problem of selecting the tuning parameter λ_k for the penalized LDA-L₁ problem (17). The simplest approach would be to take λ_k = λ, i.e. the same tuning parameter value for all components. However, this results in effectively penalizing each component more than the previous components, since the unpenalized objective value of (17), which is equal to the largest eigenvalue of ${\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}{\widehat{\mathbf{\sum }}}_b^k{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}$, is nonincreasing in k. So instead, we take the following approach. We first fix a nonnegative constant λ, and then we take ${\lambda }_k=\lambda \left|\right|{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}{\widehat{\mathbf{\sum }}}_b^k{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}\left|\right|$ where ||·|| indicates the largest eigenvalue. Note that when p ≫ n, this largest eigenvalue can be quickly computed using the fact that ${\widehat{\mathbf{\sum }}}_b^k$ has low rank. The value of λ can be chosen by cross-validation.

In the case of the penalized LDA-FL problem (19), instead of choosing λ_k and λ_k directly, we instead fix nonnegative constants λ and γ. Then, we take ${\lambda }_k=\lambda \left|\right|{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}{\widehat{\mathbf{\sum }}}_b^k{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}\left|\right|$ and ${\gamma }_k=\gamma \left|\right|{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}{\widehat{\mathbf{\sum }}}_b^k{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}\left|\right|$. λ and γ can be chosen by cross-validation.

4.2.5. Timing results for penalized LDA

We now comment on the computations involved in the algorithms proposed earlier in this section. We used a very simple simulation corresponding to no signal in the data: X_ij ~ N (0, 1) and there were four equally-sized classes. Table 1 summarizes the computational times required to perform penalized LDA-L₁ and penalized LDA-FL with the diagonal estimate (4) used for Σ̃_w. The R library penalized LDA was used. Timing depends critically on the convergence criterion used; we determine that the algorithm has “converged” when subsequent iterations lead to a relative improvement in the objective of no more than 10⁻⁶; that is, |r_i − r_i+1|/r_i+1 < 10⁻⁶ where r_i is the objective obtained at the ith iteration. Of course, computational times will be shorter if a less strict convergence threshold is used. All timings were carried out on a AMD Opteron 848 2.20 GHz processor.

Table 1.

Timing results for penalized LDA-L₁ (with λ = 0.005) and penalized LDA-FL (with λ = γ = 0.005) for various values of n and p, with 4-class data. Mean (and standard error) of running time (in seconds), over 25 repetitions. The diagonal estimate (4) was used for Σ̃_w

		p=20	p=200	p=2000	p=20000
Penalized LDA-L1	n=20	0.049 (0)	0.059 (0.002)	0.199 (0.022)	5.1 (0.851)
	n=200	0.062 (0)	0.147 (0.001)	1.182 (0.014)	11.835 (0.417)
Penalized LDA-FL	n=20	0.064 (0.003)	0.108 (0.007)	1.018 (0.102)	118.61 (9.915)
	n=200	0.075 (0.001)	0.219 (0.012)	1.835 (0.102)	118.557 (8.895)

4.3. Recasting penalized LDA as a biconvex problem

Rather than using a minorization approach to solve the nonconvex problem (12), one could instead recast it as a biconvex problem. Consider the problem

$${\text{maximize}}_{\mathit{\beta },\mathbf{u}}\{\frac{2}{\sqrt{n}}{\mathit{\beta }}^T{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}\mathbf{u}-P(\mathit{\beta })-{\mathbf{u}}^T\mathbf{u}\}\text{subject}\text{to}{\mathit{\beta }}^T{\mathbf{\sum }^{\sim }}_w\mathit{\beta }\le 1.$$ (27)

Partially optimizing (27) with respect to u reveals that the β that solves it also solves (12). Moreover, (27) is a biconvex problem (see e.g. Gorski et al. 2007): that is, with β held fixed, it is convex in u, and with u held fixed, it is convex in β. This suggests a a simple iterative approach for solving it.

Algorithm 4: A biconvex formulation for penalized LDA

1. Let β ⁽⁰⁾ be the first eigenvector of ${\mathbf{\sum }^{\sim }}_w^{-1}{\widehat{\mathbf{\sum }}}_b$.

2. For m = 1, 2, … until convergence:

   1. Let u^(m) solve

      $${\text{maximize}}_{\mathbf{u}}\{\frac{2}{\sqrt{n}}{\mathit{\beta }}^{{(m-1)}^T}{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}\mathbf{u}-{\mathbf{u}}^T\mathbf{u}\}.$$ (28)
   2. Let β ^(m) solve

      $${\text{maximize}}_{\mathit{\beta }}\{\frac{2}{\sqrt{n}}{\mathit{\beta }}^T{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{u}}^{(m)}-P(\mathit{\beta })\}\text{subject}\text{to}{\mathit{\beta }}^T{\mathbf{\sum }^{\sim }}_w\mathit{\beta }\le 1.$$ (29)

Combining Steps (b)(i) and (b)(ii), we see that β ^(m) solves

$${\text{maximize}}_{\mathit{\beta }}\{2{\mathit{\beta }}^T{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}^{(m-1)}-P(\mathit{\beta })\}\text{subject}\text{to}{\mathit{\beta }}^T{\mathbf{\sum }^{\sim }}_w\mathit{\beta }\le 1.$$ (30)

Comparing (30) to (16), we see that the biconvex formulation (27) results in the same update step as the minorization approach outlined in Algorithm 1. This biconvex formulation is very closely related to the sparse principal components analysis proposal of Witten et al. (2009), which corresponds to the case where Σ̃_w = I and a bound form is used for the penalty P (β). Since ${\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}$ is a weighted version of the class centroid matrix, our penalized LDA proposal is closely related to performing sparse principal components analysis on the class centroids matrix.

5. Examples

5.1. Methods included in comparisons

In the examples that follow, penalized LDA-L₁ and penalized LDA-FL were performed using the diagonal estimate (4) for Σ̃_w, as implemented in the R package penalized LDA. The nearest shrunken centroids (NSC; Tibshirani et al. 2002, 2003) method was performed using the R package pamr, and the shrunken centroids regularized discriminant analysis (RDA; Guo et al. 2007) method was performed using the rda R package. Briefly, NSC results from using a diagonal estimate of Σ_w and imposing L₁ penalties on the class mean vectors under the normal model, and RDA combines a ridge-type penalty in estimating Σ_w with soft-thresholding of ${\mathbf{\sum }^{\sim }}_w^{-1}{\widehat{\mathit{\mu }}}_k$. These methods are discussed further in Section 6.

The tuning parameters for each of the methods considered were as follows. For penalized LDA-L₁, λ described in Section 4.2.4 was a tuning parameter. For penalized LDA-FL, we treated λ = γ (see Section 4.2.4) as a single tuning parameter in order to avoid performing tuning parameter selection on a two-dimensional grid. Moreover, penalized LDA had an additional tuning parameter, the number of discriminant vectors to include in the classifier. NSC has a single tuning parameter, which corresponds to the amount of soft-thresholding performed. RDA has two tuning parameters, one of which controls the number of features used and the other controls the ridge penalty used to regularize the estimate of Σ_w.

5.2. A simulation study

We compare penalized LDA to NSC and RDA in a simulation study. Four simulations were considered. In each simulation, there are 1200 observations, equally split between the classes. Of these 1200 observations, 100 belong to the training set, 100 belong to the validation set, and 1000 are in the test set. Each simulation consists of measurements on 500 features, of which 100 differ between classes.

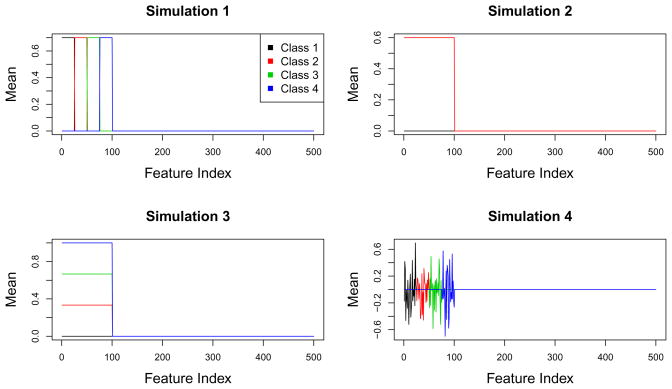
Simulation 1. Mean shift with independent features

There are four classes. If observation i is in class k, then x_i ~ N (μ_k, I), where μ_1j = 0.7 × 1_(1≤j≤25), μ_2j = 0.7 × 1_{(26≤j≤50)}, μ_3j = 0.7×1_{(51≤j≤75)}, μ_4j = 0.7×1_{(75≤j≤100)}.

Simulation 2. Mean shift with dependent features

There are two classes. For i ∈ C₁, x_i ~ N(0, Σ) and for i ∈ C₂, x_i ~ N(μ, Σ), μ_j = 0.6 × 1_(j≤200). The covariance structure is block diagonal, with 5 blocks each of dimension 100 × 100. The blocks have (j, j′) element 0.6^|j−j′|. This covariance structure is intended to mimic gene expression data, in which genes are positively correlated within a pathway and independent between pathways.

Simulation 3. One-dimensional mean shift with independent features

There are four classes, and the features are independent. For i ∈ C_k, $X_{ij}\sim N(\frac{k-1}{3},1)$ if j ≤ 100, and X_ij ~ N(0, 1) otherwise. Note that a one-dimensional projection of the data fully captures the class structure.

Simulation 4. Mean shift with independent features and no linear ordering

There are four classes. If observation i is in class k, then x_i ~ N(μ_k, I). The mean vectors are defined as follows: μ_1j ~ N (0, 0.3²) if 1 ≤ j ≤ 25 and μ_1j = 0 otherwise, μ_2j ~ N (0, 0.3²) if 26 ≤ j ≤ 50 and μ_2j = 0 otherwise, μ_3j ~ N(0, 0.3²) if 51 ≤ j ≤ 75 and μ_3j = 0 otherwise, μ_4j ~ N(0, 0.3²) if 75 ≤ j ≤ 100 and μ_4j = 0 otherwise.

Figure 1 displays the class mean vectors for each simulation.

Fig. 1.

Class mean vectors for each simulation.

For each method, models were fit on the training set using a range of tuning parameter values. Tuning parameter values were then selected to minimize the validation set error. Finally, the training set models with appropriate tuning parameter values were evaluated on the test set. Penalized LDA-FL was performed in Simulations 1–3 but not in Simulation 4, since in Simulation 4 the features do not have a linear ordering as assumed by the fused lasso penalty (see Figure 1).

Test set errors and the numbers of nonzero features used are reported in Table 2. For penalized LDA, the numbers of discriminant vectors used are also reported. Penalized LDA-FL has by far the best performance in the first three simulations, since it exploits the fact that the important features have a linear ordering. Of course, in real data applications, penalized LDA-FL can only be applied if such an ordering is present. Note that penalized LDA tends to use fewer than three components in Simulation 3, in which a one-dimensional projection is sufficient to explain the class structure.

Table 2.

Simulation results. Mean (and standard errors), computed over 25 repetitions, of test set errors, number of nonzero features, and number of discriminant vectors used

		Pen. LDA-L1	Pen. LDA-FL	NSC	RDA
Sim 1	Errors	117.48 (3)	38.4 (2)	88.96 (2.6)	96.8 (3.4)
	Features	301.16 (20.1)	159.28 (15.8)	290.28 (16.7)	226.6 (15.7)
	Components	3 (0)	3 (0)	-	-
Sim 2	Errors	90.04 (2.8)	77 (1.9)	88.44 (2.7)	112.2 (5.8)
	Features	229.36 (20.4)	170.16 (18.4)	341.28 (24.8)	414.84 (32.6)
	Components	1 (0)	1 (0)	-	-
Sim 3	Errors	150.8 (5.4)	83.44 (2.3)	276.64 (4)	291 (4.8)
	Features	147.84 (7.1)	115.92 (9.1)	439.6 (10.7)	349.32 (24.5)
	Components	1 (0)	1 (0)	-	-
Sim 4	Errors	60.56 (1.1)	-	58.28 (1.2)	57 (0.9)
	Features	311.4 (22.1)	-	135.4 (22.6)	98 (7.3)
	Components	3 (0)	-	-	-

5.3. Application to gene expression data

We compare penalized LDA-L₁, NSC, and RDA on three gene expression data sets:

Ramaswamy data

A data set consisting of 16,063 gene expression measurements and 198 samples belonging to 14 distinct cancer subtypes (Ramaswamy et al. 2001). The data set has been studied in a number of papers (see e.g. Zhu & Hastie 2004, Guo et al. 2007, Witten & Tibshirani 2009) and is available from http://www-stat.stanford.edu/~hastie/glmnet/glmnetData/.

Nakayama data

A data set consisting of 105 samples from 10 types of soft tissue tumors, each with 22,283 gene expression measurements (Nakayama et al. 2007). We limited the analysis to five tumor types for which at least 15 samples were present in the data; the resulting subset of the data contained 86 samples. The data are available on Gene Expression Omnibus (Barrett et al. 2005) with accession number GDS2736.

Sun data

A data set consisting of 180 samples and 54,613 expression measurements (Sun et al. 2006). The samples fall into four classes: one non-tumor class and three types of glioma. The data are available on Gene Expression Omnibus with accession number GDS1962.

Each data set was split into a training set containing 75% of the samples and a test set containing 25% of the samples. Cross-validation was performed on the training set and test set error rates were evaluated. The process was repeated ten times, each with a random choice of training set and test set. Results are reported in Table 3. The results suggest that the three methods tend to have roughly comparable performance. A reviewer pointed out that there is substantial variability in the number of features used by each classifier across each training/test set split. Indeed, this instability in the set of genes selected likely reflects the fact that in the analysis of many real data types, sparsity is simply an approximation, rather than a property that we expect to hold exactly.

Table 3.

Results obtained on gene expression data over 10 training/test set splits. Quantities reported are the mean (and standard deviation) of test set errors and nonzero coefficients.

		NSC	Penalized LDA-L1	RDA
Ramaswamy	Errors	16.3 (4.16)	18.8 (3.05)	24 (17.45)
	Features	2336.9 (2292.03)	14873.5 (720.29)	5022.5 (2503.35)
Nakayama	Errors	4.2 (2.15)	4.4 (1.51)	2.8 (1.23)
	Features	5908 (7131.5)	10478.7 (2116.27)	22283 (0)
Sun	Errors	15 (4.29)	15.2 (3.29)	15.7 (4.52)
	Features	30004.9 (18557.68)	21634.8 (7443.21)	54183.4 (693.23)

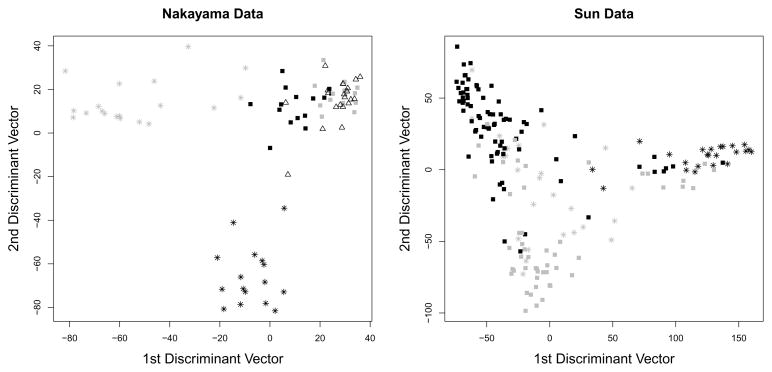
Penalized LDA-L₁ has the added advantage over RDA and NSC of yielding penalized discriminant vectors that can be used to visualize the observations, as in Figure 2.

Fig. 2.

For the Nakayama and Sun data, the samples were projected onto the first two penalized discriminant vectors. The samples in each class are shown using a distinct symbol.

6. The normal model, optimal scoring, and extensions to high dimensions

In this section, we review the normal model and the optimal scoring problem, which lead to the same classification rule as Fisher’s discriminant problem. We also review past extensions of LDA to the high-dimensional setting.

6.1. The normal model

Suppose that the observations are independent and normally distributed with a common within-class covariance matrix Σ_w ∈ ℝ^p×p and a class-specific mean vector μ_k ∈ ℝ^p. The log likelihood under this model is

$$\sum _{k=1}^K\sum _{i\in C_k}\{-\frac{1}{2}log\mid {\mathbf{\sum }}_w\mid -\frac{1}{2}\text{tr}[{\mathbf{\sum }}_w^{-1}({\mathbf{x}}_i-{\mathit{\mu }}_k){({\mathbf{x}}_i-{\mathit{\mu }}_k)}^T]\}+c$$ (31)

where c is a constant. If the classes have equal prior probabilities, then by Bayes’ theorem, a new observation x is assigned to the class for which the discriminant function

$${\delta }_k(\mathbf{x})={\mathbf{x}}^T{\widehat{\mathbf{\sum }}}_w^{-1}{\widehat{\mathit{\mu }}}_k-\frac{1}{2}{\widehat{\mathit{\mu }}}_k^T{\widehat{\mathbf{\sum }}}_w^{-1}{\widehat{\mathit{\mu }}}_k$$ (32)

is maximal. One can show that this is the same as the classification rule obtained from Fisher’s discriminant problem.

6.2. The optimal scoring problem

Let Y be a n × K matrix, with Y_ik = 1_i∈Ck. Then, optimal scoring involves sequentially solving

$${\text{minimize}}_{{\mathit{\beta }}_k\in {\mathbb{R}}^p,{\mathit{\theta }}_k\in {\mathbb{R}}^K}\{\frac{1}{n}{\left|\right|\mathbf{Y}{\mathit{\theta }}_k-\mathbf{X}{\mathit{\beta }}_k\left|\right|}^2\}\text{subject}\text{to}{\mathit{\theta }}_k^T{\mathbf{Y}}^T\mathbf{Y}{\mathit{\theta }}_k=1,{\mathit{\theta }}_k^T{\mathbf{Y}}^T\mathbf{Y}{\mathit{\theta }}_i=0\forall i<k$$ (33)

for k = 1, …, K − 1. This amounts to recasting the classification problem as a regression problem, where a quantitative coding θ_k of the K classes must be chosen along with the regression coefficient vector β_k. The solution β̂_k to (33) is proportional to the solution to (3). Somewhat involved proofs of this fact are given in Breiman & Ihaka (1984) and Hastie et al. (1995). We present a simpler proof in the Appendix.

6.3. LDA in high dimensions

In recent years, a number of authors have proposed extensions of LDA to the high-dimensional setting in order to achieve sparsity (Tibshirani et al. 2002, 2003, Guo et al. 2007, Trendafilov & Jolliffe 2007, Grosenick et al. 2008, Leng 2008, Fan & Fan 2008, Shao et al. 2011, Clemmensen et al. 2011). In Section 4, we proposed penalizing Fisher’s discriminant problem. Here we briefly review some past proposals that have involved penalizing the log likelihood under the normal model, and the optimal scoring problem.

The nearest shrunken centroids (NSC) proposal (Tibshirani et al. 2002, 2003) assigns an observation x* to the class that minimizes

$$\sum _{j=1}^p\frac{{(x_j^{\ast }-{\overline{\mu }}_{kj})}^2}{{\widehat{\sigma }}_j^2},$$ (34)

where ${\overline{\mu }}_{kj}=S({\widehat{\mu }}_{kj},\lambda {\widehat{\sigma }}_j\sqrt{\frac{1}{nk}+\frac{1}{n}})$, S is the soft-thresholding operator (24), and we have assumed equal prior probabilities for each class. This classification rule approximately follows from estimating the class mean vectors via maximization of an L₁-penalized version of the log likelihood (31), and assuming independence of the features (Hastie et al. 2009). The shrunken centroids regularized discriminant analysis (RDA) proposal (Guo et al. 2007) arises instead from applying the normal model approach with covariance matrix Σ̃_w = Σ̂_w + ρI and performing soft-thresholding in order to obtain a classifier that is sparse in the features.

Several authors have proposed penalizing the optimal scoring criterion (33) by imposing penalties on β_k (see e.g. Grosenick et al. 2008, Leng 2008). For instance, the sparse discriminant analysis (SDA) proposal (Clemmensen et al. 2011) involves sequentially solving

$${\text{minimize}}_{{\mathit{\beta }}_k,{\mathit{\theta }}_k}\{\frac{1}{n}{\left|\right|\mathbf{Y}{\mathit{\theta }}_k-\mathbf{X}{\mathit{\beta }}_k\left|\right|}^2+{\mathit{\beta }}_k^T\mathbf{\Omega }{\mathit{\beta }}_k+\lambda {\left|\right|{\mathit{\beta }}_k\left|\right|}_1\}\text{subject}\text{to}{\mathit{\theta }}_k^T{\mathbf{Y}}^T\mathbf{Y}{\mathit{\theta }}_k=1,{\mathit{\theta }}_k^T{\mathbf{Y}}^T\mathbf{Y}{\mathit{\theta }}_i=0\forall i<k$$ (35)

where λ is a nonnegative tuning parameter and Ω is a positive definite penalization matrix. If Ω = γI for γ > 0, then this is an elastic net penalty (Zou & Hastie 2005). The resulting discriminant vectors will be sparse if λ is sufficiently large. If λ = 0, then this reduces to the penalized discriminant analysis proposal of Hastie et al. (1995). The criterion (35) can be optimized in a simple iterative fashion: we optimize with respect to β_k holding θ_k fixed, and we optimize with respect to θ_k holding β_k fixed. In fact, if any convex penalties are applied to the discriminant vectors in the optimal scoring criterion (33), then an iterative approach can be developed that decreases the objective at each step. However, the optimal scoring problem is a somewhat indirect formulation for LDA.

Our penalized LDA proposal is instead a direct extension of Fisher’s discriminant problem (3). Trendafilov & Jolliffe (2007) consider a problem very similar to penalized LDA-L₁. But they discuss only the p < n case. Their algorithm is more complex than ours, and does not extend to general convex penalty functions.

A summary of proposals that extend LDA to the high-dimensional setting through the use of L₁ penalties is given in Table 4. In the next section, we will explore how our penalized LDA-L₁ proposal relates to the NSC and SDA methods.

Table 4.

Advantages and disadvantages of using the normal model (NM), optimal scoring (OS), and Fisher’s discriminant analysis (FD) as the basis for penalized LDA with an L₁ penalty

	Advantages	Disadvantages	Citation
NM	Sparse class means if diagonal estimate of Σw used. Computations are fast.	Does not give sparse discriminant vectors. No reduced-rank classification.	Tibshirani et al. (2002)
OS	Sparse discriminant vectors.	Dificult to enforce diagonal estimate for Σw, which is useful if p > n. Computations can be slow.	Grosenick et al. (2008) Leng (2008) Clemmensen et al. (2011)
FD	Sparse discriminant vectors. Simple to en-force diagonal estimate of Σw. Computations are fast using diagonal estimate of Σw.	Computations can be slow when p is large, unless diagonal estimate of Σw is used.	This work.

7. Connections with existing methods

7.1. Connection with sparse discriminant analysis

Consider the SDA criterion (35) with k = 1. We drop the subscripts on β₁ and θ₁ for convenience. Partially optimizing (35) with respect to θ reveals that for any β for which Y^TXβ ≠ 0, the optimal θ equals $\frac{{({\mathbf{Y}}^T\mathbf{Y})}^{-1}{\mathbf{Y}}^T\mathbf{X}\mathit{\beta }}{\sqrt{{\mathit{\beta }}^T{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-1}{\mathbf{Y}}^T\mathbf{X}\mathit{\beta }}}$. So (35) can be rewritten as

$${\text{maximize}}_{\mathit{\beta }}\{\frac{2}{\sqrt{n}}\sqrt{{\mathit{\beta }}^T{\widehat{\mathbf{\sum }}}_b\mathit{\beta }}-{\mathit{\beta }}^T({\widehat{\mathbf{\sum }}}_b+{\widehat{\mathbf{\sum }}}_w+\mathbf{\Omega })\mathit{\beta }-\lambda {\left|\right|\mathit{\beta }\left|\right|}_1\}.$$ (36)

Assume that each feature has been standardized to have within-class standard deviation equal to 1. Take Σ̃_w = Σ̂_w + Ω, where Ω is chosen so that Σ̃_w is positive definite. Then, the following proposition holds.

Proposition 3

Consider the penalized LDA-L₁ problem (17) where λ₁ > 0 and k = 1. Suppose that at the solution β* to (17), the objective is positive. Then, there exists a positive tuning parameterλ₂ and a positive scalar c such that cβ* corresponds to a zero of the generalized gradient of the SDA objective (36).

A proof is given in the Appendix. Note that the assumption that the objective is positive at the solution β* is not very taxing - it simply means that β* results in a higher value of the objective than does a vector of zeros. Proposition 3 states that if the same positive definite estimate for Σ_w is used for both problems, then the solution of the penalized LDA-L₁ problem corresponds to a point where the generalized gradient of the SDA problem is zero. But since the SDA problem is not convex, this does not imply that there is a correspondence between the solutions of the two problems. Penalized LDA-L₁ has some advantages over SDA. Unlike SDA, penalized LDA-L₁ has a clear relationship with Fisher’s discriminant problem. Moreover, unlike SDA, it provides a natural way to enforce a diagonal estimate of Σ_w.

7.2. Connection with nearest shrunken centroids

The following proposition indicates that in the case of two equally-sized classes, NSC is closely related to the penalized LDA-L₁ problem with the diagonal estimate (4) for Σ_w.

Proposition 4

Suppose that K = 2 and $n_1=n_2=\frac{n}{2}$. Let β̂ denote the solution to the problem

$${\text{maximize}}_{\mathit{\beta }}\{\sqrt{{\mathit{\beta }}^T{\widehat{\mathbf{\sum }}}_b\mathit{\beta }}-\lambda \sum _{j=1}^p\mid {\beta }_j{\widehat{\sigma }}_j\mid \}\text{subject}\text{to}{\mathit{\beta }}^T{\mathbf{\sum }^{\sim }}_w\mathit{\beta }\le 1$$ (37)

where Σ̃_w is the diagonal estimate (4). Consider the classification rule obtained by computing Xβ̂ and assigning each observation to its nearest centroid in this transformed space. This is the same as the NSC classification rule (34).

Note that (37) is simply a modified version of the penalized LDA-L₁ criterion, in which the between-class variance term has been replaced with its square root. Therefore, penalized LDA-L₁ with a diagonal estimate of Σ_w and NSC are closely connected when K = 2. This connection does not hold for larger values of K, since NSC penalizes the elements of the p × K class centroid matrix, whereas penalized LDA-L₁ penalizes the eigenvectors of this matrix. A proof of Proposition 4 is given in the Appendix.

8. Discussion

We have extended Fisher’s discriminant problem to the high-dimensional setting by imposing penalties on the discriminant vectors. The penalty function is chosen based on the problem at hand, and can result in an interpretable classifier. A potentially useful but unexplored area of application for our proposal is fMRI data, for which one could use a penalty that incorporates the spatial structure of the voxels.

There is a strong connection between our penalized LDA proposal and previous work on penalized principal components analysis (PCA). When P_k is an L₁ penalty, (12) is closely related to the SCoTLASS proposal for sparse PCA (Jolliffe et al. 2003). The criterion (12) and Algorithm 1 for optimizing it are closely related to the penalized principal components algorithms considered by a number of authors (see e.g. Zou et al. 2006, Shen & Huang 2008, Witten et al. 2009). This connection stems from the fact that Fisher’s discriminant problem is simply a generalized eigenproblem.

The R language software package penalized LDA implementing penalized LDA-L₁ and penalized LDA-FL will be made available on CRAN, http://cran.r-project.org/.

Appendix

Equivalence between (3) and standard formulation for LDA

We have stated Fisher’s discriminant problem as (3), but a more standard formulation is

$${\text{maximize}}_{{\mathit{\beta }}_k\in {\mathbb{R}}^p}\{{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}_k\}\text{subject}\text{to}{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_w{\mathit{\beta }}_k=1,{\mathit{\beta }}_k^T{\widehat{\mathbf{\sum }}}_w{\mathit{\beta }}_i=0\forall i<k.$$ (38)

We now show that (3) and (38) are equivalent, provided that the solution is not in the null space of Σ̂_b. It suffices to show that if α solves (3), then α^TΣ̂_wα = 1.

We proceed with a proof by contradiction. Suppose that α solves (3) and α^TΣ̂_wα < 1, α^TΣ̂_bα > 0. Let $c=1/\sqrt{{\mathit{\alpha }}^T{\widehat{\mathbf{\sum }}}_w\mathit{\alpha }}$. Since c > 1, it follows that (cα)^TΣ̂_b(cα) > α^TΣ̂_bα. And cα is in the feasible set for (3). This contradicts the assumption that α solves (3). Hence, any solution to (3) that is not in the null space of Σ̂_b also solves (38).

Note that we do not concern ourselves with solutions that are in the null space of Σ̂_b, as these are not useful for the purpose of discrimination and will arise only if too many discriminant vectors are used.

Proof of Proposition 1

Proof

Letting ${\mathbf{\sum }^{\sim }}_w^{\frac{1}{2}}$ denote the symmetric matrix square root of Σ̃_w and ${\stackrel{\sim }{\mathit{\beta }}}_k={\mathbf{\sum }^{\sim }}_w^{\frac{1}{2}}{\mathit{\beta }}_k$, (6) becomes

$${\text{maximize}}_{{\stackrel{\sim }{\mathit{\beta }}}_k}\{{\stackrel{\sim }{\mathit{\beta }}}_k^T{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{P}}_k^{\perp }{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{Y}}^T\mathbf{X}{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}{\stackrel{\sim }{\mathit{\beta }}}_k)\}\text{subject}\text{to}{\left|\right|{\mathit{\beta }}_k\left|\right|}^2\le 1,$$ (39)

which is equivalent to

$${\text{maximize}}_{{\stackrel{\sim }{\mathit{\beta }}}_k,{\mathbf{u}}_k}\{{\stackrel{\sim }{\mathit{\beta }}}_k^T\mathbf{A}{\mathbf{P}}_k^{\perp }{\mathbf{u}}_k\}\text{subject}\text{to}{\left|\right|{\stackrel{\sim }{\mathit{\beta }}}_k\left|\right|}^2\le 1,{\left|\right|{\mathbf{u}}_k\left|\right|}^2\le 1,$$ (40)

where $\mathbf{A}={\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}$. Equivalence of (40) and (39) can be seen from partially optimizing (40) with respect to u_k.

We claim that β̃_k and u_k that solve (40) are the kth left and right singular vectors of A. By inspection, the claim holds when k = 1. Now, suppose that the claim holds for all i < k, where k > 1. Partially optimizing (40) with respect to β̃_k yields

$${\text{maximize}}_{{\mathbf{u}}_k}\{{\mathbf{u}}_k^T{\mathbf{P}}_k^{\perp }{\mathbf{A}}^T\mathbf{A}{\mathbf{P}}_k^{\perp }{\mathbf{u}}_k\}\text{subject}\text{to}{\left|\right|{\mathbf{u}}_k\left|\right|}^2\le 1.$$ (41)

By definition, ${\mathbf{P}}_k^{\perp }$ is an orthogonal projection matrix into the space orthogonal to

$${({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{Y}}^T\mathbf{X}{\widehat{\mathit{\beta }}}_i={({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}{\mathbf{Y}}^T\mathbf{X}{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}{\stackrel{\sim }{\mathit{\beta }}}_i={\mathbf{A}}^T{\stackrel{\sim }{\mathit{\beta }}}_i\propto {\mathbf{u}}_i$$ (42)

for all i < k, where proportionality follows from the fact that β̃_i and u_i are the ith singular vectors of A for all i < k. Hence, ${\mathbf{P}}_k^{\perp }=\mathbf{I}-{\sum }_{i=1}^{k-1}{\mathbf{u}}_i{\mathbf{u}}_i^T$. Therefore, by (41), u_k is the kth eigenvector of A^TA, or equivalently the kth right singular vector of A. So by (40), β̃_k is the kth left singular vector of A, or equivalently the kth eigenvector of $\mathbf{A}{\mathbf{A}}^T=n{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}{\widehat{\mathbf{\sum }}}_b{\mathbf{\sum }^{\sim }}_w^{-\frac{1}{2}}$. Therefore, the solution to (6) is the kth discriminant vector.

Proof of Proposition 2

For (18), the Karush-Kuhn-Tucker (KKT) conditions (Boyd & Vandenberghe 2004) are given by

$$2{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}^{(m-1)}-\lambda \mathbf{\Gamma }-2\delta {\mathbf{\sum }^{\sim }}_w\mathit{\beta }=0,\delta \ge 0,\delta ({\mathit{\beta }}^T{\mathbf{\sum }^{\sim }}_w\mathit{\beta }-1)=0,{\mathit{\beta }}^T{\mathbf{\sum }^{\sim }}_w\mathit{\beta }\le 1,$$ (43)

where we have dropped the “k” subscripts and superscripts for ease of notation, and where Γ is a p-vector of which the jth element is the subgradient of ${\sum }_{j=1}^p\mid {\widehat{\sigma }}_j{\beta }_j\mid$ with respect to β_j; i.e. Γ_j = σ̂_j if β_j > 0, Γ_j = −σ̂_j if β_j < 0, and Γ_j is in between σ̂_j and − σ̂_j if β_j = 0.

First, suppose that for some j, |(2Σ̂_bβ^(m−1))_j| > λσ̂_j. Then it must be the case that 2δΣ̃_wβ ≠ 0. So δ > 0 and β^TΣ̃_wβ = 1. Then the KKT conditions simplify to

$$2{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}^{(m-1)}-\lambda \mathbf{\Gamma }-2\delta {\mathbf{\sum }^{\sim }}_w\mathit{\beta }=0,{\mathit{\beta }}^T{\mathbf{\sum }^{\sim }}_w\mathit{\beta }=1,\delta >0.$$ (44)

Substituting d = δβ, this is equivalent to solving (21) and then dividing the solution d̂ by $\sqrt{{\widehat{\mathbf{d}}}^T{\mathbf{\sum }^{\sim }}_w\widehat{\mathbf{d}}}$.

Now, suppose instead that |(2Σ̂_bβ^(m−1))_j| ≤ λσ̂_j for all j. Then, by (43), it follows that β̂ = 0 solves (18). By inspection of the subgradient equation for (21), we see that in this case d̂ = 0 solves (21) as well. Therefore, the solution to (18) is as given in Proposition 2.

The same set of arguments applied to (20) lead to Proposition 2(b).

Proof of Proposition 3

Proof

Consider (17) with tuning parameter λ₁ and k = 1. Then by Theorem 6.1.1 of Clarke (1990), if there is a nonzero solution β*, then there exists μ ≥ 0 such that

$$0\in 2{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}^{\ast }-{\lambda }_1\mathbf{\Gamma }({\mathit{\beta }}^{\ast })-2\mu {\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}^{\ast },$$ (45)

where Γ(β) is the subdifferential of ||β||₁. The subdifferential is the set of subgradients of ||β||₁; the jth element of a subgradient equals sign(β_j) if β_j ≠ 0 and is between −1 and 1 if β_j = 0. Left-multiplying (45) by β* yields 0 = 2β*^TΣ̂_bβ* − λ₁ ||β*||₁ − 2μβ*^TΣ̃_wβ* Since the sum of the first two terms is positive (since β* is a nonzero solution), it follows that μ > 0.

Now, define a new vector that is proportional to β*:

$$\widehat{\mathit{\beta }}=\frac{\mu }{(1+\mu )a}{\mathit{\beta }}^{\ast }=c{\mathit{\beta }}^{\ast }$$ (46)

where $a=\sqrt{n{\mathit{\beta }}^{\ast T}{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}^{\ast }}$. By inspection, a ≠ 0, since otherwise β* would not be a nonzero solution. Also, let ${\lambda }_2={\lambda }_1(\frac{1-ca}{a})$. Note that $1-ca=\frac{1}{1+\mu }>0$, so λ₂ > 0.

The generalized gradient of (36) with tuning parameter λ₂ evaluated at β̂ is proportional to

$$2{\widehat{\mathbf{\sum }}}_b\widehat{\mathit{\beta }}-{\lambda }_2\mathbf{\Gamma }(\widehat{\mathit{\beta }})(\frac{\sqrt{n{\widehat{\mathit{\beta }}}^T{\widehat{\mathbf{\sum }}}_b\widehat{\mathit{\beta }}}}{1-\sqrt{n{\widehat{\mathit{\beta }}}^T{\widehat{\mathbf{\sum }}}_b\widehat{\mathit{\beta }}}})-2{\mathbf{\sum }^{\sim }}_w\widehat{\mathit{\beta }}(\frac{\sqrt{n{\widehat{\mathit{\beta }}}^T{\widehat{\mathbf{\sum }}}_b\widehat{\mathit{\beta }}}}{1-\sqrt{n{\widehat{\mathit{\beta }}}^T{\widehat{\mathbf{\sum }}}_b\widehat{\mathit{\beta }}}}),$$ (47)

or equivalently,

$$\begin{array}{l}2c{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}^{\ast }-{\lambda }_2\mathbf{\Gamma }({\mathit{\beta }}^{\ast })\frac{ac}{1-ac}-2c{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}^{\ast }\frac{ac}{1-ac}=2c{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}^{\ast }-{\lambda }_{1}c\mathbf{\Gamma }({\mathit{\beta }}^{\ast })-2c{\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}^{\ast }\frac{ac}{1-ac}\\ =2c{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}^{\ast }-{\lambda }_{1}c\mathbf{\Gamma }({\mathit{\beta }}^{\ast })-2c\mu {\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}^{\ast }\\ =c(2{\widehat{\mathbf{\sum }}}_b{\mathit{\beta }}^{\ast }-{\lambda }_1\mathbf{\Gamma }({\mathit{\beta }}^{\ast })-2\mu {\mathbf{\sum }^{\sim }}_w{\mathit{\beta }}^{\ast }).\end{array}$$ (48)

Comparing (45) to (48), we see that 0 is contained in the generalized gradient of the SDA objective evaluated at β̂.

Proof of Proposition 4

Proof

Since n₁ = n₂, NSC assigns an observation x ∈ ℝ^p to the class that maximizes

$$\sum _{j=1}^p\frac{x_{j}S({\overline{\mathbf{X}}}_{kj},{\widehat{\sigma }}_j\lambda )}{{\widehat{\sigma }}_j^2}$$ (49)

where X̄_kj is the mean of feature j in class k, and the soft-thresholding operator S is given by (24). On the other hand, the classification rule resulting from (37) assigns x to the class that minimizes

$$\left|\sum _{j=1}^p\frac{{\overline{\mathbf{X}}}_{kj}S({\overline{\mathbf{X}}}_{1j},{\widehat{\sigma }}_j\lambda )}{{\widehat{\sigma }}_j^2}-\sum _{j=1}^p\frac{x_{j}S({\overline{\mathbf{X}}}_{1j},{\widehat{\sigma }}_j\lambda )}{{\widehat{\sigma }}_j^2}\right|.$$ (50)

This follows from the fact that (37) reduces to

$${\text{maximize}}_{\mathit{\beta }}\{{\mathit{\beta }}^T{\overline{\mathbf{X}}}_1-\lambda \sum _{j=1}^p\mid {\beta }_i{\widehat{\sigma }}_j\mid \}\text{subject}\text{to}\sum _{j=1}^p{\beta }_j^2{\widehat{\sigma }}_j^2\le 1,$$ (51)

since $\frac{1}{\sqrt{n}}{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-\frac{1}{2}}={\overline{\mathbf{X}}}_1[\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\end{array}]$ and ${\widehat{\mathrm{\sum }}}_b=\frac{1}{n}{\mathbf{X}}^T\mathbf{Y}{({\mathbf{Y}}^T\mathbf{Y})}^{-1}{\mathbf{Y}}^T\mathbf{X}$.

Since the first term in (50) is positive if k = 1 and negative if k = 2, (37) classifies to class 1 if ${\sum }_{j=1}^p\frac{x_{j}S({\overline{\mathbf{X}}}_{1j},{\widehat{\sigma }}_j\lambda )}{{\widehat{\sigma }}_j^2}>0$ and classifies to class 2 if ${\sum }_{j=1}^p\frac{x_{j}S({\overline{\mathbf{X}}}_{1j},{\widehat{\sigma }}_j\lambda )}{{\widehat{\sigma }}_j^2}<0$. Because X̄_1j = −X̄_2j, by inspection of (49), the two methods result in the same classification rule.

Proof of equivalence of Fisher’s LDA and optimal scoring

Proof

Consider the following two problems:

$${\text{maximize}}_{\mathit{\beta }\in {\mathbb{R}}^p}\{{\mathit{\beta }}^T{\widehat{\mathbf{\sum }}}_b\mathit{\beta }\}\text{subject}\text{to}{\mathit{\beta }}^T({\widehat{\mathbf{\sum }}}_w+\mathbf{\Omega })\mathit{\beta }=1$$ (52)

and

$${\text{minimize}}_{\mathit{\beta }\in {\mathbb{R}}^p,\mathit{\theta }\in {\mathbb{R}}^K}\{\frac{1}{n}{\left|\right|\mathbf{Y}\mathit{\theta }-\mathbf{X}\mathit{\beta }\left|\right|}^2+{\mathit{\beta }}^2\mathbf{\Omega }\mathit{\beta }\}\text{subject}\text{to}{\mathit{\theta }}^T{\mathbf{Y}}^T\mathbf{Y}\mathit{\theta }=1.$$ (53)

In Hastie et al. (1995), a somewhat challenging proof is given of the fact that the solutions β̂ to the two problems are proportional to each other. Here, we present a more direct argument. In (52) and (53), Ω is a matrix such that Σ̂_w + Ω is positive definite; if Ω = 0 then these two problems reduce to Fisher’s LDA and optimal scoring. Optimizing (53) with respect to θ, we see that the β that solves (53) also solves

$${\text{minimize}}_{\mathit{\beta }}\{-\frac{2}{\sqrt{n}}\sqrt{{\mathit{\beta }}^T{\widehat{\mathbf{\sum }}}_b\mathit{\beta }}+{\mathit{\beta }}^T{\widehat{\mathbf{\sum }}}_b\mathit{\beta }+{\mathit{\beta }}^T({\widehat{\mathbf{\sum }}}_w+\mathbf{\Omega })\mathit{\beta }\}.$$ (54)

For notational convenience, let $\stackrel{\sim }{\mathit{\beta }}={({\widehat{\mathbf{\sum }}}_w+\mathbf{\Omega })}^{\frac{1}{2}}\mathit{\beta }$ and ${\mathbf{\sum }^{\sim }}_b={({\widehat{\mathbf{\sum }}}_w+\mathbf{\Omega })}^{-\frac{1}{2}}{\widehat{\mathbf{\sum }}}_b{({\widehat{\mathbf{\sum }}}_w+\mathbf{\Omega })}^{-\frac{1}{2}}$. Then, the problems become

$${\text{maximize}}_{\stackrel{\sim }{\mathit{\beta }}}\{{\stackrel{\sim }{\mathit{\beta }}}^T{\mathbf{\sum }^{\sim }}_b\stackrel{\sim }{\mathit{\beta }}\}\text{subject}\text{to}{\stackrel{\sim }{\mathit{\beta }}}^T\stackrel{\sim }{\mathit{\beta }}=1$$ (55)

and

$${\text{minimize}}_{\stackrel{\sim }{\mathit{\beta }}}\{-\frac{2}{\sqrt{n}}\sqrt{{\stackrel{\sim }{\mathit{\beta }}}^T{\mathbf{\sum }^{\sim }}_b\stackrel{\sim }{\mathit{\beta }}}+{\stackrel{\sim }{\mathit{\beta }}}^T({\mathbf{\sum }^{\sim }}_b+\mathbf{I})\stackrel{\sim }{\mathit{\beta }}\}.$$ (56)

It is easy to see that the solution to (55) is the first eigenvector of Σ̃_b. Let β̂ denote the solution to (56). Consequently, β̂^TΣ̃_bβ̂ > 0. So β̂ satisfies

$${\mathbf{\sum }^{\sim }}_b\stackrel{\sim }{\mathit{\beta }}(1-\frac{1}{\sqrt{n{\widehat{\mathit{\beta }}}^T{\mathbf{\sum }^{\sim }}_b\widehat{\mathit{\beta }}}})+\widehat{\mathit{\beta }}=0,$$ (57)

and therefore $\sqrt{n{\widehat{\mathit{\beta }}}^T{\mathbf{\sum }^{\sim }}_b\widehat{\mathit{\beta }}}<1$. Now (57) indicates that β̂ is an eigenvector of Σ̃_b with eigenvalue $\lambda =\frac{\sqrt{n{\widehat{\mathit{\beta }}}^T{\mathbf{\sum }^{\sim }}_b\widehat{\mathit{\beta }}}}{1-\sqrt{n{\widehat{\mathit{\beta }}}^T{\mathbf{\sum }^{\sim }}_b\widehat{\mathit{\beta }}}}$; it remains to show that β̂ is in fact the first eigenvector.

Notice that if we let w = β̂^Tβ̂ then $\lambda =\frac{\sqrt{n\lambda w}}{1-\sqrt{n\lambda w}}$, and so $w=\frac{\lambda }{n{(1+\lambda )}^2}$. Then the objective of (56) evaluated at β̂ equals

$$-\frac{2}{\sqrt{n}}\sqrt{\lambda w}+\lambda w+w=\frac{-2\lambda }{n(1+\lambda )}+\frac{\lambda }{n(1+\lambda )}=-\frac{\lambda }{n(1+\lambda )}.$$ (58)

The minimum occurs when λ is large. So the solution to (56) is the largest eigenvector of Σ̃_b.

This argument can be extended to show that subsequent solutions to Fisher’s discriminant problem and the optimal scoring problem are proportional to each other.