Perception of across-frequency asynchrony and the role of cochlear delays

Abstract

Cochlear filtering results in earlier responses to high than to low frequencies. This study examined potential perceptual correlates of cochlear delays by measuring the perception of relative timing between tones of different frequencies. A brief 250-Hz tone was combined with a brief 1-, 2-, 4-, or 6-kHz tone. Two experiments were performed, one involving subjective judgments of perceived synchrony, the other involving asynchrony detection and discrimination. The functions relating the proportion of “synchronous” responses to the delay between the tones were similar for all tone pairs. Perceived synchrony was maximal when the tones in a pair were gated synchronously. The perceived-synchrony function slopes were asymmetric, being steeper on the low-frequency-leading side. In the second experiment, asynchrony-detection thresholds were lower for low-frequency rather than for high-frequency leading pairs. In contrast with previous studies, but consistent with the first experiment, thresholds did not depend on frequency separation between the tones, perhaps because of the elimination of within-channel cues. The results of the two experiments were related quantitatively using a decision-theoretic model, and were found to be highly correlated. Overall the results suggest that frequency-dependent cochlear group delays are compensated for at higher processing stages, resulting in veridical perception of timing relationships across frequency.

INTRODUCTION

Spectro-temporal analysis performed by the cochlea generates spatio-temporal patterns of neural firings that provide the information necessary for the brain to correctly interpret the sounds around us. Cochlear processing has often been modeled as a bank of overlapping filters with center frequencies representing specific sites along the basilar membrane (BM), with bandwidths dependent on the characteristic frequency (CF) and stimulus level (Lopez-Poveda and Meddis, 2001; Zhang et al., 2001; Irino and Patterson, 2006). The models have been developed based on findings from direct mechanical measurements in experimental animals that were performed primarily at basal sites of the cochlea, which can be accessed with little effect on the cochlea’s physiological function (Rhode, 1971; Rhode and Robles, 1974; Robles et al., 1986; Ruggero et al., 1997; Robles and Ruggero, 2001; Rhode, 2007). Only a few studies have provided data from apical sites, and those have acknowledged that the response characteristics might have been compromised by the procedures used to gain physical access to the apex (Cooper and Rhode, 1995, 1996; Rhode and Cooper, 1996; Khanna and Hao, 1999; Zinn et al., 2000). Due to the mechanical properties of the BM, the peak responses to different frequency components occurring at their respective CF places have different latencies. Because cochlear response latencies cannot be measured accurately via direct access at all sites, the BM latency-frequency functions for commonly used experimental animals (chinchilla, guinea pig, cat) have been derived from Wiener kernels of auditory-nerve responses to noise (Recio-Spinoso et al., 2005; Siegel et al., 2005; Temchin et al., 2005; Temchin et al., 2011), from phase responses of auditory-nerve fibers to pure tones (Palmer and Shackleton, 2009) or via minimum-phase computations of BM responses based on frequency-threshold tuning curves measured in auditory-nerve fibers (Temchin et al., 2011).

In humans, direct measurements from the BM or auditory nerve are not possible, and so non-invasive methods have been devised to estimate the BM latency-frequency functions for the human cochlea. The BM delays have been estimated from measurements of the compound action potential (CAP) (Elberling, 1974; Eggermont, 1979; Schoonhoven et al., 2001), derived-bands and tone-burst auditory brainstem responses (Eggermont and Don, 1980; Neely et al., 1988; Don et al., 1993; Donaldson and Ruth, 1993; Don et al., 1998; Harte et al., 2009), distortion-product, transient-evoked, and stimulus-frequency otoacoustic emissions (Neely et al., 1988; Bowman et al., 1997; Ramotowski and Kimberley, 1998; Schoonhoven et al., 2001; Shera et al., 2002; Sisto and Moleti, 2007; Harte et al., 2009), and by using latency-frequency responses obtained postmortem (Von Békésy, 1949) and then assuming a compensation term for the effects of death on the cochlear function (Ruggero and Temchin, 2007).

The latency (τ) of peak BM responses has often been described by a power law, τ = αf^–β, where f is the tone frequency α and β are constants whose values differ across studies.1 Most commonly, the estimated latencies span a range of around 10 ms, over a frequency range from 0.1 to 10 kHz, in both experimental animals and humans. Because BM latencies are closely related to tuning (Shera et al., 2010), they are expected to depend on stimulus level, due to the level dependence of filter bandwidths. The exact form of changes in BM latency-frequency function with level is unknown. Some studies have suggested that the latency-frequency function becomes shallower, exhibiting more synchronous responses across frequency as the level increases (e.g., Neely et al., 1988; Schoonhoven et al., 2001; Sisto and Moleti, 2007), while others have predicted a small effect of level in the opposite direction, i.e., a slight increase in the slope of the latency-frequency function at high levels (Ruggero and Temchin, 2007).

The frequency dependence of BM-response latency implies that physically synchronous components of a broadband stimulus are desynchronized in the process of BM filtering, such that lower-frequency components in the neural representation of the input stimulus are delayed relative to the higher-frequency components. Therefore, components that are physically delayed to mirror the BM latency-frequency function are expected to yield a synchronous response along the entire cochlea, and consequently a synchronous neural representation. Consistent with this idea, Shore and Nuttal (1985) achieved a greater synchronization of AN responses across the cochlear partition in the guinea pig, as was evidenced by the CAP, for a rising chirp designed to counteract the BM latencies than for a falling chirp or a click. Similarly, Dau et al. (2000) reported a larger amplitude of the auditory brainstem response (ABR) wave-V evoked by a rising chirp (compared with that for a click and the time-reversed version of the chirp), which was designed to align latencies of the cochlear responses across frequency, based on the BM model of de Boer (1980). The increased amplitude of ABR wave-V observed for the rising chirp suggested more synchronous stimulation across the entire BM compared with that evoked by a click. Petoe et al. (2010b) examined a few temporal and spectral measures known to reflect the degree of neural synchrony, obtained from chirp- and click-evoked ABRs. Consistent with the findings by Dau et al. (2000), at moderate levels, they found increased neural synchrony in response to a rising chirp compared with a click, as was evidenced by increased high-frequency content of the ABR-response spectrum and decreased phase variance for the prominent ABR frequency components. At high levels, despite an increased wave-V amplitude for a rising chirp, spread of excitation and an increased contribution from within-channel phase dispersion to the overall neural synchrony led to a reduction or even elimination of earlier ABR waves, increased variance in wave V latency, and decreased high-frequency content of the ABR response spectrum, indicating a disruption to the superior neural synchrony seen in response to the same chirp at lower levels (Petoe et al., 2010a).

Thus, evidence suggests that the neural stimulus presented to the brain has a modified time-frequency alignment compared with the stimulus entering the cochlea. An important question is whether this desynchronizing of components within broadband stimuli is perceived. Surprisingly few psychophysical studies have addressed this question. Patterson (1987, 1988) investigated whether frequency-dependent cochlear response delays affect the perception of timbre of harmonic complexes. In both studies, listeners were asked to discriminate complexes with components starting in cosine phase from complexes with the same amplitude spectrum but with a modified phase spectrum. The phase spectrum was manipulated by introducing monotonically increasing or decreasing phase delays of successive harmonics. Patterson (1987, 1988) found that the monotonic phase shifts were discriminated from the cosine phase when they corresponded to a total time delay of about 4–5 ms across all the components in a harmonic complex. Because the stimulus level (Patterson, 1987) and background-noise (Patterson, 1988) had no effect on the discrimination thresholds, Patterson argued that timbre discrimination for monotonic phase shifts between the components was performed using between-channel rather than within-channel timing cues. Overall, the results of Patterson’s two studies suggested that across-channel delays, on the order of cochlear response delays, could in principle affect the perception of timbre of harmonic complexes. However, since only small (although statistically significant) differences in discrimination threshold were observed depending on the direction of the phase delay with increasing harmonic frequency, Patterson (1987) concluded that cochlear “propagation delays can largely be ignored in perceptual models of hearing.” A similar conclusion was reached by Uppenkamp et al. (2001), based on results of subjective comparisons of perceived compactness of clicks, rising chirps, and their time-reversed versions (i.e., falling chirps): for chirp durations up to about 20 ms, a rising chirp (Dau et al., 2000) was judged as less compact than its time-reversed counterpart, and a click was judged to be the most compact of the three stimuli. These results led Uppenkamp et al. (2001) to suggest that across-channel cochlear delays may be eliminated at subsequent neural processing stages.

Unfortunately the interpretation of the Patterson (1987) and Uppenkamp et al. (2001) data is complicated by the fact that changes to their stimuli resulted not only in changes in across-channel synchrony, but also in changes to the within-channel waveform shapes. While Patterson (1987, 1988) argued that the changes to the waveforms at the output of each channel were minimal, Uppenkamp et al. (2001) suggested that the listeners’ judgments of stimulus compactness may have been determined by the response within individual cochlear filters, which for a rising chirp extends over a longer duration than the response to either a click or a falling chirp (see their Fig. 1). These differences in response duration are due to the phase responses of the individual cochlear filters (e.g., Kohlrausch and Sander, 1995; Oxenham and Dau, 2001a,b), and so the results of Uppenkamp et al. (2001) may provide information about within-filter phase responses, rather than across-filter differences in group delay.

Strelcyk and Dau (2009) used another approach to measure effective cochlear delays behaviorally. They presented two tones of nearby frequencies (10%–20% apart), with one tone presented to each ear, and measured the interaural time difference (ITD) necessary for the tones to be lateralized to the center of the head. They argued that the ITD should be the opposite of any difference in delay between the two tones imposed by the peripheral auditory system. Unfortunately, their interpretation is complicated by two factors. First, they defined the delay between the two tones in terms of their temporal envelopes. Although both tones had zero starting phase, the fact that they were of different frequency means that the phase difference between the two tones was continually changing. It is known that ITD perception is dominated by temporal fine structure, not temporal envelope, for tones of low frequency (<1500 Hz). Because the delay between peaks in the fine structure of the two tones varied with each cycle, the effective delays between Strelcyk and Dau’s tone pairs are difficult to define with certainty. The second issue is that lateralization between two tones separated by only 10%–20% may be determined by a common place in the cochlea with a CF between the frequencies of the tone pair, and so the measured ITD may not reflect the difference in the group delays between the cochlear locations with CFs corresponding to the tone frequencies.

Studies of asynchrony detection (Hirsh and Sherrick, 1961; Parker, 1988; Zera and Green, 1993b; Mossbridge et al., 2006, 2008; Micheyl et al., 2010) or temporal-order discrimination (Hirsh, 1959; Hirsh and Sherrick, 1961; Wier and Green, 1975; Pastore et al., 1982; Kelly and Watson, 1986; Mossbridge et al., 2006; Micheyl et al., 2010) might be useful in determining possible perceptual effects of the frequency-dependent cochlear delays but, as in the Strelcyk and Dau (2009) study, within-channel cues were potentially available to the listeners because of the relatively close frequency spacing used, or because of potentially overlapping spectral information due to splatter caused by very rapid onset/offset ramps. To our knowledge, no data reflecting the perception of solely across-channel timing differences are available to test the hypothesis that a higher-level mechanism compensates for BM across-channel delays to provide veridical perception. In this study, pairs of tones with frequency separations of at least two octaves were used to investigate the role of BM delays in the perception of across-channel timing information. To further minimize the availability of within-channel cues, bands of noise were used to mask regions of the cochlea in which the excitation by the tones in a pair could potentially overlap. In experiment 1, listeners performed subjective evaluations of the relative timing of tones in a pair. No feedback was provided in this task. If a mechanism compensating for the cochlear delays exists, then the tones that were physically gated on and off simultaneously should sound synchronous and tone pairs with a low- or high-frequency tone delayed should sound asynchronous. In contrast, if a compensating mechanism does not exist and cochlear delays are perceived, then the highest proportion of “synchronous” responses should be given to a pair with a small delay (of the order of milliseconds) of the high-frequency tone relative to the low-frequency tone. In experiment 2, the detection of a change in delay between two tones in a pair was measured as a function of the baseline delay. Finally, the results from the two experiments were compared within the quantitative framework of signal detection theory (SDT) (Green and Swets, 1966) to determine whether the results from both experiments could be explained via the same perceptual mechanisms.

EXPERIMENT 1: SUBJECTIVE JUDGMENTS OF ASYNCHRONY

Most physiological studies estimate that the BM peak response to low frequencies (∼100 Hz) is delayed by about 10 ms relative to the peak response to high frequencies (∼10 kHz). The latency-frequency function exhibits the steepest slope (i.e., the greatest change in latency per octave) in the frequency region below 1000–2000 Hz, with little difference in response times for higher frequencies (e.g., Fobel and Dau, 2004). To investigate the perceptual effects of BM delays, a tone well below 1 kHz was paired with selected tones with frequencies of 1 kHz and above. If BM-induced frequency-dependent group delays are not compensated at higher processing stages, then the point of maximal perceived synchrony should occur when the low-frequency is leading the high-frequency tone by about 10 ms. As mentioned in Sec. 1, the dispersion of cochlear delays may be greater for low-level than for high-level stimuli due to level-dependent sharpness of tuning. Therefore, the perception of relative timing for two spectrally remote tones was tested at both a low and a high stimulus level.

Stimuli and procedure

The perception of relative timing between two tones was measured for a number of delays between the tones using a method of constant stimuli. The experiment was performed for four frequency pairs tested in separate blocks. Each pair consisted of a 250-Hz low-frequency (LF) tone and one of the higher-frequency (HF) tones at 1, 2, 4, or 6 kHz. The delays were drawn from a set including 0 ms (synchronous presentation) and ±2, 4, 8, 12, 16, 20, 30, and 40 ms, where the negative sign denotes pairs with the LF tone leading and the positive sign denotes pairs with the HF tone leading. Each tone had a duration of 40 ms including 10-ms squared-cosine onset and offset ramps. The choice of 10-ms ramps was a compromise between the need to precisely define the onsets and the need to avoid audible “spectral splatter” effects (e.g., Leshowitz and Wightman, 1972).

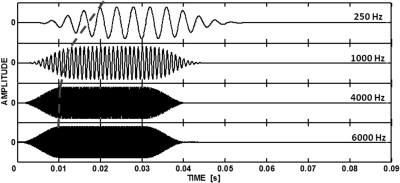
Figure 1 illustrates the waveforms at the output of BM filters centered on the frequencies of some of the tones used in the experiment. The waveforms were obtained by convolving the tones with the impulse responses of the level-dependent gammachirp filters (Irino and Patterson, 1997) with center frequencies corresponding to the respective tone frequency, for a level of 30 dB SPL (roughly corresponding to the mean SPL across the listeners needed for 20 dB SL). The 250-Hz waveform at the output of the filter is delayed relative to the waveforms with higher frequencies. The delay is highlighted in the figure by the gray dashed line connecting the first maximum (steady-state) amplitudes at the filter output. The waveform for a 1-kHz tone is only slightly delayed relative to those for the 4- and 6-kHz tones, consistent with the very shallow slope of the BM latency-frequency function for frequencies above 1–2 kHz.

Figure 1.

Waveforms at the output of gammachirp filters centered on frequencies of the test tones, for an input level of 30 dB SPL. The dashed curve connecting the first peaks of the steady-state response is used to highlight the frequency-dependent latencies of the filter maximum responses.

The experiment was performed for two tone levels, 85 dB SPL and 20 dB above the absolute threshold for the tone (i.e., 20 dB SL), determined for each listener and tone individually.

For each pair of tone frequencies, a half-octave-wide band of noise was used to mask within-channel cues potentially available in channels excited by both tones in a pair. A plausible within-channel cue for sufficiently small frequency separations could be an increase in excitation within a filter responding to both tones (i.e., an increment in the envelope of the waveform at the output of the filter due to the addition of the delayed tone). Listeners could perform the task by detecting that increment instead of judging the relative timing of responses in remote frequency channels. The noise was centered on the geometric mean of the LF and HF tones. On each trial, the stimulus obtained by adding two tones with a selected delay (including a 0-ms delay) was temporally centered in the noise, which started 400 ms before the onset and ended 400 ms after the offset of the tone pair. The overall noise level was set to 20 dB below the level of the lower-level tone in each tone pair. This noise level was determined to be sufficient for eliminating within-channel cues based on the outputs of level-dependent gammachirp filters (Irino and Patterson, 1997). The noise bands were generated in the frequency domain by setting the spectral components of a Gaussian noise outside the desired band to zero, and thus the spectral roll-offs below and above the cutoff frequencies were limited only by the gating of the noise.

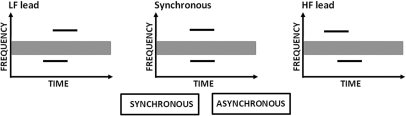
Each block of trials contained one pair of frequencies and included ten permutations of the 17 different delays between the tones, resulting in a total of 170 trials per block. Each trial contained a single tone pair. After each trial, the listeners had to decide whether the pair of tones sounded synchronous or asynchronous. Listeners were encouraged to use whatever cue they found most effective for judging the synchrony between the tones. For instance, they were told that they could focus on the onset portions of the stimuli and decide whether or not they started at the same time, or they could evaluate the overall duration (or compactness) of the tone pair. They could also focus on the dispersion of offsets, although offset cues have been found to be less effective than onset cues in detecting asynchrony (Zera and Green, 1993b; Mossbridge et al., 2008). A schematic illustration of the three types of trials that were presented within a block is shown in Fig. 2, with the two types of responses available to the listeners. The listeners were given no feedback in the experiment. For each pair of tones, listeners completed ten blocks. Since each block contained ten permutations of the delays used, each delay for each tone pair was judged a total of 100 times by each listener.

Figure 2.

Schematic illustration of the three types of trials presented to the listeners for synchrony judgments: The left panel shows a trial with the LF tone leading, the middle panel shows a trial with the tones gated simultaneously, and the right panel shows the HF tone leading. One trial was presented before the listener’s response was recorded. The available responses are shown below the plots.

To determine the levels used as a reference for 20 dB SL tones, absolute thresholds for detecting 40-ms tones with frequencies of 0.25, 1, 2, 4, and 6 kHz were measured before the main experiment. An adaptive three-interval, three-alternative forced-choice (3I-3AFC) procedure was used in combination with a 2-down 1-up tracking rule to estimate the 70.7% correct point on the psychometric function (Levitt, 1971). The intervals were marked by lights on a computer screen and were separated by 300-ms silent gaps. Two intervals contained silence and one interval, chosen at random, contained the test tone (signal). After each trial, the listeners were asked to choose the interval with the signal and respond via a computer keyboard or a mouse click. Feedback indicating the correct interval was provided immediately after the listener’s response. On the first trial the tone was presented at a clearly audible level. The level was decreased by 8 dB after two consecutive correct responses or increased by the same step after one incorrect response until two reversals were reached. The step was then reduced to 4 dB for the subsequent two reversals and to 2 dB for the final eight reversals. A track terminated after a total of 12 reversals and the threshold estimate was calculated by averaging signal levels at the last eight reversal points. Three single-run estimates were obtained for each frequency and the final threshold for each frequency and listener was computed as the mean of the three estimates.

During the experiment, listeners were seated in a double-walled sound-attenuating booth and the stimuli were presented monaurally to the left ear. All the stimuli were generated on a PC with a sampling rate of 48 kHz via a 24-bit LynxStudio Lynx22 sound card and routed to the left earphone of a Sennheiser HD 580 headset.

Listeners

Six listeners (2 males, 4 females) participated in the experiment. Their ages ranged from 18 to 56 years (median age 22 years). Their audiometric thresholds, tested using an ANSI certified audiometer (Madsen Conera), were below 15 dB HL for frequencies between 0.25 and 8 kHz in octave steps, indicating that all had normal hearing. The listeners signed informed consent prior to their participation and were paid for their services on an hourly basis. Listeners received extensive training using one selected pair of tones (usually 0.25 and 1 kHz) before data collection began. The protocol for all the experiments within this study was approved by the Institutional Review Board of the University of Minnesota.

Results

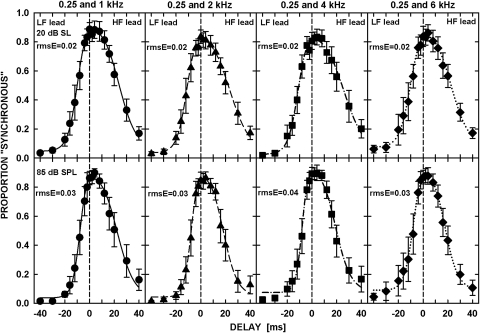
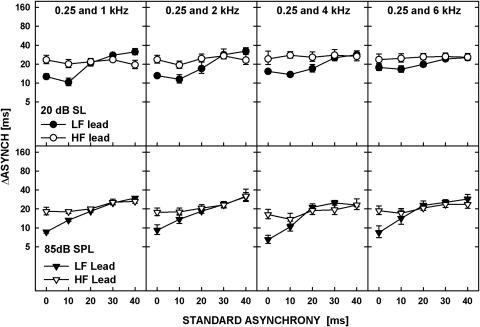
Despite some inter-individual variability, the overall patterns of results were similar, and thus data averaged across the six listeners are shown in Fig. 3. The top and bottom rows show data for the tones presented at 20 dB SL and at 85 dB SPL, respectively. Separate columns show data for different pairs of tones with frequencies specified above the top row of Fig. 3. Each panel shows the proportion of “synchronous” responses (symbols) plotted as a function of the delay between the tones in the pair. The negative delays represent stimuli with the LF tone leading and the positive delays represent the stimuli with the HF tone leading. The error bars represent 1 standard error of the mean.

Figure 3.

Proportion of “synchronous” responses averaged across six listeners (symbols) are plotted as a function of the delay between the tones. The negative values of the delay indicate low-frequency-tone lead, and the positive values indicate high-frequency-tone lead. The curves in each plot represent maximum-likelihood fits to the data (see text for details). The vertical dashed lines delineate a 0-ms delay between the tones. The upper panels show data for the tones at 20 dB SL, and the lower panels, for 85 dB SPL. Each column of panels is for a different frequency pair indicated above the upper panels.

For longer delays between the tones, the proportion of “synchronous” responses was very small, although it did not reach zero even when the LF tone was delayed by its full length (40 ms) so that it immediately followed the HF tone. As the delay between the tones decreased, the proportion of “synchronous” responses progressively increased, leading to a bell-shaped function. Simple visual inspection of the data suggested that the peaks of the functions were positioned close to the vertical dashed line representing the delay of 0 ms (i.e., simultaneous gating of the tones), with a slight tendency for a shift toward small positive delays, i.e., a small HF-tone lead. The results were generally similar for both tone levels used. In addition to the near-zero peak position, the data consistently showed asymmetry around the peak for all the tone pairs and at both presentation levels: The lower slope (LF leading) was steeper than the upper slope (HF leading).

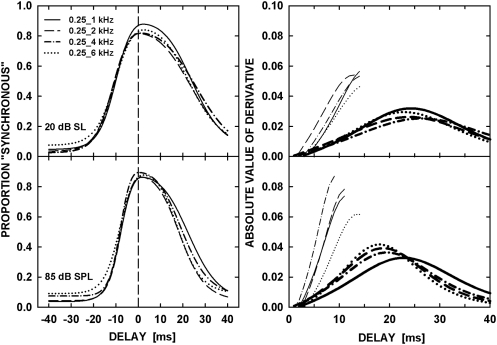
To quantify the observed effects, the average (and individual) data were fitted with a model, which is described in detail in the Appendix. The fits were obtained using a maximum-likelihood procedure with a binomial distribution (Wichmann and Hill, 2001; Dai and Micheyl, 2011). The maximum-likelihood fits are shown by the curves in Fig. 3. The accuracy of the fits was quantified by the root mean square error (rmsE) between the data and the model fits, shown in each panel. The fitted curves are replotted in Fig. 4, with all frequency separations on the same panel, for the low (upper left panel) and high (lower left panel) level, to illustrate the similarity of the synchrony judgments across the different frequency separations. The right panels of Fig. 4 show the absolute values of the derivatives of the fitted curves. To facilitate slope comparisons between derivatives corresponding to negative delays (which are indicated by thin curves) and derivatives corresponding to positive delays (thick curves), the former are reflected about the position of the peak. The points at which the derivative equals zero (i.e., the points at which the curves in these right-hand panels touch the x axis) correspond to the positions of the peak in the fitted curves shown on the left.

Figure 4.

Maximum-likelihood fits for all four frequency pairs are plotted in the left panels, for 20 dB SL (upper panel) and 85 dB SPL (lower panel). The absolute values of the derivatives of the fitted functions for the two levels are shown in the right panels, for the two levels. The values below the position of the tip in the derivative function were mirror-imaged about the position of the tip to help visualize differences between the slopes below and above the peak of the fits. The values of the derivatives corresponding to larger delays were removed to improve clarity of the plots.

The peak positions that were computed from the fits to the individual data (not shown) were subjected to a repeated-measures analysis of variance (ANOVA), with factors of frequency separation and level. Neither main effect, nor their interaction, was significant [Frequency separation: F(3,15) =1.758, p = 0.213; Level: F(1,5) = 0.062, p = 0.813; Interaction: F(3,15) = 1.354, p = 0.302]. Because of the lack of variation with frequency or level, the peak values were averaged across the eight conditions to produce an overall peak value for each subject. The mean of these values was 0.62 ms, which was not significantly different from zero [t(5) = 1.394, p = 0.222]. Thus, the point of maximum perceived synchrony did not vary with frequency separation or level and was not significantly different from zero (i.e., synchronous gating of the tones).

The steepness of the slopes on either side of the point of maximum perceived synchrony is determined in the model by the parameter α (see Appendix). A repeated-measures ANOVA on the log-transformed α values, derived from the fits to the individual data, revealed a significant effect of level [F(1,5) = 20.249, p = 0.006], but no significant effect of frequency separation [F(3,15) = 0.977, p = 0.413], and no interaction between the two factors [F(3,15) = 0.819, p = 0.458]. Inspection of Fig. 4 suggests that the effect of level reflects the fact the function is somewhat narrower at the higher (85 dB SPL) level than at the lower (20 dB SL) level, implying a slightly smaller range of delays that are perceived as being synchronous.

Finally, any asymmetry between the slope of the function at negative and positive delays is captured by the parameter β in the model (see Appendix). A repeated-measures ANOVA found no significant effect of level, frequency separation, or their interaction on the log-transformed β values taken from the fits to the individual data [Frequency separation: F(3,15) = 0.645, p = 0.501; Level: F(1,5) = 1.080, p = 0.346; Interaction: F(3,15) = 0.295, p = 0.747]. Because of the lack of variation with frequency or level, the asymmetry measures were averaged across the eight conditions to produce an overall asymmetry value for each subject. The geometric mean of these values was 2.12, which was significantly greater than unity, implying a significant asymmetry in the function [one-sample t-test on the average log-transformed β values: t(5) = 5.117, p = 0.004].

Thus, although the degree of asymmetry did not vary with frequency separation or level, it was significant, implying that LF-leading conditions were more readily identified as being asynchronous than HF-leading conditions with the same absolute delay.

Overall, the results suggest that the frequency-dependent group delays observed in the cochlea are not reflected in judgments of perceived synchrony, supporting the notion that there is a compensating mechanism at a higher stage of auditory processing (e.g., Uppenkamp et al., 2001).

EXPERIMENT 2: ASYNCHRONY DISCRIMINATION

The ability to detect a change in delay between stimuli exciting different regions of the cochlea was measured for the same tone pairs as in experiment 1. Previous studies have measured asynchrony detection (e.g., Zera and Green, 1993b; Mossbridge et al., 2006, 2008; Micheyl et al., 2010) and asynchrony discrimination (e.g., Zera and Green, 1993a). However, the contribution of within-channel cues to the results could not be ruled out because no effort was made to prevent the listeners from attending to the areas of overlapping excitation from different-frequency components while performing the tasks. In the present experiment, detection of changes in delay between two tones was measured for spectral separations of at least two octaves and in the presence of a band of noise between the tones, which was used to mask regions of potential overlap of excitation.

Stimuli and procedure

Detection of an increase in delay between two tones in a pair was measured using a 3I-3AFC procedure as a function of the baseline (standard) delay. In one condition, the low-frequency tone was delayed relative to the high-frequency tone (HF lead) and in another condition, the opposite direction of the delay was used (LF lead). As shown by the schematic illustration of the two conditions in Fig. 5, the two non-signal intervals contained a pair of tones with the same (standard) delay and the signal interval, chosen at random, had an increased delay between the tones. The standard delays used were 0, 10, 20, 30, and 40 ms. The observation intervals were separated by 500-ms gaps and were marked by lights on a computer screen. The listeners were instructed to choose the interval in which the timing between the tones was different from that in the other two intervals. The listeners responded via a keyboard or a mouse click. Feedback indicating the correct response was provided immediately after each response. The conditions (“LF lead” and “HF lead”) and the standard delays were tested in random order until all conditions had been tested once; then the conditions were repeated in a different random order. A total of three repetitions of each condition were run for each subject.

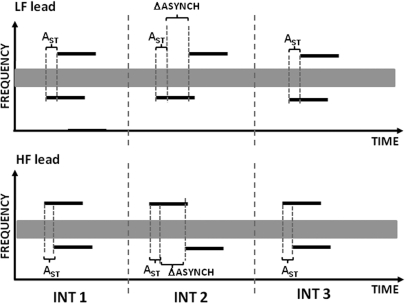
Figure 5.

Schematic illustration of the two types of runs in the experiment measuring detection of an increase in asynchrony using a 3I-3AFC procedure. The upper plot shows a run for the low-frequency-tone lead and the lower plot, for high-frequency-tine lead. When the standard asynchrony (A_ST) was equal to zero, the task is referred to as asynchrony detection. For a non-zero A_ST, the task is referred to as asynchrony discrimination.

As in experiment 1, a 250-Hz tone was paired with a 1-, 2-, 4-, or 6-kHz tone. The 3I-3AFC procedure was coupled with an adaptive 2-down, 1-up technique tracking the 70.7% correct point on the psychometric function (Levitt, 1971). The delay in the signal interval was always longer than that in the non-signal intervals and the increase in asynchrony, ΔASYNCH, in milliseconds was adaptively varied using multiplicative steps. At the beginning of a run, ΔASYNCH was large enough to be easily perceived. The value of ΔASYNCH was decreased by a factor of 2 after two consecutive correct responses and increased by the same step after one incorrect response, until two reversal points were obtained. The step size was then decreased to a factor of 1.41 for the next two reversals and to a factor of 1.19 for the final eight reversals. A run was terminated after a total of 12 reversals and the threshold from a single run was computed by geometrically averaging the values of ΔASYNCH at the last eight reversals. Because the values of ΔASYNCH appeared to be normally distributed on a log-time scale, the final threshold was calculated by geometrically averaging the three single-run estimates.

As in experiment 1, the tones had a duration of 40 ms including 10-ms squared-cosine onset/offset ramps, and two levels of 85 dB SPL and 20 dB SL were used. The noise bands used to mask potential areas of overlapping excitation on the BM were identical to those in experiment 1 except for their duration. In each condition, the noise started 300 ms before the first observation interval and continued throughout the trial, ending with the offset of the tone pair in the third observation interval. The equipment and the method of presentation (monaural to the left ear) were also the same as in experiment 1.

Listeners

The same six listeners who performed the subjective evaluations of the perceived synchrony/asynchrony in experiment 1 participated in this experiment. Listeners received about 2 h of practice before data collection began.

Results

The just-detectable changes in delay, ΔASYNCH, are plotted in Fig. 6. The data show geometric means of thresholds expressed in milliseconds from the six listeners. The top row shows data for the tones presented at 20 dB SL and the bottom row is for the tones at 85 dB SPL. Each column of panels corresponds to a different tone pair, as indicated in the legends in the upper panel. The filled and open symbols show thresholds in the LF-lead and the HF-lead conditions, respectively. The error bars represent the standard errors.

Figure 6.

Thresholds for detecting an increase in delay between two tones in a pair, averaged across six listeners are plotted as a function of the standard asynchrony. The data are plotted separately for the low-frequency tone leading (filled symbols) and the high-frequency tone leading (open symbols). The upper panels show data for the tones at 20 dB SL, and the lower, for 85 dB SPL. Different columns show data for different frequency pairs, shown in the legend of upper panels.

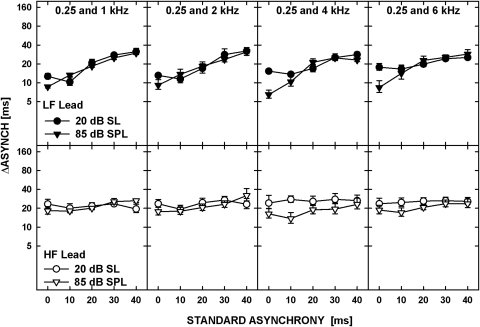
For convenience, the data for the standard delay of 0-ms will be referred to hereafter as thresholds for “asynchrony detection,” keeping in mind that simultaneous gating of the tones may not have led to the perception of simultaneity (as would be the case for uncompensated across-channel BM delays). The data corresponding to all the other values of standard delay will be considered as representing “asynchrony discrimination.” The data were analyzed using a repeated-measures ANOVA with the values of log-transformed ΔASYNCH as the dependent variable and the standard asynchrony, level, frequency order (LF lead versus HF lead), and frequency separation between the tones, as the main factors. Among the main factors, only the effect of standard asynchrony was significant [F(4,20) = 25.418, p < 0.001], reflecting the general increase in threshold with increasing standard asynchrony. The ANOVA showed no main effect of frequency separation [F(3,15) = 0.341, p = 0.796] and no significant interaction of frequency separation with frequency order [F(3,15) = 0.625, p = 0.610] or with the standard asynchrony [F(3.50,17.48) = 1.359, p = 0.211]. There was, however, a significant interaction between frequency separation and level [F(3,15) = 4.965, p = 0.014] and between frequency separation, level and frequency order [F(12,60) = 2.268, p = 0.019], reflecting a slight increase in thresholds for asynchrony discrimination with increasing frequency spacing in the LF-lead condition at 20 dB SL. Other significant interactions shown by the ANOVA were between the standard asynchrony and the frequency order [F(4,20) = 13.175, p < 0.001], reflecting the trend for the thresholds for the LF- and HF-lead conditions to converge at larger standard asynchronies, and between the standard asynchrony and level [F(4,20) = 5.822, p = 0.003], reflecting the trend for lower thresholds for asynchrony detection (data for a 0-ms delay) at 85 dB SPL than at 20 dB SL. The effects of level can be seen more clearly in Fig. 7, in which the data from Fig. 6 are replotted so the thresholds for the LF-leading and HF-leading conditions at both levels are shown in the top and bottom panels, respectively.

Figure 7.

Data replotted from Fig. 6. The upper panel shows the data for the low-frequency tone leading, for two levels of the tones, 20 dB SL (circles) and 85 dB SPL (triangles). Lower panels show the data for the high-frequency tone leading. Each column is for a different frequency pair as shown by the legends in the upper panels.

The data in Fig. 6 show that at a 0-ms delay, thresholds for the LF-tone leading were consistently lower than those for the HF-tone leading. To test the significance of the difference between asynchrony-detection thresholds in the LF- and HF-lead conditions, an ANOVA was performed using log-transformed thresholds for the 0-ms delay as the dependent variable and the tone order (LF versus HF), frequency separation, and level as the main factors. The ANOVA showed that thresholds in the LF-lead condition were significantly lower than those for the HF-lead condition [F(1,5) = 12.665, p = 0.016]. There was a significant effect of level indicating that asynchrony-detection thresholds were lower at 85 dB SPL than at 20 dB SL [F(1,5) = 16.152, p = 0.010]. In contrast to the previously published studies, which showed an increase in asynchrony detection thresholds with increasing frequency separation between different components (Parker, 1988; Zera and Green, 1993a; Mossbridge et al., 2006), the data for the 0-ms delay showed no effect of frequency separation [F(3,15) = 0.300, p = 0.825]. The lack of the effect of frequency separation on asynchrony detection in our study may be due to the use of large frequency separations between the tones and the presence of noise masking the areas of overlapping excitation, which both reduced the availability of within-channel cues.

EXPERIMENT 2 A: EFFECT OF PHASE ON ASYNCHRONY DETECTION

In the design of the stimuli for this study and in the model presented in the Appendix, an implicit assumption was that in the absence of within-channel cues, listeners use the relative timing between the internal representations of the temporal envelopes of the tones to make decisions about synchrony/asynchrony. Intuitively, this is likely the case at higher frequencies where phase-locking involved in encoding fine structure of the stimuli becomes less reliable (Kim and Molnar, 1979). However, for a 250-Hz tone used in our experiments, the fine structure is strongly represented in the auditory-nerve responses and the timing of the phase-locked neural spikes could affect the timing of the perceived onset/offset. To test for the potential effect of temporal fine structure on the results, the detection of asynchrony between two tones was measured for different values of the starting phase of the 250-Hz tone.

Stimuli and procedure

Thresholds for the detection of asynchrony were measured for a pair consisting of 250 Hz and 4 kHz, for three values of the starting phase of the 250-Hz tone, 0°, 90°, and 180°. The 3I-3AFC procedure and the adaptive tracking technique were identical to those used in experiment 2. Since only asynchrony detection was measured, the delay between the tones in the non-signal intervals was 0 ms. In separate blocks, the 250-Hz tone was delayed relative to the 4-kHz tone or vice versa. The 4-kHz tone always started in a sine (0°) phase. The gating and the duration of the tones were the same as in experiment 2. The tones were presented at 85 dB SPL. All the other experimental details, including the masking noise and the apparatus, were the same as in experiment 2.

Listeners

Four out of the six listeners who participated in experiment 2 were recruited to participate in this control experiment. The listeners were considered well-practiced so the data collection commenced without any additional training. Although the listeners performed asynchrony detection for the 250-Hz tone starting at a 0° phase in experiment 2, this condition was re-run to make sure no significant changes in performance occurred between the two experiments.

Results and discussion

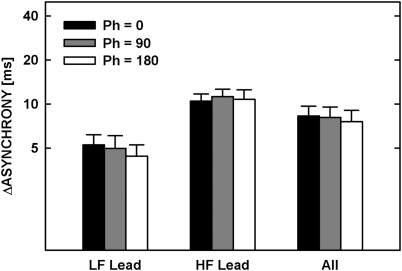
Figure 8 shows thresholds averaged across the four listeners. The bars denoted by “All” represent thresholds averaged across LF-lead and HF-lead conditions. No systematic variation in asynchrony-detection threshold as a function of the 250-Hz tone starting phase was observed in either condition. A repeated-measures ANOVA with the starting phase and the frequency order as the main factors showed that the effect of the starting phase was not statistically significant [F(2,6) = 3.040, p = 0.123]. Consistent with the results of experiment 2, asynchrony detection was significantly better when the LF tone was leading [F(1,3) = 11.987, p = 0.041]. There was no significant interaction between the starting phase and the frequency order [F(1.22,3.66) = 0.339, p = 0.636]. The lack of a main effect of, or interaction with, starting phase is consistent with the hypothesis that the temporal-envelope rather than fine-structure cues were used when comparing the relative timing of remote-frequency tones, or at least that differences in perceived timing produced by changes in the temporal fine structure were too small to produce a reliable effect on thresholds.

Figure 8.

Thresholds for detecting asynchrony between 250-Hz and 4-kHz tones averaged across four listeners. Different bars show thresholds for different starting phases of the 250-Hz tone, as described in the legend. Different set of bars show mean thresholds for the LF-lead and HF-lead conditions, and for the data from both conditions (All).

MODEL PREDICTIONS FROM SIGNAL DETECTION THEORY

The results of experiments 1 and 2 are in qualitative agreement with each other: steeper slopes of synchronous-response functions when the LF tone was leading in experiment 1 corresponded to smaller thresholds for asynchrony detection when the LF tone was leading in experiment 2. However, due to the fact that these data were obtained using very different tasks (one-interval identification versus three-interval discrimination), direct quantitative comparisons between the data of the two experiments are difficult. In order to meaningfully relate the results of the two experiments, we transformed the proportions of “synchronous” judgments measured in experiment 1 into d′, Green and Swets, 1966), providing a measure of the discriminability of the asynchrony from no asynchrony. We then used the results to compute “predicted” thresholds corresponding to a d′ of 1.26, the d′ value corresponding to the 70.7%-correct thresholds measured using the 3I-3AFC task in experiment 2.

The model, on which our d′ calculations in the first step were based, is described in detail in the Appendix. The model was used to fit the proportion of “synchronous” responses measured in experiment 1 (see example in Fig. 9, top panel). The results of these fits were used to compute d′ as a function of delay. Finally, interpolation was used to find the threshold for asynchrony detection (based on a 0-ms reference) corresponding to d′ = 1.26 (see example in Fig. 9, bottom panel). As shown by the vertical arrows in the bottom panel of Fig. 9, for this listener and condition, the model predicted asynchrony-detection thresholds of 4.9 ms in the LF-lead condition, and 14.5 ms in the HF-lead condition. This was done separately, for each listener and each of the conditions tested in experiment 1.

Figure 9.

The psychometric function (line) fitted to the data (symbols) of one listener (upper panel) and the d′ function (lower panel) obtained from the SDT-based model. The vertical dashed line in the upper panel represents the position of the peak in the psychometric function. The horizontal dashed line in the lower panel represents d′ = 1.26, and the vertical arrows point to the delays representing asynchrony-detection thresholds predicted by the model.

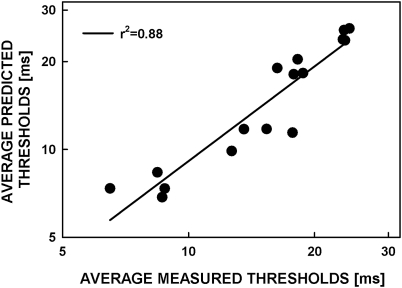
Figure 10 shows asynchrony-detection thresholds predicted by the model plotted against the thresholds observed in experiment 2 for the 0-ms standard asynchrony. In both cases, geometric means were computed for the six listeners. The predicted and observed thresholds were highly correlated with each other (Pearson correlation coefficient for the mean across 6 listeners of the log-transformed predicted thresholds and of the corresponding log-transformed observed thresholds, across the 16 test conditions: r = 0.94, r²= 0.88, p < 0.0001, n = 18). The linear regression function, shown by the line in Fig. 10, had a slope of 1.08 indicating a very good quantitative agreement between the model predictions and the data. Indeed, the results of a repeated-measures ANOVA comparing the log-transformed predicted and observed thresholds showed no significant difference [F(1,5) = 0.447, p = 0.533].

Figure 10.

Thresholds for the detection of asynchrony predicted from subjective asynchrony judgments plotted versus the thresholds measured in the 3I-3AFC asynchrony-detection task. The latter correspond to the (geometric) mean thresholds measured in the 0-ms-delay-standard condition of Experiment 2, while the former were computed, using the signal-detection-theory model described in the Appendix, based on the subjective judgments of synchrony measured in Experiment 1.

These model outcomes demonstrate a strong degree of quantitative agreement between the results of the two experiments, and they support the idea that the results from these two experiments reflect the same underlying perceptual mechanisms.

DISCUSSION

Relationship between BM latencies and across-frequency synchrony perception

Based on physiological evidence from animal and human studies, the latency of the BM response to the 250-Hz tone is expected to be greater than the latency of the response to each of the higher-frequency tones paired with it in our two experiments. If the across-channel timing of BM responses were preserved at all stages of auditory processing, the perception of synchrony of each two-tone complex would require delaying the high-frequency tone by an interval mirroring the difference in BM latency for the two frequencies. Thus, in the absence of a central mechanism compensating for differences in across-channel cochlear delays, the peak of the function relating the proportion of “synchronous” responses to the delay between the tones in Fig. 3 should correspond to a negative delay (LF lead) for all the tone pairs tested. An alternative scenario, put forth by Uppenkamp et al. (2001), proposes a higher-level mechanism that compensates for cochlear across-channel delays. Such a mechanism would predict that peaks of the functions in Fig. 3 should correspond to simultaneous gating of the tones, i.e., a 0-ms delay, irrespective of their frequency separation. As shown by the position of the zero value in the derivative functions in Fig. 4 (right panel), the position of the peak in the functions fitted to the data (Fig. 3) was nearly the same for all the tone pairs, but it did not correspond to a negative delay. Instead, the maximum proportion of “synchronous” responses was close to a 0-ms delay between the tones, with a small shift toward positive delays that did not reach statistical significance. The position of the peak was robust to the frequency separation and level of the tones, suggesting that regardless of level, the neural transmission of low frequencies is accelerated compared with that of frequencies above 1 kHz resulting in veridical perception of across-frequency timing. In other words, the data suggest that at the input to the decision stage, the relative timing of neural responses to low versus high frequencies does not reflect the relative timing of the BM responses.

The results from experiment 2 cannot be interpreted as directly in terms of BM delay. Taken in isolation, the fact that LF-leading conditions led to lower asynchrony detection thresholds than the HF-leading conditions might be interpreted as supporting the idea that the perceptual latency for LF tones is longer than that for HF tones, in line with expectations based on frequency-dependent BM latencies. However, this interpretation is not consistent with the results of experiment 1. In fact, as shown by the modeling, the results from experiment 2 are also consistent with alignment of latencies at the perceptual level.

A comparison of the synchronous-response functions in Fig. 3 and the data in Fig. 5 of the study by Uppenkamp et al. (2001) reveals interesting similarities when the differences between the slopes on both sides of the peak are considered. The listeners of Uppenkamp et al. compared the compactness of rising and falling chirps of the same duration, for durations up to about 20 ms. As the duration of the chirp increased, the delay between the lowest and highest frequency in the chirp increased but, unlike the pairs of tones used in this study, their stimuli swept through all intervening frequencies. Despite this important difference, the perceived compactness decreased more for a given increase in the duration of the rising chirp (and thus a given increase in delay of the highest relative to the lowest frequency in the chirp) than it did for the same increase in duration of the falling chirp. Uppenkamp et al. explained their results in terms of the within-channel interactions between the direction of the frequency glides in the stimuli and the glides in the impulse responses of BM filters (e.g., Carney et al., 1999). However, given the similarity of their results and the results of our experiment, which precluded within-channel cues, it is possible that the findings of Uppenkamp et al. also reflect across-channel processing.

The asymmetric shape of the synchronous-response function in experiment 1 can account for higher thresholds for asynchrony-detection observed for the HF-tone leading than for the LF-tone leading in experiment 2. This dependence of sensitivity to asynchrony on the frequency order resembles the asymmetry in timbre-discrimination thresholds reported by Patterson (1987) for stimuli with monotonic phase increases/decreases applied to successive harmonics. Thresholds for detecting a timbre difference were larger when the comparison was made between a complex with all harmonics starting in cosine phase and a complex in which the starting phases of the lower-frequency components were monotonically delayed with decreasing harmonic number (and thus, decreasing frequency) than when the cosine-phase complex was compared with a complex with a reversed direction of the monotonic phase shift. Patterson reported that the difference in threshold for timbre discrimination between the two conditions was statistically significant. His result is consistent with the higher asynchrony-detection thresholds observed in the HF- than LF-lead condition, suggesting that performing both tasks involved using across-channel cues.

Envelope versus fine-structure timing cues

The implicit assumption of this study was that listeners compare the relative timing between tones that are remote in frequency by using the timing between the neural representations of the envelopes. Because of this assumption, the envelopes were identical for all the tones used. For a 250-Hz tone, the auditory-nerve responses are strongly phase-locked to the fine structure but the starting phase of the 250-Hz tone paired with a 4-kHz tone had no effect on detecting asynchrony between the tones. This result supports the use of the temporal envelope as a reasonable approximation of the neural response to a tone-burst for the purposes of synchrony perception. The 10-ms ramp used for all the tones likely resulted in energy splatter around 250 Hz, although no audible clicks were present at the onset and offset of the 250-Hz tone. Spread of energy toward higher frequencies could have resulted in a decreased difference in response latency between the 250-Hz tone and the higher-frequency tones. To minimize differences in spectral splatter, Neely et al. (1988) used longer ramps for low-frequency tones than for higher-frequency tones when estimating BM latency-frequency function from measurements of ABR responses and otoacoustic emissions. Recently, Ruggero and Temchin (2007) argued that the use of different ramp durations by Neely et al. contributed to artificially large differences in latency across frequency. Ruggero and Temchin based their criticism on physiological data showing that first spike latencies in neural responses show strong dependence on stimulus ramp duration (e.g., Heil and Irvine, 1997). In addition, the effect of stimulus level on first spike latency has been shown to vary depending on ramp duration (Kitzes et al., 1978; Heil and Irvine, 1997). Ruggero and Temchin (2007) argued that using constant ramp duration across frequencies, as was done in the present experiments, is the most appropriate design for experiments in which effects of BM response latencies across frequencies are measured.

Effects of frequency separation on asynchrony detection

Studies of BM latency suggest that the differences in latencies are relatively small at high frequencies. Therefore, we did not expect to find BM-related differences between the pairs of frequencies we used, because all our HF tones were at or above 1 kHz (see Fig. 1). In line with expectations, no differences in the peak of the synchrony perception function were observed between the different tone pairs (Figs. 34).

Previous studies have suggested that across-frequency asynchrony detection deteriorates with increasing frequency separation between the test stimuli (Parker, 1988; Zera and Green, 1993a; Mossbridge et al., 2006). Our findings do not support this conclusion: the synchrony perception function did not broaden (Fig. 4) and asynchrony detection thresholds did not worsen (Fig. 6) with increasing frequency separation. The apparent discrepancy between our results and those of previous studies may be because the earlier conclusions were based on experiments using stimuli for which within-channel cues were potentially available. For smaller frequency separations, listeners might have detected an increment in the envelope of the stimulus at the output of the channels excited by different components of the stimuli when the delayed components were added. This cue could be more effective than the relative-timing cue (e.g., Oxenham, 2000), and thus could dominate performance for close frequency spacing. The cue would become less salient and possibly unavailable as the frequency separation increased (and thus the possibility for within-channel interaction decreased). The poorer asynchrony-detection thresholds may therefore have reflected a decreasing contribution of within-channel cues with increasing frequency separation. In the present study, large frequency separations and the use of noise bands positioned spectrally between the test tones prevented within-channel cues. An analysis of the transfer characteristics of the level-dependent gammachirp (Irino and Patterson, 1997) filters suggested that the frequency separation between our tones and the masking noise made the possibility of using within-channel cues unlikely.

Asynchrony detection versus discrimination

Our results support earlier conclusions that asynchrony detection is generally better than asynchrony discrimination (Mossbridge et al., 2006; Micheyl et al., 2010). It has been argued that asynchrony detection may involve broadly tuned coincidence-detection mechanism, encountered as early as in the cochlear nucleus (Palmer and Winter, 1996), whereas asynchrony discrimination may involve more complex timing comparisons, which could explain why thresholds for asynchrony discrimination are larger than thresholds for asynchrony detection. However, in our data, clear differences between asynchrony-detection and asynchrony-discrimination thresholds were found only for cases in which the LF tone led in the asynchronous interval, particularly at the higher sound level; for the HF-tone leading conditions, thresholds remained roughly the same for all baseline values of asynchrony, including zero (Fig. 7). Again, the difference between our results and those of previous studies may be due to the fact that within-channel cues were likely eliminated in our experiments. Within-channel cues may permit asynchrony detection through a change in the envelope near the onset (and offset) of the composite waveform. For asynchrony discrimination a more complex task involving comparisons of the relative timing of the changes in the envelope would be expected to produce higher thresholds.

Our finding of roughly constant thresholds for larger values of baseline asynchrony (and for all values of baseline asynchrony for the HF-leading conditions) is in line with the results of Zera and Green (1993a), who found that detecting an asynchrony of one component did not depend on the amount of asynchrony between the components of a complex tone. Both our results and those of Zera and Green do not follow Weber’s law, which predicts that thresholds should be proportional to the baseline asynchrony. Alternative decision rules, such as considering the overall duration of the composite stimulus, also produce no simple relationship between thresholds and baseline differences.

Effects of level

The reported effects of level on the BM latency-frequency function measured indirectly using non-invasive techniques in humans are inconsistent across studies. The latency-frequency functions estimated using otoacoustic emissions or ABR responses become shallower with increasing stimulus level (Neely et al., 1988; Schoonhoven et al., 2001; Sisto and Moleti, 2007). In contrast, Ruggero and Temchin (2007) argued that stimulus level has very little effect on the BM latency-frequency function and the effect is to slightly increase across-frequency latencies at high levels. The synchronous-response functions from experiment 1 showed that the position of the peak did not change when the level of the stimuli was increased from 20 dB SL to 85 dB SPL. However, the synchronous-response functions were wider, i.e., the slopes of the functions on both sides of the peak were shallower, for the 20-dB SL than for the 85-dB SPL tones. In agreement with the broader synchronous-response distribution, asynchrony-detection thresholds were higher at the lower level (Fig. 7).

The synchronous-response functions in the top left panel of Fig. 4 also exhibit a smaller difference between the slopes below and above the peak compared with those in the bottom left panel of Fig. 4, thus predicting a smaller difference between thresholds in the LF- lead and HF-lead conditions, for the 20-dB SL than the 85-dB SPL tones. Although the difference between asynchrony detection in the two conditions was significant at both levels, the data for a 0-ms delay in Fig. 6 are consistent with this prediction of the difference being smaller for the 20-dB SL tones than for the 85-dB SPL tones. In summary, changes in the pattern of results with level in experiment 1 are consistent with the changes in asynchrony-detection thresholds with level observed in experiment 2.

The changes in the width of the distribution of synchronous responses, and in asynchrony-detection thresholds with level, may reflect level-dependent changes in the distribution of neural responses to onsets at central sites of auditory processing. Physiological evidence suggests that distributions of first-spike latencies in neurons that likely encode onsets in the cochlear nucleus become sharper with increasing level (Kitzes et al., 1978). Sharpening of the distribution of first-spike latency suggests more precise coding of information received by putative coincidence detectors, for high-level tones. However, with no direct physiological measures of neural response to the specific stimulus configurations used in the present experiments, the possible neural bases remain conjectural.

Possible origins of the asymmetry in temporal synchrony judgments and thresholds

Both experiments provide consistent evidence for an asymmetry between LF-leading tone pairs and HF-leading tone pairs, whereby LF-leading tone pairs are less likely to be perceived as synchronous, and more likely to be discriminated from a truly synchronous tone pair, than HF-leading tone pair with the same absolute delay. The origins of this novel perceptual asymmetry are unclear. One possibility is that the asymmetry reflects a form of adaptation to the statistics of natural sounds, as determined by the physics of sound generation and transmission through resonant structures, such as the human vocal apparatus. Low-frequency resonators typically have a longer impulse response, and thus longer latency, than high-frequency resonators with the same quality factor (Q). This is because the absolute bandwidth (in Hz) of low-frequency resonators is usually smaller, leading to a longer latency in a minimum-phase system (e.g., Shera et al., 2010). Thus, broadband sounds that are generated synchronously may end up with the low-frequency portions lagging the high-frequency portions (depending on the transmission path of the sound), but the opposite will rarely occur. It may be, therefore, that our auditory system is more tolerant of low-frequency delays than of high-frequency delays, because the low-frequency delays are more likely to occur in natural environments.

An analogy of this argument can be found in human perceptual judgments of the synchrony between auditory and visual stimuli. Observers are more likely to judge a visual stimulus leading an auditory stimulus as being synchronous than they are to judge an auditory stimulus leading a visual stimulus (e.g., van Eijk et al., 2008), presumably because light travels faster than sound and so light-leading asynchronies are much more common in the natural environment than are sound-leading asynchronies.

Although this explanation based on natural sound occurrences has some appeal, we are not aware of any demonstrations that the time scale of asynchronies in natural acoustic environments match those found in the present experiment. Furthermore, there are as yet no fully explored neural correlates for this effect in the auditory system.

SUMMARY AND CONCLUSIONS

The role of the frequency-dependent BM-response latency in the perception of relative timing between spectrally remote tones was investigated using two different psychoacoustic tasks. The tones were paired so that their BM-response latencies were expected to differ, based on physiological estimates in laboratory animals and electrophysiological and otoacoustic-emission measurements in humans. In experiment 1 the proportion of “synchronous” responses was measured as a function of the delay between the two tones. Since the task involved subjective judgments, the listeners were given no feedback. In experiment 2 the listeners detected an increase in delay between tones in a pair and correct-response feedback was provided. The results can be summarized as follows.

In experiment 1, a LF and HF tone tended to be judged most synchronous when they were gated synchronously. The position of the peak in the synchrony judgment function remained roughly constant for different pairs of frequencies (with the lower frequency fixed at 250 Hz) and for the two levels tested (20 dB SL and 85 dB SPL). The distribution of synchronous and asynchronous judgments was asymmetric, with the LF-leading pairs being judged as asynchronous more often than the HF-leading pairs for the same physical delay. The distribution of responses did not vary across the range of frequency separations tested, but became narrower overall at the higher of the two stimulus levels tested. There are currently no obvious neural correlates that can explain this perceptual asymmetry between the LF- and HF-leading tones and its level dependence, although they may result from properties of the natural acoustic environment.

In experiment 2, asynchrony detection thresholds were typically lower for the LF-tone leading conditions than for the HF-tone leading conditions. Several key features of the detection and discrimination results, including the difference of asynchrony-detection thresholds between the LF- and HF-leading pairs, the lack of effect of frequency separation and the effects of stimulus level, could be explained quantitatively using a simple SDT model with parameters fitted to the data from experiment 1. The success of the model suggests a link between perceived asynchrony and performance in asynchrony detection and discrimination tasks.

Overall, the results suggest that the frequency-dependent group delay produced by cochlear filtering is compensated for at a higher processing level, resulting in veridical perception of across-frequency synchrony.

APPENDIX: A SIGNAL-DETECTION-THEORY MODEL OF ASYNCHRONY DETECTION

This appendix details the mathematical model that was used to relate quantitatively the proportions of “synchronous” judgments measured in experiment 1 to the asynchrony-detection thresholds measured in experiment 2. The main assumptions of the model are as follows.

• (1)Listeners’ judgments in the two experiments were based on perceived differences between the onset times of the two (low- and high-frequency) tones presented in a trial. We denote these onset times t₁ and t₂, where the subscript refers to the temporal position of the corresponding tone (first or second). Note that we use onset times, because onsets are known to play a dominant role in asynchrony-detection tasks (Zera and Green, 1993b; Mossbridge et al., 2006). However, this choice entails no loss of generality; the model would work equally well, and its predictions would be unchanged, if another metric, such as tone-offset times, were used instead of the differences in onset times. The perceived difference between the tone onset times is represented as a unidimensional random variable, Δ.
• (2)Conditioned on a given difference, δ, between the physical tone onset times, where,

$$\delta =t_2-t_1,$$ (A1)

the variable, Δ, has a Gaussian distribution with a constant standard deviation of σ, and an expected value that depends non-linearly on δ, as given by

$$E[\Delta (\delta )]=e^{{[\delta -{\delta }_0/\alpha ]}^2}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\mathrm{if}\hspace{1em}\delta -{\delta }_0<0,$$ (A2)

and

$$E[\Delta (\delta )]=e^{{[\delta -{\delta }_0/\beta \alpha ]}^2}\mathrm{\hspace{1em}\hspace{1em}\hspace{1em}}\mathrm{if}\hspace{1em}\delta -{\delta }_0\ge 0,$$ (A3)

where the dependence of Δ on δ is made explicit.

The variable, δ₀, is introduced to account for the possibility that, due to delays of cochlear (or some other) origin, a physical onset asynchrony of 0 ms may not correspond to a zero perceived onset asynchrony, even in the absence of any internal noise. The “scale” parameter, α, controls the rate at which the value of the exponential arguments in Eqs. A2, A3 increase with the magnitude of the difference between the physical onset times; α is inversely related to this rate. The coefficient, β, makes it possible for this rate to differ, depending on the sign (or direction) of the perceived difference; values of β larger than 1 imply a faster rate for “negative” perceived differences—which correspond to the situation in which the low-frequency tone was perceived as leading—than for “positive” perceived differences—which correspond to the situation in which the low-frequency tone was perceived as lagging.

Since, as mentioned above, the standard deviation of Δ was constant and equal to σ, the index of detectability of signal detection theory, d′, which is traditionally defined as the standardized distance between the expected values of the two conditional probability distributions corresponding to the two alternatives being discriminated in a yes-no task, is related to Δ(δ) by,

$$d\text{'}(\delta )=\frac{\Delta (\delta )}{\sigma }.$$ (A4)

The probability of a “synchronous” response corresponds to the probability that the perceived onset-time difference falls below the listener’s decision criterion, c, i.e.,

$$P_s(\delta )=\Phi (c-d\text{'}[\delta ]),$$ (A5)

where Φ denotes the cumulative standard normal function.

The model described by Eqs. A1, A2, A3, A4, A5 was used to fit the proportions of synchronous judgments measured in each listener using a maximum-likelihood procedure. The number of “synchronous” responses corresponding to a given P_s(δ) was assumed to be distributed according to a binomial distribution with the parameter n (number of trials) set to 100, the number of trials per delay condition per listener in experiment 1 (Wichmann and Hill, 2001; Dai and Micheyl, 2011). The negative logarithm of the likelihood of the data given the model was minimized using MATLAB’s (The MathWorks, Natick, MA) fminsearch function, which implements the Nelder-Mead simplex algorithm.

Figure 9 shows a representative example of best-fitting psychometric function [P_s(δ), upper panel] and corresponding d′(δ) function (lower panel) for one particular listener and test condition. The d′(δ) functions, which were computed separately for each listener and each condition, were used to compute “predicted” asynchrony-detection thresholds, which could be directly compared to those measured in experiment 2. This was achieved by interpolating each obtained d′(δ) function to find the abscissas (physical delays) of the points at which d′(δ) intersected the horizontal line representing d′ = 1.26 corresponding to 70.7% in the 3I-3AFC task that was used in experiment 2.