Normalization as a canonical neural computation

Abstract

There is increasing evidence that the brain relies on a set of canonical neural computations, repeating them across brain regions and modalities to apply similar operations to different problems. A promising candidate for such a computation is normalization, in which the responses of neurons are divided by a common factor that typically includes the summed activity of a pool of neurons. Normalization was developed to explain responses in the primary visual cortex and is now thought to operate throughout the visual system, and in many other sensory modalities and brain regions. Normalization may underlie operations such as the representation of odours, the modulatory effects of visual attention, the encoding of value and the integration of multisensory information. Its presence in such a diversity of neural systems in multiple species, from invertebrates to mammals, suggests that it serves as a canonical neural computation.

The brain has a modular design. The advantages of modularity are well known to engineers: modules that can be replicated and cascaded, such as transistors and web servers, lie at the root of powerful technologies. The brain seems to apply this principle in two ways: with modular circuits and with modular computations. Anatomical evidence suggests the existence of canonical microcircuits that are replicated across brain areas, for example, across regions of the cerebral cortex^1,2. Physiological and behavioural evidence suggests that canonical neural computations exist — standard computational modules that apply the same fundamental operations in a variety of contexts. A canonical neural computation can rely on diverse circuits and mechanisms, and different brain regions or different species may implement it with different available components.

Two established examples of canonical neural computations are exponentiation and linear filtering. Exponentiation, a form of thresholding, operates at the level of neurons and of networks³ — for example, in the mechanism that triggers eye and limb movements^4–6. This operation has multiple key roles: maintaining sensory selectivity⁷, decorrelating signals⁸ and establishing perceptual choice^9,10. Linear filtering (that is, weighted summation by linear receptive fields) is a widespread computation in sensory systems. It is performed, at least approximately, at various stages in vision¹¹, hearing¹² and somatosensation¹³. It helps to explain a vast number of perceptual phenomena¹⁴. It may also play a part in sensorimotor¹⁵ and motor systems¹⁶.

A third kind of computation has been seen to operate in various neural systems: divisive normalization. Normalization computes a ratio between the response of an individual neuron and the summed activity of a pool of neurons. Normalization was proposed in the early 1990s to explain non-linear properties of neurons in primary visual cortex^17–19. Similar computations²⁰ had been proposed previously to explain light adaptation in retina^21–24, size invariance in the fly visual system²⁵ and associative memory in the hippocampus²⁶. Evidence that has accumulated since then suggests that normalization plays a part in a wide variety of modalities, brain regions and species.

Here, we review this evidence and suggest that normalization is a canonical neural computation in sensory systems and possibly also in other neural systems. We introduce normalization by describing results from the olfactory system of invertebrates. We then describe its operation in retina, in primary visual cortex, in higher visual cortical areas and in non-visual cortical areas, and discuss its role in sensory processing and in the modulatory effects of attention. Finally, we review the multiple mechanisms and circuits that may be associated with normalization, and the behavioural measurements that are captured well by normalization. Two independent sections define the basic elements of the normalization equation and the many roles that have been proposed for normalization in relation to optimizing the neural code.

Normalization in the invertebrate olfactory system

The fruitfly (Drosophila melanogaster) senses odours through receptor neurons, each of which expresses a single odorant receptor. Receptor neurons project to the antennal lobe, a brain region that is analogous to the olfactory bulb in vertebrates. The response R of an antennal lobe neuron increases with the activity I of the receptor neurons that drive it²⁷:

$$R=\gamma \frac{I^n}{{\sigma }^n+I^n}$$ (1)

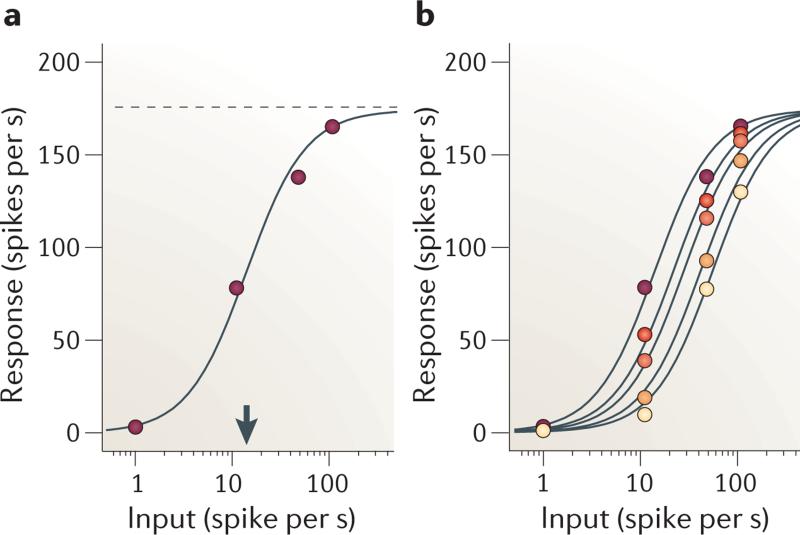
The parameters γ, σ and n determine the shape of the response curve (FIG. 1a). A mask odorant that does not drive an antennal lobe neuron nonetheless suppresses the responses to a test odorant that does drive the neuron (FIG. 1b). The interaction of the two odorants is accurately described²⁷ by the normalization equation:

$$R=\gamma \frac{I^n}{{\sigma }^n+I_m^n+I_n}$$ (2)

Here, I is the response of receptor neurons that drive the antennal lobe neuron (which responds to the test odorant), and I_m are the pooled responses of the other receptor neurons (which respond to the mask odorant). As I_m appears as an additive term in the denominator, increasing it has the same effect as increasing σ in equation 4: it shifts the response curve to the right on a logarithmic scale (FIG. 1b).

Figure 1. Normalization in the olfactory system of the fruitfly.

a | Responses of olfactory neurons in the antennal lobe to a single test odorant, as a function of activity in the presynaptic receptor neuron. γ and σ are constants (shown by the dotted line and the arrow). b | Responses of olfactory neurons in the antennal lobe to test odorant in the presence of mask odorants of increasing concentration (lower concentrations are shown by lighter colours). Curves are fits of the normalization model (equation 5), with I_m free to vary with mask concentration. Data from REF. 27.

Normalization in the retina

The retina needs to operate in a wide range of light intensities. Across visual environments (for example, an overcast night and a sunny day) light intensities range over 10 factors of 10 (REFS 28,29). Within a given visual scene the variation is typically smaller, but still more than a factor of 10 (REF. 30). The retina uses anatomical solutions (rod and cone photoreceptors and an adjustable pupil) for some of this wide range. For the rest of the range, light adaptation adjusts the sensitivity of neurons through normalization (FIG. 2a), resulting in responses that represent contrast (deviations from the mean over recent time and local space) rather than absolute intensities.

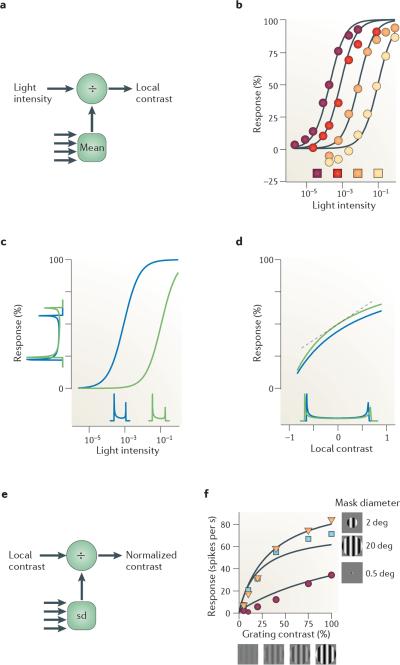
Figure 2. Normalization in retina.

a | Light adaptation operates on light intensity to produce a neural estimate of contrast (multiple arrows indicate light intensities from multiple locations). b | Responses of a turtle cone photoreceptor to light of increasing intensity. The intensity of the coloured squares reflects background intensity. Curves are fits of normalization model (equation 5) with n = 1. c | Light adaptation moves the operating point to suit images of differing intensity. Histograms on abscissa indicate distributions of light intensity for a sinusoidal grating under dim illumination (shown in blue) and bright illumination (shown in green). Histograms on ordinate indicate distributions of responses, which are more similar to one another than the light intensity distributions. d | The same data as in part c | plotted as a function of local contrast (Weber contrast) rather than light intensity. Light adaptation makes responses roughly proportional to local contrast. The linear approximation given by equation 6 is shown (indicated by the dotted line). e | Contrast normalization operates on the neural estimate of contrast and normalizes it with respect to the standard deviation (sd) of nearby contrasts (multiple arrows indicate local contrast from multiple locations). f | Effects of contrast normalization. Responses of a neuron in lateral geniculate nucleus (which receives input from the retina) as a function of grating contrast and size. deg, degrees. Data in part b, from REF. 24. Data in part f, from REF. 40.

Photoreceptor responses increase with the intensity of a stimulus (FIG. 2b). Their sensitivity (the position of the intensity–response curve on the intensity axis) depends on background light intensity^{22–24,31,32} (FIG. 2b). Increasing background intensity shifts the response curve to the right on a logarithmic axis^23,24,31,32, placing the steepest portion of the curve (where the cell is most sensitive to changes) near the background intensity (FIG. 2b). As with a mask odorant in insect olfaction, equation 5 fits this effect well. Here, the background intensity constitutes the additive term I_m in the denominator, and the exponent n is 1.

Normalization makes photoreceptors adjust their operating point to discount mean light intensity (FIG. 2c). For example, consider two images differing only by a scaling factor (for example, because of different illumination³³). Their distributions of light intensities are shifted laterally on a logarithmic axis (FIG. 2c). Normalization makes the photoreceptor responses shift accordingly, so that the responses to both images are similar³⁴.

This adjustment of sensitivity approximates a neural measure of visual contrast (FIG. 2c,d). If background light is sufficiently high (I_m >> σ), equation 5 can be rewritten (through a Taylor series) as:

$$R-R_m\alpha C$$ (3)

Here, R_m is the response to the background light I_m. C is local contrast, the relative deviation of local light intensity from the mean:

$$C=(I-I_m)∕I_m$$ (4)

The approximation in equation 6 assumes that local contrast C is moderate (so that C² and higher can be ignored). This condition is often met in natural scenes, in which local contrast is typically low³⁰.

The key factor in determining local contrast is the spatial and temporal scale over which one computes the mean light intensity I_m. Computing it over a scale that is too wide or long would entail large deviations from the mean, so equation 6 would no longer apply and light adaptation would no longer provide a measure of contrast. At the other extreme — computing local contrast over a tight spatial scale and brief temporal scale — estimates of mean intensity would become unreliable because of noise (variability inherent in the photoreceptor responses)²⁹.

Following light adaptation, signals in retina are thought to feed into a second normalization stage, which performs contrast normalization (FIG. 2e). This stage adjusts responses to one location in an image based on the contrast in a surrounding spatial region^35–40. Conceptually, it is useful to consider contrast normalization as separate from light adaptation^29,30, but mechanistically the two stages may overlap in bipolar cells. Light adaptation is thought to operate in photoreceptors and bipolar cells, whereas contrast normalization is thought to occur in bipolar cells and ganglion cells⁴¹, and to become stronger in subsequent stages of visual processing.

Under contrast normalization, responses are no longer proportional to local contrast C_j (the output of the first normalization stage). Instead, the response R_j of neuron j is divided by a constant σ plus a measure of overall contrast⁴⁰:

$$R_j=\gamma \frac{{\Sigma }_i{w}_i{C}_i}{\sigma +\sqrt{{\Sigma }_k{\alpha }_k{C}_k^2}}$$ (5)

Here, the weights w_i (positive or negative) define the spatial profile of the summation field (typically, a centre-surround difference of Gaussians), and the weights α_k (positive) define the spatial profile of the suppressive field (typically, a large Gaussian⁴⁰). The responses of neurons at the output of the retina (as measured in the lateral geniculate nucleus (LGN)) are characterized well by this equation, in which the normalization in the denominator corresponds to the standard deviation of contrasts over a region of the visual field⁴².

A common way to probe contrast normalization is to use gratings that vary in overall contrast and size (FIG. 2f). As predicted by the model, increasing grating contrast leads to response saturation when gratings are shown in a large window, but not when they are shown in a small window⁴⁰ (FIG. 2f). For small windows, local contrast is zero in most of the suppressive field, so the denominator has a small role in equation 8. For larger stimuli, increasing grating contrast increases local contrast not only in the numerator but also in the denominator, and responses saturate. Response saturation, therefore, is due to contrast and not to the evoked response: it is strongest for largest stimuli, which evoke weaker responses than smaller stimuli.

Normalization in primary visual cortex

Normalization is thought to operate not only in retina but also at multiple subsequent stages along the visual pathway. Indeed, the normalization model was first developed to account for the physiological responses of neurons in primary visual cortex (V1)^{17–19,43–45}.

Here, we describe the normalization model for a population of V1 neurons differing in preference for stimulus position and orientation. This characterization of the responses of neural populations^46–48 encompasses previous descriptions of single neurons^19,43. In the model, the responses of a population of V1 neurons are given by:

$$R(x,\theta )=\frac{D{(x,\theta )}^n}{{\sigma }^n+N{(x,\theta )}^n}$$ (6)

Here, x and θ indicate the preferred position and orientation of each neuron in the population (the only two stimulus attributes that we consider in this simplified explanation). The numerator contains the stimulus drive D, which results from each neuron's summation field and determines the selectivity for stimulus position and orientation. The normalization factor N in the denominator, in turn, is determined by the suppressive field α(x,θ), which provides weights with which to pool the stimulus drive received by each of the neurons (BOX 1). The normalization factor typically responds to a broader set of stimuli than the summation field. So a neuron that responds to stimuli with particular spatial positions and orientations can be suppressed by stimuli with a broader range of spatial positions and orientations. The exponent n in V1 neurons is generally between 1.0 and 3.5, with an average of about 2 (REFS 48–50).

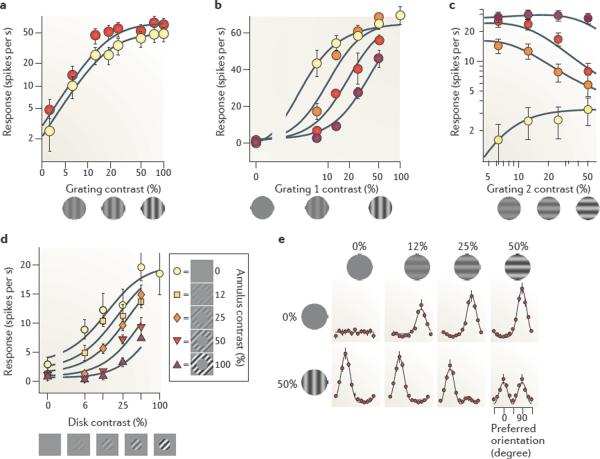
Normalization explains why responses of V1 neurons saturate with increasing stimulus contrast, irrespective of stimulus orientation, and therefore irrespective of firing rate⁴⁹ (FIG. 3a). Normalization explains this behaviour^17–19,43 because both the stimulus drive and the normalization factor are proportional to grating contrast c:

$$R=\gamma (\theta -\phi )\frac{c^n}{{\sigma }^n+c^n}$$ (7)

Here, γ is the neuron's tuning curve for orientation, which depends on the difference between the neuron's preferred orientation θ and the stimulus orientation φ. This characterization of the responses is a separable function of contrast and orientation, so the responses saturate with contrast regardless of stimulus orientation (FIG. 3a), and orientation tuning is invariant with contrast^51,52.

Figure 3. Normalization in primary visual cortex.

a | Contrast saturation. Responses as a function of grating contrast for gratings having optimal orientation (shown in red) and suboptimal orientation (shown in yellow). b | Cross-orientation suppression. Responses to the sum of a test grating and an orthogonal mask grating (colours indicate mask contrast, from 0% (shown in yellow) to 50% (shown in dark red)). c | Transition from drive to suppression. Grating 1 had optimal orientation and grating 2 had suboptimal orientation. Grating 2 could provide some drive to the neuron when presented alone (shown in yellow) but became suppressive when grating 1 had moderate contrasts (shown in red). d | Surround suppression. A grating contained in a central disk was surrounded by a grating in an annulus. The annulus elicited minimal responses when presented alone, but suppressed responses to the central disk. e | Effects of normalization on population responses. Each dot indicates the response of a population of neurons selective for a given orientation, and each panel indicates the population responses to a stimulus. Stimuli are gratings of increasing contrast, presented alone (top) or together with an orthogonal grating (bottom). Data in part a from REF. 43; data in part b from REF. 56; data in part c from REF. 43; data in part d from REF. 142; data in part e from REF. 48.

Another non-linear phenomenon that is captured by normalization is cross-orientation suppression (FIG. 3b). The responses of a V1 neuron to a test grating that drives responses are suppressed by superimposing on the test grating a mask grating that is ineffective in eliciting responses when presented alone — for example, because its orientation is orthogonal to the neuron's preferred orientation^43,53–56. Normalization explains this effect because the suppression in the denominator increases with both test contrast c_t and mask contrast c_m, whereas the stimulus drive increases only with test contrast c_t (the summation field does not respond to the mask):

$$R=\gamma \frac{c_t^n}{{\sigma }^n+c_m^n+c_t^n}$$ (8)

The effect of increasing mask contrast, therefore, is to increase the denominator, which shifts the curve to the right on a logarithmic contrast axis (FIG. 3b). This is remarkably similar similar to the effect in the fruitfly antennal lobe of adding a non-preferred odorant (FIG. 1b), or increasing background light intensity in photoreceptors (FIG. 2b). In all of these cases, the responses to a preferred stimulus are effectively divided by the strength of a non-preferred stimulus.

Normalization also explains the more general case in which the mask does provide some drive to the neuron, for example, because its orientation is close to the preferred one (FIG. 3c). In this case, normalization makes an important prediction^43,57: the mask should evoke activity when presented alone, but it should become suppressive in the presence of a more effective stimulus. To see how this prediction arises, consider the response of a neuron (equation 9) to the sum of two stimuli with contrasts c₁ and c₂:

$$R=\frac{w_1{c}_1+w_2{c}_2}{\sigma +c_1+c_2}$$ (9)

w₁ >> w₂ measure the degree to which stimulus 1 and 2 drive the neuron (and for simplicity we are setting the exponent n to 1). When stimulus 1 is absent (c₁ = 0), responses increase with stimulus 2 contrast. If instead stimulus 1 has sufficiently high contrast c₁, one can ignore the term w₂c₂ in the numerator. Therefore c₂ appears only in the denominator, where it exerts a purely suppressive effect.

Another widespread phenomenon in V1 that is explained by normalization is surround suppression^58,59 (FIG. 3d). A neuron's responses to stimuli inside the summation field can be suppressed by placing additional stimuli in the surrounding region^60,61. Normalization accounts for this phenomenon⁵⁸ (FIG. 3d) for similar reasons to those discussed in relation to cross-orientation suppression: the suppressive field covers a larger region of visual space than does the summation field.

Normalization correctly predicts that the V1 population exhibits strong winner-take-all competition in response to sums of stimuli with different contrasts⁴⁸ (FIG. 3e). When a low-contrast vertical grating is added to a high-contrast horizontal grating, the population responses mostly reflect the high-contrast grating (FIG. 3e), even though the low-contrast grating was perfectly able to elicit strong responses when presented alone (FIG. 3e). Normalization provides winner-take-all competition because the presence of multiple stimuli effectively raises the constant in the denominator, reducing the sensitivity of the neurons to the point that the weaker stimuli become unable to drive them (FIG. 3b). An exponent n > 1 strengthens this effect, but normalization can provide winner-take-all competition even when the exponent in the numerator is 1 (see FIG. 3e).

Normalization in other cortical areas

There is evidence for normalization downstream from area V1, and particularly in visual cortical area MT^62–64, where neurons are selective for visual motion (speed and direction). An established model of MT responses^62,63 involves a summation field that operates on the population activity of V1, followed by a normalization stage. The summation field determines the selectivity for velocity, and the normalization stage helps to make this selectivity independent of spatial pattern⁶³. The presence of normalization in MT would explain a number of suppressive phenomena that have been observed⁶⁵, but it is challenging to determine whether normalization is computed de novo in MT or simply inherited from the V1 inputs⁶⁴. Indeed, normalization in area V1 can profoundly shape the pattern of population activity (FIG. 3d), and thereby have strong effects on MT neurons that receive inputs from V1 (REF. 48).

Other examples of normalization in visual areas beyond V1 lie in the ventral pathway, where visual neurons are thought to perform a series of transformations that lead to object recognition⁶⁶. Models of object recognition propose that information is combined from multiple features to construct object representations. In one such model⁶⁷, a large set of summation fields extract features, and each successive visual cortical area integrates features by a non-linear pooling operation. The non-linear pooling operation selects the largest responses (winner-take-all) and feeds those forward to the next stage of integration. This winner-take-all competition can result from the normalization model⁴⁸ (FIG. 3d), particularly when the exponent is large⁶⁸ (BOX 2). Normalization, in this model, serves a role in the non-linear pooling that underlies feature integration. As predicted by such a model, there is evidence for suppression in ventral stream area V4 and the inferotemporal cortex (IT) when a non-preferred stimulus (or object) is presented with a preferred stimulus^69,70. Some of the best current computer vision systems for visual object recognition follow a similar architecture as the model of the ventral visual pathway, with alternating stages of linear filtering and non-linear pooling through normalization. Normalization plays an important part in these computer vision systems as it enhances the accuracy of object recognition⁷¹.

There is also evidence for normalization in cortical areas that are devoted to other sensory modalities, and in particular in primary auditory cortex^72–74 (A1). It has been known for a long time that responses of A1 neurons to sounds depend on sound intensity and context. For example, the spectrotemporal receptive field provides only a rough approximation to an A1 neuron's responses, and it seems to change depending on the stimulus set that is used to measure it^72,73,75. Responses of A1 neurons show a roughly logarithmic dependence on sound intensity (the commonly used decibel scale), but the responses can be shifted to the right on the logarithmic intensity axis by increasing intensity of a background noise⁷⁶. These non-linear behaviours are qualitatively reminiscent of normalization: we have seen similar effects in the olfactory system (FIG. 1) and in two stages of the visual system (FIGS 2–3). In fact, the deviations from linearity can be characterized quantitatively by the normalization equation⁷⁴. First, A1 responses increase with a measure of spectrotemporal auditory contrast that is analogous to spatiotemporal visual contrast (equations 6 and 7). Second, A1 responses saturate with auditory contrast (equation 4). Third, the responses can be suppressed by superimposing a noise stimulus that does not evoke responses in the neuron when presented alone (equation 5). Normalization may be a widespread phenomenon in auditory processing: similar divisive effects as those seen in mammalian area A1 have been characterized in the auditory midbrain of the owl⁷⁷.

Normalization seems to be at work not only in individual sensory modalities but also at the stage of multisensory integration⁵⁷. A prime example is provided by neurons in the cortical medial superior temporal area (MST) of primates, which are thought to integrate visual cues and vestibular cues about head, body and eye movements to estimate heading. Some of these neurons are driven more strongly by visual cues, and others are driven more strongly by vestibular cues, but many seem to have their activity modulated by both modalities. The nature of the interaction is divisive, as in equation 12. In the numerator there is a contribution by both modalities that is often biased in favour of one modality, whereas the denominator sums signals from both modalities. Normalization thus explains why neurons that integrate sensory inputs from different modalities weigh each modality depending on its strength⁷⁸, why multisensory enhancement decreases with stimulus intensity (also known as the `principle of inverse effectiveness')⁵⁷, and possibly why stimuli of the non-preferred modality can both drive the cell when presented alone and suppress it when presented with a stimulus of the preferred modality. We have already illustrated analogous effects of normalization in V1 (FIG. 3c).

In addition to sensory systems, there is evidence that the cortex uses normalization when encoding the value associated with different actions^79,80. For example, neurons in the lateral intraparietal area (LIP) of the macaque monkey encode the value of saccadic eye movements, but they are modulated by relative rather than absolute value: the neural representation of saccadic value is explicitly dependent on the values of the other available alternatives. The responses of a LIP neuron increase with the reward value (magnitude of juice reward) of a saccade target presented within the neuron's response field, and the responses decrease with the value of saccade targets simultaneously presented outside the response field. The normalization equation fits the responses to various combinations of reward values well. Other models (such as those based on absolute value or relative value computed differently from the normalization equation) do not fit the data as well. Rational choice theory assumes that options are assigned absolute values that are independent of the values of other available alternatives. However, animals and humans violate this assumption, suggesting that normalization may help to explain violations of rational choice theory⁷⁹.

Normalization and visual attention

The normalization model has been extended to explain how responses in visual cortex are modulated by attention⁴⁶. In the extended model, attention multiplicatively enhances the stimulus drive before normalization. As the normalization model can exhibit winner-take-all competition (FIG. 3e), even a small enhancement can provide a substantial advantage to the attended stimulus.

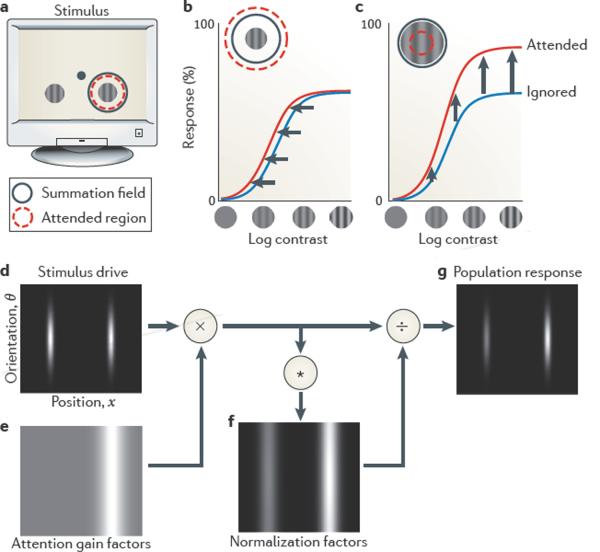
A typical experiment that probes spatial attention involves two spatially separate stimuli, and attention is directed towards one of them (FIG. 4a). Recordings in visual cortex indicate that the neurons that respond to the attended stimulus show stronger responses (FIG. 4b,c). To model this experiment, consider a population of neurons whose responses R(x,θ) depend on preferred position x and preferred orientation θ (equation 9). The stimulus drive D(x,θ) is largest for the neurons whose preferred positions and orientations match the stimuli (FIG. 4d). The effect of attention is simulated in the model by an array of attentional gain factors A(x,θ). This array depends on the range of attended locations and features; in the case of spatial attention (as in this example) it is narrow in space and broad in orientation (FIG. 4e). In other conditions it can instead be narrow in orientation (or other features) and broad in space (feature-based attention). The attentional gain factors multiply the stimulus drive, so that they affect both the numerator and the denominator of the normalization equation (FIG. 4f). The resulting output firing rates R(x,θ) are largest at the attended location (FIG. 4g).

Figure 4. Attentional modulation of responses in visual cortex and predictions of the normalization model of attention.

a | A typical attention experiment. A pair of gratings is presented, one on each side of the fixation point (shown by a dot). The task engages attention around one of the gratings (shown by a red circle). One of the gratings lies in the summation field of a recorded neuron (shown by a dashed circle). b | In some experiments, attending to the stimulus in the summation field (shown by a red curve) changes contrast gain (leftward shift) relative to attending the opposite side (shown by a blue curve). The normalization model of attention predicts this result when the attended region is large and the stimulus is small relative to the summation and suppressive fields (shown in the inset). c | In other experiments, attention changes response gain (upward scaling). The model predicts this result for large stimulus size and small attended region (shown in the inset). d | Stimulus drive D(x,θ) for a population of neurons indexed by their preference for stimulus position x (abscissa) and orientation θ (ordinate) (the grey level indicates the stimulus drive for each neuron). e | Attentional gain factors A(x,θ) when attending to the stimulus on the right (the red circle in a) without regard to orientation (light grey indicates a value of 1 and white indicates a value >1). The attentional gain factors are multiplied point-by-point (×) with the stimulus drive. f | Normalization factors N(x,θ) are computed from the result of this multiplication, by pooling over space and orientation (shown by the asterisk) through convolution with the suppressive field α(x,θ). g | The output firing rates R(x,θ) of the population can be computed by dividing the stimulus drive (÷) by the normalization factors. Figure is modified, with permission, from REF. 46 © (2009) Cell Press.

Although conceptually simple, the model can explain a seeming discrepancy in the literature about the effects of attention on responses of neurons in visual cortex (FIG. 4b–c). Different experiments have reported ostensibly conflicting outcomes⁴⁶: a change in contrast gain (FIG. 4b), a change in response gain (FIG. 4c) or a combination of the two. According to the model, the discrepancy stems from differences in the size of the stimulus and the spread of attention (that is, the extent of the attentional gain factors), relative to the sizes of the summation and suppressive fields. The model predicts that attention increases contrast gain when the stimulus is small and attention is broad (FIG. 4b), because the attentional gain factors multiply the stimulus drive and the normalization factor by the same amount. The model predicts that attention increases response gain when the stimulus is large and attention is narrowly focused (FIG. 4c), because the attentional gain factors multiply the entire summation field (which appears in the numerator of the normalization equation) but only the centre of the suppressive field (in the denominator). These predictions were further confirmed by a behavioural study that systematically manipulated stimulus size and attention spread⁸¹.

Circuits and mechanisms underlying normalization

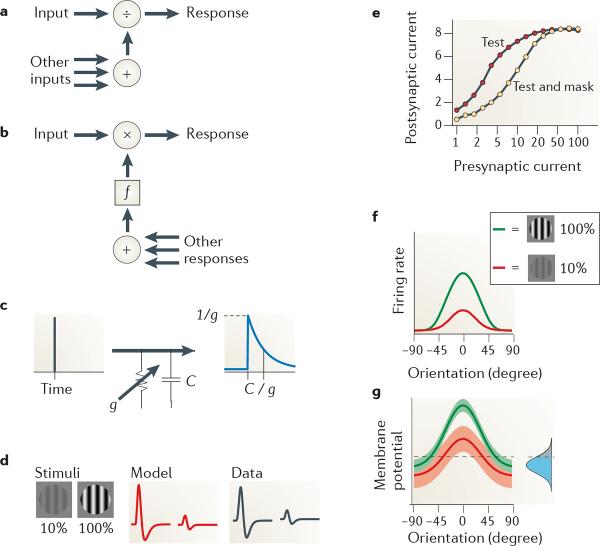
A large body of research has sought to identify the specific biophysical and cellular mechanisms that are responsible for normalization. Much of this research has focused on the role of GABA-mediated inhibition, which has often been suggested to underlie the operation of division. This emphasis has proven useful in the olfactory system of the fruitfly²⁷ but less so in mammalian V1, where GABA inhibition seems to play little or no role in essential aspects of normalization⁸². Therefore, it is unlikely that a single mechanistic explanation will hold across all systems and species: what seems to be common is not necessarily the biophysical mechanism but rather the computation. Moreover, in some systems (for instance, the visual system) normalization seems to result from multiple circuits and mechanisms operating in concert and cascading across multiple stages. In the visual system, for example, contrast normalization is thought to be progressively strengthened in retina, LGN, V1 and MT. Below, we review some key mechanisms that have been proposed, with an emphasis on research performed in visual cortex, where the debate is most open.

Although there are notable exceptions (for example, much of light adaptation operates in single photoreceptors), normalization generally involves pooling a larger set of signals than those received by any single neuron. Therefore, its most useful explanations are those based on networks of neurons.

A key question concerns the basic arrangement of such networks (FIG. 5a,b). The normalization equation operates on neural signals (both in the numerator and in the denominator) that have not themselves been normalized. A simple way to obtain such signals would be through a feedforward network that taps them before they have been subjected to normalization (FIG. 5a). Such an arrangement has been proposed for the visual system of the housefly (Musca domestica)²⁵, for the olfactory system of the fruitfly⁸³ and for some aspects of normalization in the mammalian visual cortex⁸⁴. However, normalization can also be achieved in a feedback circuit (FIG. 5b). It is well known to electrical engineers that gain control can be implemented using either a feedforward or a feedback system. A feedback circuit has been traditionally proposed for primary visual cortex, where signals in the denominator have been thought to originate from lateral feedback within V1 (REFS 19,43–45) or from feedback from higher visual areas⁸⁵. The origin of divisive signals is generally hard to distinguish based on responses alone, that is, unless the underlying anatomy is known and the signals themselves can be manipulated at various stages in the circuit. Some models, therefore, are agnostic as to the origin of divisive signals^18,25.

Figure 5. Some networks and mechanisms that have been proposed for normalization.

a | The connections underlying normalization can be arranged in a feedforward manner, in which signals contributing to the denominator have not been normalized themselves. b | An alternative configuration involves feedback. The function f performs the appropriate transformation of signals so that they can be multiplied by the input, giving rise to division in steady state^43,44. c | A resistor–capacitor (C) circuit and its transformation of an impulse into an exponential response. Conductance g determines both response gain and time constant. d | Effect of stimulus contrast on impulse responses of a lateral geniculate nucleus (LGN) neuron. Increasing contrast (left part) causes impulse responses to be weaker and faster, both in the model (middle part) and in the data (right part). e | Synaptic depression as a mechanism for normalization. Depression changes the relationship between presynaptic current and postsynaptic current (arbitrary units) in a divisive way. f,g | Noise as a mechanism for normalization (arbitrary units). The transformation between stimulus-driven membrane potential (g) and firing rate (f) depends on signals originating from the rest of the brain in the form of `ongoing activity', modelled from the point of view of a single neuron as noise added to the membrane potential (shown by the inset Gaussian curve in g). Data in part d from REF. 35; data in part e from REF. 84; data in parts f and g from REF. 143.

A clue to the nature of divisive signals is given by their timing and sensory properties. For example, in visual cortex, normalization signals that originate near a neuron's preferred position (responsible, for example, for cross-orientation suppression (FIG. 3b)) resemble LGN responses more than V1 responses: they exhibit broad selectivity for stimulus attributes⁵⁶, lack of adaptability⁵⁶ and extremely short delay⁸⁶. These characteristics might suggest a feedforward arrangement (FIG. 5a). Conversely, normalization signals that reach a neuron from a broader region of visual space (responsible, for example, for surround suppression (FIG. 3d)) resemble V1 responses in many ways, such as orientation selectivity⁵⁹, susceptibility to adaptation⁸⁷ and longer delay⁸⁸. These characteristics suggest a feedback arrangement (FIG. 5b). It is possible, therefore, that phenomena such as cross-orientation suppression and surround suppression might be mediated by different mechanisms that operate in concert within the computational framework of normalization.

A second set of questions concerns the nature of the biophysical mechanisms that perform division. One of the very first proposals was shunting inhibition^25,43,45. Shunting inhibition increases membrane conductance without introducing depolarizing or hyperpolarizing synaptic currents (FIG. 5c). Conductance increases could be obtained either through channels with a reversal potential close to the resting potential^25,43 (for example, GABA type A (GABA_A) receptors permeable to Cl⁻ ions) or by concomitant increases in excitation and inhibition, balanced so that there is an increase in conductance with no net synaptic current⁴⁵. It is easy to see how conductance controls the gain of membrane potential responses, as this follows directly from Ohm's law: the membrane potential response V to a synaptic input current I is scaled by membrane conductance g as V = I / g. It is less obvious to see how conductance controls the gain of firing rate responses, because spiking itself introduces large, albeit brief, conductance increases⁸⁹. It is now agreed that the effect of conductance increases on firing rates is divisive, but only if the source of increased conductance varies in time⁹⁰. This variation could be achieved if the conductance changes were evoked by the noisy activity of other neurons⁹¹.

The shunting inhibition hypothesis makes a strong prediction: that normalization should affect not only the amplitude of the responses but also their time course. Increasing the conductance of a resistor–capacitor circuit such as the cellular membrane reduces not only the gain but also the time constant of the responses (FIG. 5c). The reduction in time constant is another way to reduce responsiveness, as briefer responses allow for less temporal summation. This prediction is valid in the retina during light adaptation^35,92 and during contrast normalization³⁵ (FIG. 5d). The evidence for conductance increases in normalization, however, is mixed. In V1, for example, intracellular measurements show that conductance does grow with stimulus contrast, but it is not invariant with orientation^93,94 as it would be if it reflected only the strength of normalization.

More generally, inhibition seems to have a role in some but not all forms of normalization. In the olfactory system of the fruitfly, normalization seems to be due to presynaptic inhibitory connections between neurons in the antennal lobe⁸³, because blocking inhibition with a GABA antagonist greatly reduces the suppressive effect of a mask stimulus²⁷. However, in V1 the normalization mechanisms underlying contrast saturation (FIG. 3a) or cross-orientation suppression (FIG. 3b) do not seem to rely on GABA_A inhibition: they are unaffected by blockage of GABA_A receptors⁸². Inhibition in V1 may contribute to surround suppression⁹⁵ (FIG. 3d), but this remains controversial⁹⁶.

Alternative mechanisms have been proposed that could explain normalization phenomena without relying on inhibition. Some of these explanations rely on non-linearities in the afferent input^27,84,97. In particular, a mechanism that could provide the appropriate non-linearity is synaptic depression⁹⁸: if a synapse is engaged in transmitting both test signals and mask signals, its effectiveness is reduced in a way that resembles the divisive effect required by normalization⁸⁴ (FIG. 5e). Explanations of this kind, however, can only explain divisive effects provided by the same afferents that feed the numerator of the normalization equation. In area V1, for example, they could explain phenomena of cross-orientation suppression (FIG. 3b) but not phenomena of surround suppression (FIG. 3d).

Other possible mechanisms rely on the effect of fluctuations in membrane potential on firing rate responses⁵¹ (FIG. 5f,g). The membrane potential of neurons is not only dependent on the afferent signals that are meant to drive the neuron but also on other signals originating from the rest of the brain in the form of ongoing activity⁹⁹. In neurons such as those in area V1, the resulting fluctuations in membrane potential are essential in making the neuron fire: without them, many stimuli would evoke membrane potential fluctuations that are too small to reach spike threshold^100,101. Consequently, the amplitude of ongoing activity controls the responsiveness of the neurons. The ongoing activity is weaker in V1 when stimulus contrast increases⁵¹, so the neurons become less responsive, mimicking divisive suppression.

Finally, an intriguing possibility is that normalization in some systems may rely on amplification rather than suppression. In visual cortex, for example, a canonical microcircuit has been proposed^1,2 to amplify and shape responses inherited from the LGN. This circuit and more recently proposed circuits, such as one centred on balanced amplification¹⁰², suggest an alternative path to normalization. Instead of increasing normalization by increasing suppression, these circuits may increase normalization by decreasing amplification.

Behavioural evidence for normalization

Psychophysical studies of visual pattern perception have paralleled research on the neurophysiological response properties of neurons in the visual cortex. The prevailing view has been that judgments about pattern discrimination and pattern appearance are limited by neural signals in early visual cortical areas such as area V1. Consistent with this view, it has been possible to use normalization equations that summarize responses of V1 neurons to make specific predictions about human perception.

The simultaneous contrast–contrast illusion, for example, is created by surrounding a central texture patch with a textured background¹⁰³. When the central texture patch is surrounded by a high-contrast pattern, the bright points of the central patch appear dimmer and, simultaneously, the dark points appear lighter. To explain this illusion with the normalization model, we must adopt a decision rule, a testable hypothesis that predicts behavioural performance from the pooled activity of a population of neurons. It has been proposed that perceived contrast is a monotonic function of the average activity of neurons with summation fields centred on the patch. The normalization model suggests that each of these neurons is suppressed by the pooled activity of a larger number of neurons, including those with summation fields in a surrounding spatial region. The responses of these surrounding neurons increase with background contrast. Hence, when there is a high-contrast background the suppression is stronger, and perceived contrast of the central texture patch is lower. Indeed, the normalization model has been used to explain the appearance of this illusion¹⁰⁴.

The psychophysics of superimposed and surround suppression parallels the physiology. Surround suppression, as measured behaviourally, depends on whether the orientations and spatial frequencies of target and surround are matched^103–106, unlike a superimposed mask for which the suppression is largely nonspecific¹⁰⁷. Surround suppression, as measured behaviourally, is also slightly delayed, unlike a superimposed mask for which the suppression is immediate¹⁰⁶. Both of these results parallel the physiological findings^86,88.

Analogous behavioural markers of normalization should be measurable in the other domains, for example, olfactory behaviour in the fruitfly while manipulating the concentrations of two or more odorants, and choice behaviour in human and non-human primates while manipulating the reward values of two or more alternative options.

Deficits in computations related to normalization have been linked with amblyopia^108–110, epilepsy^111,112, major depression^113,114 and schizophrenia^67,115–121. This suggests the possibility that the origin of these brain disorders may lie not in a particular brain area or system (such as the prefrontal cortex in schizophrenia), but instead in computational deficits, and that normalization may be one of the fundamental computations that is compromised in these disorders.

Discussion

We have seen that divisive normalization is a widespread computation in disparate sensory systems, and that it may also play a part in cognitive systems (for example, those that encode value). Why is normalization so widespread? A tempting answer would be to see it as a natural outcome of a very common mechanism or network; a canonical neural circuit. However, there seem to be many circuits and mechanisms underlying normalization and they are not necessarily the same across species and systems. Consequently, we propose that the answer has to do with computation, not mechanism. Normalization is thought to bring multiple functional benefits to the computations that are performed by neural systems (BOX 2). Some of these benefits may be more important for some neural systems than for others.

Some of the literature that we have reviewed concerns aspects of normalization that are still the subject of intense research. A key set of questions concerns circuits and mechanisms that result in normalization. As reviewed above, these circuits and mechanisms are understood for some systems but not for others. Understanding these circuits and mechanisms is fundamental, especially if, as suggested earlier, deficits in normalization are indeed at the root of psychiatric, neurological or developmental disorders.

Another question for further exploration is the degree to which normalization resembles — in computational terms or in underlying circuitry — the more general non-linear interactions that constitute `gain modulation'. Gain modulation is the multiplicative control of one neuron's responses by the responses of another set of neurons. It arises in a wide range of contexts¹²², including in the interaction of proprioceptive and visual signals in the parietal cortex^15,123, in the coordinate transformation needed for visually guided reaching^15,122,123 and in invariant object recognition¹²². A variety of studies address the computational advantages of gain modulation^15,124,125 and its possible underlying biophysical mechanisms^{90,91,122,126}. In its simpler forms, normalization is a special case of gain modulation in that the signals controlling gain are a superset of the signals that determine the responses. However, when the normalization model is expanded to include distinct gain factors, as in the normalization model of attention, it incorporates more general aspects of gain modulation.

Because normalization is a computation that is repeated modularly in a number of brain systems, we propose that it should be considered a canonical neural computation. Under this proposal, normalization should be added to a short list of known canonical neural computations. These include not only two well-established computations that we have already mentioned — linear filtering and exponentiation — but also other computations, such as recurrent amplification, associative learning rules, coincidence detection, population vectors and constrained trajectories in dynamical systems. Identifying and characterizing more modular computations of this kind will provide a toolbox for developing a principled understanding of brain function.

Understanding canonical neural computations could help us to understand brain function in a number of ways. First, it would provide a single language to describe the functional specialization of different brain areas. Second, as we have discussed above, a computational understanding of normalization provides a platform for characterizing behaviour and for characterizing cellular mechanisms. Finally, understanding canonical neural computations such as normalization may also shed light on psychiatric, neurological and developmental disorders. If this hypothesis is correct for some of these disorders, then elucidation of these neural computations, and of the underlying mechanisms and microcircuits, is a fundamental mission.

Online at-a-glance summary

• Normalization computes a ratio between the response of an individual neuron and the summed activity of a pool of neurons.

• The normalization model was developed to explain responses in the primary visual cortex (V1), and has been seen to operate in a variety of other regions of the visual system: light adaptation in the retina, contrast normalization in the retina and lateral geniculate nucleus, and visual processing in higher visual cortical areas beyond V1.

• Normalization has also been proposed to be at the root of the modulatory effects of visual attention on neural responses in visual cortex.

• Normalization is seen in multiple species and brain regions. These include olfactory processing and representation in the fruitfly antennal lobe, the encoding of value in posterior parietal cortex, multisensory integration of visual motion and vestibular signals, and auditory processing in primary auditory cortex.

• A variety of different (feedforward and feedback) neural circuits and mechanisms might perform normalization, including presynaptic inhibition, shunting inhibition, synaptic depression, changes in the amplitude of ongoing activity and balanced amplification.

• The effects of normalization can be measured behaviourally.

• The computational benefits of normalization include maximizing sensitivity, providing invariance with respect to some stimulus dimensions at the expense of others, facilitating the decoding of a distributed neural representation, facilitating the discrimination among representations of different stimuli, providing max-pooling (winner-take-all competition) and reducing redundancy.

• Understanding canonical neural computations such as normalization may shed light on psychiatric, neurological and developmental disorders.

Box 1 | The normalization equation.

The normalization model is defined by a simple equation, the normalization equation. This equation specifies how the normalized response R_j of neuron j depends on its inputs D_k (which are not normalized):

$$R_i=\gamma \frac{D_j^n}{{\sigma }^n+{\Sigma }_k{D}_k^n}$$ (10)

The numerator is the neuron's driving input D_j; in sensory systems, this driving input provides the stimulus drive to the responses. Its units depend on the system under study. They could be in units of stimulus intensity in a sensory system, or in spikes per s if the input is considered to arise from another neuron. The denominator is a constant σ plus the normalization factor, which is the sum of a large number of inputs D_k, the normalization pool. The constants γ, σ and n constitute free parameters that are typically fit to empirical measurements: γ determines overall responsiveness, σ prevents division by zero and determines how responses saturate with increasing driving input, and n is an exponent that amplifies the individual inputs.

This operation is called `normalization' by analogy to normalizing a vector. In this vector, each element of the vector is one of the inputs (D_j) and the exponent is n = 2. If the normalization factor is the same for all neurons in the population, then the activity of the whole population of neurons is scaled (normalized) by the same number.

In a sensory system, the normalization equation is often used in combination with a summation field (or linear receptive field) that determines the neuron's selectivity for stimulus attributes. In that case the stimulus drive D_j to neuron j is taken to be a weighted sum of sensory inputs:

$$D_j={\Sigma }_k{w}_{jk}{I}_k$$ (11)

Here, the I_k are activities of afferent neurons, and the weights w_jk specify the summation field of neuron j. A number of variations of the normalization equation have been applied to model different systems:

Different inputs D_k can be assigned different weights α_jk in the normalization pool. These weights define a suppressive field. The suppressive field may differ across neurons (hence the subscript_j). For example, neurons in primary visual cortex whose summation fields are centred on different spatial locations would have suppressive fields that are centred at corresponding locations.

A baseline response β can be added to the numerator (to account for the spontaneous activity of the inputs). Doing so allows the normalization pool to affect not only the driven responses but also the resting (spontaneous) activity of the neuron.

The exponent n can be the same in the numerator and denominator, as in equation 1, and it is applied to the individual inputs before being pooled. The exponent can also be applied to the output of the entire normalization pool, or different exponents m, n and p can be used in the numerator and denominator.

The normalization signal can be averaged over a period of recent time to model adaptation, such as light adaptation in retina or contrast adaptation in visual cortex. Combining these variations results in the following equation:

$$R_j=\gamma \frac{{\left({\Sigma }_k{w}_{jk}{I}_k\right)}^n+\beta }{{\sigma }^n+{\left({\Sigma }_k{\alpha }_{jk}{I}_k^m\right)}^p}$$ (12)

This expression encompasses various implementations of the model that have been found to characterize different neural systems. When applying the model to a given neural system, however, it is best to strive for simplicity and have as few parameters as possible — for example, as in equation 1.

A typical way to characterize systems exhibiting normalization is to fit the normalization equation to the responses of a neuron to stimuli that drive that neuron, to stimuli that drive other nearby neurons, and to various combinations of these stimuli. More recent approaches involve fitting the equation to the responses of a large population of neurons at once⁴⁸.

Box 2 | Normalization and neural coding.

Theoreticians have offered several (not mutually exclusive) rationales for normalization, most of which are related to coding efficiency.

Maximizing sensitivity. Normalization adjusts the gain of the neural responses to efficiently use the available dynamic range, maximizing sensitivity to changes in input. Light adaptation in the retina enables high sensitivity to subtle changes in visual features over a huge range of intensities (FIG. 2). Normalizing reward values yields a representation that can distinguish one dollar from two dollars and one million dollars from two million dollars, that is, widening the effective dynamic range of the reward system.

Invariance with respect to some stimulus dimensions. Normalization in the antennal lobe of the fly is thought to enable odorant recognition and discrimination regardless of concentration^27,127. Normalization in retina discards information about the mean light level to maintain invariant representations of other visual features^35,128 (for example, contrast). Normalization in V1 discards information about contrast to encode image pattern (for example, orientation)^17,19,48,49 (FIG. 3e), optimizing discriminability regardless of contrast¹²⁹. Normalization in the visual cortical area MT is thought to encode velocity independent of spatial pattern^62,63. Normalization in the ventral visual pathway may contribute to object representations that are invariant to changes in size, location, lighting and occlusion⁶⁸.

Decoding a distributed neural representation. Visual area MT is thought to encode visual motion in the responses of a population of neurons tuned for different speeds and directions. These responses can be interpreted as discrete samples of a probability density function in which the firing rate of each neuron is proportional to a probability; the mean of the distribution estimates stimulus velocity and the variance of the distribution measures the uncertainty in that estimate⁶³. Mean and variance can be computed simply as weighted sums of the firing rates if they are normalized to sum to a constant, the same constant for any stimulus.

Discriminating among stimuli. Normalization can make the neural representations of different stimuli more readily discriminable by a linear classifier^{27,127,129,130}. The response of n neurons to a stimulus is a point in n-dimensional space. The points belonging to similar stimuli cluster together. A linear classifier discriminates stimulus categories by drawing hyperplanes between the clusters. This is difficult if some stimuli evoke strong responses (points far from the origin) but others evoke weak responses (points near the origin); the hyperplane that defines the boundary far from the origin can fail near the origin, and vice versa. Normalization prevents this problem from arising.

Max-pooling (winner-take-all). Normalization can cause a neuronal population to operate in two regimes, averaging the inputs when these are approximately equal and computing a winner-take-all competition (max-pooling, selecting the maximum of inputs) when one input is considerably larger than the rest⁴⁸ (FIG. 3e). Max-pooling is thought to operate in multiple neural systems and to underlie perceptual decisions by selecting the neuronal subpopulation (or psychophysical channel) with the largest responses^131–135. Models of object recognition propose multiple stages of max-pooling (winner-take-all)⁶⁷. Attention might interact with normalization to shift the computation from averaging to max-pooling, thus selecting the subpopulation with largest responses and suppressing the rest, similar to the `biased competition' model¹³⁶.

Redundancy reduction. A neural representation is thought to be inefficient when its outputs are redundant^137–139. Normalization can reduce this redundancy. Normalization contributes to statistical independence of V1 responses to natural images^140,141. Natural images tend to be similar at nearby locations (for example, along a contour). Consequently, the response of a V1 summation field can be estimated from the responses of V1 summation fields that are selective for nearby locations. Normalization removes the dependence, making the representation more efficient^140,141. Likewise, responses of the population of antennal lobe neurons (post-normalization) in the fly olfactory system are more statistically independent than are the (pre-normalization) olfactory receptor neurons^27,127.

Biographies

Matteo Carandini is the GlaxoSmithKline/Fight for Sight Chair in Visual Neuroscience at University College London, UK. His research uses a variety of electrical and optical methods to characterize the computations performed by neural circuits, the interplay between sensory-driven activity and ongoing activity in visual cortex, and how neural activity supports visually guided behaviour. He obtained an M.Sc. in mathematics from the University of Rome, Italy (1990) and a Ph.D. in neural science, from New York University, USA (1996). He carried out postdoctoral work at Northwestern University, Evanston, Illinois, USA, and worked as an assistant professor at the Swiss Federal Institute of Technology, Zurich, Switzerland (1998–2002) and as a research scientist in the Smith-Kettlewell Eye Research Institute, San Francisco, California, USA (2002–2006). He received a McKnight Scholar award in 2005 and was made a European Research Council Advanced Investigator in 2009. Since 2011 he has been a Wellcome Trust Senior Investigator.

David J. Heeger is Professor of Psychology and Neural Science at New York University. His research spans an interdisciplinary cross-section of engineering, psychology and neuroscience, using functional MRI and computational theory to quantitatively investigate brain and behaviour. He received a B.A. in mathematics (1983) and a Ph.D. in computer science from the University of Pennsylvania, USA (1987). He carried out postdoctoral work at the Massachusetts Institute of Technology (MIT), USA, and has worked as a research scientist at the US National Aeronautics and Space Administration (NASA) Ames Research Center and as an assistant and then associate professor at Stanford University, California, USA (1991–2002). In 1987 he received the David Marr Prize in computer vision and in 1994 the Alfred P. Sloan Fellowship in neuroscience. He has also been awarded the Troland Award in psychology from the National Academy of Sciences (2002) and the Sokol Award in the Sciences from New York University (2006).