Current and selectivity in a model sodium channel under physiological conditions: Dynamic Monte Carlo simulations

Abstract

A reduced model of a sodium channel is analyzed using Dynamic Monte Carlo simulations. These include the first simulations of ionic current under approximately physiological ionic conditions through a model sodium channel and an analysis of how mutations of the sodium channel’s DEKA selectivity filter motif transform the channel from being Na⁺ selective to being Ca²⁺ selective. Even though the model of the pore, amino acids, and permeant ions is simplified, the model reproduces the fundamental properties of a sodium channel (e.g., 10 to 1 Na⁺ over K⁺ selectivity, Ca²⁺ exclusion, and Ca²⁺ selectivity after several point mutations). In this model pore, ions move through the pore one at a time by simple diffusion and Na⁺ versus K⁺ selectivity is due to both the larger K⁺ not fitting well into the selectivity filter that contains amino acid terminal groups and K⁺ moving more slowly (compared to Na⁺) when it is in the selectivity filter.

INTRODUCTION

Together with the potassium channel, the neuronal sodium channel is one of the two ion channels necessary for action potential propagation. Ion selectivity and permeation in potassium channels have been studied in great detail [1–5] since its crystal structure was determined [6] to understand how it conducts K⁺ instead of Na⁺. Significantly less work has been done on sodium-selective channels.

Na⁺ selectivity is seen not only in channels, but also in transporters and sodium-activated proteins like thrombin. Both crystal structures and recent theoretical work have shown that there are a number of mechanisms by which Na⁺ can be selected over K⁺. The leucine transporter LeuT is a case in point. It has two sodium binding sites [7] (and possibly three [8]) that are both rich in carbonyl and hydroxyl oxygens, but that select Na⁺ by quite different mechanisms [9]. The binding sites are similar to those of the aspartate transporter Glt_Ph [10] so two mechanisms may also be at work there. Thrombin also binds Na⁺ in an oxygen-rich environment [11].

The molecular details of Na⁺ selectivity in sodium channels is still unknown. What is known is that there are wildly different amino acid motifs present in sodium-selective ion channels. Three examples are the neuronal, epithelial, and bacterial sodium channels. These produce Na⁺ over K⁺ selectivity with completely different amino acids in the selectivity filter. Neuronal sodium channels have the DEKA locus made of an aspartate, glutamate, lysine, and alanine [12] that seem to face the permeation pathway (given their homology with L-type calcium channels for which this is true [13]). Epithelial channels (ENaC, also known as amiloride-sensitive sodium channels) have a (G/S)XS motif on each of its three different subunits [14–17] that also face the permeation pathway [18]. The bacterial sodium channels NaChBac [19] and NavAb [20] share the selectivity filter motif TLESW on each of their four identical subunits. The glutamate side chains of NavAb do not seem be facing the permeation pathway [20]. Both the neuronal and NaChBac channels have been mutated to produce Ca²⁺ over Na⁺ selectivity. For example, the mutations DEKA→DEEA and DEEE [12] and TLESW→TLEDW [21] produce calcium-selective channels. These mutations were made because many kinds of calcium channels have four aspartates and/or glutamates producing their selectivity properties. The DEKA mutations are consistent with this Ca²⁺ selectivity motif if both the aspartate and glutamate are fully charged. On the other hand, the NaChBac mutation calls into question the charge state of the native glutamate (why would eight negative charges produce a calcium channel, but not the usual calcium channel motif of four?).

NavAb is the only one with a crystal structure [20], but, because of its very recent publication, no theoretical analysis of either glutamate charge state or Na⁺ selectivity have been done. This is important because each kind of selectivity filter motif must be analyzed individually before any overarching mechanism can be deduced. In fact, Nature may use several distinct mechanisms for Na⁺ selectivity in channels, especially given the very different amino acid sequences of the three sodium channels types discussed above. This possibility is also borne out by recent theoretical studies that show that there are many ways to get Na⁺ over K⁺ selectivity (and vice versa) [3–5, 9, 22–24]. In this paper we study the selectivity mechanism of neuronal sodium channels.

Recent theoretical studies of sodium channels with the DEKA locus have generally fallen into three classes of simulations: Brownian dynamics (BD), molecular dynamics (MD), and Monte Carlo (MC). Each of these approaches have their strengths and weaknesses. For example, Vora et al. [25] used BD to show that Na⁺ versus Ca²⁺ selectivity in sodium channels is primarily an electrostatic effect. While preventing Ca²⁺ from entering the cell is an important aspect of sodium channel selectivity, the primary aspect is Na⁺ versus K⁺ selectivity. This was not addressed by Vora et al. [25].

Lipkind and Fozzard [26], on the other hand, did explore Na⁺ versus K⁺ selectivity using MD. While they studied several mutations, they did not simulate the wild-type DEKA locus directly, instead assuming that the AEKA mutant would give similar results to DEKA, as it does in experiments [27]. Their simulations showed that Na⁺ and K⁺ produced different configurations of the selectivity filter due to different electrostatic interactions between the ions and amino acids. By considering only electrostatic energies, they assume that entropic effects can be neglected so that differences in electrostatic interaction are enough to quantify selectivity. However, recent calculations in pores similarly crowded with ions and amino acid side chains show that entropic effects can contribute significantly to selectivity [28–30]. Lastly, Lipkind and Fozzard did not consider Na⁺ and K⁺ currents. Their analysis then assumes that the difference in electrostatic “happiness” of the ions determines selectivity. Instead it is possible (although admittedly unlikely) that the lower electrostatic energy of Na⁺ causes it to be trapped in the filter and not be conducted (e.g., like in the L-type calcium channel where a trapped Ca²⁺ blocks the pore, but is itself not conducted [31].)

Boda et al. [32] also studied Na⁺ versus K⁺ selectivity. Like Lipkind and Fozzard [26], Boda et al. [32] did not consider ion current, considering only ion partitioning from the bath into the channel and the relative amounts of Na⁺ and K⁺ accumulating in and near the filter, which we will call binding selectivity. Using equilibrium MC simulations, they found that selectivity in their model pore did not stem from electrostatic differences, but rather from size exclusion; the larger K⁺ could not fit into the selectivity filter nearly as easily as Na⁺. It was, however, electrostatics that caused Ca²⁺ to be rejected from the selectivity filter.

In this paper, we continue where Boda et al. left off. Using the same model of the pore, we consider not only binding selectivity (the relative occupancy of the pore), but extend the results to dynamic selectivity (the relative current through the pore). We do this using a different kind of MC simulation (Dynamic Monte Carlo, DMC) that allows us for the first time to compute ionic currents through a model sodium channel with approximately physiological ion concentrations. With DMC we can quantify both ion concentration and velocity throughout the pore in the DEKA locus and various mutants, including some that Heinemann et al. [12] showed to be Ca²⁺ over Na⁺ selective. We reproduce that result and identify the differences in ion accumulation and velocity that produce that transition. We also explore the mechanism of Na⁺ versus K⁺ selectivity by varying different model parameters. Our main goal is to describe a mechanism of selectivity using simple physics.

THEORY AND METHODS

Model of the selectivity filter

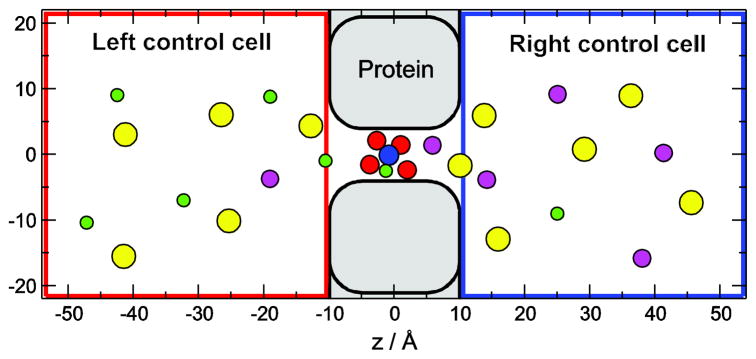
The simulation cell is shown in Fig. 1. The pore consists of a cylindrical part representing the selectivity filter (|z| < 0.5 nm) and two vestibules to the left and right of it (0.5 <|z| <1 nm). This is the part of the cell for which the DMC simulations were performed. Both the channel protein and the membrane in which it is embedded are defined by a hard wall that the ions cannot cross. The role of this channel wall is to confine ions to the selectivity filter. Unless otherwise stated, the radius of the filter is 0.35 nm.

Figure 1.

The simulation cell consists of two control cells, where concentrations are controlled by GCMC simulations, and a protein/membrane region that contains the channel. Four O^1/2− ions (red spheres) representing the COO− groups of E and D amino acid side chains as well as a NH₄⁺ ion (blue sphere) representing the amino group of the lysine (Lys⁺) are confined within the selectivity filter (|z| < 0.36 nm, |r| < R −0.14 nm, where r is the distance from the axis and R_f is the radius of the selectivity filter), but they are mobile otherwise. Green, magenta, and yellow spheres represent Na⁺, K⁺, and Cl⁻ions, respectively.

The baths on the two sides of the membrane are modeled by two rectangular control cells that are analogous to the dual control grand canonical molecular dynamics simulation technique [33, 34]. The dimensions shown in Fig. 1 are typical in our simulations. Periodic boundary conditions are applied in the x and y dimensions. In the z dimension, the control cells are externally confined by hard walls, while they are confined by the membrane/protein on the other side. The control cells and the DMC cell are “open” where they are in contact, meaning that ions can move between these cells when MC displacement steps are made. The ionic concentrations in the control cells are controlled by grand canonical Monte Carlo (GCMC) simulations where individual ion insertion/deletions were performed. The chemical potentials that correspond to prescribed ionic concentrations were determined using the Adaptive GCMC method of Malasics et al. [35, 36]. In our simulations, the baths (control cells) start at the entrances of the channel. In reality, there are transition zones of the size of at least a Debye length in these regions with considerable resistances. Because we were primarily interested in the transport mechanisms inside of the channel, we do not consider the role of these zones in this work.

We assume that the terminal groups of DEKA locus amino acids hang into the selectivity filter where they coordinate the passing cations. The model of the selectivity filter assumes that these side chains are quite flexible and the terminal groups have considerable mobility in the selectivity filter. Because of this, we assume that the COO⁻ groups of the glutamate and aspartate amino acids are indistinguishable and so we model each COO⁻ group as two half-charged oxygen ions (O^1/2−) with diameters 0.28 nm placed in the selectivity filter. The amino group of the basic lysine is represented as a positively charged ammonium ion (NH₄⁺) with diameter 0.3 nm (denoted Lys⁺). All these structural ions are allowed to move anywhere within the selectivity filter, but they cannot leave the filter. Such reduced models of selectivity filters with flexible side chains have proven very useful and insightful for both calcium and sodium channels [28–32, 37–50]. In keeping with the simplified nature of our model pore, we assume that these side chains are infinitely flexible, which of course overestimates their mobility.

Water is represented as an implicit solvent with a dielectric constant 78.5. This assumes that there is water in the pore. Our pore is ~0.24 nm wider than the NavAb selectivity filter where Na⁺ is believed to be conducted mostly hydrated [20], allowing for even more hydration in our model pore. The presence of charged and polar amino acids would also act to keep waters in the pore. (However, in both NavAb and our model pore, only atomic simulations can determine how much water is present, something that should be done in the future.)

The dielectric constant of the protein is also 78.5, reflecting a number of polar side chains near the DEKA locus (see, for example, Fig. 3 of Ref. [20]). The lack of a dielectric interface also makes the simulations significantly faster. We have shown previously that a lower protein dielectric constant increases the number of times an ion enters the pore, but, since our pore is almost always singly-occupied, it does not change the mechanism of selectivity [32].

The permeant ions of the bathing electrolytes are modeled as charged, hard spheres with Pauling diameters (0.19, 0.198, 0.266, 0.362 nm were used for Na⁺, K⁺, Ca²⁺, and Cl⁻, respectively). The temperature of the system is 298.15 K. Coulomb interactions between charges were computed for the central simulation cell only and were not computed for the charges’ periodic images, but this did not affect our results.

Lastly, a technical note. We did not use water-mediated effective interaction potentials between the ions as done by Im and Roux [51] (and others). These are short-range ion-ion interaction potentials that can be added to Coulomb and Lennard-Jones (LJ) potentials and are calibrated to reproduce bulk pair correlation functions of ions derived from MD simulations. Without these, the LJ potentials used by Im and Roux [51] reproduced those pair correlation functions poorly; the peaks were shifted by ~0.1 nm and significantly reduced in size. We do not experience this problem because we do not use LJ potentials, but rather hard-sphere potentials. This shifts the peak to the contact radius, which is at the same location as the MD ones, and the peak has a significant amplitude above bulk [52]. Although this amplitude is still below that of the MD, it is significantly larger than the LJ result of Im and Roux. Therefore, we do not believe that not using water-mediated interaction potentials will significantly affect our results.

Dynamic Monte Carlo method

In equilibrium (Metropolis) MC simulations, an ion is chosen at random and moved to a random new location. The move is accepted with a probability that ensures a Boltzmann distribution. A similar idea is used in DMC. A randomly-chosen ion from a randomly-chosen ion species (with the probability weighted according to its mole fraction) is moved to a new random position within a maximum displacement (r_max) of its old position. The distance r_max (described in more detail below) is generally small (on the order of the mean free path) so that the path taken by the ion resembles that of a MD or BD ion trajectory.

The DMC method is based on the idea that the sequence of configurations generated by a series of random particle displacements can be interpreted as a dynamic evolution of the system in time [53–55]. DMC reproduces dynamic properties such as the mean-square displacement, although it does not generate deterministic trajectories. In contrast to MD, DMC does not guarantee an absolute measure of physical time; it only ensures proportionality. Time is expressed as the number of trial MC steps (MCS). Our simulations were performed using the DMC algorithm of Rutkai and Kristóf [55] because it ensures that the relative dynamics of the ion species is correct.

The key parameter of the algorithm is the maximum displacement r_max. Calculations in Ref. [55] show that the main determinant of r_max is the density of the all-atom system being modeled. In MD simulations with explicit waters, r_max is adjusted to match the mean free paths in the DMC results and MD simulations of the same system [55]. In an implicit solvent model, however, it is not the mean free path of the ion gas that determines r_max. Like in BD where dynamic interactions with water are taken into account with a random force in the Langevin equation, a small value for r_max must be used for DMC with implicit water to approximate the mean free path of the ions in explicit water. We used the value 0.1 nm because it is in the ballpark of values used in liquids. Although we observed some sensitivity of our quantitative results to the value of r_max, we did not change the 0.1 nm value in our calculations, because we are interested in qualitative results. Changing r_max did not influence our qualitative conclusions.

DMC has parallels with other dynamic particle simulation methods. In MD simualtions, ions are moved deterministically in the direction of the force acting on them. In BD simulations, they move in these directions only on average because, while these deterministic forces are still present, the random forces expressing collisions with water change the trajectories stochastically. In DMC simulations, ions are also moved in the directions of forces on average because moves attempted into the direction of decreasing energy are accepted with higher probability.

The total flux of ion species i through the channel in z-direction ( $J_i^{(z)}$) was calculated by counting the net movement of particles for species i from left-to-right and from right-to-left through a properly selected x–y reference plane in a given MCS time interval. Although the total flux of species i is constant inside the pore due to conservation of mass, the flux profile $J_i^{(z)}(z)$ can also be determined from the sum of the z-components of the accepted displacements of particles. This procedure has two benefits. First, $J_i^{(z)}(z)$ computed this way provides the opportunity to crosscheck the results obtained by counting particles crossing the entrance of the pore. Second, the drift velocity $v_i^{(z)}(z)$, which is the average distance covered by the individual particles of species i in the z-direction per MCS, can be calculated from the equation

$$J_i^{(z)}(z)=n_i(z)v_i^z(z)$$ (1)

where n_i (z) is the number of ions per unit (axial) distance (i.e., the ion concentration integrated over the cross-sectional area at z). All the results that we will show in this work provide constant $J_i^{(z)}(z)$ profiles and the value of this constant agreed with the value obtained from counting ions crossing the channel. For ease of notation, we drop the (z) superscript for J_i.

The typical length of the simulations was 10¹¹ MC moves, including about 50% particle insertions and deletions in the GCMC simulations for the control cells.

In our simulations, the driving force for the ions is only their concentration gradients. An applied voltage to drive the ions is not currently part of the simulation. A membrane potential contributes to the conductance and is an important driving force for the ions and can affect ion-ion correlations. Since we ignore these, it is best to interpret our simulations as occurring at small voltages. However, in unpublished work on the ryanodine receptor calcium channel where current-voltage curves are computed, one of the authors (DG) has found only small changes in response to applied voltages (even up to ~100 mV) to ion density profiles like those we show later of both permeating and protein ions. Therefore, we do not expect the selectivity mechanism we describe to change with an applied voltage.

RESULTS AND DISCUSSION

Mechanism of ion permeation

Experimental measurements of Na⁺ Ussing flux ratio [56] indicate that there is no flux coupling as ions cross the sodium channel; Rokowski et al. [57] measured it to be 0.97±0.03. The Ussing flux ratio is more than 1 when ions exchange momentum, such as during single-file permeation. On the other hand, an Ussing flux ratio of 1 indicates a diffusive process. This is what we find in our model.

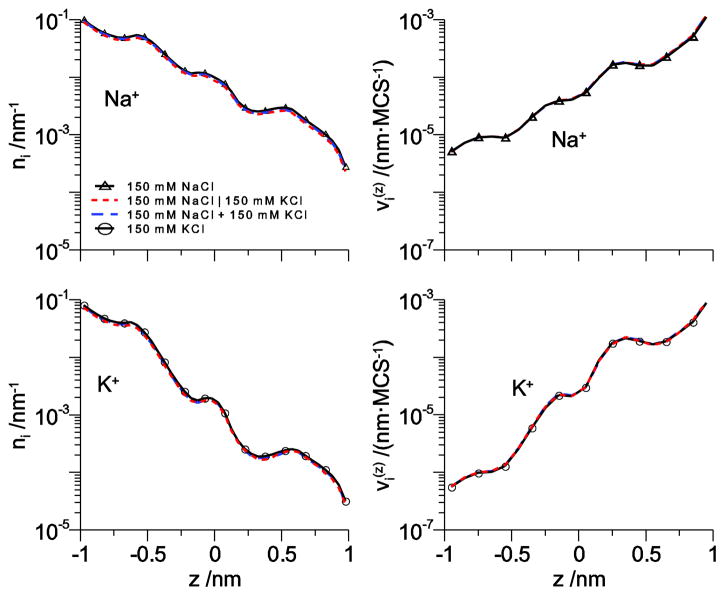
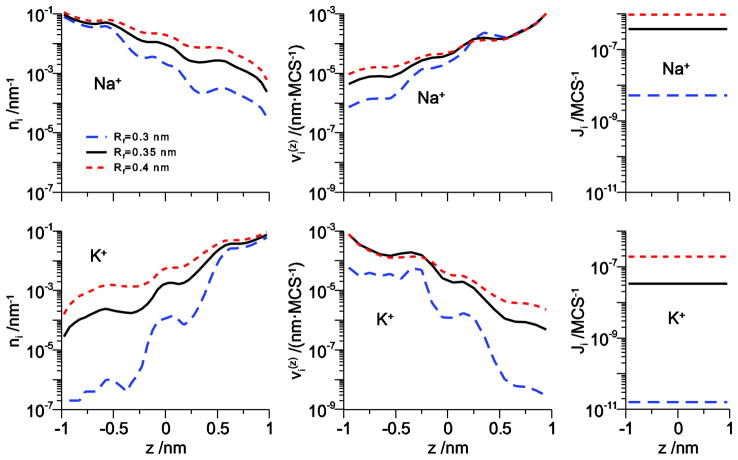
To see this, we consider the conduction of Na⁺ and K⁺ through our model pore at 150 mM bath concentration. Fig. 2 shows both the line density n (z) and the drift velocity $v_i^{(z)}(z)$ for both Na⁺ and K⁺ and Fig. 3 shows the line densities for the amino acid terminal groups, the four O^1/2− of the aspartate and glutamate and the NH₄⁺ of the lysine. In Fig. 2, several cases are shown: (1) no K⁺ is present and only Na⁺ is in the left bath, (2) no Na⁺ is present and only K⁺ is in the left bath, (3) both Na⁺ and K⁺ are in the left bath and neither is in the right bath, and (4) Na⁺ and K⁺ are on separate sides of the membrane (physiological). The results of all of these simulations are the same, indicating that the ions do not interact as they cross the pore.

Figure 2.

The line density n (z) (left column) and ion velocity $v_i^{(z)}(z)$ (right column) across the channel for Na⁺ (top row) and K⁺ (bottom row) for Na⁺ and K⁺ at 150 mM concentration in one bath. Triangles: 150 mM NaCl in the left bath; dotted line: 150 mM NaCl in the left bath and 150 mM KCl in the right bath (for clarity, the K⁺ profiles have been reversed to run from −1 to 1 so they can be directly compared to the other curves); dashed line: 150 mM NaCl and 150 mM KCl in the left bath; circles: 150 mM KCl in the left bath. All other bath concentrations are 0.

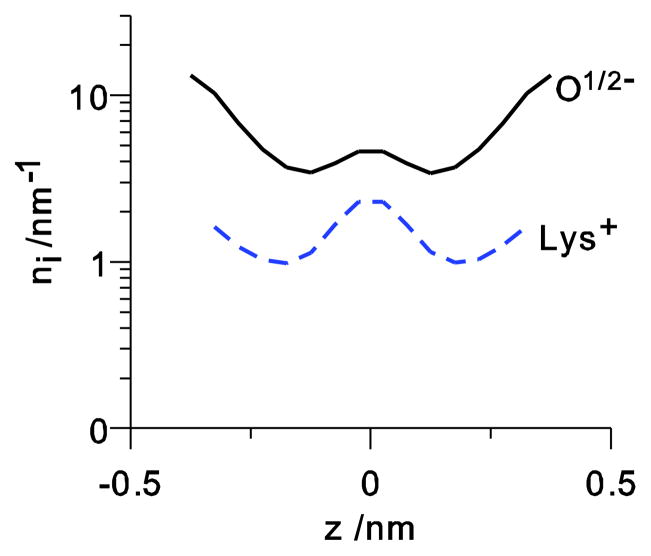
Figure 3.

The line density profiles of the four O^1/2− and the lysine (NH₄⁺) for the bi-ionic conditions where Na⁺ and K⁺ are at 150 mM concentration in the left and right baths, respectively.

To understand why this is, we analyzed the percent of times that the ions spent in the selectivity filter. The results are shown in Table 1. The selectivity filter is empty the vast majority of the time (>98%). In a previous study, Boda et al. showed that this is because cations tend to accumulate just outside the selectivity filter, preferring to screen from there because it is entropically unfavorable to enter the filter that is occupied by amino acid side chains [32]. When ions are in the filter, it is almost always a single ion. In fact, the ratio of times of one Na⁺ to two cations in the filter is ~400:1. This indicates that one ion is not being “kicked” by another to move across the pore as in a knock-on or knock-off mechanism (as proposed by Vora et al. [25]). Combined with the fact that the filter does not mind being empty, it seems ions cross the pore by simple diffusion, with a single cation entering an empty selectivity filter, diffusing across, and leaving an empty pore until the next cation enters. This mechanism would give an Ussing flux ratio of 1, consistent with the experiments Rokowski et al. [57].

Table 1.

The percentage of all DMC steps is shown for each combination of ions in the selectivity filter. For the data shown here, 150 mM of each Na⁺ and K⁺ were in both baths on each side of the membrane. The results for other conditions shown in Fig. 2 are similar.

Percentage of ion combinations in the selectivity filter
0 Na+ & 0 K+	1 Na+ & 0 K+	2 Na+ & 0 K+	0 Na+ & 1 K+	1 Na+ & 1 K+	0 Na+ & 2 K+
98.5964%	1.1092%	0.0015%	0.2916%	0.0013%	<0.0001%

The classical picture of ion permeation usually involved single filing of ions with ions hopping over energy barriers. One example of this kind of modeling for sodium channels was done by Ravindran et al [58]. Since our pore contains at most one cation, we cannot assess whether ions can pass each other or not. However, our analysis indicates ion diffusion through the selectivity filter that contains the terminal groups of the DEKA amino acids; there are no static energetic barriers to overcome. This can be seen, for example, in the velocity profiles of the ions in Fig. 2. There are no deep wells where an ion is “stuck”.

As a result, our model pore has a linear current versus mole fraction relationship for mixtures of Na⁺ and K⁺. This is consistent with the experiments of Ravindran et al. [58] on batrachotoxin-modified sodium channels who found only a small nonlinearity in their mole fraction measurements. Their current versus mole fraction curves (done under symmetric ion conditions) were slightly superlinear for positive voltage and slightly sublinear for negative voltages, indicating an asymmetry in the pore structure that is not included in our symmetric model pore.

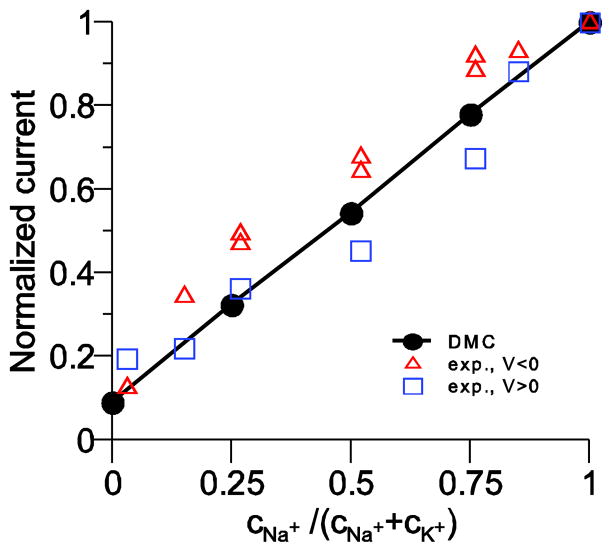
A direct comparison with their data is not possible because our simulations only give ion flux as ions per MCS not ions per second. We can, however, compare normalized currents. This is done in Fig. 4 where the current is normalized to the current at Na⁺ mole fraction 1. The comparison shows not only that the model reproduces the experiment, but also that the model reproduces the correct Na⁺ to K⁺ current ratio. The difference in Na⁺ and K⁺ currents are solely due to the difficulty that the larger K⁺ has moving through the crowded selectivity filter.

Figure 4.

Normalized current versus mole fraction of Na⁺ in mixtures of Na⁺ and K⁺. Our model results are the line and the experiments are the symbols. The squares are for an applied voltage of +50 mV and the triangles for −50 mV. The experiments are performed under symmetric ionic conditions, while the simulations were done with ions only in one bath because we cannot presently apply a voltage across the membrane. However, we expect that the results are comparable because the large voltages used in the experiments would drive ions in only one direction.

Mechanism of Na⁺ versus K⁺ selectivity

This ability of Na⁺ to more easily move through the selectivity filter (as compared to K⁺), is an important aspect of Na⁺ versus K⁺ selectivity, which is the sodium channel’s most important physiological role. In vivo, it is the ratio of inward Na⁺ flux and outward K⁺ flux that ultimately defines the selectivity of the sodium channel. Therefore, we will focus on this quantity.

Experiments—unable to directly measure individual Na⁺ and K⁺ fluxes—show that the Na⁺ to K⁺ permeability ratio of wild-type sodium channels ranges between ~12 [59] and ~33 [27]. As shown in Table 2, our model channel has a Na⁺ to K⁺ flux ratio of 11, in line with these permeability ratios. Interestingly, the flux ratio is not the same as the occupancy ratio for these ions (Table 2); that is, each ion species’ current is not proportional to the average number of that species in the filter (N_i for species i).

Table 2.

The ratios of Na⁺ to K⁺ current (J_Na⁺ / J_K⁺), Na⁺ to K⁺ occupancy (N_Na⁺ / N_K⁺) in the filter and in the entire pore for different pore radii (R_f). Occupancy is the average number of ions whose centers are in the filter (| z |< 0.5 nm) or in the whole channel (| z |<1 nm). In all cases, there was 150 mM NaCl in the left bath and 150 mM KCl in the right bath, the physiological separation of ions. The amino acid (aa) space-filled fraction is shown in the last column.

Ratios of Na+ to K+ currents and occupancy
filter ions	filter radius Rf	JNa+ / JK+	NNa+ / NK+ (filter)	NNa+ / NK+ (channel)	aa space-filled fraction
DEKA (4 O1/2 +Lys+)	0.35 nm	11.12	3.75	1.62	0.156
DEKA	0.3 nm	326	8.39	1.62	0.213
DEKA	0.4 nm	5.04	2.70	1.57	0.120
4 O1/4− +Lys0	0.35 nm	9.86	3.55	1.52	0.156
4 O1/4−, no Lys	0.35 nm	6.51	2.89	1.55	0.121

In general, Na⁺ occupies the pore 3.75 times more often than K⁺ (Table 2), meaning that the channel is Na⁺ selective over K⁺ from an ion binding (accumulation) point of view. This is how Boda et al. [32] defined selectivity in their equilibrium simulations of the sodium channel. Our simulations are consistent with those results, but they also show that not only is K⁺ excluded from the space between protein side chains (as previously shown [32]), but—on average—it moves through the pore more slowly so the Na⁺ to K⁺ flux ratio is 3 times larger than the occupancy ratio (Table 2).

We can analyze how crowding of the selectivity filter lumen affects both ion occupancy and flux ratios by changing some parameters in our model. Boda et al. [32] showed that Na⁺ versus K⁺ selectivity was sensitively affected by the filter radius (R_f). Making the pore more narrow makes the pore more crowded by increasing the fraction of the available space taken up by the amino acids. This increased Na⁺ binding affinity, while making the pore less crowded by increasing the filter radius had the opposite effect.

The density and velocity profiles of Na⁺ and K⁺ show that the same thing is true when the pore radius changes in the DMC simulations. Fig. 5 shows that while decreasing the pore radius affects Na⁺, it has a disproportionate effect on K⁺, both on concentration and velocity. For example, on the dilute side (right for Na⁺ and left for K⁺ under these bi-ionic conditions) both Na⁺ concentration and velocity decrease <1 order of magnitude in the 0.3 nm-radius pore compared to the 0.35 nm-radius pore. However, K⁺ concentration decreases more than two orders of magnitude and K⁺ velocity decreases one order of magnitude. Together, these combine to decrease Na⁺ flux by <100 fold (Fig. 4, right column) while K⁺ flux decreases >1000 fold. This indicates that K⁺ is not only found less often in this more narrow channel than Na⁺, but also that when it is there it moves much more slowly (compared to the wider pore).

Figure 5.

The line density n (z) (left column) and ion velocity $v_i^{(z)}(z)$ (right column) across the channel for Na⁺ (top row) and K⁺ (bottom row) for Na⁺ and K⁺ at 150 mM concentration in one bath as the pore radius R_f is varied.

Table 2 summarizes the effect of different filter radii on both occupancy ratio (N_Na⁺ / N_K⁺) and flux ratio (J_Na⁺ / J_K⁺). For our reference radius of 0.35 nm, the amino acid terminal group ions (the 4 O^1/2− and Lys⁺) occupy 15.6% of the available space in the cylinder that defines the selectivity filter. This increases to 21.3% for a filter radius of 0.3 nm and decreases to 12.0% for 0.4 nm. These seemingly small differences make large nonlinear changes in both the occupancy and the flux ratios (Table 2).

When the pore is more narrow, the occupancy ratio increases from 3.75 to 8.39, in line with the results of Boda et al. [32]. However, the flux ratio jumps disproportionately from 11.12 to 326 (Table 2). Now K⁺ has a more difficult time getting into the filter (as measured by the change in occupancy ratio), but it has an even more difficult time moving to the other side of the pore (as measured by the change in flux ratio). The story is reversed when the pore is wider. Compared to the 0.35 nm-radius pore, the Na⁺ to K⁺ occupancy ratio drops 28% to 2.70 while the flux ratio drops 55% to 5, indicating easier K⁺ entry and substantially easier K⁺ movement in the wider pore.

To underscore the idea that it is the crowding within the selectivity filter that drives Na⁺ versus K⁺ selectivity in our model, we consider two other selectivity filters. Both of these are unphysical, but are included to illustrate that we can change the crowding in different ways and get the same Na⁺ versus K⁺ selectivity. In the first channel, we keep both the space-filled fraction of the amino acid ions and the net charge of the filter unchanged (at 15.6% and −1, respectively), but remove the charge from the lysine (Lys⁺→Lys⁰) and compensate by halving the charge of the oxygens (O^1/2− →O^1/4−). Table 2 shows that this pore has Na⁺ to K⁺ flux and occupancy ratios similar to the WT DEKA locus. In the second pore, we remove the lysine from the filter and keep the −1 net charge of the pore by again halving the charge of the oxygens (O^1/2− →O^1/4−). The decreased space-filled fraction of the amino acids of 12.0% is the same as the wide pore considered earlier when the pore radius was 0.4 nm. Table 2 shows that these two pores have similar Na⁺ to K⁺ flux and occupancy ratios. These ratios, on the other hand, are reduced compared to the case when Lys⁰ is present. This indicates that in this model the role of the bulky terminal group of the lysine is to exclude K⁺ from the filter (as suggested earlier [32]) and be an obstacle in the permeation pathway of K⁺.

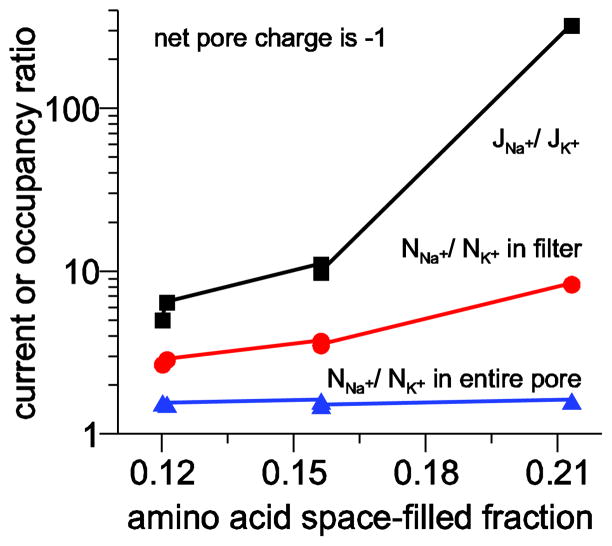
The selectivity versus crowding relationship is summarized in Fig. 6 where the Na⁺ to K⁺ flux and occupancy (both in the filter and in the entire pore) ratios are plotted as a function of amino acid space-filled fraction. Not only does this graph illustrate that two channels with the same crowding have similar selectivity, it illustrates the very nonlinear relationship between these variables even in seemingly dilute filters (e.g., increasing space-filled fraction from 12% to 16% produces large changes in both flux and filter occupancy ratios). This relationship is especially steep for the flux ratio, which can change by more than an order magnitude.

Figure 6.

Relationship between crowding and Na⁺ versus K⁺ selectivity. Flux ratio is shown with squares, filter occupancy ratio with circles, and pore occupancy ratio with triangles. The channels are those described in Table 2 and all have a net charge of −1.

Mutating a sodium channel into a calcium channel

An important aspect of sodium channels that a model should explain is their close relationship to calcium channels. Specifically, Heinemann et al. [12] showed that point mutations of either the lysine or the alanine of the DEKA locus to glutamate confer Ca²⁺ selectivity on a sodium channel. Further mutation studies showed that stepping the pore charge from −1 to −4 by adding one negative charge at a time (e.g., DEKA→DEKE→DEEA→DEEE) produced more and more Ca²⁺-selective channels [60]. Because these are simple point mutations, a model of sodium channels should strive to explain how this transition occurs.

In our model pore we make these three mutations by adding two more O^1/2− for every added glutamate and removing the Lys⁺ in some cases. This changes both the charge of the pore and the crowding. Previous studies by our co-workers and us have shown how a DEEE locus (using the same model of the pore, ions, and amino acids) is selective for Ca²⁺ over monovalents [28, 29, 31, 37–49], including two extensive analyses of the energetics of selectivity [28, 29]. In short, the four charges of the glutamates attract cations into the pore, but, because the filter is very crowded, it is energetically easier for small multivalent ions (e.g., Ca²⁺) to find space and be coordinated by the glutamate oxygens [37]. Our co-workers and we have also shown that with equilibrium MC simulations that the DEKA to DEEA mutation changes the pore from Na⁺ selective to Ca²⁺ selective [32].

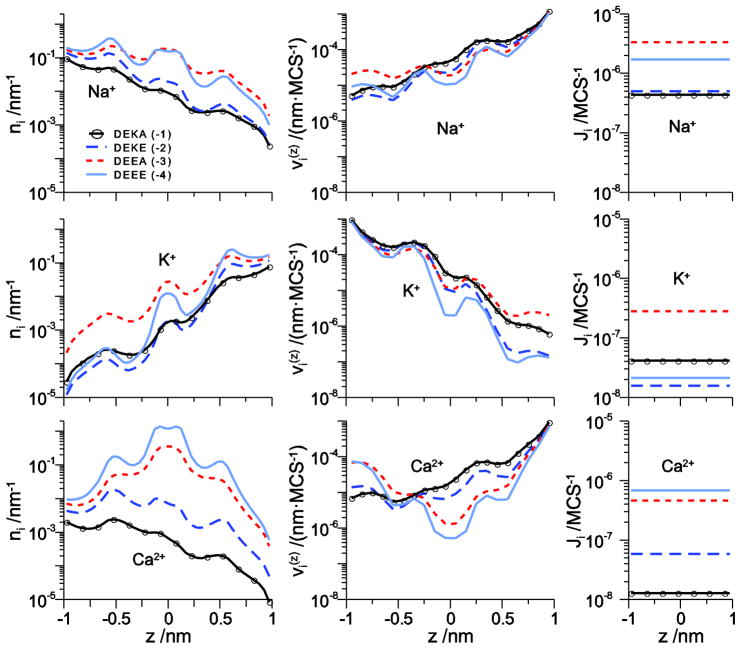
Here, for the first time we explore the transition from monovalent cation selectivity to Ca²⁺ selectivity as the pore charge is varied from −1 to −4. The concentration and velocity profiles of Na⁺, K⁺, and Ca²⁺ under approximately physiological ionic conditions is shown in Fig. 7 for DEKA, DEKE, DEEA, and DEEE selectivity filters. For the Na⁺ selective DEKA locus (solid line with circles), Ca²⁺ is rarely in the filter (it has low filter concentration) because it is not electrostatically favorable for a +2 charge to move through the pore with −1 net charge, as shown previously [32]. As the net charge of the filter increases from −2 to −3 to −4 (long-dashed, dashed, and solid lines, respectively), the Ca²⁺ concentration in the filter increases. The Na⁺ and K⁺ concentrations also increase, but proportionately much less than Ca²⁺. The net effect is more Ca²⁺ in the filter than monovalents; the pore is Ca²⁺ selective.

Figure 7.

The line density n_i (z) (left column) and ion velocity $v_i^{(z)}(z)$ (right column) across the channel for Na⁺ (top row), K⁺ (middle row), and Ca²⁺ (bottom row) for Na⁺ and K⁺ at 150 mM concentration in the left and right baths, respectively, and 3 mM Ca²⁺ in the left bath. The different lines are for different mutations of the filter amino acids: DEKA with net charge −1 (solid line with circles), DEKE with net charge −2 (long-dashed line), DEEA with net charge −3 (dashed line), and DEEE with net charge −4 (solid line).

At the same time that cation concentrations are increasing in the filter, their velocities are generally decreasing (with the exception of Ca²⁺ velocity in the left vestibule). The increased charge and crowding is slowing the ions down. In fact, Ca²⁺ velocity is decreased by almost two orders of magnitude. However, because Ca²⁺ concentration in the filter increased by more than two orders of magnitude, Ca²⁺ flux actually increases as the filter charge increases (Fig. 7, right column). This was found in our simulations of the EEEE calcium channel locus: the large charge of the filter binds Ca²⁺ very effectively. significantly reducing its velocity in the filter.

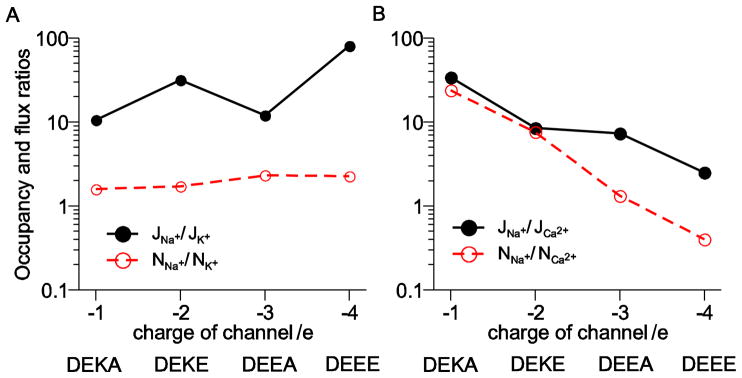
The selectivity properties of these four channels is summarized in Fig. 8. There flux and occupancy ratios for Na⁺ versus K⁺ (Fig. 8A) and Na⁺ versus Ca²⁺ (Fig. 8B) are shown. For all these channels the Na⁺ to K⁺ occupancy ratio is relatively constant, but because the pore crowding changes with each mutation, the flux ratio does change. (The Na⁺ to K⁺ flux ratio is not monotonic because the DEKE filter with −2 charge is less crowded than the DEEA filter with −3 charge.)

Figure 8.

Occupancy and flux ratios for the DEKA locus and three mutations (DEKE, DEEA, and DEEE) plotted as a function of net filter charge. (A) Ratios for Na⁺ and K⁺. (B) Ratios for Na⁺ and Ca²⁺.

On the other hand, both the Na⁺ to Ca²⁺ occupancy and flux ratios decrease monotonically as the pore becomes more and more Ca²⁺ selective. For the DEKA and DEKE loci, the Na⁺ and Ca²⁺ flux and occupancy ratios are similar, while they are very different for the DEEA and DEEE loci; the Na⁺ to Ca²⁺ occupancy ratio is much smaller than the flux ratio. This is because the DEEE locus binds Ca²⁺ more effectively than Na⁺, but it does not conduct the Ca²⁺ well due to the its limited mobility (Fig. 7). This is in agreement with our previous DMC simulations of a calcium channel [61].

CONCLUSION

We have performed the first direct particle simulations of ionic current through a model sodium channel under both bi-ionic (Fig. 2) and approximately physiological ionic concentrations (Fig. 7). These show that, in this model, a single ion moves through the pore at one time via a simple diffusion mechanism. Na⁺ versus K⁺ selectivity is due to a combination of the larger K⁺ having a more difficult time (compared to Na⁺) fitting into the selectivity filter and having a more difficult time moving through the pore when it does get in. We have also shown the transition of concentration and velocity profiles for a series of mutations that change the Na⁺-selective DEKA locus into the Ca²⁺-selective DEEE locus (Fig. 7).

The mechanism of selectivity we find relies on the pore being narrow, a concept that goes all the back to Mullins [62]. A narrow pore is also part of potassium channel selectivity, but our pore is narrow in a very different way than potassium channels are narrow. Potassium channel selectivity filters are narrow enough to force single filing of ions; the protein acts like a tight sleeve through which the ions travel [6]. This forces waters to be stripped off the ions and become resolvated in the protein atoms [2, 3, 5, 22, 23, 63]. Selectivity is then the balance of two large energies, dehydration and coordination by the protein.

Our model selectivity filter is several angstroms wider than a potassium channel or NavAb sodium channel filter [6, 20]. At 0.7 nm in diameter, it is wide enough to accommodate a substantially hydrated Na⁺ ion. Although not having explicit water in the model is a limitation in exploring this point, even the more narrow NavAb sodium channel is believed to conduct Na⁺ ions “in a mostly hydrated form” [20]. This is probably necessary for all Na⁺ over K⁺ selectivity because, if there were substantial ion dehydration, the dehydration energies would favor K⁺ selectivity. (The impact of ion dehydration does, however, deserve more attention and is part of our on-going work [64].) The exclusion of K⁺ is then by size because the amino acid side chains take up space within the permeation pathway. It has previously been shown how this can lead to Na⁺ over K⁺ selectivity even in systems without the confining geometry of a pore [30, 37, 65]. The role of the pore then is to provide a filter that is crowded with enough amino acid side chains to hinder K⁺, but not a filter that is so narrow and crowded that it forces substantial ion dehydration, like the potassium channel does.

The model we have used is the simplest possible, and possibly overly simple. It includes only hard-sphere ions to represent both the permeant ions and amino acid terminal groups. It does not include other physics like ion dehydration or a different dielectric constant for the protein (the effect of which our co-workers and we have analyzed in previous studies [32, 42, 43]). Extra physics may be necessary to explain some of the experimental results that we do not reproduce. For example, the DEEA and DEEE pores do not seem to distinguish between Na⁺ and K⁺ [60] like our model pores do (Fig. 8A). Also, mutations of the lysine to other basic amino acids (histidine and arginine) decrease Na⁺ versus K⁺ selectivity [27]. Our model would predict the opposite because these amino acids would increase pore crowding. However, it is quite plausible (and, unfortunately, impossible to rule out) that it is not possible to form, in vivo, the narrow pore required for Na⁺ versus K⁺ selectivity with these much more bulky amino acids.

There is then certainly room for improvement in the model, but our purpose for the simulations is not a detailed model of reality. Rather, it is to show that with some very simple physics it is possible to recreate the fundamental—and physiologically most important—properties of neuronal sodium channels. These include Na⁺ versus K⁺ selectivity and Ca²⁺ exclusion, as well as the close kinship that sodium channels share with calcium channels. To our knowledge, no other model of a sodium channel has demonstrated all of these properties or computed ionic currents that exhibited these properties.

Highlights.

• Selectivity and permeation in model sodium channel studied with Dynamic Monte Carlo

• Ion permeation is single ion moving by simple diffusion

• Model reproduces Na⁺ vs. K⁺ selectivity, Ca²⁺ exclusion, DEKA to DEEE mutations

• Na⁺ vs. K⁺ selectivity: K⁺ excluded from crowded pore and moves slower through pore

• Point mutations DEKA→DEEE makes calcium channel, reproducing experiments