Nuclear Resonance Vibrational Spectra of Five-Coordinate Imidazole-ligated Iron(II) Porphyrinates

Abstract

Nuclear resonance vibrational spectra have been obtained for six five-coordinate imidazole-ligated iron(II) porphyrinates, [Fe(Por)(L)] (Por = tetraphenylporphyrinate, octaethylporphyrinate, tetratolylporphyrinate or protoporphyrinate IX and L = 2-methylimidazole or 1,2-dimethylimidazole). Measurements have been made on both powder and oriented crystal samples. The spectra are dominated by strong signals around 200–300 cm⁻¹. Although the in-plane and out-of-plane vibrations are seriously overlapped, oriented crystal spectra allow their deconvolution. Thus, oriented crystal experimental data, along with DFT calculations, enable the assignment of key vibrations in the spectra. Molecular dynamics are also discussed. The nature of the Fe–N_Im vibrations has been elaborated further than was possible from resonance Raman studies. Our study suggests that the Fe motions are coupled with the porphyrin core and peripheral groups motions. Both peripheral groups and their conformations have significant influence on the vibrational spectra (position and shape).

Introduction

The five-coordinate histidine-ligated deoxyhemoglobin and -myoglobin species have been of interest in many fields; a variety of methods have been used to study these proteins and their model complexes. Among them, vibrational spectroscopy provides an incisive probe of their structure, dynamics, and reactivity. For example, resonance Raman¹ and infrared difference spectroscopy² have been intensively applied in such studies. But selection rules inherent to infrared and Raman spectroscopies restrict the observation of many important active-site vibrations. In fact, in-plane vibrations of the heme Fe, which would probe the strength of the Fe–N_p bonds,³ are Raman inactive.^{1, 4} At low frequencies, solvent absorption and other experimental challenges also limit infrared studies. So reactive modes, such as doming modes at low frequencies,^{5, 6} are rarely identified with these traditional techniques.

The shortcomings of optical techniques can be overcome with nuclear resonance vibrational spectroscopy (NRVS), a synchrotron-based technique. NRVS is selective for vibrations involving displacement of Mössbauer active nuclei[these include ⁸³Kr, ¹¹⁹Sn, ¹⁵⁷Eu, and especially ⁵⁷Fe.^7–22 The NRVS experiment can be thought of as Mössbauer spectroscopy with vibrational sidebands.²³ Distinct from Raman and infrared spectroscopy, NRVS is not subject to the optical selection rules. All iron–ligand modes can be observed, including many that had not been previously observed. For hemes, these include in-plane Fe vibrations, which have not been reported in resonance Raman investigations, and the Fe–imidazole stretch, which has not been identified in six-coordinate porphyrinates. Other low frequency vibrations, including heme doming, can also be investigated by NRVS. Thus, the NRVS experiment can provide the complete set of bands corresponding to modes that involve motion of the iron atom. On the other hand, only iron vibrations are observed, which eliminates solvent interference.

As models of deoxyhemoglobin and deoxymyoglobin, imidazole-ligated, five-coordinate iron(II) species have been intensively studied. One of these, [Fe(TPP)(2-MeHIm)], has been investigated previously by NRVS.²⁴ In that investigation, Rai et al.²⁴ have reported the iron normal mode dynamics study, and have applied normal mode calculations to assign all the important iron modes, including in-plane and out-of-plane modes. In this paper, we present more complete NRVS studies on six model complexes of deoxymyoglobin, [Fe(TPP)(2-MeHIm)], [Fe(OEP)(2-MeHIm)], [Fe(TPP)(1,2-Me₂Im)], [Fe(OEP)(1,2-Me₂Im)], [Fe(PPIX)(2-MeHIm)] and [Fe(TTP)(1,2-Me₂Im)], based on porphyrins with different peripheral substituents (TPP, TTP, OEP, PPIX) and different axial ligands (2-methylimidazole and 1,2-dimethylimidazole). Instead of classical normal mode calculations, density functional theory (DFT) has been used for mode analysis on the complete molecules rather than a truncated model system. These quantum chemical calculations do not rely on empirical force constants or require prior knowledge of related molecules to constrain the potential. Through DFT calculations, Fe-involving vibrational dynamics can be predicted.^{10, 11, 13, 25–32} Our studies show that their vibrations are congested over the 200–300 cm⁻¹ region and both in-plane and out-of-plane modes are seriously overlapped. Based on experimental powder, oriented single-crystal measurements and DFT calculations, all of the important iron modes have been assigned, and the influence of peripheral substituents and their conformations on the iron-associated vibrations has been discussed.

Experimental Section

Porphyrin Synthesis

⁵⁷Fe-enriched porphyrinates were prepared using a modified small-scale metalation procedure described by Landergren and Baltzer.³³ The ⁵⁷Fe₂O₃ used in the ⁵⁷Fe labeled complexes was purchased from Cambridge Isotopes. All imidazoles were purchased from Sigma-Aldrich. The syntheses of [Fe(OEP)(2-MeHIm)],³⁴ [Fe(OEP)(1,2-Me₂Im)]³⁴ and [Fe(TPP)(1,2-Me₂Im)]³⁵ were described previously. [Fe(TTP)(1,2-Me₂Im)] was prepared as the same method as that for [Fe(TPP)(1,2-Me₂Im)]. Micelle-encapsulated [Fe(PPIX)(2-MeHIm)] was prepared by dissolving ⁵⁷Fe-enriched Fe(PPIX)(Cl), purchased from Frontier Scientific, in 0.1 M phosphate buffer pH 7.0 containing ~0.5 M 2-MeHIm and 1% (w/v) cetyltrimethylammonium bromide (CTAB), concentrating to approximately 80 mM, deoxygenating under a stream of argon gas, and and adding an excess of sodium dithionite.

NRVS Measurements and Analysis

NRVS measurements were performed at Sector 3-ID-D of the Advanced Photon Source at Argonne National Laboratory. The sample was placed in a monochromatic X-ray beam, whose energy was scanned through the 14.4 keV ⁵⁷Fe resonance using a high-resolution monochromator³⁶ with an energy bandwidth (full width at half-maximum) of 8 cm⁻¹ (1.0 meV). X-rays were distributed across a 4 × 1 mm² beam cross section and arrived as a train of pulses 70 ps wide at 154-ns intervals, with an average flux of 2 × 10⁹ photons/s = 4.6 microW at 14.4 keV incident on the sample. An avalanche photodiode detected photons emitted by the excited ⁵⁷Fe atoms, which arrive with a delay on the order of the 140 ns ⁵⁷Fe excited-state lifetime. The counter was disabled during a time interval containing the arrival time of the X-ray pulse, to suppress the large background of electronically scattered 14.4 keV photons, which arrived in coincidence with the X-ray pulse.

Polycrystalline powders were prepared by immobilization of the crystalline material in Apiezon M grease. The samples were loaded into polyethylene sample cups and mounted on a cryostat cooled by a flow of liquid He, with X-ray access through a beryllium dome. Crystals of [Fe(TPP)(2-MeHIm)] and [Fe(OEP)(2-MeHIm)] were mounted in an inert-atmosphere dry box. The crystals were mounted in a 2-mm-diameter, thin-walled (0.01 mm), boron-rich, X-ray diffraction capillary tubes that were purchased from the Charles Supper Company. The crystals were immobilized in the capillary tube with a small amount of Dow Corning high-vacuum grease. The capillary tube was sealed and secured to a small length of 18-gauge copper wire with epoxy. The copper wire was then secured with epoxy to a brass mounting pin. The copper wire allowed for enough flexibility to make minor adjustments in the orientation of the crystal. The brass mounting pin, holding the crystal, was then mounted on a eucentric goniometer head to allow for further fine adjustments in the orientation of the crystal. Data were recorded in two orthogonal orientations related by rotation about an axis orthogonal to the X-ray beam. Crystal orientations were verified by X-ray diffraction before and after the NRVS measurements. A stream of cold N₂ gas from a Oxford Instruments cryocooler controlled the crystal temperature during NRVS measurements.

[Fe(OEP)(2-MeHIm)] crystallizes in space group P1̄ with a single porphyrin in the asymmetric unit so all porphyrin planes are parallel to each other in the crystal structure. An ⁵⁷Fe-enriched single crystal with dimensions 2.0 × 0.5 × 0.4 mm³ was oriented with a selected crystallographic plane parallel both to the X-ray beam and to the goniometer rotation axis. The chosen {6, 6, 17} plane lies 1.3° from the mean plane of the four pyrrole nitrogens. This procedure ensures that only Fe motion parallel to the porphyrin plane contributes to the NRVS signal recorded in the original orientation. A second data set, recorded after a 90° rotation about the goniometer axis, sampled Fe motion perpendicular to the porphyrin plane.³⁷

A spectrum recorded as a function of X-ray energy consists of a central resonance, due to recoilless excitation of the ⁵⁷Fe nuclear excited state at E₀ = 14.4 keV, together with a series of sidebands corresponding to creation or annihilation of vibrational quanta of frequency ν̄. The sidebands have an area proportional to the mean squared displacement of the Fe and are displaced from the recoilless absorption by an energy hcν̄.^{38, 39} Normalization of this spectrum according to Lipkin’s sum rule⁴⁰ yields the excitation probability S(ν̄) with peak areas for each mode representing the mean-square amplitude of the Fe. Subtraction of the central resonance results in a vibrational excitation probability S′(ν̄).

The program PHOENIX⁴¹ removes temperature factors, multiphonon contributions, and an overall factor proportional to inverse frequency from S′(ν̄) to yield an Fe-weighted vibrational density of states (VDOS), which defines the vibrational properties at all temperatures for a harmonic system. Within the harmonic approximation, the Fourier-log deconvolution procedure employed by PHOENIX is rigorous for a single ⁵⁷Fe site in an oriented sample or in a randomly oriented sample that is vibrationally isotropic.

Measurements were recorded at low temperatures to minimize multiphonon contributions. The requirement that the ratio S′(ν̄)/S′(−ν̄) equal the Boltzmann factor exp(hcν̄/k_BT) yields the sample temperature. Temperatures determined in this way are more reliable than the readings from a sensor mounted below the sample, which are typically 10–15 K lower. For randomly oriented powder samples, we obtained 15 K for [Fe(OEP)(2-MeHIm)], 35 K for [Fe(OEP)(1,2-Me₂Im)], 27 K for [Fe(TPP)(1,2-Me₂Im)], 35 K for [Fe(PPIX)(2-MeHIm)], 21 K for [Fe(TTP)(1,2-Me₂Im)]. For single crystal samples, we found 140 K (90 K) for the in-plane (out-of-plane) orientation of the [Fe(OEP)(2-MeHIm)] crystal and 110 K for the [Fe(TPP)(2-MeHIm)] crystal.⁴²

Computational Methods

DFT calculations provided optimized structures and detailed vibrational predictions for the quintet states of [Fe(TPP)(2-MeHIm)], [Fe(OEP)(2-MeHIm)], [Fe(TPP)(1,2-Me₂Im)], and [Fe(OEP)(1,2-Me₂Im)]. Calculations were performed with Gaussian 03,⁴³ using the 6–31G* basis set for N, O, C, and H atoms, Ahlrichs’s VTZ basis set for the Fe atom,⁴⁴ and the Becke-Lee-Yang-Parr composite exchange correlation functional (B3LYP).^{45, 46} Cartesian coordinates for the optimized structures are given in the Supporting Information.

The kinetic energy distribution (KED) is determined for each vibrational mode from the relative Cartesian displacements of individual atoms, as described previously.⁴⁷ From this, the vectors

$${\overrightarrow{e}}_{j\alpha }=m_j^{1/2}\frac{\partial \overrightarrow{r_j}}{\partial Q_{\alpha }}=\frac{m_j^{1/2}\overrightarrow{r_j}}{\sqrt{{\displaystyle {\sum }_i}{m}_i{r}_i^2}}.$$ (1)

which describe the linear transformation from the normal coordinates Q_α to mass-weighted Cartesian displacement r⃗_j of atom j can be derived. The mode composition factor $e_{j\alpha }^2$ is the fraction of kinetic energy of mode α on atom j and it determines the area contributed by mode α to the VDOS of atom j. Choosing a Gaussian line-shape L(ν̄ − ν̄_α) with appropriate width (greater than or equal to the experimental resolution) and choosing the Fe atom we define the partial VDOS

$$D_{\widehat{k}}(\overline{\nu })={\displaystyle \sum _{\alpha }}{(\widehat{k}·{\overrightarrow{e}}_{\mathit{\text{Fe}},\alpha })}^{2}L(\overline{\nu }-{\overline{\nu }}_{\alpha })$$ (2)

for Fe along the unit vector k̂. The partial VDOS is appropriate for comparison of vibrational predictions with data on oriented crystals. The total VDOS D(ν̄) = D_x(ν̄) + D_y(ν̄) + D_z(ν̄) on the other hand is used for unoriented samples (such as powders). To facilitate comparison with experiment, the partial VDOS is normalized as follows:

$${\displaystyle \int }{D}_{\widehat{k}}(\overline{\nu })d\overline{\nu }=1.$$ (3)

Results

NRVS measurements

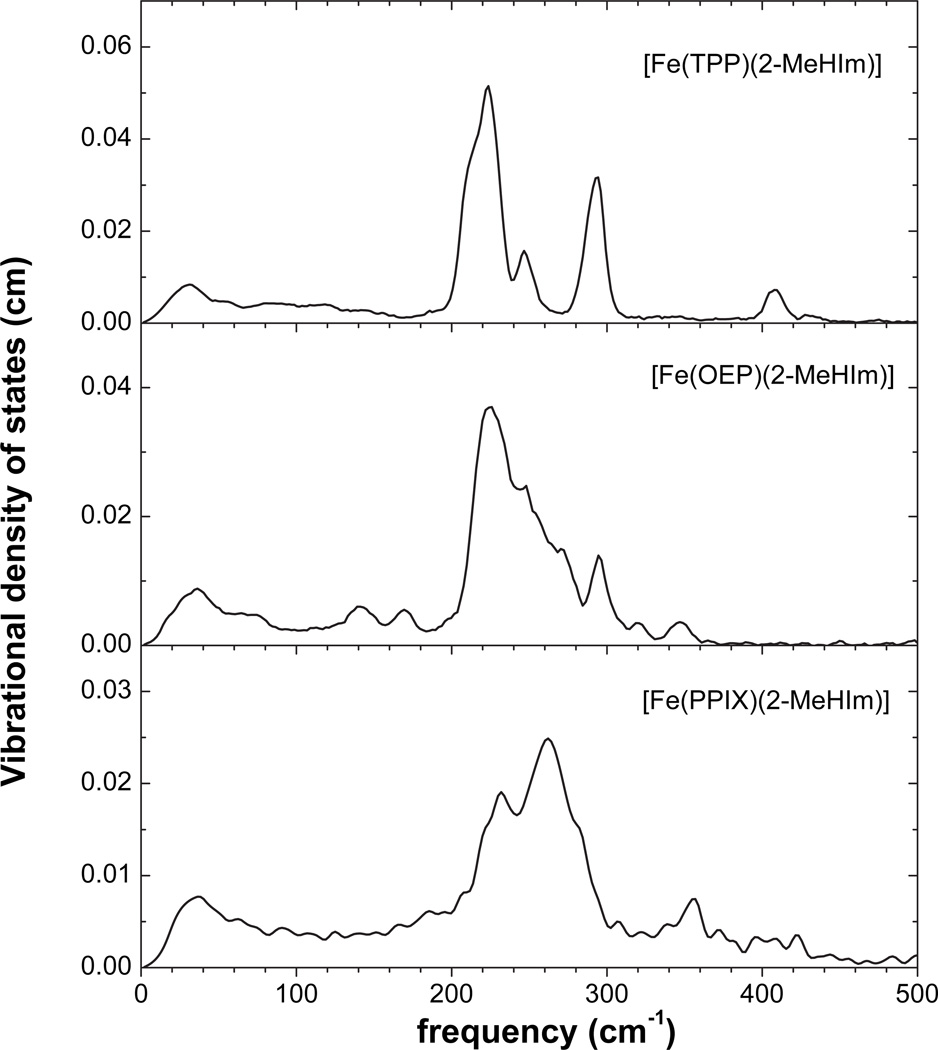
The Fe-weighted vibrational density of states (VDOS) D(ν̄) derived from excitation probabilities S(ν̄) for three high-spin iron(II) porphyrinates coordinated by the hindered imidazole 2-methylimidazole are shown in Figure 1 and those coordinated with 1,2-dimethylimidazole are displayed in Figure 2. Since the NRVS signal is weighted by the Fe mean-squared displacement, vibrations involving all Fe ligands contribute prominently to the experimental VDOS. Spectra were taken either as Apiezon grease mulls or as a micelle; both types of spectra can be regarded as a powder spectrum with no preferential orientations of the molecules. The use of a hindered imidazole is necessary to limit coordination at the iron(II) center to a single imidazole (and a high-spin iron center) rather than two imidazole ligands (and a low-spin iron center).

Figure 1.

Experimental NRVS spectra of polycrystalline (powder) samples of 2-methylimidazole-ligated species. [Fe(TPP)(2-MeHIm)] (crushed single crystals, upper panel), [Fe(OEP)(2-MeHIm)] (crushed single crystals or microcrystalline, center panel), and [Fe(PPIX)(2-MeHIm)] (CTAB micelle, lower panel).

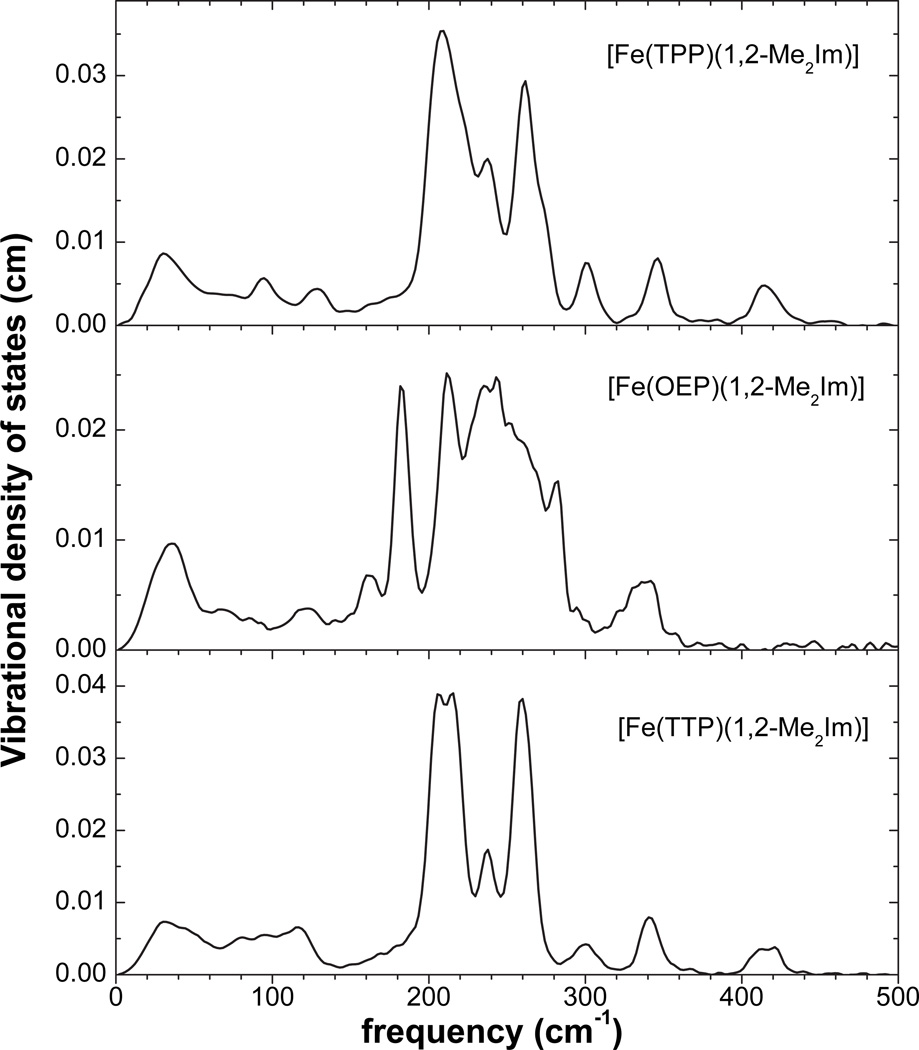
Figure 2.

Experimental NRVS spectra of polycrystalline (powder) samples of 1,2-dimethylimidazole-ligated species. [Fe(TPP)(1,2-Me₂Im)] (microcrystalline, upper panel), [Fe(OEP)(1,2-Me₂Im)] (microcrystalline, center panel), [Fe(TTP)(1,2-Me₂Im)] (microcrystalline, lower panel).

The compounds are all five-coordinate iron(II) porphyrinates, but differ in the axial ligand and porphyrin peripheral substituents. These factors lead to significant variations in vibration modes; inspection of the two sets of spectra reveals some common features and some differences as well. As shown in Figure 1, the observable vibrations for 2-methylimidazole-ligated species are all below 500 cm⁻¹. Spectra are clearly dominated by strong signals between 200 and 300 cm⁻¹ with weaker signals found at both higher and lower frequencies. Spectra of iron(II) porphyrinates with 1,2-dimethylimidazole (Figure 2) show similar patterns but with greater complexity in the 200–300 cm⁻¹ region.

Besides the common features, the spectra also show some differences. In the range between 200 and 300 cm⁻¹, for the OEP and PPIX species with substituents on the pyrrole β position, there are very broad bands with some shoulders. Whereas for TPP and TTP with meso phenyl substituents, there are three relatively sharp bands. For the same porphyrin, with an axial ligand change, the spectra show some difference. The spectra of 1,2-dimethylimidazole-ligated species are more complex than the 2-methylimidazole-ligated species. For TPP derivatives, the 1,2-Me₂Im species has six relatively sharp bands above 200 cm⁻¹, instead of four for the 2-MeHIm species. For OEP derivatives, the 1,2-dimethylimidazole-ligated species has two more sharp bands around 200 cm⁻¹ than its 2-methylimidazole-ligated species.

Computational Results

Oriented single-crystal NRVS spectra allows the basic assignment of out-of-plane and in-plane vibrational modes. Further insight into the vibrational dynamics were obtained from DFT calculations that were performed on four derivatives and compared with the experimental results. These are summarized in Table 1. DFT calculations must be carried out on the complete molecule rather than a truncated model system because of the known importance of the porphyrin peripheral groups on the Fe vibrational dynamics.²⁴

Table 1.

Summary of NRVS experimental measurements and DFT calculations.

Complex	NRVS Experiment		DFT Calculation
Fe(OEP)(2-MeHIm)]	Powder	Single-crystal	yes
Fe(TPP)(2-MeHIm)]	Powder	Single-crystal	yes
Fe(TPP)(1,2-Me2Im)]	Powder		yes
Fe(OEP)(1,2-Me2Im)]	Powder		yes
Fe(PPIX)(2-MeHIm)]	Powder		no
Fe(TTP)(1,2-Me2Im)]	Powder		no

The calculations predict the overall structural features expected for a high-spin iron(II) complex,^{35, 48, 49} such as large Fe–N_p and Fe–N_Im bond distances and a significant out-of-plane displacement of the iron(II) atom. A comparison of the experimental and calculated structural data is shown in Table 2. For [Fe(TPP)(2-MeHIm)], the average calculated Fe–N_p distance is 2.090(10) Å, similar to the observed distance (2.073(9) Å). But the Fe–N_Im distance (2.196 Å) is a slightly longer than the observed value (2.127(3) Å). The out-of-plane displacement, ΔN⁴, of iron (0.30 Å) and the relative orientation of imidazole to the closest N_p—Fe–N_Im (27.7°) are in excellent agreement with the experimental data (0.32 Å and 24.0°, respectively). For the three other complexes, the calculated Fe–N_Im distances are again larger than the observed (Table 2). Such differences may influence the prediction of the iron vibrations to some extent and will be discussed in the next section.

Table 2.

Comparison of calculated and experimental structural parameters.

Complex	Fe–Npa,b	Fe–Nimb	ΔN4b,c	Δb,d	ϕe,f	ref.
[Fe(TPP)(2-MeHIm)]·1.5C6H5Cl	2.073(9)	2.127(3)	0.32	0.38	24.0	49
(calcd.)	2.090(10)	2.196	0.30	0.37	27.7
[Fe(OEP)(2-MeHIm)]	2.077(7)	2.135(3)	0.34	0.46	19.5	34
(calcd.)	2.104(3)	2.170	0.40	0.48	45.2
[Fe(TPP)(1,2-Me2Im)]	2.079(8)	2.158(2)	0.36	0.42	20.9	35
(calcd.)	2.090(2)	2.205	0.30	0.38	44.5
[Fe(OEP)(1,2-Me2Im)]	2.080(7)	2.171(3)	0.37	0.45	10.5	34
(calcd.)	2.092(2)	2.203	0.30	0.40	45.4

^aAveraged value.

^bin Å.

^cDisplacement of iron from the mean plane of the four pyrrole nitrogen atoms.

^dDisplacement of iron from the 24-atom mean plane of the porphyrin core.

^eValue in degrees.

^fDihedral angle between the plane defined by the closest N_p–Fe–N_Im and the imidazole plane in degrees.

The calculations predict all 3N-6 vibrational normal modes with real frequencies, which range from 10 cm⁻¹ to about 3650 cm⁻¹. ${\displaystyle \sum }{e}_{\mathit{\text{Fe}}}^2$ for the modes above 800 cm⁻¹ is less than 0.5%, suggesting that the experimental range 0−800 cm⁻¹ is large enough to offer a comprehensive picture of the Fe vibrational dynamics. Since the NRVS signal is weighted by the Fe mean-squared displacement, vibrations involving all Fe ligands contribute prominently to the experimental VDOS. The ${\displaystyle \sum }{e}_{\mathit{\text{Fe}}}^2$ of features in 0–500 cm⁻¹ is > 98% for all complexes. This is consistent with the experimental results, so all figures in the paper are presented in the range of 0–500 cm⁻¹.

Discussion

The NRVS spectrum encompasses all vibrations with iron motion. The powder spectra show both in-plane and out-of-plane iron vibrations, so the difficulty of making all of the vibrational assignments with often congested spectra is evident. In order to assign these vibrations, we have developed the use of oriented crystal measurements that allows the partitioning of the iron vibrations into modes that have predominant in-plane or out-of-plane character. DFT calculations also provide assistance in spectral assignments. The calculations can not only help the assignment of the vibrations, but also describe the vibrational dynamics of the ⁵⁷Fe probe nucleus. Since the calculations are performed on isolated molecules, they do not include intermolecular interactions, and some predictions of the observed vibrational frequencies are not precise. Nevertheless, the gas-phase calculations reproduce the pattern of vibrational amplitudes and the qualitative directions of Fe motion determined from measurements on oriented crystals. Thus the oriented crystal spectra, along with DFT-based vibrational assignments, have proven essential in understanding the iron dynamics in model complexes.⁴⁷

In this section, we emphasize a detailed discussion of the assignments of iron modes and their dynamics by comparison of the DFT calculation with NRVS observations. Although there can be differences in the DFT predictions that depend on choice of functional and basis set, careful consideration of the predicted and experimental intensities and the character of the vibrations, obtained from oriented single-crystal measurements, provides the best current process for assigning all observed iron modes.

Analysis of the spectra

For [Fe(TPP)(2-MeHIm)] and [Fe(OEP)(2-MeHIm)], both powder and single-crystal NRVS have been measured; DFT calculations have also been performed on the complete molecules. The iron vibration assignments and dynamics are described as below. Further, we have carried out additional measurements on four other derivatives and additional DFT calculations for two. Unfortunately, practical issues⁵⁰ limited measurements for the remaining four to the powder spectra, but the measurements do provide useful additional data.

In-plane porphyrin modes

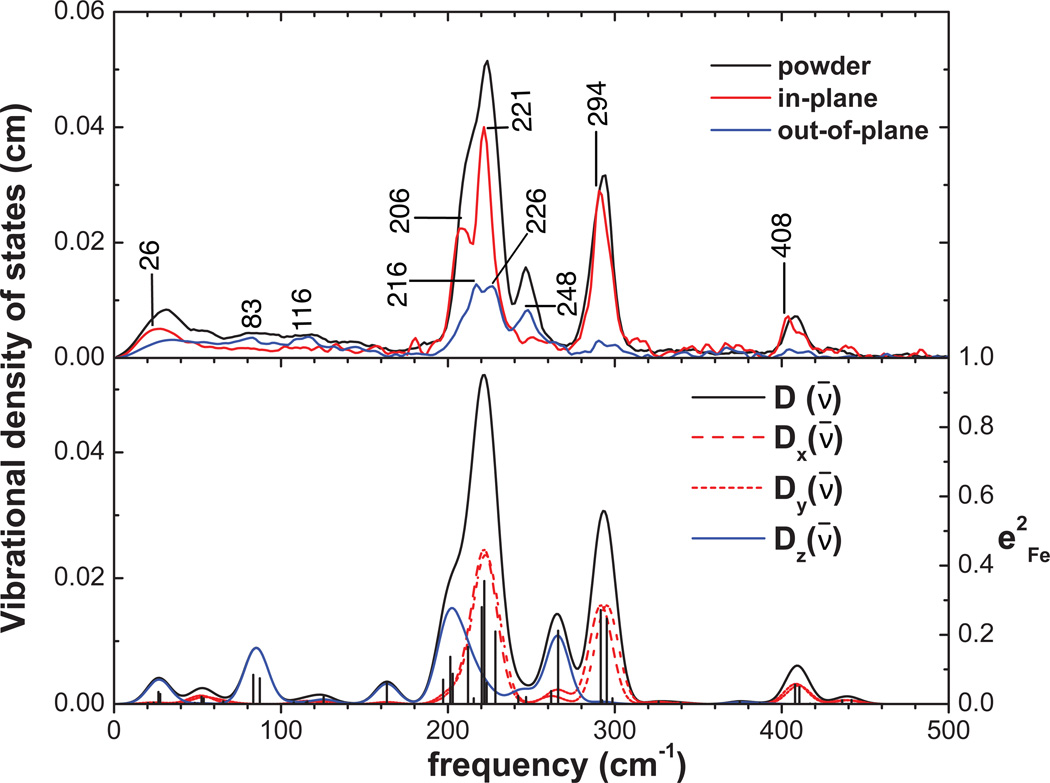
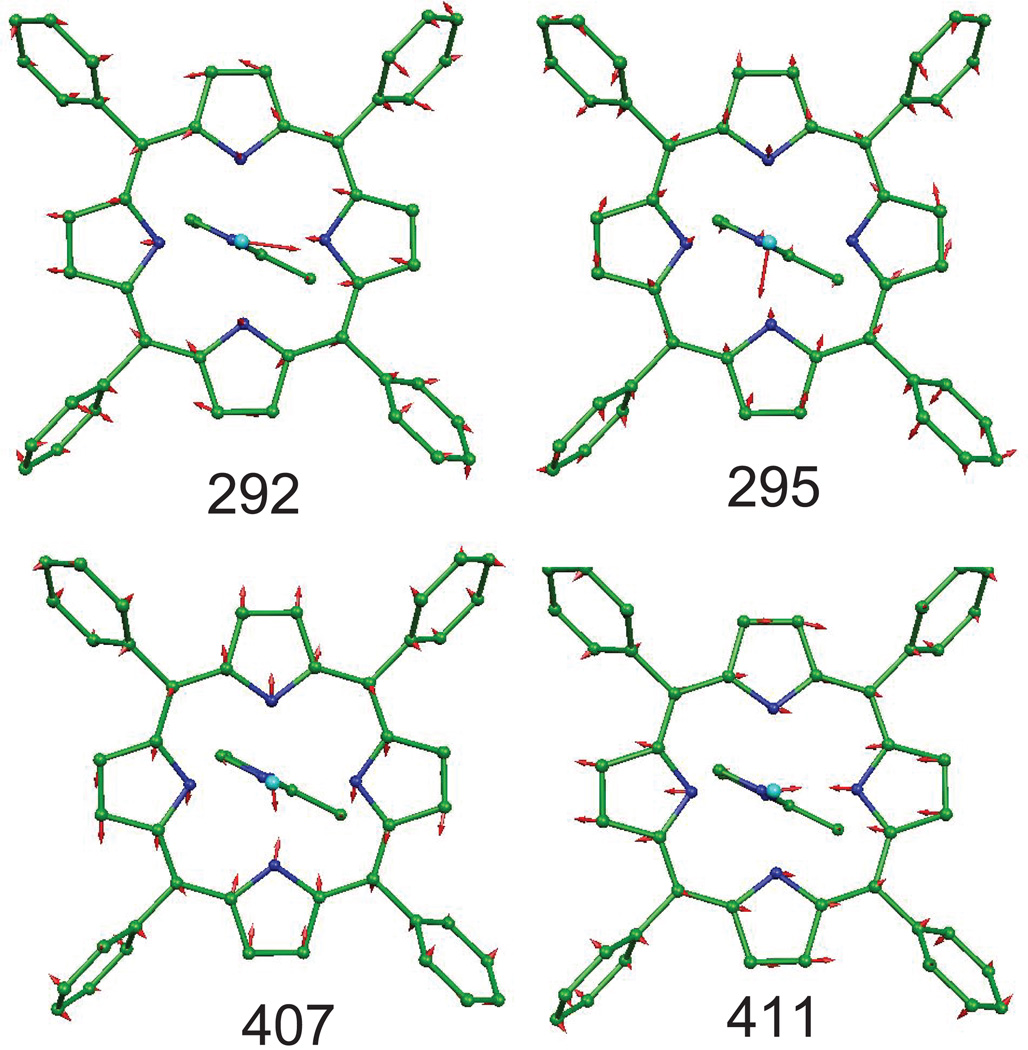
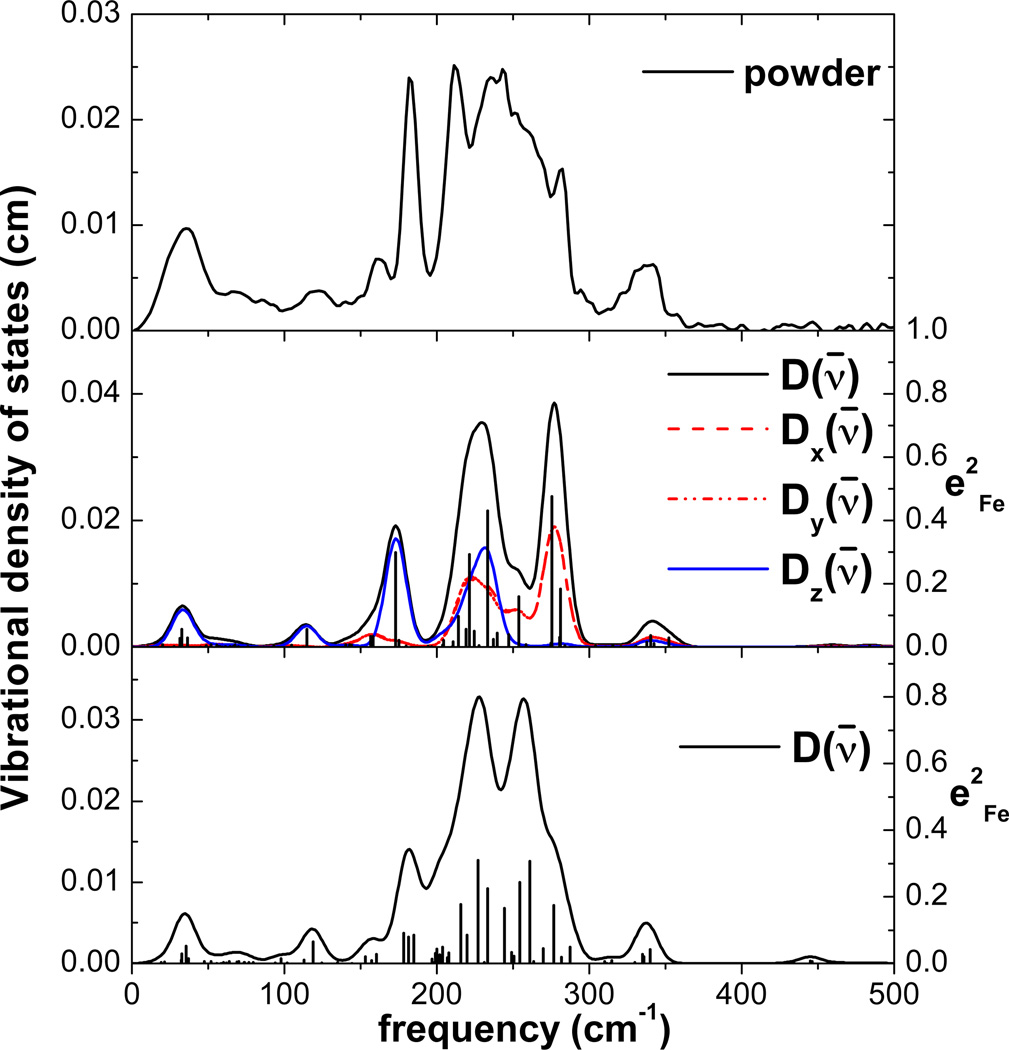
The porphyrin in-plane modes involving a nonzero displacement of iron are usually Raman inactive,⁵¹ but they can be readily detected by ⁵⁷Fe NRVS, which is not limited by the optical selection rules.²⁴ For [Fe(TPP)(2-MeHIm)], as shown in Figure 3, experimentally determined VDOS for the oriented crystal has been compared with that determined for the polycrystalline powder. Its powder spectrum shows four peaks above 200 cm⁻¹ at 224, 248, 294 and 408 cm⁻¹. Very weak overtones and combinations that we previously identified in the unprocessed experimental signal above 408 cm⁻¹ (ref. 52) are removed during the calculation of the VDOS for the oriented crystals. The single-crystal measurements clearly reveal that the peaks at 294 and 408 cm⁻¹ are in-plane vibrational modes, whereas the one at 248 cm⁻¹ is an out-of-plane mode. Both in-plane and out-of-plane modes overlap to form a broad band around 220 cm⁻¹; with in-plane modes at 206 and 221 cm⁻¹ and out-of-plane modes at 216 and 226 cm⁻¹. Consistent with the observed data, these in-plane modes have also been predicted by the DFT calculations. The predicted frequencies and corresponding $e_{\mathit{\text{Fe}}}^2$ values are listed in Table S1. For a four-fold symmetric Fe coordination environment, such in-plane Fe modes will occur as degenerate pairs. The direction of Fe motion in one mode of the pair will be orthogonal to that in the other mode. Binding of a fifth ligand will break the four-fold symmetry of the Fe environment, and lift the degeneracy of the in-plane mode pairs. That is the case for the predicted 292/295 cm⁻¹ and 408/411 cm⁻¹ pair of modes. The DFT calculation predicts a pair of modes at 292/295 cm⁻¹ with nearly equal Fe amplitudes as shown in Figure 4, the predicted splittings are smaller than the experimental resolution and so appear as a single feature at the observed 294 cm⁻¹ band. Such modes have been reported in [Fe(TPP)(NO)]⁴⁷ as well. In these modes, the Fe motion points to a pyrrole nitrogen atom directly and the trans pyrrole rings move with and opposed to the iron motion. The other predicted pair of modes at 408/411 cm⁻¹ have a similar pattern and correspond to the observed 408 cm⁻¹ band. As shown in Figure 4, iron motion is again along the Fe–N_p directions, but now the two adjacent pyrrole rings move in the same direction as the iron atom. The higher frequency pair also shows reduced iron amplitudes and larger pyrrole motions.

Figure 3.

Comparison of the experimental VDOS determined from NRVS measurements on [Fe(TPP)(2-MeHIm)] (upper panel) with the DFT-predicted VDOS on (lower panel). The spectra in the top panel have been normalized so that the following relationship is followed: D(ν̄) = 2D_ip(ν̄) + D_oop(ν̄).

Figure 4.

Two DFT-predicted pairs of in-plane Fe modes contributing to the pair of experimental features at 294 and 408 cm⁻¹ in [Fe(TPP)(2-MeHIm)]. Arrows represent the mass-weighted displacements of the individual atoms. For ease of visualization each arrow is 100 (m_j/m_Fe)^1/2 times longer than the zero-point vibration amplitude of atom j. Color scheme: cyan = iron, green = carbon, blue = nitrogen. In this and other figures, hydrogens are omitted for clarity.

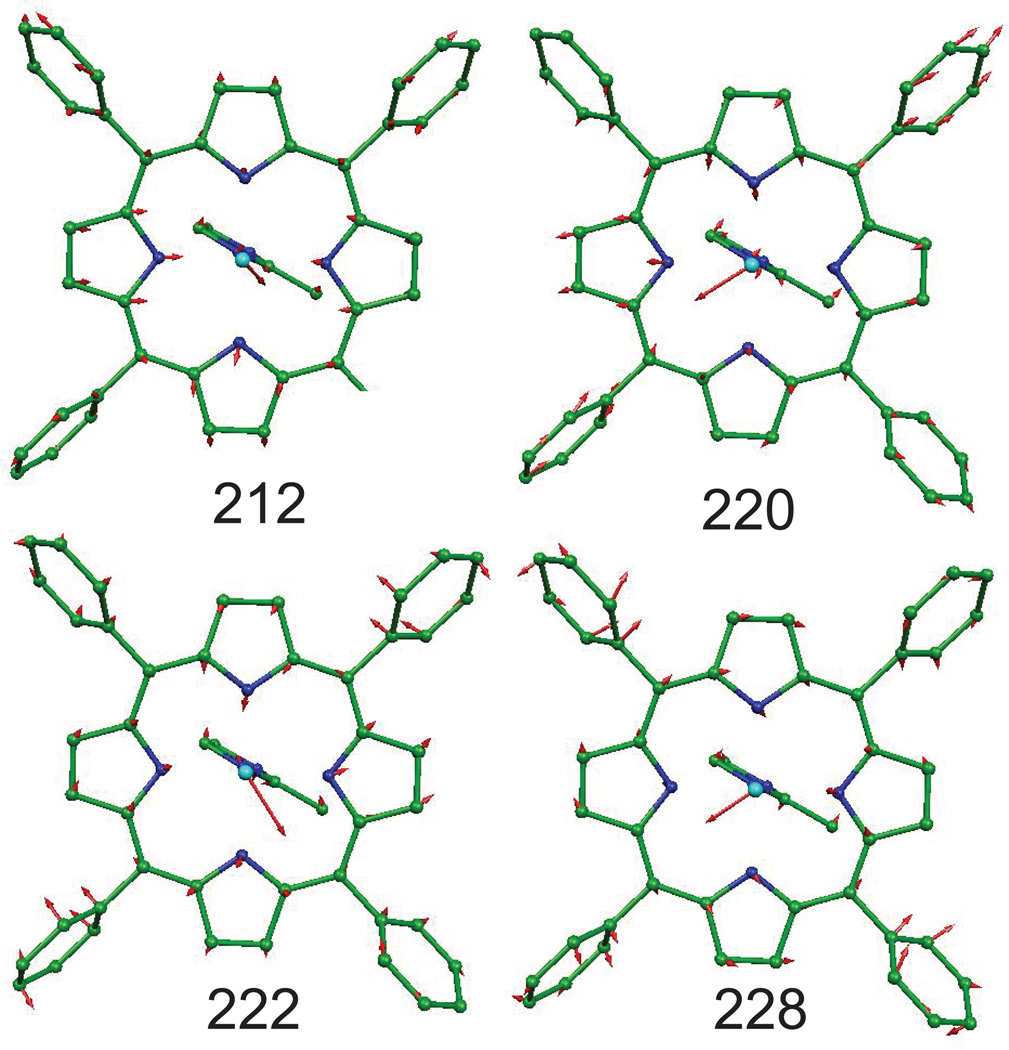
A complex situation occurs in the 200–230 cm⁻¹ region where four in-plane modes, at 212, 220, 222 and 228 cm⁻¹, have been predicted as shown in Figure 5. The four modes all have Fe motions pointing to the meso carbon atoms of porphyrin. These modes contribute to the observed two bands at 206 and 221 cm⁻¹ in the single-crystal measurements in Figure 3. The three predicted modes at 220, 222, and 228 cm⁻¹ cannot be resolved at the experiment resolution, so appear as a single feature with much larger area than the mode at 212 cm⁻¹.

Figure 5.

Four DFT-predicted in-plane Fe modes contributing to the pair of experimental features at 212 and 221 cm⁻¹ in [Fe(TPP)(2-MeHIm)].

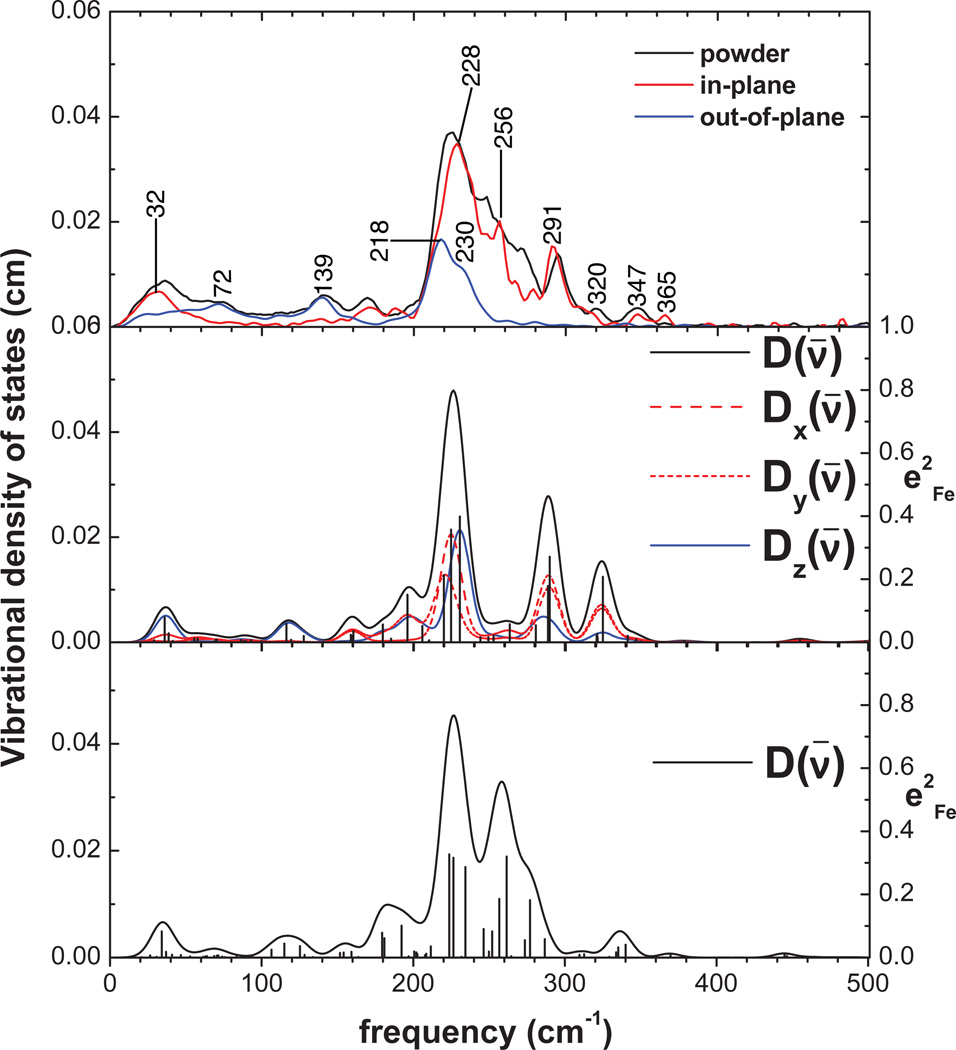
The peripheral substituents have a significant effect on the NRVS spectra. Thus, the β-substituted porphyrin complex, [Fe(OEP)(2-MeHIm)], shows much broader bands in the 200–300 cm⁻¹ range compared to the meso-substituted porphyrin complexes. Figure 6 compares the experimentally determined VDOS for the oriented [Fe(OEP)(2-MeHIm)] crystal with that determined for the polycrystalline powder. As shown in Figure S1, the data above 200 cm⁻¹ show in-plane modes at 228, 256 (shoulder), 291, 320 (shoulder), 347, 365 cm⁻¹ and out-of-plane modes at 218 and 230 cm⁻¹ (shoulder). The DFT prediction suggests that two in-plane modes, at 220 and 224 cm⁻¹ as shown in Figure S1, contribute to the Fe–N_p stretch mode. The predicted mode at 230 cm⁻¹ has both in-plane and out-of-plane contributions. The three modes are believed to contribute to the observed bands at 228 cm⁻¹ in the oriented crystal measurement. Other in-plane Fe modes predicted from the DFT calculation appear to match the experimental values as well. A predicted mode at 263 cm⁻¹ (Figure S2) showing in-plane iron motion coupled with imidazole distortion corresponds to the observed 256 cm⁻¹ shoulder. The predicted 288/289 cm⁻¹ pair have similar motions as the 292/295 cm⁻¹ pair in [Fe(TPP)(2-MeHIm)]. They correspond to the observed band at 291 cm⁻¹. The DFT calculation has also predicted an in-plane mode at 324 cm⁻¹ (Figure S2), which probably corresponds to the observed weaker band at 320 cm⁻¹ in the powder spectrum.

Figure 6.

Comparison of the experimental VDOS determined from NRVS measurements on [Fe(OEP)(2-MeHIm)] (upper panel) with the DFT-predicted VDOS using the observed conformation of the peripheral ethyl groups (all down, center panel), and an energy minimized conformation (four up and four down, lower panel). The spectra in the top panel have been normalized so that the following relationship is followed: D(ν̄) = 2D_ip(ν̄) + D_oop(ν̄).

For the above two complexes, the predicted in-plane Fe modes are generally in good agreement with the experimental observed in-plane features in average frequency and amplitude especially for [Fe(TPP)(2-MeHIm)]. Conformational issues may contribute to larger deviations for [Fe(OEP)(2-MeHIm)]. Nevertheless, it is most likely that the predicted modes represent reliable descriptions of the modes responsible for the corresponding experimental features.

Fe–imidazole vibrations

The heme iron to imidazole bond is a particularly important linkage in biology and, hence, has received much attention. A knowledge of the vibrational frequency of this bond provides insight into the following issues: 1) the strength of the Fe–N_Im bond, which may have functional significance,⁵³ 2) hydrogen bonding of the proximal histidine to a peptide oxygen,⁵⁴ 3) the repulsion between the porphyrin nitrogen and the imidazole hydrogens from the proximal histidine,⁵⁵ and 4) the tilt of the Fe–N_Im bond from the heme normal.⁵⁶ Unlike the in-plane modes, the iron-imidazole stretch(es) are expected to be Raman active in five-coordinate histidine-ligated proteins including the oxygen carrying/storage proteins deoxymyoglobin and -hemoglobin. The nature of a strong Raman peak near 220 cm⁻¹ in deoxymyoglobin and -hemoglobin^{57, 58} has been probed by isotopic labeling studies that include ⁵⁷Fe/₅₄Fe, ¹⁵N_p/¹⁴N_p, ²H/¹H substitutions⁵¹ and ¹⁵N histidine labeling and site-direct Mb mutants.⁵⁹ The shifts from the varying isotopic studies were compared with a number of simplified vibrational models, none of which totally predicted the shifts in complete suite of experiments. The models all predict significant motion of both iron and histidine but with differing amounts of histidine atom motions. Moreover, the frequency and Raman intensity of the ~220 cm⁻¹ mode are found to be sensitive to the global protein structure.^60–64 A resonance Raman study by Palaniappan and Bocian⁶⁵ that excited the NIR charge transfer band III gave a peak at 224 cm⁻¹. To our knowledge the differences remain unexplained.

As noted above, the in-plane and out-of-plane modes are strongly overlapped in these five-coordinate derivatives. Only oriented single-crystal measurements allows detailed assignments. The first derivative examined, [Fe(TPP)(2-MeHIm)], has out-of-plane modes consistent with simultaneous large motion of iron and imidazole at 216, 226, and 248 cm⁻¹ (Figure 3 (top)). The spectral features for [Fe(OEP)(2-MeHIm)] are slightly simpler with modes observed at 218 and 231 cm⁻¹ (Figure 6 (top)).

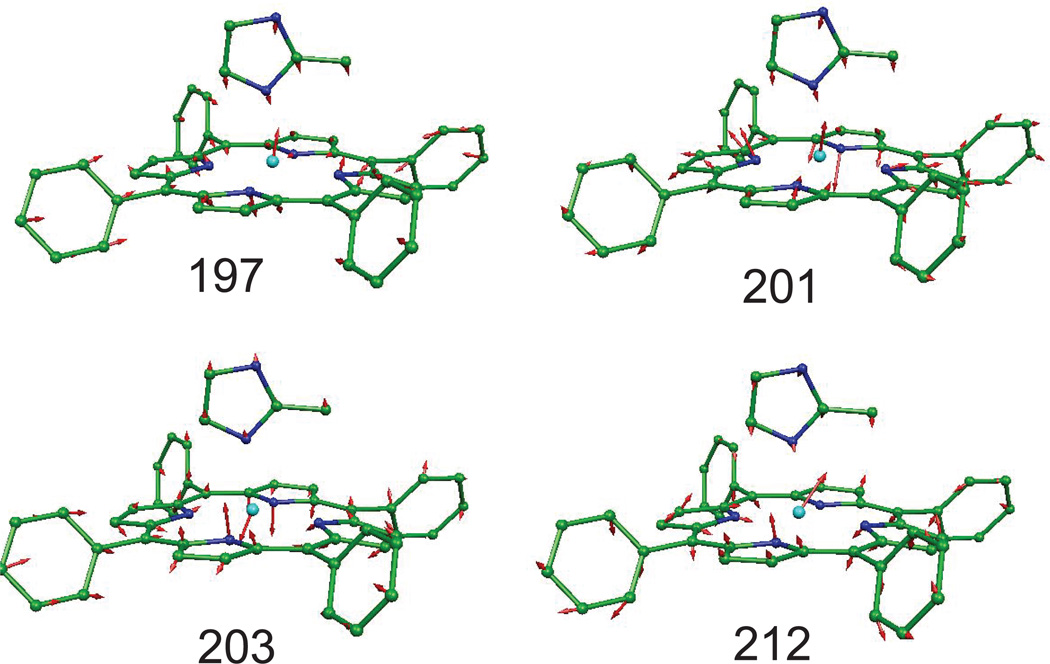
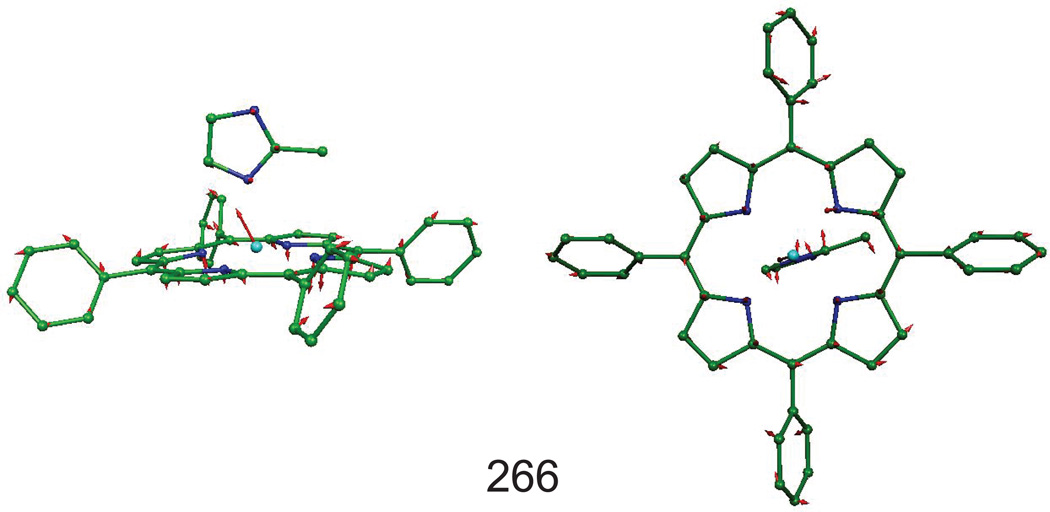
The DFT calculations predict multiple out-of-plane Fe modes, especially for [Fe(TPP)(2-MeHIm)] where five major modes involving both iron and imidazole motion at 163, 197, 201, 203, and 212 cm⁻¹ are predicted. But as shown in Figure 7, none are predicted to be a pure Fe–N_Im stretching mode. These predicted modes (Figure 7) are expected to contribute to the observed out-of-plane vibrations at 216 and 226 cm⁻¹. The three lower predicted frequencies are separated by differences smaller than the resolution of the NRVS experiment (~8 cm⁻¹). The observed mode at 248 cm⁻¹ is associated with a predicted mode at 266 cm⁻¹ (Figure 8) with the dominant iron out-of-plane motion coupled with an imidazole bending motion as well as porphyrin ring motions. These motions are similar to that predicted at 230 cm⁻¹ (observed at 231 cm⁻¹) for [Fe(OEP)(2-MeHIm)] as seen in Figure S1. The observed 218 cm⁻¹ band in [Fe(OEP)(2-MeHIm)] is predicted by DFT to have three components, the two at 196 and 206 cm⁻¹ have strong out-of-plane character whereas the final possible contributor is predicted to be a mode with mixed in-plane and out-of-plane contributions at 220 cm⁻¹. The character of these modes is shown in Figure S3. Interestingly, the powder spectrum of [Fe(PPIX)(2-MeHIm)] shows less apparent complexity than that of the OEP analogue (Figure 1).

Figure 7.

Four DFT-predicted out-of-plane Fe modes contributing to the pair of experimental features at 216 and 226 cm⁻¹ in [Fe(TPP)(2-MeHIm)].

Figure 8.

The out-of-plane Fe mode, predicted at 266 cm⁻¹, contributing to the experimental feature at 248 cm⁻¹ in [Fe(TPP)(2-MeHIm)].

The NRVS data for the 2-MeHIm derivatives suggest that there are at least two distinct modes with significant out-of-plane character in the region expected for the Fe–N_Im stretch. Is this expectation mirrored in the results found for deoxymyoglobin and related derivatives? Argade et al.⁵¹ have used both iron and pyrrole ¹⁵N-isotope labeled deoxymyoglobin and Wells et al.⁵⁹ have used ¹⁵N-enriched protein to examine the resonance Raman spectrum. The band observed at 220 cm⁻¹, and seen in all five-coordinate histidine heme proteins, shows a significant downshift of 1.7 cm⁻¹ for ⁵⁷Fe–⁵⁴Fe, or 1.25 cm⁻¹ for ¹⁵N-enriched protein, and is clearly seen to have Fe–N_Im stretch character. This band clearly corresponds to the lower frequency band seen in the 2-MeHIm complexes for which the experimental NRVS data and DFT predictions show stretching character as well as coupling to porphyrin vibrations. Is there a second band at slightly higher frequency in the proteins comparable to that seen in the NRVS spectra of the low molecular weight complexes? The band at 243 cm⁻¹ in deoxymyoglobin is the obvious candidate; however, the studies of Argade et al.⁵¹ showed no (or less than 0.4 cm⁻¹) iron isotope sensitivity for this band. They did show that the band displayed a 1.5 cm^{−1 15}N-isotope shift which was taken as involvement of out-of-plane pyrrole ring-folding vibrations. The DFT predictions of the 230 cm⁻¹ band for [Fe(OEP)(2-MeHIm)] or 248 cm⁻¹ band for [Fe(TPP)(2-MeHIm)] do show this type of porphyrin atom motions, but also clearly confirm the experimentally seen out-of-plane motion of iron. Resonance Raman studies of [Fe(PPIX)(2-MeHIm)] show 218 and 257 cm⁻¹ peaks with only the former showing sensitivity to pentadeuteration of the axial imidazole.⁵⁸ We thus conclude that resonance Raman is not observing the second (230–250 cm⁻¹) low-frequency band with significant iron out-of-plane character; only NRVS reveals this frequency. Contributions from porphyrin vibrations account for the failure of two-body models to explain the isotope shifts of the “iron-histidine” mode,⁵⁹ and the DFT predictions are clearly consonant with the complexity of the modes.

The frequency of the Fe–N_Im stretch is expected to be related to the Fe–N_Im bond length and to differences in the mass of the coordinated imidazole. The measurements on the 1,2-dimethylimidazole derivatives were made to explore these possible effects. As shown in Table 2, the axial bond distance differences between the two imidazoles shows that the 1,2-dimethylimidazole derivatives are slightly longer than those of 2-methylimidazole, and would thus be consistent with a decreased Fe–N_Im stretching frequency. The mass difference would also suggest a lower frequency value for 1,2-dimethylimidazole derivatives. As shown in a comparison of Figures 1 and 2 there is a general shift to the entire spectrum of 1,2-dimethylimidazole derivatives to lower frequencies consistent with these expectations. It is obvious that the 248 cm⁻¹ band in [Fe(TPP)(2-MeHIm)] shifts to 238 cm⁻¹ in [Fe(TPP)(1,2-Me₂Im)] and [Fe(TTP)(1,2-Me₂Im)]. Calculations suggest these all correspond to similar iron motion. For the lower frequency at around 220 cm⁻¹, both spectra of [Fe(TPP)(1,2-Me₂Im)] and [Fe(TTP)(1,2-Me₂Im)] suggest a shift as well. In the [Fe(OEP)(1,2-Me₂Im)] derivative, a band at 235 cm⁻¹ shows similar iron motion as the 230 cm⁻¹ band in [Fe(OEP)(2-MeHIm)]. But in [Fe(OEP)(1,2-Me₂Im)], a well resolved band at 182 cm⁻¹ is predicted to have significant out-of-plane and Fe–N_Im stretch character. The shift from 218 cm⁻¹ in the 2-MeHIm analogue does seem larger than would be expected. Unfortunately, the lack of oriented crystal data has limited our ability to make more definitive assignments. Although the generally expected trends to lower frequency are often seen, there are bands where the shifts are smaller than expected or even in the opposite direction. This might be expected as these are not pure modes but have substantial mode mixing with porphyrin modes. The complete powder spectra and DFT-predictions for [Fe(OEP)(1,2-Me₂Im)] and [Fe(TPP)(1,2-Me₂Im)] are given in Figures 9 and S4, respectively. In resonance Raman studies, both Hori and Kitagawa⁶⁶ and Desbois and Lutz⁶⁷ compared the Fe–N_Im stretch in 2-MeHIm and 1,2-Me₂Im derivatives and found a 9 to 11 cm⁻¹ shift to lower frequency for the 1,2-Me₂Im species.

Figure 9.

Comparison of the experimental VDOS determined from NRVS measurements on [Fe(OEP)(1,2-Me₂Im)] (upper panel) with the DFT-predicted VDOS from DFT calculations using the observed conformation of the peripheral ethyl groups (center panel, four up and four down) and an energy minimized conformation (lower panel, alternating two up, two down).

Differing peripheral group conformations also appear to have an effect on the observed spectra. Notably, the ethyl groups in [Fe(OEP)(2-MeHIm)] and [Fe(OEP)(1,2-Me₂Im)] have different conformations in their crystal structures.³⁴ In [Fe(OEP)(2-MeHIm)], all ethyl groups are away from imidazole, while in [Fe(OEP)(1,2-Me₂Im)], four adjacent ethyl groups are towards imidazole and the other adjacent four are away from it. A limited set of DFT calculations on different conformations have been performed. One set of DFT calculations for [Fe(OEP)(2-MeHIm)] are based on the single-crystal structure conformation and a second set of calculations are based on an optimized structure in which four ethyl groups are towards imidazole side and the other four are away from it. As shown in Figure 6, the predicted spectra are significantly different, especially in the region around 260 cm⁻¹. For [Fe(OEP)(1,2-Me₂Im)], one set of calculations are based on the single-crystal structure and a second set are based on an optimized structure in which ethyl groups arrange as two up-two down-two up-two down (pseudo S₄ symmetry). As shown in Figure 9, the predicted spectra again show substantial differences. These data, along with the experimental data on the OEP derivatives, suggest a real influence of ethyl group conformations on the vibrational spectra.

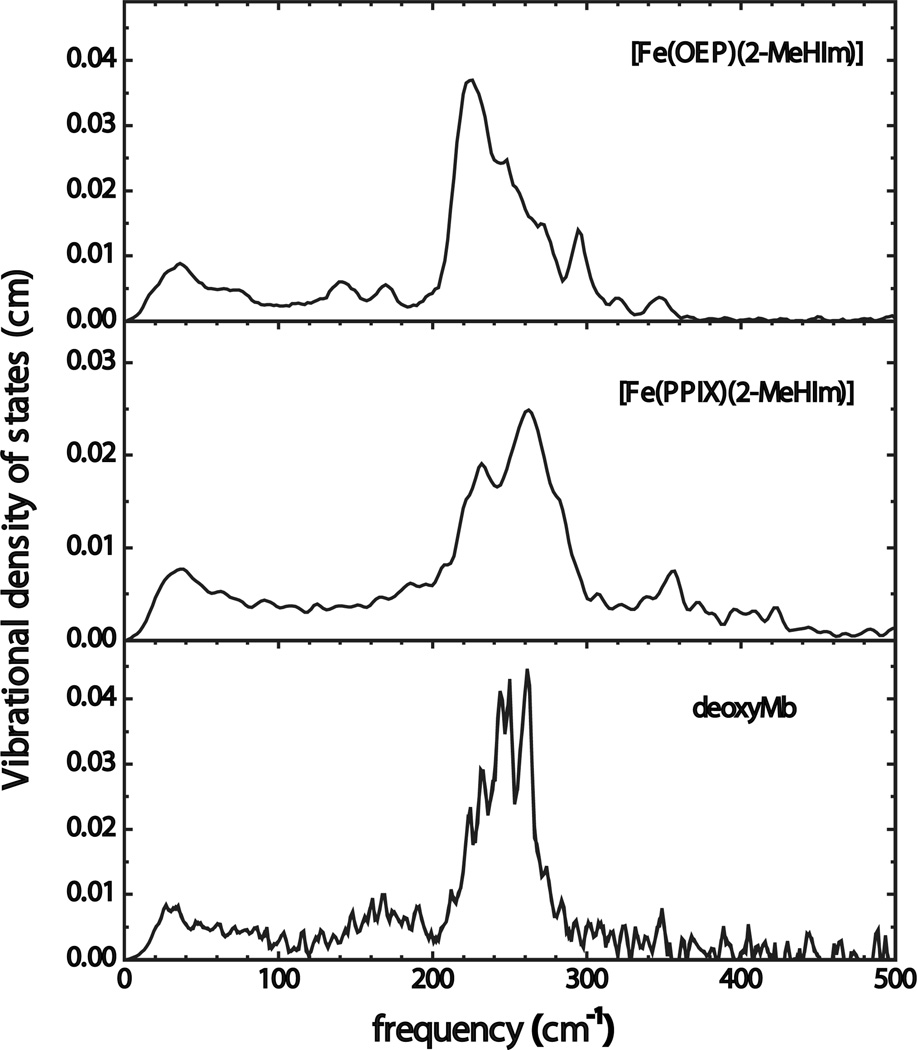
Figure 10 presents interesting and perhaps somewhat ambiguous results. The observed NRVS spectrum of ⁵⁷Fe-labeled deoxymyoglobin taken as a frozen solution⁶⁸ is compared with the NRVS data of low molecular weight analogues [Fe(OEP)(2-MeHIm)] and [Fe(PPIX)(2-MeHIm)]. Although the in-plane and out-of-plane modes in deoxymyoglobin are as likely to overlapped in the low molecular weight species, the narrowness of the total signal and the sharpness of the spectral features compared to the the low molecular weight species is striking. The broader nature of the spectrum for [Fe(PPIX)(2-MeHIm)] might reflect that a variety of conformations for the peripheral are accessible in the micelle form of the sample, relative to the likely single conformation of the porphyrin in the protein.

Figure 10.

Comparison of the experimental VDOS determined from NRVS measurements on [Fe(OEP)(2-MeHIm)] (upper panel) with [Fe(PPIX)(2-MeHIm)] (center panel) and deoxyMb (lower panel).

Doming and Other Low Frequency Modes

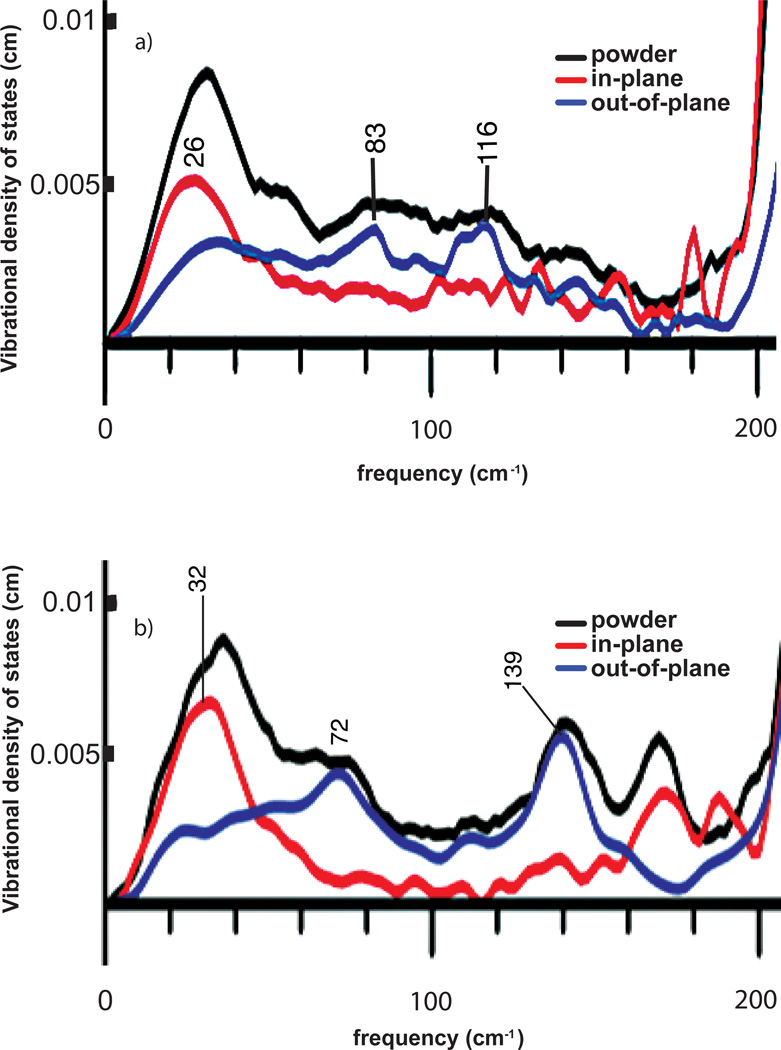
The most significant mode in the low frequency region is the doming mode, an important out-of-plane mode involving a large iron displacement perpendicular to the heme plane with opposing motion of the outer portion of the porphyrin core. Such a mode is of particular interest due to its biological roles, such as in Perutz’s model for hemoglobin cooperativity,⁶⁹ and in other models for protein control of reactions at the active sites of heme proteins.^{5, 70, 71, 72} Experimental identification of such modes are crucial to understand the reactive dynamics. The doming mode usually occurs below 150 cm⁻¹, an experimentally difficult region of the vibrational spectrum, but NRVS is an ideal technique to probe the dynamics of iron in such a frequency range. The doming mode is often substantially mixed with low-frequency modes involving porphyrin peripheral groups and thus contribute to the NRVS signal at multiple frequencies. As out-of-plane modes, these modes can be distinguished from in-plane modes by the oriented crystal measurements. As shown in Figures 3 and 6, the low frequency vibrations are dominated by out-of-plane iron motions. There are at least three bands for those measured species except [Fe(PPIX)(2-MeHIm)] which has a broad (unresolved) signal over this region. An expanded view of the 0–200 cm⁻¹ region of Figures 3 and 6 is given in Figure 11.

Figure 11.

Expanded view of the 0 – 200 cm⁻¹ region for (top) [Fe(TPP)(2-MeHIm)] and (bottom) that for [Fe(OEP)(2-MeHIm)].

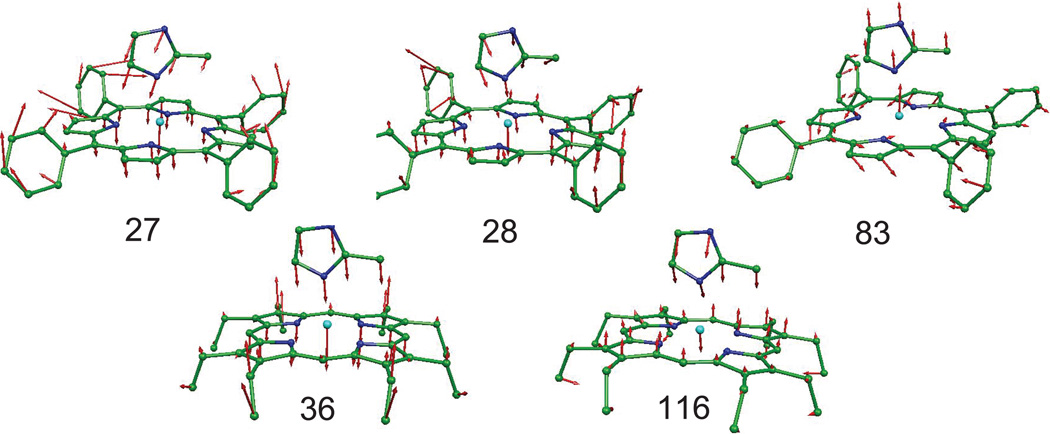
In the very lowest portion of this frequency range (usually below 50 cm⁻¹), there are also contributions from the lattice translation or phonon modes as well as intramolecular modes. Consequently, it can be difficult to conclusively separate the lowest frequency molecular modes from the phonon modes. In a few instances, for example [Fe(OEP)(NO)], molecular modes in this region have been conclusively observed.⁷³ Earlier studies proposed that this low frequency vibration involved translation of the iron and porphyrin core perpendicular to its mean plane, counterbalanced by motion of the four phenyl groups in the opposite direction.^{24, 74} The calculated modes for [Fe(TPP)(2-MeHIm)] shown in Figure 12 are in accord with this proposal, with the band in the 40–60 cm⁻¹ region. DFT predicts similar motion in [Fe(OEP)(2-MeHIm)] with counterbalancing ethyl group motion similar to the contributions of the phenyl groups in the TPP analogue.

Figure 12.

Predicted oop modes at 27, 28 and 83 cm⁻¹ for [Fe(TPP)(2-MeHIm)](top); the predicted mode at 87 cm⁻¹ is similar to the 83 cm⁻¹ mode. Predicted out-of-plane modes at 36 and 116 cm⁻¹ for [Fe(OEP)(2-MeHIm)] (bottom).

There are two out-of-plane features in [Fe(TPP)(2-MeHIm)], observed at 83 and 116 cm⁻¹ (Figure 3), that are clearly seen in the oriented crystal spectra, although they are not well-resolved in the powder data. These appear to be related to calculated doming modes at 83 and 87 cm⁻¹. A representation of one of these modes is shown in Figure 12. Its near-degenerate partner has the motions of the porphyrin core atoms rotated by 90° around the heme normal. The modes observed in a related five-coordinate, [Fe(TPP)(NO)] complex,⁴⁷ were observed at 74 and 128 cm⁻¹. The 128 cm⁻¹ mode was predicted to have strong doming mode character whereas the 74 cm⁻¹ mode was strongly mixed with motion of the axial NO and porphyrin vibrations. Although only powder data are available for [Fe(TPP)(1,2-Me₂Im)], bands analogous to those of [Fe(TPP)(2-MeHIm)] are observed at 94 and 128 cm⁻¹.

A similar pattern is seen for [Fe(OEP)(2-MeHIm)] and [Fe(OEP)(NO)] where bands at 72 and 139 cm⁻¹ are the doming modes seen in the imidazole complex, whereas the doming mode is observed at 158 cm⁻¹ in the NO complex. Two generalizations are to be noted. First, in comparing tetraarylporphyrin derivatives with octaethylporphyrin derivatives, the corresponding frequencies in this low frequency region are always in the order OEP > TPP. Second, the doming mode observed for the low-spin NO derivatives is at a higher frequency than those observed for the five-coordinate imidazole species. Observation of the doming mode at 142 cm⁻¹ for [Fe(OEP)(Cl)]⁷⁶ suggests that the spin state may be a more important factor than ligand mass.

Vibrational influence of porphyrin substituents

A recent investigation of ferric porphyrin halides used NRVS measurements and vibrational correlation analysis of DFT predictions to demonstrate the strong influence of peripheral substituents on the vibrational dynamics of the Fe,⁷⁶ reinforcing more qualitative observations for nitrosyl complexes.⁴⁷ Similarly, comparison with the dynamics of the smaller, more symmetric compound [Fe(P)(Im)]⁷⁷ provides a useful perspective on the more complex imidazole-ligated porphyrins considered here (see Table 3). DFT calculations for [Fe(OEP)(NO)] suggest that peripheral group conformations can have significant effects on the lower frequency regions as well.⁷⁸

Table 3.

Correlation of calculated normal modes with Fe vibrations of the [Fe(P)(Im)] model calculation. All frequencies are expressed in cm⁻¹.

	[Fe(P)(Im)]	[Fe(TPP)(2-MeHIm)]	[Fe(OEP)(2-MeHIm)]
γ9 (doming)	66	83, 87	116, 128
imidazole translation	169	163	180, 196
γ6 (inverse doming)	237	266, 212, 201, 203, 197	230
ν53	247	222, 292	220
ν53	255	228, 295, 220	224
ν50	395	408	324, 289
ν50	394	411	288

The ν₅₃ mode pair at 247 and 255 cm⁻¹ dominates the predicted Fe dynamics parallel to the porphine plane in [Fe(P)(Im)], with smaller contributions from the ν₅₀ mode pair (394/395 cm⁻¹). (There is no evidence of the interaction between the ν₅₃ and the γ₂₃ modes predicted and observed for the analogous [Fe(P)(Cl)] and [Fe(P)(Br)] compounds.⁷⁶) Peripheral substitutions weakly influence the ν₅₀ modes, which remain a minor contribution to the VDOS of [Fe(TPP)(2-MeHIm)] (Figure 3) and weaken further for [Fe(OEP)(2-MeHIm)] (Figure 6). However, the ν₅₃ modes interact strongly with phenyl distortions in [Fe(TPP)(2-MeHIm)], resulting in splitting of the dominant in-plane vibrations to clusters of in-plane modes that account for observed peaks at 220 and 294 cm⁻¹. Interaction with peripheral vibrations in [Fe(OEP)(2-MeHIm)] also splits the in-plane ν₅₃ contribution in a complex pattern, which calculations further reveal depend on the conformation of the ethyl substituents (Figure 6).

Three modes determine the predicted Fe dynamics perpendicular to the heme plane of [Fe(P)(Im)]. The doming mode (γ₉ at 66 cm⁻¹) and an “inverse doming” mode (γ₆ at 238 cm⁻¹), which reverses the relative phase of the Fe and pyrrole tilting motions, interact with a 169 cm⁻¹ mode dominated by translational motion of the imidazole ligand. (The γ₇ mode contributes little to the Fe dynamics of [Fe(P)(Im)] in the quintet state, as previously noted,⁷⁷ in contrast with the analogous [Fe(P)(Cl)].⁷⁶) Imidazole modifications and the addition of peripheral substituents also alter the out-of-plane Fe motions.

The dominant γ₆ contribution predicted for [Fe(OEP)(2-MeHIm)] is to a single vibration at 230 cm⁻¹, while complex interactions with other porphyrin distortions in [Fe(TPP)(2-MeHIm)] distribute the predicted γ₆ contribution between a 266 cm⁻¹ mode and a cluster of modes in the 200 – 220 cm⁻¹ region. The observed splitting, between features at 220 and 250 cm⁻¹, is smaller. The 66 cm⁻¹ doming frequency predicted for [Fe(P)(Im)] shifts to frequencies near 85 and 120 cm⁻¹, respectively, for the [Fe(TPP)(2-MeHIm)] and [Fe(OEP)(2-MeHIm)] predictions. The observed frequencies appear somewhat higher, possibly because of lattice effects that the gas phase calculations fail to capture. An imidazole translation mode is predicted at 163 cm⁻¹ for [Fe(TPP)(2-MeHIm)]. In [Fe(OEP)(2-MeHIm)], imidazole translation interacts with an in-plane vibration to yield predicted modes at 180 and 196 cm⁻¹. The contribution of imidazole translation to the experimental VDOS is not apparent for either compound.

Interestingly, our results indicate that the influence of peripheral substitution is less apparent for the most common biological heme, protoporphyrin IX. This mirrors our experience with the analogous compound [Fe(PPIX)(Cl)], where simply substituting substituent mass for the mass of the β-hydrogens captured many of the differences of the Fe VDOS with respect to [Fe(P)(Cl)].⁷⁶ The primary exception is the doming mode γ₉, which contributes to several modes in the predicted spectrum of [Fe(PPIX)(Cl)] and is not clearly resolved experimentally for either [Fe(PPIX)(Cl)] or [Fe(PPIX)(2-MeHIm)]. Neither the [Fe(PPIX)(2-MeHIm)] nor the deoxyMb VDOS resolve a feature near 59 cm⁻¹ that could account for sharp bands observed at 115 and 168 cm⁻¹ in the Raman signal scattered from a deoxyMb solution excited in resonance with a weak near-IR band and considered as possible overtones of the doming mode.⁶⁵ Two clearly resolved features near 230 and 260 cm⁻¹ dominate the [Fe(PPIX)(2-MeHIm)] VDOS and must represent the contributions of γ₆ and ν₅₃, respectively. This conclusion is consistent with our earlier description of the analogous features in deoxyMb as stretching of the axial and equatorial Fe-N bonds.²⁰ The increased breadth of these features in [Fe(PPIX)(2-MeHIm)], as compared with noticeably sharper bands in deoxyMb, may reflect conformational variations of the side chains in the noncrystalline [Fe(PPIX)(2-MeHIm)] sample.

Summary

We have used NRVS, which provides all iron vibrational frequencies, to study a series of six different five-coordinate imidazole-ligated iron(II) porphyrinates. Both powder and oriented crystals have been measured for [Fe(TPP)(2-MeHIm)] and [Fe(OEP)(2-MeHIm)] and powder spectra have been obtained for [Fe(TPP)(1,2-Me₂Im)], [Fe(OEP)(1,2-Me₂Im)], [Fe(PPIX)(2-MeHIm)], and [Fe(TTP)(1,2-Me₂Im)]. The oriented crystal spectra allow the deconvolution of the in-plane and out-of-plane modes and, along with the aid of DFT calculations, the iron vibrational modes have been assigned. The study reveals that many iron vibrations are mixed with porphyrin core and peripheral group vibrations. In addition to the effects of varying peripheral groups, the conformation of the peripheral groups, especially for ethyl groups, can strongly influence the vibrational spectra. These effects may lead to spectral broadening. Previously unidentified imidazole dependent iron–imidazole modes have now been identified. Finally, the use of NRVS provides details of the vibrational spectra that have not been accessible by other techniques.