ANFIS-based approach for predicting sediment transport in clean sewer

Abstract

The necessity of sewers to carry sediment has been recognized for many years. Typically, old sewage systems were designated based on self-cleansing concept where there is no deposition in sewer. These codes were applicable to non-cohesive sediments (typically storm sewers). This study presents adaptive neuro-fuzzy inference system (ANFIS), which is a combination of neural network and fuzzy logic, as an alternative approach to predict the functional relationships of sediment transport in sewer pipe systems. The proposed relationship can be applied to different boundaries with partially full flow. The present ANFIS approach gives satisfactory results (r² = 0.98 and RMSE = 0.002431) compared to the existing predictor.

1. Introduction

In sewer networks, the deposition of solids occurs occasionally due to the intermittent nature of flow [1]. The longer the deposits remain in the sewer the more likely that the sediment properties change and can eventually become consolidated or cemented, especially during dry weather flows. Such permanent deposits in pipe inverts will change the nature of the velocity and boundary shear distributions, which affects the sediment carrying capacity and hydraulic resistance of sewers. Previous works on sediment transport with no deposition include those of May et al. [2], Mayerle et al. [3] and Vongvisessomjai et al. [4].

Sewer system designs must satisfy two major criteria: high flow and low flow criteria. During high flows, sewer systems must convey the design discharge. For low flows, sewers should be free from sediment deposit as much as possible. Traditionally, a fixed minimum flow velocity for non-deposition, such as 0.6 m/s [5] is used as a low flow criterion. This criterion may be inadequate because the loading and sediment characteristics vary considerably under different environmental conditions [4] with permission from ASCE.

Sediment transport equations which are applicable for both conditions in sewers, namely rigid boundary (clean pipes) and loose boundary (pipes with deposited beds) are being derived to meet the challenging condition of flow. Few previous works on sediment transport with no deposition include those by Mayerle et al. [3], Ab Ghani [6], May et al. [2], Cigizoglu [7], Dogan et al. [8]. Kisi [9] applied ANN and ANFIS approaches to estimate suspended sediment. Yang et al. [10] used ANN to evaluate total sediment load formulae and prediction of sediment load concentration in rivers using neural networks [11]. Recently Ab Ghani and Azamathulla [12] have attempted gene-expression programming (GEP) for sediment transport in sewer pipe systems.

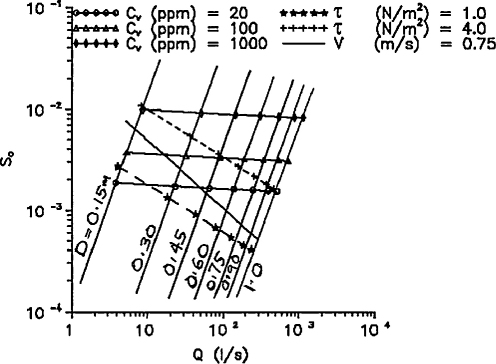
The present study investigates the hydraulic characteristics of the flow in channels with a circular cross-section with different bed roughness, and their effects on sediment transport capacity (Fig. 1) [13]. The pipe channel can be represented by a trapezoidal section, especially at low depths; at high depths, the cross-section is influenced by the ‘crowing’ effect of the pipe, through the changes in velocity and shear distributions due to changes in cross-sectional shapes [1].

Fig. 1.

Q-S0-D plot: clean pipe.

Reprinted from Ab Ghani [6].

The present study presents multiple regression model and adaptive neuro-fuzzy inference system (ANFIS), as an alternative approach to predict the functional relationships of sediment transport in sewer pipe systems.

2. Data collection

The experimental data were collected from Ab Ghani [6] and Vongvisessomjai et al. [4]. Models were generated from the collection of cumulative data. The sediment transport data for clean pipe with diameter 100–150 mm consisted of 118 sets. As for the present study, 85% (98 sets) data has been using for training data and 15% for testing data.

3. Multiple linear regression

The sediment transport rate in channels with a circular cross-section or pipe channels depends on many factors, such as flow depth (y_o), bed slope (S_o), sediment size (d₅₀), density of sediment (ρ_s), kinematic viscosity (ν) and density (ρ) of fluid, friction factor (λ), pipe diameter (D), and gravitational constant (g). But, not all the parameters will have significant effect on the result. Therefore, sensitivity test was performed to investigate the effect of each parameter on the model result, followed by dimensionless analysis to determine the functional relationship of limiting velocity.

From the dimensional analysis using Buckingham Π Theorem, an expression was obtained considering the parameters $V_s=f(g,R,d_{50},{\lambda }_s,D_{gr},C_v,\Delta )$ as:

$$\frac{V}{\sqrt{\Delta g{d}_{50}}}=f\left(\frac{d_{50}}{R},{\lambda }_s,D_{gr},{\lambda }_s,C_v\right)$$ (1)

The following equation was obtained on the basis of nonlinear regression to describe bed load transport with a limiting velocity for no deposition (clean pipes):

$$\frac{V_s}{\sqrt{g\Delta d}}=0.22D_{gr}^{-0.27}{C}_v^{0.16}{\left(\frac{d_{50}}{R}\right)}^{-0.29}{\lambda }_s^{-0.51}$$ (2)

where V_s is the limiting velocity, D_gr is dimensionless grain size, $D_{gr}=d{((Ss-1)/{\nu }^2)}^{1/3}$, R is hydraulic radius, d₅₀ is sediment size, Δ is relative density of sediment in water (ρ_s/ρ) − 1, λ_s is overall friction factor, ${\lambda }_s=0.851D_{gr}^{0.03}{C}_v^{0.04}{\lambda }_c^{0.86}$, λ_c is the clear water friction factor of the channel.

This simple regression equation could produce a good prediction of sediment transport in clean pipes as it yielded r² = 0.94, RSME = 0.084, AAE = 0.061. However, this method was not as efficient as the new soft computing technique, such as artificial neural networks (ANNs), evolutionary computation (EC), fuzzy logic (FL) and genetic programming, which have been successfully applied in water engineering problems in the last two decades. Although many successful attempts have been made, a wider application of theoretical models is restricted by their heavy demand in terms of computing capacity and time. Thus, this study will attempt a new soft computing technique, Adaptive Neuro-Fuzzy Inference System (ANFIS) to obtain a new sediment transport equation for the bed load transport in pipes with no deposition.

4. Overview of Adaptive Neural Fuzzy Inference System (ANFIS)

ANFIS is a combination of Fuzzy Inference System (FIS) and ANNs, which is a successful invention by Jang [14]. It is a multilayer feed-forward network, which uses neural network learning algorithms and fuzzy reasoning to map an input space to an output space. The fuzzy decision rules are implemented as membership functions (MFs) and the model learns the best fitting parameters of the MFs. A membership function (MF) is a curve that defines how each point in the input space is mapped to a membership value (or degree of membership) between 0 and 1. FIS, was based on if-then rules, such that we can obtain the relation between input and output variables by these rules. Since in conditions which input and output data have high uncertainty, the classic estimating method, regression for instance, do not considered uncertainty of data well, and we use FIS as a prediction model.

5. Implementation of ANFIS model

In the ANFIS model, fuzzy subtractive clustering algorithm was used to design an initial rule base. Subtractive clustering is a fast, one-pass algorithm for estimating the number of clusters and the cluster centers in a set of data [15]. In this study, the genfis2 function was applied to generate a model using data by using clustering. The genfis2 function is a fast, one-pass method that does not perform any iterative optimization. When fuzzy systems are designed by using fuzzy clustering, each cluster corresponds to a fuzzy rule. Hence, the number of clusters determines the number of rules. A sample command-line is as follow:

$$\text{fismat}=\text{genfis}2(\text{datin},\text{datout},0.5);$$

In general, as the number of rules is increased, the difference between the predicted and the obtained values decreases and more complex relations can be modeled with a large number of rules. A crucial point in the rule base design is selecting the number of rules. The present study focuses on developing various models with different cluster radius, in order to determine the number of clusters by studying the rules and the results obtained from each model.

For the regression analysis, after obtaining an equation, it would be verified by using the testing data by equating each data in the equation. As for ANFIS model, it would generate itself to compute the predicted value. It is vital to define the criteria by which the performance of the model and its prediction accuracy are evaluated in the model development process. The correlation coefficient (r) and the root mean square error (RMSE) were used in the current study. The root mean square error, RMSE describes the average difference between predicted values and measured values, as expressed by:

$$\text{RMSE}={\left(\frac{\sum {(X-Y)}^2}{n}\right)}^{1/2}$$ (3)

The correlation coefficient, r represents the degree of association between the predicted and the measured values as depicted below:

$$r=\frac{\sum xy}{\sqrt{\sum x^2\sum y^2}}$$ (4)

First, an attempt was made to assess the significance or influence of each input parameter on $V_s/\sqrt{g\Delta d}$. Table 1 compares the ANFIS models, with one of the independent parameters removed in each case, and deleting any independent parameter from the input set yielded larger RMSE and lower r² values. These five independent parameters have non-negligible influence on $V_s/\sqrt{g\Delta d}$ and so the functional relationship given in Eq. (2) is used for ANFIS modeling in this study.

Table 1.

Models for sensitivity analysis.

Model set	Dependent variables	Independent variables	Error
			r2	RMSE
1	$\frac{V}{\sqrt{\Delta g{d}_{50}}}$	d50/R, λs, Dgr, Cv	0.98	0.002431
2	$\frac{V}{\sqrt{\Delta g{d}_{50}}}$	λs, Dgr, Cv	0.96	0.0567
3	$\frac{V}{\sqrt{\Delta g{d}_{50}}}$	d50/R, Dgr, Cv	0.93	0.1489
4	$\frac{V}{\sqrt{\Delta g{d}_{50}}}$	d50/R, λs, Cv	0.89	1.458
5	$\frac{V}{\sqrt{\Delta g{d}_{50}}}$	d50/R, λs, Dgr	0.85	2.3765

6. Result and discussion

Table 1 shows 5 models being set up for sensitivity analysis as shown below by using regression approach. Table 1 shows the sensitivity analysis done for the 5 models. Model with the least errors and highest r² value were used in the present analysis. Accordingly, model $((d_{50}/R),{\lambda }_s,D_{gr},{\lambda }_s,C_v)$ has been selected for further analysis as the parameters give the most significant effect on determining the relation of limiting velocity (V_s). Eq. (1) was deduced through the regression analysis, based on the 85% (98 sets) training data, a quite acceptable results with RMSE = 0.084, r² = 0.94 was obtained.

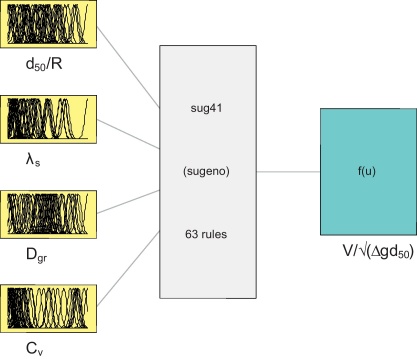
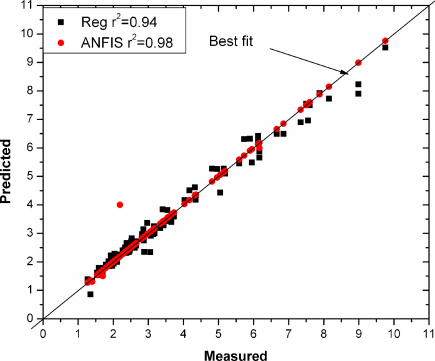
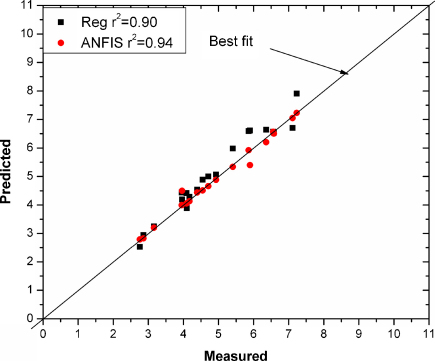
Fig. 2 shows the scenario of the ANFIS model using cluster radius of 0.1. The inputs had 4 parameters $((d_{50}/R),{\lambda }_s,D_{gr},C_v)$, output layer had 1 parameter $V/\sqrt{\Delta g{d}_{50}}$, and the model generated 63 rules. Table 2 shows the comparison of errors from ANFIS and regression model. The performance of the ANFIS model was compared with the regression analysis and also the proposed ANFIS approach gave satisfactory results compared to the existing predictor [4] which produced r² = 0.75 only. Overall, particularly for laboratory measurements, the ANFIS models could give better predictions than the traditional regression models. The ANFIS model produced the lowest errors r² = 0.98, and RMSE = 0.002431 for the training data (Fig. 3), and r² = 0.94, and RMSE = 0.005678 for the testing data (Fig. 4).

Fig. 2.

Scenario of the ANFIS model using cluster radius of 0.1 (63 rules).

Table 2.

Errors measures—ANFIS and regression analyses.

Model	Data sets	RMSE	r2
Regression	Training	0.08393	0.94
	Testing	0.37646	0.90
ANFIS	Training	0.18527	0.98
	Testing	0.17388	0.94
Vongvisessomjai et al. [4]	Testing	3.234	0.75

Fig. 3.

Observed versus predicted $V/\sqrt{\Delta g{d}_{50}}$ by ANFIS and regression (training).

Fig. 4.

Observed versus predicted $V/\sqrt{\Delta g{d}_{50}}$ by ANFIS and regression (testing).

7. Conclusions

Sediment transport in pipes is a complex phenomenon. The nature and motivation of traditional models differ significantly. These approaches are normally capable to make predictions within about one order-of-magnitude of the actual measurements. A single bed load transport model for storm sewers is given in Eq. (2). To overcome the complexity and uncertainty associated with bed load estimation, this study demonstrated that an ANFIS model could be applied for accurate prediction. The ANFIS model successfully predicted the bed load transport in storm sewers. The high value of the coefficient of determination (r² = 0.98), and RMSE = 0.002431, indicate that the ANFIS model is an excellent fit for the measured data. Thus the proposed ANFIS model is robust and useful for the practitioners.