Abstract
We introduce the software tool NTRFinder to search for a complex repetitive structure in DNA we call a nested tandem repeat (NTR). An NTR is a recurrence of two or more distinct tandem motifs interspersed with each other. We propose that NTRs can be used as phylogenetic and population markers. We have tested our algorithm on both real and simulated data, and present some real NTRs of interest. NTRFinder can be downloaded from http://www.maths.otago.ac.nz/~aamatroud/.
INTRODUCTION
Genomic DNA has long been known to contain ‘tandem repeats’: repetitive structures in which many approximate copies of a common segment (the ‘motif’) appear consecutively. Several studies have proposed different mechanisms for the occurrence of tandem repeats (1,2), but their biological role is not well understood.
Recently, we have observed a more complex repetitive structure in the ribosomal DNA of Colocasia esculenta (taro), consisting of multiple approximate copies of two distinct motifs interspersed with one another. We call such structures nested tandem repeats (NTRs), and the problem of finding them in sequence data is the focus of this article. Our motivation is their potential use for studying populations: for example, a preliminary analysis suggests that changes in the NTR in taro have been occurring on a 1000 year time scale, so a greater understanding of this NTR offers the potential to date the early agriculture of this ancient staple food crop.
The problem of locating tandem repeats is well known, as their implication for neurological disorders (3,4), and their use to infer evolutionary histories has urged some researchers to develop tools to find them. This has resulted in a number of software tools, each of which has its own strengths and limitations. However, the existing tools were not designed to find NTRs, and consequently do not generally find them. In this article, we present a new software tool, NTRFinder, which is designed to find these more complex repetitive structures.
We report here the algorithm on which NTRFinder is based and report some of the NTRs it has identified, including an even more complex structure where copies of four distinct motifs are interspersed.
Sequences, edit operations and the edit distance
A DNA sequence is a sequence of symbols from the nucleotide alphabet Σ = {A,C,G,T}. We define a DNA segment to be a string of contiguous DNA nucleotides and define a site to be a component in a segment. For a DNA segment
 |
xi ∈ Σ is the nucleotide at the i-th site and |X| = n is the length of X.
Copying errors happen in DNA replication due to different external and internal factors. These changes include substitution, insertion, deletion, duplication and contraction. We refer to these as ‘edit operations’. By giving each type of edit operation some specific weight, we can in principle find a series of edit operations which transforms segment x to segment y, whose sum of weights is minimal. We will refer to this sum as the ‘edit distance’, and denote it by d(x, y). For the purposes of this article, the edit operations allowed in calculating the edit distance are restricted to single nucleotide substitutions, and single nucleotide insertions or deletions (indels).
Classification of tandem repeats
Many classifications of tandem repeat schemas have been introduced in the computational biology literature. We list some which are commonly used:
(Exact) tandem repeats: an ‘exact tandem repeat’ (TR) is a sequence comprising two or more contiguous copies XX…X of identical segments X (referred to as the motif).
k–Approximate tandem repeats: a k–approximate tandem repeat (k–TR) is a sequence comprising two or more contiguous copies X1X2…Xn of similar segments, where each individual segment Xi is edit distance at most k from a template segment X.
Multiple length tandem repeats: a multiple length TR is a TR where each repeat copy is of the form Xxn, where n is a constant larger than one and d(X, x) is greater than some threshold value k.
Examples
-
• TR:
AGG AGG AGG AGG AGG. The motif is AGG.
-
• 1 − TR:
AGG AGC ATG AGG CGG. The motif is AGG.
-
• MLTR:
GACCTTTGG ACGGT ACGGT ACGGT
GACCTTTGG ACGGT ACGGT ACGGT.
The motifs are x = ACGGT and X = GACCTTTGG, with n = 3.
NTRs
In this section, we introduce a more complex repetitive structure, the NTR, also referred to as a ‘variable length tandem repeat’ (5). Let X and x be two segments (typically of different lengths) from the alphabet Σ = {A,C,G,T}, such that d(X,x) is greater than some threshold value k.
Definition 1. —
An ‘exact nested tandem repeat’ is a string of the form
where n > 1, si ≥ 1 for each 0 < i < n, and sj ≥ 2 for some j ∈ {0, 1, · · · , n}. The motif x is called the TR and the motif X is the ‘interspersed repeat’. The concatenations of the tandem repeats
alone, and of the interspersed motifs X alone, both form exact TRs.
Example —
x = ACGGT, X = GACCTTTGG, n = 7, s0 = 0, s1 = 3, s2 = 5, s3 = 2, s4 = 4, s5 = 1, s6 = s7 = 2, so
In practice, we expect any NTRs occurring in DNA sequences to be approximate rather than exact. In what follows we will write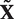 
to mean an approximate copy of the motif X, and 
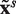to mean an approximate TR consisting of s (not necessarily identical) approximate copies of the motif x.
Definition 2. —
A (k1, k2)-approximate NTR is a string of the form
where n and si satisfy the same conditions as in Definition 1, and
is a k1-approximate TR with motif x, and
is a k2-approximate TR with motif X.
Examples —
• NTR:
AGG AGG CTCAG AGG CTCAG AGG AGG AGG CTCAG.
The motifs are AGG, CTCAG.
• (1, 2)–NTR:
AGA AGG CTTCG AGG CTCAG AG AGA AGG CTTCG AGG CTCAG AAG.
The motifs are x = AGG, X = CTCAG.
Related work
Various algorithms have been introduced to find exact TRs. Such algorithms were developed mainly for theoretical purposes, namely, to solve the problem of finding squares in strings (6–10). These algorithms are not easily adapted to finding the approximate TRs that usually occur in DNA.
A number of algorithms (11,12) consider motifs differing only by substitutions, using the Hamming distance as a measure of similarity. Others, e.g. (13–17), have considered insertions and deletions by using the edit distance. Most of these algorithms have two phases, a scanning phase that locates candidate TRs, and an analysis phase that checks the candidate TRs found during the scanning phase.
The only algorithm designed to look for NTRs is that of Hauth and Joseph in (5), which searches for tandem motifs of length at most 6 nt.
MATERIAL AND METHODS
In this section, we present the algorithm we have developed to search for NTRs in a DNA sequence. The algorithm requires several preset parameters. These are: k1 and k2 which bound the edit distances from the tandem and interspersed motifs; and the motif length bounds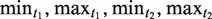 
. Other input parameters are discussed below.
Search phase —
Our search is confined to seeking NTRs with motifs of length
and
A (k1, k2)–NTR must contain a k1 − TR, so we begin by scanning the sequence for approximate TRs. To do this, we have chosen to adapt the TR search algorithm of Wexler et al., in which the sequence is searched for tandem motifs of length l1 by scanning the sequence with two windows w1 and w2 of width w, at distance l1 apart. This may be adapted to find non-adjacent copies of the tandem motif (as occur in NTRs) by holding w1 fixed, and moving w2 further away.
The user may set the k1, k2 values, preset with default values
 |
 |
following Domaniç and Preparata (2007), with matching probability pm given the default value pm = 0.8.
Once a TR has been found and its full extent determined, the right-most copy of the repeated pattern is taken as the current TR motif x, and further approximate copies of x are sought, displaced from the TR up to a distance of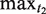 
nucleotides to the right. This is done by moving the second scanning window w2 to the right, while holding the first fixed in the current copy of x. If no further approximate copies of x are located, this TR is abandoned, and the TR search continues to the right. If a displaced approximate copy of x is observed, then both x and the interspersed segment X are recorded in a list, as we have found a candidate NTR. Further contiguous copies of x are then sought, with the rightmost copy x replacing the previous template motif.
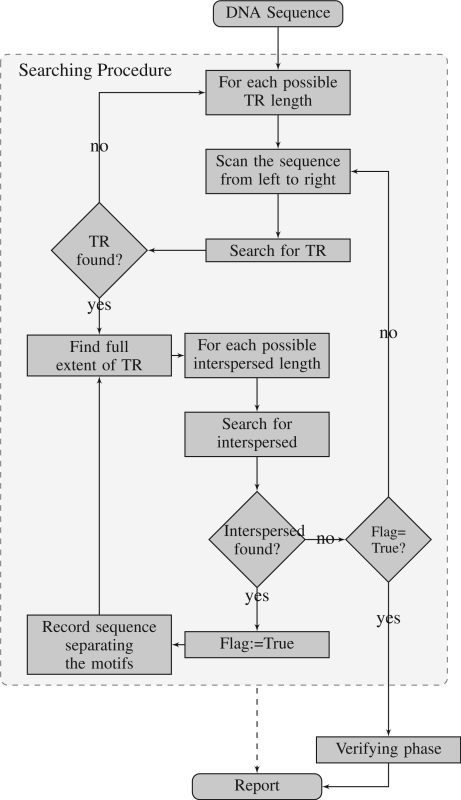
The steps above are repeated with successive motifs x and interspersed segments copied to the list, until no additional copies of the last recorded motif x are found. This search phase is illustrated in Figure 1.
Figure 1.
Flowchart of the NTRFinder algorithm.
At this point, the algorithm builds consensus patterns for x and X using majority rule. After constructing the two consensus patterns, the algorithm moves to the verification phase.
Example —
An example will help illustrate the procedure. Suppose that S contains an NTR of the form
The algorithm will scan from the left until it locates the TR consisting of three copies of x between X0 and X1. It will then start searching for additional non-adjacent copies of x to the right, locating the first copy to the right of X1. Having found this, it will record the intervening segment X1, and then continue the TR search from this point until the full extent of the TR between X1 and X2 is found.
This procedure is repeated once more, locating the TR between X2 and X3, recording the segment X2, and then searching for further copies to the right. At this point, no more copies of x are found, and the process of verification begins. The segments X0, X3 and the initial copy of x are found during this stage.
Verification phase —
Each candidate NTR is checked to determine whether it meets the NTR definition. This is accomplished by aligning the candidate NTR region, together with a margin on either side of it, against the consensus motifs x and X, using the nested wrap-around dynamic programming algorithm of Matroud et al. (18). The nested wrap-around dynamic programming parameters are set to be 2 for a match, −5 for a mismatch and −7 for a gap. These parameters were chosen following Wexler et al. (17). The nested wrap-around dynamic programming algorithm has complexity O(n|x||X|), where n is the length of the NTR region and |x| and |X| are the length of the tandem motif and the length of the interspersed motif, respectively.
A remark on tandem repeat detection, and the role of verification
The definition of a k-TR requires that each repeat be a distance at most k from some template motif. However, this template is unknown during the search phase. We follow Wexler et al.'s algorithm of comparing each repeat copy with the preceding copy. Comparisons between adjacent copies will not miss any TRs, provided the distance threshold is set appropriately, but may result in false positives due to ‘drift’. Such false positives are eliminated during the verification phase, when the candidate TR is aligned against the consensus motif.
Suppose that x1x2…xn is a k-TR with motif x. Then since d(x, xi) ≤ k we have
 |
by the triangle inequality. It follows that a TR search that correctly detects when d(xi, xi+1) ≤ d will find all (d/2)-TRs.
We note, however, that a segment x1x2…xn satisfying d(xi, xi+1) ≤ d for all i need not be a TR, since xj may ‘drift’ away from xi as j increases. A simple example is
 |
in which adjacent copies are distance 1 apart, but the first and last copies are distance 4 apart.
RESULTS
Tests on simulated data
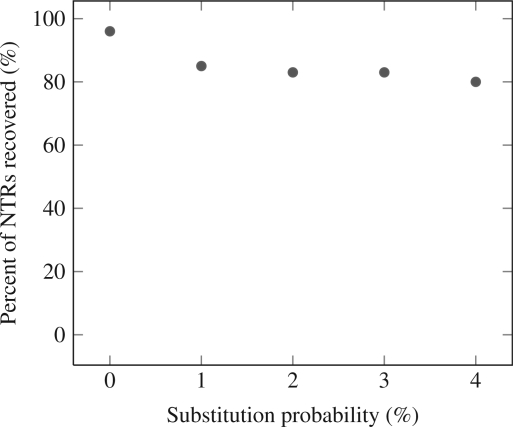
In order to measure the accuracy of NTRFinder, we generated synthetic sequence data containing NTR subsequences with varying probabilities of substitution and insertion/deletion (indels), and determined the proportion of the NTRs that were found by NTRFinder. In our simulation, we first generated one random DNA sequence of 100 000 nt, with each nucleotide occurring with probability 0.25. Within this sequence, we embedded 100 exact NTRs with repeats of randomly generated motifs X and x of varying lengths. From this sequence, we generated four additional sequences by introducing indels and substitutions. Indels were introduced to each sequence with a constant probability of 1% per site, and substitutions were introduced with varying probabilities of 1, 2, 3 and 4% per site. NTRFinder recovered 95, 84, 83, 83 and 80% of the NTRs, respectively. These results are plotted in Figure 2. No false positives were detected.
Figure 2.
Percentage of NTRs found in the synthetic sequences.
The first phase of NTRFinder uses a modification of ATRhunter's algorithm. In Wexler et al. (17), the authors report that ATRhunter has a 74–90% success rate for finding ATRs in synthetic sequences, with average score of an ATR over all sequences being 238 with a standard deviation of 116. These results suggest the accuracy of the Wexler algorithm provides the major limitation on the accuracy of NTRFinder.
Tests on real sequence data
To test NTRFinder on real sequence data, we searched all IGS sequences available in GenBank. The IGS sequences were chosen because we already knew of an NTR in the IGS region of C. esculenta. We also searched the entire Human Y chromosome from Fujita et al. (19).
The size ranges used for this search were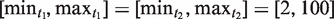 
, with the parameters k1 and k2 set to their default values. NTRs found in IGS sequences are listed in Table 1. We searched 27 IGS sequences and found NTRs in 12 of them.
Table 1.
NTRs found in some IGS sequences searched from GenBank and an additional unpublished sequence (C. esculenta)
| Species and accession number | NTR structure (s0, s1, … , sn) | |x| | Start index |
|---|---|---|---|
| |X| | End index | ||
| Nicotiana sylvestris X76056.1 | (0,1,2,3,4,2,3,2,3,3,3,5,4,3,2,3,3,1,2,5,3,5,4,2,2,4,3) | 10 | 960 |
| 13 | 2111 | ||
| Brassica juncea X73032.1 | (9,12,2,6,2,5,4,1) | 21 | 1403 |
| 30 | 2605 | ||
| Brassica olerecea | (1,1,1,3,3,1,3,2,1,1,2,1,3,1,1,2,1,2,1,1,2) | 30 | 1031 |
| 44 | 2902 | ||
| Brassica olerecea X60324.1 | (1,1,1,3,3,1,3,1,3,2,1,1,2,1,3,1,1,2,1,2,1,1,2) | 30 | 1036 |
| 44 | 3133 | ||
| Brassica rapa S78172.1 | (1,2,2,3,3,2,2,2,3) | 12 | 385 |
| 45 | 1337 | ||
| Brassica campestris X73031.1 | (6,4,4,7,4,4,4,3,1) | 21 | 1558 |
| 51 | 2580 | ||
| Colocasia esculenta Not published | (5,3,1,6,10,5,10,9,13,14,15,4) | 11 | 725 |
| 48 | 2384 | ||
| Nicotiana tomentosiformis Y08427.1 | (1,1,2,2,1,2,4,2,1) | 20 | 1016 |
| 46 | 1969 | ||
| Arabidopsis thaliana CP002685.1 | (3,2,1,1) | 13 | 32 189 |
| 17 | 32 365 | ||
| Zea mays AJ309824.2 | (2,2,1) | 19 | 2984 |
| 52 | 3113 | ||
| Olea europea AJ865373.1 | (3,1,3,6,5,6,4,3,4) | 75 | 961 |
| 11 | 3743 | ||
| Herdmania momus X53538.1 | (3,1,1,1,1,0) | 107 | 6363 |
| 91 | 7642 |
NTRs found in the Human Y chromosome are listed in Table 2. All NTRs found in the Y chromosome appear to be in the pseudoautosomal region.
Table 2.
NTRs found in the Human Y chromosome
| NTR structure (s0, s1, … , sn) | |x| | Start index |
|---|---|---|
| |X| | End index | |
| (1,2,2,1,2,1,2,1,1,2,2,2,2,1) | 12 | 143 865 |
| 56 | 144 880 | |
| (7,22,23,12,14,4) | 2 | 234 183 |
| 88 | 234 767 | |
| (1,1,2,1,1,1,1,,1,1,1,1,1,1,1,1,1,1,1,1) | 15 | 465 369 |
| 14 | 466 397 | |
| (1,1,1,2,1,1,1,1,1,1,1,1,1,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1) | 11 | 647 659 |
| 16 | 649 721 | |
| (17,15,31,28,72,62) | 2 | 901 237 |
| 49 | 902 037 | |
| (3,6,8,11,7,6,4,4,5,4,11) | 12 | 1 279 754 |
| 32 | 1 280 875 | |
| (26,27,25,25,25,20,17,13,26) | 1 | 1 397 128 |
| 48 | 1 397 735 | |
| (1,2,1,2,1,2,2,2,2,2,1,2,1,1,1,2,2,2,1,2,2,1,1) | 16 | 1 516 157 |
| 22 | 1 517 560 | |
| (1,1,2,6,2,2,2,1,2) | 19 | 1 626 578 |
| 35 | 1 627 258 | |
| (1,1,1,0,2,1) | 19 | 2 102 194 |
| 56 | 2 102 594 | |
| (2,2,2,1,2,1,1,1,1,2,6) | 21 | 2 164 541 |
| 15 | 2 165 091 |
More complex structures
In addition to the NTRs in Table 2, NTRFinder also reported an NTR in Linum usitatissimum (accession number gi∣164684852∣ gb∣EU307117.1∣) which on further analysis by hand turned out to have a more complex structure. The IGS region of the rDNA of this species contains an NTR with four motifs interspersed with each other. The four motifs are w=GTGCGAAAAT, x=GCGCGCCAGGG, y=GCACCCATAT and z=GCGATTTTG, and the structure of the NTR has the form
 |
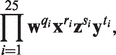where qi ∈ {1, 2, 3}; ri ∈ {1, 2}; si ∈ {0, 1}; ti ∈ {0, 1}.
Running time
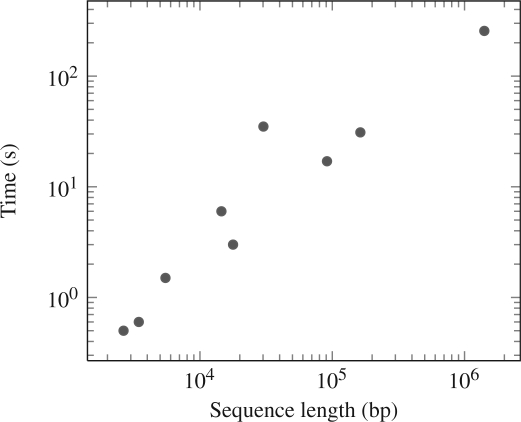
The running time for NTRFinder searching some sequences from GenBank is shown in Figure 3. It can be seen that the run time is approximately linear in the length of the sequence. However, it must be noted that the run time depends not only on the length of the input sequence, but also on the number of TRs and NTRs found in the sequence. The program spends most of the time verifying any TRs found.
Figure 3.
Running time of NTRFinder (on a Pentium Dual core T4300 2.1 GHz) plotted against segment length on a log–log scale. The search was performed on segments of different lengths, with the minimum and maximum TR lengths set to 8 and 50, respectively. The distribution suggests the running time is approximately linear with the sequence length.
DISCUSSION
In the last decade, a number of software tools to find TRs have been introduced; however, little work exists on more complex repetitive structures such as NTRs. The problem of finding NTRs is addressed in this study. The motivation for our study is the potential use of NTRs as a marker for genetic studies of populations and of species.
We have done some analysis on the NTR in the intergenic spacer region in C. esculenta (taro), noting some variation in the NTRs derived from domesticated varieties sourced from New Zealand, Australia and Japan. Further varieties are currently being analyzed.
CONCLUSION
The NTR structure is a complex structure that requires further analysis and study. The number of copy variants in the NTR region and the relationships between these copies might suggest a TR generation mechanism. In this article, we have introduced a new algorithm to find NTRs. The first phase of the algorithm has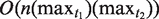 
time complexity, while the second phase (the alignment) needs 
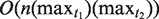space and time, where n is the length of the NTR region, and 
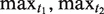are the maximum allowed lengths of the tandem and interspersed motifs.
FUNDING
The Allan Wilson Centre for Molecular Ecology and Evolution. Funding for open access charge: Allan Wilson Centre.
Conflict of interest statement. None declared.
ACKNOWLEDGEMENTS
We thank Andrew Clarke and Peter Matthews, for providing data and useful background about taro, and Hussain Matawa, for assisting in the development of the program interface. We would also like to thank the anonymous reviewers for their help in improving the manuscript.
REFERENCES
- 1.Weitzmann MN, Woodford KJ, Usdin K. DNA Secondary Structures and the Evolution of Hypervariable Tandem Arrays. J. Biol. Chem. 1997;272:9517–9523. doi: 10.1074/jbc.272.14.9517. [DOI] [PubMed] [Google Scholar]
- 2.Wells RD. Molecular basis of genetic instability of triplet repeats. J. Biol. Chem. 1996;271:2875–2878. doi: 10.1074/jbc.271.6.2875. [DOI] [PubMed] [Google Scholar]
- 3.Macdonald ME, Ambrose CM, Duyao MP, Myers RH, Lin C, Srinidhi L, Barnes G, Taylor SA, James M, Groot N. A novel gene containing a trinucleotide repeat that is expanded and unstable on huntington's disease chromosomes. the huntington's disease collaborative research group. Cell. 1993;72:971–983. doi: 10.1016/0092-8674(93)90585-e. [DOI] [PubMed] [Google Scholar]
- 4.Fu YH, Pizzuti A, Jr, Fenwick RG, King J, Rajnarayan S, Dunne PW, Dubel J, Nasser GA, Ashizawa T, de Jong P, et al. An unstable triplet repeat in a gene related to myotonic muscular dystrophy. Science. 1992;255:1256–1258. doi: 10.1126/science.1546326. [DOI] [PubMed] [Google Scholar]
- 5.Hauth AM, Joseph DA. Beyond tandem repeats: complex pattern structures and distant regions of similarity. Bioinformatics. 2002;18(Suppl. 1):S31–S37. doi: 10.1093/bioinformatics/18.suppl_1.s31. [DOI] [PubMed] [Google Scholar]
- 6.Apostolico A, Preparata FP. Optimal off-line detection of repetitions in a string. Theor. Comput. Sci. 1983;22:297–315. [Google Scholar]
- 7.Crochemore M. An optimal algorithm for computing the repetitions in a word. Inf. Process. Lett. 1981;12:244–250. [Google Scholar]
- 8.Kolpakov R, Kucherov G, Logiciel TG. Theoretical Computer Science. Springer; 2001. Finding approximate repetitions under hamming distance; pp. 170–181. [Google Scholar]
- 9.Main MG, Lorentz RJ. An o(n log n) algorithm for finding all repetitions in a string. J. Algorithms. 1984;5:422–432. [Google Scholar]
- 10.Stoye J, Gusfield D. Simple and flexible detection of contiguous repeats using a suffix tree. Theor. Comput. Sci. 2002;270:843–856. [Google Scholar]
- 11.Delgrange O, Rivals E. Star: an algorithm to search for tandem approximate repeats. Bioinformatics. 2004;20:2812–2820. doi: 10.1093/bioinformatics/bth335. [DOI] [PubMed] [Google Scholar]
- 12.Landau GM, Schmidt JP, Sokol D. An algorithm for approximate tandem repeats. J. Comput. Biol. 2001;8:1–18. doi: 10.1089/106652701300099038. [DOI] [PubMed] [Google Scholar]
- 13.Benson G. Tandem repeats finder: a program to analyze DNA sequences. Nucleic. Acids Res. 1999;27:573–580. doi: 10.1093/nar/27.2.573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hauth AM, Joseph D. Beyond tandem repeats: complex pattern structures and distant regions of similarity. ISMB. 2002:31–37. doi: 10.1093/bioinformatics/18.suppl_1.s31. [DOI] [PubMed] [Google Scholar]
- 15.Domaniç NO, Preparata FP. A novel approach to the detection of genomic approximate tandem repeats in the levenshtein metric. J. Comput. Biol. 2007;14:873–891. doi: 10.1089/cmb.2007.0018. [DOI] [PubMed] [Google Scholar]
- 16.Sagot MF, Myers EW. Identifying satellites and periodic repetitions in biological sequences. J. Comput. Biol. 1998;5:539–554. doi: 10.1089/cmb.1998.5.539. [DOI] [PubMed] [Google Scholar]
- 17.Wexler Y, Yakhini Z, Kashi Y, Geiger D. Finding approximate tandem repeats in genomic sequences. J. Comput. Biol. 2005;12:928–942. doi: 10.1089/cmb.2005.12.928. [DOI] [PubMed] [Google Scholar]
- 18.Matroud AA, Hendy MD, Tuffley CP. An algorithm to solve the motif alignment problem for approximate nested tandem repeats in biological sequences. J. Comput. Biol. 2011;18:1211–1218. doi: 10.1089/cmb.2011.0101. [DOI] [PubMed] [Google Scholar]
- 19.Fujita PA, Rhead B, Zweig AS, Hinrichs AS, Karolchik D, Cline MS, Goldman M, Barber GP, Clawson H, Coelho A, et al. The UCSC genome browser database: update 2011. Nucleic Acids Res. 2010;39:D876–D882. doi: 10.1093/nar/gkq963. [DOI] [PMC free article] [PubMed] [Google Scholar]