Quantum dynamics in continuum for proton transport II: Variational solvent-solute interface

Abstract

Proton transport plays an important role in biological energy transduction and sensory systems. Therefore it has attracted much attention in biological science and biomedical engineering in the past few decades. The present work proposes a multiscale/multiphysics model for the understanding of the molecular mechanism of proton transport in transmembrane proteins involving continuum, atomic and quantum descriptions, assisted with the evolution, formation and visualization of membrane channel surfaces. We describe proton dynamics quantum mechanically via a new density functional theory based on the Boltzmann statistics, while implicitly model numerous solvent molecules as a dielectric continuum to reduce the number of degrees of freedom. The density of all other ions in the solvent is assumed to obey the Boltzmann distribution in a dynamic manner. The impact of protein molecular structure and its charge polarization on the proton transport is considered explicitly at the atomic scale. A variational solute-solvent interface is designed to separate the explicit molecule and implicit solvent regions. We formulate a total free energy functional to put proton kinetic and potential energies, the free energy of all other ions, the polar and nonpolar energies of the whole system on an equal footing. The variational principle is employed to derive coupled governing equations for the proton transport system. Generalized Laplace-Beltrami equation, generalized Poisson-Boltzmann equation and generalized Kohn-Sham equation are obtained from the present variational framework. The variational solvent-solute interface is generated and visualized to facilitate the multiscale discrete/continuum/quantum descriptions. Theoretical formulations for the proton density and conductance are constructed based on fundamental laws of physics. A number of mathematical algorithms, including the Dirichlet to Neumann mapping (DNM), matched interface and boundary (MIB) method, Gummel iteration, and Krylov space techniques are utilized to implement the proposed model in a computationally efficient manner. The Gramicidin A (GA) channel is used to validate the performance of the proposed proton transport model and demonstrate the efficiency of the proposed mathematical algorithms. The proton channel conductances are studied over a number of applied voltages and reference concentrations. A comparison with experimental data verifies the present model predictions and confirms the proposed model.

I Introduction

Ion channels, which are proteins with pores and embedded in lipid-bilayer formed membranes, selectively permitting the permeation of certain ions, have attracted great interests in biological, biomedical and bioengineering studies. They are fundamental components in various biological processes, from cardiac cycles to human sensory systems. For example, human sensory systems are a part of the nervous system that is responsible for processing of vision, hearing, somatic sensation (touch), taste and olfaction (smell). Sensory systems consist of sensory receptors, neural pathways, and parts of the brain involved in sensory perception. However, human brain recognizes only electric signals, whereas external stimuli are chemical, physical, mechanical, thermal, acoustic, and photonic ones. It is ion channels that transfer external stimuli into electric signals acceptable by the brain. Therefore, the importance of ion channels to biological science and biomedical engineering cannot be over emphasized.

Ion flux across a cell membrane through protein channels usually results in biological current or the shift of the cell membrane from its resting potential so that the down stream signal transduction process is activated. The depolarization or hyperpolarization of the cell membrane is an essential step in biological sensory systems. For example, in the human vision system, the resting potential of cone cells or rod cells in the retina is maintained at around −40 mV by the inward sodium flux and outward potassium flux through corresponding channels. When struck by a photon, the cis-retinal changes its configuration to all-trans retinal, this photoisomerization causes conformational change in the opsin and leads to a series of signal transduction cascades. As a consequence, the Na⁺ channel is inhibited while the K⁺ channel keeps open, so the cell becomes hyperpolarized. The voltage-gated calcium channel is then closed due to this hyperpolarization and the photoreceptor cell is “switched off", by which an excitatory signal is sent down the neural pathway. It is the synergy of the Na⁺, K⁺ and Ca⁺ channels that leads the visual photontransduction, in which the optical signal is converted into the electric signal. In the human hearing sensory system, hair cells or cilia, which are located in the basilar membrane in the cochlea of the inner ear, are deflected mechanically by the acoustic vibration. As a consequence, mechanically gated K⁺ channels are open and then the change in voltage opens voltage-gated Ca⁺ channels that control the release of neurotransmitters. By this means, the acoustic signal is converted into an electrical nerve signal.

As a special cation, the proton transport is of crucial importance and plays a major role in many biochemical processes, such as cellular respiration, ATP synthase, photosynthesis and denitrification.²⁶ Energy transduction in bioenergetic systems requires the generation of large proton concentration gradients. For example, the chemical energy is stored as proton concentration gradient that drives ATP generation in mitochondria. For plants, light energy is transferred into a proton concentration gradient to create ATPs in chloroplasts.¹⁹ Voltage-gated proton channels are also vital in phagocytes, such as human neutrophils, during the respiratory burst process. The proton efflux through proton channels balances the electron movement generated by the NADPH oxidase and assists the production of extracellular reactive oxygen species which kill bacteria. Because of these important biological roles, as well as frequently serving as the target for rational drug design, proton channels have attracted great interests in experimental, theoretical and computational explorations.

The structure and function of channel proteins play an essential role in ion permeation. Most research activities are focused on a few ion channel properties: (i) The gating of ion channels. Ion channels are not always open or close. Based on the mechanism controlling the open/close status, they are categorized as ligand-gated ion channel (i.e., the channel is open only when the specific ligand is bound to the extracellular receptor domain), voltage-gated ion channel (i.e., the channel is open/close by the regulating membrane electrostatic potential) and other gating channels, such as mechanical, acoustic, photonic and thermal stimuli. (ii) The selectivity of the ion channel. When an ion channel is open, it is not open to all the ion species, only certain ions can penetrate. In this sense, ion channels are also classified by the permeating ions, such as potassium channels, sodium channels, and proton channels, etc. (iii) The efficiency of ion conductance. When an ion channel is open and conducts a specific ion species, the efficiency of ion conductance is of major interest, which is measured by the current-voltage (I–V) curve. Technological advance in the past few decades makes it possible to measure I–V curves through a single channel for a variety of ion channels under physiological conditions. These techniques are considerably empowered by the genetic engineering technology to identify the gating mechanism. (iv) Structural analysis. Many channel protein structures have been discovered by X-ray crystallography, nuclear magnetic resonance (NMR) and cryoelectron microscopy. Channel protein structural information is usually deposited in the Protein Data Bank (PDB) (http://www.pdb.org/pdb/home/home.do).

Apart from the molecular structure of the channel protein, the transport mechanism of ion transport is also important. Regular ions are prohibited to permeate the membrane because of a large energy barrier formed by the lipid bilayer. They can only permeate through the membrane with the assistance of ion channels. The basic permeation mechanism of regular ions, such as the sodium, potassium or calcium are considered to be hydro-diffusion, driven by the electrostatic potential and concentration gradient. The diffusivity is significantly reduced in the channel region, because of possible ion dehydration/rehydration processes, and the limited mobility of water molecules. The proton permeation across the membrane is quite different. Although the main mechanism of the proton transport is not fully understood yet,⁴⁰ it is believed that protons have properties distinguished from those of other cations and have significantly different conductivity. The motion of regular ions in solvent is usually described as diffusion, while the proton is interchangeable with protons that form water molecules. Protons translocate through a succession of hops in the hydrogen-bond network as indicated by the Grotthuss theory.³⁰ The protons can even permeate a membrane when the channel protein is absent, as long as an efficient hydrogen band chain is formed. Furthermore, the proton has the lightest mass among all ions and an effective radius that is about 10⁵ times smaller than other ions because H⁺ has no electron.¹⁹ The light mass and tiny size greatly facilitate proton transfer reaction and electrostatic interactions with surrounding molecules.²⁹ Due to these unique biological properties, the mobility of protons in bulk solution is fivefold higher than that of other cations.⁵

There are several strategies in modeling general ion transport processes. Molecular dynamics (MD) provides one of the most detailed descriptions in modeling biomolecular systems and there are several user-friendly packages available, such as AMBER,³¹ CHARMM,²⁷ etc. However, the use of MD in modeling ion permeation is still limited due to the significant barrier of predicting the channel conductance in sense of total simulation time needed versus the necessarily small time step.¹⁶ Brownian dynamics (BD)¹⁵ and the Poisson-Nernst-Planck (PNP) theory⁹ are utilized to study ion channels based on the mean-field approximation. In the former approach, ions are treated as explicit particles, while the water molecules are treated by continuum approximation. In the PNP approach, the ions of interest are also modeled by the continuum description through the electro-diffusion theory. The atomic detail of the channel protein is retained in these two approaches to estimate electrostatic potentials, whose gradient drives the ion motion. Both the BD and PNP models have a number of similarities in their initial setups and computational approaches.^21,28,33 Recently, we have developed matched interface boundary (MIB) based computational techniques^8,24,44,47 to overcome numerical challenges in the solution of the PNP equations for ion channels.⁴⁵ Our techniques are rigorously second-order convergent for complex geometries, non smooth interfaces and singular charges of membrane channel proteins. More recently, we have proposed a Poisson-Boltzmann-Nernst-Planck (PBNP) model⁴⁶ to reduce the computational cost of multiple ion systems ^1†. In the PBNP model, one only needs to solve the Nernst-Planck equation for one ion species and can represent the detailed density profiles of other ion species in the system by the Boltzmann distribution.⁴⁶

There is an agreement that the BD theory and PNP model may be expected to work well for regular ions, but not for protons,¹⁶ which have lighter mass and whose transfer involves the hydrogen bond making and breaking as mentioned earlier. The special proton transport processes need to be studied quantum mechanically. Some investigators have explored proton channels via Feynman path integral simulations and quantum energy levels of protons are computed by the Schrödinger equation.^32–34 Several interesting theoretical models are proposed in the last decade for proton systems.^7,38,40 Nevertheless, the field remains open and the molecular mechanism, as well as the quantum mechanism of proton transport is yet to be investigated.

Recently, we have introduced a multiscale/multiphysics framework, the quantum dynamics in continuum (QDC), to study proton transport over transmembrane proteins.¹¹ Due to the special properties and transport mechanism, the proton dynamics was described quantum mechanically via a density functional theory approach, while other mobile ions are treated implicitly to reduce the number of degrees of freedom. Quasi-equilibrium state and the Boltzmann distribution are assumed for the density of all other ions in the solvent. The water molecules are treated as a dielectric continuum by using the mean field approximation. The impact of protein molecular structure and its charge polarization on the proton transport is considered explicitly at the atomic detail. A total free energy functional is constructed to put proton kinetic and potential energies as well as electrostatic energy of all ions on an equal footing. The variational principle is employed to derive nonlinear governing equations for the proton transport system. Generalized Poisson-Boltzmann equation and Kohn-Sham equation are obtained from the variational framework. Theoretical formulations for the proton density and proton conductance are constructed based on fundamental principles. Our QDC model is validated by the experimental data for the Gramicidin A channel protein at a variety of ion concentration and voltage settings.

In the QDC model, the multiscale discrete-continuum description requires the separation of the discrete atomic domain from the continuum solvent domain. The static solvent excluded surface (SES)³⁵ is employed in our earlier treatment to separate solvent and solute.¹¹ Such an SES is ad hoc and does not reflect the true physical interface which varies when the ion permeates. A similar problem exists in implicit solvent models. In 2005, we introduced curvature-controlled partial differential equations (PDEs), i.e., geometric PDEs, for solvent-solute interface generation.⁴³ Such an approach differs from the use of PDEs for surface smoothing because the starting point is atomic information, instead of an existing surface. The first variational molecular surface of macromolecules, the minimal molecular surface (MMS), was introduced in 2006.³ The MMS has the smallest surface free energy (or surface area) for a given set of atomic coordinates and radii.^3,4 Recently, to accommodate the impact of potential interactions in the surface formation, we have proposed potential driven geometric flows for the construction of molecular surfaces of proteins.² Most recently, we have introduced differential geometry based multiscale models in which the discrete atomic domain is separated from the continuum solvent domain by the interface determined via differential geometry theory of surfaces.⁴² One of our differential geometry based multiscale models is a multiscale solvation model which optimizes the surface area, volume, solvent-membrane protein interaction, and electrostatic energies.^12,13,42 Both Eulerian and Lagrangian formulations of the differential geometry based multiscale model of solvation are constructed to couple polar and nonpolar contributions to the protein solvation process.^12,13

The objective of the present work is to incorporate the variational solvent-solute interface (VSI) to our QDC model to study the proton transport through membrane proteins. The combination of the QDC and the VSI is a new multiscale model. Unlike our previous multiscale models, this new model involves quantum mechanical description and Boltzmann statistics. In the spirit of our earlier differential geometry based multiscale models,^12,13,42 we construct the total energy functional to put multiscale/multiphysics/multidomain descriptions of the proton transport on an equal footing. The total energy functional consists of the proton energy and the solvation free energy of the system. The proton energy is described by the quantum formalism and includes the kinetic and potential contributions. The solvation free energy encompasses the polar (i.e., electrostatic) and nonpolar components. By using the variational principle, we derive three governing equations. First, the generalized Laplace-Beltrami equation is obtained for the membrane protein-solvent interface evolution. Additionally, the generalized Poisson-Boltzmann equation gives rise to the electrostatic potential of the system. Finally, the generalized Kohn-Sham equation describes the proton transport. These three equations are coupled and a dynamic iteration algorithm is proposed to update all of the nonlinear components. The present generalized Kohn-Sham equation differs much from the classical Kohn-Sham, which is for electrons. A number of mathematical algorithms, including the Dirichlet to Neumann mapping (DNM), the MIB method, and Krylov space techniques are utilized to implement the proposed model in a computationally efficient manner. Discussions are provided for the impact of the present multiscale VSI. A comparison with experimental measurement validates the present new differential geometry based multiscale model.

The rest of the present paper is organized as follows. Section II is devoted to the theory and model. The general setup and variables of interests are described first, followed by the model incorporating quantum mechanical treatment of protons, the continuum description of solvent, and atomic detail of protein structure and charges. A total energy functional is constructed to assemble the polar, non-polar and proton energy components. Section III outlines the derivation of three governing equations: the generalized Laplace-Beltrami, Poisson-Boltzmann and Kohn-Sham equations, and their corresponding numerical challenges and treatments. In Section IV, we present formalisms for proton density and transport from fundamental principles. A surface-dynamics driven self-consistent iteration algorithm is proposed. In Section V, we employ a commonly used channel protein, the Gramicidin A (GA), to demonstrate the performance of the proposed theoretical model and validate the proposed computational algorithms. Visualization of the variational interface of the GA is presented, and electrostatic properties are analyzed with a number of combinations of model parameters to gain a basic understanding of the GA channel. The conductance of protons under various external voltages and concentrations are simulated. Comparison is made with experimental measurements in the literature. This paper ends with a brief conclusion.

II Theory and model

In this section we provide the theoretical formulation of the quantum dynamics in continuum (QDC) model with the variational solvent-solute interface (VSI).

II.A Kinematics of the model

As indicated by Fig. 1(a), a proton transport system could be extremely complicated in terms of its biological structure, dynamics and transport process. Our goal is to model the dynamics of proton transport and to predict the proton conductance with the variational solvent-membrane protein interface. The model is built up on a multidomain, multiscale, and multiphysics fashion, which is sketched in Fig. 1(b).

Figure 1.

(a) Illustration of the complicated channel protein and membrane system; (b) Illustration of the multiscale model setup. The z− direction is considered as the transport direction.

In the sense of multidomain, the full domain Ω is divided into two subregions. One is the solvent domain Ω_s that consists of the extracellular/intracellular solvent region (or bath region) and the channel pore region; the other is the macromolecular subdomain Ω_m which includes the membrane protein(s) as well as lipid bilayers. Therefore, we have Ω = Ω_s ∪ Ω_m. It is worth pointing out that Ω_m and Ω_s overlap with each other at the so-called solute-solvent interface Ω_b,¹² i.e., Ω_b = Ω_s ∩ Ω_m ≠ ∅. The main reason is that wavefunctions of the solvent and the solute overlap at the atomic level. Furthermore, since the ion transport is a dynamic process with the cooperation of the channel protein, the interface of solute and solvent should not be considered as “frozen”. Therefore, the deformation of the solvent-membrane protein interface during the ion permeation should be described based on the fundamental laws of physics. To this end, a characteristic function S(r) : ℝ³ → ℝ is employed to indicate the overlapping solute-solvent interface. The S(r) is defined as one (S = 1) in the van der Waals volume of the biomolecule and zero (S = 0) in the aqueous solvent. In the solvent-membrane protein interface region Ω_b, S(r) takes transition values between zero and one. With the assistance of S(r), all model parameters are continuously defined on the multiple domains. The governing equation of S(r) is derived from the variational principle and it is the variational solvent-solute interface (VSI) that makes the current model significantly different from our previous one,¹¹ in which a fixed solvent excluded surface (SES) is employed to separate the solvent and macromolecule.

The solute (i.e., macromolecule) and solvent are treated in microscopic atomic detail and with macroscopic continuum approximation, respectively. For the biomolecular subdomain, the structural data of the channel protein and lipid bilayers are either generated from molecular dynamics simulations, or downloaded from the PDB, whose data are mostly collected from X-ray crystallography or nuclear magnetic resonance (NMR) experiments. The force field parameters, such as atomic van der Waals radii and point charges, are obtained from the CHARMM force field.²⁷ This detailed structural information, represented as charge density ρ_f (r), is crucial to establish the electrostatic potential, whose distribution near the channel pore plays a dominant role in regulating the ion species and transport process. In contrast, explicit description of the solvent is extremely expensive, so the solvent is approximated by the dielectric continuum to reduce the computational burden. In the solvent subdomain, there are three types of materials, ions of interest (i.e., protons), all other ion species and water molecules. The number density of the proton is denoted as n(r) so the corresponding charge density is ρ_p (r) = qn(r), where q is the elementary charge or charge carried by a single proton. The charge density for all other ion species, similarly is defined as

$$\rho \prime (\mathbf{r})={\displaystyle \sum _j^{N_c^{\prime }}}{q}_j{n}_j^{\prime }(\mathbf{r}),$$

with $N_c^{\prime }$ being the total number of other ion species in the solvent, $n_j^{\prime }(\mathbf{r})$ and q_j being the number density and charge of the jth ion species. The water molecules are modeled as a dielectric continuum.

Different physical principles are applied to protons and all other ion species. A fundamental assumption is that all other ions are essentially in a quasi-equilibrium state in the bath region and their densities $n_j^{\prime }(\mathbf{r})$ can be well described by the Boltzmann distribution except for those at the solvent-membrane protein interface. This approach has been carefully validated in our PBNP model.⁴⁶ Near the solvent-membrane protein interface, the density distribution of ions might be better described by the density functional theory of solution, or integral equations, in which the dispersion interaction between solvent and solute can be better accounted. However, such a treatment will lead to additional computational cost. In the present work, the solvent-solute interactions are accounted with short range interaction potentials.

The physics for protons in the channel pore is of central interest and is sharply different from that of other ion species. There are many evidences which indicate the quantum mechanical behavior of proton transfer in biomolecular systems and proton channels.^6,17 The first reason is that the small proton mass enhances the quantum tunneling effect in the proton transport. Additionally, a narrow channel morphology in many proton channels may lead to severe geometric confinement, which consequently promotes quantum effects. Finally, hydrogen-bonded chain of water molecules assisted proton translocation is quantum mechanical in origin.^32–34 Although theoretical models were proposed in the last decades,^7,38,40 the detailed mechanism of proton dynamics and transport is not fully understood yet. For these reasons, we treat protons quantum mechanically via a quantum formalism which describes how a quantum mechanical proton scatters through electrostatic and generalized-correlation potential fields. By this consideration, the number density of protons is expressed in terms of its wavefunction. The electrostatic potentials include interactions between protons represented by a self-consistent mean field approximation, the interactions between protons and fixed ions from membrane proteins and lipid bilayers, and the interactions between protons and other ion species in the system. The generalized-correlation potential is due to the impacts of the continuum solvent, the proton van derWaals interactions with the solvent, other ions and biomolecules, the effect of ion-water clusters, dispersion effect, and possible break-down of hydrogen-bonded chain in a narrow channel, etc.

Finally, in the spirit of our differential geometry based multiscale models,^10,12,42 a total energy functional framework is utilized to incorporate surface variation, quantum mechanical description and continuum description. Governing equations for the molecular surface generation, electrostatic potential of the system and the proton dynamics are derived from the Euler-Lagrange variation. Solutions to these coupled equations give rise to proton dynamics and transport process, which describes how quantum mechanical protons scatter through an electrostatic and generalized-correlation potential landscape with the presence of the variational channel wall.

II.B Free energy components

Before the overall energy functional is constructed, various free energy components in the multiscale model of the quantum dynamics in continuum are described in this subsection. The whole transport process involves a number of interactions which can be mainly classified as polar and nonpolar components, and generalized correlations. Consequently, the free energy of the transport model consists of corresponding polar, nonpolar, and correlation contributions.

II.B.1 Non-polar free energy functional

This subsection focuses on the nonpolar free energy of the system, which is considered as an important complement of the polar free energy. Since solvent molecules are treated implicitly, many well-known intermolecular interactions, such as London dispersion interactions, Debye (induced dipole) interaction, dipole-dipole interactions and van der Waals interactions, can be modeled as surface energy, mechanical work, and additional solvent-membrane protein interactions in the solvation analysis.^12,41,42 The corresponding nonpolar free energy functional takes the form

$$G_{\text{np}}[S]=\gamma A+p(\text{Vol})+{\displaystyle {\int }_{{\mathrm{\Omega }}_s}}{\rho }_0{U}_{\mathit{\text{ss}}}d\mathbf{r}.$$ (1)

The first term is the surface energy, with A being the surface area and γ the surface tension. It measures the disruption of intermolecular binding and/or intramolecular bonds that occurs when the surface of a macromolecule is created in the solvent. The second term is the mechanical work of creating the vacuum of a biomolecular size in the solvent. Here Vol represents the volume occupied by the molecule of interest, and p is the hydrodynamic pressure. Both surface energy and mechanical work are hydrophobic in nature. These hydrophobic terms are partially compensated by the third term, an interaction potential, which represents the attractive dispersion and other possible effects near the solvent-membrane protein interface. In this term, ρ₀ is the solvent density, which is in general a position-dependent function ρ₀ = ρ₀(r) to describe the solvent response to the macromolecule near the solvent-membrane protein interface, but assumed to be a constant bulk solvent density for simplicity in our current work. The solvent-solute interaction potential U_ss (r) is modeled by the van der Waals potential while many other potential forms can be used as well. This term couples polar and nonpolar solvation effects.

In differential geometry based solvation models,^12,13,42 the characteristic function S(r) is utilized to recast the nonpolar free energy in an appropriate form. For the surface area term in Eq. (1), the concept of the mean surface area of a family of isosurfaces which are subsets of points satisfying {S(r) = c}; where 0 ≤ c ≤ 1, is the range of S. Meanwhile, we make use of the coarea formula from the geometric measure theory to convert the area integral into a global volume integral.⁴² Such a term has been carefully validated in our recent work.¹² Finally, the mean surface area can be described by a volume integral. With the natural expressions of second and third terms of Eq. (1) in volume integrals, the non-polar free energy functional can be given as^12,42

$$G_{\text{np}}[S]={\displaystyle \int }\gamma |\nabla S(\mathbf{r})|d\mathbf{r}+{\displaystyle \int }pS(\mathrm{r})d\mathbf{r}+{\displaystyle \int }{\rho }_0(1-S(\mathbf{r}))U_{\mathit{\text{ss}}}d\mathbf{r}.$$ (2)

II.B.2 Electrostatic free energy in the system

Let Φ (r) be the electrostatic potential on the whole domain. In order to build up the electrostatic free energy, one needs to define the permittivity and total charge density in the system. In the present work, both the membrane and channel protein are treated as the same dielectric medium, and the interface between them is erased and a constant dielectric constant ε_m is assumed on Ω_m. On the other hand, the solvent in bath regions and in the channel pore has different biological characteristics, therefore a position dependent dielectric constant ε_s (r) is imposed on the solvent domain Ω_s. In fact, ε_s (r) in the channel region can differ much from that in the bulk region. Taking into account the solute-solvent interface, the general dielectric function of the system depends on the characteristic function S(r) and is given by

$$\epsilon (S)=(1-S){\epsilon }_s+S{\epsilon }_m$$ (3)

As shown in our earlier work,¹² the profile of ε(S) is very smooth.

The total charge density of the system consists of partial charges on channel proteins/membrane, charges carried by the mobile ions in the solvent, which are further categorized into the ions of interests and other ion species, i.e.,

$$\begin{array}{cc}{\rho }_{\text{total}}(\mathbf{r})\hfill & ={\rho }_f(\mathbf{r})+{\rho }_p(\mathbf{r})+\rho \prime (\mathbf{r})\hfill \\ \hfill & ={\rho }_f(\mathbf{r})+\mathit{\text{qn}}(\mathbf{r})+{\displaystyle \sum _j^{N_c^{\prime }}}{q}_j{n}_j^{\prime }(\mathbf{r}).\hfill \end{array}$$ (4)

As mentioned in earlier sections, the charge density of protein/membrane is described at the atomic scale. In the present treatment, we assume that coordinates of atoms in membrane protein and lipid bilayer are given and do not change during the proton transport process. This is certainly an approximation and can be easily removed by a combination of the present formulation with our multiscale MD formalism.^23,42 Although the coordinates do not change, the solvent-membrane protein interface are allowed to vary in the present model. Without changing the coordinates, the biomolecules still significantly contribute to ion dynamics and transport by electrostatic interactions. The fixed charges in the channel protein and nearby lipid bilayers determine the fundamental characteristics of the channel and provide the primary environment for proton transport. Since the total number of fixed charges is not too large (i.e., up to thousands), with the assumption that the positions of them are essentially fixed, the explicit discrete description is actually affordable. In this sense, one has

$${\rho }_f(\mathbf{r})={\displaystyle \sum _{i=1}^{N_a}}{Q}_i\delta (\mathbf{r}-{\mathbf{r}}_i)$$ (5)

where N_a is the total number of fixed charges, Q_i and r_i are the point charge and position of the ith atom, respectively. The electrostatic solvation free energy of the membrane-protein domain can be given by

$$G_{\text{Elec}-\text{Mol}}[S,\mathrm{\Phi },{\rho }_f]={\displaystyle \int }S(\mathbf{r})\left\{\mathrm{\Phi }{\rho }_f-\frac{{\epsilon }_m}{2}|\nabla \mathrm{\Phi }(\mathbf{r}){|}^2\right\}d\mathbf{r}.$$ (6)

Apart from ions of interest, there are many other ions in the solvent region, particularly in the extracellular and intracellular solvent regions. In the present model, all other ions are treated in a classical manner. Specifically, no detailed description is given to individual ions and their distributions are assumed to obey the Boltzmann distribution, i.e., the charge density of other ions is given by, in terms of electrostatic potential Φ (r)^11,46

$$\rho \prime ={\displaystyle \sum _j^{N_c^{\prime }}}{q}_j{n}_j^{\prime }(\mathbf{r})={\displaystyle \sum _j^{N_c^{\prime }}}{q}_j{n}_j^0{e}^{-\frac{q_j\mathrm{\Phi }(\mathbf{r})-{\mu }_j}{k_{B}T}},$$ (7)

where $n_j^0$ is the bulk reference density of the jth ion species. Notice that the Boltzmann distribution of other ion species with respect to the potential has been modified with the μ_j, the generalized electro-chemical potential of the jth ion species, which may have the position dependence at a non-equilibrium setting.^36,45

Under this approximation, the electrostatic solvation free energy of the solvent domain can be given as

$$G_{\text{Sol}}[S,\mathrm{\Phi }]={\displaystyle \int }(1-S(\mathbf{r}))\left[\mathrm{\Phi }(\mathbf{r}){\rho }_p(\mathbf{r})-\frac{{\epsilon }_s(\mathbf{r})}{2}{|\nabla \mathrm{\Phi }(\mathbf{r})|}^2-k_{B}T{\displaystyle \sum _j^{N_c^{\prime }}}{n}_j^0\left(e^{-\frac{q_j\mathrm{\Phi }(\mathbf{r})-{\mu }_j}{k_{B}T}}-1\right)\right]d\mathbf{r}.$$ (8)

Note that the electrostatic free energy functional of other ions in Eq. (8) is similar in spirit to that of Sharp and Honig,³⁹ Gilson et al,²⁵ Chen et al¹² and Wei.⁴² It should be pointed out that G_Sol[S, Φ] covers more than electrostatic free energy in the solvent. All the components of free energies of other ion species, including the internal potential energy, kinetic energy, entropy and chemical potential are absorbed in the last term in Eq. (8).

II.B.3 Proton energies

In fact, the polar and nonpolar free energies of the system discussed above complete the solvation free energy functional.^12,42 However, for proton transport, we need to consider the proton kinetic energy of motion and the proton potential energy of various interactions. As discussed in the Introduction, protons behave quantum mechanically. Therefore, we develop a quantum theory for protons. To reduce the number of degrees of freedom, it is convenient to construct a density functional description of protons. However, the present density functional theory of protons differs much from the classic density functional theory of electrons. The density functional theory of protons is formulated according to the Boltzmann statistics; while the density functional theory of electrons obeys the Fermi-Dirac statistics.

Kinetic energy

The fundamental kinetic energy of a proton is given by $\frac{{\mathbf{p}}^2}{2m(\mathbf{r})}$, where p is the momentum and m is proton effective mass. In the coordinate representation, the kinetic energy of protons in the whole system can be given as

$$G_{\text{Kin}}[S,{\mathrm{\Psi }}_E]={\displaystyle \int }(1-S(\mathbf{r})){\displaystyle \int }\frac{{\hslash }^2{e}^{-(E-{\mu }_p)/k_{B}T}}{2m(\mathbf{r})}|\nabla {\mathrm{\Psi }}_E(\mathbf{r}){|}^2\mathit{\text{dEd}}\mathbf{r},$$ (9)

where Ψ_E and E are the proton wavefunction and corresponding energy, μ_p is the generalized electrochemical potential of protons. The Boltzmann factor weights different energy contributions. The relation between the wavefunction and number density of the proton is the following:

$$n(\mathbf{r})=\langle \mathbf{r}|n_H|\mathbf{r}\rangle ={\displaystyle \int }{\mathrm{\Psi }}_E(\mathbf{r}){\mathrm{\Psi }}_E^{†}(\mathbf{r})e^{-\frac{E-{\mu }_p}{k_{B}T}}\mathit{\text{dE}}={\displaystyle \int }{|{\mathrm{\Psi }}_E(\mathbf{r})|}^2{e}^{-\frac{E-{\mu }_p}{k_{B}T}}\mathit{\text{dE}},$$ (10)

where ${\mathrm{\Psi }}_E^{†}(\mathbf{r})$ is the complex conjugate of Ψ_E(r) and the proton density operator n_H is given by

$$n_H=e^{-\frac{H-{\mu }_p}{k_{B}T}},$$ (11)

where H is the Hamiltonian of the system. The Boltzmann statistics is adopted in the present work. The proton density is constrained by the total number of protons (N_p) in the computational domain

$${\displaystyle \int }(1-S(\mathbf{r}))n(\mathbf{r})d\mathbf{r}={\displaystyle {\int }_{{\mathrm{\Omega }}_s}}n(\mathbf{r})d\mathbf{r}=N_p.$$ (12)

Electrostatic potential energy

Protons have a number of electrostatic interactions with the environment. First, protons interact repulsively among themselves

$$U_{\text{Ion}-\text{Ion}}(\mathbf{r})=\frac{1}{2}{\displaystyle \int }\frac{q^{2}n(\mathbf{r})n(\mathbf{r}\prime )}{\epsilon (S)|\mathbf{r}-\mathbf{r}\prime |}d\mathbf{r}\prime .$$ (13)

These interactions lead to a term that is nonlinear in density n and the resulting equations are to be solved iteratively.

Additionally, interactions between protons in the solvent and fixed charges in biomolecules are described as

$$U_{\text{Ion}-\text{Fix}}(\mathbf{r})={\displaystyle \sum _{i=1}^{N_a}}\frac{\mathit{\text{qn}}(\mathbf{r})Q_i}{\epsilon (S)|\mathbf{r}-{\mathbf{r}}_i|}.$$ (14)

Computationally, this contribution can be handled by the so-called Dirichlet to Neumann mapping approach.¹⁰

Finally, interactions between protons and other ion species are of the form

$$U_{\text{Ion}-\text{Other}}(\mathbf{r})={\displaystyle \sum _{j=1}^{N_c^{\prime }}}{\displaystyle \int }\frac{{\mathit{\text{qq}}}_{j}n(\mathbf{r})n_j^{\prime }(\mathbf{r}\prime )}{\epsilon (S)|\mathbf{r}-\mathbf{r}\prime |}d\mathbf{r}\prime .$$ (15)

Therefore, the electrostatic potential energy functional of protons is

$$G_{\text{Elec}}[S,n]={\displaystyle \int }(1-S(\mathbf{r}))[U_{\text{Ion}-\text{Ion}}(\mathbf{r})+U_{\text{Ion}-\text{Fix}}(\mathbf{r})+U_{\text{Ion}-\text{Other}}(\mathbf{r})]d\mathbf{r}.$$ (16)

Generalized correlation potential

The electrostatic potential plays a significant role in the transport process. However, there are many other interactions in the system that are also important for proton transport. These additional interactions, denoted as generalized correlations, include van der Waals interactions, dispersion interactions, proton-water dipolar interactions, proton-water cluster formation or dissociation, proton spin effects, proton-channel protein interaction etc. For example, one of generalized correlation effects is an energy barrier to the ion transport due to the change in the solvation environment from the bulk water to a relatively dry channel pore.

As discussed in our earlier work, the generalized correlation potential can also be modeled as a functional of the local ion density n(r) and the density gradient ∇n, i.e., U_GC[n,∇n]

$$G_{\text{GC}}[S,n]={\displaystyle \int }(1-S(\mathbf{r}))U_{\text{GC}}[n,\nabla n]d\mathbf{r}$$ (17)

where

$$\begin{array}{cc}\frac{\partial U_{\text{GC}}[n,\nabla n]}{\partial n}\hfill & =V_{\text{GC}}[n]\hfill \\ \hfill & =V_{\text{GC}}^{\text{Ion}-\text{Ion}}[n]+V_{\text{GC}}^{\text{Ion}-\text{Sur}}[n],\hfill \end{array}$$ (18)

where the ∇n dependence has been omitted as a first order approximation. Here $V_{\text{GC}}^{\text{Ion}-\text{Ion}}[n]$ is for the interaction among protons themselves, which represents those short range interactions and possible collisions; while the interactions between protons and the surrounding molecules, which may include many-body proton-water collisions, proton-protein interactions and dehydration effects, are simply modeled as energy $V_{\text{GC}}^{\text{Ion}-\text{Sur}}[n]$, which can be considered as related to the relaxation time of ions.¹¹

External potentials

One additional energy term should be introduced to account for the interaction between protons and infinitely large extra/intra-cellular surroundings. This energy is expressed by external potential U_Exter as the following:

$$G_{\text{Ext}}[S,n]={\displaystyle \int }(1-S(\mathbf{r}))U_{\text{Ext}}[n]d\mathbf{r}$$ (19)

where

$$\begin{array}{cc}\frac{\partial U_{\text{Ext}}[n]}{\partial n}\hfill & =V_{\text{Ext}}(\mathbf{r})\hfill \\ \hfill & =V_{\text{extra}}(\mathbf{r})+V_{\text{intra}}(\mathbf{r})\hfill \end{array}$$ (20)

where V_extra and V_intra are potentials for extracellular and intracellular positions, respectively. Because much of extracellular and intracellular surrounding is not explicitly described, V_Ext is non-hermitian and the detailed derivation is referred to our earlier work.¹¹ The external potential energies approximate the truncation effect of finite simulation region from the realistic infinitely large one, as well as various experimental conditions. Of course, external potentials can be dropped when the system is closed and no external field is applied.

II.C Total free energy functional of the system

Before assembling all energy components of the system, one needs to check the consistence and possible redundancy as shown in our earlier differential geometry based multiscale models.⁴² Indeed, fixed charges on the protein/membrane, protons and all other ion species make up all the charge sources in the present system. These charge sources are considered in electrostatic energies in Eqs. (6) and (8). It is interesting to note that, had dielectric function described a homogeneous dielectric medium, i.e., ε(S) = C with C being a constant, the electrostatic potential energies in Eqs. (13), (14) and (15) would be the solution of the Poisson equation

$$\mathit{\text{qn}}(\mathbf{r})\mathrm{\Phi }(\mathbf{r})=\frac{1}{2}{\displaystyle \int }\frac{q^{2}n(\mathbf{r})n(\mathbf{r}\prime )}{\epsilon (S)|\mathbf{r}-\mathbf{r}\prime |}d\mathbf{r}\prime +{\displaystyle \sum _{i=1}^{N_a}}\frac{\mathit{\text{qn}}(\mathbf{r})Q_i}{\epsilon (S)|\mathbf{r}-{\mathbf{r}}_i|}+{\displaystyle \sum _{j=1}^{N_c^{\prime }}}{\displaystyle \int }\frac{{\mathit{\text{qq}}}_{j}n(\mathbf{r})n_j^{\prime }(\mathbf{r}\prime )}{\epsilon (S)|\mathbf{r}-\mathbf{r}\prime |}d\mathbf{r}\prime .$$ (21)

Therefore, the effect of proton electrostatic potential energies has been accounted in Eqs. (6) and (8). Consequently, the total energy functional of the proton system includes the non-polar free energy in Eq. (2), electrostatic energies in Eqs. (6) and (8), the kinetic energy in Eq. (9), the generalized correlation energy (17) and the external potential energy in Eq. (19)

$$G_{\text{Total}}\left[S,\mathrm{\Phi },n\right]={\displaystyle \int }\{\gamma |\mathrm{\nabla }S(\mathbf{r})|+pS(\mathbf{r})+{\rho }_0(1-S(\mathbf{r}))U_{\mathit{\text{ss}}}+S(\mathbf{r})\left[-\frac{{\epsilon }_m}{2}{|\mathrm{\nabla }\mathrm{\Phi }|}^2+\mathrm{\Phi }{\rho }_f\right]+(1-S(\mathbf{r}))[-\frac{{\epsilon }_s(\mathbf{r})}{2}{|\mathrm{\nabla }\mathrm{\Phi }|}^2+\mathrm{\Phi }{\rho }_p-k_{B}T{\displaystyle \sum _j^{N_c^{\prime }}}{n}_j^0\left(e^{-\frac{q_j\mathrm{\Phi }-{\mathrm{\mu }}_j}{k_{B}T}}-1\right)]+(1-S(\mathbf{r}))\left[{\displaystyle \int }\frac{{\hslash }^2{e}^{-(E-{\mu }_p)/k_{B}T}}{2m(\mathbf{r})}{|\mathrm{\nabla }{\mathrm{\Psi }}_E(\mathbf{r})|}^2\mathit{\text{dE}}+U_{\text{GC}}[n]+U_{\text{Ext}}[n]\right]+(1-S(\mathbf{r}))\lambda \left[\frac{N_p}{V_{\mathrm{\Omega }}}-{\displaystyle \int }{e}^{-\frac{E-{\mu }_p}{k_{B}T}}{|{\mathrm{\Psi }}_E(\mathbf{r})|}^2\mathit{\text{dE}}\right]\}d\mathbf{r}.$$ (22)

where V_Ω = ∫ dr and the additional term in last row of Eq. (22) is the Lagrange multiplier for the constraint of the proton density.

The total energy functional (22) represents a multiphysical and multiscale framework that contains the continuum approximation for the solvent, while explicitly takes into account the channel protein in discrete atomic detail. More importantly, it mixes the classical theory of electrostatics and quantum mechanical description on an equal footing. Similar energy frameworks have been developed in our recent work for biomolecular systems^13,42 and nano-electronic devices.¹⁰

III Governing equations

The present multiscale system has three unknown functions: the characteristic function S(r), the electrostatic potential Φ(r) and the proton number density n(r), which is actually further linked to the wavefunction Ψ_E (r). All other functions are either to be explicitly given or depend on these variables. The governing equations for S, Φ and Ψ_E are to be derived from the total free energy functional by the variational principle via the Euler-Lagrange equation. This multiscale variational framework approach was developed in our recent work.^10,42

III. A Generalized Laplace-Beltrami (LB) equation

By variation of Eq. (22) with respect to the characteristic function S(r), we have

$$-\mathrm{\nabla }·\left(\mathrm{\gamma }\frac{\mathrm{\nabla }S}{|\mathrm{\nabla }S|}\right)+p-{\rho }_0{U}_{\mathit{\text{ss}}}+\left[-\frac{{\epsilon }_m}{2}{|\mathrm{\nabla }\mathrm{\Phi }|}^2+\mathrm{\Phi }{\rho }_f\right]+\left[\frac{{\epsilon }_s(\mathbf{r})}{2}{|\mathrm{\nabla }\mathrm{\Phi }|}^2-\mathrm{\Phi }{\rho }_p+k_{B}T{\displaystyle \sum _j^{N_c^{\prime }}}{n}_j^0\left(e^{-\frac{q_j\mathrm{\Phi }-{\mu }_j}{k_{B}T}}-1\right)\right]-\left[{\displaystyle \int }\frac{{\hslash }^2{e}^{-(E-{\mu }_p)/k_{B}T}}{2m(\mathbf{r})}{|\mathrm{\nabla }{\mathrm{\Psi }}_E(\mathbf{r})|}^2\mathit{\text{dE}}+U_{\text{GC}}[n]+U_{\text{Ext}}[n]\right]+\lambda \left[{\displaystyle \int }{e}^{-\frac{E-{\mu }_p}{k_{B}T}}{|{\mathrm{\Psi }}_E(\mathbf{r})|}^2\mathit{\text{dE}}-\frac{N_p}{V_{\mathrm{\Omega }}}\right]=0.$$ (23)

In Eq (23), $\nabla ·\left(\gamma \frac{\nabla S}{|\nabla S|}\right)$ is a generalized Laplace-Beltrami operator, which is a generalization of the usual Laplacian operator to a smooth manifold of the solvent-macromolecular interface.^2,42 In general, γ can be a function of the position γ = γ(r) to account for surface hydrophobicity at different locations of the macromolecule. For simplicity, it is treated as a position independent parameter in our present work. By solving Eq. (23), we can obtain a “physical solvent-solute interface”, S(r). However, it is difficult to solve this equation directly. As discussed in earlier work,^2,4,42 the solution of this elliptic PDE can be attained via a parabolic PDE with an artificial time

$$\frac{\partial S}{\partial t}=|\mathrm{\nabla }S|\left[\mathrm{\nabla }·\left(\gamma \frac{\mathrm{\nabla }S}{|\mathrm{\nabla }S|}\right)+V_{\text{LB}}\right],$$ (24)

where S : Ω × [0, ∞) ↦ ℝ. As $\frac{\partial S}{\partial t}=0$, the initial profile of S evolutes into a steady state solution, which solves the original Eq. (23). Note that Eq. (24) has the same structure as the potential driven geometric flow equation proposed in our earlier work.²

The generalized Laplace-Beltrami (LB) potential V_LB is defined as

$$V_{\text{LB}}=-p+{\rho }_0{U}_{\mathit{\text{ss}}}+\left[\frac{{\epsilon }_m}{2}{\left|\mathrm{\nabla }\mathrm{\Phi }\right|}^2-\mathrm{\Phi }{\rho }_f\right]-\left[\frac{{\epsilon }_s(\mathbf{r})}{2}{\left|\mathrm{\nabla }\mathrm{\Phi }\right|}^2\mathrm{-}\mathrm{\Phi }{\rho }_p+k_{B}T{\displaystyle \sum _j^{N_c^{\prime }}}{n}_j^0\left(e^{-\frac{q_j\mathrm{\Phi }-{\mu }_j}{k_{B}T}}-1\right)\right]+\left[{\displaystyle \int }\frac{{\hslash }^2{e}^{-(E-{\mu }_p)/k_{B}T}}{2m(\mathbf{r})}{\left|\mathrm{\nabla }{\mathrm{\Psi }}_E(\mathbf{r})\right|}^2\mathit{\text{dE}}+U_{\text{GC}}[n]+U_{\text{Ext}}[n]\right]-\lambda \left[{\displaystyle \int }{e}^{-\frac{E-{\mu }_p}{k_{B}T}}{\left|{\mathrm{\Psi }}_E(\mathbf{r})\right|}^2(\mathbf{r})\mathit{\text{dE}}-\frac{N_p}{V_{\mathrm{\Omega }}}\right].$$ (25)

It is this LB potential V_LB that makes Eq. (24) not closed. The electrostatic potential Φ and wavefunction Ψ_E are to be coupled to other governing equations. It is quite straightforward to calculate the first and second rows of V_LB, while the third and fourth rows involve the integration of explicit wavefunctions with respect to energy E. A practical and more efficient treatment will be given in later sections.

Equation (24) is solved with the Dirichlet boundary condition, i.e., S = 0 on ∂Ω × [0,∞). For the initial condition S(r, 0), it is defined as

$$S(\mathbf{r},0)=\{\begin{array}{cc}1,\hfill & \mathbf{r}\in D_{\mathrm{m}}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (26)

where we define the initial molecular domain to be $D_m={\displaystyle {\cup }_{i=1}^{N_a}}\{\mathbf{r}:|\mathbf{r}-{\mathbf{r}}_i|<r_i^{\text{VDW}}+r_p\},\text{with}{r}_i^{\text{VDW}}$ and r_p being atomic van der Waals radius and the probe radius, respectively. Standard central finite difference scheme is employed to discretize the spatial derivative while upwind scheme is utilized for the temporal derivative.^12,13

III.B Generalized Poisson-Boltzmann (PB) equation

The governing equation for the electrostatic potential can be derived by the variation of functional (22) with respect to electrostatic potential Φ

$$-\mathrm{\nabla }·(\epsilon (S)\mathrm{\nabla }\mathrm{\Phi }(\mathbf{r}))-(1-S){\displaystyle \sum _{j=1}^{N_c^{\prime }}}{n}_j^0{e}^{\frac{-q_j\mathrm{\Phi }(\mathbf{r})-{\mu }_j}{k_{B}T}}=(1-S)n(\mathbf{r})q+S{\rho }_f(\mathbf{r}).$$ (27)

Equation (27) is a generalized Poisson-Boltzmann equation^12,42 describing the electrostatic potential with three types of charge sources: the ions of interest, other ions species in the solvent described by the continuum approximation and the fixed point charges in biomolecules. This equation is not closed because S(r) and n(r) need to be evaluated from other governing equations.

It is meaningful, as stated in the previous sections, that the electrostatic potential Φ(r) relies on a smooth solute-solvent boundary or a characteristic function S(r) with transition values. This variational approach is the so called Eulerian formulation.^12,42 However, solving the proceeding Kohn-Sham equation requires a sharply defined solvent-solute boundary.¹¹ Fortunately, a Lagrangian formulation¹³ of this variation approach has been formulated on a sharp solvent-solute interface and shown to be mathematically equivalent to the Eulerian formulation and lead to consistent results in the solution of the generalized PB equation and in the solvation free energies for a large set of compounds. Therefore, we utilize the solvent-solute interface in the Lagrangian formulation for the generalized PB and Kohn-Sham equations. This is the so-called variational solvent-solute interface (VSI) and obtained by setting the interface Γ as a level set of the characteristic function S, i.e., Γ = {r ∈ ℝ³|S(r) = c}, where 0 < c < 1 is a constant.

Considering Eq. (27), the generalized Poisson-Boltzmann equation at the VSI limit is

$$-\mathrm{\nabla }·(\epsilon (\mathbf{r})\mathrm{\nabla }\mathrm{\Phi }(\mathbf{r}))-{\lambda }_s{\displaystyle \sum _{j=1}^{N_c^{\prime }}}{q}_j{n}_j^0{e}^{-\frac{q_j\mathrm{\Phi }-{\mu }_j}{k_{B}T}}={\lambda }_{s}qn(\mathbf{r})+{\lambda }_m{\displaystyle \sum _{i=1}^{N_a}}{Q}_i\delta (\mathbf{r}-{\mathbf{r}}_i)$$ (28)

where the permittivity ε(r) (also called dielectric coefficient) and the project functions λ_m(r) and λ_s(r) are defined as^13,23

$$\epsilon (\mathbf{r})={\epsilon }_m{\lambda }_m+{\epsilon }_s{\lambda }_s$$ (29)

and

$$\begin{array}{cc}{\mathrm{\lambda }}_m(\mathbf{r})=\{\begin{array}{cc}1\hfill & \mathbf{r}\in {\mathrm{\Omega }}_m\hfill \\ 0\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s\hfill \end{array},\hfill & {\mathrm{\lambda }}_s(\mathbf{r})=\{\begin{array}{cc}0\hfill & \mathbf{r}\in {\mathrm{\Omega }}_m\hfill \\ 1\hfill & \mathbf{r}\in {\mathrm{\Omega }}_s\hfill \end{array}\hfill \end{array}$$ (30)

where the computational domain is divided into two subdomains, Ω = Ω_m ∪Ω_s, with Ω_m and Ω_s denoting the solute and solvent accessible regions, respectively. The domains Ω_m and Ω_s are separated by an interface Γ = Ω_m∩Ω_s. Here, ε_m = ε₀ε_m and ε_s = ε₀ε_s are the permittivities of the macromolecule and the solvent, respectively, where ε₀ is the permittivity of vacuum and ε_α (α = m, s) are relative permittivities.

Recall the fact that the electrostatic potential Φ(r) is defined throughout the domain Ω, which is inhomogeneous with respect to the dielectric constant ε(r). Therefore, we need to physically impose continuity matching conditions at the interface Γ of two adjunctive subregions. The continuity matching conditions are given as

$${[\mathrm{\Phi }]|}_{\mathrm{\Gamma }}={\mathrm{\Phi }}^{+}(\mathbf{r})-{\mathrm{\Phi }}^{-}(\mathbf{r})=0,$$ (31)

$${[\epsilon \mathrm{\nabla }\mathrm{\Phi }·\overrightarrow{\mathrm{n}}]|}_{\mathrm{\Gamma }}={\epsilon }^{+}\mathrm{\nabla }{\mathrm{\Phi }}^{+}(\mathbf{r})·\overrightarrow{n}-{\epsilon }^{-}\mathrm{\nabla }{\mathrm{\Phi }}^{-}(\mathbf{r})·\overrightarrow{n}=0$$ (32)

where superscripts “⁺” and “⁻” represent the limiting values of a certain function at two sides of interface Γ, and n⃗ is the unit outward normal direction of Γ. Consequently, Eqs. (31) and (32) guarantee the continuities of the potential function and its flux. Equation (28) has discontinuous coefficient ε(r) across the sharp interface Γ, which is very complex in general for biomolecules. Additionally, charge sources consist of a large number of delta functions, which may cause computational difficulties. Fortunately, all of the above-mentioned challenges can be successfully handled by the matched interface and boundary (MIB) method^8,24,44,47 and the Dirichlet-to-Neumann mapping (DNM) scheme.^11,24

III.C Generalized Kohn-Sham (KS) equation

In the present multiphysics model, the proton number density n(r) in Eq. (27) is related to the wavefunction Ψ_E(r), which is governed by the generalized Kohn-Sham equation. This equation is obtained by the variation of the total free energy functional (22) with respect to wavefunction ${\mathrm{\Psi }}_E^{†}$

$$H{\mathrm{\Psi }}_E(\mathbf{r})=-\mathrm{\nabla }·\frac{{\hslash }^2}{2m(\mathbf{r})}\mathrm{\nabla }{\mathrm{\Psi }}_E(\mathbf{r})+V(\mathbf{r}){\mathrm{\Psi }}_E(\mathbf{r})=E{\mathrm{\Psi }}_E(\mathbf{r}),$$ (33)

where we set the Lagrange multiplier λ = E. Here

$$V(\mathbf{r})=q\mathrm{\Phi }(\mathbf{r})+V_{\text{GC}}[n]+V_{\text{Ext}}(\mathbf{r})$$

is the effective potential, which includes electrostatic, generalized correlation and external contributions. As mentioned earlier, the external potential can be omitted for a closed system without external fields.

Equation (33) appears to be the conventional Kohn-Sham equation. However, there are some important differences. First, the exchange correlation potential, which is crucial to electrons, is not presented. In the present theory, we use the generalized correlation potential to represent many unaccounted interactions. We assume the Boltzmann statistics for the ions of interest at ambient temperature. Additionally, we define the density as in Eq. (10), instead of the conventional choice for electrons: n_electron(r) = ∑_j |Ψ_j (r)|². This definition is partially due to the Boltzmann statistics and partially due to the spectrum of the present Kohn-Sham operator. Technically, the Hamiltonian of the generalized Kohn-Sham equation (33) has an absolute continuous spectrum. As such, a Boltzmann factor in the density definition is indispensable. In fact, the present Hamiltonian may support discrete spectra as well, if the potential interactions are strong enough. However, we do not consider this situation in the present work. In contrast, the Kohn-Sham operator for electrons has discrete spectra. Finally, unlike the conventional Kohn-Sham equation for electrons, the present generalized Kohn-Sham equation is not a closed one. It is inherently coupled to the generalized Laplace-Beltrami equation (23) and the generalized Poisson-Boltzmann equation (27). This coupled system endows us the flexibility to deal with complex multiphysics in a multiscale fashion — the quantum dynamics in continuum model with the VSI.

IV Solution protocol

Equations (23), (27) and (33) form a strongly coupled system and they need to be solved iteratively. Specifically, the characteristic function S(r) defines the solute and solvent sub-regions where different components of the electrostatics Φ(r) and the wavefunction Ψ_E (r) are calculated, while it also depends on the generalized LB potential which includes Φ(r) and Ψ_E (r) as building blocks. Once S(r) is determined, solving Φ(r) and n(r) (or Ψ_E (r)) is a self-consistent process, as indicated by their own governing equations. This situation results in a nonlinear system with three variables, one needs to predetermine two of them to solve for the third one and the whole loop is a complex self-consistent iteration procedure. It will be an interesting mathematical problem to analyze the system in view of existence, uniqueness of the solution, and to design robust algorithms to attain the solution. Unfortunately, this problem is still open.

In our previous work,^12,13 the dynamical coupling of the generalized PB and LB equations is well addressed. In our other work,^10,11 the generalized Gummel iteration is proposed to solve the self-consistent iteration of the generalized PB and KS equations. In this section, we propose a new strategy, the surface driven dynamical iteration to solve the system of three governing equations. In this tactic, the characteristic function S(r) serves as the leading variable in the dynamic evolution that initiates the internal self-consistent iteration of Φ(r) and n(r).

A set of model parameters needs to be carefully chosen to initiate the numerical simulation. These parameters include the surface tension γ, pressure p, ρ₀ for nonpolar free energy, dielectric constant ε_m and ε_s for electrostatics, α and $V_{\text{GC}}^{\text{Ion}-\text{Sur}}$ for proton generalized correlation and effective mass m(r) of protons. More detailed discussion about these parameters is referred to our earlier work.^11,12

IV.A Transport properties

The goal to solve Eqs. (23), (27) and (33) is to compute transport properties, such as density n(r) and current I. From Eq. (10) one can see that the wavefunction Ψ_E (r) is a fundamental element to construct necessary physical observables. For computational purpose, the relation (11) can be revised for the non-equilibrium transport as¹¹

$$n_H=\frac{i}{\pi }{\displaystyle \sum _{\alpha }}{\displaystyle \int }{e}^{-\frac{E-{\mu }_{\alpha }}{k_{B}T}}G(E)V_{\alpha }^{\mathit{\text{ah}}}{G}^{†}(E)\mathit{\text{dE}},\alpha =\text{extra},\text{intra},$$ (34)

where G is the Green’s operator

$$G(E)={(E-H)}^{-1}$$ (35)

and μ_extra, μ_intra are the external electrical field energies at extracellular and intracellular electrodes, respectively. Here $V_{\text{extra}}^{\mathit{\text{ah}}}\text{ and }{V}_{\text{intra}}^{\mathit{\text{ah}}}$ are the anti-Hermitian components of the external potentials.¹¹

Another important quantum observable, the proton current, is defined by the standard probability flux¹¹

$$I=q\text{Tr}\frac{1}{2}(n_H{\upsilon }^{†}+\upsilon n_H)$$ (36)

$$=q{\displaystyle {\int }_{{\mathrm{\Omega }}_s}}{\displaystyle \int }\frac{\mathrm{\hslash }}{2mi}\left[{\mathrm{\Psi }}_E^{*}(\mathbf{r})\mathrm{\nabla }{\mathrm{\Psi }}_E(\mathbf{r})-{\mathrm{\Psi }}_E(\mathbf{r})\mathrm{\nabla }{\mathrm{\Psi }}_E^{*}(\mathbf{r})\right]e^{-\frac{E-{\mu }_p}{k_{B}T}}\mathit{\text{dEd}}\mathbf{r},$$ (37)

where Tr is the trace operation and $\frac{1}{2}(n_H{\upsilon }^{†}+\upsilon n_H)$ is the symmetrized current operator with υ being the velocity vector. Similarly, one obtains the practical expression as¹¹

$$I=\frac{q}{h}\text{Tr}{\displaystyle \int }G(E)V_{\text{intra}}^{\mathit{\text{ah}}}{G}^{†}(E)V_{\text{extra}}^{\mathit{\text{ah}}}\left[e^{-\frac{E-{\mu }_{\text{extra}}}{k_{B}T}}-e^{-\frac{E-{\mu }_{\text{intra}}}{k_{B}T}}\right]\mathit{\text{dE}}.$$ (38)

Practically, properly discretized formulations for Green’s operator G and external potentials $V_{\alpha }^{\mathit{\text{ah}}},(\alpha =\text{extra},\text{intra})$ need to be set up for Eqs. (34) and (38).¹¹ In fact, Eq. (33) is not solved explicitly for the wavefunction. Instead, with total Hamiltonian of proton and proper VSI, Eq. (34) is implemented and contributes back to the source term of the generalized PB equation and generalized LB potential.

IV.B Internal iteration of electrostatics and proton number density

At this stage, let us assume that S(r) is obtained or as an initial guess and consider the iteration of Eqs. (27) and (33). The proton number density n(r) and the electrostatics potential Φ(r) are assumed to have the following intrinsic connection^10,11

$$n(\mathbf{r})=ℱ(\mathrm{\Phi }(\mathbf{r}),{\overline{\mu }}_p(\mathbf{r})),$$ (39)

where ℱ (Φ, μ̄_p) = n₀e^{−(qΦ−μ̄_p)/k_BT} is the Boltzmann function and n₀ is the reference number density of the protons. The intermediate value of μ̄_p(r) equals μ_p in bath regions and the quantity in the channel pore can be easily found once ρ_p and Φ̃(r) are available. Based on this argument, Eq. (28) is written as a new nonlinear equation

$$-\mathrm{\nabla }·(\epsilon (S)\mathrm{\nabla }\mathrm{\Phi }(\mathbf{r}))-(1-S){\displaystyle \sum _{j=1}^{N_c^{\prime }}}{n}_j^0{e}^{\frac{-q_j\mathrm{\Phi }(\mathbf{r})-{\mu }_j}{k_{B}T}}=(1-S)n_0{e}^{-\frac{q\mathrm{\Phi }-{\overline{\mu }}_p(\mathbf{r})}{k_{B}T}}+S{\rho }_f(\mathbf{r}).$$ (40)

Equation (40) can be solved by various inexact Newton’s methods with the μ̄_p (r) recovered from the Φ(r) and n(r) from the previous step. After solving Eq. (40), one proceeds the iteration to the next loop. It has been verified that this generalized Gummel iteration with the relaxation method can achieve good convergence.^10,11 Furthermore, relation (39) offers an alternative but more convenient way to calculate the generalized LB potential that is contributed by the protons in the solvent.

IV.C External surface dynamics driven iteration

The characteristic function S(r) can be updated once the Φ(r) and n(r) are obtained. However, it is extremely difficult to directly calculate the generalized LB potential in the form of (25) because the wavefunction Ψ_E (r) is not explicitly solved¹¹ and the integral with respect to the energy E will cost extra computation. The introduced intermediate function μ̄_p (r) can overcome this difficulty. With the knowledge of Φ(r) and n(r) (and hence μ̄_p (r)), the original total functional (22) is essentially equivalent to, based on equation (40)

$$G_{\text{Total}}[S,\mathrm{\Phi }]={\displaystyle \int }\{\mathrm{\gamma }|\nabla \mathrm{S}(\mathbf{r})|+pS(\mathbf{r})+{\rho }_0(1-S(\mathbf{r}))U_{\mathit{\text{ss}}}+S(\mathbf{r})\left[-\frac{{\epsilon }_m}{2}{|\mathrm{\nabla }\mathrm{\Phi }|}^2+\mathrm{\Phi }{\rho }_f\right]-(1-S(r))[\frac{{\epsilon }_s(\mathbf{r})}{2}{\left|\mathrm{\nabla }\mathrm{\Phi }\right|}^2+k_{B}T{\displaystyle \sum _j^{N_c^{\prime }}}{n}_j^0\left(e^{-\frac{q_{j^{\mathrm{\Phi }-{\mu }_j}}}{k_{B}T}}-1\right)]-(1-S(\mathbf{r}))\left[k_{B}T{n}^0\left(\text{exp}\left(-\frac{q\mathrm{\Phi }-{\overline{\mu }}_p(\mathbf{r})}{k_{B}T}\right)-1\right)]\right\}d\mathbf{r}.$$ (41)

As a consequence, the generalized LB potential (25) can be rewritten as:

$$V_{\text{LB}}=-p+{\rho }_0{U}_{\mathit{\text{ss}}}+\left[\frac{{\epsilon }_m}{2}{|\mathrm{\nabla }\mathrm{\Phi }|}^2-\mathrm{\Phi }{\rho }_f\right]-\frac{{\epsilon }_s(\mathbf{r})}{2}{|\mathrm{\nabla }\mathrm{\Phi }|}^2-k_{B}T{\displaystyle \sum _j^{N_c^{\prime }}}{n}_j^0\left(e^{-\frac{q_j\mathrm{\Phi }-{\mu }_j}{k_{B}T}}-1\right)-k_{B}T{n}^0\left[\text{exp}\left(-\frac{q\mathrm{\Phi }-{\overline{\mu }}_p(\mathbf{r})}{k_{B}T}\right)-1\right].$$ (42)

With the above treatment, there is no need to explicitly calculate the wavefunction Ψ_E (r) and integrations. Instead, having Φ(r) and n(r) available, one can evaluate the quasi-chemical potential via Eq. (39), which is a simple algebraic equation, and insert the quasi-chemical potential in Eq. (42) to obtain the generalized LB potential. Consequently, Eq. (24) is closed at the current step. Various numerical schemes, such as upwind method,⁴ can be employed to solve the time evolution problem to obtain the characteristic function S(r) for the next loop.

IV.D The work flow of the self-consistent iteration

In principle, any two variables of S(r),Φ(r) and n(r) can be initialized for the calculation of the third one, and the whole iteration can continue. In other words, any of the three variables can be used to lead the iteration of other two. It is this mathematical flexibility that brings us the complexity of numerical simulation. Based on our successful experience,^10–13 the dynamic evolution of the characteristic function S(r) is utilized to lead the self-consistent iteration of Φ(r) and n(r). Here we assemble all the components together and give a main work flow for the numerical simulation of these coupled equations.

• Step 0. Preparation. All the necessary preparations for the whole loop are accomplished in this step, which include:

  • –
    0.1. The channel protein of interest is downloaded from the PDB. Partial charges, positions, radii of all atoms are determined by CHARMM force field²⁷ and related software packages, such as PDB2PQR.²⁰ The prepared channel structure is then embedded in a proper computational domain.
  • –
    0.2. Generate the initial condition S(r; 0) for Eq. (24).

• Step 1 (Surface dynamics). Solving the generalized Laplace-Beltrami equation (24) with Φ^m (r) and n^m(r) (initial guess as zero if m = 0). Calculate total energy $G_{\text{Total}}^m$ through Eq. (41). Note that index m is for the external or surface driven dynamic evolution loop.

• Step 2 (Self-consistent). This step is considered as the internal self-consistent iteration of electrostatics Φ^m,l(r) and proton number density n^m,l(r), where superscripts l is added for the internal iteration:

  • –
    2.1. With ${\overline{\mu }}_p^{m,l}(\mathbf{r})$, solve generalized Poisson-Boltzmann equation (40) to attain updated Φ^m,l+1(r).
  • –
    2.2. Solve Eq. (34) to attain new density n^m,l+1(r).
  • –
    2.3. Recover ${\overline{\mu }}_p^{m,l+1}(\mathbf{r})$ via Eq. (39).

• Step 3 (Self-consistent convergence check). If ‖Φ^m,l+1 −Φ^m,l‖ < ε₁ and ‖n^m,l+1 − n^m,l+1‖ < ε₂, where ε₁ and ε₂ are predefined internal error tolerances, set Φ^m+1(r) = Φ^m,l+1, n^m+1(r) = n^m,l+1(r) and go to Step 4, otherwise go to Step 2.1.

• Step 4 (Dynamic energy convergence check). Update energy $G_{\text{Total}}^{m+1}$ with S^m+1(r), Φ^m+1(r) and ${\overline{\mu }}_p^m(\mathbf{r})$. If the total energy is convergent, go to step 5 otherwise go to Step 1.

• Step 5 (Proton current calculation). Calculate the proton current via Eq. (38).

Figure 2 gives an explicit graphic illustration of the above work flow.

Figure 2.

Work flow of the overall surface driven self-consistent iteration.

V Numerical experiments

In this section, we carry out numerical experiments to demonstrate the utility of the proposed multiscale/multiphysics QDC model. The validity of the proposed model for proton transport and related performance analysis are presented based on a specific channel protein, the Gramicidin A (GA, PDB code: 1MAG).

V.A Gramicidin A as a water-filled pore for proton transport

The GA channel protein exists in the soil bacterial species Bacillus brevis and is one of the best studied realistic channels, both structurally and functionally. The GA is a dimer in a bilayer membrane, and consists of two head-to-head β-helical parts. Two parts of the dimer have an identical sequence: FOR-VAL-GLY-ALA-DLE-ALA-DVA-VAL-DVA-TRP-DLE-TRP-DLE-TRP-DLE-TRP-ETA. It forms a narrow pore of about 4Å in diameter and 25Å in length. The GA is known to select small monovalent cations, bind bivalent cations, while reject anions. Due to its well-defined structure and abundant experimental data, the GA has been used as a testbed for highly accurate numerical algorithms⁴⁵ and newly developed Poisson-Boltzmann-Nernst-Planck model in our earlier work.⁴⁶ Indicated by sufficiently many experimental evidences, the GA is a water-filled pore in which roughly twelve water molecules are aligned. Hydrogen band chain can form within the water chain, which sustains proton transport through the Grotthuss-type mechanism. Because of the simple structure and fruitful biological conclusion of the GA, we utilize it to validate the proposed model and algorithm.

In the present work, the GA structure is downloaded from the PDB, and the data file is processed by the PDB2PQR package, in which the radii and partial charges are adopted from the CHARMM force field.²⁷ Figure 3 gives an illustration of the GA protein in a 3D display for the structure in atomic details, Fig. 3 (a) shows the atomic structure of the protein from which amino-acid and their relative positions can be easily obtained. Figure 3 (b) displays the structure from the top view from which a channel pore can be easily recognized.

Figure 3.

3D illustration of the Gramicidin A (GA) channel structure with atoms and bonds. (a) Side view (b) Top view.

V.B Variational solvent-solute interface (VSI) of the GA system

With the prepared structural information, we solve the coupled equations by following the work flow in Fig. 2. We first check the resulting VSI, with a comparison to the SES which is adopted in our earlier work. In the LB potential (25), the solute-solvent interaction potential U_ss is taken as the full 12-6 Lennard-Jones pair potential since it can offer the smallest root mean square (RMS) error for the testing set of solvation calculations^12,13

$$U_{\text{ss}}={\displaystyle \sum _i}{V}_i^{\text{LJ}}(\mathbf{r})={\displaystyle \sum _i{\overline{\epsilon }}_i\left[{\left(\frac{{\sigma }_i+{\sigma }_s}{|\mathbf{r}-{\mathbf{r}}_i|}\right)}^{12}-2{\left(\frac{{\sigma }_i+{\sigma }_s}{\left|\mathbf{r}-{\mathbf{r}}_i\right|}\right)}^6\right],}$$ (43)

where ε̄_i is the well-depth parameter, σ_i and σ_s are the radii of solute and solvent, respectively. In our calculation, σ_s is chosen to be 0.65 Å as a good fitting solvent radius. The value of ε̄_i can be determined by the formula ${\overline{\epsilon }}_i\left[{\left(\frac{{\sigma }_i+{\sigma }_s}{|\mathbf{r}-{\mathbf{r}}_i|}\right)}^{12}-2{\left(\frac{{\sigma }_i+{\sigma }_s}{|\mathbf{r}-{\mathbf{r}}_i|}\right)}^6\right]=D_i$, where r is on the vdW surface of the atom and constant D_i is assumed as constant D = 1.¹² The surface tension γ is used as a fitting parameter and its initial value is chosen as γ = 1/15. Correspondingly, the hydrodynamic pressure is taken as p = 0.5γ. The grid resolution is taken as Δx = Δy = Δz = 0.5Å and the time step is Δt = (Δx)²/5. When the characteristic function S(r) is calculated, the isosurface function value c = 0.5 is adopted to determine the sharp solute-solvent surface Γ, which is convenient for other two governing equations.

Figure 4 provides the VSI and SES in top view and side cross-section view, respectively. It should be noted that the SES is independent of the physiological conditions such as ion concentration or transmembrane voltage differences. It only depends on the parameter used in the generating software package. The SES of the GA is generated via the MSMS package³⁷ with water probe radius 1.3 Å and density 10. Once generated, it keeps fixed and is applied to various simulation conditions. However, the generation of the VSI is an iteration process as stated in the earlier sections. As indicated by generalized LB equation (24), the mechanism of evaluating the characteristic functions S(r) is the diffusion associated with the generalized LB potential, which contains the impact from the electrostatics and ionic concentration. The VSI showed in Figs. 4(c) and (d) are calculated under the transmembrane potential of 0.2 mV and with the ionic concentration of 0.1M.

Figure 4.

Morphology of the GA with the solvent exclusion surface (SES) and variational solvent-solute interface (VSI) (a) Mouth of the channel pore in the SES; (b) Side view of the GA channel in the SES; (c) Mouth of the channel pore in the VSI; (b) Side view of the GA channel in the VSI.

Comparing Figs. 4(a) and (b) and Figs. 4(c) and (d), it can be seen that the SES is relatively “skinny”. Many geometric singularities, such as cusps and self-intersecting surfaces, can occur.⁴⁵ These singularities may bring computational difficulties to the designed interface schemes and are unphysical in the solvent-solute interface. On the contrary, the VSI admits a smooth appearance because of the diffusion mechanism, gives less-intensive sharp changes near the solvent-solute boundary, and incorporates interactions with the external ionic condition as well as transmembrane voltages. All of these characteristics endows the VSI with physical sense, and many good results in applications are obtained.^12,13

The VSI also results in different characteristics for the channel pore. Because the SES gives a “skinny” surface configuration, it leaves a relatively wider channel pore as shown in Fig. 4(b)) than the VSI does (Fig. 4(d)). On the other hand, the channel wall formed from the VSI is much smoother than that from the SES. Figure 5 unveils this characteristics by the comparison of areas of cross-section along the channel generated by the SES and the VSI. The red solid and blue dashed curves represent the areas of the channel cross-sections that perpendicular to the transport direction, with the VSI and SES, respectively. Both of area calculations agree with the experimental conclusion that the radius of the channel pore is roughly 4Å in diameter. It can be seen that the VSI gives less-significant change in area along the transport direction. An explanation of the present VSI is that it partially takes care of the size effect of the solvent via the van der Waals interaction potential.

Figure 5.

Comparison of the GA channel pore areas along the transport direction computed with SES and the VSI. The unit of area is Ų. The red solid curve is for the VSI and the blue dashed line for the SES.

V.C Electrostatic properties of the GA system

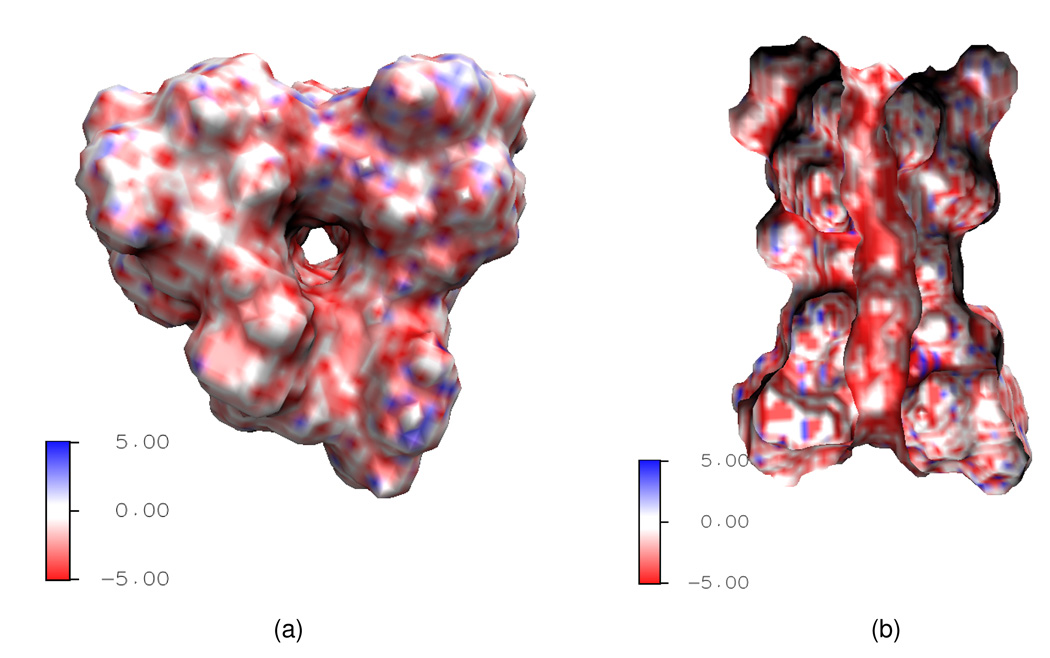
Next, we examine the surface electrostatic distribution in the GA channel protein, which plays the most significant role in the proton transport. Figure 6 shows the calculated electrostatic potential mapped on the VSI in this system. Although the GA is neutral in general, its surface electrostatic potential is mostly negative near the channel mouth as indicated by the red color in the graph. Furthermore, as shown in Fig. 6(b), the inner wall of the channel pore is also intensively negatively charged. This fact indicates the selectivity of the GA channel — it selects positive ions.

Figure 6.

3D illustration of the Gramicidin A (GA) channel structure and surface electrostatic potential. The negative surface electrostatic potential as indicated by the intensive red color on the channel upper surface and inside the channel pore implies that the GA selects positive ions. (a) Top view of the GA channel; (b) Side view of the GA channel.

The electrostatics of the channel system greatly depends on the dielectric constants used in Eq. (27). We have explored the proper range of the dielectric constant of each component in biological sense and tested a wide range of values in order to obtain a reasonable prediction in our earlier work.¹¹ The study on the dielectric constant ε_m of the molecule in the ion transport problem is quite fruitful and there is a general agreement that ε_m could be taken as a constant that slightly greater than 2, which is the value used in the solvation study. While the dielectric constant ε_s for the solvent should be position dependent. The dielectric constant ε_bath = 80 is the value widely accepted in the literature for the bath water region. However, since the mobility of the water molecules in the channel pore is restricted because of the small radius, the dielectric constant ε_ch remains mysterious and various values are tested in reported simulations.¹¹

Figure 7 quantitatively displays the electrostatic potential of the GA channel and the corresponding density of monovalent cations based on the Boltzmann distribution, with three different values of ε_ch. All quantities are averaged on the cross-section along the channel axis. Here ε_m is taken as 5 and the reference ionic density is set to 0.1M. The vertical dash lines indicate the entrance (left) and exit (right) of the GA channel. Although the GA protein is overall neutral in charge, it possesses a negative environment in the channel region and this fact leads to a large potential well. Near the entrance and the exit of the channel, there are two local potential minima (the valley near the dash line) and a major barrier in the middle of the channel. Accordingly, in the density profile, there are two peaks at the positions where two potential minima present and the density is lower in the middle part of the channel. These electrostatic profiles agree well with the biological properties of the GA channel. The magnitude of the electrostatic potentials responds directly to the change of ε_ch value, as showed in Fig. 7(a). When ε_ch decreases from 80, which is the commonly used value for the solvent, to the smaller values suggested by biological observations, the contrast between the energy wells near the entrance/exit and the barrier in the middle becomes sharper. This phenomenon verifies the impact of ε_ch value and leads us to prefer a smaller value in our model. For the ion density profile shown in Fig. 7(b), changes in the peaks with respect to the changes of ε_ch are quite clear. As ε_ch doubles, the magnitudes of the density at the peaks decrease half accordingly, as expected.

Figure 7.

Electrostatic potential and charge density of the GA channel along the z-axis obtained with ε_m = 5 and $n_p^0=0.1$ M (Red: ε_ch = 20; Green: ε_ch = 40; Blue: ε_ch = 80). (a) Electrostatic potential profiles in the channel; (b) Proton density profiles in the channel.

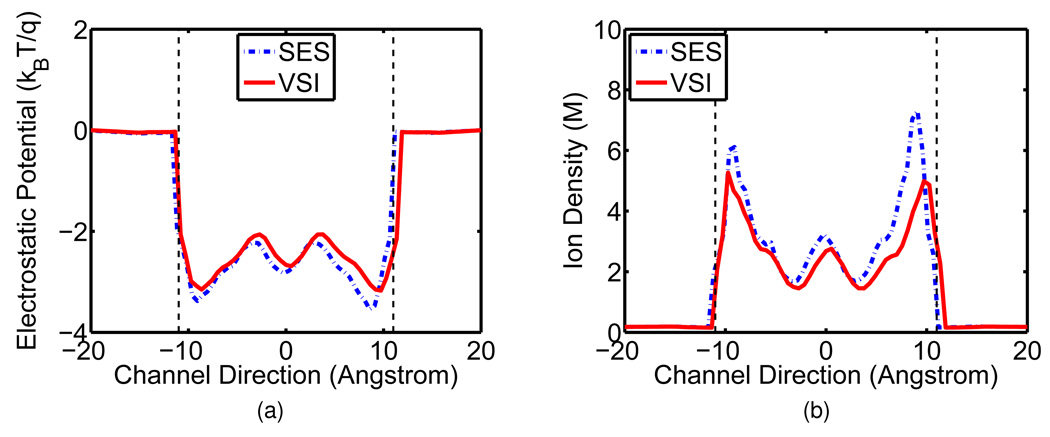
Figure 8 gives electrostatic potentials and corresponding ionic densities calculated with the SES and the VSI. The red solid curves are the quantities evaluated from the VSI while the blue dashed ones are from the SES. Comparing to the characteristics from the SES, the electrostatic potential with the VSI is slightly shifted at the entrance and major part of the channel while decreased at the exit. Consequently, the ionic density is lowered at most part of the channel except at the very end region.

Figure 8.

Electrostatic potential and corresponding density of GA, with the SES and the VSI. Red solid lines are for the VSI and blue dashed lines are for the SES.

V.D Proton conductivity in the GA channel

Proton conductivity in a channel protein provides a validation to transport expression (38) and generalized Kohn-Sham equation (33). The efficiency of proton transport mainly depends on the proton scattering process. The efficiency of solving Eq. (33) can be enhanced if one takes advantages of the geometry of the channel pore and considers the property of the total proton Hamiltonian. Since the channel pore has a long, narrow and tube-like shape, it is a reasonable approximation to decouple the scattering direction, or the z direction, from x – y plane, see Fig. 1(b). Along the transport direction, in which protons cross the channel protein or scatter back to the solvent, the Kohn-Sham operator has an absolutely continuous spectrum. In contrast, protons are greatly confined in other directions by the channel wall. Therefore the Kohn-Sham operator is essentially compact and has a discrete spectrum. Based on this characteristics, the 3D overall effective potential V (r) in Eq. (33) can be converted to a series of scattering potentials (or called eigenvalues), from which the proton current is evaluated via Eq. (38).¹¹ Furthermore, because of the Boltzmann distribution, higher energy levels contribute less in the overall current. Only the first few lowest eigenvalues are needed in most practical simulations.

We illustrate eigenvalues on Fig. 9. Clearly, these eigenvalues create potential barriers for proton scattering. Only first three are displayed in the figure, but in actual calculations, the first fifteen eigenvalues are employed to obtain sufficiently accurate results. For a comparison, all the solid lines are eigenvalues from the VSI and dashed lines are from the SES. Here red, green and blue colors represent the first, second and third lowest eigenvalues, respectively.

Figure 9.

The first three eigenvalues that used for the proton scattering, with the SES and the VSI. Solid lines are the eigenvalues computed with the VSI while the dashed lines are those computed from the SES.

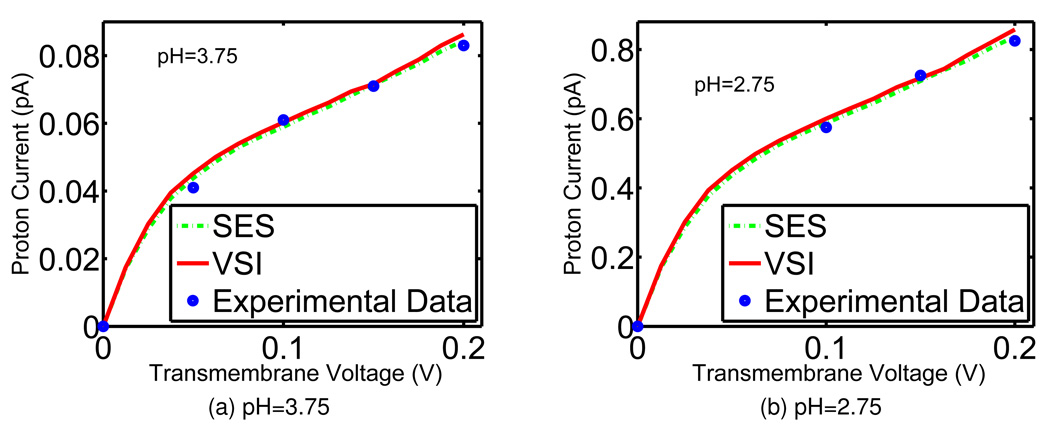
Figure 10 displays simulated results of proton conductance through Eq. (38), compared with experimental data from the literature³⁸ for the GA channel. The blue dots in each figure represent available experimental observations for certain voltage biases, while the red and green curves are our model predictions calculated with sufficiently many voltage samples. The model parameters are chosen to match the experimental data but all of the choices are taken within the range of physical measurements. The dielectric coefficients are taken as ε_m = 5, ε_ch = 30 and ε_bath = 80, according to the discussion in previous sections. The diffusion coefficient of protons is used to model the generalized correlation potentials and is taken as 3.6 × 10⁻⁹ m²/s in the channel, less than a half of the value in the bulk environment. In Eq. (17), the relative weighting parameter is set to α = 0.227. Taking into account above considerations, we can conclude that experimental data and the present predictions agree quite well and this agreement validates our quantum dynamics in continuum model.

Figure 10.

Voltage-current relation of proton translocation of GA at different concentrations. Blue dots: experimental data of Eisenman et al;²² Red solid curves: model prediction with the VSI, green dashed lines: prediction from the SES.

Apart from I–V curves, conductance-concentration relation (C-C curve) is another measurement under given voltages for proton transport. Figure 11 illustrates such a relationship with a comparison between experimental data and model predictions. The conductance of the channel is calculated with various proton concentrations as indicated by the horizontal axis at a given voltage bias. The conductance-concentration relation is computed with the same set of parameters as that in Fig. 10. At lower proton concentrations (i.e., pH value being greater than 2), the agreement between our prediction and experimental data is quite good. At relatively higher concentrations, the conductance saturates against the concentration as expected. It corresponds to the sub-linear characteristics or the flat tail of the C-C curve. The numerical simulations slightly overestimate the observed conductance.

Figure 11.

Conductance-concentration relation of proton translocation at a fixed voltage. Voltage bias=0.05V; Blue triangles: experimental data of Eisenman et al;²² Red curve: model prediction with VSI.

The experimental data used in this work are reported by Eisenman et al.²² They are also employed to validate a proton transport model proposed by Schumaker et al.³⁸ In fact, many other sets of experimental data are available for proton conductance under different experimental conditions.^1,14,18 For example, lipid membrane can vary from positively charged to negatively charged. In general, it is impossible to fit all the experimental data by a single group of parameters because of the difference in experimental conditions. Nevertheless, it can be observed that our simulation curves, especially for the I–V curves under the current set of parameters have shown similar qualitative shapes. Therefore, the present model can fit to other experimental data by slightly adjusting model parameters to reflect the different experimental conditions. Note that Akeson and Deamer¹ also reported I–V curves of proton conductance for the F₁F₀ ATPases studies. In their results, a severe saturating or sublinear character was found for proton concentration of 10 mM and there was an obvious superlinear pattern for 1.0 M hydrogen chloride (HCl). By just tuning the parameter values, we do not capture this characteristics using our model. In fact, this set of experimental data was also found difficult for another theoretical model of proton transport in the literature.³⁸ Experimental data of GA shown in Fig. 11 exhibits a “shoulder” region between the pH value 1 and 2 (or the −2 and −1 of the log₁₀[H⁺]). It is believed that the shoulder is due to the change in the rate-determining mechanism from the Grotthuss-type one to the hydrodynamic conduction of hydronium ions.¹⁹ These details are not in our model now but will be considered in the future.

VI Concluding remarks

Ion transport across membrane proteins is of paramount importance to the normal function of living cells and biological systems. As a special cation, the proton has its special mechanism to transport through membrane proteins and plays essential roles in energy transduction and cellular respiration. The present work introduces a quantum dynamics in continuum (QDC) model with a variational solvent-solute interface (VSI) for the prediction and analysis of proton transport process in biomolecular systems. The proposed model is of multiphysics and multiscale in nature. In the present approach, protons are treated quantum mechanically due to their small effective masses, small radius, and channel geometric confinement. Additionally, since the primary interactions in proton transport are of ion-ion electrostatic type, a dielectric continuum treatment of solvent medium provides a reasonable approximation to the effect of numerous solvent molecules. Most importantly, this treatment dramatically reduces the dimensionality of the system. As such, our approach is called a QDC model. In contrast, the atomic details of the protein essentially determine the electrostatic potential and regulate channel so that the membrane protein is described explicitly. Moreover, we use the VSI to separate the continuum solvent domain from the discrete charge domain of the protein. This treatment is in the same spirit as that of our earlier differential geometry based multiscale models.⁴²

It is believed that proton transport in the ion channel is a physical system so that it must obey the fundamental laws of physics. Therefore, the variational principle applies. In the present work, we introduce a multiscale/multiphysics variational paradigm to accommodate all the aforementioned treatments of the ions, the membrane protein and the lipid bilayer in a unified framework. We construct a total free energy functional which encompasses the kinetic and potential energies of protons, the polar or electrostatic energies of ions and fixed charges, along with the nonpolar energy in the proton transport system. The first variation is carried out via the Euler-Lagrange equation to derive the governing equations for the system. A generalized Poisson-Boltzmann equation is obtained for the electrostatic potential. Additionally, a generalized Kohn-Sham equation is resulted for the state of protons in the system. Finally, a generalized Laplace-Beltrami equation is presented for the VSI. Expressions for proton density and proton flux across the membrane are derived from fundamental principles as well.

The numerical computation of the proposed coupled equations involves a number of mathematical issues. A major issue is that the Laplace-Beltrami potential in the generalized Laplace-Beltrami equation has to be approximated by a density related expression to avoid the direct evaluation of the proton wavefunctions. Additionally, one needs to take care of the linearization of coupled nonlinear partial differential equations (PDEs) using the Gummel iterations and/or inexact Newton iterations, and the solution of elliptic PDEs with discontinuous coefficients (i.e., piecewise dielectric constants), and singular sources (i.e., Dirac delta functions for protein charges). Fortunately, we have developed many computational tools in the past to deal with these issues. For example, we utilize the Dirichlet to Neumann mapping (DNM) method²⁴ to handle singular charges, and the matched interface and boundary (MIB) method^8,24,44,47 to accurately deal with the discontinuous coefficients. The coupling of three equations is achieved by a surface driven self-consistent iteration.

A popular protein structure, the Gramicidin A (GA) channel protein, is employed in our numerical experiments to validate the proposed model and demonstrate the performance of the proposed numerical techniques. We give a detailed visualization of the VSI along with the solvent excluded surface. The electrostatic property of the GA channel is analyzed with the proposed new model against a large number of model parameters. Proton transport properties, i.e., the current voltage (I–V) curves and conductance-concentration curves, are investigated over a large number of combinations of applied voltages and reference bulk concentrations. We have compared our model predictions against experimental data, which validates the present QDC-VSI model.