Dipole characterization of single neurons from their extracellular action potentials

Abstract

The spatial variation of the extracellular action potentials (EAP) of a single neuron contains information about the size and location of the dominant current source of its action potential generator, which is typically in the vicinity of the soma. Using this dependence in reverse in a three-component realistic probe + brain + source model, we solved the inverse problem of characterizing the equivalent current source of an isolated neuron from the EAP data sampled by an extracellular probe at multiple independent recording locations. We used a dipole for the model source because there is extensive evidence it accurately captures the spatial roll-off of the EAP amplitude, and because, as we show, dipole localization, beyond a minimum cell-probe distance, is a more accurate alternative to approaches based on monopole source models. Dipole characterization is separable into a linear dipole moment optimization where the dipole location is fixed, and a second, nonlinear, global optimization of the source location. We solved the linear optimization on a discrete grid via the lead fields of the probe, which can be calculated for any realistic probe + brain model by the finite element method. The global source location was optimized by means of Tikhonov regularization that jointly minimizes model error and dipole size. The particular strategy chosen reflects the fact that the dipole model is used in the near field, in contrast to the typical prior applications of dipole models to EKG and EEG source analysis. We applied dipole localization to data collected with stepped tetrodes whose detailed geometry was measured via scanning electron microscopy. The optimal dipole could account for 96% of the power in the spatial variation of the EAP amplitude. Among various model error contributions to the residual, we address especially the error in probe geometry, and the extent to which it biases estimates of dipole parameters. This dipole characterization method can be applied to any recording technique that has the capabilities of taking multiple independent measurements of the same single units.

1 Introduction

Spatial sampling of EAP’s has become routine with the use of various multisite recording techniques (McNaughton et al. 1983; Drake et al. 1988; Gray et al. 1995; Nordhausen et al. 1996). As model calculations (Moffitt and McIntyre 2005; Gold et al. 2006; Pettersen and Einevoll 2008) predict and experimental studies (Drake et al. 1988; Buzsaki and Kandel 1998; Henze et al. 2000) show, there is a systematic dependence of the shape and size of the extracellular action potential (EAP) waveform on the recording probe’s position relative to the neural source. Despite its availability, this implicit spatial information about the spike sources is rarely exploited. Here we focus on the feasibility of characterizing the current source of spiking single units, including spatially localizing them.

Characterizing the action potential source from the EAP waveform is a classic example of an inverse problem. Like other inverse problems, it does not have a unique solution (Helmholtz 1853a), so it is necessary to introduce constraints and assumptions about the source and the electrical medium. Since the results generally depend on these constraints and assumptions (Malmivuo and Plonsey 1995), accurate source localization requires an adequate source model.

For modeling the dynamic distributed current sources of spiking neurons, the choice of a model amounts to a tradeoff based on the number of model parameters. Models with many parameters can capture the details of the source, while models with a small number of parameters are more useful in constraining the inverse problem. At the many-parameter extreme are the detailed compartmental (forward) models. These have been used in a few EAP modeling studies (Moffitt and McIntyre 2005; Gold et al. 2006; Pettersen and Einevoll 2008) and localization studies (Drake et al. 1988). This realistic approach is data limited: it operates with a large number of parameters that are difficult to verify, diminishing its use in inverse problems. Moreover, the implied reconstruction of neural architecture is costly and remains impractical for routine application.

At the other extreme is the simplest source model, the monopole, determined by 4 parameters, readily suited to source characterization from recordings made with tetrodes (Gray et al. 1995; Maldonado et al. 1997; Jog et al. 2002; Aur et al. 2005; Chelaru and Jog 2005; Aur and Jog 2006; Lee et al. 2007) and larger multi-contact probes (Henze et al. 2000; Blanche et al. 2003, 2005; Du et al. 2009). The monopole model implies a r⁻¹ radial EAP falloff. As discussed later, the falloff reported in real neurons or their realistic models is closer to r⁻² over the range of typical recording distances, and thus, the monopole model generically leads to an underestimation of the cell-probe distance. The improved accuracy of localization, at the cost of only a modest increase in complexity (6 parameters instead of 4), motivates our choice of a dipole source model. The principle of current conservation makes an additional argument against the monopole model: currents passing in and out of the whole neuron sum to zero at all times, making the monopole an increasingly poor approximation as the distance from the currents is increased. Acquisition of the data necessary to fit a dipole model is readily achieved with contemporary polytrodes (Blanche et al. 2005; Du et al. 2009) or (as in this study), by tetrodes in multiple recording positions. (The quantitative stepping method using a single electrode was pioneered by Rosenthal et al. (1966)).

With this as motivation, here we solve the inverse problem of dipole spike source characterization. We use a three-component realistic probe + brain + source model to find the position and the moment vector of the equivalent dipole current source of single neurons from multisite recording. We model the brain with a homogeneous, isotropic, resistive volume conductor because evidence in our data (and elsewhere) supports these simplifications and because they make our goal to solve our phenomenological localization task greatly more convenient. However these are not essential assumptions: our approach requires only that the medium is quasi-static and linear, and that the conductivity tensor is symmetric. We separate the dipole optimization into the linear optimization of the dipole moment from the nonlinear optimization of the dipole location. Dipole moments were locally optimized on a discrete spatial grid using a linear operator built of the lead fields. The lead fields summarize, independent of the source, the electrical properties and geometry of the volume conductor and the probe. They were numerically solved in a reciprocal forward problem by the finite element method (FEM). On the discrete space of local solutions, the globally optimal dipole was solved for by Tikhonov regularization, the joint minimization of error norm and dipole moment norm. We used a variant of the L-curve method to identify the optimal relative weight of the two norms.

We demonstrate the method applied to recordings made with tetrodes (Thomas Recording, Gmbh) from neurons in the visual cortex. We address how model error in probe geometry could influence the accuracy of neuron localization and discuss the applicability of the method to multisite recording technologies that use different contact configurations.

2 Methods

2.1 Data acquisition and spike preprocessing

The physiological preparation, data acquisition apparatus, and preprocessing of extracellular action potentials (EAP’s, or simply “spikes”) were described in detail in a companion paper (Mechler et al. 2011). Briefly, spike activity of neurons was visually stimulated and recorded repeatedly at positions of incremental depths (5–10 µm apart) along the tetrode penetration in the visual cortex of anaesthetized cats and monkeys. The recording tetrodes were commercially acquired from the manufacturer (Thomas Recording GmbH). Using the Cheetah (Neuralynx) multichannel spike acquisition system, analogue extracellular potentials were amplified, filtered (300-to-9,000 Hz pass-band), digitally sampled (at 22,222 Hz) and, if above a threshold, stored.

Before source localization analysis, recorded spike waveforms were preprocessed in a three-stage off-line procedure. First, spikes were sorted into clusters that corresponded to putative single cell sources, done separately for each recording location of the probe. An automated clustering algorithm (Klustakwik, by Ken Harris) was used to identify spike clusters for candidate single-units. The algorithm, operating in a multidimensional “feature space” that used waveform energy or peak voltages on each channel as coordinates, was used conservatively, i.e., with a tendency to err by splitting clusters rather than mixing them. Next, user input, via a graphical user interface (SpikeSort 3D; Neuralynx), was used to finalize clusters: certain candidate clusters were manually fused, and noisy clusters were eliminated. Our criteria to combine two clusters were that their corresponding waveforms were scaled versions of similarly-shaped spikes, and that their projections into the “feature space” were continuous. The interspike interval in each final cluster had to be no shorter than a criterion 1.3 ms absolute refractory period. Second, these finalized clusters identified at one recording position were linked with finalized clusters identified at the adjacent recording positions, on the basis of similarity of spike waveforms and relationships among the clusters; this was also aided by the same graphical user interface. Because the step size was kept small enough (≤10 µm), cluster configuration in feature space typically changed in an orderly fashion and provided a useful aid in tracing the same unit across steps. The relative size of clusters (in terms of spike counts) was a similarly useful characteristic of unit identity. These cluster characteristics, unlike correlations in waveform shape (or a difference-of-waveform norm), remain robust aids of cluster tracing even when new clusters appear or an old one disappear across a pair of consecutive recording positions. Additionally, for the candidate set of clusters to be linked, the noise covariance (across the four channels) had to be similar at each tetrode position. This criterion was included to ensure that there was no new “noise source” (e.g., a new unit included in the cluster) as the tetrode progressed. The linked clusters were taken to represent the spike waveforms of a single neuron, recorded at all tetrode positions. Third, for each cell and recording site, spikes were re-sampled and re-centered via cubic spline interpolation before averaging.

2.2 Spatial and temporal sampling of the EAP

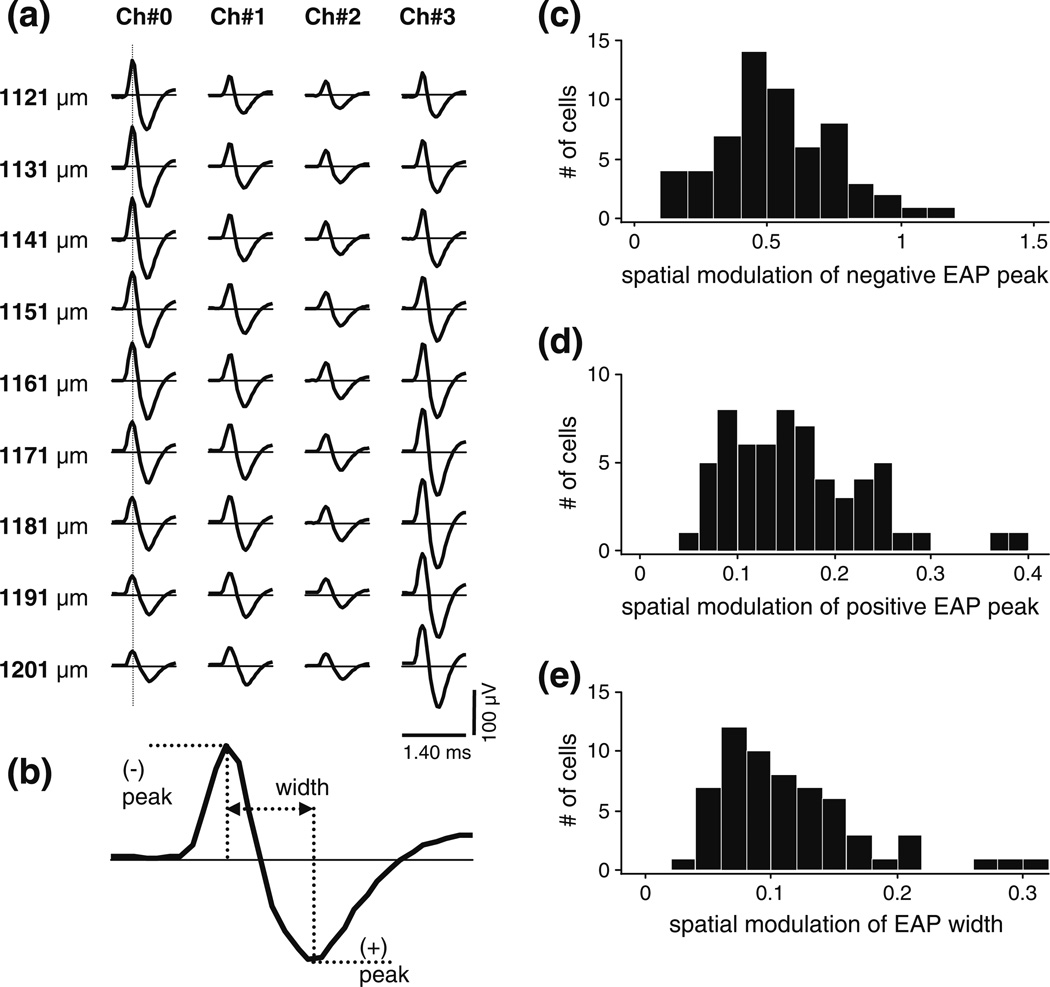
Figure 1(a) is a typical example of the spatial sample of the EAP waveforms recorded from a single unit. (Note that by convention negative extracellular potentials, corresponding to intracellular depolarization or fast sodium influx in the neuron, are plotted above the zero line.) It illustrates an important fact about this data, namely that the spatial variation in the EAP waveform (both across channels at fixed probe position, and across probe positions) was dominated by size change.

Fig. 1.

Analysis of the spatial variation of the size and shape of the extracellular action potential (EAP) waveform. (a) Example data set recorded from a single unit (cell 4) with a tetrode (06–3200, see Table 1) in 9 equally spaced positions. Rows, labeled by nominal depth along the penetration, show the mean spike waveforms registered by the 4 channels of the tetrode; data from different channels are organized in separate columns. The vertical line indicates the sampling spatial EAP amplitudes at a fixed moment in time (here at the peak). By convention, negative extracellular potentials are plotted above the zero line. (b) Definition of the positive and negative peaks and the width of an EAP. We define an index of the spatial variation of these features by their relative spatial modulation, i.e., by the ratio of the difference of the spatial maximum and minimum to the spatial mean. (c) The distribution of the index of spatial variation of EAP size (the negative EAP amplitude) in the entire sample (N=61) of visual cortical neurons. The sample median was 0.51. (d) The distribution of an index of the spatial variation of EAP shape (the relative size of negative peak over positive peak) in the entire sample. The sample median was 0.15. (e) The distribution of another index of the spatial variation of EAP shape (width). The sample median was 0.10. Note that the horizontal scales in panels (c), (d), and (e) differ

The spatial variation of the shape (or temporal waveform) of the EAP was a secondary phenomenon. This is shown by the population analysis summarized by the histograms in Fig. 1(c, d and e). Figure 1(b) defines the size and shape parameters we selected for the population analysis. Size was measured by the negative EAP peak amplitude; shape measured by the relative size of the positive over the negative EAP amplitude, and the EAP width defined by the elapsed time between the two peaks. The spatial variation for any measure was characterized by the relative spatial modulation, i.e., by the difference between the maximum and minimum divided by the spatial mean. The size modulation (Fig. 1(c)) was large in the sample of 61 visual cortical neurons (median 0.51). In comparison, the shape modulation was modest: e.g., the median EAP width modulation (Fig. 1(d)) was only 0.1, and the median modulation of EAP peak amplitude ratio was not much larger (0.15). These findings were underscored by model-independent quantification of the shape of the EAP waveforms. From principal components analysis of the waveforms (with their mean not removed), we have found that the first principal component (mean magnitude) accounted for 97% of the variance in the spatial variation of the EAP temporal waveform. Thus shape modulation accounted for no more than 3% of the variance, and the waveforms could be well approximated as spatiotemporally separable. This approximation was made possible most likely because the probed brain volume was relatively small (≈40×40×90 µm³), limiting the frequency-dependent spatial filtering effects that can be observed in spatially more extensive samples of EAP and LFP (Destexhe et al. 1999).

For dipole characterization, we selected the temporal sample corresponding to the negative peak on the EAP waveforms (vertical dotted line in Fig. 1(a)). This choice assumes that the time of negative peak EAP corresponded across all recording positions and could be used to align the waveforms of the different spatial samples. (We had to make some assumption of this kind to enable a temporal alignment of EAP’s that were recorded non-simultaneously, i.e., at sequential tetrode positions). Support for approximate local synchrony of EAP peaks (coincident within ~0.1 ms for recording sites within ~100-to-200 µm from the location of the largest signal) comes from multisite recordings of spikes from pyramidal neurons (Henze et al. 2000; Blanche et al. 2005; Somogyvari et al. 2005; Du et al. 2009).

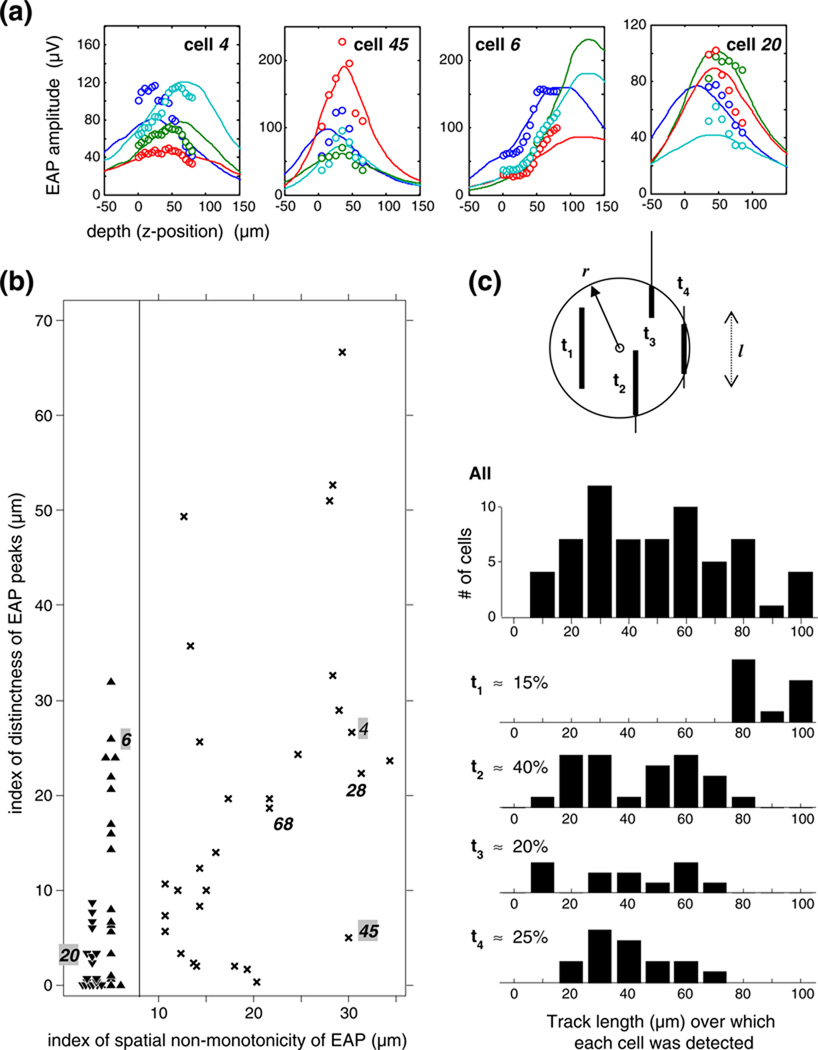
In order for the spatial variation of the EAP to be informative about the location of the source, it must be sampled over a sufficiently large spatial extent and with sufficient resolution so that its spatial dependence can be determined. As shown in Fig. 2(b), EAP spatial variation can be characterized by two indices: the index of non-monotonicity and the index of peak distinctness. The non-monotonicity index measures (in µm) the average absolute distance of the channel peaks from the nearest extreme sample position; small values indicate that the EAP sample is approximately monotonic increasing (e.g., cell 6; its EAP data shown in Fig. 2(a)) or decreasing (e.g., cell 20), and high values indicate that the EAP sample has a discernible peak on one or more channels (e.g., cells 4 & 45). The index of peak distinctness measures (in µm) the average lag of the z-coordinate of the channel maxima behind the maximum on the leading channel; large values indicate that EAP maxima on the lagging channels are spatially well separated from the leading channel (e.g., cells 4 & 6) and low values indicate that they overlap (e.g., cells 20 & 45). The joint distribution of these two indices in the entire sample is shown on the right. The two indices are uncorrelated and the data scatter widely, indicating great shape diversity in the spatial variation of the EAP of neurons of visual cortex as probed by the tetrode in a limited range. Each of the 4 examples shown in Fig. 2(a) is characteristic of a particular subset of the sample in which one or the other index takes a high or low value. Only in about half of the cells did the EAP sample have a discernable spatial peak on most channels; the EAP sample varied monotonically in the other half of the cells. As explained by the stick and ball model of random penetrations in Fig. 2(c), this is expected (scenarios t₁ and t₄ and corresponding histograms and fractions). In the majority of those cells whose EAP sample on most channels had discernable peaks, the peaks on the lagging channels were spatially well separated (by >10 µm) from the leading channel. An average ≈ 25 µm EAP peak separation is expected for our tetrodes (given their size and tetrahedral contact configuration) if we assume that the EAP was well behaved, but peak separation could be blurred by physical processes (e.g., noise and field distortions, including the possibility of a partial fluid shunt) that are at work under experimental conditions. As a result of these processes, a spatial overlap of discernable EAP peaks can occur (e.g., cell 45), but this is not typical of our sample, as the scattergram of Fig. 2(b) shows. We add that since the localization procedure assesses the spatial gradients from the collection of recording channels, the source localization problem can be solved even if the data do not include a discernible peak or if peaks are not cleanly separated.

Fig. 2.

Characterization of the diversity of the spatial variation of the EAP amplitude recorded with a stepped tetrode. (a) EAP variation is shown for four cells (tetrode channels are labeled by color); each represents high or low values of either of two shape indices: the index of non-monotonicity and the index of peak distinctness (see text for their definition). The continuous lines are the predictions from the optimal dipole fit. (b) The joint distribution of two indices of spatial EAP variation in the entire sample (N=61). Each symbol represents one cell: up triangles, monotonic increasing EAPs; down triangles, monotonic decreasing EAPs; 'x' symbols, discernible EAP peaks. The vertical line separates the cells of monotonic EAPs from cells of peaking EAPs. Examples featured in the text are numbered. (c) The linear spatial span of EAP’s. Analysis of the distribution of the measured linear span of detectable signal levels in the entire sample (‘All’). The stick and ball model (inset) helps to explain how such distributions depend on the relative size of the full linear span of spatial samples (sticks with fixed length l) detectability radius of neurons (ball with radius r). The thickened portion of a stick indicates the range of detectable EAP’s recorded from an isolated single cell within the full linear span of spatial samples. Their relative position defines 4 subsets of neurons: neurons whose spikes were isolated either (t₁) at all positions sampled; or (t₂) beginning with the first sample and ending before the last; or (t₃) beginning after the first sample and continuing through to the last; or (t₄) beginning after the first sample, and ending before the last. The vertical axes in (t₁)-(t₄) are omitted for clarity but the same vertical scale applies as in ‘All’

For spatial extent, a reasonable rule of thumb is to match the neuron’s detection radius. In these experiments, spatial sampling was accomplished by stepping through multiple recording positions in visual cortex. The total linear sample range, averaged over 12 tracks, was l=90±10 µm. This choice was informed by our prior informal observations of the spatial range over which individual single neurons could be isolated in visual cortex, and by data from other brain areas (Gerstein and Clark 1964; Rosenthal et al. 1966; Drake et al. 1988; Blanche et al. 2005).

As seen in Fig. 2(c), this choice does, in fact, cover the typical range over which a neuron’s spike waveform can be recorded. The neuron “cell 45” in Fig. 2(a) was held in isolation along a 60-um-long segment of the penetration, typical of our sample. The top histogram in Fig. 2(c) shows the distribution of the total length of the tracks along which a cell was held isolated (mean track length 54 µm, N=61 neurons). This histogram, and those of the 4 disjoint subsets analyzed further below, shows that our choice of ≈ 100 µm for the total linear range of spatial samples was commensurate with the detection radius for the recorded neurons.

For spatial sampling, our choice of a 5–10 µm step along the tetrode track was determined by an empirical tradeoff between two factors. If the distance between two recording sites is too large (in our experience, >10–15 µm in visual cortex), changes in the size and the shape of action potentials recorded from most single units may be too large to make reliable matches between the waveforms recorded at different step positions. If the step size is too small (<5 µm in visual cortex), adjacent steps are redundant, and there is a risk of a larger accumulated positional error due to starting and stopping the microdrive. (We used a Thomas Recording apparatus that has an accuracy of a few microns over a course of several hundred microns, as measured under the light microscope).

We arrive at a similar estimate of the useful range of step size by considering, in an alternative to the empirical approach, the 1/r² falloff of the dipole potential. Between two recording sites separated by 20 µm at an average distance of ≈ 50 µm from a dipole source, the dipole potential could change dramatically, by up to 125%, depending on step direction. The corresponding change would be rather modest, no more than 25%, if the sites were only 5 µm apart. Such fast, dipole-like, spatial attenuation of EAP is indicated by extracellular recordings (Henze et al. 2000) and realistic model simulations (Gold et al. 2006) of pyramidal neurons in rat hippocampus.

2.3 Signal statistics

To provide a benchmark for the sizes of spike waveforms necessary for source analysis, and also to help interpret the goodness of model fits, we determined the RMS noise in the recordings. We estimated this noise from the difference between individual samples of a spike waveform and its average, which typically represented hundreds of samples. This yielded an RMS noise in single tetrode channels that ranged between 12 and 35 µV (Fig. 3, histogram in dark bars); the mean, averaged across channels, tetrodes and recording sites, was 21 µV. These relatively large noise levels likely reflect the high level of neuronal background activity that characterizes visual cortex even under anesthesia. The estimated amplitude of the component of this noise that is due to thermal fluctuations was in the 10–17 µV range, as determined by Johnson’s equation of noise power at room temperature from the per channel tetrode input impedance (1–2 MOhm) and the recording bandwidth (6-to-9 kHz). Assuming that thermal noise is independent of other noise sources, we therefore estimate that thermal noise and the combination of all other noise sources (non-thermal instrumentation noise and background electrical activity) contributed comparably on average.

Fig. 3.

Distribution of signal (open bars) and noise (dark bars) in extracellular action potential (EAP) data recorded from single units with Thomas tetrodes in visual cortex (N=61). Noise level is defined by per-channel RMS amplitude; the mean (range) was 21 (12–35) µV. Signal level is defined by the spatial minimum of EAP peak amplitude on the tetrode channel that registered the largest peak; the mean (range) was 91 (25–313) µV

To analyze the signal-to-noise of detection and isolation, we define signal level as the spatial minimum of EAP peak amplitude on the tetrode channel that registered the largest peak. The open bars in Fig. 3 show the distribution of the signal thus defined. Reliable single unit discrimination of the typical single unit in this sample demanded that the EAP amplitude on the channel with the largest EAP amplitude exceeded ~91 µV or 4.3 times the RMS noise (Fig. 3). (For comparison, spike detection i.e., spike-background discrimination, was already reliable at a ratio of 2 or larger). Because of the large spike sample size (ranging from several dozens to several thousand per neuron per recording position) the mean spike waveform estimates were quite reliable in spite the considerable noise (95% confidence limits were typically ± 2 µV, a small fraction of the amplitudes).

These signal statistics are similar to what other laboratories reported for their tetrode or polytrodes (Henze et al. 2000; Musial et al. 2002; Blanche et al. 2005; Du et al. 2009).

2.4 Finite element model of lead fields

A concept key to our solving the inverse problem is the lead field (Malmivuo and Plonsey 1995). The lead field of an electrode quantifies the electrode’s sensitivity to a point dipole current source as a function of the source location. Each contact of a tetrode has a lead field that summarizes the electrical properties and geometry of the volume conductor and the probe from that contact’s point of view. To determine the lead fields we used FemLab (Comsol AB, Sweden), a finite-element model toolbox implemented in the Matlab environment. A critical aspect of this computation is determining the mesh. We used the following procedure. First, a tetrahedral mesh (~10^5 elements) was set up on the 4×4 mm cylindrical volume of the entire brain-tetrode model. Volume element size was then adapted to the characteristic curvature of the tetrode shaft and wires, to maintain a FemLab quality control parameter of 0.3 or higher, as recommended for 3-D problems. (Further details of the analysis of mesh quality are presented for a tetrode example in Fig. 7). The resulting large number of volume elements reflects the need for the mesh to accommodate smooth element variation between the vastly different spatial scales and curvatures characterizing the vicinity of the probe contacts and the homogeneous peripheral regions of the brain block; a similarly high element count was reported for an FEM model of a silicone probe inserted in rat brain (Moffitt and McIntyre 2005). The lead field is the solution of a forward problem, described by the Poisson equation (see Eq. 1c in Results), with the boundary condition that current is injected through the lead. Using Quadratic Lagrange elements, an incomplete LU factorization or a geometric multigrid preconditioner, and an iterative stationary linear (Good Broyden) solver (tolerance ~10⁻⁶), the solution converged in a few dozen steps, based on this mesh. The typical lead field computation required a few hundred megabytes of memory and was completed within a few hundred seconds on a workstation with an Intel Core Duo (2.4 MHz) CPU. The lead fields were then interpolated on a regular cylindrical mesh with the azimuth sampled in 10-deg steps, and the z-axis in 5-µm steps. The radial samples, {5,10,15,…,50, 60,70,…,150, 165,180,…,300, 350,400,…} um, were piece-wise equidistant but asymptotically logarithmic. Our mesh sampling strategy reflects a tradeoff between the conflicting requirements of preserving the equidistant z-axis resolution of the EAP data, preserving the approximate radial symmetry of the probe, keeping spatial resolution constant within the entire region of interest, and keeping the size of the numerical problem manageable. The resulting mesh resolution was reasonably similar (radial samples were <=10 um apart and tangential samples <=26 µm apart), and at least a factor of 2 better than the measured scatter radius, everywhere within the volume of 150-µm radius around the tetrode tip where 95% of the cells isolated in this study were localized.

Fig. 7.

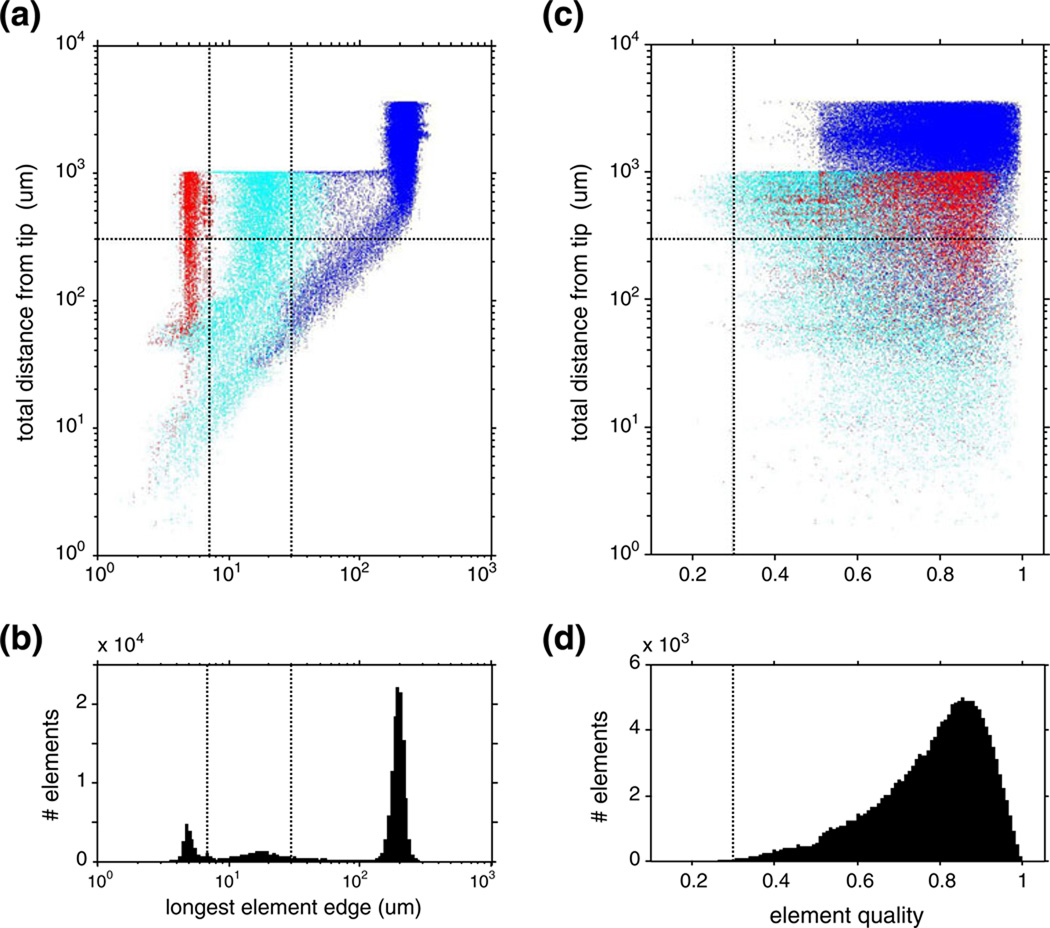
(a) The distribution of element size of the finite element mesh, as a function of the distance from the tetrode tip. Colors indicate different domains in the finite element model: wire domain (red), gray matter in neighborhood of tetrode (cyan), and more distant elements (blue). The horizontal dotted line indicates the radius of the region of interest; the vertical dotted lines indicate the characteristic size of tetrode features (see details in text). (b) The marginal histogram of the data in (a). (c)–(d) Distribution of the element quality analyzed similarly to element size. The vertical dotted line indicates minimum element quality recommended for 3-d problems

We chose as the region of interest a spherical volume of 300-µm radius, centered on the tetrode tip, and set the radius of the modeled brain volume to 2 mm. The 300 µm radius was thought to be larger than the anticipated largest cell-probe distance (the localization results verified this assumption), and the 2-mm radius of the modeled brain volume was large enough to ensure that the grounding artifact, a distortion in the lead fields arising from the finite model size, was negligible within the region of interest. We arrived at this choice via auxiliary simulations. We varied the model size and estimated the upper bound of the size of the grounding artifact as the distortion of the potential of a monopole placed at the center of the region of interest. The monopole attenuates as ~1/r, more slowly than any other multipole, and it is thus the most sensitive to distortions. In a model cylinder of 0.5 mm radius, the distortion (excess attenuation) of monopole potential could exceed 50% towards the boundary of the region of interest. However, in a model cylinder of 2 mm radius, the distortion was capped at 8%. So we chose this radius for all lead field calculations. The error in the lead fields relevant to our results had to be much smaller because the distortion in the monopole potential gradient, which is the analogue of lead fields, was <1% at ≈ 150 µm, the estimated cell-probe distance of the furthest-localized cell in our sample.

Further analysis—the dipole optimization—is a focus of this paper and these methods are presented in detail in Section 3. The computations were all done by custom software written in Matlab.

2.5 ‘Exact-probe’ and ‘approximated-probe’ sets

We define as the “exact-probe” set the cells (N=43) for which the tip geometry of the tetrode that recorded them was scanned and used in the FEM model. To document the effect of error in model geometry, we have included in the analysis cells that we recorded with tetrodes whose tips could not be scanned. For these neurons, defined as the ‘approximated-probe’ set (N=21), we substituted for tetrode geometry in the FEM model the reconstructed tip of the tetrode that represented the median contact separation among the measured tetrodes in our study (listed 2nd in Table 1.).

Table 1.

Parameters used to model tetrode geometry

Tetrode	dcore (µm)	ϕtip/2 (deg)	htip (µm)	Acont (µm2)	rCE (µm)	SCE (µm)	SEE (µm)	dshaft (µm)	hshaft (µm)
03–0591	7	18.5	11	121	17	54	36	63	95
06–3200	8	25	9.5	118	17	40	36	56	60
07–0087	5	26.5	5	44	13.5	30	28	50	50
07–0088	6.5	25	7	78	13.5	32	28	50	54

d_core: diameter of lead wires;

ϕ_tip/2: half cone angle;

h_tip: cone height of exposed central contact (=1/2d_core tan(ϕ_tip/2);

A_cont: exposed contact area $(=\pi d_{\text{core}}^2/\text{sin}({\varphi }_{\text{tip}}/2)$ for both center and eccentric);

r_CE: the distance between the center and the eccentric wires, measured center-to-center;

S_CE: center-to-center separation of center-eccentric contacts (=r_CE/sin(ϕ_tip/2));

S_EE: center-to-center arc separation of eccentric-eccentric contacts, (=2πr_CE/3);

d_shaft: shaft diameter;

h_shaft: cone height of entire tip below shaft cylinder.

Note that S_CE and S_EE (~30-to-50 µm) are comparable to 2–3 cell body diameters in neocortex

2.6 Sharing data and code

Upon publication, lead field models along with the Matlab code of the dipole optimization algorithm described in this study will be made available on the ModelDB public database (http://senselab.med.yale.edu/ModelDB/default.asp)

3 Results

3.1 Dipole characterization—theory

In overview, our approach is as follows. We frame the 3-d localization of a spiking neuron in terms of characterizing the equivalent single dipole current source. That is, we seek the size and location of the current dipole moment that, given the material properties and geometry of multi-contact probe and the brain, best accounts for the extracellular action potentials measured at the contact sites of the probe. Because of noise and because the model is approximate, solutions are sought via optimizing some objective function. Conveniently, dipole optimization is separable into a linear component (optimization of the dipole moment assuming a particular source location) and a nonlinear component (optimization of the source location). We frame the linear problem in terms of a “lead field matrix”, which summarizes the geometry and the electrical properties of the tissue and the probe. (A rigorous introduction of the lead field is given further down in this section). We frame the nonlinear optimization as a Tikhonov regularization problem that jointly minimizes the error norm and dipole size, and we solve it with a variant of the L-curve method.

To formalize these notions, cortical gray matter is modeled by a volume conductor of finite dimensions, its material properties characterized by the conductivity, σ_GM, generally a tensor. Embedded in the volume conductor is a multi-contact probe (e.g., tetrode or polytrode) built of some good insulating material (‖σ_insulator‖≪‖σ_GM‖), which, in turn, encapsulates the electrode wires, made of some metal of high ohmic conductivity (σ_electrode≫‖σ_GM‖). The electrode wires are exposed to the volume conductor at the positions of the contacts (measurement locations). Thus different material domains in this system are defined by their different conductivity. The default coupling between two contiguous domains is current continuity, where the normal current outflow of one domain is equal to the inflow into the domain on the other side of the boundary (i.e., n₁₂(σ₁∇V₁) = n₁₂(σ₂∇V₂), where V_k, σ_k is the potential and the conductivity, respectively, inside domain k, n₁₂ is the unit surface normal pointing from domain 1 to 2, and ∇ is the gradient operator). On the external boundaries of the system, the boundary conditions are current- or voltage-clamped, depending on the component that contacts the boundary. Where an insulator contacts the boundary, the boundary condition is that no normal current flows, i.e., that n(σ∇V) = 0. Where a probe wire contacts the boundary, the boundary condition is that n(σ∇V) = j_inj, where j_inj is the amount of current injected (nonzero only for the wire whose lead field is being calculated). Where the brain meets the boundary, the boundary condition is that V=0, i.e., that the brain is grounded.

Since our goal is to develop a phenomenological model of the EAP for the purpose of localizing neurons, we do not intend to provide a fully realistic biophysical model of EAP generation and propagation in the extracellular medium. Towards this goal, we make certain simplifying assumptions about the source and the media. By doing so, we do not intend to imply that the phenomena we ignore by these assumptions do not exist, merely that their presence in our data is limited and that modeling them is not essential to our goal. We make 3 basic assumptions and 4 non-essential simplifying assumptions about the electrical properties of the tissue.

The 3 basic assumptions are quasi-stationarity linearity and symmetry of material tensor; they hold for most bioelectric phenomena (certainly for the spatio-temporal scale of the EAP records we model) and, crucially, they make the lead field approach possible (Plonsey 1963; Plonsey and Heppner 1967; Malmivuo and Plonsey 1995).

The quasi-stationary approximation assumes that we can ignore the induction of magnetic fields by changing electric fields, and vice-versa, and also that the field develops instantaneously at all points. It is guaranteed to hold at the low temporal frequencies (10² to 10⁴ Hz) that characterize action potential waveforms. As a consequence, the electric field, E, is the gradient of the potential, Φ, i.e., E = −∇Φ.

Linearity is the principle of superposition and it holds at the low field strengths characteristic of bioelectrical phenomena. It has two important consequences. First, the relationship between current, j, and electrical field is linear, i.e., j = −σE, where the conductivity, σ, is a tensor in general. Second, it guarantees that the “forward problem”, i.e., the relationship of sources and resulting electric fields, is a linear one.

The third assumption is that the conductivity tensor in the above equation is symmetric; this is not known to be violated in biologic tissue. Because of these 3 assumptions, the principle of reciprocity, which is required by the lead field approach (see below), holds.

If no further assumptions are made, then the material properties of the medium are summarized by the conductivity tensor, σ̂(x,ω), which is complex-valued and depends on both temporal frequency and spatial position. Capacitive, non-ohmic, phenomena are handled by including permittivity in the model as the imaginary part of the conductivity, i.e., σ̂ = σ + iωε. Anisotropy is handled by the tensor formalism of the material properties. Inhomogeneity and frequency-dependence are formalized by allowing the dependence on these variables as arguments, i.e., as in σ(x,ω) and ε(x, ω).

We first consider the general forward problem: given some probe geometry, the material properties of the tissue and the probe, the above boundary conditions, and a general current source distribution, Q, what is the spatial distribution of the voltage? The governing equation of the quasi-stationary linear forward problem, stating current conservation, takes the form

$$\nabla \cdot \left(\widehat{\mathbf{\sigma }}(x,\omega )\nabla {\tilde{V}}_{\omega ,x}\right)=Q_{\omega ,x}.$$ (1a)

The Ṽ_ω,x Fourier components of the potential can be solved by integration, frequency-by-frequency and the potential in the temporal domain can be obtained by an inverse Fourier transform. Numerical (e.g., finite element method or FEM) implementation of this general model is straightforward: FEM can handle a complex, frequency-dependent, conductivity tensor. In inhomogeneous media the lead fields are not translation invariant and they must be calculated for each contact in each position, which may be slightly inconvenient but the associated computational burden is manageable.

The non-essential assumptions amount to neglecting any one of the above 4 dependencies in σ̂(x,ω): they are not required by our approach that utilizes lead fields. Isotropy neglects directional variation of conductivity, and thus simplifies conductivity to a scalar, σ̂(x,ω), that may be complex and may retain the spatial and temporal dependence. High degree of isotropy in the gray matter (but not in white matter) of neocortex is empirically well supported (Logothetis et al. 2007), making this assumption likely to have the least associated error of the four. Homogeneity is also well-approximated in the gray matter of neocortex (Logothetis et al. 2007) (if not in hippocampus (Lopez-Aguado et al. 2001)), and this justifies eliminating spatial dependence in the conductivity, which in turn simplifies the governing equation of the forward problem to the Poisson equation

$$\widehat{\sigma }(\omega ){\nabla }^2{\tilde{V}}_{\omega }=Q_{\omega },$$ (1b)

where σ̂(ω) is a complex frequency-dependent scalar.

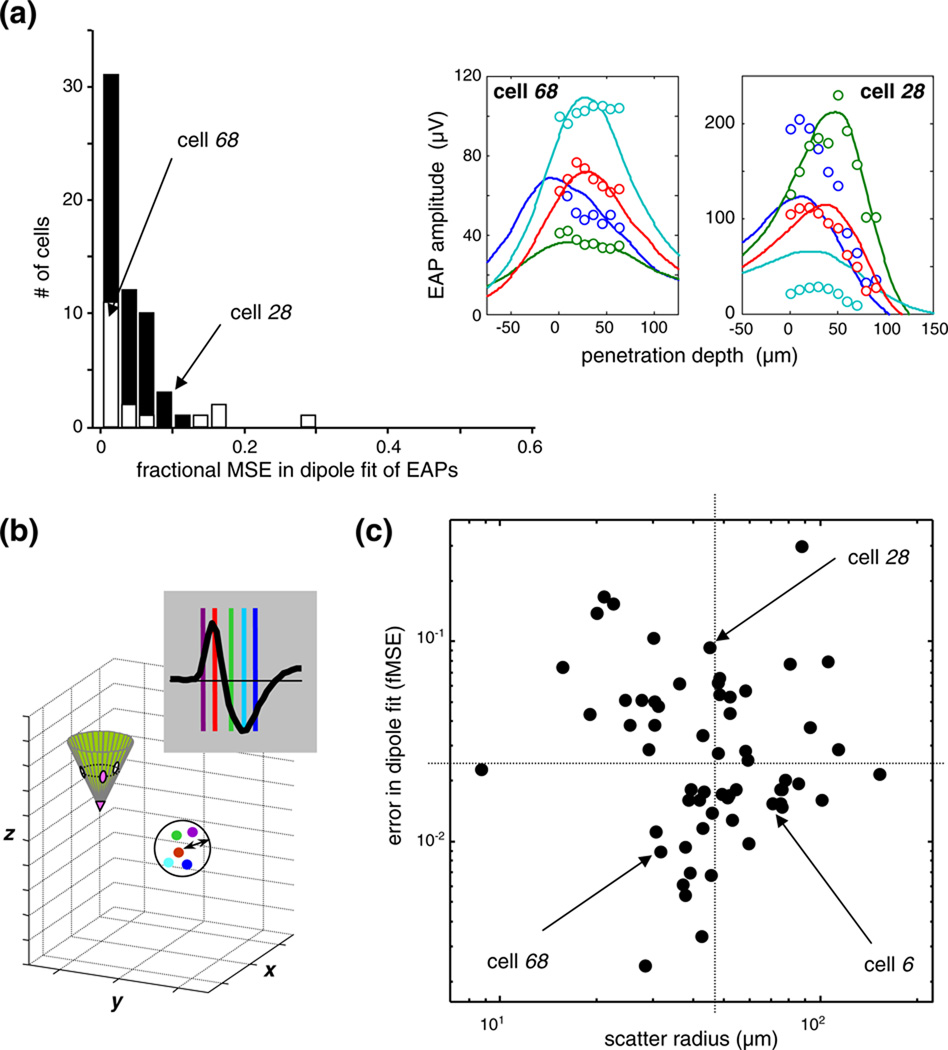
Neglecting frequency dependence reduces conductivity to a (complex-valued) constant and permits seeking a solution in the time domain. The assumption of resistive (ohmic) media neglects permittivity (and all capacitive and phase-related phenomena), and simplifies conductivity to a real-valued constant. Thus, with this assumption we neglect a host of biophysical mechanisms in the tissue that give rise frequency-dependent spatial filtering by the extracellular media (Bédard et al. 2004, 2006; Bédard and Destexhe 2009). However, the resistive volume conductor approximation is justified for EAP modeling in the gray matter of neocortex by experimental evidence that suggest either that the associated error is negligible (Logothetis et al. 2007), or that it is small, <10% (Plonsey and Heppner 1967; Gabriel et al. 1996). (In our model, this is the most costly of the four non-essential assumptions in terms of associated errors.) Note that this small error depends on the specifics of the spectrum of the material properties: models of local field potentials (LFP), in contrast to EAP’s, may not afford neglecting the capacitive contributions to the conductivity at frequencies <100 Hz (Gabriel et al. 1996). Furthermore, analysis of our own data provides assurance that the impact of the resistive volume conductor approximation on the accuracy of cell localization is limited. Since our dipole source is free to change position, size, and direction at each point in time, the dipole localization (analyzing each time point separately) allowed the model to retain a phenome-nological capacity to generate spatiotemporally inseparable EAP’s at the cost of localization inaccuracy. Yet we report that the scatter of the dipole location over the duration of the action potential is quite limited (see Fig. 10). This is likely because within the small brain volume (≈[50 µm]³) to which our EAP samples are typically confined, shape per se accounts for only a small fraction of EAP variation (see Fig. 1.).

Fig. 10.

(a) The error in the optimal dipole fits. The histogram shows the sample distribution of the fractional mean-squared error, i.e., the summed squared difference between model fit and EAP data, as a fraction of the summed squared data. Histograms from the “exact-probe” cells (dark bars; N=43), to the “approximated-probe” cells (open bars; N=18) are stacked. For definition of these subsets, see Section 2. The quality of the fit and the size of the error are indicated by two examples in the insets, one with a slightly better than typical fit (cell 68; fMSE 0.009), and the other with an atypically poor fit (cell 28, fMSE 0.094). Further examples of the typical in the sample are illustrated by the 4 cells shown in Fig. 2(a); the fMSE for those cells were 0.034 for cell 4; 0.015 for cell 45; 0.039 for cell 6; 0.018 for cell 20. (b) Definition of the scatter radius—a measure of the error in dipole localization (see text for details). (c) The joint distribution, in log-log coordinates, of the fMSE error in the dipole fit (horizontal axis) and the error in dipole localization (vertical axis). Arrows indicate cells 6 (third example in Fig. 2(a)) as well as cells 28 and 68, the same two as in (a). The horizontaland vertical dotted lines indicate the sample medians. Note that the localization error (abscissa) and the fitting error (ordinate) are not correlated.

When all 4 non-essential assumptions are adopted, conductivity is reduced to a real-valued constant, σ, and the forward problem is governed by the Poisson equation in the time domain:

$$\sigma {\nabla }^{2}V=Q.$$ (1c)

This is the version of the forward problem that we consider here, with the current source distribution Q reduced to a single dipole current p_s at a known location x_s, so Q = p_s at x_s, and Q = 0 elsewhere. (The specific material properties and the geometry of the model of the brain and probe are given below in separate sections entitled “The volume conductor model of cortex” and “Modeling a multi-contact probe and its lead field”.) Because Eq. (1) is linear, we can calculate its solution for a general dipole moment p_s by superimposing the solution for the projection of this dipole moment onto each of the three coordinate axes. This superposition is conveniently carried out in terms of a vector-valued kernel, L_ek(x̂). L_ek(x̂) has three components, each indicating the potential generated by a unit dipole along one coordinate axis. The subscript e_k indicates the contact at which the potential is measured, and the argument x̂ indicates the dipole position relative to the contact position, x_ek(i.e., x̂_s = x_s − x_ek). With this notation, the potential recorded by electrode e_k located at x_ek for a dipole moment p_s located at x_s is given by:

$$V_{e_k}={\mathbf{L}}_{e_k}({\mathbf{x}}_s-{\mathbf{x}}_{e_k})\cdot {\mathbf{p}}_s.$$ (2)

The kernels L_ek (x̂), which are meant to realistically capture the non-negligible field distortions from the non-ideal probe, quantify the sensitivity of the probe contacts to various source configurations. Thus, they are appropriately called the lead fields (owing to the concept’s origins in EKG studies).

Note that the well-known spatial dependence of the dipole potential in an infinite homogeneous volume conductor is

$$V_{e_k}=\frac{1}{4\pi \sigma }\frac{({\mathbf{x}}_s-{\mathbf{x}}_{e_k})\cdot {\mathbf{p}}_s}{\parallel {\mathbf{x}}_s-{\mathbf{x}}_{e_k}{\parallel }^3},$$ (2a)

implying that the lead field of an ideal point probe is L_idealprobe(x̂) = (1/4πσ)(x̂)/‖x̂‖³.

A lead field, according to the reciprocity principle of lead field theory (Helmholtz 1853b; Plonsey 1963) is the solution of a “reciprocal” forward problem, namely, the forward problem that results from interchanging the roles of current source and measuring device. In the present context, the reciprocal forward problem consists of injecting a current, I_e at the position of the electrode contact, x_e, and measuring the electric field, E_s = ∇V_s, at the position of the dipole. According to the reciprocity principle,

$${\mathbf{E}}_s\cdot \mathbf{p}=V_{\mathrm{e}}{I}_{\mathrm{e}}.$$ (3)

By substituting Eq. (3) in Eq. (2), we find that the lead fields are the current-normalized electric field solutions in the reciprocal forward problem in which current is injected through the electrode:

$${\mathbf{L}}_{\mathrm{e}}={\mathbf{E}}_s/I_{\mathrm{e}}.$$ (4)

Once the lead fields are calculated, they can be used with Eq. (2) to obtain a fast solution of the forward problem for any dipole source configuration.

We note that an analogous treatment can be formulated for monopole sources and the lead potential, of which the lead field is the gradient. Specifically, if the current source is a monopole volume current j_s (a scalar) at location x_s, we can re-write Eq. (3) of the reciprocity law via two substitutions: the monopole is substituted for the dipole source and the potential Φ_s is substituted for electrical field E_s at the source location that results from injecting the current I_e to electrode. With these, we get the lead potential

$$L_{e_k}={\Phi }_s/I_{\mathrm{e}},$$ (4’)

a scalar valued kernel, that solves the forward problem for monopole source(s):

$$V_{e_k}=L_{e_k}({\mathbf{x}}_s-{\mathbf{x}}_{e_k})\cdot j_s$$ (2’)

Consistency of Eqs. (2) and (2’) is readily obtained by using Eq. (2’) with two equal monopole sources of opposite polarity that are spatially removed, and attaining the dipole limit by spatial differentiation at the location of the source. Furthermore, all equations describing dipole optimization below will be valid for monopole optimization by substituting a monopole (scalar) for the dipole moment (vector) and the lead potential matrix (of scalars) for the lead field matrix (of vectors).

The great advantage of lead fields is that it focuses on the critical element for the solution of forward problems: the relative spatial position (emphasized by the notation x̂) of the current source and the lead. That is, within the interior of a sufficiently large homogeneous volume conductor medium, the lead field kernels rigidly translate as the probe is repositioned. This property of lead fields is particularly advantageous for analyzing multisite arrays whose contacts are related by a combination of translation and rotation: it is only necessary to calculate the lead field for one probe; the remainder can be obtained by symmetry. Numerical techniques to solve the lead fields with the finite element method and the results for various probe examples are presented below in a separate section.

We next assume that the lead fields have been obtained, and turn to the problem of optimizing dipole parameters. Let U_E = {U_e1,…,U_eN}^T denote the spatial sample of an EAP recorded by probe contacts in fixed measurement positions X_E = {x_e1,…,x_eN}^T. Suppose that we want to determine the location x_s (in electrode-independent coordinates) and dipole moment vector p = [p_x, p_y, p_z]^T that best accounts for these measurements. Each electrode contact, e_k, at its location, x_ek, has its corresponding lead field, L_ek(x̂_S), and the corresponding dipole potential at x_ek is given by Eq. (2). Using the notation

$${\mathbf{L}}_{\mathbf{E}}({\mathbf{x}}_S)={\{{\mathbf{L}}_{e1}({\mathbf{x}}_S-{\mathbf{x}}_{e1}),\dots ,{\mathbf{L}}_{eN}({\mathbf{x}}_S-{\mathbf{x}}_{eN})\}}^T,$$ (4A)

where L_E is an [N × 3] matrix, we can formulate the dipole optimization problem as a dual minimization

$$\underset{\left\{\mathbf{p}\right\},\left\{{\mathbf{x}}_s\right\}}{\text{min}}\parallel {\mathbf{U}}_{\mathbf{E}}-{\mathbf{L}}_{\mathbf{E}}({\mathbf{x}}_S)\cdot \mathbf{p}\parallel .$$ (5)

Note that for a fixed source location, x_S, the problem is reduced to the dipole moment minimization

$$\underset{\mathbf{p}}{\text{min}}\parallel {\mathbf{U}}_{\mathbf{E}}-{\mathbf{L}}_{\mathbf{E}}({\mathbf{x}}_{\mathbf{S}})\cdot \mathbf{p}\parallel .$$ (6)

The optimization problem in equation (6) is overdetermined (N>3) and linear, and can be solved by matrix inversion:

$$\begin{array}{l}\tilde{\mathbf{p}}={\mathbf{L}}_{\mathbf{E}}^{+}({\mathbf{x}}_{\mathrm{S}}){\mathbf{U}}_{\mathbf{E}}\hfill \\ {\mathbf{L}}_{\mathbf{E}}^{+}={({\mathbf{L}}_{\mathbf{E}}^{\mathrm{T}}{\mathbf{L}}_{\mathbf{E}})}^{-1}{\mathbf{L}}_{\mathbf{E}}^{\mathrm{T}}\hfill \end{array}$$ (7a,b)

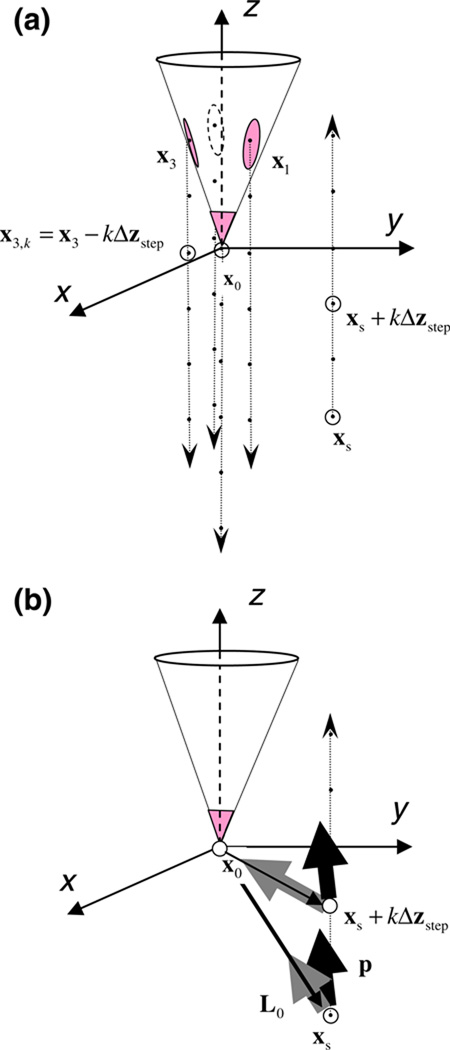
where ${\mathbf{L}}_{\mathbf{E}}^{+}$ denotes the [3×N] left pseudo-inverse of L_E (Unless the probe is a linear array of contacts, ${\mathbf{L}}_{\mathbf{E}}^{+}$ is full column rank.) The logic of the linear optimization procedure makes use of the rigidly translating lead field as illustrated in Fig. 4.

Fig. 4.

Schematics of dipole optimization procedure using translated lead fields of a moving tetrode. (a) During data collection, the tetrode moves down (down arrows) the path of penetration in steps of size Δz_step, yielding measurements of the same source at 4n_step spatial points (black dots). From the probe’s point of view used in the analysis, real movement of the tetrode is equivalent to virtual movement of the source in the opposite direction (up arrow). x_s and x_i, i={0,1,2,3}, denotes the Cartesian coordinates of the position of the source and the ith lead in the first step, respectively, relative to the (moving) tetrode tip (x₀). (b) The tetrode lead registers the extracellular action potential of a single unit that is characterized by a single dipole current source with moment p. The dipole moment vector is translated to a new position relative to the probe at each step (x_s + kΔz_step). At each step, the model prediction of the probe potential is the scalar (dot) product of the dipole moment vector of the source, p, and the lead field vector of the probe at that relative position, L_i(x). Thus for a fixed physical source position, the dipole interacts with the lead field in a set of translated virtual positions. See text for the details of dipole optimization

We note that from a statistical perspective, it is more appropriate to use noise normalized error minimization than the simple residual error measure implicit in Eq. (6). Noise normalization uses the Mahalanobis distance to weigh the contribution of the residual error by C⁻¹, the inverse of the spatial noise covariance matrix, essentially recasting the error norm in terms of levels of significance. Then the dual minimization problem is formulated as

$$\underset{\left\{\mathbf{p}\right\}\left\{x_S\right\}}{\text{min}}\parallel {\mathbf{C}}_{\mathrm{n}}^{-1/2}({\mathbf{U}}_{\mathbf{E}}-{\mathbf{L}}_{\mathbf{E}}({\mathbf{x}}_{\mathrm{S}})\cdot \mathbf{p})\parallel ,$$ (5’)

and the linear solution for the optimal dipole is obtained by the pseudo inverse of the covariance-weighted lead field matrix:

$$\begin{array}{l}\tilde{\mathbf{p}}={\mathbf{L}}_{\mathrm{E}}^{\prime +}({\mathbf{x}}_S){\mathbf{U}}_{\mathbf{E}}\hfill \\ {\mathbf{L}}_{\mathbf{E}}^{\prime +}={({\mathbf{L}}_{\mathbf{E}}^{\mathbf{T}}{\mathbf{C}}^{-1}{\mathbf{L}}_{\mathbf{E}})}^{-1}{\mathbf{L}}_{\mathbf{E}}^{\mathbf{T}}{\mathbf{C}}^{-1}\hfill \end{array}$$ (7’b)

To carry the optimization with the above noise normalization through the regularization step, we need only to substitute ${\mathbf{L}}_{\mathbf{E}}^{\prime +}$ (Eq. (7’b) for ${\mathbf{L}}_{\mathbf{E}}^{+}$ (Eq. (7b)) in every equation below. This formalism makes it transparent that noise normalization only makes a difference when the noise covariance matrix is significantly different from the identity. Interestingly, for our data recorded with the stepped tetrode, the noise covariance is nearly the identity (save for a scale factor), and thus noise normalization makes no difference to the optimal dipole recovered from these data. This is a consequence of two special features of our data: (1) the asynchronous recording at different tetrode positions, and (2) an approximate translation invariance of channel noise. Because of (1), spatial noise correlation was zero between measurements made at different tetrode positions (thus the only non-zero elements in the matrix were restricted to the disjoint 4×4 diagonal sub-matrices). Because of (2), per channel noise levels and channel cross-talk were comparable at all probe positions. Translation invariance was well approximated probably only because the probed volume was small enough and the stimulation was reproducible enough for the neural noise (often the dominant noise component) to change little across sites. And of course thermal electrode noise is expected to be translation invariant. (Notice that (1), and possibly (2) cannot be expected to hold for the entire set of recording sites on a spatially extended stationary multisite probe. Thus noise normalization gains importance for analyzing data recorded with those probes.)

After the linear dipole optimization is solved in separation, the joint minimization over x_s and p reduces to a single minimization over x_s, in which the optimal p is chosen for each x_s via Eq. (7). Thus, the joint minimization (Eq. (5)) reduces to

$$\underset{{\{\mathbf{x}}_S\}}{\text{min}}\parallel {\mathbf{U}}_{\mathbf{E}}-{\mathbf{L}}_{\mathbf{E}}({\mathbf{x}}_S){\mathbf{L}}_{\mathbf{E}}^{+}({\mathbf{x}}_S){\mathbf{U}}_{\mathbf{E}}\parallel .$$ (8)

The dependence on x_s implied by Eq. (8) is in general complicated and nonlinear, and there is no analytic solution to the global optimization problem. Instead, we choose a large and dense discrete set of trial positions X_S = {x_S}, and determine the minimum within that set:

$$\underset{{\mathbf{x}}_S\in {\mathbf{X}}_S}{\text{min}}\parallel {\mathbf{U}}_{\mathbf{E}}-{\mathbf{L}}_{\mathbf{E}}({\mathbf{x}}_S){\mathbf{L}}_{\mathbf{E}}^{+}({\mathbf{x}}_S){\mathbf{U}}_{\mathbf{E}}\parallel .$$ (9)

As is generally the case with source localization problems, the residual error, plotted as a function of model parameters, typically lacks a robust global minimum. That is, beyond a certain minimum cell-probe separation, near-optimal fits can be obtained for widely different source geometries. As a result, the specific model parameters at which the minima occur are determined by noise in the data, and do not represent robust or physically meaningful solutions. To circumvent this difficulty, we need to impose constraints other than just error minimization. For this, we use Tikhonov regularization (Tikhonov and Arsenin 1977): among all the solutions that have a comparably small error norm (Eq. (8)), we choose the one that is the most economical, i.e., the one in which the solution norm (the source magnitude) is the smallest.

To implement this approach, the objective function (Eq. (9)) is replaced by one that takes into account both the error norm and the model norm. The relative weighting of these factors is controlled by a regularization parameter, j. Specifically, we consider the objective function

$$\underset{{\mathbf{x}}_S\in {\mathbf{x}}_S}{\text{min}}\left\{\parallel {\mathbf{U}}_{\mathbf{E}}-{\mathbf{L}}_{\mathbf{E}}({\mathbf{x}}_S){\mathbf{L}}_{\mathbf{E}}^{+}({\mathbf{x}}_S){\mathbf{U}}_{\mathbf{E}}{\parallel }^2+j^2\parallel {\mathbf{L}}_{\mathbf{E}}^{+}({\mathbf{x}}_S){\mathbf{U}}_{\mathbf{E}}{\parallel }^2\right\}.$$ (10)

In the j→0 limit, Eq. (10) turns into Eq. (9) and the regularized solution is identified by the absolute minimum of the residual, usually at the cost of an unrealistically large dipole moment and source distance. In the j→∞ limit, the regularized solution minimizes the dipole size at the cost of near-maximal fitting error. Values between these two extremes represent the tradeoff between the two optimization principles. Thus, the crux of the problem is to choose the value of the Tikhonov parameter j in a principled fashion.

To determine the Tikhonov parameter, we used a variant of Hansen’s L-curve method (Hansen and Oleary 1993). The starting point is a log-log plot of the two quantities that constitute the objective function Eq. (10): on the abscissa, the model norm, $\parallel {\mathbf{L}}_{\mathbf{E}}^{+}({\mathbf{x}}_S){\mathbf{U}}_{\mathbf{E}}\parallel$, and on the ordinate, the error norm, $\parallel {\mathbf{U}}_{\mathbf{E}}-{\mathbf{L}}_{\mathbf{E}}({\mathbf{x}}_S){\mathbf{L}}_{\mathbf{E}}^{+}({\mathbf{x}}_S){\mathbf{U}}_{\mathbf{E}}\parallel$ (the squaring in Eq. (10) can be omitted because in log-log coordinates it merely scales both axis by a factor 2). Each of these quantities are determined (via Eq. (7)) for dipoles placed at the discrete set of trial positions X_S = {x_S}. The lower envelope of this scatter plot, parametric in j, takes the shape of an “L”, and the corner of the L provides a natural definition of the globally optimal solution and the corresponding optimal regularization parameter. With discrete data (following (Hansen and Oleary 1993)), the corner point is determined by smoothly interpolating through the discrete points at the vertices of the convex hull, and then choosing the discrete sample that is closest to the point of largest curvature.

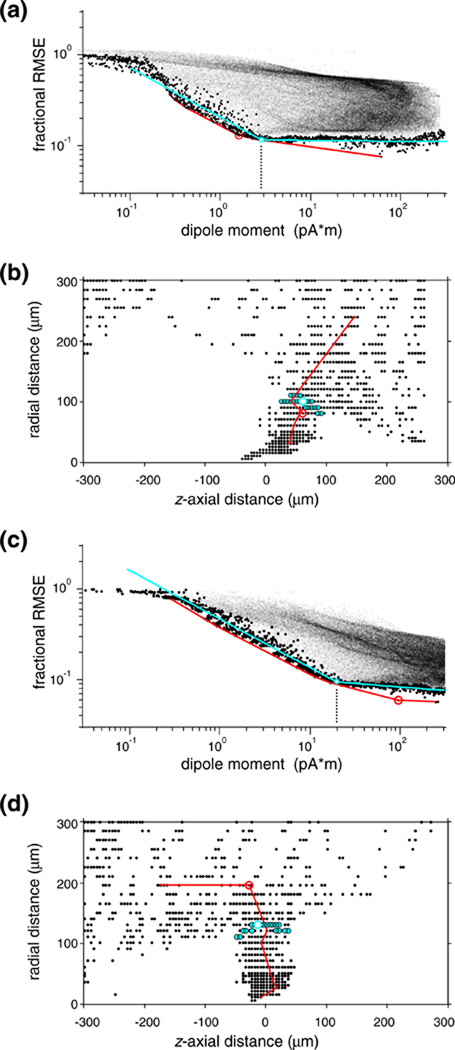
The log-log plot of dipole moment versus fit error is shown for two examples in Fig. 5(a and c). The L-shaped lower convex envelop and its encircled corner point are plotted in red. We found that it was necessary to improve the robustness of this estimate, since often there were odd local minima that “trapped” the point with largest curvature on the convex hull in the range of unrealistically large dipole moments. For example, the optimal dipole moment (≈100 pA*m) thus identified for the cell shown in Fig. 5(c) is ≈ 5 times larger than the more robust estimate (≈20 pA*m), and ≈ 20 times larger than the typical moment (≈5 pA*m) in our sample.) We therefore modified the Hansen procedure as follows. First, we defined a “lower bound” subset (data points highlighted as black circles in Fig. 5(a and c)) of the joint distribution of dipole norm and residual norm. Within the data range where the lower bound could be well approximated by a piece-wise linear (“L”-shaped) trace, ${\text{log}}_{10}(\parallel {\mathbf{L}}_{\mathbf{E}}^{+}({\mathbf{x}}_S){\mathbf{U}}_{\mathbf{E}}\parallel )$ was densely binned. Within each bin the data point with $\underset{\tilde{\mathbf{p}}}{\text{min}}({\text{log}}_{10}(\parallel {\mathbf{U}}_{\mathbf{E}}-{\mathbf{L}}_{\mathbf{E}}({\mathbf{x}}_S){\mathbf{L}}_{\mathbf{E}}^{+}({\mathbf{x}}_S){\mathbf{U}}_{\mathbf{E}}\parallel ))$ was selected, and the union of these bin-by-bin minima defined the lower bound subset. We chose a bin width (< 0.01 log units) that allowed a dense sampling of the log model norm but still yielded a large enough sample within each bin to reliably estimate the minimum log error norm. Then, we fit a smooth function to this lower bound subset: either two intersecting line segments in log-log coordinates (shown as the cyan curves in Fig. 5(a and c)), or a descending parabola and its smooth linear continuation in the log-linear coordinates (not shown but yielding very similar results). Finally, the globally optimal dipole (highlighted as a white circle in Fig. 5(a and c)) was defined by the data point that was closest to the corner point on the fitted curve. The metric we used for L-curve fitting in the log-log coordinates weighted the two coordinates equally (representing equal multiples with equal weights), and the metric we used in log-linear coordinates normalized both coordinates by dividing them with their full range used in the L-curve fitting. But this choice was not critical: the relative weights assigned to the two data coordinates had negligible influence on the resulting globally optimal dipole, because the densely sampled vicinity of the corner point of the L-curve (highlighted by a cyan disk) mapped compactly in space (dipole location coordinates plotted in cyan symbols in Fig. 5(b and d)). The empirical L-curve fits were generally very good (they explained on average more than 90% of the variance in the lower bound set). Furthermore, the L-curve fits had a much smaller scatter than the estimates from the convex envelope (standard deviation and range of log dipole moment was reduced by 60% and 1 log unit, respectively). This great improvement in confidence in the estimates of optimal dipoles did not come at a price of bias towards larger moments: the difference between the sample medians of the dipole moments estimated with the two methods was <8% and not significant (p>0.8, Wilcoxon’s ranksum-test). (The slight but consistent offset apparent between the descending limbs of our empirical L-curve and the lower convex envelope might suggest, misleadingly, such a bias but the offset between the two curves is generated by an essentially vertical shift).

Fig. 5.

L-curve regularization of the optimal dipole for a single visual neuron. (a) The joint distribution of the size (abscissa) of the locally optimal dipole source and the associated residual error (ordinate) between the predicted and measured EAP’s. Each of these model dipoles (fine dots) was calculated by Eq. (7) at one of the node points of a regular cylindrical mesh covering a finite volume surrounding the recording tetrode. Large dots mark data in the lower bound subset, the red line indicates the tangent envelope, and the smooth cyan curve is a 4-parameter empirical L-curve fitted to the lower bound. The L-shaped pattern suggests two model regimes. On the steep left segment, models increasingly well capture genuine physical features of the data at the cost of small increases in the dipole size (and, implicitly, cell-probe separation). The shallow segment to the right corresponds to the noise limit that allows no further improvement in capturing physical features. The optimal equivalent dipole is defined as the data point nearest to the corner point of the L (open circle). The cyan circular halo indicates the neighborhood of the 30 data nearest to the corner point. The point with the largest curvature on the tangent envelope (red circle) corresponds to a similar dipole. (b) Dipole localization of neurons via L-curve regularization is robust. The mapped locations of the locally optimal dipoles that fell within the lower bound subset are plotted in small symbols; the open circle marks the globally optimal dipole. Confirming that the optimization principle was realized, the 30 nearest neighbors of the L-curve corner (indicated by cyan halo in (a)), are mapped in a compact volume (cyan symbols) that represents a choke-point in the distribution; dipoles from the noise-limited flat right limb of the L-curve are mapped in an explosively expanded volume. Cell 10. (c)-(d): another example, illustrating the unstable nature of the prediction by the tangent envelop in discrete sample. In contrast to the corner of the L-curve (cyan circle), the point with the largest curvature on the tangent envelope (red circle) corresponds to physiologically unrealistic dipole parameters). Cell 37

3.2 Volume conductor model of cortex

As reasoned in Section 3.1, we approximated the extracellular action potential in cortex in a quasi-stationary manner and modeled brain tissue as a linear, isotropic and piecewise homogeneous, frequency-independent, resistive medium. Some of the implications and validity of these assumptions are also discussed below in Section 4.5.

The model brain block was a 4-mm high cylinder, with the top 2 mm representing homogeneous gray matter and the bottom 2 mm representing homogeneous white matter. Control calculations indicate that including or omitting a WM domain makes essentially no difference to our results. The probe penetrated the brain along the axis of the brain cylinder and its tip was positioned at halfway down the gray matter. The block diameter (4 mm) was chosen large enough to make outer boundary effects negligible within a smaller volume of interest (≈0.6 mm diameter) centered on the site of the recording probe. The outer boundary of the brain cylinder was grounded, except at the top where it was insulated; a selected tetrode lead was clamped at a unit voltage or current, and all other domain boundaries on the probe were insulated.

We choose the geometric mean of two extremes, white matter (σ_WM = 0.15 S/m) and cerebrospinal fluid (σ_CSF ≈ 1.35 S/m) for the gray matter conductivity. This choice (σ_GM = 0.45 S/m) reflects values measured for σ_GM in various cortices and species (Ranck 1963; Li et al. 1968; Vigmond et al. 1997; Lopez-Aguado et al. 2001). Other recent modeling studies used somewhat lower values (σ_GM = 0.30–0.38 S/m (Moffitt and McIntyre 2005; Gold et al. 2006, 2007)). The value of the scalar conductivity has no effect on the dipole location, only the dipole moment size (see Section 4).

3.3 The multi-contact probe model and its lead fields

Single unit recording made with multi-contact probes typically occur at cell-probe separations that are a few multiples of the characteristic contact separation. Since at these short distances, the details of the probe geometry may crucially influence the lead fields, we created a numerical model of the recording probe—in our case, a tetrode. We used tetrodes commercially acquired from the manufacturer, Thomas Recording GmbH, and the parameter range reported here reflects specifications tailored to use in our laboratory.

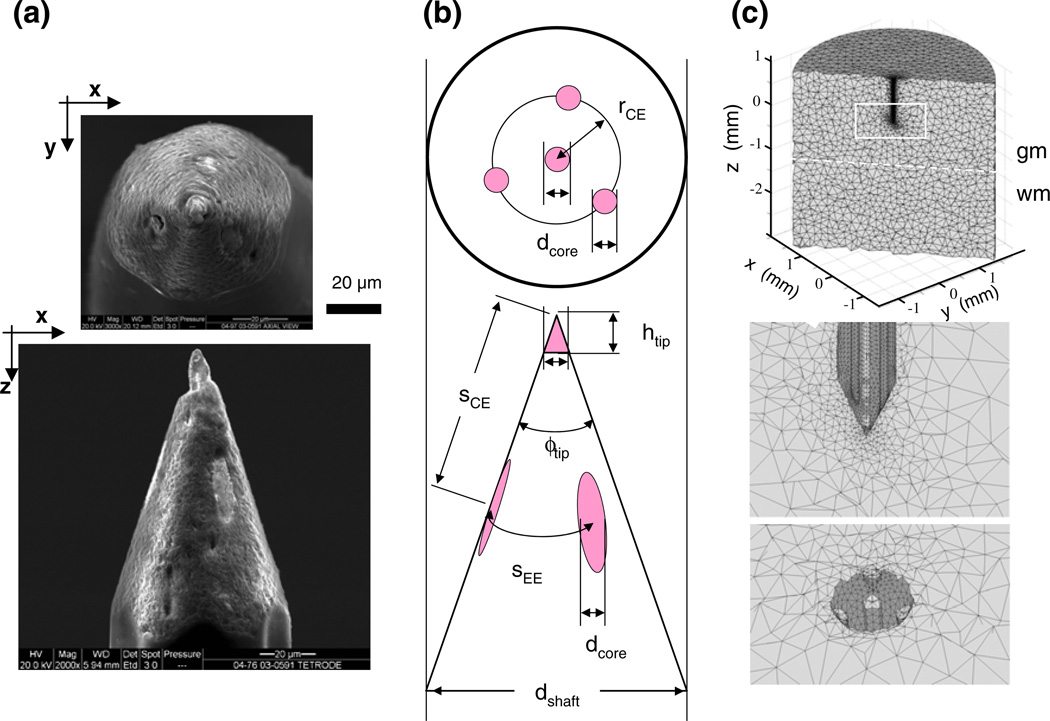
The contacts are in a tetrahedral configuration on the Thomas tetrode. The probe geometry is shown by the scanned eletronmicroscopy images in Fig. 6(a). The overall shape is that of a sharpened pencil: the cylinder of the quartz-insulated shaft is ground to a cone at the tip in a sharp angle to expose the contacts in a tetrahedral configuration; the 4 embedded parallel microwires are made of platinum-tungsten alloy (PtW); one microwire placed in axial position, emerging as the central contact at the center of the tip (the point of the pencil); three are at equal angles in a concentric arrangement around the central one, emerging as eccentric contacts along the tip’s sloping portion. The geometry of the design guarantees approximate equality of the exposed areas of the three eccentric contacts and the central contact, and approximate equality of their input impedances.

Fig. 6.

The geometry of a Thomas tetrode and its finite element model. This tetrode is the first one listed in Table 1. (a) Scanning electron microscopy images of the cleaned, untreated tip of the tetrode with axial view (top) and lateral view (bottom). The lighter contact surfaces of the PtW wire leads contrast well with the quartz coat. (b) The critical geometry parameters used in the tetrode models (defined and listed for each reconstructed tetrode in Table 1). (c) The tetrahedral mesh of the finite element model of the probe-brain system, viewed in three cross-sections; top, vertical on-axis cut showing overall dimensions; middle, same cut but zoomed-in on the tetrode tip area where elements representing the lead wires are visible; and bottom, cut in the x-y plane at the z-level where the core wires are exposed as contacts. Note that element size varies extensively; it is smallest near the tetrode tip

The manufacturer supports adjustment of several shape parameters (Fig. 6(b)). These include the diameter of the wires and the quartz cylinder within the last several hundred microns of the conical tip (5-to-9 µm and 50-to-90 µm, respectively), and the angle of the conical tip, adjusted by grinding (18–25 deg range, half-angle measured in the plane of the long axis). These values yielded contact impedances of 1.4±0.25 MOhm at 1 kHz (individually tested by Thomas Recording), and good selectivity in single unit isolation. The cone angle and the inter-wire separation together determined the inter-contact separation.

For 4 of the 7 tetrodes used in this study, the critical geometric details of the tetrode tip and shaft were reconstructed from high-resolution scanning electron-microscopic (SEM) images that were taken after the completion of the stepping experiments, as in Fig. 6(a). The contact surfaces of the PtW wire leads were easily discernable, and the resolution (spatial dimensions are indicated by horizontal scale bar) allowed precise measurement of the critical geometry parameters (Table 1) The tetrode of Fig. 6(a) is listed as the first row in Table 1.

The core wires were modeled as thin cylinders shaved at the exposed contact area to mesh with the conical tip surface. The specific conductivity of the model conductor (σ_PtW =1.5×10⁷ S/m) was set to the mean conductivity of the platinum (σ_Pt = 0.94×10⁷ S/m) and tungsten (σ_W = 1.78×10⁷ S/m), reflecting a real alloy that contained an equal mix of the two components. The infinitesimal conductivity of the insulating quartz shield (σ_qz = 10⁻¹⁴ S/m) was modeled by the ideal insulator (σ_vacuum = 0 S/m), to reduce the accumulation of numerical rounding errors. The overall dimensions and the relative scale of the various components of the finite element model (FEM) are illustrated by images in Fig. 6(c).

High computational accuracy requires (a) that element size is small enough, i.e., size is adapted to the characteristic size of the compartmental features in the model and (b) that element quality is high, i.e., the distortion of tetrahedral volume elements from the ideal equilateral shape is small. Both criteria are important, but they need not correlate. Therefore we examined the distribution of both element size and element quality, both as a function of the distance from the tetrode tip (where the smallest feature and the largest curvature were located). As the analysis below details, both criteria were met.

The two criteria are analyzed in Fig. 7. We examine the quality of the mesh (~1.6*10⁶ elements) used to model tetrode 06–3200 (the second in Table 1; similar results were obtained for the other tetrodes). Because element size needs to adapt to the characteristic size of model features, we plot the distribution of element size separately for three kinds of elements: metal wires (7-µm diameter) in red; gray matter within a 30-µm wide neighborhood of the tetrode in cyan; everything else in blue. We chose a 30-µm cutoff because this corresponds to the size of tetrode features of interest (exposed tip length; tip separation; shaft radius). The two vertical lines, one at 7 µm and one at 30 µm, indicate these scales; the horizontal line at 300 µm indicates the radius of the region of interest.

Element size (Fig. 7(a)), measured by the longest of the 6 edges of the tetrahedral elements, was well-adapted to the characteristic size of the compartmental features, and was progressively smaller for elements nearer to the tetrode tip. Specifically, element size within the wires domain (red) was smaller than the wire diameter in 94% of the elements (96% within the region of interest), and element size within the gray matter neighborhood of the tetrode (cyan) was smaller than those features in 90% of the elements (95% within the region of interest). As shown in the marginal histogram (Fig. 7(b)), these three subsets correspond to 3 distinct modes in the distribution of element size, with peaks at ≈ 5 µm, ≈ 20 µm, and ≈ 200 µm.

Element quality is defined by the ratio of the volume of the actual element to that of an ideal element whose edge equals the root-mean-square average edge length in the actual element, and is shown in Fig. 7(c). Element quality was better than the minimum acceptable for 3-d models (0.3, a criterion recommended by FemLab and shown as a vertical line, Fig. 7(c)) in all but 20 of the ≈ 21,000 elements within the region of interest. Typical element quality was much higher (mode ≈ 0.85; median >0.7 within each of the above spatial domains), as shown by the marginal histogram (Fig. 7(d)).

The lead fields of all 4 contacts obtained with FEM on the same random mesh were then interpolated on the same regular cylindrical grid centered on the tetrode axis. The lead field was directly computed via FEM for only one of the three eccentric tetrode contacts; for the other two, fields were computed from the first by rotation and interpolation, utilizing the three-fold symmetry in the tetrode design.

Figure 8 shows the lead fields calculated for one of our measured tetrodes (listed second in Table 1). For the center lead, there is near-perfect radial symmetry for distances beyond ≈ 25 µm from the tip, and the distance dependence closely approximates the ~r⁻² expected for the electric field of a point source. For the eccentric lead, there is a substantial departure from radial symmetry up to at least 100 µm. Contour lines are kidney-shaped, with lower field values and a more rapid fall-off in directions behind the shaft (i.e., opposite to the exposed area of the eccentric lead analyzed and between the other eccentric contacts). In these directions, falloff is faster than ~r⁻². This behavior is expected from geometric considerations, and also applies to planar polytrodes (Moffitt and McIntyre 2005). For the other tetrodes listed in Table 1, the lead fields were very similar, despite a considerable difference in contact area across tetrodes. This is because away from the shaft, the ~r⁻² falloff dominates, independent of contact area or the tip angle.

Fig. 8.

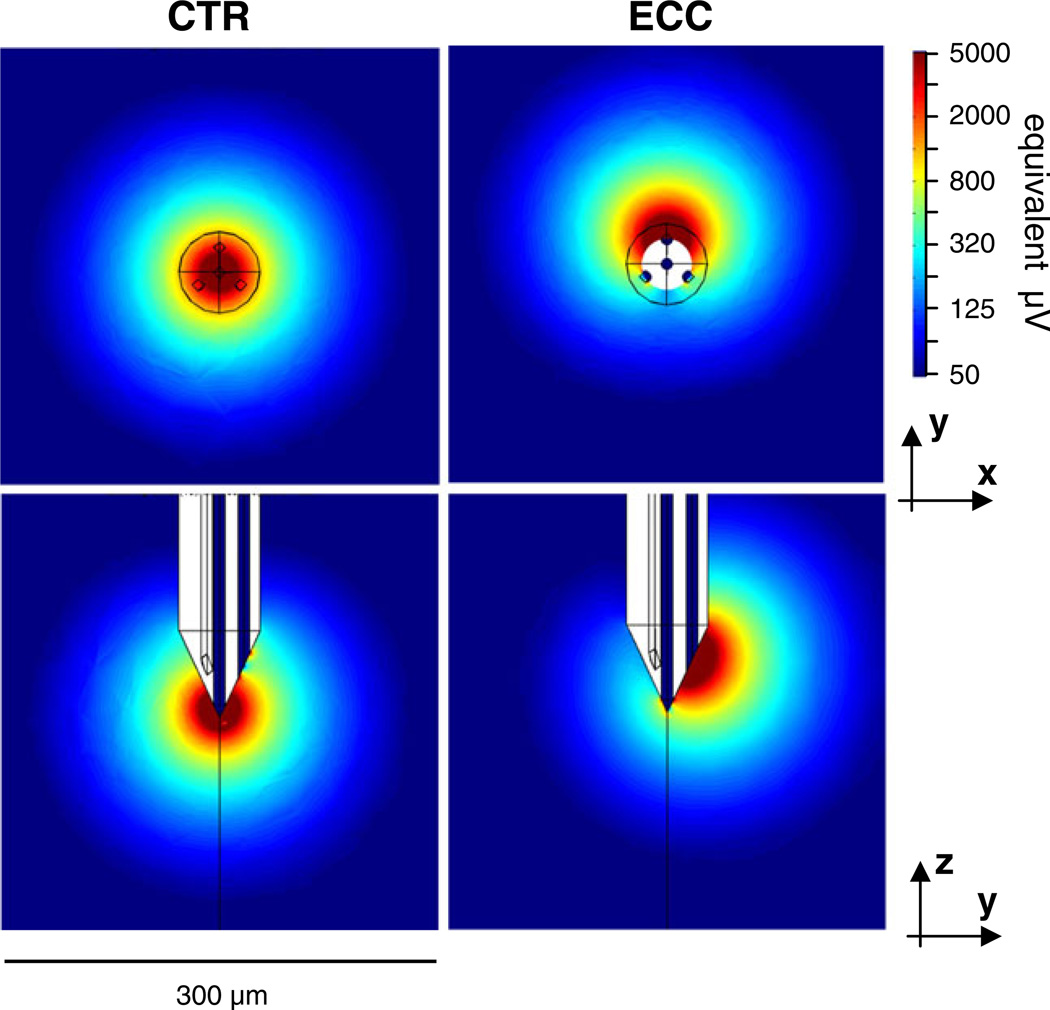
The lead fields of a Thomas tetrode, calculated by the finite element method for one of the tetrodes. The parameters of the tip geometry for this tetrode (#03–0591) are listed in Table 1. The images show the lead field strength in color scale for two planar cross-sections for the center lead on the left (x-y plane through the tip point; y-z plane through the vertical axis of the probe), and for one eccentric lead on the right (x-y plane through the center point of the exposed lead surface). The color bar indicates the lead field strength on a log scale after conversion to equivalent probe potentials (µV) that the probe would register for a dipole source whose dipole moment equals 5pA*m (see text for explanation) and whose vector is iso-oriented with the lead field vector at each position in space. The lead field vectors at each point in space are oriented approximately in the direction of the gradients

To get a sense of the physiological significance of the lead fields, we use the forward equation (Eq. (2)) to determine the distance at which a dipole of a given size produces a probe voltage of a given size. The size of the equivalent dipole of a typical neuron recorded in visual cortex is 5 pA*m (Mechler et al. 2011); we use this dipole moment magnitude as the standard for lead field comparison. For an optimally-oriented 5 pA*m dipole current source and voltages registered by the contact in the range 50–250 µV (typical EAP amplitudes in our data) the distance range is ≈ 50-to-150 µm (the range outside cyan ring in Fig. 8). For comparison, typical recording noise, combining neuronal (multiunit) and thermal sources, falls in the <50 µV range (see Fig. 3); this corresponds to a source distance of ≈ 150 µm and beyond (the peripheral deep blue regions of Fig. 8).

To quantify these observations, we used the 5 pA*m standard dipole source and calculated the r_{25 µV}, r_50µV, and r_100µV lead field radii with the corresponding criterion signal level set near the mean noise level (≈25 µV), the observed empirical signal detection threshold (≈50 µV), and the median EAP amplitude for single unit discrimination (≈100 µV), respectively. The three cover the characteristic signal range in our recordings in visual cortex in log steps. r_100µV and r_50µV can be thought of as the median and maximum single unit recording radius of a contact, respectively, and r_25µV as the median radius for multiunit recording. For each criterion, we calculated the radius along the principal axes of field symmetry and listed the mean and range in Table 2 for the 4 reconstructed tetrodes.

Table 2.

Tetrode lead field radii

		r100µV	r50µV	r25µV
Tetrode	Lead	(µm)	(µm)	(µm)
03–0591	CTR	92±4	131 ±4	187±3
	ECC	101 ±2 (71)	139±3 (109)	195 ±3 (167)
0603–3200	CTR	93±3	132±3	187±2
	ECC	99±3 (64)	139±4 (108)	194±5 (167)
0703–0087	CTR	95±2	134±2	189±1
	ECC	99±2 (74)	138±4 (116)	194±5 (175)
0703–0088	CTR	93±3	132±3	187±2
	ECC	98±2 (75)	137±3 (116)	193±5 (171)

Field radii are defined at 3 criteria: r_100µV, for characteristic (median) single unit signal levels required by unit isolation (at 4 times the characteristic noise levels), r_50µV, for characteristic signal detection threshold (at 2 times the characteristic noise levels), and r_25µV, for characteristic noise levels. The criterion field strengths are in equivalent probe potential (µV) obtained with a 5pA*m dipole source (typical for neurons in visual cortex) aligned with the field everywhere. Entries are mean ± the half-range of the radii measured along the x- and z-axis for the center lead, and along the cardinal directions within the tangent plane and along its surface normal in front for the eccentric lead. The smaller radii enclosed by the parenthesis are along the surface normal pointing behind the tetrode; they highlight the asymmetry specific to the eccentric leads

Lead fields radii were very similar despite considerable variation in contact area and tip angle among the tetrodes. Across the 4 tetrodes listed in Table 2, the variation of lead field radii of the central contacts (e.g., r_50µV range 131–135 µm) and the eccentric contacts (r_50µV range 137–139 µm) was no larger than the variation with direction for each contact. The small variation with direction indicates almost perfect radial symmetry for the entire center lead field, and in the front hemi-sphere of the eccentric lead. The almost exact doubling of radius for a 4-fold drop in signal level indicates that at these distances the lead fields are well approximated by a perfect point source (r⁻² falloff). All these together confirm that these criterion distances are far enough and the geometry details of the tetrode tip do not affect the lead fields.

There is one notable exception to this rule: the lead field radii of the eccentric leads differ significantly from the central lead. Indicating elevated sensitivity compared to the central lead, the eccentric field spreads out 5–10% more in front of the tangent plane of the eccentric lead (compare, for each tetrode in Table 2, the ‘CTR’ radius with the larger of the two ‘ECC’ radii). Conversely, indicating reduced sensitivity, the eccentric field is 20–30% more compressed on the opposite side of the tetrode (compare, for each tetrode in Table 2, the ‘CTR’ radius with the smaller of the two ‘ECC’ radii (in parenthesis)). These distortions result in the kidney-shaped equipotential contours shown in Fig. 8.

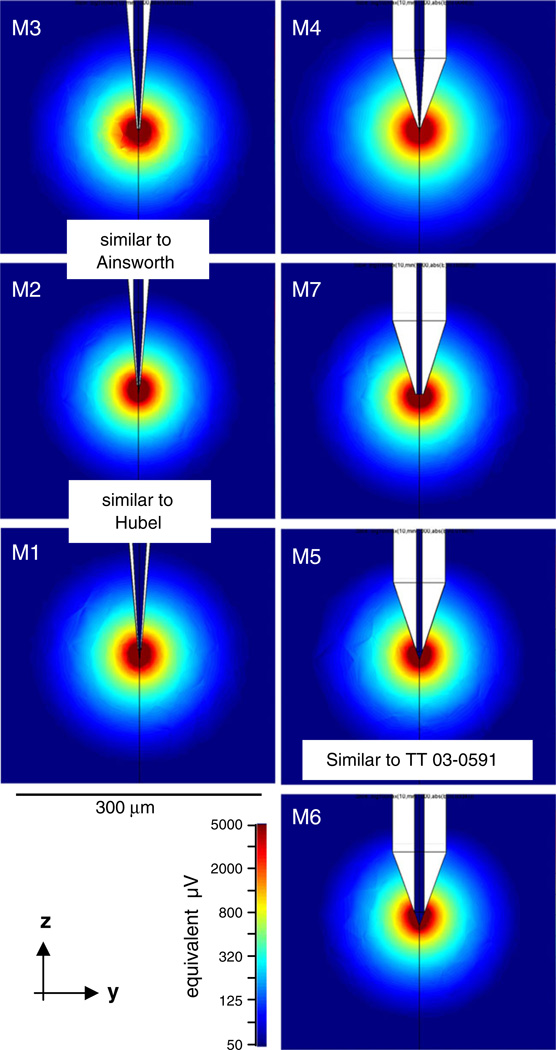
To better understand how lead field radius depends on tip geometry of the electrode, we simulated the lead fields for sharp microelectrodes modeled with various tip geometries (Fig. 9), ranging from very fine sharp tips (M1-M3) approximating the reported shape of single electrodes traditionally used in cortical electrophysiology to blunt tips that are identical to the central lead of a one of our tetrodes (M5). The parameters of these models are listed in Table 3. Although the exposed tip area ranges over two orders of magnitude, the lead field radius r_50µV barely changes. This indicates that the geometry of the tip per se has little influence on the sensitivity of single electrodes. The same principle extends to multi-contact probes as well (see Section 4).

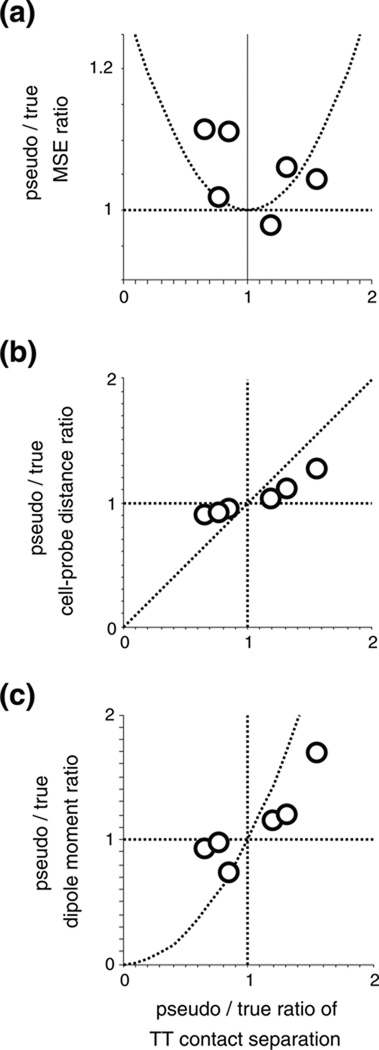
Fig. 9.

The lead fields of sharp electrodes modeled with a wide variety of tip shapes. Spatial scale and field strength are as in Fig. 8. Lead field geometry depends only weakly on the details of the tip geometry. The radius of the lead fields defined at a criterion field strength (or equivalent signal strength) is weakly anti-correlated with exposed tip area (models are vertically ordered with increasing tip area) and with the cone angle of the shaft, and does not depend significantly on the cone angle of the exposed tip. Most notably, the typical lead fields of our tetrodes (e.g., M5) are very similar in size to those of typical sharp electrodes (all other panels). Specifically, M1 and M2 are similar to tips fabricated by Hubel (Hubel 1957), and M2 and M3 are similar to tips fabricated by Ainsworth (Ainsworth et al. 1977). The varied geometry parameters and the resulting field radii are summarized in Table 3. Other details of the lead field modeling were the same as used for the tetrodes (see Fig. 8) and text

Table 3.

Single electrode models

Model	dcore (µm)	ϕtip/2 (deg)	dtip (µm)	htip (µm)	Atip (µm2)	ϕshaft/2 (deg)	dshaft (µm)	hshaft (µm)	r100µV (µm)	r50µV (µm)	r25µV (µm)
1	24	3.5	2	10	43	5	36	200	92±2	132±3	186±4
2	12	3.5	1.6	10	30	5	36	200	86±2	123 ±3	175±3
3	12	3.5	0.8	3	4	5	36	200	97±0	139±0	201 ±0
4	12	3.5	1	5	8.5	5	65	90	106±2	150±3	217±4
5	7	19	7	10	116	19	65	90	89±4	126±5	179±5
6	12	19	12	16.7	322	19	65	90	85±5	122±5	176±6
7	6	90	6	0	26	19	65	90	97±2	136±1	192±2

M1-M3: sharp tips and shafts; M4-M7: wider shafts and variously sharp tips. The varied geometry parameters included the core diameter (d_core), exposed tip diameter at its top (d_tip), exposed tip cone height (h_tip), cone angle of the shaft (ϕ_tip), exposed tip area (A_tip), shaft diameter (d_shaft), shaft cone height (h_shaft), the cone angle of the shaft (ϕ_shaft). Lead field radii are defined at 3 criteria, as in Table 2. Entries are mean ± the half-difference of the radii measured along the horizontal (x-dir) and vertical (z-dir)

3.4 The dipole account of EAP and localization error

We used the lead fields of reconstructed tetrodes, in conjunction with the L-curve regularization method, to solve the optimal equivalent point dipole source for each of 61 visual cortical neurons. The dipole fit to the EAP data was characterized by the fractional mean squared error (fMSE), i.e., the ratio of the spatial mean of the squared errors over the spatial mean of the squared EAP amplitudes. The quality of the fit is indicated by two examples in the insets of Fig. 10(a). The one on the left was a slightly better than typical fit (cell 68; fMSE 0.009), the one on the right was an atypically poor fit (cell 28, fMSE 0.094). Further examples of what was typical in the sample are illustrated by the 4 cells shown in Fig. 2(a) (all with fMSE in the 0.02-to-0.04 range).

The histogram in Fig. 10(a) shows the distribution of the fMSE in our sample (N=61). The sample is the sum of the two subsets (open and dark bars, respectively, shown stacked), that will be discussed below. In the entire sample, fMSE was, very small (mean ≈ 0.04) except in a minority of cells (range: 1% to 30%). The sample means for the two sets were not significantly different (2-sample t-test, p>0.05).

The residual error lumps together data error (noise, neuronal spike variability, errors in spike sorting and probe position) with modeling error (in tetrode geometry; volume conductor; source model; regularization of discrete data). The fMSE indicates that all these factors were small in most cells. However, a goodness-of-fit statistic (a sum of F-statistics across spatial positions) that characterized the optimal dipole fit was significant for each cell in our sample. This test (not shown) indicated that error in the fit was more than could be accounted for by errors in the voltage measurements. Moreover, in the exact-probe set (dark bars; Fig. 10(a)), there was a weak negative correlation between fMSE and inferred cell-probe distances (slope = −0.3, p-value ~0.11; not shown). That is, the dipole model gave a slightly poorer fit for the nearest cells. Since the details of the true source and/or probe geometry are likely to be more significant for the cells nearest to the probe, the latter analysis suggests that at least some of the MSE represents error contributed by model error in the source model.

In line with the above, the error in the dipole fit was a poor predictor of the error in dipole localization. To estimate the latter, we defined the scatter radius of the smallest spherical volume that includes the dipole locations estimated at 5 different characteristic moments in the time course of the action potential (as illustrated in Fig. 10(b)). The sample median of the scatter radius (vertical dotted line in Fig. 10(c)) was 51 µm (and not significantly different in the two subsets). Figure 10(c) shows the joint distribution of the scatter radius and the fitting error—they were uncorrelated. Arrows indicate cells 6 (third example in Fig. 2(a)) as well as cells 28 and 68, the same two as in (a).

3.5 The effect of probe geometry error

One source of modeling error is an error in the probe geometry; this is of practical importance since often the probe geometry is not known exactly and must be estimated. As the above analysis of the approximated-probe set (open bars; Fig. 10(a)) shows, this source of error is a significant contributor to the residual.

Figure 10(a) shows the distribution of the fractional MSE separately in the exact-probe dataset (N=43; dark bars) and the approximated-probe dataset (N=18; open bars); the two are stacked. The sets were defined in Section 2. To recap, for the exact-probe set, the tip geometry of the recording tetrode was scanned and used in the FEM model. For the approximated-probe set, this was not possible and, as the best guess approximation, we used the reconstructed geometry of the tetrode that represented the median contact separation (row 2, Table 1.) in our study. In the exact-probe set, MSE was, on average, 3% (range: 1% to 11%), but in the approximated-probe set the error blows up to more than double (mean 6%, range 1% to 30%), with the difference likely indicating the contributions by model errors in probe geometry.

The lower quality fits raise the possibility that model error in probe geometry could also result in a bias in dipole localization. To address this issue directly, we introduced probe geometry errors in a controlled fashion. For this analysis we selected neurons that were recorded with one of 3 tetrodes whose geometry was known (from SEM), and with which at least 10 neurons were recorded. For each cell, we compared the dipole fit obtained with a model based on the tetrode actually used (‘true data’), with the dipole fit obtained with a model based on one of the other reconstructed tetrodes (‘pseudo-data’). Since the “true-pseudo” sample pair of fitted parameters strongly correlated, the slope of their regression was extracted as their pseudo vs. true ratio. (There are 3 tetrodes, thus there are 3*2=6 possible distinct pseudo-data pairings of spike data collected with one tetrode and the geometry of another of the 3 tetrodes. Thus the number of distinct pseudo vs. true ratio comparisons is 6, one for each of the pseudo-data sets, even though there are only 3 unique true data sets.) Since the three tetrodes differed in mean contact separation, we could determine whether there was a systematic dependence of dipole parameters on this specific geometrical factor.

Figure 11(a) shows, as expected, that the pseudo-data always produced a larger fractional MSE than the true data. Figure 11(b and c) show that this error is, in fact, associated with a bias in the dipole fit. If the true probe separation is smaller than assumed (pseudo/probe ratio >1), the distance to the source is overestimated (Fig. 11(b)), as is the estimated dipole strength (Fig. 11(c)). These biases, and the observation that the bias in the estimated dipole strength is more severe, can be understood from an analysis of the nature of the EAP (see Section 4).

Fig. 11.

Determination of errors in dipole characterization attributable to errors in modeling probe geometry. To analyze the effects of geometry error in a controlled fashion, we compared localization calculations based on the tetrode actually used to record each dataset (“true data”), with parallel calculations carried out as if the recording tetrode was one of the other two measured tetrodes (“pseudo-data”). We then summarized this comparison for each pseudo-data vs. true-data pair by regressing values obtained for three parameters ((a): fractional MSE, (b): estimated cell-probe distance, (c): estimated dipole moment) from pseudo-data, against their values obtained from the true data. The three panels show how these regression slopes depend on the geometry error, as quantified by the ratio of contact separation for the pseudo-data tetrode vs. true-data tetrode. Unity ratio on the horizontal axis means no error in probe geometry; unity ratio on the vertical axis means no distortion in a dipole measure. The three tetrodes are the first three listed in Table 1, and their respective mean contact separation was 45 µm; 38 µm; and 29 µm. The dotted curves are the prediction of an idealized error analysis (see Section 4)

4 Discussion

The principal contribution of our study is the recognition that the dipole is an appropriate source model for localizing neurons from spatial samples of their extracellular action potentials, and the development and implementation of a method, combining lead field theory and Tikhonov regularization, to carry out dipole localization. To demonstrate the capabilities of the method, we applied it to recordings in visual cortex, obtained with a tetrode probe moved to multiple recording positions along a track.

Although dipole models are commonly used for source localization in EEG and related techniques (see, e.g., (Malmivuo and Plonsey 1995)), it is new to single neuron source characterization. While at first glance these problems might appear quite similar, there is a fundamental difference: in EEG source localization, the recording geometry is well within the far-field regime. That is, the recording electrodes are several cm from the source, and the current flow (within a sheet of cortical neurons) is over distances that are orders of magnitude smaller. Thus, the equivalent dipole model is a direct representation of the source. Here, the recording geometry is very different: the spatial extent of the current source is comparable to its distance to the recording electrode. This has implications both for the optimization procedure (the need for a robust regularization procedure), and the interpretation of the optimal dipole that it identifies. Specifically, even though the geometry is not within the far-field regime, the equivalent dipole accounts for the spatial dependence of the potential, and thereby provides an accurate estimate of the location of the source. These considerations favor the use of a dipole model over simpler alternatives, such as a monopole. Furthermore, current conservation requires that the true equivalent current monopole of the whole neuron is zero at all times. Thus, the monopole approximation, unlike any other multipole approximation, is expected to fail as the distance from the currents is increased.

In the following, we discuss the support, interpretation, and limitations of the dipole localization, the use of the lead fields, and the adaptability of the method to other multi-contact probes.

4.1 Support for the dipole source model

The basic objective of the inverse problem approach to neural source characterization is to obtain an accurate estimate of the cell location relative to the probe position. Because inverse problems are ill-posed, a model must be imposed—and different source models may fit the data equally well. For example, a monopole model can fit a locally sampled, moderately noisy, dipole field just as well as the correct dipole model (Supplement 2A). Thus a goodness-of-fit measure by itself is an insufficient guide to model selection. In contrast, localization accuracy is heavily dependent on model selection, because alternative models differ in their ability to accurately capture the spatial attenuation of extracellular potential (Supplement 2A). Thus, approximating this attenuation over the range of typical cell-probe separation becomes the critical issue in selecting a point multipole for the source model. As we review below, the available evidence favors the choice of a dipole source model for cell-probe separations that are larger than ≈30 to 50 µm.

A standard approach to the analysis of the potential due to a distributed source is the multipole expansion (e.g., (Milstein and Koch 2008)). For a multipole source, the potential, V, is related to the distance from the source via a power function, V ~ r^−k. The integer exponent is characteristic of the multipole: k = 1 for the monopole; k = 2 for the dipole; k = 3 for the quadrupole; etc.

However, the spatial attenuation of the extracellular potential of real neurons does not fit this simple picture but, rather, it accelerates with the distance from the cell. Nevertheless, it can be locally approximated by r^−k, provided that the exponent, k, increases gradually with r. Thus, even though a real neuronal source may be quite complex, a single-term multipolar expansion can provide a good approximation to its radial falloff, within a restricted range of distances.

With this approach in mind, we have re-analyzed several published studies (see Supplement 1). As summarized here, they support the dipole approximation within the distance range of interest. Evidence comes from two directions: modeling studies and experimental measurements. The modeling studies include analytic results of Pettersen and Einevoll (2008), simulations of simplified models of a soma plus a passive dendritic arbor (Rall 1962; Pettersen and Einevoll 2008), and simulations of models with realistic neuronal morphology and membrane properties (Moffitt and McIntyre 2005; Gold et al. 2006; Lee et al. 2007; Milstein and Koch 2008; Pettersen and Einevoll 2008). In all models, the extracellular potential is characterized by a dipolar falloff (~r⁻²) for a range (r₀≤ r ≤ 200 µm) of radial distances that covers most of the cell-probe distances typical in single unit recordings with extracellular probes. Within the immediate r < r₀ neighborhood of the soma, spatial attenuation is slower than predicted by a dipole and may or may not be well fit by a monopole model. The short-distance bound r₀ of the dipole regime varied from 20 to 50 µm, depending on cell size and membrane properties: r₀ was larger in models of pyramidal cells in cat layer 5 than in rodent CA1 (the first are 30–50% larger), and larger in models where dendrites were endowed with active membrane conductances (probably because this made the current sources more spread out).

Experimental evidence (also see Supplement 1) is only available from rodent hippocampus where the cells are small, but only for cell-probe distances greater than 50 µm, where it is consistent with the dipole approximation; it does not permit assessment of the radius r₀ below which the dipole approximation breaks down. These technically demanding studies consisted of simultaneously recording from neurons with an intracellular and an extracellular probe (Cohen and Miles 2000; Henze et al. 2000). Samples were small (N<25), and each cell only contributed to one or two distance points over a limited spatial range. Thus, while these data are demonstrably consistent with the dipolar approximation in the range (>50 µm), they cannot be used to distinguish among alternative forms for the radial dependence. (In rat hippocampus, the extracellular probe can get very near the cells— ≈ 20 µm (Buzsaki 2004)— where the dipole regime may not hold.)

4.2 The “local lobe” interpretation of the dipole source model

The equivalent dipoles identified by the above models for the short-to-intermediate cell-probe distances differ from the dipoles that characterize the far-field (r≫500 µm) potential. Since the apical dendrite defines the cell axis and it is a relatively large current source among dendrites, symmetry considerations predict that the in the far-field regime, the overall dipole of the cell must be aligned with the soma-apical dendrite axis of the pyramidal neuron. But within 200 µm from the soma, the probe is within (or close to) the dendritic arbor. Thus, it more heavily weighs the contributions from currents in local over distant dendrites (Gold et al. 2006), and the equivalent dipole at short-to-intermediate distances mostly reflects contributions from the soma and the largest basal segments of the dendritic arbor that are nearest to the probe.

In the companion paper (Mechler et al. 2011), we analyzed the moment vector of the equivalent dipole in a population of visual cortical neurons (the same as used here for the illustration of dipole characterization method applied to tetrode recordings) and reported that the moment vector of the equivalent dipole of isolated neurons tends to point toward the probe. This surprising result contrasts with the expectation from the standard “far-field” interpretation of the equivalent dipole (in which the moment vector is fixed in space by the morphology of the neuron, independent of the direction to the probe). However, this near-field dipole that rotates toward the probe makes sense, once we recognize that (1) the probe tends to pick up activity in the nearest lobe of the soma-dendritic arbor, and that (2) the dendritic arbor of most cortical cells tend to have an approximate and chunky radial symmetry (see e.g., Sholl (1953)). Then no matter what direction the probe approaches from, the nearest lobe of the arbor will be oriented from the soma toward the probe. These notions are best summarized by the “local lobe” interpretation of the near-field dipole.

The local lobe interpretation has quantitative support from cellular morphology. In terms of cellular geometry, the “local lobe” is understood to be a portion of the dendritic tree whose trunk is one of the primary dendrites anchored at the soma (including but not limited to the primary apical dendrite). The measured deviations of the moment vectors from the cell-probe axis are in good correspondence with the solid angle (≈50 deg cone) that is occupied by the average dendritic tree of a single primary dendrite (“the local lobe”) on the typical visual cortical neuron.

The local lobe interpretation has qualitative support from cellular biophysics. The current contributions of the local lobe are likely to be dominated by the soma compartment and the trunk or root segment of the primary dendrite. At peak AP time, large inward Na⁺–currents make the soma region of the neuron act as the dominant sink (−), and while all dendrites play the role of the (distributed) current source (+), only the potential contributions from the currents in the nearest large dendrites of the arbor are large enough to register at the probe. We can estimate the effective sink-source separation from elementary biophysical principles, using the notion of a length constant from cable theory. Pettersen and Einevoll (2008) analyzed the AC length constants for ball-and-stick model neurons. Assuming realistic soma diameter and stick lengths of a few hundred µm (basal dendrites of neurons in the cortex are about this long), they calculated a ≈ 50 µm length constant at 1 kHz (the temporal frequency characteristic of action potentials). There are two features of real neurons that will tend to make the effective sink-source separation on the local lobe shorter than this. First, the real dendrites are branching trees, not sticks, and currents flowing into the side branches accelerate the rate of current loss in the radial direction away from the soma, making the length constant genuinely shorter. Second, the dendritic arbor on a real neocortical neuron has many lobes, each corresponding to one primary dendrite, and because of symmetry considerations the superimposed fields of all the other lobes together act to weaken the field of the local lobe at hand. This makes the length constant of the effective or equivalent dipole of the local lobe to appear even shorter than it is. Thus we think that the characteristic spatial separation of the effective sink and source currents of the local lobe is short, at most a few multiples of 10 µm.

In summary, the recovered equivalent dipole is like a rotating elastic vector pinned at the cell body: it rotates towards the probe position, and it may stretch to indicate the size of the nearest dendritic currents, but its location will continue to approximate the soma independent of the probe position.

4.3 Localization error due to adopting the dipole as a source model

Simple computer simulations (Supplement 2B) indicate that the optimal dipole can well localize a model source whose radial potential attenuation follows the pattern identified by studies cited above. However, at sufficiently close distances to a neuronal source, the dipole regime breaks down: it overestimates the falloff rate of the potential and, as a result, overestimates the distance from the source.

The shape of the radial EAP falloff offers an account for this, and provides for a comparison of the errors incurred by dipole and monopole models. For a single-term multipole source model, the exponent of the model multipole (k_model = 1 for monopole, k_model = 2 for dipole) is the main factor in the localization error. The reason for this is that a probe array provides two robust quantities: the average potential V, and its local gradient V′. For a multipole model, potential falls off as V(r) = cr^−k, so r ≈ −kV/V′. Thus, the average localization error is determined by the ratio of exponents describing the true local EAP falloff and the one used in modeling it:

$$r_{\text{model}}/r_{\text{cell}}~k_{\text{model}}/k_{\text{cell}}.$$ (11)

This is also demonstrated in computer simulations of realistic spatial sampling of the EAP in Supplement 2A. As summarized above (see Supplement 1 for details), the true local EAP falloff exponent, k_cell, varies around 2 (1.5 ≤ k_cell ≤ 2.5) at the distances 50 µm ≤ r ≤ 200 µm typical for extracellular probes in neocortex. Accordingly the dipole model (k_model = 2) will keep localization error within ±25% for most cells, and will have, on average, very little bias. However, a monopole model (k_model =1) will systematically underestimate the same distances by 50%. Conversely, at very short cell-probe distances (r ≤ 30 µm) a monopole is likely the better approximation, and the dipole would lead to a systematic overestimation of distances by as much as 100%.

4.4 Localization error due to model error in probe geometry

The above analysis also allows one to understand how model errors in probe geometry affect localization error. Again we consider the regime in which the most reliable measurements provided by the probe are the average voltage, and its spatial gradient. Assume that the contact separation is modeled as Δs̃, but its true value is Δs. Since voltage gradient is determined by voltage difference divided by probe separation, the error in probe separation leads to a reciprocal error in the voltage gradient, Ṽ′ ≈ ΔV/Δs̃ ≈ V′(Δs/Δs̃), but there is no corresponding error in the estimate of the average voltage. As seen above, the estimated source distance is also inversely proportional to the estimated voltage gradient (r ≈ −kV/V′). Thus, an error in the estimate of probe separation is expected to produce a proportional bias in the estimated distance to the source: r̃ ≈ −kV/Ṽ′ ≈ rV′/Ṽ′, or, by substituting the above expression for the erroneous voltage gradient,

$$\tilde{r}/r=\mathrm{\Delta }\tilde{s}/\mathrm{\Delta }s.$$ (12)

Because the equivalent source is forced to account for the measured EAP amplitudes, V, the bias in the estimated equivalent source size is expected to be the same fraction raised to the k-th power:

$$\parallel \tilde{\mathbf{p}}\parallel /\parallel \mathbf{p}\parallel ={(\mathrm{\Delta }\tilde{s}/\mathrm{\Delta }s)}^k.$$ (13)

Because k>1, the error is larger in the source size than its distance. As seen in Fig. 11, the empirical analysis of probe model error is qualitatively consistent with this analysis. The bias in estimated distance (Fig. 11(b)) is somewhat less than the prediction of strict proportionality most likely because there is, additionally, a contribution of errors in the measured data. The bias in estimated source size (Fig. 11(c)) is larger than the bias in estimated distance, in keeping with a dipolar (k=2) model. This analysis of geometry error is relevant to twisted wire tetrodes, since their tips can flay (Jog et al. 2002). As a result, model-based localization methods that use the nominal (i.e., smaller than true) contact separation would underestimate the distance of cells and their equivalent source size.

4.5 Localization error due to error in volume conductor model

In this subsection, we consider the 4 non-essential assumptions (resistivity, isotropy homogeneity, frequency-independence) of the volume conductor model of gray matter that are known to be violated by the biophysics of cortical tissue to some degree. (We do not review quasistationarity linearity, and the symmetry of material tensors; these are fundamentally well-grounded approximations of the biophysics and required by the lead field approach of our method).

By far the largest error is in neglecting the capacitive effect and it is still very small (Plonsey and Heppner 1967): from the measured spectra of gray matter conductivity and permittivity (Gabriel et al. 1996), we estimate that the ratio of capacitive over ohmic contributions to impedance is near constant (frequency-independent) and small (≤10%) in the entire frequency band (300-to-6,000 Hz) of EAP’s, and the related voltage-current phase shift is ≤0.1 rad. (This is in contrast to the low-frequency band (10–100 Hz) relevant for LFPs, in which, the same data (Gabriel et al. 1996) shows, permittivity is non-negligible and its ratio to conductivity (0.2-to-0.9) is strongly frequency-dependent.

We further assumed that the volume conductor is (1) isotropic and (2) homogeneous. Both assumptions are expected to hold as first approximation on the spatial scale of the cell body of neurons (~10 um), especially within the same cortical layer. At the core of these assumptions is the observation that the more conductive, interstitial, space of the neuropil has a richly interconnected structure on an order of magnitude smaller scale that permits local averaging (Robinson 1968). Their validity on larger spatial scales in gray matter rests on direct biophysical measurements in studies that sought for physiologically realistic tissue parameters to be used in current source density analysis of evoked potentials and EEG data (for a review, see e.g., Mitzdorf (1985)).

If homogeneity holds, the key model parameter is the value of the scalar conductivity. This parameter may not be known precisely, but errors in its value do not influence localization accuracy. This is because scalar conductivity is fully absorbed by the estimated dipole moment size: it scales in proportion with conductivity (‖p‖~σ). (See also Eqs. (1c, 4, and 7a,b)) Thus, an error in the conductivity leads to a proportional error in the size of the estimated moment, but no error in its estimated position. The conductivity we used (σ_GM=0.45 S/m) was 30–50% higher than in some other studies (e.g., Moffitt and McIntyre (2005) and Gold et al. (2006)), but we also note that the passage of an electrode may result in local edema that elevates conductivity in the electrode’s vicinity.

Strict homogeneity, though, is only an approximation: laminar changes in density of cell bodies and processes and extracellular ion concentrations lead to changes in tissue conductivity by as much as a factor of 2 (Lopez-Aguado et al. 2001). This distorts cell localization and apparent source size not unlike the optical distortion of objects by refraction at a liquid-air boundary. Specifically, a step change in the tissue conductivity alters not only the potential but also its gradient near the domain boundary (Moffitt and McIntyre 2005), resulting in a bias in the cell position inferred from models that assume homogeneity. While the lead field calculation and regularization methods used here immediately extend to models that include laminar variations in conductivity, the bias is likely negligible except in the vicinity of large conductivity jumps.

4.6 The use of lead fields

Lead fields play a central role in our approach and are very helpful in understanding probe performance at a conceptual level. They were originally developed for EKG design, but because of their conceptual importance they have been adopted to diverse applications in neurophysiological investigation. They facilitate the analysis and design of probe sensitivity in single unit recording both for tetrodes (as done in this study) and multi-contact probes (see below), or in chronic neural prosthetics (Mitzdorf 1985). They are similarly helpful in studying the activation fields of stimulating electrodes used in deep brain stimulation (McIntyre et al. 2004; Wei and Grill 2005; Butson and McIntyre 2006).

Lead fields of a recording probe, in particular, are useful because they can summarize contact sensitivity to all possible source positions with the accuracy of the details of the modeled geometry. Analytic approaches to source localization ignore the probe geometry and thus are unable to capture field distortions around the probe, which can be quite large and hard to intuit (see, e.g., the eccentric lead fields of the Thomas tetrode in Fig. 8; similar effects were shown for contacts on a silicon polytrode by Moffitt and McIntyre (2005)). Because of these field distortions, the sensitivity of contacts of the probe can be very different to a source lying in a given direction and distance from the probe.

Lead field analysis helps determine the recording volume of a probe. This holds both for single electrodes and multi-contact probes, but there is an important distinction rooted in the way that these probes isolate neurons. What is common to both scenarios is that at a given signal level, the lead fields of an individual contact on the multi-contact probe and a sharp single electrode are very similar in size (Figs. 5 and 6). Furthermore, the size is largely independent of tip shape and, consistent with the results of Moffitt and McIntyre (2005), of contact area beyond a very short distance from the contact (a distance commensurate with the characteristic length of the contact). (Tip shape and contact area matter for other electrode properties: the first determines the mechanics of penetration and the ability of the probe to get close to cells; the second determines electrode noise via input impedance). However, despite the comparable lead field size, the recording radius of sharp single electrodes is thought to be smaller than of most tetrodes (e.g., ≈50 µm for single electrode in cat sensorimotor cortex (Rosenthal et al. 1966) versus ≈ 70 µm for wire tetrodes in cat visual cortex (Gray et al. 1995)). This is likely because the single electrode has to be moved closer to the source to achieve high S/N that is demanded by reliable single unit isolation on a single channel.

The shape and size of the recording volume of a multi-contact probe as a whole depends on the relationship between the lead fields. Taking advantage of the signal variation across different contacts, the multi-contact probe achieves single unit isolation at lower signal levels and thus in a larger recording volume than single electrodes. To a first approximation, the recording volume of multi-contact probes is the union of the recording volume of each contact. However, synergy between leads may refine this overall volume. For example, the recording radius measured for the same tetrodes (from the same data) as used here (Mechler et al. 2011) could be more closely approximated by the radius of individual lead fields (as defined above, for the isolation threshold) than the larger radius of the union of lead fields.

4.7 Applicability to other multisite recording techniques

As is apparent from the discussion above, our approach to dipole localization is readily applicability to multi-contact arrays, including silicon blades. The extensive translational or rotational symmetries of the contact array on these large probes can be greatly exploited in lead field calculations. Because of this, and because the regularization technique does not depend on the specifics of the probe geometry dipole localization procedure is applicable.

These probes have a number of advantages over tetrodes that can help improve spatial localization of neurons. Here we highlight these probe features; owing to ongoing technological innovation, the list will doubtless grow in the future.

One advantage is spatial: a sufficiently long stationary blade can sample an entire cortical minicolumn without the need to move the probe (Csicsvari et al. 2003; Blanche et al. 2005). Furthermore, with these probes the accuracy of cell isolation (“spike clustering”) may improve (Blanche et al. 2005) as the number of spatial EAP samples increases, which can be achieved even if contact density is not as high as on tetrodes—because spike-triggered averaging driven by large spikes helps uncover small signals. To support dipole characterization, the critical requirement is that contact spacing should be sufficiently dense to allow for at least 6 but preferably many more EAP samples from the typical target neuron. Typical polytrodes currently in use appear to be just short of achieving a sufficient density. For example, on a probe on which contacts were 50 µm apart in a 3-column rectangular layout, discriminable spikes were recorded by fewer than 6 contacts in half of the single neurons in cat visual cortex (Blanche et al. 2005). This suggests that even a modest increase in probe density will substantially benefit source localization. This is readily achievable: contact separation on some more recently developed silicon polytrodes is already approaching ≈ 20 µm (Henze et al. 2000; Bartho et al. 2004; Buzsaki 2004; Du et al. 2009) that formerly only tetrodes could reach.

It is important for source localization that the temporal correspondence of the spatial EAP samples is correct. From this perspective, multi-contact probes have the additional benefit that they yield automatically correct temporal alignment of the spatial sample. The correct temporal alignment of course extends to all waveforms of the same source, including the small signals uncovered by spike-triggered averaging. Since these small samples have a potentially large spatial span, including them all for source localization does not immediately translate to improved localization. This is because a spatially extensive sample would likely include significant contributions from a correspondingly larger domain of the distributed source of the neuron, more than just a local lobe of the arbor. To accurately capture this would likely require a source model more complex than the simple dipole.