Image Similarity and Tissue Overlaps as Surrogates for Image Registration Accuracy: Widely Used but Unreliable

Abstract

The accuracy of nonrigid image registrations is commonly approximated using surrogate measures such as tissue label overlap scores, image similarity, image difference, or transformation inverse consistency error. This paper provides experimental evidence that these measures, even when used in combination, cannot distinguish accurate from inaccurate registrations. To this end, we introduce a “registration” algorithm that generates highly inaccurate image transformations, yet performs extremely well in terms of the surrogate measures. Of the tested criteria, only overlap scores of localized anatomical regions reliably distinguish reasonable from inaccurate registrations, whereas image similarity and tissue overlap do not. We conclude that tissue overlap and image similarity, whether used alone or together, do not provide valid evidence for accurate registrations and should thus not be reported or accepted as such.

I. Introduction

Quantifying the accuracy of nonrigid image registration is inherently difficult. Whereas a satisfactory gold standard database for evaluating the accuracy of rigid inter-modality registration of head images has been available for over a decade [1], no such gold standard yet exists for nonrigid registration (see Murphy et al. [2] for an overview of the current state-of-the-art of validating nonrigid registration). Rigid registration accuracy is comparatively easy to quantify because the rigid registration error at any given point is completely determined by errors at three non-collinear landmarks [3].

By contrast, nonrigid registration error can be quantified with certainty only at the available landmarks and with increasing uncertainty as distance from these landmarks increases. A very dense set of landmarks, which is generally not available, would thus be required to gain a complete, global understanding of registration accuracy. For inter-subject registration in particular, not all landmarks identifiable in one subject, such as branching points of cortical sulci, may even exist in another subject, even when both are normal controls.

Surrogate measures of registration accuracy are, therefore, commonly used when comparing different registration algorithms. A selection of such surrogates have recently been made available in a software package, the Nonrigid Image Registration Evaluation Program (NIREP), which evaluates inter-subject, single-modality nonrigid registrations of magnetic resonance (MR) brain images using region-of-interest overlap, intensity variance, inverse consistency error, and transitivity error [4].

The purpose of this paper is to demonstrate experimentally that several popular surrogate measures, including a subset of the measures provided by NIREP, are only weakly related to registration accuracy. We achieve this by designing a completely inaccurate “registration” algorithm, which nonetheless appears to “outperform” state-of-the-art nonrigid registration techniques when evaluated in terms of tissue overlap, image similarity, and inverse consistency error. Of the tested criteria, only overlap of sufficiently small and localized labeled regions survives as a reliable discriminator between good and bad registrations.

The timeliness and relevance of our study is underscored by 19 papers published in the last ten years in premier peer-reviewed international journals (Table I) or presented at major peer-reviewed international conferences (Table II). Each of these publications quantifies or compares accuracy of image registration based exclusively on image similarities or brain tissues overlaps, both surrogate measures that we demonstrate herein to be unreliable and thus insufficient.

TABLE I.

Peer-reviewed journal articles depending on unreliable surrogates

No. Publication		Summary of Problematic Methodology
1	R. W. So, T. W. Tang, and A. C. Chung, “Non-rigid image registration of brain magnetic resonance images using graph-cuts,” Pattern Recognition, vol. 44, no. 10–11, pp. 2081–2092, 2011.	Claims “consistently higher registration accuracy” of proposed method based on tissue overlap scores, despite recovering known deformations.
2	S. Liao and A.C.S. Chung, “Feature based nonrigid brain MR image registration with symmetric alpha stable filters,” IEEE Transactions on Medical Imaging, vol. 29, no. 1, pp. 106–119, 2010.	Uses tissue overlap scores to compare new vs. existing registration algorithms.
3	A.M. Siddiqui, A. Masood, and M. Saleem, “A locally constrained radial basis function for registration and warping of images,” Pattern Recognition Letters, vol. 30, no. 4, pp. 377–390, 2009.	Compares transformation models using post-registration values of CC, MSD, and MI similarity measures.
4	H. Nam, R.A. Renaut, K. Chen, H. Guo, and G.E. Farin, “Improved inter-modality image registration using normalized mutual information with coarse-binned histograms,” Communications in Numerical Methods in Engineering, vol. 25, no. 6, pp. 583–595, 2009.	Applies known deformations, but then only uses intensity L2 error for comparison of registration results.
5	J. Larrey-Ruiz, R. Verdú-Monedero, and J. Morales-Sánchez, “A fourier domain framework for variational image registration,” Journal of Mathematical Imaging and Vision, vol. 32, no. 1, pp. 57–72, 2008.	Applies known deformations, but then only uses intensity PSNR, MI, and CR for comparison of registration results.
6	P. Zhilkin, M.E. Alexander, and J. Sun, “Nonlinear registration using variational principle for mutual information,” Pattern Recognition, vol. 41, no. 8, pp. 2493–2502, 2008.	Uses MSD and MI and measures of registration accuracy.
7	C. Frohn-Schauf, S. Henn, and K. Witsch, “Multigrid based total variation image registration,” Computing and Visualization in Science, vol. 11, no. 2, pp. 101–113, 2008.	Compares registration methods based on post-registration L2 image differences.
8	D.C. Paquin, D. Levy, and L. Xing, “Multiscale deformable registration of noisy medical images,” Mathematical Biosciences and Engineering, vol. 5, no. 1, pp. 125–144, 2008.	Uses post-registration correlation coefficient to “demonstrate the accuracy” of the proposed registration method.
9	D.C. Paquin, D. Levy, and L. Xing, “Hybrid landmark and multiscale deformable registration,” Mathematical Biosciences and Engineering, vol. 4, no. 4, pp. 711–737, 2007.	Uses difference images, CC and MSD to demonstrate registration “accuracy,” even though in one example 20 landmarks are used to drive the registration.
10	S. Tang and T. Jiang, “Nonrigid registration of medical image by linear singular blending techniques,” Pattern Recognition Letters, vol. 25, no. 4, pp. 399–405, 2004.	Uses post-registration SSD and MI to “evaluate […] accuracy” of proposed registration method against others.
11	B.C. Vemuri, J. Ye, Y. Chen, and C.M. Leonard, “Image registration via level-set motion: Applications to atlas-based segmentation,” Medical Image Analysis, vol. 7, no. 1, pp. 1–20, 2003.	Shows “difference image between evolved/transformed source image and the target image as a qualitative measure of the accuracy of the registration algorithm”; also uses CC to compare with other registration methods.

PSNR = Peak Signal to Noise Ratio; CR = Correlation Ratio; CC = Correlation Coefficient; SSD = Sum of Squared Differences; MI = Mutual Information

TABLE II.

Peer-reviewed conference articles depending on unreliable surrogates

No. Publication		Summary of Problematic Methodology
1	S. Liao and A.C.S. Chung, “Non-rigid image registration with uniform gradient spherical patterns,” in Medical Image Computing and Computer-Assisted Intervention, 12th International Conference, MICCAI 2009, vol. 5761 of Lecture Notes in Computer Science, pp. 696–704, Springer-Verlag, Berlin/Heidelberg.	Claims “proposed method gives the highest registration accuracy” based on tissue overlap scores.
2	M.R. Sabuncu, B.T.T. Yeo, K. Van Leemput, T. Vercauteren, and P. Golland, “Asymmetric image-template registration,” in Medical Image Computing and Computer-Assisted Intervention, 12th International Conference, MICCAI 2009, Proceedings, Part I, vol. 5761 of Lecture Notes in Computer Science, pp. 565–573, Springer-Verlag, Berlin/Heidelberg.	Compares registration algorithms to “quantify the quality of alignment” based on image MSD and tissue Dice overlap scores.
3	T. Rohlfing, E.V. Sullivan, and A. Pfefferbaum, “Subject-matched templates for spatial normalization,” in Medical Image Computing and Computer-Assisted Intervention, 12th International Conference, MICCAI 2009, Proceedings, Part II, 2009, vol. 5762 of Lecture Notes in Computer Science, pp. 224–231, Springer-Verlag, Berlin/Heidelberg.	Uses tissue overlap scores to show more accurate spatial normalization to different atlases.
4	S. Liao and A.C.S. Chung, “Non-rigid image registration with uniform spherical structure patterns,” in Information Processing in Medical Imaging, 21st International Conference, IPMI 2009, Proceedings, vol. 5636 of Lecture Notes in Computer Science, pp. 163–175, Springer-Verlag, Berlin/Heidelberg.	Claims “proposed method achieves the highest registration accuracy” based on brain tissue overlap scores.
5	H. Li, Y. Lin, and A. Wang, “An medical image registration approach using improved Hausdorff distance combined with particle swarm optimization,” in Proceedings, IEEE Computer Society Fourth International Conference on Natural Computation, IEEE ICNC 2008, pp. 428–432.	Claims that “proposed algorithm produces more accurate results” by comparing post-registration CC, MSD, and PSNR.
6	T.W.H. Tang and A.C.S. Chung, “Non-rigid image registration using graph-cuts,” in Medical Image Computing and Computer-Assisted Intervention, MICCAI 2007, Proceedings, Part I, vol. 4791 of Lecture Notes in Computer Science, pp. 916–924, Springer-Verlag, Berlin/Heidelberg.	Claims “accuracy of our approach significantly better than other methods” base on absolute image difference and brain tissue overlap scores.
7	T. Chen, T.S. Huang, W. Yin, and X.S. Zhou, “A new coarse-to-fine framework for 3D brain MR image registration,” in Proceedings, First International Workshop on Computer Vision for Biomedical Image Applications, CVBIA 2005, vol. 3765 of Lecture Notes in Computer Science, pp. 114–124, Springer-Verlag, Berlin/Heidelberg.	Claims that “a method can be affirmed as relatively more accurate than others if it consistently obtains higher similarity values” and uses image CC and CR to this effect.
8	Z.-Y. Long, L. Yao, and D.-L. Peng, “Fast non-linear elastic registration in 2d medical image,” in Medical Image Computing and Computer-Assisted Intervention - MICCAI 2004. Proceedings, Part I, vol. 3216 of Lecture Notes in Computer Science, pp. 647–654, Springer-Verlag, Berlin/Heidelberg.	Compares “performance” of different filters for elastic registration via image MSD.

PSNR = Peak Signal to Noise Ratio; CR = Correlation Ratio; CC = Correlation Coefficient; SSD = Sum of Squared Differences

Our work shows in particular the ease with which one can disguise a misconceived registration algorithm as a valuable contribution by selective reporting of unsuitable evaluation criteria. Specifically, we demonstrate that overlap of tissue classes and image similarity cannot be used in isolation for determining the feasibility of a registration strategy. We therefore establish, once and for all, that these must be supplemented with measures more reliably related to misregistration to form a valid set of evaluation criteria.

II. Methods

A. Test Data

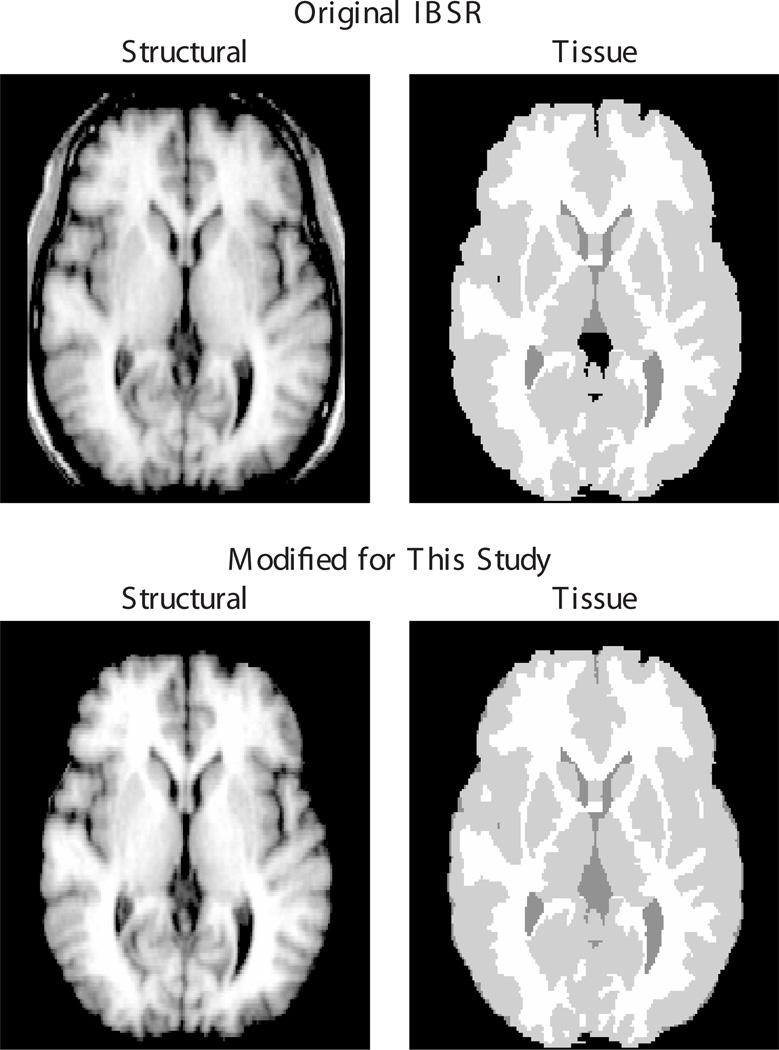
Our experiments used 18 modified T₁-weighted MR images publicly available from the Internet Brain Segmentation Repository (IBSR) [5]. These images are provided with manual expert segmentations of gray matter (GM), white matter (WM), and some cerebrospinal fluid (CSF), as well as labelings of 43 anatomical structures. For our study, we modified these data as follows (examples of original vs. modified images are shown in Fig. 1).

Fig. 1.

Original (top row) and modified (bottom row) image data of the IBSR_01 subject. In the modified data, non-brain tissue was removed from the structural images to facilitate inter-subject registration, and missing CSF labels (note, for example, the third ventricle) were added to previously unlabeled regions inside the brain masks.

First, non-brain regions were removed from all structural images, which were provided without faces but not fully skull stripped. Removing non-brain tissue prior to registration is generally accepted as a means of simplifying the inter-subject registration problem and thus increasing the quality of the computed registrations [6, 7].

Second, all pixels within the identified brain mask that were not assigned to one of the three “tissue” types were assigned to CSF, because the provided segmentations are complete only for GM and WM but leave most CSF pixels unlabeled. Filling in missing CSF pixels allows us to perform a more complete and consistent evaluation of tissue overlaps after registration.

B. A Deceptive Registration Algorithm

We describe in this section an algorithm that computes a coordinate transformation between two images, which “pretends” to be a co-registration and is designed to perform well on certain surrogate measures of registration performance, but completely disregards any actual mapping of corresponding anatomical points. We have implemented this algorithm in the aptly named “Completely Useless Registration Tool” (CURT), which is publicly available in source code as part of the Computational Morphometry Toolkit (CMTK) [8].

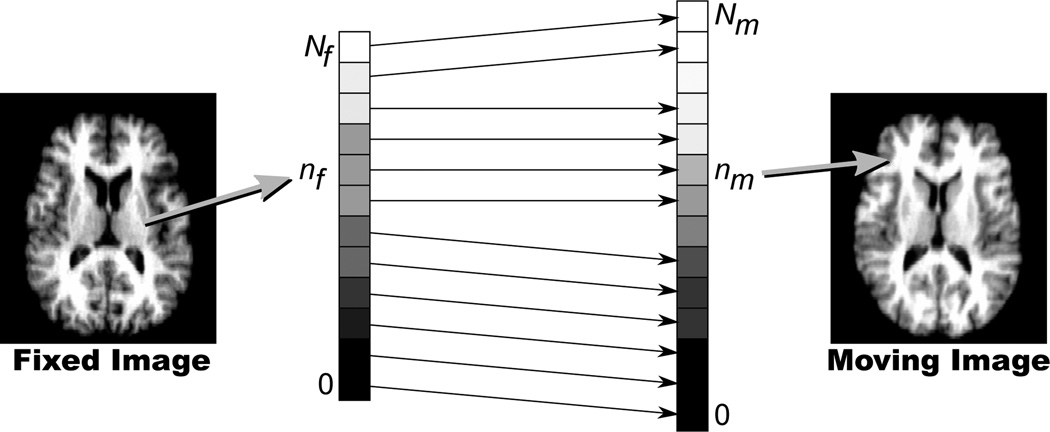
The algorithm is simple: to compute the transformation from a fixed image to a moving image, the N_f pixels in the fixed image and the N_m pixels in the moving image are independently sorted by increasing intensity values. The n_f-th pixel (as counted by increasing intensity) in the fixed image then maps to the n_m-th pixel in the moving image, which is computed as follows:

$$n_m=\lfloor N_m\frac{n_f}{N_f}\rfloor$$ (1)

This is also illustrated in Fig. 2. One way to interpret the algorithm is as a geometrically unconstrained, closed-form optimization of the rank correlation criterion recently proposed by Birkfellner et al. [9] to perform rigid 2D/3D image registration.

Fig. 2.

Schematic illustration of rank order-based mapping of a pixel from the fixed image (left) to the moving image (right) via correspondence of pixels sorted by increasing intensities. See text for details and notation.

C. Comparison Methods: SyN and FFD Registration

For comparison, two established nonrigid registration algorithms are used. Both are readily available in source code, which should allow interested readers to replicate our experiments and confirm our results. The algorithms are:

1. the symmetric diffeomorphic normalization method (“SyN”) by Avants et al. [10] as implemented in Release 1.9.1 of the ANTs software package [11], and

2. our own implementation [12] (available as part of CMTK [8]) of Rueckert’s free-form deformation (FFD) registration algorithm [13] based on a cubic B-spline transformation model.

Besides being freely available, the two comparison algorithms were chosen because both the SyN algorithm and Rueckert’s own implementation of the FFD registration (IRTK) [14] were consistently among the top performers (with SyN considered one of the two overall “winners”) in a comprehensive recent comparison study [7]. They can, therefore, be considered the current state of the art in nonrigid registration. For each algorithm we used generic parameter settings recommended by the software authors for inter-subject MR brain image registration, i.e., the parameters were not specifically optimized for the particular set of images to be registered.

It is common practice to perform an affine pre-registration stage before nonrigid registration to eliminate differences in image pose, orientation, and scale. For SyN, we used the built-in affine registration, which is based on multi-resolution optimization of mutual information [15, 16]. For the FFD algorithm, we used CMTK’s affine registration tool based on multi-resolution optimization [17] of normalized mutual information [18]. For the CMTK affine registrations in particular, we report below the same overlap and similarity measures as for the other three methods to serve as a reference baseline.

D. Experimental Setup

We performed a round-robin, leave-one-out evaluation protocol, in which the anatomical MR image of each of the 18 IBSR cases is registered to the anatomical image of each of the remaining 17 cases (registrations are directed, i.e., registration of A to B is different from registration of B to A). This is repeated for each registration algorithm, resulting in 306 registrations per algorithm, each aligning a different pair of images from two different subjects.

For every computed registration, the moving anatomical image was reformatted into the space of the fixed image, as were the moving tissue segmentation and region label images. Each reformatted anatomical moving image was then compared with the fixed anatomical image using three different similarity measures (see Section III-A). The reformatted tissue and region label images were also compared to their respective fixed images, which serve as the gold standard for the respective labelings, using a volume overlap measure (see Sections III-B and III-C). Finally, for each image pair and each registration algorithm the inverse consistency error in millimeters between forward and backward transformations was also computed (see Sections III-D).

III. Results

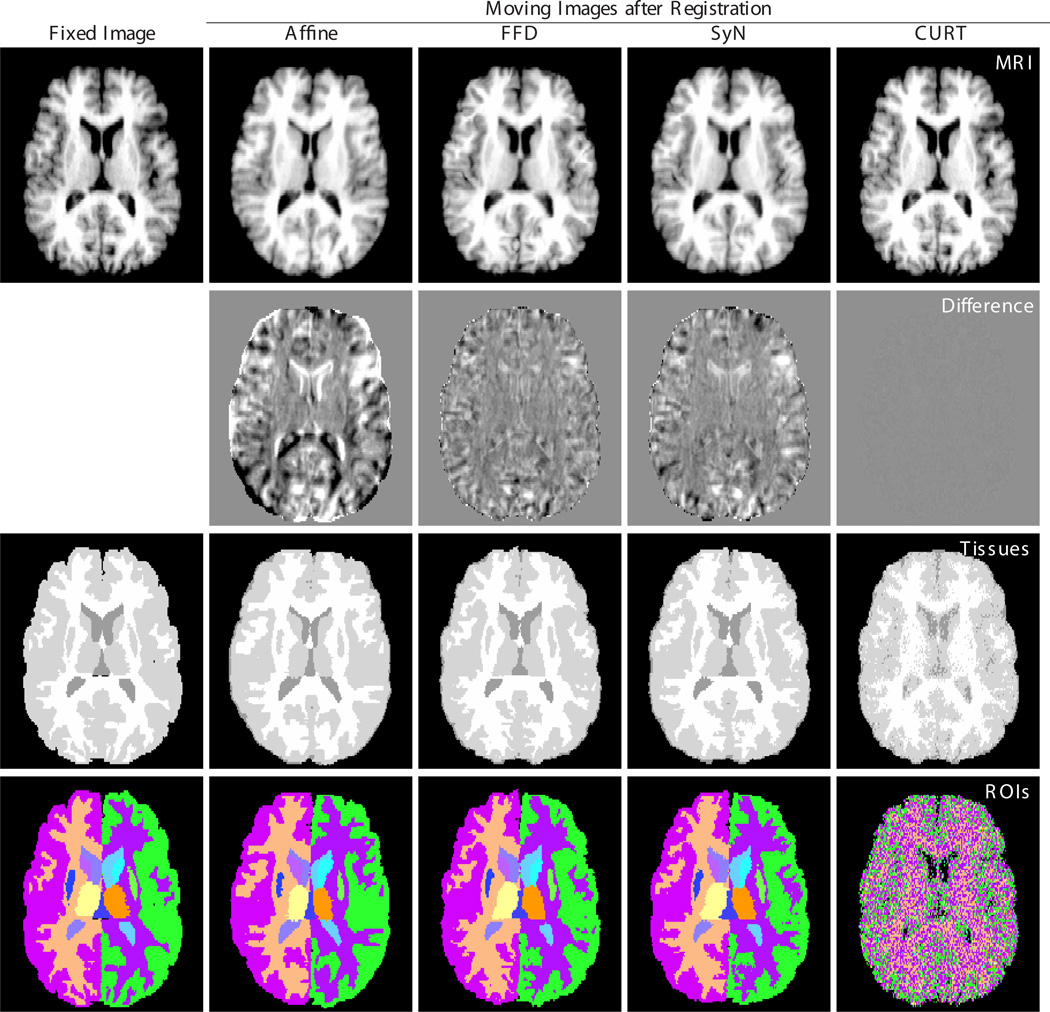
Examples of co-registered and reformatted images are shown in Fig. 3. Three observations are visually obvious:

1. The anatomical image reformatted using the CURT transformation is virtually indistinguishable from the the fixed image. This observation is particularly relevant because it suggests that even expert visual inspection of reformatted or subtraction images would not be able to detect CURT’s entirely inappropriate transformations.

2. The tissue image reformatted using CURT shows readily discernible errors throughout the brain, but note that for the other registration algorithms errors are localized along tissue boundaries, where they are hard to detect visually.

3. The region label image reformatted using CURT is essentially random and shows no resemblance to the gold standard label map of the fixed image.

The following subsections put each of these observations into a quantitative context.

Fig. 3.

Reformatted images after registration of one image pair (IBSR_01 to IBSR_02) using different registration algorithms. Columns from left to right: Fixed image (IBSR_01), and moving image (IBSR_02) after affine, FFD, SyN, and CURT registration. Rows from top to bottom: structural MR image, difference images (all with identical window/level settings), three-compartment tissue segmentation, and region labels provided by the IBSR.

A. Image Similarity Measures

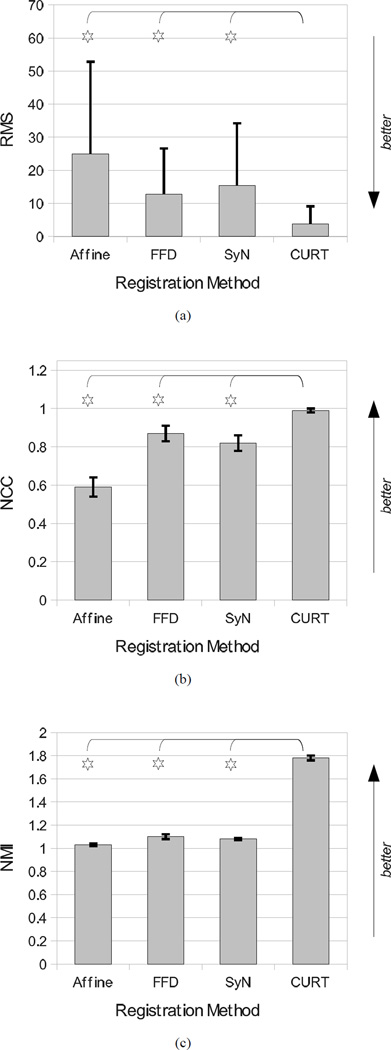
Shown in Table III are the post-registration values of three image-based similarity measures that are also commonly used to evaluate image registrations: Root of Mean Squares (RMS), Normalized Cross Correlation (NCC), and Normalized Mutual Information (NMI). These values quantify the residual image difference (RMS) or final image similarity (NCC; NMI), respectively, between the fixed and the reformatted moving anatomical images. CURT scored significantly better on all three similarity measures, which confirms the qualitative observation in Fig. 3 that it produced a reformatted image that is nearly identical to the reference image.

TABLE III.

Image-based similarity measures after registration

Similarity Measure	Affine	FFD	SyN	CURT
RMS*	24.9 ± 27.9†	12.7 ± 13.9†	15.4 ± 18.8†	3.8 ± 5.1
NCC	0.59 ± 0.05†	0.87 ± 0.04†	0.82 ± 0.04†	0.99 ± 0.01
NMI	1.03 ± 0.01†	1.10 ± 0.02†	1.08 ± 0.01†	1.78 ± 0.02

Values are mean ± standard deviation for Root of Mean Squares (RMS), Normalized Cross Correlation (NCC), and Normalized Mutual Information (NMI) after registration over all 306 pairwise, directed registrations of the 18 IBSR images to one another. Smaller values are better for RMS, larger values are better for NCC and NMI.

^†marks results significantly different from those obtained by CURT (p < 10⁻⁷ or smaller; two-sided paired t-tests).

^*Due to different intensity ranges among the original IBSR images, RMS values were computed from images that were globally normalized to identical intensity means and standard deviations.

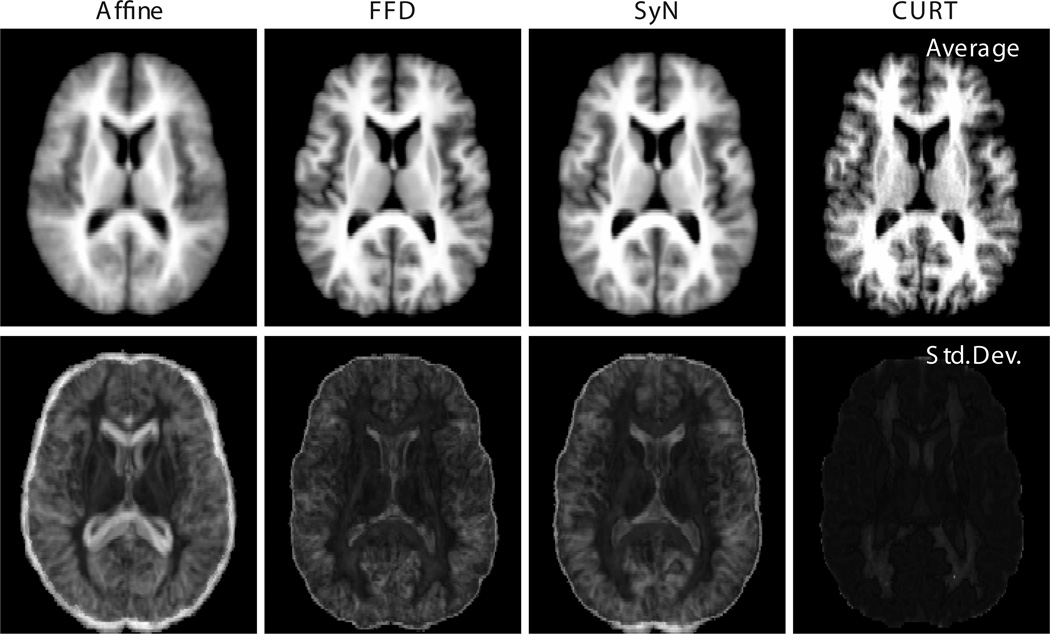
These observations apply equally when an entire group of co-registered images is considered, rather than just a single image pair. To this end, Fig. 4 shows the pixel-wise average and standard deviation images of reformatted images IBSR_02 through IBSR_18, all registered to IBSR_01. The “sharpness” of the average image and the magnitude of the standard deviation image are somewhat popular measures for the performance of groupwise registration algorithms (e.g., [19]). Again, CURT seemingly outperforms the other registration algorithms in that it produces a more crisp average and appreciably lower across-image standard deviation.

Fig. 4.

Groupwise average (top row) and standard deviation (bottom row) images of IBSR_02 through IBSR_18 after registration to IBSR_01 using each of the four registration algorithms. To obtain consistent intensity ranges, the pixel intensity values in each reformatted image were globally rescaled to match mean and standard deviation of the reference image intensities. All average images, as well as all standard deviation images, are shown using identical gray scales.

B. Tissue Overlap Measures

We report overlap scores of tissue labels (and, below, region labels) expressed as the Jaccard index, which for two sets of pixels, A and B, is defined as

$$J_{A,B}=\frac{|A\cap B|}{|A\cup B|}$$ (2)

Perfect overlap of A and B scores J_A,B = 1, no overlap at all scores J_A,B = 0.

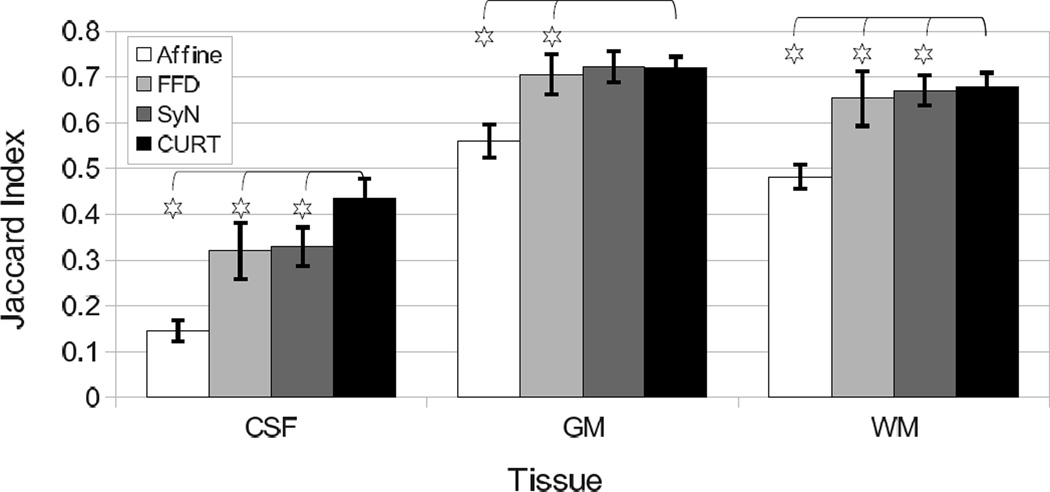
Table IV summarizes the overlap scores of three tissue types (GM, WM, CSF) for the four registration algorithms. CURT scored significantly higher than all other algorithms on all tissue types except SyN on GM (no significant difference, p > 0.73; two-sided paired t-test).

TABLE IV.

Tissue class overlaps after registration

Tissue	Affine	FFD	SyN	CURT
CSF	0.145 ± 0.023†	0.320 ± 0.061†	0.329 ± 0.042†	0.435 ± 0.043
GM	0.559 ± 0.036†	0.705 ± 0.044†	0.722 ± 0.034	0.721 ± 0.023
WM	0.482 ± 0.027†	0.653 ± 0.060†	0.670 ± 0.033†	0.678 ± 0.031

Values are mean ± standard deviation of Jaccard index, J, for each tissue between reference and co-registered moving images over all 306 pairwise, directed registrations of the 18 IBSR images to one another.

^†marks results significantly different from those obtained by CURT (p < 10⁻⁶; two-sided paired t-tests).

It is worth noting that between the two “real” nonrigid registration algorithms, SyN performed better than FFD in terms of tissue overlap scores (Table IV), whereas FFD performed better than SyN in terms of image similarity (Table III). See the Section IV-C for discussion of a possible explanation of this inconsistency and its implications for registration evaluation criteria.

The Dice coefficient [20] of volume overlap, which is also frequently reported [21], can be readily obtained from the Jaccard index via D = 2J/(1 + J) (see[22]); thus the relative comparison between the different methods remains unaffected when representing these results as Dice coefficients.

C. Region Overlap Measures

The overlap scores for labeled anatomical regions achieved by the four different registrations are summarized in Table V. Only labels are listed that appear in all 18 IBSR images, and these labels are listed in their entirety, because only a complete list of regions can provide assurance that the results are not subject to selection bias towards a particular desired outcome. Analogous to tissue labels, overlaps are reported as Jaccard index values.

TABLE V.

Region label overlaps after registration

Region	Affine	FFD	SyN	CURT
leftCerebralWhiteMatter	0.47 ± 0.03	0.65 ± 0.06	0.66 ± 0.04	0.23 ± 0.01
leftCerebralCortex	0.52 ± 0.04	0.68 ± 0.05	0.69 ± 0.04	0.22 ± 0.01
leftLateralVentricle	0.38 ± 0.11	0.68 ± 0.13	0.70 ± 0.10	0.02 ± 0.01
leftInferiorLateralVentricle	0.06 ± 0.05	0.15 ± 0.08	0.19 ± 0.01	0.00 ± 0.00
leftCerebellumWhiteMatter	0.48 ± 0.05	0.57 ± 0.12	0.67 ± 0.04	0.01 ± 0.01
leftCerebellumCortex	0.60 ± 0.06	0.75 ± 0.06	0.79 ± 0.04	0.03 ± 0.01
leftThalamus	0.66 ± 0.07	0.73 ± 0.05	0.76 ± 0.04	0.01 ± 0.00
leftCaudate	0.48 ± 0.10	0.62 ± 0.09	0.65 ± 0.09	0.00 ± 0.00
leftPutamen	0.57 ± 0.09	0.69 ± 0.06	0.74 ± 0.03	0.01 ± 0.00
leftPallidum	0.47 ± 0.10	0.53 ± 0.10	0.61 ± 0.05	0.00 ± 0.00
leftHippocampus	0.40 ± 0.09	0.55 ± 0.07	0.58 ± 0.06	0.00 ± 0.00
leftAmygdala	0.37 ± 0.12	0.46 ± 0.10	0.50 ± 0.08	0.00 ± 0.00
leftAccumbens	0.31 ± 0.13	0.42 ± 0.13	0.49 ± 0.08	0.00 ± 0.00
leftVentralDC	0.53 ± 0.08	0.61 ± 0.06	0.64 ± 0.05	0.00 ± 0.00
rightCerebralWhiteMatter	0.47 ± 0.03	0.65 ± 0.06	0.66 ± 0.04	0.23 ± 0.01
rightCerebralCortex	0.52 ± 0.04	0.67 ± 0.05	0.69 ± 0.04	0.22 ± 0.01
rightLateralVentricle	0.36 ± 0.11	0.66 ± 0.12	0.68 ± 0.10	0.01 ± 0.01
rightInferiorLateralVentricle	0.07 ± 0.05	0.14 ± 0.08	0.19 ± 0.09	0.00 ± 0.00
rightCerebellumWhiteMatter	0.47 ± 0.06	0.57 ± 0.11	0.66 ± 0.04	0.01 ± 0.01
rightCerebellumCortex	0.59 ± 0.07	0.75 ± 0.06	0.79 ± 0.03	0.03 ± 0.01
rightThalamus	0.67 ± 0.07	0.72 ± 0.06	0.76 ± 0.05	0.01 ± 0.00
rightCaudate	0.49 ± 0.10	0.60 ± 0.10	0.63 ± 0.10	0.00 ± 0.00
rightPutamen	0.59 ± 0.07	0.67 ± 0.07	0.75 ± 0.03	0.01 ± 0.00
rightPallidum	0.49 ± 0.09	0.51 ± 0.11	0.62 ± 0.04	0.00 ± 0.00
rightHippocampus	0.40 ± 0.10	0.56 ± 0.07	0.60 ± 0.06	0.00 ± 0.00
rightAmygdala	0.38 ± 0.12	0.43 ± 0.12	0.49 ± 0.09	0.00 ± 0.00
rightAccumbens	0.27 ± 0.14	0.40 ± 0.13	0.48 ± 0.08	0.00 ± 0.00
rightVentralDC	0.53 ± 0.08	0.61 ± 0.07	0.64 ± 0.05	0.00 ± 0.00
thirdVentricle	0.34 ± 0.11	0.48 ± 0.10	0.52 ± 0.09	0.00 ± 0.00
fourthVentricle	0.29 ± 0.14	0.54 ± 0.08	0.59 ± 0.07	0.00 ± 0.00
brainStem	0.63 ± 0.08	0.80 ± 0.04	0.81 ± 0.03	0.01 ± 0.00

Values are mean ± standard deviation of Jaccard index, J, for each region label between reference and co-registered moving images over all 306 pairwise, directed registrations of the 18 IBSR images to one another. Only labels are listed here that appear in all 18 IBSR images, i.e., labels such as “lesion” and “vessel” have been excluded.

For all individual regions, the SyN algorithm achieved better overlap than the FFD registration, which in turn achieved better overlap than affine-only registration. CURT achieved virtually no overlap, with the exception of the four spatially unspecific regions of cerebral white matter and cerebral cortex (i.e., GM) for the left and right side separately. Even for these four regions, which are essentially maps of hemispheric white matter and gray matter without further subdivision, CURT’s overlap scores are substantially below those of even the affine registration.

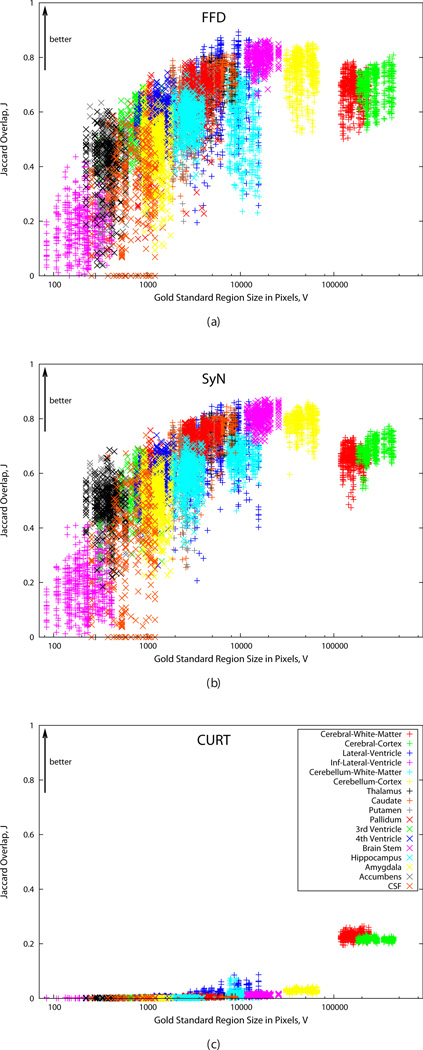
Due to the quasi-random nature of correspondences computed by CURT, it is reasonable to expect that it would perform better for larger regions than for smaller ones. This is confirmed by Fig. 5, which shows the Jaccard overlap scores for FFD, SyN, and CURT plotted against gold standard region size in pixels.

Fig. 5.

Plots of Jaccard overlap scores, J (larger values are better), after registration vs. gold standard region size in pixels. (a) FFD, (b) SyN, (c) CURT. All plots use the same axis scales. Correspondence between plot symbols and ROIs is shown in (c). For bilateral regions, both left and right region values are plotted separately but using the same symbol.

In particular the overlap scores for the previously identified, unspecific cortical regions, “Cerebral White Matter” and “Cerebral Cortex”, show that CURT performed better than would be expected based the region sizes. By comparison, FFD and SyN appear to perform less well on these regions than would be expected, perhaps due to their complex shapes and large inter-individual variability. This difference further confirms the findings of the previous section that overlap scores of spatially unspecific regions are less sensitive for revealing CURT as a biologically implausible registration algorithm.

D. Inverse Consistency Error

For each pair of fixed and moving images, A and B, and for each registration algorithm, the inverse consistency error [23] between the forward transformation, T_AB, and the backward transformation, T_BA, is computed as follows:

$$E_{\text{IC}}={\displaystyle \sum _{{\overrightarrow{x}}_i\in \text{Brain}A}}\sqrt{{\left[{\overrightarrow{x}}_i-T_{\mathit{\text{BA}}}\left(T_{\mathit{\text{AB}}}\left({\overrightarrow{x}}_i\right)\right)\right]}^2}$$ (3)

It should be noted that the SyN algorithm simultaneously computes the forward and inverse (i.e., backward) transformation consistent with one another, up to discretization effects. However, this algorithm still uses a non-symmetric initial affine alignment. Therefore, when the algorithm is run a second time with fixed and moving image switched, two independently computed initial affine transformations are used, which are not in general inverses of each other. Thus, the two resulting forward deformations are also not guaranteed to be perfectly inverse consistent.

In mathematical terms, SyN applied once to register image A to B produces T_AB and T_AB⁻¹, but running it in the opposite direction produces T_BA. Whereas the simultaneously computed T_AB and T_AB⁻¹ are almost perfectly consistent (mean E_IC=0.03 mm over all registrations), the separately computed T_AB andT_BA are not (mean E_IC=26.2 mm).

Comparing the different registration algorithms, the results in Table VI show that CURT produces transformations that have, on average, lower inverse consistency errors than FFD registration and also lower than SyN when the latter is run separately to compute forward and backward mapping. This is explained by the fact that CURT is almost symmetric by construction: when mapping from image A to B and back to A, most pixels will end up in their original location, resulting in zero inverse consistency error. Only pixels for which

$$n_f\ne \lfloor N_f\frac{\lfloor N_m\frac{n_f}{N_f}\rfloor }{N_m}\rfloor$$ (4)

map elsewhere and will incur a very large inverse consistency error because their final location is essentially random. However, because the number of these pixels is relatively small when N_f ≈ N_m, the mean inverse consistency error over all pixels is also small. (If N_f = N_m then the mapping is indeed perfectly inverse-consistent.)

TABLE VI.

Inverse consistency errors

	Affine	FFD	SyN	CURT
Inverse Consistency Error [mm]	25.8 ±16.3	26.2 ± 15.1	26.2 ± 16.2*	6.4 ± 9.0

Values are mean ± standard deviation of inverse consistency errors in mm over 306 registrations per algorithm.

^*For simultaneously computed forward and backward transformations per image pair, the consistency error for SyN is 0.03 ± 0.04mm. The larger value in the table is due to inconsistent initial affine transformations when the algorithm is run separately for the forward and backward direction. See text for details.

It may also be of general interest to observe that the inverse consistency error after FFD registration is essentially the same as after affine registration. This may suggest that FFD registration itself does not add much inconsistency on top of what is already present in its input transformation.

E. Results Summary

Selective interpretation of the quantitative results presented here could suggest that the CURT “registration” algorithm significantly outperformed the other two nonrigid registration algorithms as it achieved significantly better tissue overlap scores and image similarity measures (Figs. 6 and 7). It furthermore produced lower inverse consistency errors than FFD registration and two-pass forward/backward SyN (Table VI).

Fig. 6.

Summary graphs over all 306 image pairs comparing the post-registration image similarities after affine, FFD, SyN, and CURT registrations. (a) RMS image difference, (b) NCC image correlation, and (c) NMI image similarity. Stars mark results for which CURT differs significantly from the other algorithms (the remaining algorithms were not tested against one another).

Fig. 7.

Summary graph over all 306 image pairs comparing the tissue overlap scores of affine, FFD, SyN, and CURT registrations. Stars mark results for which CURT differs significantly from the other algorithms (the remaining algorithms were not tested against one another).

Also in terms of other commonly used measures of registration performance, such as computational complexity or need for fine-tuning of parameters, CURT seemingly outperformed the other methods: it requires no affine pre-registration, has no tunable parameters (which makes it easy to apply) and is very fast (less than 1 s on a single CPU, compared with tens of minutes for SyN and one to two hours for the FFD algorithm).

IV. Discussion

A. Implications of This Study

The aim of this paper was to demonstrate that tissue overlap, image similarity, and inverse consistency error are not reliable surrogates for registration accuracy, whether they are used in isolation or combined. Even expert visual inspection of reformatted, subtraction, or variance images cannot always reliably distinguish accurate from inaccurate registrations. This is true for both pairwise (Fig. 3) and groupwise (Fig. 4) presentation of registration results.

While it could be argued that our findings are obvious and well-known, the real importance of our work is further highlighted by the fact that peer-reviewed literature continues to rely on evaluation criteria that we have now proven to be inadequate beyond any doubt. The papers listed as examples in Tables I and II all appeared in respected, peer-reviewed international journals and conference proceedings between 2003 and 2011. Using image similarity and tissue overlap to evaluate registration accuracy appears to be still considered acceptable for many authors and reviewers.

It is important to note that we are not claiming that registration algorithms “validated” using the criteria discounted herein, such as the ones listed in Tables I and II, are necessarily inaccurate. What our results demonstrate, however, is that these evaluations of registrations do not provide sufficient positive evidence to establish accurate registrations. This is true even though low scores of tissue overlap, for example, might still be useful to establish negative evidence by detecting inaccurate registrations. Already published studies aside, the obvious consequence going forward is to insist on the use of more valid measures in the consideration of future publications.

Of the criteria tested in our study, only overlap of sufficiently local labeled ROIs could distinguish reasonable from poor registrations. One reason for this is that smaller, more localized ROIs approximate point landmarks, and their overlap thus approximates point-based registration error. This effect can be seen in Fig. 5, which illustrates that CURT’s apparent performance, while still substantially below that of the other algorithms, increases with region size and is better than expected for large, spatially unspecific regions.

Tissue overlap, then, fails as a surrogate for registration accuracy because brain tissues are distributed throughout the brain, i.e., tissue does not “encode” spatial location, and also because there is a strong relationship between tissue type and MR image intensity. The latter relationship is of course exactly what CURT exploits to perform well on this criterion.

The simplicity and ridiculously implausible mapping of the CURT algorithm do not diminish the importance of our conclusions. Rather, by being unquestionably inaccurate, CURT allows us to test accuracy measures without ground truth or gold standard. Equally important, its simplicity underscores how easily the validity of these measures is undermined. At the same time, the method could be obfuscated by complicated description, hidden in a closed-source implementation, and published as a superior registration algorithm.

A possible Abstract to this effect might read as follows: “We introduce a new nonrigid registration algorithm based on a closed-form solution to maximizing the Rank Correlation criterion. The new algorithm produces more accurate registrations than two state-of-the-art methods as judged by image similarity and tissue overlap scores. It is also two to three orders of magnitude faster, requires no affine preregistration, and has no tunable parameters.”

While this Abstract would be factually correct and fully supported by the experimental data presented herein, the underlying algorithm is inadequate and certainly does not produce accurate registrations. More reliable performance measures should, therefore, be expected to support claims of superior registration accuracy. Our results have identified overlap of localized anatomical ROIs as one suitable, immediately available alternative.

At least for inter-subject registration of MR brain images the necessary labeled data have been provided to the community for years from several sources such as the IBSR [5] and LPBA40 data sets [24, 25]. More recently, NIREP [4] has provided data as well as software tools for registration performance evaluation. An even more comprehensive evaluation data set for longitudinal (within-subject) thoracic CT registration has recently become available from the EMPIRE10 Challenge [26, 27], which uses as evaluation criteria the alignment of lung boundaries, major fissures, and up to 100 landmark pairs, as well as singularities in the deformation fields.

B. Limitations of This Study

We have not considered herein some other common evaluation strategies for nonrigid image registration. One of the most frequently used techniques is to apply a known deformation to an image, and then attempt to recover it by registration. Such evaluations do quantify actual registration errors (and thus accuracy), but are limited by different weaknesses, such as their inability to quantify the accuracy of registrations between two actual, independent images.

Another strategy is to compare the deformation field obtained by registration to one computed using a bio-mechanical (e.g., finite element [28]) simulation, but this method cannot be applied to inter-subject registration problems, and the accuracy of the bio-mechanical model prediction itself is unknown and variable [29].

Due to these limitations, and because studies that quantify accuracy without application of known deformations are plentiful, exclusion of these techniques from consideration does not reduce the relevance of our results. Indeed, we note that some studies listed in Tables I and II actually apply known deformations, yet proceed to ignore these in the evaluation and use only image similarity or tissue overlap to support claims of accuracy.

The algorithm used by us to purposely break accuracy surrogate measures, CURT, is clearly limited to same-modality registration, but the vast majority of “real” nonrigid registration algorithms in the literature have been evaluated on this exact type of problem. Whether or not these published algorithms would also perform well on multi-modality data is purely speculative. Thus, limiting CURT’s evaluation to single-modality registration problems does not reduce the relevance of our findings at all.

The most fundamental difference between CURT and “real” registration algorithms is its complete lack of regularization (Tikhonov or otherwise) of the inherently ill-posed registration problem, as well as the entirely unconstrained transformation model. CURT’s seemingly “superior” performance on the tested evaluation criteria can thus be readily explained as the result of data overfitting. On the other hand, many regularized algorithms adjust the degree of regularization using a parameter such as a constraint weight factor (e.g., [30]) or the width of a smoothing kernel (e.g., [31, 32]). There is no a priori correct value for either type of parameter, and if they are adjusted to optimize the registration outcome in terms of achieved image similarity, this can defeat the very purpose of regularization to prevent overfitting.

C. Recommendations and Caveats

The first step towards reporting valid and reliable evaluations of registration performance is to use correct terminology. The magnitude of registration error is fundamentally a quantity that represents a distance in space. Thus, only quantities measured in meters can be registration errors to begin with, and only actual errors should be labeled as such. All other quantities, including differences in transformation parameters (e.g., rotation angles, kernel function coefficients) are at best surrogate measures, they should be clearly labeled as such, and their predictions be carefully interpreted.

Ideally, actual registration errors measured at a large number of densely distributed landmarks (i.e., identifiable anatomical locations) should become the standard for reporting registration errors. Although this type of analysis has long been impeded by the inefficiency of manual landmark localization, recent work such as that by Murphy et al. [2] on semi-automatic gold standard construction, including a dense set of corresponding anatomical landmarks, may help make direct quantification of nonrigid registration accuracy more common.

In addition to point landmarks, other features such as surfaces or lines (e.g., cortical sulci [33]) can also be used to quantify registration accuracy directly using appropriate distance measures. It is worth mentioning, however, that registration error can be measured only in the direction perpendicular to surface and line features, which leads to residual uncertainty of the error estimate tangential to the landmark structure.

The final and perhaps most important recommendation is to make the evaluation of registration performance as independent as possible from the registration itself. Some obvious dependencies exist between images used for registration and features derived from them for evaluation. For example, the validity of evaluation using tissue overlap scores is compromised by the near-monotonic relationship between image intensities and tissue labels. Similarly, when registration algorithms use different data representations (e.g., diffusion tensor images vs. scalar maps derived from these) or channels (e.g., different channels of a multi-echo MRI), then features used for evaluation of the transformations should not be obtained from either representation (or channel).

In other cases, dependencies may be more subtle and harder to safeguard against. In our work, the difference between global metric computation used in FFD registration and local computation used in SyN registration may not appear to be of much importance to the comparison methodology. Nonetheless, it is one possible explanation for our inconsistent findings by which FFD outperformed SyN in terms of (globally computed) image similarity (Table III), whereas SyN outperformed FFD in terms of tissue overlap scores (Table IV).

V. Conclusion

Tissue label overlap scores and image similarity measures are not reliable criteria to establish registration accuracy. Because test data sets and reference standards are publicly available for more valid evaluation of registration accuracy using landmarks and labeled anatomical structures, these should be used instead. With any test data set, registration evaluation results should always be reported in their entirety (i.e., for all image pairs and all available performance measures) to avoid selection bias.