The Statistics of Calcium-Mediated Focal Excitations on a One-Dimensional Cable

Abstract

It is well known that various cardiac arrhythmias are initiated by an ill-timed excitation that originates from a focal region of the heart. However, up to now, it is not known what governs the timing, location, and morphology of these focal excitations. Recent studies have shown that these excitations can be caused by abnormalities in the calcium (Ca) cycling system. However, the cause-and-effect relationships linking subcellular Ca dynamics and focal activity in cardiac tissue is not completely understood. In this article, we present a minimal model of Ca-mediated focal excitations in cardiac tissue. This model accounts for the stochastic nature of spontaneous Ca release on a one-dimensional cable of cardiac cells. Using this model, we show that the timing of focal excitations is equivalent to a first passage time problem in a spatially extended system. In particular, we find that for a short cable the mean first passage time increases exponentially with the number of cells in tissue, and is critically dependent on the ratio of inward to outward currents near the threshold for an action potential. For long cables excitations occurs due to ectopic foci that occur on a length scale determined by the minimum length of tissue that can induce an action potential. Furthermore, we find that for long cables the mean first passage time decreases as a power law in the number cells. These results provide precise criteria for the occurrence of focal excitations in cardiac tissue, and will serve as a guide to determine the propensity of Ca-mediated triggered arrhythmias in the heart.

Introduction

Clinical and experimental studies have shown that sudden death is initiated by an ill-timed beat that originates from a focal region of the heart. These excitations, also known as ectopic foci, induce excitation wave fronts that break to form reentrant electrical propagation that can lead to ventricular tachycardia, and subsequently ventricular fibrillation (1,2). However, the precise mechanism for the initiation of these focal excitations is not well understood. In particular, it is not well understood what governs the timing, location, and morphology of these excitations (3). Mechanistic insights into these properties are important to understand the essential factors that initiate various arrhythmias. For instance, it is critical to understand the factors that govern the timing of a focal excitation with respect to the action potential (AP), because that will determine whether the excitation can propagate in the heart. Also, it is important to understand the electrophysiological factors that make certain cell types more prone to ectopic activity. A deeper understanding of these factors will be essential for a rational development of antiarrhythmic strategies that target ectopic foci.

Cardiac cell electrophysiology is a complex process involving the electrical system, dictated by voltage-sensitive ion channels, which regulate the membrane potential, and calcium (Ca) cycling, which is the back-and-forth flow of Ca between intracellular Ca stores and the cell interior (4). Ca release from the sarcoplasmic reticulum (SR), the main internal store, occurs within thousands of spatially distributed synapse-like junctions, referred to as “Ca release units” (CRUs), where voltage-sensitive membrane channels are in close proximity to Ca-sensitive ryanodine receptors, which are the main ion channels that regulate the flow of Ca from the SR. In this way, Ca release can be triggered by an opening of a membrane channel that will deliver enough Ca into the CRU to induce RyR channel openings via the process of calcium-induced-calcium release. Once Ca is released into the cell, it initiates a variety of signaling processes, and also interacts with Ca-sensitive membrane channels that shape the time course of the AP. Therefore, the membrane voltage is bidirectionally coupled to the intracellular Ca cycling activity so that a disruption in Ca cycling can feed-back on the electrical activity of the cell (4–7).

Many experimental studies have demonstrated that a variety of arrhythmias is related to abnormalities in Ca cycling at the cellular level (8–10). These studies show that, under certain conditions, Ca release from the SR can occur in the form of Ca waves, where the release of Ca in one CRU can diffuse and induce release at a neighboring CRU (10). This spatiotemporal Ca release process is often referred to as “spontaneous Ca release” (SCR), because these waves originate due to the random fluctuations of RyR channels, rather than the opening of a trigger membrane current (11). Now, once SCR occurs, Ca is released into the cell and can induce a membrane depolarization due to Ca-sensitive membrane channels such as the sodium-calcium exchanger, which delivers an inward current in response to an increase in intracellular Ca (12,13). SCR is believed to be arrhythmogenic because it can occur during the cardiac cycle and therefore disrupt the electrical rhythm of a paced cardiac cell. On the tissue scale, if enough cells in a region of cardiac tissue exhibit SCR, then inward currents in this group of cells can summate to induce a propagating electrical excitation (3,7). These excitations, which are referred to as “ectopic beats” (or “focal excitations”) are believed to initiate various arrhythmias. In particular, it has been proposed that atrial fibrillation is caused by excitations that originate from the pulmonary veins (14,15).

In this article, we present a minimal model of focal excitations that is due to spontaneous Ca release. In particular, we will address the following two questions: 1), What factors govern the timing of Ca-mediated focal excitations? 2), What factors determine the length scale of these excitations? The first of these questions is important because, for an ectopic beat to propagate, it must occur when cardiac cells in tissue are in their rest state. Thus, a detailed understanding of the statistics of the timing of SCR will yield insight on the potential for an ectopic excitation to induce an arrhythmia. Secondly, because the heart is highly heterogeneous it will be valuable to understand which regions are prone to these focal excitations.

To address these questions we will develop a minimal model of Ca-mediated ectopic activity in cardiac tissue. This model will account for the stochastic properties of SCR within individual myocytes, along with the bidirectional coupling between voltage and calcium. We will then apply this model to investigate how SCR in a population of myocytes can induce ectopic activity in cardiac tissue.

A Minimal Model of Ca-Mediated Ectopic Activity

Voltage and calcium dynamics near the resting potential

A focal excitation in the heart will occur when there is sufficient inward current, within a group of cells in cardiac tissue, to raise the membrane potential above an excitation threshold. This threshold is set by the sodium current, denoted by I_Na, which increases rapidly as the voltage approaches a threshold V_c, which is typically in the range –60 mV < V_c < –50 mV. Thus, to model the initiation of an ectopic beat, it is only necessary to consider the voltage dynamics between the resting potential at V_m ∼ –80 mV and the voltage threshold V_c. In this regime, the dominant potassium current is the inward rectifier potassium current (I_K1), which is responsible for holding the membrane at the resting potential. In this study, we will consider membrane excitations that are induced by SCR, which influences the voltage via the sodium-calcium exchanger (I_NaCa), which allows sodium ions into the cell in response to an increase in intracellular Ca. Therefore, in the relevant voltage range the ionic current across the membrane can be effectively modeled as

$$I_{ion}=I_{Na}+I_{K1}+I_{NaCa}.$$ (1)

Near the resting potential, I_Na is modeled using an activation gate variable (the m-gate), which is a sharp sigmoid function of voltage that rises rapidly from zero at a threshold voltage (16). In this study, we will incorporate this feature in our model by describing the sodium current as I_Na = g_NaΘ(V – V_c), where Θ is a Heaviside step function with threshold V_c ∼ –50 mV, and where g_Na is the conductance of the sodium channel. To proceed, close to the resting potential we can linearize I_K1 and approximate it as I_K1 = g_k(V – V_m), where g_k is the current conductance. To describe I_NaCa, we note that this is an inward current that responds to a rise in the intracellular Ca concentration. During SCR, this current is activated by the release of Ca due to spontaneous Ca waves that propagate inside the cell. These waves are nucleated at local sites in the cell and propagate and extinguish at cell boundaries, or by colliding with each other. Nucleation of these Ca waves is a stochastic process that depends on RyR channel fluctuations in the cell, and can be well described by a Poisson process with a rate that is dependent on the SR Ca load (7,10). To model these features, we will describe the exchanger current using a simple form

$$I_{NaCa}\left(t\right)=I_x·\eta \left(t\right),$$ (2)

where η(t) is a random variable that can take the value 0 or 1 (depending on whether SCR is active in the cell or not, respectively). Here, I_x describes the average amplitude of the exchanger current during SCR. Note that this quantity is dependent on the amount of Ca released in the cell. However, in this study we will not model this time dependence and simply treat I_x to be a constant parameter. To describe the nucleation of SCR we simply let the random variable η make a 0 → 1 transition with a rate α. This rate can be determined directly from experimental measurements of the timing of Ca wave sources in a cardiac cell (10), i.e., α is simply the exponential decay rate of the latency distribution of the first Ca spark that induces SCR (at fixed SR load). To proceed, we denote, by T_scr, the average time it takes for a Ca wave to form, propagate, and then extinguish at the cell boundaries (or by colliding with other waves). We model this process by letting η make the 1 → 0 transition with a rate β = 1/T_scr. Thus, we can model the timing of SCR using the simple reaction scheme

$$0\begin{array}{c}\alpha \\ \rightleftharpoons \\ \beta \end{array}1,$$ (3)

so that the fraction of cells in a population exhibiting SCR will be p_o = α/(α + β). Note that although this is a crude approximation to the complex spatiotemporal features of SCR, it does capture key features such as the correct timing statistics and the average duration.

To model a one-dimensional cable of cells, we apply the discrete cable equation

$$\frac{d{u}_i}{dt}=g_j\left(u_{i+1}+u_{i-1}-2u_i\right)-g_k{u}_i+I_{Na}\left(u_i\right)+I_x{\eta }_i\left(t\right),$$ (4)

where u_i = V_i –V_m is the voltage difference of the i^th cell above the resting membrane potential, and where g_j is the gap junction conductance between cells. To avoid boundary effects, we will apply periodic boundary conditions so that u₁ = u_n, where n is the number of cells on the cable. Here, all conductances are measured per unit capacitance, and have units of mS/μF = ms⁻¹, while currents are in units of A/F.

In this study, we will explore the timing of ectopic activity over a wide range of system parameters. Thus, we will pick model parameters that can differ substantially from the known physiological values. In this way, our study will be relevant to potential disease states where the current conductance can differ substantially from their physiological values. The system parameters are determined as follows:

The gap junction conductance (g_j)

This parameter is chosen so that the effective diffusion coefficient of voltage in cardiac tissue is the experimentally measured value D = 5 × 10⁻⁴ cm²/ms. Noting that D = g_jd², where d is the length of a cell, this gives g_j = 5 ms⁻¹, using a standard value of d = 100 μm. Thus, we will consider gap junction conductances in the range 1 ms⁻¹ < g_j < 10 ms⁻¹.

The I_K1 conductance (g_k)

The maximum I_K1 conductance typically varies over a wide range depending upon cell type and physiological conditions. In this study we will consider system properties in the range 0.05 ms⁻¹ < g_k < 1 ms⁻¹, which includes conductances from a range of ionic models (16,17).

The strength of the sodium-calcium exchanger (I_x)

To estimate I_x, which is the average current due to the sodium-calcium exchanger during SCR, we will follow Schlotthauer and Bers (18), who claim that the total charge pumped out of the cell during SR Ca release in rabbit myocytes is ∼1 C/F. Assuming this charge is pumped out of the cell in ∼500 ms, a typical duration of SCR, then this gives I_x ∼ 2 A/F. However, during diseased states this current is substantially upregulated and so we will consider a much broader range 1 A/F < I_x < 15 A/F.

SCR statistics

To fix the rate constants of the reaction scheme in Eq. 3 we will rely on recent experimental data from Wasserstrom et al. (10), who measured SCR activity after rapid pacing at high SR loads. There, it was found that SCR typically occurs after ∼300 ms, for a duration typically ∼100 ms. Thus, we will choose system parameters consistent with these findings so that β = 0.009 (ms)⁻¹ and α = 0.003 (ms)⁻¹. This choice determines that the fraction of cells undergoing SCR, at any given time, is p_o ∼ 0.25.

Note that these parameters correspond to Ca overload conditions. Under normal physiological conditions, SCR rarely occurs, and Ca-mediated ectopic activity is unlikely to occur.

Dependence of the MFPT on the number of cells

On a cable, cell-to-cell coupling will require that a minimum number of cells must cross the sodium current threshold to induce sufficient inward current to form a propagating excitation. This question has been explored in the classic work of Noble (19) and Rushton (20), who referred to the minimum length of tissue above threshold as the liminal length. In this picture, an ectopic excitation will form when the maximum voltage on the tissue reaches a voltage V_th > V_c. For this to occur, a liminal length of tissue, which we will denote by l_n, must be above the threshold voltage V_c. Noble (19) estimated V_th to be roughly 10–20 mV larger than V_c, depending on physiological parameters, such as the strength of the sodium current and the degree of electrotonic coupling. In this study, we will consider the case when the sodium current conductance is large so that near threshold, the sodium current is much larger than the repolarizing potassium current, i.e., I_Na ≫ I_K1. In this limit, V_th ∼ V_c, and an ectopic excitation occurs the moment any one cell on the cable reaches V_c. Although this is a major simplification, it will serve as starting point to understand the stochastic properties of Ca-mediated ectopic activity in cardiac tissue. Thus, the timing of an ectopic beat on our cable is dictated by the average time duration for any one cell in the tissue to reach u_c = V_c − V_m for the first time. We will denote this time, referred to as the mean first passage time (MFPT), as T_e. The goal is then to understand how T_e depends on the relevant physiological parameters.

To solve for the MFPT, we simulate the time evolution of Eq. 4 and record the time t_c for a point on the cable to reach u_c for the first time. The MFPT is then computed as the average t_c over 10⁵ independent simulations. As a starting point, we have picked parameters of our model such that the MFPT for a single isolated cell to reach u_c is roughly a few hundred milliseconds. We have chosen initial conditions on our cable such that the state of the i^th cell is assigned a value η_i = 1 with probability p_o, η_i = 0 with probability 1 − p_o, and where u_i = 0 mV. In Fig. 1 A, we plot the mean first passage time T_e versus the number of cells in the cable (n), showing that T_e increases rapidly with n for small system sizes, reaches a peak at a cell number n_p that is roughly in the range of 15–30 cells, and then gradually decreases with increasing n. Furthermore, we find that this nonmonotonic behavior is robust and is observed for a range of gap junction conductances. In Fig. 1 B, we also plot the corresponding first passage time distribution for t_c for three system sizes. This result shows that the MFPT has a broad distribution with a variance that is comparable to the mean. To ensure that our computation of the MFPT is accurate, we have computed the variance of T_e computed using 50 averages of 2000 independent simulations. The variance computed in this fashion is <1% of our computed average and smaller than the symbol size showing in Fig. 1 A.

Figure 1.

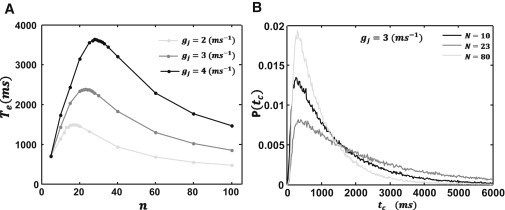
System size dependence of the mean first passage time. (A) Plot of the MFPT T_e versus number of cells n. Plots are for three values of the gap junction conductance g_j. The model parameters used are g_k = 0.1 ms⁻¹, I_x = 6.0 A/F, ν_c = 31.4 mV, α = 0.003 ms⁻¹, β = 0.009 ms⁻¹, and Δx = 150 μm. (B) Plot of the first passage time probability distribution for three system sizes. Distribution was computed using 10⁵ independent simulations.

Statistics of Ectopic Activity on a Short Cable

Condition for an ectopic beat

In this section, we will investigate the MFPT on a short cable. As a starting point, we note that if the voltage varies on a length scale much larger than the size of a single myocyte, the discrete cable equation can be well approximated by the standard cable equation

$$\frac{\partial u}{\partial t}=I_{ion}+D\frac{{\partial }^{2}u}{\partial x^2}.$$ (5)

In this approximation, a current perturbation on the cable can be shown to decay exponentially with a length constant, referred to as the electrotonic length (or space constant), which is given by l_e = n_ed, where $n_e=\sqrt{g_j/g_k}$. In this article, we will refer to n_e as the space constant, which, under physiological conditions is roughly n_e ∼10, so that the electrotonic length is ∼1 mm (using d = 100 μm). For a cable with n cells, such that n ≲ n_e, the spatial variations of voltage are small. In this regime, we can take the spatial average of both sides of Eq. 5 and drop the diffusion term because it is small. This gives

$$\frac{du}{dt}=-g_{k}u+\langle l_x\eta \left(t\right)\rangle ,$$ (6)

where $u\left(t\right)=\left(1/L\right){\int }_0^{L}u\left(x,t\right)dx$ and where $\langle I_x\eta \left(t\right)\rangle =\left(1/n\right){\sum }_{i=1}^n{I}_x{\eta }_i\left(t\right)$, so that the voltage difference relaxes to u(t) = 〈I_xη(t)〉/g_k in a time τ_k ∼ 1/g_k, which is in the range 1–20 ms. Now, because this relaxation time is smaller than the mean duration of SCR (∼100 ms), then the average voltage can be approximated by its steady-state value

$$u\left(t\right)=\frac{I_x}{g_k}\frac{k\left(t\right)}{n},$$ (7)

where k(t) is the number of cells, among the n cells on the cable, which exhibits SCR (i.e., have value η_i(t) = 1 at time t). Therefore, the condition for an AP to fire on our cable (u(t) ≥ u_c is just k ≥ k_c = n p_c, where p_c is

$$p_c=\frac{I_k}{I_x},$$ (8)

and where I_k = g_ku_c, so that p_c is simply the ratio of outward/inward currents at the threshold potential u_c.

The MFPT

To determine the timing of spontaneous excitations in a small tissue, we have to compute the average time for k to exceed the threshold k_c for the first time. To compute this time, we write a master equation for P(k,t), which is the probability that k cells exhibit SCR at time t. The master equation is

$$\frac{dP\left(k,t\right)}{dt}=w_{k-1}^{+}P\left(k-1,t\right)+w_{k+1}^{-}P\left(k+1,t\right)-\left(w_k^{+}+w_k^{-}\right)P\left(k,t\right),$$ (9)

where w⁺_k = α(n − k), w⁻_k = βk. Pury and Cáceres (21) have solved this problem exactly and find that the first passage time from k = 0 to k_c, with reflecting boundary conditions at the origin, is given by the exact expression

$$T_e=\sum _{k=0}^{kc}\frac{1}{w_k^{+}}+\sum _{k=0}^{k_c-1}\frac{1}{w_k^{+}}·\sum _{i=k+1}^{k_c}\prod _{j=k+1}^i\frac{w_j^{-}}{w_j^{+}}.$$ (10)

To confirm this result in Fig. 2, we plot the logarithm of Eq. 10 versus the number of cells along with the numerically computed MFPT using Eqs. 6 and 7. Our results show excellent agreement between the analytic and numerical solutions. Furthermore, we observe that logT_e increases linearly with cell number, showing that the MFPT is exponentially dependent on the number of cells on our cable.

Figure 2.

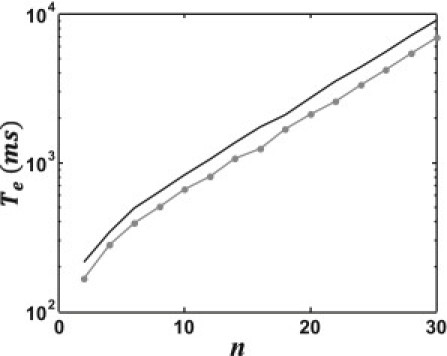
Plot of the logarithm of the MFPT T_e versus number of cells n. (Solid line) MFPT computed by numerically solving the spatial average of the discrete cable equation, Eq. 6. (Circles) Computed using the steady-state voltage (Eq. 7); (shaded line) determined using the exact solution for the MFPT given in Eq. 10.

However, the dependence of T_e on system parameters is not clearly evident from Eq. 10. To extract this dependence, we will evaluate this expression in the limit of large n (see Doering et al. (22) for similar computations). In this limit, the MFPT is given by

$$Te\sim \frac{1}{\alpha \log \left(\lambda s\right)}\sqrt{\frac{\pi s}{2n}}\exp \left(n\left(F\left(p_c\right)-F\left(p_o\right)\right)\right),$$ (11)

where p_o = α/(α + β), s = p_c/(1 − p_c), and where F(x) = (1 − x) log(1 − x) + x log(λx), with λ = β/α. Note that the behavior of T_e is dominated by the exponential term, which for small p_o and p_c gives

$$\log T_e\sim \frac{n{\left(p_c-p_o\right)}^2}{2p_o}.$$ (12)

This result demonstrates that the MFPT is exponentially sensitive to the number of cells n on the cable, the critical fraction of cells necessary for an excitation p_c, and finally, the fraction of cells p_o undergoing SCR. These findings have important implications on the timing of ectopic beats in small tissue sizes, and will be described in more detail in the Discussion.

Ectopic Activity on a Long Cable

Reaction rate theory

In this section, we will investigate the properties of an ectopic beat on a long cable where the number of cells exceeds the space constant n_e. In this case, the MFPT will be dictated by fluctuations of the membrane potential that will allow a cell on the cable to cross the threshold for membrane excitation. For this to occur, we expect that a larger-than-average fraction of cells within a region of tissue undergoes SCR simultaneously, so that the local inward currents are sufficient to raise the voltage beyond threshold. Thus, we seek to determine the MFPT for a cell on the cable to reach threshold, and the necessary number of cells in that vicinity that must undergo SCR for this to occur. Similar problems have been addressed in a variety of contexts such as the escape rate of a polymer trapped in a potential well (23), and the nucleation of a critical droplet from a metastable state (24) (see Hänggi et al. (25) for an extensive review of the literature). In all these problems, progress has been made by studying the spatiotemporal dynamics of a field w(x,t) that obeys the stochastic partial differential equation (PDE)

$$\frac{\partial w}{\partial t}=D\frac{{\partial }^{2}w}{\partial x^2}-V^{\prime }\left(w\right)+\xi \left(x,t\right),$$ (13)

where V(w) is a potential function, and ξ(x,t) is a white noise term that satisfies 〈ξ(x,t)ξ(x′,t′)〉 = Γδ(x − x′)δ(t − t′) and 〈ξ(x,t)〉 = 0, where Γ denotes the strength of the noise. The deterministic part of Eq. 13 can be viewed as the gradient flow of the energy functional

$$E\left[w\left(x\right)\right]=\underset{0}{\overset{L}{\int }}\left[\frac{D}{2}{\left(\frac{\partial w}{\partial x}\right)}^2+V\left(w\right)\right]dx,$$ (14)

where L is the system size. Thus, the system will evolve toward the locally stable minima of the energy and will fluctuate around the local minima due to the random noise term. However, on rare occasions, these fluctuations can be large enough that our system will cross from one metastable minima to another. If we denote w₁(x) to be a configuration in the vicinity of a metastable minima, and w₂(x) to a configuration of a rare fluctuation, then the transition rate (j) between these two configurations is of the order

$$j\sim j_0\exp \left(-\frac{\Delta E}{\Gamma }\right),$$ (15)

where ΔE = E[w₂(x)] −E[w₁(x)], and where j_o is a prefactor that will depend on the system size (24). Physically, ΔE corresponds to the energy necessary to nucleate a particular large fluctuation from equilibrium, while j_o will represent the attempt frequency for that fluctuation to occur. In the following section we will show that, under reasonable assumptions, Eq. 13 can be used to describe the fluctuations of voltage near the resting potential of the cell, so that we can estimate the rate of focal excitations, and hence the MFPT, using Eq. 15.

Mapping to a stochastic PDE

To cast our problem in the form given by Eq. 13, we will coarse-grain our cable into groups of m cells such that m ≪ n_e. However, we will choose m large enough such that voltage fluctuations of a coarse-grained region can be well approximated by Gaussian statistics. To proceed, we write the average sodium-calcium exchanger current within a coarse-grained region of cells as

$$I_x^m\left(t\right)=\frac{1}{m}\sum _{i=1}^m{I}_x{\eta }_i\left(t\right),$$ (16)

which can be written as $I_x^m\left(t\right)=I_{x}k/m$, where k is the number of cells that exhibit SCR (i.e., are in the state 1 according to the reaction scheme in Eq. 3). As shown earlier, k will satisfy the master equation given by Eq. 9, which, for m large enough can be well approximated by the corresponding Fokker-Planck equation for the fraction of active cells z = k/m (26). This gives

$$\frac{\partial P\left(z,t\right)}{\partial t}=-\frac{\partial }{\partial z}\left[f\left(z\right)P\left(z,t\right)\right]+\frac{1}{2m}\frac{{\partial }^2}{{\partial z}^2}\left[h\left(z\right)P\left(z,t\right)\right],$$ (17)

where f(z) = α(1 − z) − βz and h(z) = α(1 − z) − βz. The steady-state probability distribution for the fraction of active cells is then

$$P\left(z\right)=\frac{\mathbb{N}}{h\left(z\right)}\exp \left[2m{\int }_0^{z}Q\left(y\right)dy\right],$$ (18)

where Q(y) = f(y)/h(y), and ℕ is a normalization constant. This probability distribution is peaked around the average p_o = α/(α + β), so that expanding around the average yields a Gaussian distribution of the form P(x) = ℕ exp[−ax²/2], where a = m/p_o(1 − p_o). Therefore, the average current for a coarse-grained region of m cells can be approximated by $I_x^m\left(t\right)\approx I_x{p}_o+\xi \left(t\right)$, where ξ(t) is a Gaussian random variable with 〈ξ(t)〉 = 0 and $\langle \xi \left(t\right)\xi \left(t^{\prime }\right)\rangle =\left(I_x^2/m\right)p_o\left(1-p_o\right)\delta \left(t-t^{\prime }\right)$. To proceed, we coarse-grain our system by averaging the voltage for adjacent blocks of m cells, which we denote by 〈u〉_m, and define a new variable $w={\langle u\rangle }_m-I_x{p}_o/g_k$, where, for convenience we have shifted the voltage so that the average resting potential is at w = 0. If the electrotonic length is much larger than spatial variations of w, then we can approximate the spatiotemporal dynamics of the coarse-grained cable as

$$\frac{\partial w}{\partial t}=D_m\frac{{\partial }^{2}w}{\partial x^2}-g_{k}w+\xi \left(x,t\right),$$ (19)

where 〈ξ(x,t)〉 = 0, and 〈ξ(x,t)ξ(x′,t′)〉 = Γδ(x − x′)δ(t − t′), with $\Gamma =I_x^2{p}_o\left(1-p_o\right)/m$, and where D_m = g_j(md)². This completes our mapping to the form given in Eq. 13. However, we note here that Eq. 19 can only be strictly justified when n_e is large enough that the number of cells in a coarse-grained region can be modeled by Gaussian statistics. Thus, in one dimension where n_e ∼ 10 we do not expect Eq. 19 to provide a quantitative description of the system. However, as we will demonstrate later, qualitative features of the MFPT are captured using this approach.

Optimal fluctuations

To determine the MFPT for an ectopic beat to fire in our tissue, we note that this beat will be caused by a fluctuation of the membrane voltage such that the peak voltage of that fluctuation is equal to the critical threshold w_c = u_c − I_xp_o/g_k. In a large system, we expect that the MFPT for such an occurrence will be determined by local fluctuations that maximize the rate j given in Eq. 15. These fluctuations correspond to membrane voltage configurations that minimize the energy difference ΔE. For this to occur, we expect that a larger-than-average fraction of cells, within a segment of size l of the tissue, to exhibit SCR, so that the peak voltage in this section reaches threshold. To construct the shape of this critical fluctuation, we will consider a voltage fluctuation that is due to a constant driving current in a localized segment of size l. Assuming steady state, we can construct these solutions by solving 0 = D_mw_xx − g_kw + I(x), where I(x) = I for |x| ≤ l/2 and zero otherwise. Here, I is a constant that is fixed by the requirement that the maximum voltage is at threshold. The solutions are w₁(x) = a₀ + a₁e^ax + a₂e^−ax for −l/2 < x < l/2 and w₂(x) = be^{−b|x−l/2|} for |x| > l/2. Matching boundary conditions and requiring that our localized solution reaches threshold at its maximum value (w₁(0) = w_c) gives w₁(x) = A(1 −exp(αl/2) Cosh(ax)) and w₂(x) = Bexp(−α|x −l/2|), where $\alpha =\sqrt{g_k/D_m}$ and where A = w_c/(1 − exp(−αl/2)) and B = (A/2)(1 − exp(−αl)). To proceed, we directly evaluate the energy of the kink solution and then minimize the energy with respect to the size of the excitation l. The optimal solution occurs for l = 0 and w(x) = w_cexp(−α|x|), valid for all x.

The liminal length

Our analysis above reveals that the optimal voltage fluctuation corresponds to the smallest region of tissue such that the center of that region reaches the threshold voltage. To generate this optimal solution, the inward current at a point on the cable would have to be infinite. However, this cannot occur in our discrete cable equation (Eq. 4) because the magnitude of the sodium-calcium exchanger is bounded by I_x. Thus, the optimal fluctuation predicted using Eq. 19 cannot be attained in a realistic cable. However, a key insight from the reaction rate computation is that the optimal fluctuation is simply the smallest region of cells that can cross threshold. To determine the size of the shortest segment such that one point of the segment is at threshold, we solve the steady-state solutions of the coarse-grained PDE given in Eq. 19, but with a driving term such that all cells in a segment of size l have current I_x. Thus, we look for stationary solutions of 0 = D_mw_xx − g_kw + I(x), where I(x) = I_x − I_xp_o for |x| < l/2 and I(x) = 0 for |x| > l/2. Setting the maximum voltage at x = 0 to be at threshold (w₁(0) = w_c) and solving for the number of cells n_l = l/d gives

$$n_l=2\sqrt{\frac{g_j}{g_k}}\left|\log \left(\frac{1-p_c}{1-p_o}\right)\right|,$$ (20)

which gives the smallest region of active cells that can reach threshold. Hereafter, we will refer to this quantity as the liminal cell number, and l_m = n_ld as the liminal length for SCR-induced focal excitations on a one-dimensional cable. Thus, we predict that in a long cable, excitations that cross threshold will be most likely due to a group of n_l cells that undergo SCR simultaneously. Note that it is important to distinguish l_m from l_n, which is the minimum number of cells necessary to cross the sodium threshold. In general, we expect l_m > l_n, because a larger number of cells needs to undergo SCR to raise a segment of length l_n above threshold. To compute the timing of an ectopic beat on a cable, we evaluate the energy of this minimal excitation. Noting that T_e ∼ 1/j (25), we find that

$$\log T_e\sim \sqrt{g_k{g}_j}\frac{u_c^2}{I_x^2{p}_o},$$ (21)

which is valid for small p_c and p_o (indicating that the MFPT depends exponentially on system parameters).

Numerical simulations

The key predictions of reaction theory are that 1), the MFPT for a long cable is dictated by a region of n_l cells that undergo SCR simultaneously, and 2), the timing of these excitations are exponentially sensitive to a combination of system parameters as shown in Eq. 21. To confirm these predictions, we have directly simulated the discrete cable equation. To compute the MFPT, we solved Eq. 4 on a cable of n = 150 cells and computed the time t_c until one point of the cable reached the threshold u_c. To compute the MFPT, we averaged t_c over 10⁵ independent simulations. In Fig. 3, A–E, we plot logT_e versus the physiological parameters shown in Eq. 21. As shown, the qualitative predictions of Eq. 21 are consistent with our simulation results. However, we do not get a precise match with the exponents predicted analytically. This is partly due to the fact that the exponential dependence ensures that the MFPT becomes very large even for small changes in system parameters. This makes it computationally very demanding to study the MFPT over a wide range of parameters.

Figure 3.

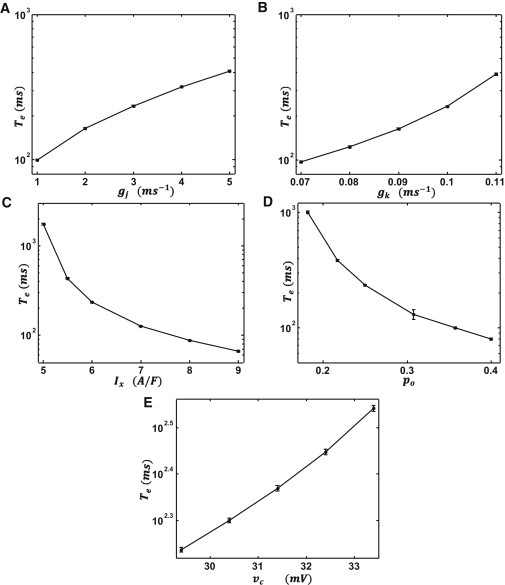
Numerical simulation of the exponential dependence of the mean first passage time T_e as a function of system parameters. Plot of T_e versus (A) the gap junction conductance g_j, (B) I_K1 conductance g_k, (C) the strength of the sodium-calcium exchanger I_x, (D) the probability of SCR p_o, and (E) the voltage threshold ν_c. (Error bars) Computed from the variance of 50 groups of 2000 independent simulations. (Error bars not shown are smaller than the symbol size.) To estimate the parameter dependence we estimate the slope of a least-squares fit of a log(log(T_e)) versus log(x)graph, where x denotes the parameter in question. The line fits give $\log Te\sim \left\{g_j^{0.2},g_k^{0.6},I_x^{-0.7},p_o^{-0.6},{\nu }_c\right\}$.

The next step is to compute the number of cells that must undergo SCR for the voltage to cross threshold in that vicinity. To do this, we compute the correlation length of the random variable η_i(t) in the vicinity of that point on our cable where the voltage crosses threshold. In practice, we will compute the correlation function

$$C\left(k\right)=\frac{\langle {\eta }_l\left(t_c\right){\eta }_{l+k}\left(t_c\right)\rangle -p_o^2}{p_o\left(1-p_o\right)},$$ (22)

where η_l(t_c) is the state of the l^th cell at which the voltage crosses u_c at time t_c. Assuming η_i are uncorrelated random numbers governed by the reaction scheme shown in Eq. 3, then C(0) = 1 and C(k) = 0 for k ≠ 0. However, near the threshold we expect that a larger-than-average fraction of cells will exhibit SCR. Thus, the decay rate of C(k) will give a measure of the number of cells underlying the excitation. In Fig. 4 A, we compute C(k) for the cell that crosses threshold for the first time, along with an arbitrary cell on the cable. As expected, C(k) decays slowly in the vicinity of the threshold voltage but decays to zero for an arbitrary cell. Fitting the correlation function to an exponential function C(k) ∝ exp(−k/n_cor) gives an estimate n_cor for the size of our optimal fluctuations. In Fig. 4, B–D, we plot n_cor and the liminal cell number n_l as a function of system parameters. Our results show that the liminal length and the local correlation length are comparable, and exhibit a similar dependence on system parameters. In Fig. 4, B and C, we found that n_l > n_cor, indicating that our measure of n_cor typically underestimates the size of the focal excitation. We also found that, numerically, n_cor exhibits only a weak dependence on the SCR probability p_o, whereas n_l decreases more rapidly when p_o is increased.

Figure 4.

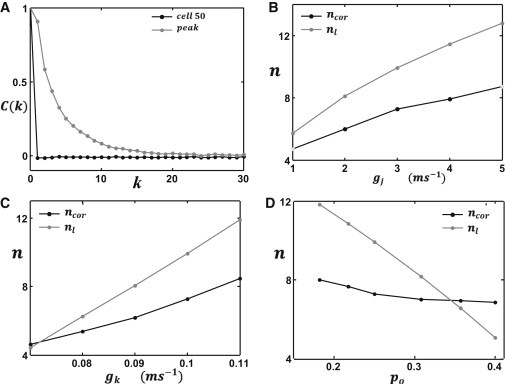
Comparison between numerical and analytical predictions for the liminal length. (A) The correlation function C(k) computed near the peak voltage (gray line) and near an arbitrary cell (black line). In this simulation we have picked the 50th cell on the cable. (B–D) The liminal length (n_l) computed analytically using Eq. 20 (gray line) along with the correlation length (n_cor) near the peak voltage (black line): computed as a function of (B) gap junction conductance g_j, (C) I_K1 conductance g_k, and (D) SCR probability p_o.

The Dependence of the MFPT on System Size

The reaction rate theory described earlier showed that, to leading order, the timing of an ectopic beat is determined by a local fluctuation that brings the voltage to threshold. Now, in a long cable this excitation can occur at any location so that we expect the excitation rate j to increase with system size. Indeed, this is confirmed by our numerical simulations in Fig. 1 showing that T_e decreased with n, for large n. However, this effect is not captured by the exponential term in Eq. 15 because the energy of the optimal fluctuation is independent of system size. Hence, the system size dependence of the rate is only accounted for in the prefactor j_o, which is generally difficult to calculate for spatially extended systems. Here, we present an alternative statistical theory of the size effect. Our approach follows statistical arguments, originally developed by Weibull (27), that have been applied to determine the size dependence of the strength of materials (28). To apply this theory we first note that cells a distance n_e apart are essentially statistically independent, so that we can treat a cable of n cells to be an aggregate of k = n/n_e independent regions. Therefore, if we know the statistics of the MFPT for each segment of n_e cells then we can determine the statistics of the cable. To determine the MFPT of k independent systems, we write the first passage time distribution (FPD) as

$$P_k\left(t\right)=k{P}_1\left(t\right){\left(1-{\int }_0^t{P}_1\left(t^{\prime }\right)d{t}^{\prime }\right)}^{k-1},$$ (23)

where P₁(t) is the FPD of a segment of n_e cells. Following Weibull (27) and Bažant (28), we note that in the limit of large n, the MFPT will be dominated by the tail of the distribution P₁(t). If we assume a power-law tail for small t,

$$P_1\left(t\right)\propto t^{\mu },$$ (24)

then it is straightforward to show that the MFPT for large n behaves like

$$T_e\left(n\right)\sim n^{\gamma },$$ (25)

where γ = −1/(1 + μ). Thus, for large systems we expect that the MFPT decreases as a power law, with an exponent that is determined by the tail of the FPD for a segment of n_e cells.

To confirm that these arguments apply to our system, we have simulated a cable of cells in which the number of cells is large. In Fig. 5 A, we plot logT_e versus log(n) where the number of cells ranges from 600 to 5000 cells. As shown, the data are well approximated by a straight line fit, indicating that, indeed, T_e has an approximate power-law dependence on the number of cells on the cable. Computing the slope of the straight line fit for a range of gap junction conductances shows that the exponent varies in the range −1/3 to −1/5. To confirm that this exponent is dictated by the tail of the first passage time distribution P₁(t), we have directly computed this distribution using a cable of n_e ∼ 20 cells, with periodic boundary conditions. In Fig. 5 B, we have plotted logP₁(t) versus logt showing that, indeed, the tail of the first latency distribution grows as a power law with an exponent μ in the range 2–3. Finally, we confirm that the power-law exponent approximately satisfies γ ∼ −1/(1 + μ), which is consistent with the predictions of the Weibull statistical theory.

Figure 5.

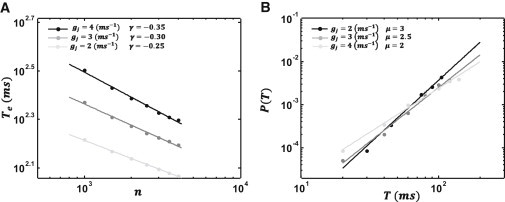
(A) Log-log plot of the mean first passage time versus the number of cells on a long cable. (Inset) Simulation points are fitted with a straight line with slope γ. Each curve corresponds to the indicated gap junction conductance. (B) Log-log plot of first passage time distribution as a function of time for a cable of size n_e. (Inset) Points are fitted with a straight line with slope μ.

Discussion

To induce an arrhythmia, a focal excitation must propagate in cardiac tissue, and therefore must occur when the tissue is in the rest state. This is likely to occur if the trigger occurs during the diastolic interval after the action potential duration (APD). Thus, we expect focal activity to be dangerous when APD < T_e < APD + DI. Under normal physiological conditions, T_e is large (≫1 s) and typically does not occur within the cardiac cycle. However, our findings suggest that this timing can be substantially reduced by a small change in system parameters. In particular, we find that for a cable that is shorter than the electrotonic length constant, the MFPT T_e is exponentially sensitive to the fraction of cells undergoing SCR (p_o), the ratio of inward/outward currents at threshold (p_c), and the number of cells in the tissue (n). In particular, from Eq. 12 we observe that T_e is exponentially sensitive to Δp = p_c − p_o, so that a rough but quantitative criteria for a focal excitation to occur within a cardiac cycle is

$$p_o\sim p_c=\frac{I_k}{I_x}$$ (26)

because, when this condition is met, T_e is likely to be small. To estimate p_c, we follow Schlotthauer and Bers (18), who measured the onset of delayed-after-depolarizations in rabbit myocytes, which are induced by SR Ca release invoked by a caffeine application. In that experiment, u_c ∼ 15 mV, so that using g_k ∼ 0.2 ms⁻¹ gives I_k = g_ku_c ∼ 5 A/F. Also, taking I_x ∼ 10 A/F gives p_c ∼ 0.5, which implies that roughly half the cells in tissue must undergo SCR simultaneously for the threshold to be reached. During heart failure, it is generally believed that g_k can decrease by roughly a factor of 2 and I_x is enhanced up to four times (29). Under these conditions, p_c ∼ 1/16, so that the fraction of cells that must undergo SCR simultaneously is substantially decreased. However, to evaluate p_o is generally difficult because one will have to count the fraction of cells in tissue that exhibit SCR at any given time. Recent experimental advances in optical mapping show that SCR activity in a population of cells can be observed (8). Indeed, the findings in Wasserstrom et al. (10) show that a substantial fraction of cells exhibit SCR after an AP. Given this data, Eq. 26 can potentially serve as a useful rule of thumb to evaluate the propensity for SCR-induced ectopic activity in cardiac tissue.

The MFPT, as shown in Fig. 1, increases rapidly for small n, reaches a peak at n ∼ n_p, and then gradually decreases for large n. To understand this behavior, we have analyzed the statistical properties of threshold crossing in a spatially extended system. Our results can be summarized as follows:

• 1.n < n_p: In this case, we find that the timing of focal excitations increases exponentially with the number of cells n. This effect is due to the strong electrotonic coupling between cells in tissue, which requires a critical fraction of cells to undergo SCR simultaneously for the average voltage to cross threshold. Increasing the number of cells leads to a rapid increase of the MFPT of excitation, because more cells must undergo SCR simultaneously.
• 2.n ∼ n_p: The exponential growth of the MFPT ceases once n ∼ n_p and begins to decrease with increasing n. The explanation for this effect is simply that, for large n, it is possible to fit more liminal lengths of size n_l on the cable. Because focal excitations can originate from any one of these sections of size n_l, then the MFPT will decrease once n ≫ n_l. Indeed, we find numerically that n_p and n_l depend on system parameters in roughly the same way, although our numerical findings show that n_p is roughly twice larger than n_l. This difference is likely due to the fact that our derivation of n_l assumed a large system whereas n_p is computed using periodic boundary conditions. Note that in these simulations we have implemented periodic boundary conditions to eliminate edge effects. In fact, we find that when we impose nonflux boundary conditions on our cable, the ectopic excitation tends to originate at the boundaries. This is because of the reduced electrotonic load at the edges.
• 3.n ≫ n_p: for very long cables, we found that the MFPT decreased as a power law in the number of cells. Furthermore, we showed that the power-law exponent is related to the first passage time statistics of an ensemble of independent sections of size n_e. This result gives a quantitative relationship between the timing of focal excitations and the numbers of cells in tissue.

There are several physiological implications of the size dependence described above. As a starting point, let us consider a more realistic three-dimensional block of tissue of size n_x × n_y × n_z. Then our results imply that the MFPT of focal excitations from this block will be strongly dependent on each spatial dimension. In particular, if a dimension of the tissue, say n_x, is <n_l, then we expect the MFPT to decrease significantly. This is because the electrotonic load, at least in that dimension, will drop significantly, i.e., a lesser fraction of cells will be required for a region in the block to cross threshold. Thus, in general, given uniform electrophysiological properties, we expect focal activity to occur in regions of the heart where the electrotonic load on cells is minimal. The interesting finding here is that we have computed, at least in one dimension, an estimate of the length scale n_l after which this effect becomes important.

Now, one can argue that because the MFPT also decreases for large n, then we expect that ectopic beats should occur from regions of the heart with the most cells. This is certainly true, although we argue here that this is unlikely, because the MFPT decreases slowly (a power law with fractional exponent) with n for large n, but decreases exponentially fast with n for small cables. Because the power-law decrease is slow, we expect that focal activity will be dominated by the regions of the heart that are spatially constricted, rather than regions where there are the most cells. Furthermore, we expect the MFPT in three dimensions to be much larger than in one dimension, because there is a much larger number of cells within a sphere with a liminal length radius. Now, because we expect a similar fraction of cells to exhibit SCR within the liminal volume to reach threshold, then the waiting time for this fraction to be reached will be exponentially larger. These results are consistent with experimental findings, showing that ectopic beats tend to occur in the Purkinje fiber system rather than the bulk myocardium (8). Because a Purkinje fiber diameter is ∼10 cells, we expect the electrotonic load to be less than in bulk myocardium because there will be less electrotonic load on the cells. Thus we predict that, given uniform electrophysiology in the Purkinje fiber system, focal excitations are likely to originate from the narrowest parts of the network.

Our analytic results reveal how the timing and morphology of focal excitations depends on the physiological parameters of the system. This is important as it will give insight on how these parameters influence the probability of occurrence of an ectopic beat. On long cables we find that the current conductance of I_K1 and the gap junction plays a crucial role. Expanding our expression for the liminal length (Eq. 20) for small p_o and p_c, we find that $n_l\sim \sqrt{g_j{g}_k}{\nu }_c/I_x$, showing that, as expected intuitively, the liminal length of tissue must grow with g_j, g_k, and ν_c, and decrease with increasing I_x. However, even more importantly, we find that the timing of these excitations scales exponentially with system parameters. Hence, we expect that small changes in electrophysiological properties, such as ion channel conductances, can dramatically alter the timing and location of ectopic foci. This result, may explain why ectopic beats tend to occur in specific regions, such as the pulmonary veins, where ion channel characteristics differ from that in the bulk myocardium (30,31).

A major limitation of this study is that we have only included a very crude treatment of the sodium channel. To fully connect with experiments, it will be important to describe more precisely the dynamics near the threshold for excitation. For example, it is likely that the precise time constants of activation and inactivation can dramatically alter our estimates for the liminal length. We expect that the details of this process will influence the timing and morphology of Ca-mediated focal excitations. Furthermore, it will be essential in the future to analyze the problem in higher dimensions. In three dimensions, the number of cells within the liminal length will be significantly larger, which implies that the MFPT will be exponentially longer than in one dimension. Also, the much larger number of cells will strengthen the requirement that p_o ∼ p_c for an excitation to occur. However, the main results of our findings should hold—namely, the exponential dependence of the MFPT on system parameters and the presence of a well-defined liminal length in cardiac tissue, along with the power-law dependence on the number of cells in large tissue sizes.