Abstract
All-atom molecular dynamics (MD) computer simulations have been applied successfully to duplex DNA structures in solution for some years and found to give close accord with observed results. However, the MD force fields have generally not been parameterized against unusual DNA structures, and their use to obtain dynamical models for this class of systems needs to be independently validated. The four-way junction (4WJ), or Holliday junction, is a dynamic DNA structure involved in central cellular processes of homologous replication and double strand break repair. Two conformations are observed in solution: a planar open-X form (OPN) with a mobile center and four duplex arms, and an immobile stacked-X (STX) form with two continuous strands and two crossover strands, stabilized by high salt conditions. To characterize the accuracy of MD modeling on 4WJ, we report a set of explicit solvent MD simulations of ∼100 ns on the repeat sequence d(CCGGTACCGG)4 starting from the STX structure (PDB code 1dcw), and an OPN structure built for the same sequence. All 4WJ MD simulations converged to a stable STX structure in close accord with the crystal structure. Our MD beginning in the OPN form converts to the STX form spontaneously at both high and low salt conditions, providing a model for the conformational transition. Thus, these simulations provide a successful account of the dynamical structure of the STX form of d(CCGGTACCGG)4 in solution, and provide new, to our knowledge, information on the conformational stability of the junction and distribution of counterions in the junction interior.
Introduction
The DNA four-way junction (4WJ), also known as the Holliday junction, is involved in central cellular processes of homologous replication and double strand break repair. Two conformations are observed in solution, a planar open-X form (OPN) with a mobile center and four duplex arms, and an immobile stacked-X (STX) form with two continuous strands and two crossover strands. The STX conformation requires adequate shielding of phosphate charges, and is stabilized by high salt conditions. In the course of a joint experimental and theoretical project, which involves structure prediction of the complex between two HU proteins and a DNA 4WJ (1), we require validation of molecular dynamics (MD) applied to a corresponding uncomplexed 4WJ. MD force fields have generally not been parameterized against unusual DNA structures, and the ability of a duplex DNA MD force field to transfer successfully to unusual DNA structures has yet to be fully determined. Analogous transferability to RNA structures has been documented by Sponer and co-workers (2,3), and is found to be quite complex.
We report herein a study of MD on 4WJs based on all-atom, explicit solvent MD simulations of ∼100 ns using the AMBER 9 suite of programs including the recent improvements on DNA force fields (4) and monovalent ions (5). In this study, MD was performed on the repeat sequence d(CCGGTACCGG)4 from two different starting structures, the STX structure (PDB #1dcw) and a model built OPN structure of the same sequence, both in two different salt conditions. Our study also includes a control MD on the corresponding duplex DNA sequence, d(CCGGTACCGG)2. This investigation focuses on the dynamics of the junction with respect to conformational stability, the transition from the OPN to STX form, and characterization of the water and ion atmosphere of the junction compared with corresponding results on duplex DNA.
There are five specific questions we address in the current study: 1), what is the dynamical stability of the MD models obtained for d(CCGGTACCGG)4; 2), what level of agreement is obtained between the MD calculated and experimentally observed results; 3), what new information is obtained on dynamics of the system, such as the thermal dispersion of structures in the MD ensemble and the conformational stability of the STX and OPN forms; 4), how does the structure of the DNA at and around the junction compare with that of corresponding duplex DNA; and 5), what distribution of water and mobile ions is predicted for the junction? More specifically, our simulations aim to address how phosphate charges in the junction are compensated for by counterions, and how the MD distribution of these ions compares with the Manning-like condensation of counterions around duplex DNA.
Background
The four-stranded DNA junction originally proposed by Holliday (6) has been implicated in a number of cellular processes including homologous recombination, DNA repair, replication restart, and viral integration (7). Distinct conformational forms of Holliday junctions have been identified in solution using a number of methods including single molecule fluorescence resonance energy transfer (FRET) (8). The solution conformation of 4WJs was initially assessed by gel mobility (9,10), later confirmed by FRET (11,12), and directly visualized by single-molecule FRET (13). These experiments were mainly performed on longer junctions of different nucleic acid sequence that were immobile. Our investigations have focused on a junction composed of homologous sequences of 10 basepairs (bp) whose structure has been determined by x-ray crystallography (14). At physiological conditions the preferred conformation of a 4WJ is generally the STX form in which there are two continuous and two crossover strands. The crossover at the junction results in essentially coaxial duplex arms with an interduplex angle (IDA) of ∼60° and a torsion angle between junction arms (Jtwist) of ∼40° (15). The STX form is capable of adopting either an antiparallel or a parallel conformation, and the parallel conformation was predicted to be the more biologically significant structure for homologous recombination (16). However, experimental evidence has shown that the antiparallel conformation is the more commonly observed solution structure (9,13,17,18). Under low salt conditions, 4WJs typically adopt the square planar OPN conformation in which the IDA relating the adjacent duplex arms is ∼90° and the Jtwist angle between junction arms is presumably ∼0°.
The first crystal structure of a DNA Holliday junction was solved by Ortiz-Lombardia et al. (19) for the sequence d(CCGGGACCGG)4 in the STX antiparallel conformation with two G:A mismatches. There have since been a number of x-ray crystallographic structures of Holliday junctions reported for STX forms (20,21) and for OPN or hybrid forms complexed with proteins (22,23). The symmetric d(CCGGTACCGG)4 (ApC) junction and the G:A mismatch junction served as the basis for further crystallographic studies by Eichman et al. (14), which focused on the nature of the conserved ACC core of the STX form adopted in several known crystal structures. However, subsequent studies have shown that the requirement of an ACC core is not as strict as initially suspected (24).
The Eichman et al. crystal structure of the ApC 4WJ (Fig. 1 A) is an antiparallel STX form composed of four strands of DNA. The two outer strands (labeled I and III) wrap around the outside of the structure and the two inner strands (labeled II and IV) crossover between the pseudoduplexes and make an abrupt turn at the positions of strand exchange (A16pC17 and A36pC37 of the ACC core of the junction; Fig. 1 B). The bps between the outer and inner strands form two pseudocontinuous DNA duplexes, each made up of a 6 bp arm stacked on a 4 bp arm. The ∼41° Jtwist between the ApC pseudoduplexes is shallower than the ∼60° Jtwist estimation for affixed Holliday junctions obtained by gel electrophoresis and FRET (9,11,25,26), and for 4WJ analogs obtained by atomic force microscopy (27). Contacts between adjacent duplexes occur around the A16pC17 and A36pC37 steps of crossover strands II and IV at the junction, and between the phosphate oxygen atoms of C2 and G30; C22, and G10 near the ends of each arm (Fig. 1, A and C) (14).
Figure 1.
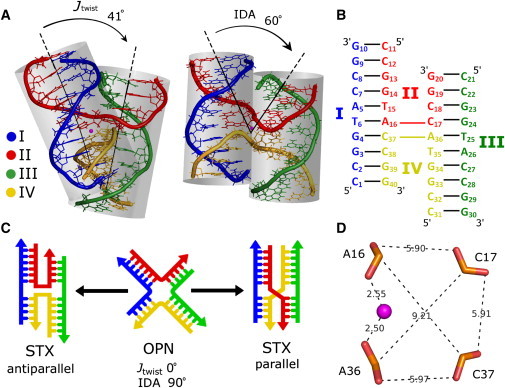
(A) Crystal structure of 1dcw, the inverted repeat d(CCGGTACCGG)4 (ApC) junction resolved to 2.1 Å. In the center of the junction in pink is a crystallographically resolved sodium ion. Strands I and III are linear; II and IV are crossover strands. The reported Jtwist and IDA angles between the pseudoduplexes are ∼41° and ∼60°, respectively. (B) Strand sequence and numbered base layout for the ApC junction. Junction bases refer to A16pC17 and A36pC37 of strands II and IV. (C) A schematic representing the canonical stacked-X and open-X conformations of a Holliday junction, denoted STX and OPN, respectively. The STX form is characterized by either an antiparallel or parallel directionality, the former of which applies to the ApC junction. (D) Phosphate group atoms in the junction crossover site of bases A16, C17, A36, and C37, and the crystallographically resolved sodium ion in pink. Distances are shown in angstroms.
The essential perturbations in structures of the DNA arms in the ApC junction are present in the backbone torsion angles between A16pC17 and A36pC37 of the crossover strands and the low helical twist angles for the bp steps in the crossover region. The sugar-phosphate backbone parameters are relatively unperturbed even where the inner strands crossover, and compensatory rotation is instead localized around the β (P-O5′-C5′-C4) torsion angles of the backbone and the glycosidic χ angles. The helical twist at the d(G14pT15/A16∗C17) bp step at the junction (denoted ∗) is 34°, which is well within the range of twist values observed in DNA duplexes (14). The bp steps flanking the junction are overwound at the 4 bp arm and underwound at the 6 bp arm. Thus, in this structure the overwinding at one side of the junction is compensated for by the underwinding of the other side such that overall B-form structure is essentially maintained (14). The minor grooves of both pseudoduplexes are on one face of the junction, whereas the major groove surfaces are connected smoothly across the junction on the other face.
The experimentally observed conformation of the 4WJ (STX versus OPN) is highly dependent on salt concentration, with STX forms stabilized at physiological salt concentrations, and the OPN form favored at low salt for which there is more phosphate-phosphate separation (8–10). In the STX form of the ApC junction, the four phosphate groups of bases A16, C17, A36, and C37 of crossover strands II and IV are located within ∼6−9 Å of one another (Fig. 1 D), resulting in a strong negative region of electrostatic potential around the junction. In the OPN form, the analogous four equidistant phosphate groups are ∼27 Å from one another, and thus require less screening for the structure to be electrostatically stable. A peak in crystallographic electron density of the ApC junction was assigned to a sodium ion bridging the O2P oxygen atoms of the A16 and A36 bases of strands II and IV at the junction (Fig. 1 D). As noted by Eichman et al. (14), the gaps between the adjacent neighboring arms of the ApC junction are also locations of high negative electrostatic potential, and additional counterions are expected to be required to counterbalance the anionic repulsions.
Plausible computational models of DNA structure and motions based on AMBER MD simulations including explicit solvent date back to the development of the second generation force field by Cornell et al. known as parm94 (28). The first MD simulations on DNA using parm94 provided a successful description of the B-form double helix; for reviews see (29) and (30). MD on DNA using CHARMM has been reported by MacKerell and co-workers (31). An AMBER model of DNA has been compared with both crystallographic and NMR results on the prototype d(CGCGAATTCGCG)2 duplex and found to be in close accord with the experimental results (32). Subsequent application of MD on DNA in general can be followed in a series of review articles (33–35), an MD on d(CGCGAATTCGCG) has recently been extended up to 1 μs (36). A recent collaboration was formed to test MD on DNA and investigate sequence effects on structure based on trajectories for all 136 permutations of tetranucleotide bp steps (37–39). This collaboration characterized the stability of the simulations, the agreement between MD and experiment, and investigated context effects on bp step geometries. However, an ergodic problem was encountered in the behavior of the α/γ backbone in long MDs based on the parm99 force field (28,40). This problem was subsequently remedied by Perez et al. (4) with a modification included in the AMBER force field parmbsc0, which is the most current force field for use in MD on DNA. In a recent study of a DNA minicircle (41), initial results based on the AMBER parm94 force field showed some problems, but MD based on the parmbsc0 force field resulted in an improved dynamical model (42).
Molecular modeling and simulations on Holliday junctions began with the elucidation of the stereochemistry by von Kitzing et al. (43,44). An initial set of computer models of static structures for Holliday junctions was set forth by Srinivasan and Olson (45). Westhof and co-workers (46) predicted metal ion binding sites for a number of 4WJs including the ApC junction in a dielectric continuum using Brownian dynamics, and found that Brownian dynamics counterions were preferentially localized in the minor groove of the OPN structures, and the major grove of the STX structures. Yu et al. (47) reported a 6 ns MD simulation on the ApC junction based on the CHARMM27 force field (31), used the results to deduce conformational models for transitions within Holliday junctions, proposed a schematic framework for the classification of these changes, and provided theoretical evidence for a tetrahedral OPN junction. However, these results were derived from the initial portion of a simulation that proved to be dynamically unstable after 6 ns.
Materials and Methods
Three sets of MD simulations are reported herein; each with both a minimal salt (MS) electroneutral condition, and a physiological 200 mM NaCl condition denoted high salt (HS). The three systems are 1), the ApC junction beginning from the STX form (crystal structure 1dcw) (denoted STX-MS and STX-HS), 2), the ApC junction beginning from a modified OPN model obtained from Olson and built using 3DNA (48) (denoted OPN-MS and OPN-HS), 3), and a corresponding canonical B DNA d(CCGGTACCGG)2 duplex (denoted CBD-MS and CBD-HS) built using the make-NA web server (49). All six simulations were performed for over 100 ns of MD. Five repeat MD trajectories with different distributions of initial velocities were performed for the OPN-MS system to assure simulations of this system are reproducible. See the Supporting Material, section S7, for additional details.
All simulations were carried out with the PMEMD version of the AMBER 9.0 suite of programs (50). The parm99 force field using the parmbsc0 (4) and ions08 (5) modifications were used for DNA and monovalent ions, respectively. The systems were solvated in an octahedral box of TIP3P water molecules (51), extending to a minimum boundary distance of 12 Å from all DNA atoms. Minimization, heating to 300 K, and subsequent MD of the DNA, ions, and water were carried out by standard procedures. A 9 Å nonbonded van der Waals cutoff was employed along with the particle mesh Ewald method treatment of long-range electrostatics (52,53). A constant pressure of 1 atm and the temperature of 300 K were maintained during the MD using Berendsen coupling (54), and SHAKE (55) was applied to fix all the covalent bonds to hydrogen atoms. A 2 fs time step was used in all simulations.
MD stability and sampling was assessed with root mean-square deviation (RMSD) and principal component analysis (PCA) of the covariance matrices (Supporting Material, sections S.5.1–S.5.4). We assessed the convergence of each simulation by calculating the RMSD of the DNA backbone with respect to the average structure for 25 ns blocks of trajectory snapshots (Figs. S1–S6). The Curves+ program of DNA analysis (39,56,57) was used to examine bp and bp step parameters and the axis behavior of the pseudoduplex arms. The helix axes generated using Curves+ were also used to calculate Jtwist values for 4WJ structures. Average water and ion density histograms and ion occupancies were calculated using the ptraj (50,59) module of AmberTools 1.2 (Supporting Material, section S3).
The focus of this work is an overall assessment of AMBER MD simulations of the ApC junction compared with the corresponding 2.1 Å crystal structure solved by Eichmann et al. (14). Although this crystal structure provides the most highly resolved experimental STX structure of the ApC junction, the MD simulations involved in this study provide a model for the structure in solution. It should also be noted that there are no available experimental results for the OPN form of the ApC junction in solution. Thus, the observed and calculated results are not expected to be identical, but should be in close accord if the MD model is plausible.
Results
Dynamical stability of MD on 4WJ
The junction was examined in the OPN and STX conformations under both HS and MS conditions for a total of 100 ns for each simulation. We calculated the RMSD of OPN-HS, OPN-MS, STX-HS, and STX-MS DNA backbone atoms with respect to the 1dcw crystal structure for the first 30 ns of each simulation (Fig. 2 A). All four simulations equilibrated in ∼4–8 ns and remained stable over the remainder of their 100 ns trajectories (Fig. S7). The first two principal components of the STX-MS simulation are displayed as a time progression alongside their corresponding population distribution plots (Fig. 2 B). The PCA shows a single well-populated ensemble of trajectory snapshots for the two STX systems (Fig. S10, A and B). The junction remained stacked for 100 ns of MD and we found only minor salt concentration effects. The OPN-HS and OPN-MS MD transitioned from the OPN form to the STX form, and the HS transition is depicted in greater detail (see Fig. 5) (The PCA are provided in Fig. S10, C and D). The starting OPN structure and final antiparallel STX structure are shown in Fig. 2 C, with junction bases (A16, C17, A36, and C37) shown highlighted in cyan. The MD average structures from the equilibrated portions of the four simulations and the 1dcw crystal structure are superimposed in Fig. 2 D. The four simulations all folded into the antiparallel STX form, and are in close agreement with backbone RMSD values of ∼4 Å from the STX crystal structure and ∼1 Å from one another.
Figure 2.
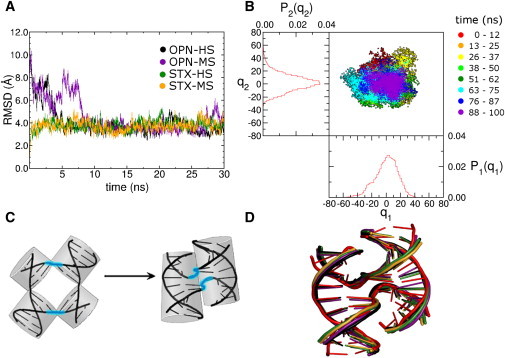
(A) Backbone RMSD of OPN-HS, OPN-MS, STX-HS, and STX-MS all referenced to crystal structure 1dcw. End bps are omitted. All four starting conditions converged to the same antiparallel STX conformation, with both OPN-HS and OPN-MS transitioning from OPN to STX. (B) PCA of the covariance of atomic fluctuation for MD on STX-MS. The time progression of the simulation is denoted by progression through the visible spectrum with red indicating the initial portion of the simulation and purple the end portion. The corresponding population distribution plots are shown in red. (C) OPN model starting conformation and STX ending/starting conformation. Junction bases are highlighted in cyan. (D) Superposition of average converged structures from OPN-HS (black), OPN-MS (purple), STX-HS (green), and STX-MS (yellow) with the 1dcw crystal structure (red). Backbone RMSD between the average STX-HS structure and 1dcw is ∼3.3 Å, and for the backbone of junction bases 16, 17, 36, and 37 is ∼2.8 Å.
Figure 5.
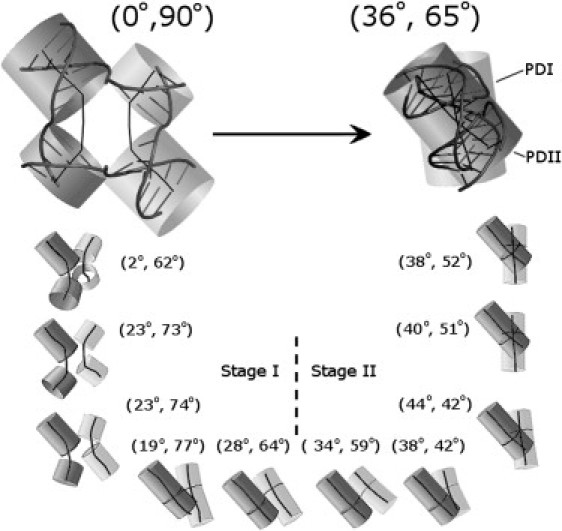
Progression from OPN to STX for the OPN-HS system in 1 ns intervals for 11 ns of MD. Twist and bend angles for each interval is shown as (Jtwist, IDA) next to their corresponding structures. Stage I roughly corresponds to the bending step, and Stage II roughly corresponds to the twisting step. The final structure is an average representative of the 11th ns, after which the structure remains stacked with minor thermal fluctuations. The two pseudoduplexes (PDI, PDII) are shown in two shades of gray with the central bend axes in black.
Atomic fluctuations (B-factors) are plotted as a function of sequence for the equilibrated structures of STX-HS and OPN-HS in Fig. 3. Bases 1–10; 21–30 correspond to linear strands I and III and 11–20; 31–40 correspond to crossover strands II and IV (Fig. 1 A). The largest fluctuations occur near the ends of each arm of the junction, and the regions corresponding to the center of the junction near bases A16, C17, A36, and C37 show the lowest fluctuation values, indicating the center of the STX junction is a region with a high degree of stability. Junction bases are expected to be well stabilized in the HS condition due to adequate phosphate shielding, and indeed both STX-HS and OPN-HS simulations equilibrated to form STX structures with junction phosphates stabilized in close proximity.
Figure 3.
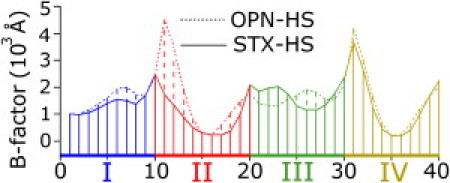
B-factors by sequence for OPN-HS and STX-HS averaged from 90–100 ns of MD. The junction bases 16, 17, 36, and 37 appear more stable, whereas the end bases 1, 10, 11, 20, 21, 30, 31, and 40 appear most dynamic. MD calculated B-factors are atomic positional fluctuations multiplied by (8/3)π2.
Comparison of MD on 4WJ and duplex B DNA
A comparison of the bp helical parameters x-displacement (XDP) and inclination (INC) for the first pseudoduplex arm of STX-HS (STX-PDI), and the duplex DNA CBD-HS are compared in Fig. 4. Basepair parameters XDP and INC can be used in combination to describe the geometries of both canonical A and B forms of DNA, and as a result can be used to distinguish between the two forms. The bp parameters for STX-PDI and CBD-HS closely parallel one another in the case of both XDP and INC, and in general, fall between the canonical A-DNA and B-DNA values for these parameters. Application of the t-tests reveal that the differences for XDP and INC for the two MD structures are not statistically significant (see the Supporting Material, section S.6.2). The corresponding results for the bp step parameters roll, twist, tilt, and rise (Fig. S11) indicate comparable results regarding statistical insignificance (Table S2).
Figure 4.
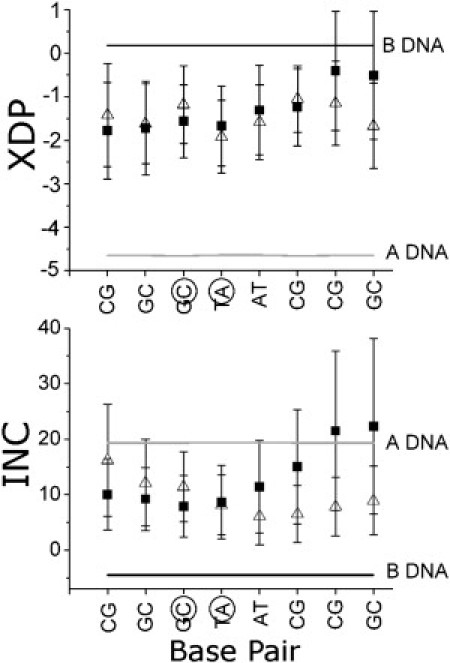
DNA bp parameters XDP and INC, capable together of characterizing canonical B DNA or A DNA. Black squares refer to parameter values of the equilibrated MD average for CBD-HS, and white triangles are the parameter values of the equilibrated MD average for a STX-HS pseudoduplex arm (STX-PDI). Standard values for B DNA and A DNA are shown in black and gray, respectively, and junction bases are circled on the x axis. Error bars indicate one standard deviation.
MD water and ion distributions
See Fig. 6 for the MD calculated high-density water and ion distributions for the STX-HS simulation. The 1dcw crystal structure indicates a sodium ion at a position interior to the junction, but more ions are expected to be present in the regions that are not resolved crystallographically. The MD results show two main peaks in the calculated maximum ion density centered at distances of ∼5 Å from the ion in the crystal structure, and a number of other significant peaks in ion density around the STX structure as well.
Figure 6.
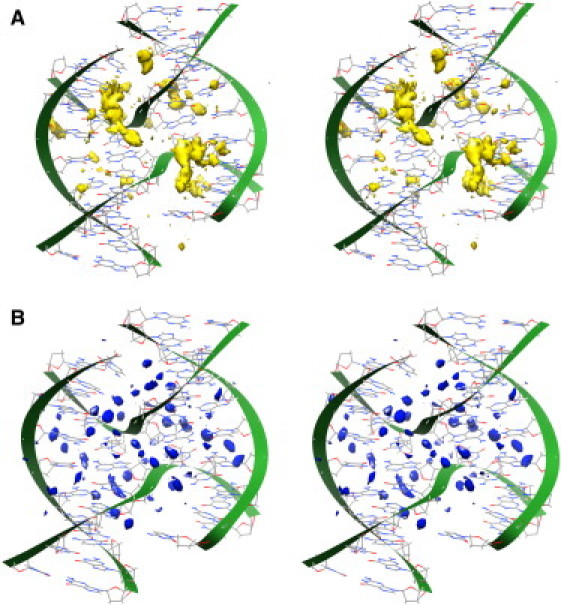
MD predictions for the regions of high density for (A) Na+ ions and (B) water molecules for the equilibrated portion of MD on STX-HS. Images are depicted in cross-eye stereo. The two regions of primarily high ion density are within ∼7 Å of one another and ∼5 Å of the crystallographically resolved Na+ ion in 1dcw (Fig. 1).
Further analysis of the dynamical structure of ions inside the junction is provided in terms of the calculated phosphate oxygen-sodium ion radial distribution function (RDF), see Fig. 7. Results on this for duplex DNA have been reported previously and found to support the counterion condensation theory (60–62). There are four phosphate groups that are closely involved in the structure of the stacked junction, and the average ion occupancy within 5 Å of the phosphate oxygen atoms is seen to compensate for ∼52% of the negative charges on the DNA backbone in the region. Thus, we do find evidence for a Manning-like counterion condensation within the junction, but with a smaller extent of charge compensation compared to duplex DNA (60).
Figure 7.
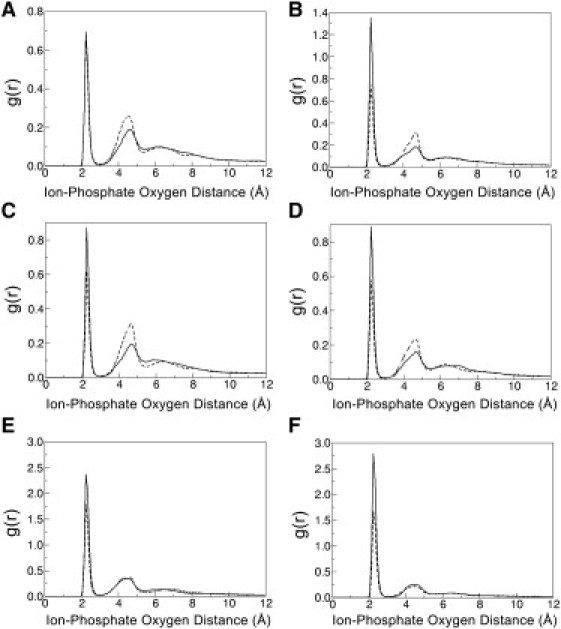
Radial distribution functions for Na+ ions within 12 Å of phosphate group oxygen atoms in junction bases A16, C17, A36, and C37 for (A) STX-HS, (B) STX-MS, (C) OPN-HS, and (D) OPN-MS, and for the phosphate oxygen atoms of (E) CBD-HS, and (F) CBD-MS. The solid lines refer to the O1P oxygen atoms, and the dashed lines to the O2P oxygen atoms. Data are taken from 80 ns of stable MD.
Discussion
Our MD results show that AMBER with the latest nucleic acid force field is capable of predicting a plausible solution structure of the ApC 4WJ. Simulations STX-MS, STX-HS, OPN-MS, and OPN-HS all equilibrated to the STX form of the junction and maintained stable convergence throughout the equilibrated portion of each 100 ns simulation (Fig. 2 and Figs. S1–S4). The average backbone RMSD between the four average equilibrated structures is ∼1 Å, and the close agreement of within ∼4 Å backbone RMSD of the 1dcw crystal structure serves to validate the ability of the force field to describe the dynamics of the 4WJ STX solution structure. It should be noted, however, that the crystal structure may differ to some extent from the solution structure, which is dynamic and capable of undergoing thermal breathing and fluctuations. This is evident in Fig. 2 A, where the backbone RMSD plot reveals a small degree of continuous fluctuation within ∼1 Å of the average structure.
A more thorough investigation of the convergence of each simulation is examined using PCA, which examines the substate sampling throughout the trajectory of the simulation (see the Supporting Material, section S.5.4). PCA results for STX-MS (Fig. 2 B) indicate a relatively narrow sampling of individual substates over the course of the MD simulation, with similar results having been observed in STX-HS (Fig. S10 A). PCA results for the OPN simulations displayed a similarly narrow sampling of substates, but only after the initial transition from OPN to STX (Fig. S10, C and D). A narrow sampling of substates is indicative of a stable MD simulation.
The OPN to STX transition for the OPN-HS simulation is represented in greater detail in nanosecond intervals in Fig. 5. The progression from OPN to STX can be characterized by monitoring the changes in Jtwist and IDA angles over time. This particular stacking process can be roughly described by two main stages, a pseudoduplex formation unbending stage (stage I), and a stacking/twisting stage (stage II). In stage I, a decrease in the IDA angle between arms that contain the eventual crossover strands and a corresponding increase in the IDA angle between arms that contain the eventual continuous strands forms the two pseudoduplexes. As the pseudoduplexes form, they begin to twist relative to one another, leading to an increase in the Jtwist. In stage II the junction phosphates approach one another and the two newly formed pseudoduplexes continue to stack and twist relative to one another, leading to a further increase in the Jtwist angle. This MD calculated progression provides one possible mechanism for how a junction might transition from the OPN form to the STX form. The reverse of this pathway may also account for one possible unstacking mechanism in solution characterized by an untwisting step, followed by an unbending step wherein the opening in the center of the junction is formed.
The average bp and bp step parameters XDP and INC for STX-PDI and CBD-HS over an equilibrated portion of the MD are examined in detail in Fig. 4 to assess how the pseudoduplexes of the junction behave when compared to an MD predicted structure of duplex DNA in solution. STX-PDI is the pseudoduplex consisting of bases 1–10, 11–16, and 37–40, whereas STX-PDII consists of bases 17–20, 21–30, and 31–16. The bp parameter results for STX-PDI and STX-PDII are statistically indistinguishable, and so for simplicity, only STX-PDI will be used in the comparison with the duplex DNA. A t-test indicates that the differences in parameter data for STX-PDI and CBD-HS are also not statistically significant (see the Supporting Material, section S6). This implies that, despite the presence of two crossover points connecting to a neighboring pseudoduplex, the dynamical structures of the 4WJ pseudoduplexes are behaving similar to that of the corresponding duplex DNA in solution. A second observation is that both STX-PDI and CBD-HS parameters also tend to fall between the values for canonical A and canonical B DNA in solution. Together, the implications of these results are that the MD predicted structure of the junction shows characteristic DNA duplex behavior without specific regard to the junction crossover point, and that any sequence effects present in CBD-HS for this sequence are either negligible or are expressed equally in STX-PDI.
The water and ion distributions for the 1dcw simulation shown in Fig. 6 predict details of ordered ion and water density around the stacked structure in solution not resolved in the crystal structure. Two peaks of ion density are consistently observed throughout the equilibrated MD simulation within ∼5 Å of the ion resolved in the crystal structure. This suggests there is likely a need for several cations near the junction phosphates in the STX form to neutralize the opposing negative charges enough for the junction to stack. Fig. 7 contains RDF plots of Na+ ions with respect to phosphate oxygen atoms for junction bases in STX and OPN simulations, and for the CBD simulations. The six RDF plots are similar in shape with a large peak at a distance of ∼2 Å and a smaller peak at ∼4.5 Å, showing the presence of ordered ion shell structures within ∼5 Å of phosphate oxygen atoms for both the junction and B DNA.
The center of the junction of the STX form is defined as bases A16, C17, A36, and C37 (Fig. 2 B) of the structure, with the two phosphates of bases C37 and C17 of the crossover strands separated by only ∼6 Å (Fig. 1 D). A calculation of the average occupancy of Na+ ions within 5 Å of a junction phosphate oxygen is ∼52%, indicating that roughly half of the charge on the junction phosphates is compensated for by local counterions. There are six phosphates encompassed within a ∼10 Å region around the center of mass of the junction crossover phosphates, and the average number of sodium ions observed within this region over a portion of equilibrated MD accounts for ∼67% of the negative phosphate charge. The number of observed chloride ions within 10 Å of the junction at a given time was zero, thus the net charge of the junction is obtained by the inclusion of phosphate groups and Na+ ions only.
Conclusions
Overall, this study indicates that MD based on the AMBER parmbsc0 DNA force field provides a reasonable description of the dynamical structure of d(CCGGTACCGG)4 in aqueous solution. The simulations remained stable over 100 ns of MD, and the RMSD was ∼4 Å between each of the four junction simulations and the crystal structure, and ∼1 Å between the average structures of each simulation. The results indicate the salt concentration affected equilibration time and the transitional pathway, but the equilibrated prediction structure for all four systems was the STX form. The transition from the modeled OPN structure to the STX structure for system OPN-HS was examined with respect to IDA and Jtwist angles at 1 ns intervals for 11 ns (Fig. 5). Over the course of the transition, the IDA decreased from 90° to ∼60° and the Jtwist increased from 0° to ∼40°, similar to FRET data obtained for other 4WJ structures and consistent with the crystal structure for the STX form.
Analysis of the water and ion atmosphere of the junction revealed that in the STX form four of the junction phosphates are neutralized by ∼52% and six are neutralized by ∼67% by local counterion condensation. Comparison of the 4WJ pseudoduplexes to corresponding duplex DNA in solution returned statistically indistinguishable results for DNA bp and bp step parameters used to characterize nucleic acid geometry. This is consistent with what has been previously observed in 4WJ crystal structures. One notable open issue is that the minimal salt systems STX-MS and OPN-MS did not equilibrate to an open 4WJ structure. There is no direct experimental determination of the low salt form of the d(CCGGTACCGG)4 sequence, but an open form would be anticipated from the behavior of related systems. Subsequent spectroscopic and computational studies will address this issue.
Acknowledgments
This work was supported by the National Science Foundation (MCB-0843656 to I.M.) and the National Institutes NIH National Research Service Award (NRSA) NIH NRSA Postdoctoral Fellowship (F32-GM-87101). General support was provided via National Institute of General Medical Services (NIGMS) training grant GM-008271. This work was partially supported by the National Science Foundation through the TeraGrid resources provided by grant number CHE10004 utilizing the Ranger Cluster at the Texas Advanced Computing Center.
Supporting Material
References
- 1.Wheatley, E. G., S. N. Pieniazek, …, D. L. Beveridge. 2011. Structure prediction of a novel protein-DNA complex. HU with a DNA four-way junction. In Innovations in Biomolecular Modeling and Simulations. In press.
- 2.Banáš P., Hollas D., Otyepka M. Performance of molecular mechanics force fields for RNA simulations. Stability of UUCG and GNRA hairpins. J. Chem. Theory Comput. 2010;6:3836–3849. doi: 10.1021/ct100481h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ditzler M.A., Otyepka M., Walter N.G. Molecular dynamics and quantum mechanics of RNA: conformational and chemical change we can believe in. Acc. Chem. Res. 2010;43:40–47. doi: 10.1021/ar900093g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pérez A., Marchán I., Orozco M. Refinement of the AMBER force field for nucleic acids: improving the description of alpha/gamma conformers. Biophys. J. 2007;92:3817–3829. doi: 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Joung I.S., Cheatham T.E., 3rd Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B. 2008;112:9020–9041. doi: 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Holliday R. A mechanism for gene conversion in fungi. Genet. Res. 2007;89:285–307. doi: 10.1017/S0016672308009476. [DOI] [PubMed] [Google Scholar]
- 7.Lilley D.M., White M.F. The junction-resolving enzymes. Nat. Rev. Mol. Cell Biol. 2001;2:433–443. doi: 10.1038/35073057. [DOI] [PubMed] [Google Scholar]
- 8.Lilley D.M. Structures of helical junctions in nucleic acids. Q. Rev. Biophys. 2000;33:109–159. doi: 10.1017/s0033583500003590. [DOI] [PubMed] [Google Scholar]
- 9.Duckett D.R., Murchie A.I., Lilley D.M. The structure of the Holliday junction, and its resolution. Cell. 1988;55:79–89. doi: 10.1016/0092-8674(88)90011-6. [DOI] [PubMed] [Google Scholar]
- 10.Duckett D.R., Murchie A.I., Lilley D.M. The role of metal ions in the conformation of the four-way DNA junction. EMBO J. 1990;9:583–590. doi: 10.1002/j.1460-2075.1990.tb08146.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Clegg R.M., Murchie A.I., Lilley D.M. The solution structure of the four-way DNA junction at low-salt conditions: a fluorescence resonance energy transfer analysis. Biophys. J. 1994;66:99–109. doi: 10.1016/S0006-3495(94)80765-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Clegg R.M., Murchie A.I., Lilley D.M. Fluorescence resonance energy transfer analysis of the structure of the four-way DNA junction. Biochemistry. 1992;31:4846–4856. doi: 10.1021/bi00135a016. [DOI] [PubMed] [Google Scholar]
- 13.McKinney S.A., Déclais A.C., Ha T. Structural dynamics of individual Holliday junctions. Nat. Struct. Biol. 2003;10:93–97. doi: 10.1038/nsb883. [DOI] [PubMed] [Google Scholar]
- 14.Eichman B.F., Vargason J.M., Ho P.S. The Holliday junction in an inverted repeat DNA sequence: sequence effects on the structure of four-way junctions. Proc. Natl. Acad. Sci. USA. 2000;97:3971–3976. doi: 10.1073/pnas.97.8.3971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Watson J., Hays F.A., Ho P.S. Definitions and analysis of DNA Holliday junction geometry. Nucleic Acids Res. 2004;32:3017–3027. doi: 10.1093/nar/gkh631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sigal N., Alberts B. Genetic recombination: the nature of a crossed strand-exchange between two homologous DNA molecules. J. Mol. Biol. 1972;71:789–793. doi: 10.1016/s0022-2836(72)80039-1. [DOI] [PubMed] [Google Scholar]
- 17.Joo C., McKinney S.A., Ha T. Exploring rare conformational species and ionic effects in DNA Holliday junctions using single-molecule spectroscopy. J. Mol. Biol. 2004;341:739–751. doi: 10.1016/j.jmb.2004.06.024. [DOI] [PubMed] [Google Scholar]
- 18.Murchie A.I., Clegg R.M., Lilley D.M. Fluorescence energy transfer shows that the four-way DNA junction is a right-handed cross of antiparallel molecules. Nature. 1989;341:763–766. doi: 10.1038/341763a0. [DOI] [PubMed] [Google Scholar]
- 19.Ortiz-Lombardía M., González A., Coll M. Crystal structure of a DNA Holliday junction. Nat. Struct. Biol. 1999;6:913–917. doi: 10.1038/13277. [DOI] [PubMed] [Google Scholar]
- 20.Hays F.A., Teegarden A., Ho P.S. How sequence defines structure: a crystallographic map of DNA structure and conformation. Proc. Natl. Acad. Sci. USA. 2005;102:7157–7162. doi: 10.1073/pnas.0409455102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Khuu P., Ho P.S. A rare nucleotide base tautomer in the structure of an asymmetric DNA junction. Biochemistry. 2009;48:7824–7832. doi: 10.1021/bi900829b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Biertümpfel C., Yang W., Suck D. Crystal structure of T4 endonuclease VII resolving a Holliday junction. Nature. 2007;449:616–620. doi: 10.1038/nature06152. [DOI] [PubMed] [Google Scholar]
- 23.Ghosh K., Lau C.K., Van Duyne G.D. Peptide trapping of the Holliday junction intermediate in Cre-loxP site-specific recombination. J. Biol. Chem. 2005;280:8290–8299. doi: 10.1074/jbc.M411668200. [DOI] [PubMed] [Google Scholar]
- 24.Hays F.A., Vargason J.M., Ho P.S. Effect of sequence on the conformation of DNA holliday junctions. Biochemistry. 2003;42:9586–9597. doi: 10.1021/bi0346603. [DOI] [PubMed] [Google Scholar]
- 25.Cooper J.P., Hagerman P.J. Gel electrophoretic analysis of the geometry of a DNA four-way junction. J. Mol. Biol. 1987;198:711–719. doi: 10.1016/0022-2836(87)90212-9. [DOI] [PubMed] [Google Scholar]
- 26.Cooper J.P., Hagerman P.J. Geometry of a branched DNA structure in solution. Proc. Natl. Acad. Sci. USA. 1989;86:7336–7340. doi: 10.1073/pnas.86.19.7336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mao C., Sun W., Seeman N.C. Designed two-dimensional DNA Holliday junction arrays visualized by atomic force microscopy. J. Am. Chem. Soc. 1999;121:5437–5443. [Google Scholar]
- 28.Cornell W.D., Cieplak P., Kollman P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1995;117:5179–5197. [Google Scholar]
- 29.Cheatham T.E., 3rd, Kollman P.A. Molecular dynamics simulation of nucleic acids. Annu. Rev. Phys. Chem. 2000;51:435–471. doi: 10.1146/annurev.physchem.51.1.435. [DOI] [PubMed] [Google Scholar]
- 30.Cheatham T.E., 3rd, Young M.A. Molecular dynamics simulation of nucleic acids: successes, limitations, and promise. Biopolymers. 2000-2001;56:232–256. doi: 10.1002/1097-0282(2000)56:4<232::AID-BIP10037>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 31.MacKerell A.D., Jr., Banavali N., Foloppe N. Development and current status of the CHARMM force field for nucleic acids. Biopolymers. 2000-2001;56:257–265. doi: 10.1002/1097-0282(2000)56:4<257::AID-BIP10029>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- 32.Arthanari H., McConnell K.J., Bolton P.H. Assessment of the molecular dynamics structure of DNA in solution based on calculated and observed NMR NOESY volumes and dihedral angles from scalar coupling constants. Biopolymers. 2003;68:3–15. doi: 10.1002/bip.10263. [DOI] [PubMed] [Google Scholar]
- 33.Beveridge D.L., McConnell K.J. Nucleic acids: theory and computer simulation, Y2K. Curr. Opin. Struct. Biol. 2000;10:182–196. doi: 10.1016/s0959-440x(00)00076-2. [DOI] [PubMed] [Google Scholar]
- 34.Giudice E., Lavery R. Simulations of nucleic acids and their complexes. Acc. Chem. Res. 2002;35:350–357. doi: 10.1021/ar010023y. [DOI] [PubMed] [Google Scholar]
- 35.Beveridge D.L., Dixit S.B., Thayer K.M. Molecular dynamics simulations of DNA curvature and flexibility: helix phasing and premelting. Biopolymers. 2004;73:380–403. doi: 10.1002/bip.20019. [DOI] [PubMed] [Google Scholar]
- 36.Pérez A., Luque F.J., Orozco M. Dynamics of B-DNA on the microsecond time scale. J. Am. Chem. Soc. 2007;129:14739–14745. doi: 10.1021/ja0753546. [DOI] [PubMed] [Google Scholar]
- 37.Beveridge D.L., Barreiro G., Young M.A. Molecular dynamics simulations of the 136 unique tetranucleotide sequences of DNA oligonucleotides. I. Research design and results on d(CpG) steps. Biophys. J. 2004;87:3799–3813. doi: 10.1529/biophysj.104.045252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Dixit S.B., Beveridge D.L., Varnai P. Molecular dynamics simulations of the 136 unique tetranucleotide sequences of DNA oligonucleotides. II: sequence context effects on the dynamical structures of the 10 unique dinucleotide steps. Biophys. J. 2005;89:3721–3740. doi: 10.1529/biophysj.105.067397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lavery R., Zakrzewska K., Sponer J. A systematic molecular dynamics study of nearest-neighbor effects on base pair and base pair step conformations and fluctuations in B-DNA. Nucleic Acids Res. 2010;38:299–313. doi: 10.1093/nar/gkp834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Várnai P., Zakrzewska K. DNA and its counterions: a molecular dynamics study. Nucleic Acids Res. 2004;32:4269–4280. doi: 10.1093/nar/gkh765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lankas F., Lavery R., Maddocks J.H. Kinking occurs during molecular dynamics simulations of small DNA minicircles. Structure. 2006;14:1527–1534. doi: 10.1016/j.str.2006.08.004. [DOI] [PubMed] [Google Scholar]
- 42.Mitchell J.S., Laughton C.A., Harris S.A. Atomistic simulations reveal bubbles, kinks and wrinkles in supercoiled DNA. Nucleic Acids Res. 2011;39:3928–3938. doi: 10.1093/nar/gkq1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.von Kitzing E. Modeling DNA structures. Prog. Nucleic Acid Res. Mol. Biol. 1992;43:87–108. doi: 10.1016/s0079-6603(08)61045-4. [DOI] [PubMed] [Google Scholar]
- 44.von Kitzing E., Lilley D.M., Diekmann S. The stereochemistry of a four-way DNA junction: a theoretical study. Nucleic Acids Res. 1990;18:2671–2683. doi: 10.1093/nar/18.9.2671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Srinivasan A.R., Olson W.K. Computer models of DNA four-way junctions. Biochemistry. 1994;33:9389–9404. doi: 10.1021/bi00198a004. [DOI] [PubMed] [Google Scholar]
- 46.van Buuren B.N., Hermann T., Westhof E. Brownian-dynamics simulations of metal-ion binding to four-way junctions. Nucleic Acids Res. 2002;30:507–514. doi: 10.1093/nar/30.2.507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Yu J., Ha T., Schulten K. Conformational model of the Holliday junction transition deduced from molecular dynamics simulations. Nucleic Acids Res. 2004;32:6683–6695. doi: 10.1093/nar/gkh1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Karymov M.A., Chinnaraj M., Lyubchenko Y.L. Structure, dynamics, and branch migration of a DNA Holliday junction: a single-molecule fluorescence and modeling study. Biophys. J. 2008;95:4372–4383. doi: 10.1529/biophysj.108.135103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Macke T.J., Case D.A. Modeling unusual nucleic acid structures. In: Leontis N.B., SantaLucia J. Jr., editors. Molecular Modeling of Nucleic Acids. American Chemical Society; Washington, DC: 1998. pp. 379–393. [Google Scholar]
- 50.Case D.A., Darden T.A., Kollman P.A. University of California; San Francisco, CA: 2006. AMBER 9. [Google Scholar]
- 51.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 52.Darden T., York D., Pedersen L. Particle mesh Ewald: an N-log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 53.Essmann U., Perera L., Pederson L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8594. [Google Scholar]
- 54.Berendsen H.J.C., Postma J.P.M., Haak J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3691. [Google Scholar]
- 55.Ryckaert J.P., Ciccotti G., Berendensen H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 56.Lavery R., Sklenar H. The definition of generalized helicoidal parameters and of axis curvature for irregular nucleic acids. J. Biomol. Struct. Dyn. 1988;6:63–91. doi: 10.1080/07391102.1988.10506483. [DOI] [PubMed] [Google Scholar]
- 57.Lavery R., Sklenar H. Defining the structure of irregular nucleic acids: conventions and principles. J. Biomol. Struct. Dyn. 1989;6:655–667. doi: 10.1080/07391102.1989.10507728. [DOI] [PubMed] [Google Scholar]
- 58.Reference deleted in proof.
- 59.Case D.A., Cheatham T.E., 3rd, Woods R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Manning G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Q. Rev. Biophys. 1978;11:179–246. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- 61.Record M.T., Jr., Anderson C.F., Lohman T.M. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening, and ion effects on water activity. Q. Rev. Biophys. 1978;11:103–178. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
- 62.Young M.A., Jayaram B., Beveridge D. Intrusion of counterions into the spine of hydration in the minor groove of B-DNA: fractional occupancy of electronegative pockets. J. Am. Chem. Soc. 1997;119:59–69. [Google Scholar]
- 63.Lavery R., Moakher M., Zakrzewska K. Conformational analysis of nucleic acids revisited: Curves+ Nucleic Acids Res. 2009;37:5917–5929. doi: 10.1093/nar/gkp608. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


