Exploring the Symmetry and Mechanism of Virus Capsid Maturation Via an Ensemble of Pathways

Abstract

Many icosahedral viruses undergo large-scale conformational transitions between icosahedrally symmetric conformations during their life cycles. However, whether icosahedral symmetry is maintained along the transition pathways for this process is unknown. By employing a simplified and directed structure-based potential we compute an ensemble of transition pathways for the maturation transition of bacteriophage HK97. We observe localized symmetry-breaking events, but find that the large-scale displacements are dominated by icosahedrally symmetric deformation modes. We find that all pathways obey a common mechanism characterized by formation of pentameric contacts early in the transition.

Introduction

Spherical viruses display icosahedral symmetry in their protein shell (capsid), and many high-resolution structures of capsids have been determined (1). These spherical capsids typically consist of 60T copies of a single protein subunit arranged in an icosahedral lattice, where T is the triangulation number that describes the architecture of the capsid. T can take on only a select set of integer values according to T = h² + k² + hk, where h and k are nonnegative integers (2). The subunit proteins form five-member (pentamer) and six-member (hexamer) oligomers. A complete icosahedral shell consists of 12 pentamers and 10(T – 1) hexamers. The organization of a T = 7 shell is displayed in Fig. 1 A.

Figure 1.

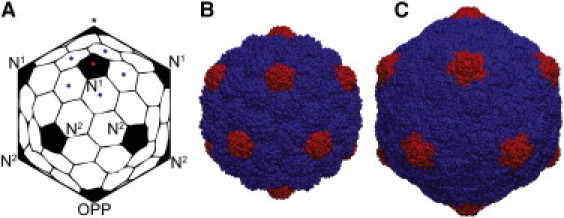
T = 7 capsids. (A) An idealized representation of a capsid, with the pentamers labeled as first neighbors (N¹), 2nd neighbors (N²), or opposite (OPP) of the pentamer denoted by ^⋆. In a T = 7, each pentamer (red dot) is surrounded by five unique hexamers (blue dots). (B) The immature PHII structure of HK97 (PDB 3e8k). (C) The mature HII structure of HK97 (PDB 1ohg).

One of the most pronounced and heavily studied capsid transitions is the maturation of the bacteriophage HK97. HK97 is a double-stranded DNA virus of T = 7 organization. The life cycle of HK97 involves formation of a precursor capsid (Prohead I), followed by cleavage of the 102 N-terminal residues of the coat protein, which induces a change to the metastable Prohead II (PHII) form (Fig. 1 B) (3). The transition from PHII to the mature Head II (HII) state (Fig. 1 C) is triggered by DNA packaging, but in vitro, the transition can be achieved in the absence of DNA by lowering the system pH (4). The transition to HII involves significant expansion and a morphological change from a spherical to a faceted shape (5–7). A chemical change also occurs in the formation of isopeptide bonds (cross-links) between residues Lys¹⁶⁹ and Asn³⁵⁶ on neighboring subunits (5). An analogous maturation transition can also be achieved in cross-link-deficient mutant particles in which the cross-linking lysine is mutated (K169Y), resulting in what is known as the Head I (HI) structure, which is morphologically identical to the HII state (8). Although the cross-links provide thermodynamic stability to the HII particle (9,10), the ability of the mutant particle to both swell and facet (HI) clearly implies that the structural maturation transition is not dependent on cross-linking (8,11,12). A combined computational and experimental AFM study on HK97 was recently performed in which the mechanical properties were examined during stages of the maturation process (13). Significant changes to the mechanical behavior of HK97 were observed at low cross-linking levels and also in the cross-link-deficient mature HI particle (as compared to the immature PHII state). High-resolution crystal structures of both the PHII (6) and HII (14) structures are available.

X-ray crystallography and cryo-electron microscopy (cryo-EM) are extremely powerful tools for determining structures that are thermodynamically stable, but these methods are not capable of determining unstable intermediate structures at atomic resolution. Furthermore, both of these techniques employ icosahedral averaging, and therefore, all solved spherical-virus capsid structures reflect icosahedral symmetry. Recently, the time-course behavior of virus dynamics has been studied with biochemical techniques (10,15), and the development of site-directed spin labeling of capsids is a promising technique for obtaining dynamical structural information (16). Given the challenges of studying virus dynamical properties experimentally, theory and computation have been important tools for understanding these phenomena. Hence, much insight into virus structure, dynamics, and mechanics has come from theoretical and computational studies (17,18).

The transition of HK97 from PHII to HII has been studied using normal-mode analysis (NMA) of an elastic network model (ENM) (19) and a Gaussian network model (20). It was shown that the transition could be achieved by displacements along a few low-frequency icosahedral normal modes. Since both endpoints observe icosahedral symmetry and NMA provides an orthogonal basis, only icosahedral normal modes yield nonzero projections onto the displacement vector describing the transition. However, if the virus spontaneously breaks symmetry (through a thermal fluctuation), then icosahedral modes cannot exist. Therefore, for a nonsymmetric structure, the question arises as to whether the system first restores symmetry and proceeds along an icosahedral preserving pathway, or, alternatively, the system proceeds on an off-icosahedral pathway and then restores symmetry at a later point along the transition. Nonicosahedral structures were observed in a recent computational study on virus swelling (21), though it is unclear whether the observed swelling behavior was related to the pH-induced biological swelling for that system, and the methods employed in that study are not well established. Group-theory analysis has indicated that symmetry does break in virus swelling transitions (22), however this analysis was performed in six-dimensional space and it is unclear what the implications are in three dimensions. Studies on the equilibrium dynamics of capsids using all-atom molecular dynamics (MD) (23,24) and network models (20,25) have shown that the dominant equilibrium motions are nonicosahedral, and that therefore the systems do break symmetry. In an ensemble of capsids, there is an obvious entropic benefit to breaking symmetry, but this is an equilibrium property of the system. In this article, we will address the nonequilibrium behavior of HK97 as it transitions from PHII to HII.

Materials and Methods

The structure of the HII capsid was obtained from the VIPER database (1) (Protein Data Bank (PDB) code 1ohg). The contacts and interaction parameters for HII were defined based upon the Karanicolas and Brooks Cα Gō model (26,27). In this model, contacts are identified based upon hydrogen bonding and side chain-side chain (SC-SC) interactions. The SC-SC interaction strength is based upon the Miyazawa-Jernigan contact energies (28). Nonnative, nonbonded contacts interact through a purely repulsive (r⁻¹²) term; bonded terms include pseudobond, angle, and dihedrals. We employ a native contact potential form (V), consistent with the Onuchic et al. Cα Gō model (29)

$$V_{ij}={ϵ}_{ij}\left[5{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-6{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{10}\right],$$ (1)

where ε is the interaction strength, σ is the native contact distance, and r is the separation between beads i and j. This form is slightly different from Karanicolas and Brooks, who used a 12-10-6 potential form to account for desolvation effects (26,27). Although that model was used in protein folding studies in which large changes in solvent-accessible surface area occur, we are considering a transition between compact states and therefore have not included the additional desolvation term.

The model was implemented in the GROMACS simulation package, version 4.5.4 (30). We first conducted native-state simulations to determine an appropriate simulation temperature. The HII simulations were performed using Langevin dynamics with a friction factor of 0.1 amu/ps, an integration time step of 10 fs, and a nonbonded cutoff distance of 33 Å. The heat capacity (C_v) and fraction of native contacts (Θ) are plotted against the simulation temperature in Fig. 2. C_v shows a single sharp peak at 330 K. We selected 270 K for our simulation temperature, where the native state maintains ∼ 85% of the native contacts. From the native-state simulation at 270 K we determined our convergence criterion values for the radial swelling coordinate, $\overline{R}$ (${\overline{R}}^{\star }=288.8\AA$), a coordinate measuring the degree of buckling (puckering of pentamers), β (${\beta }^{\star }=57\AA$), and for the fraction of native contacts, (${\Theta }^{\star }=0.833$). Although ${\overline{R}}^{\star }$ and β^★ are set equal to the averages observed in the native-state simulation, Θ^★ is set equal to 99% of the average Θ-value from the native state. This choice for Θ^★ is based on the slow convergence of Θ, and our primary interest is in the macromolecular structural properties ($\overline{R},\beta$), which converge quickly. A contact is defined as being formed when the pair distance is less than or equal to 1.2 times the native contact distance. The calculation of β involves the five residues Asp²⁹⁰, Asn²⁹¹, Glu²⁹², Gly²⁹³ and Arg²⁹⁴, which are located at the center of the capsomers (hexamers and pentamers). The radial position of each capsomer is calculated from the center of geometry of the 25 (pentamer) or 30 (hexamer) residues for that capsomer, and then the difference between the radial pentameric position, R_pent, and the average radial position of the neighboring hexamers, $R_{hex}^i$, is calculated,

$$\beta =R_{pent}-\frac{1}{5}\sum _{i=1}^5{R}_{hex}^i.$$ (2)

Figure 2.

Native-state simulations. Fraction of native contacts and C_v are plotted against temperature.

Both the PHII and HII models consist of 117,600 residues/beads; missing residues in PHII were modeled by doing a local structural alignment with the Head I structure (PDB 2fs3). Simulations started with the PHII configuration were conducted with the same parameters as described for HII above. Each of the transition trajectories was computed using 16 cpu cores via two HP DL1000/DL160 nodes with dual quad-core Intel Xeon 2.27GHz processor, connected with Infiniband fabric using Qlogic QDR or DDR cards. The simulations ran at a speed of ∼15 ns/day, each trajectory was run for ∼300 ns, requiring ∼20 days to complete.

The NMA was performed by constructing an ENM of the initial icosahedrally symmetric PHII structure using only the Cα positions. The network of elastic bonds were defined using a 12 Å cutoff, and the Hessian matrix was diagonalized using the rotation-translation of blocks (RTB) method (31,32),which treats sections of proteins as rigid blocks. We employed a blocking scheme based upon secondary structural elements, which resulted in 11 blocks/protein. The projections of the icosahedral modes onto the displacement vector is simply the normalized dot product, $P_d^{Ii}=Ii\cdot d/\left(\left|Ii\right|\times \left|d\right|\right)$, and the overlap is the sum of squares of the projections. The intermediate structures used to compute d-vectors were taken as the first snapshot, which reached Θ-values of {0.66, 0.67,…, 0.83}.

Results and Discussion

Thermodynamic studies have indicated that the transition from PHII to HII is very favorable (10), but the long timescale for the transition (minutes) (11) indicates a large barrier and/or a very rugged energy landscape governs the dynamics between these states. The timescale for the transition is far beyond what can be computed using naive MD approaches. Furthermore, the largest MD simulation to date has been of a T = 3 virus (4.5 million atoms) (33); a solvated HK97 system would likely be an order of magnitude larger and is recalcitrant to study with an all-atom representation. Therefore, to make this problem tractable, we have reduced both the level of atomic detail (coarse-graining), and the timescale for the transition. To allow the transition to proceed rapidly, we have constructed a potential energy surface in which HII is favored but no (significant) barrier separates PHII from HII. The model is a coarse-grained Gō model in which the potential is based upon the native contacts of the system. The contacts are determined from an all-atom structure, but then the interactions are mapped onto a single bead/residue (Cα-based) model, and the strength of the interactions is weighted based upon residue type (26,27). This model represents a funneled energy landscape in which the native state resides at the basin of the funnel; this class of model has been extensively used in protein folding studies (34). Further details of the model and simulation protocols are presented in the Materials and Methods section.

In this study, HII was chosen as the native/target state and the potential function was built for that structure. The potential energy of the HII structure was –3.33×10⁵ kJ/mol. We have no a priori knowledge about the ruggedness of the energy landscape, so to test whether the landscape is completely smooth, we minimized the PHII structure using a steepest-descents algorithm. During the minimization, the potential energy rapidly drops from 6.72×10⁷ to –1.75×10⁵ kJ/mol. RMSD calculations show that the structure moves only 1.8 Å away from the initial PHII configuration and remains 56.6 Å away from the HII state, indicating that there is ruggedness in the landscape. Using the minimized PHII configuration, we performed Langevin dynamics simulations and computed trajectories of the transition into the native (HII) configuration. The scale for the potential energy change during these transitions is given by the difference between the HII and minimized PHII energies (∼ 1.5×10⁵ kJ/mol). We computed 66 transition trajectories in which each simulation was started with a different initial velocity distribution. We considered several convergence criteria to detect when the transition was complete in a given simulation. The convergence criteria we considered were the fraction of native contacts (Θ), mean radius ($\overline{R}$), and a buckling coordinate (β). This transition has been termed a buckling transition and has been predicted based on continuum elasticity theory (35). For the shell to buckle into the faceted shape (Fig. 1 C), 12 disclination (buckling) events must occur, namely, that each pentamer must radially push away from its neighboring hexamers. In a T = 7 capsid (see Fig. 1 A), each pentamer is surrounded by five unique hexamers,. We compute the buckling of each pentamer (β) as the difference between the radial position of the center of a pentamer and the average radial position of the center of each of the neighboring hexamers. The target values $\left\{{\Theta }^{\star },{\overline{R}}^{\star },{\beta }^{\star }\right\}$ for convergence were determined from a native-state simulation of HII. The convergence variables for a sample trajectory are presented in Fig. 3 A, and the potential energy profile over the first 100 ns is shown in Fig. 3 B.

Figure 3.

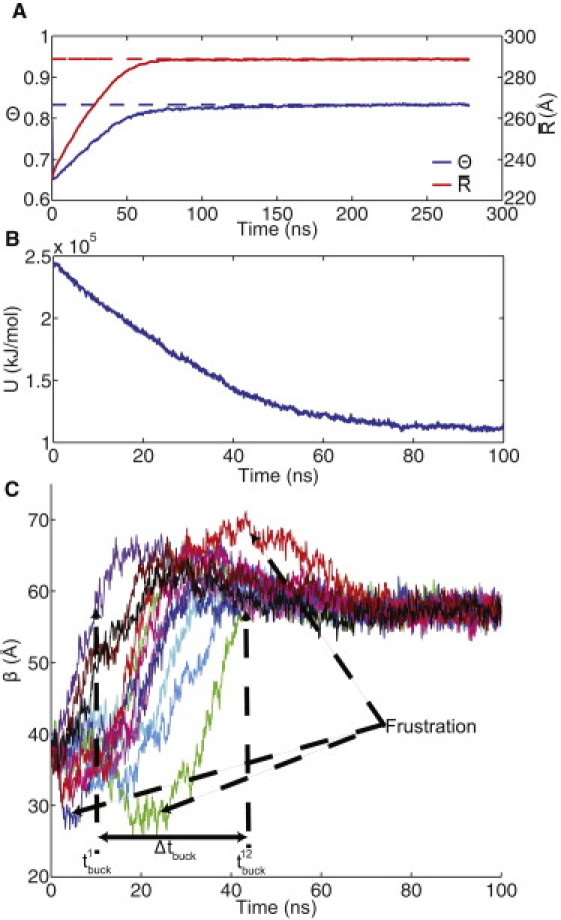
Convergence of a sample trajectory. (A) The fraction of native contacts and the mean radius value over the course of the trajectory (solid lines); also shown are the target values, Θ^★, and ${\overline{R}}^{\star }$ (dashed lines). (B) The potential energy (U) profile over the first 100 ns of the trajectory. (C) The buckling variable (β) for each of the 12 pentameric sites.

Our measure of symmetry breaking is displayed in Fig. 3 C and is denoted as Δt_buck, which is the time difference between the first ($t_{buck}^1$) and last ($t_{buck}^{12}$) buckling event. Each of the pentameric sites in the PHII structure initially has $\beta =37\AA$; the values of $t_{buck}^{1-12}$ are determined by the time when each pentameric site first reaches a β-value equal to ${\beta }^{\star }(57\AA )$. If the buckling events do not occur simultaneously (i.e., a large Δt_buck), this indicates a breaking of symmetry. To understand what constitutes a significant symmetry-breaking event (as opposed to thermal noise), we must analyze the complete set of transition trajectories. Another interesting feature we see in the sample trajectory is that over-buckling and under-buckling (flattening) occur instead of each pentamer proceeding directly to the target buckled configuration. We denote these as frustration events in Fig. 3 C, as they are similar to the idea of topological frustration in protein folding, where a protein may partially (over)fold and then have to unfold to reach the native state.

We analyzed the ensemble of trajectories to collect statistics on the transition behavior. In Fig. 4, A–C, we present histograms of the convergence times with respect to Θ^★, ${\overline{R}}^{\star },$ and β^★, respectively. It can be seen that β is a faster variable than $\overline{R}$, which itself is faster than the native contact convergence, Θ. The finding that β progresses faster than $\overline{R}$ appears to be qualitatively consistent with experimental findings that early-stage intermediates, known as EI-I and EI-II, appear more faceted than the late-stage EI-III intermediate structure (11). The distribution of our symmetry-breaking variable (Δt_buck) is shown in Fig. 4 D, and it appears to be a normal distribution. It is interesting that (Δt_buck) is normally distributed, which indicates that the most probable path has an intermediate degree of symmetry-breaking.

Figure 4.

Histograms of convergence times and symmetry-breaking. The histograms of the times to reach Θ^★,${\overline{R}}^{\star }$, and β^★ are shown in A–C, respectively. (D) Histogram of symmetry breaking.

We further examine the trajectories with extreme values in Δt_buck. The most cooperative trajectory has Δt_buck = 10.4 ns (Fig. 5 A), whereas the trajectory with the most extreme display of symmetry-breaking has Δt_buck = 51.1 ns (Fig. 5 B). The trajectory with the smallest Δt_buck displays fluctuations that can be attributed to thermal noise, whereas the trajectory with the largest Δt_buck has several pentamers that lag behind the leading pentamers. The potential energy of these trajectories is compared in Fig. 5 C; it can be seen that through the first 30 ns the energies are similar, but the cooperative trajectory has a slightly lower energy during the period of 30–70 ns during which the trajectory shown in Fig. 5 B exhibits a large degree of symmetry breaking. Several snapshots from the trajectory presented in Fig. 5 B are shown in Fig. 5 D, to illustrate the asymmetric configurations observed in the transition.

Figure 5.

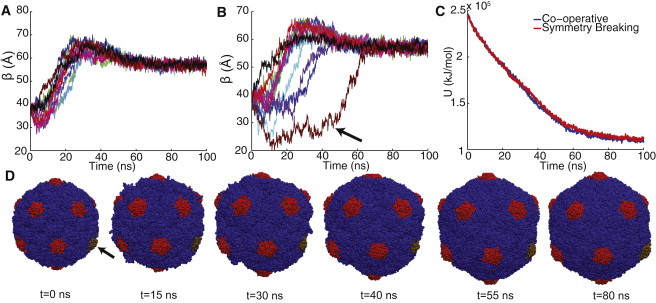
Symmetry conserving and breaking pathways. (A) Buckling of the most cooperative trajectory. (B) Buckling of the trajectory with the most significant degree of symmetry breaking. (C) Potential energy profiles of the trajectories shown in A (cooperative) and B (symmetry-breaking) (D) Snapshots from the symmetry-breaking trajectory shown in B. The brown trend in B corresponds to the brown pentamer in D (arrows).

We examine whether there is coupling between pentamer buckling events or whether the order is random. For each trajectory, once the first pentamer buckles, we label the other pentamers as either first neighbors (N¹), second neighbors (N²), or opposite (OPP); there are five N¹, five N² and a single OPP, as described in Fig. 1 A. When the second pentamer buckles, we identify if it is of type N¹, N², or OPP, and do the same for all subsequent buckling events. By examining the complete set of trajectories we can calculate, for each buckling event, the distribution of pentamer positions. The buckling of neighboring pentamers does not appear to be coupled, and overall, the order of buckling seems to be random. The complete distribution of buckling events is presented in Table 1.

Table 1.

Order of pentamer buckling

Buckling event	2	3	4	5	6	7	8	9	10	11	12
N1	0.38	0.41	0.42	0.47	0.45	0.55	0.61	0.48	0.30	0.45	0.47
N2	0.53	0.55	0.41	0.47	0.50	0.36	0.32	0.38	0.55	0.48	0.45
OPP	0.09	0.05	0.17	0.06	0.05	0.09	0.08	0.14	0.15	0.06	0.08

Values in columns 2–12 are with respect to the first buckled pentamer. For each buckling event, the observed fraction of pentamer type is reported.

Although we do observe varying degrees of convergence times and symmetry breaking in the pathways, it is still possible that there is a consistent mechanism for the transition. We consider whether there is consistency in either the pentameric contacts or the hexameric contacts forming first. In Fig. 6 A, we plot the fraction of native hexameric contacts (Θ_hex) versus fraction of native pentameric contacts (Θ_pent) for all trajectories. We observe a consistent behavior, i.e., a single reaction tube, in which the pentameric contacts form first, followed by the hexameric contacts. This observation is consistent with our finding that β is faster than $\overline{R}$.

Figure 6.

Mechanism and characterization of transition pathways. (A) The fraction of native pentameric (Θ_pent) and hexameric contacts (Θ_hex) are plotted in black for all 66 trajectories, and a single sample trajectory (same trajectory as in Fig. 3) is shown in red. (B) The squared mode projections of the normal modes of PHII projected onto displacement vectors between PHII and intermediate states. The first two icosahedral modes (I1 and I2) and the sum of the low-frequency nonicosahedral (NI) modes are shown for all trajectories. (Inset) Same projection calculation, but with the displacement vectors calculated between subsequent intermediate structures and the projections averaged over all trajectories.

In light of previous studies on the normal-mode characterization of the HK97 structural transition (19,20), we also examine the ability of normal modes to characterize our pathways. We construct an ENM of PHII and determine the normal modes. A displacement vector (d) is calculated between PHII and HII and we compute the projections, P, of the normal modes onto d. Consistent with previous results, we find that the two lowest-frequency nondegenerate (icosahedral) normal modes account for most of the displacement. The lowest-frequency icosahedral mode, I1, has a projection onto d of $P_d^{I1}=0.90$, and the second-lowest icosahedral mode I2 has a projection of $P_d^{I2}=0.33$, giving a total overlap of Ov = 0.92, where $Ov={\left(P_d^{I1}\right)}^2+{\left(P_d^{I2}\right)}^2$. I1 is a breathing mode (uniform swelling), whereas I2 is more responsible for the faceting and buckling features (19). To understand whether these modes also characterize intermediate structures along the pathway, we extracted intermediate structures along each of the pathways (selection of intermediates is described in the Materials and Methods section). We then compute d-vectors between PHII and each of the intermediate structures and project the 100 lowest-frequency normal modes onto each of the d-vectors. Of the 100 lowest-frequency modes, only two are icosahedrally symmetric (I1 and I2). In Fig. 6 B, we display the squared projection of I1, I2 and the sum of squared projections of all the nonicosahedral modes (NI). We observe that small displacements are not well characterized by the low-frequency normal modes; these are presumably high-frequency motions, whereas larger displacements are dominated by normal modes, and specifically the icosahedral normal modes. To further support that smaller deformations are not characterized by low-frequency modes, we compute d-vectors between subsequent intermediate structures (e.g., structure i + 1 − structure i) and perform the same projection analysis, again using the normal modes of PHII. These modes provide a representative basis for the low-frequency space, and we observe that these local displacements are largely high-frequnecy (see Fig. 6 B, inset).

Conclusions

In this study, we have provided new, to our knowledge, structural and mechanistic insight into virus maturation. We have shown that the transition of HK97 obeys a consistent mechanism, characterized by the formation of pentameric contacts driving the system toward the buckled configuration. There is a spread of behaviors with regard to the order of pentamer buckling and the degree of symmetry breaking. However, the large-scale, collective motions of the system follow the low-frequency icosahedrally symmetric modes, which supports the idea that even under nonequilibrium conditions, the dynamics of capsids are still governed by icosahedral motions. These results support the assumption/constraint of icosahedral symmetry in future modeling and experimental studies on virus capsids.

The picture that emerges from this study is that all pathways fall into a common channel in the free-energy landscape that guides the system toward the mature state. Progress toward the mature state (i.e., motion along the reaction coordinate (Θ)) is largely icosahedral; nonicosahedral motions introduce the configurational diversity and symmetry-breaking features. The width of the channel represents the configuration entropy of the ensemble, and as the system approaches the native state, the channel narrows as the enthalpy of a symmetric state outweighs the entropy of a nonsymmetric state. While we observe nonsymmetric intermediates, the dominant collective behavior is characterized by modes available to icosahedrally symmetric states.