Rigidity Matching between Cells and the Extracellular Matrix Leads to the Stabilization of Cardiac Conduction

Abstract

Biomechanical dynamic interactions between cells and the extracellular environment dynamically regulate physiological tissue behavior in living organisms, such as that seen in tissue maintenance and remodeling. In this study, the substrate-induced modulation of synchronized beating in cultured cardiomyocyte tissue was systematically characterized on elasticity-tunable substrates to elucidate the effect of biomechanical coupling. We found that myocardial conduction is significantly promoted when the rigidity of the cell culture environment matches that of the cardiac cells (4 kiloPascals). The stability of spontaneous target wave activity and calcium transient alternans in high frequency-paced tissue were both enhanced when the cell substrate and cell tissue showed the same rigidity. By adapting a simple theoretical model, we reproduced the experimental trend on the rigidity matching for the synchronized excitation. We conclude that rigidity matching in cell-to-substrate interactions critically improves cardiomyocyte-tissue synchronization, suggesting that mechanical coupling plays an essential role in the dynamic activity of the beating heart.

Introduction

Cardiovascular diseases are a major cause of death in modern society and affect millions of people worldwide. Studies on common potentially fatal cardiac diseases have high priority in the scientific and medical communities. Cardiac reentries (high-frequency rotating waves) are known to be responsible for many dangerous cardiac arrhythmias and are precursors of ventricular fibrillation that leads to sudden death (1–4). Thus, it is important that we understand how such undesired wave dynamics originate. To reveal underlying mechanisms and causes, different models of heart function are generally used, such as in vivo and in vitro systems of cardiac tissue. Although in vitro cultures often show generic rather than realistic features, they are easy to maintain and observe. Cardiac tissue culture is a type of in vitro experimental system that uses the hearts of neonatal mammals to reengineer heart tissue on a two-dimensional substrate. Generally, it is used to examine the activities of newly developed medical drugs (5), the nonlinear activity of wave dynamics (4–6), and stem-cell development (7).

Adhesion is an important cell property that is not only controlled by biochemical mechanisms, but is also regulated by the ability of cells to sense their mechanical and molecular microenvironment to determine the structural organization within the cell (8–10), such as the extracellular matrix, cytoskeleton, and force generation through molecular motors (11,12). Typical examples include cell migration (13,14) and the differentiation of stem cells (4,15). Thus, substrate rigidity plays an important role in the in vitro experiments to realistically model the extracellular matrix as in vivo experiments exhibit.

Substrate rigidity can be modulated by the use of different types of soft gels such as agar gels (16) and fibrin gels (17). A gel that was recently introduced for tissue engineering is elasticity-tunable photocurable styrenated gel (18,19), the local rigidity of which can be precisely adjusted by controlling the duration of irradiation with visible light. The resulting gels exhibit rigidities from a few kPa up to 1 MPa, and hence open the possibility to mimic the extracellular matrix in the cell environment.

In this study, we systematically investigated the influence of rigid substrates to the calcium conduction of confluent cardiomyocyte monolayers of neonatal rats. The records of spontaneous calcium-waves were analyzed by obtaining the power-spectrum for substrates with different rigidities. The main entrainment-frequency showed an increase with the increase in substrate rigidity, and the entrainment stability of spontaneous originated waves become maximized when the substrate rigidity and cell rigidity (∼4 kiloPascals) matches.

For verification of the effect of rigidity matching, the threshold of calcium alternans was analyzed in rapid rate-paced tissues. It was found that when the rigidity of the cell culture substrate matches that of the cardiac cell tissue, the threshold of the period to induce calcium alternans increases significantly.

Our experimentally obtained results suggest that when tissue and substrate have the same rigidity, the cell-to-substrate interactions critically improve synchronization features in cardiomyocyte tissue.

For clarification of the experimental results, additionally we adapted a simple excitable numerical model to simulate the cell-substrate interaction. Despite the simple nature of the numerical model, our model reproduces the essential features in our experiment by taking mechanical cell-coupling into account.

Methods

Cell isolation

Primary cell cultures of neonatal rat ventricular myocytes were prepared as described previously (20). Briefly, hearts isolated from 2-day-old Wistar rats were minced and treated with collagenase. The isolated cells were collected by centrifugation and preplated for 1 h. After the supernatant was collected again, the cells were plated on 18-mm-diameter glass or gel-prepared coverslips coated with fibronectin (12 μg/ml) at a cell density of 2.6 × 10³ cells/mm². Cell constructs were incubated in Dulbecco's modified Eagle's medium with 10% fetal bovine serum, and 1% penicillin streptomycin for 24 h under humidified conditions at 37°C and 5% CO₂. The medium was replaced by a contraction medium, which consisted of minimum essential medium with 10% calf serum, 1% penicillin streptomycin, and cytosine arabinofuranoside (a proliferation inhibitor) to minimize the number of fibroblasts (21,22).

All animal protocols were carried out in strict accordance with the guidelines for animal experimentation from the Animal Research Committee, Kyoto University (Kyoto, Japan). The protocol was approved by the Animal Research Committee, Kyoto University.

Immunofluorescence

Observations were performed four days after plating. Cells were labeled with the Ca²⁺-sensitive fluorescent dye Fluo-8 (Fluo-8 AM; ABD Bioquest, Sunnyvale, CA). The medium was replaced with Tyrode solution at room temperature. The cells were studied within 2 h after loading.

Photocurable gel fabrication

Photocurable styrenated gelatin was prepared as previously described (23). Styrenated gelatin (30 wt %) and sulfonyl-camphorquinone (2.5 wt % of gelatin; Toronto Research Chemicals, North York, Ontario, Canada) were mixed in phosphate-buffered saline (PBS). The mixture was centrifuged to remove the colloidal coagulations. The photocurable gel solution was spread between the previously prepared vinyl-silanized glass substrate and raw glass substrate coated with poly(n-isopropylacrylamide) for easy detachment, which were kept under 45°C. The sample was than illuminated with visible light at 100 mW/cm² (measured at 568 nm) for 150–300 s. A metal halide light source (MME-250; Moritex, Tokyo, Japan) was used. Light intensity was measured using a photodiode power meter (S120C; ThorLabs, Tokyo, Japan). Finally, the hardened gel was detached from the raw glass substrate in PBS and then kept in PBS overnight under incubation and shaking conditions to remove unreacted solution and make it swell sufficiently.

Determination of rigidity

The rigidity of gels and cell tissue was determined by nanoindentation analysis using atomic force microscopy. Indentation-force measurements were performed by atomic force microscopy (AFM) (NVB100; Olympus Optical, Tokyo, Japan) (AFM controller and software, Nanoscope IIIa; Veeco Instruments, Plainview, NY) using a silicon-nitride cantilever with a pyramidal tip and a nominal spring constant of 0.02 N/m (OMCL-TR400PSAHW; Olympus Optical) in PBS. The Young's modulus, E, of the obtained force-indentation curves was analyzed by nonlinear least-squares fitting to the Hertz model (24,25) considering the case of a conical indenter,

$$F=\frac{2E}{\pi \tan \alpha \left(1-{\mu }^2\right)}{\delta }^2,$$ (1)

where the semivertical angle is α = 30° and the Poisson ratio is μ = 0.5. A more detailed description on the nanoindentation method is provided in Fig. S1 in the Supporting Material.

Time-lapse and image acquisition

Fluorescence was observed with an inverted microscope (IX-70; Olympus Optical) with a ×2.0 magnification objective lens (PLAPON, N.A. = 0.08; Olympus Optical) in combination with a ×0.35 intermediate lens (26). Raw images were obtained with an electron-multiplying charge-coupled device camera (iXon DV887ECS-UVB; Andor Technology, Belfast, Northern Ireland) with 64 × 64 pixels at a 14-bit resolution with 200 frames/s after 8 × 8 binning for the conduction velocity and calcium alternans measurements, and 128 × 128 pixels with 50 frames/s after 4 × 4 binning for measurements of spontaneous activation dynamics. High-magnification images were obtained by confocal laser scanning fluorescence microscopy (LSM510; Carl Zeiss, Peabody, MA) using an ×20 magnification objective lens (UPlanSApo, N.A. = 0.75; Olympus Optical).

Electrical stimulation

Electrical stimulation of 6 V was applied with 10-ms bipolar pulses delivered through 1-mm-spaced platinum electrodes on the edge of the sample without touching the tissue. The pacing period was decreased systematically from 700 ms in steps of 50 ms and 10 ms, respectively, until calcium instabilities could be recognized (see Fig. 1).

Figure 1.

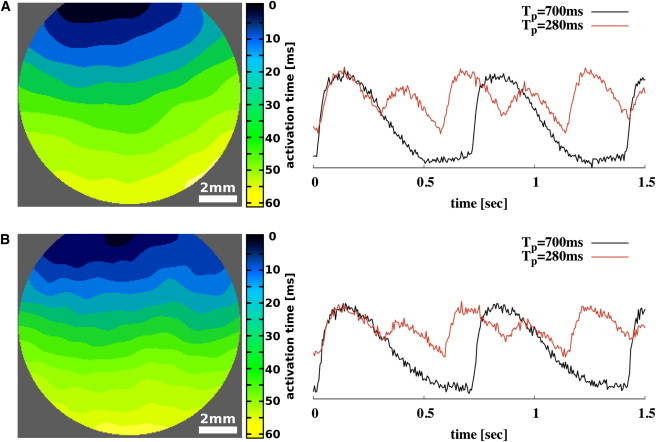
Activation-time maps (left) and single-pixel recording of the cytosolic calcium of confluent cardiac tissue culture on glass (A) and on gel-substrate with a rigidity of 4.2 kPa (B). Single-pixel recordings are shown for 700-ms and 280-ms entrained, high-frequency paced tissues that exhibit stable calcium transient alternans for 280-ms entrained tissues.

Data analysis

Activation time mapping and data obtained from conduction velocity measurements were processed by the image-analysis software ImageJ (National Institutes of Health, Bethesda, MD) with custom plug-ins as previously introduced (27). Data regarding spontaneous activation dynamics were analyzed by MATLAB (R2010a; The MathWorks, Natick, MA) with custom programs.

Results

We cultured neonatal cardiac cell tissue on microelastic gel surfaces that spanned the range of cell rigidity found during the developmental process in cardiac culture (11 gel rigidities between 2.3 kPa ∼10.2 kPa, and glass as a control) (25). In this approach, the wave activity of a large collection of cell cultures is recorded (n = 33) and a power spectrum is obtained by Fourier transformation. Fig. 2, A and B, exemplarily shows two single-pixel recorded cytosolic-calcium transients and normed frequency spectra of confluent tissue for constant entrained activity and erratic activity (fast activity followed by periods of quiescence), respectively. Both forms of activity are found in tissue cultures of different substrate rigidities. The unnormalized power spectra of all of the experimental samples, regardless of substrate rigidity, are summed over all single pixel recordings (shown similarly in Fig. 1 B) of all experiments to a combined spectrum and subsequently scaled to its maximum value that is approximately at 710 ms (Fig. 2 C). Three cycle-length (CL) bands of wave activity are distinct and numbered serially:

• 1.Low-period activity (CL > 0.9 s) due to occasional activity delays.
• 2.High-period wave bursts (CL = 0.6 s ∼0.9 s) corresponding to the region with the main CL band.
• 3.Rare events of extremely high-frequency bursts (CL = 0.3 s ∼0.6 s).

Figure 2.

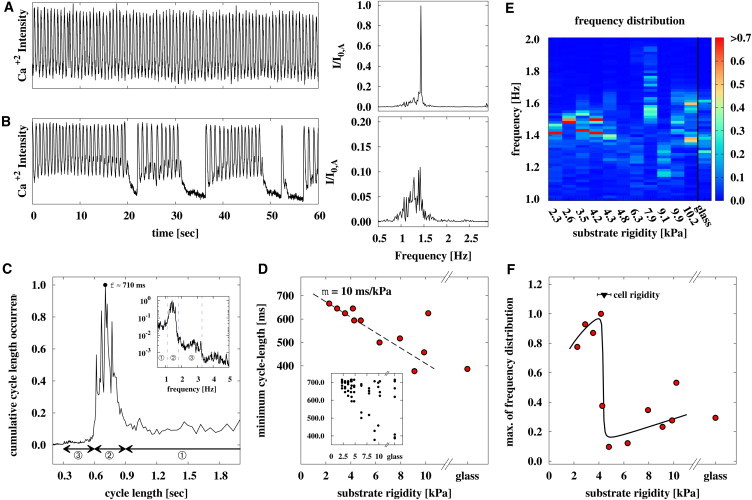
Spontaneous wave activity shows most constant activity when cardiac cell tissue is cultured on soft substrates of equal rigidity. (A and B) Examples of two single-pixel recorded cytosolic-calcium transients and normed frequency spectra of confluent tissue cultured on 3.5 kPa gel substrates showing a constant transient and transient with delays, respectively. We confirmed that tissue cultured on different gel substrates or glass shows similar patterns. (C) Relative cycle length distribution of all samples (n = 33, two 60-s records) shows distinct cycle length (CL) bands: 1), high-period activity (CL > 0.9 s) due to occasional activity delays; 2), low-period wave bursts (CL = 0.6 s ∼0.9 s) corresponding to the region with the main frequency band; and 3), rare events of extremely high-frequency bursts (CL = 0.3 s ∼0.6 s). Most CLs are observed at a period of 710 ms. (D) A linear increase in the minimum spontaneous CL with maximum occurrence of target waves is shown. (Inset) CL of spontaneous waves with maximum amplitude of each sample. (E) Map of combined power spectrum depending on substrate rigidity and wave frequency (CL⁻¹) shows a pronounced frequency band for lower rigidities (≤4.2 kPa), and dispersed frequency distribution for higher rigidities (≥4.3 kPa). The most stable frequency (cycle length) is seen for tissue cultured on substrates with rigidity of 4.2 kPa. (F) Maximum of the combined power spectrum (most stable CL occurrence) dependent on the substrate rigidity. A local maximum can be found at ∼4.2 kPa, which is consistent with the cell rigidity of 4.4 ± 0.6 kPa determined by AFM indentation measurements on glass substrates.

Further, we determined the main cycle length of each sample for the lower threshold of wave activity (CL < 710 ms) depending on the cell rigidity. We found a linear dependency between lower rigidities (m = 10 ms/kPa) and increasing dispersion for greater rigidities when we considered the minimum cycle length for each rigidity (Fig. 2 D). This suggests that the minimum main cycle length is proportional to the adhesion strength of cells, because the adhesion strength increases monotonically with increasing substrate rigidity, and the strongest adhesion occurs on glass (15).

We obtained the combined power spectrum depending on rigidity to evaluate the underlying relation between substrate rigidity and the frequency (cycle length) of natural activation sites (Fig. 2 E). Each obtained power spectrum was normalized by integrating over its area, and subsequently all rigidity-dependent power spectra were scaled to the highest exhibited frequency occurrence. We found that lower rigidities (≤4.2 kPa) show pronounced frequency (CL) domains; however, the wave activity on gels with greater rigidities shows a broad distribution of wave frequencies (CL). This result corresponds well with the cell rigidity (4.4 ± 0.6) kPa that is determined by AFM indentation measurements similarly to the rigid substrates. The cell rigidity marks the threshold between the pronounced frequency domains and the broad frequency distribution of soft and hard rigidities, respectively. Fig. 2 F shows the maxima of the combined power spectra depending on the substrate rigidity that the tissue is cultured on. The maximum at 4.2 kPa corresponds well with the cell rigidity similar to that with Fig. 2 E. The strong difference between tissue cultured on soft and hard substrates is due to the difference in the power spectrum. Higher values indicate more constant beating-frequencies than lower values, as shown in Fig. 2, panels A and B, respectively. Thus, cardiac cells beat most constantly when cardiac tissue is cultured on substrates that exhibit the same or lower rigidity as the cell-tissue.

To measure the cycle-length distribution, we obtained the power spectra by Fourier transformation (FT), rather than by defining an arbitrary intensity level and measuring the duration from activation to activation as has been done in previous studies (28). Both methods lead to comparable results but exhibit pros and cons. One advantage of using FT is that it can also detect low intensity peaks that may have gone previously undetected by having utilized a constant intensity level. However, detailed information such as calcium transient duration (CTD) and calcium transient interval (CTI) are not able to be measured by using FT. For comparison of both methods, we prepared Fig. 2 E corresponding to cycle-length distribution (see Fig. S3 A). Both plots show, quantitatively, the same distribution, considering that the frequency f = 1/ CL, respectively.

To emphasize the found effect, we extracted the calcium transient duration (CTD) and calcium transient interval (CTI) of each wave to show the CTD and CTI interaction at an intensity level of 50%. The CTI and CTD for calcium signaling is performed in a way comparable to the action potential duration and diastolic interval measurements for the membrane potential of cardiac cells (29,30) (see Fig. S2 A). Fig. 3, A–C, shows the relative CTD-CTI occurrence in a normalized histogram for all substrates, soft substrates with rigidities <4.25 kPa, and hard substrates with rigidities >4.25 kPa, respectively. The difference between panels B and C of Fig. 3 shows clearly the stabilization of the conduction system when the substrate rigidity is softer than the cell rigidity. Larger substrate rigidities lead to a broad distribution of CTD-CTI values; however, smaller rigidities lead to a focused CTD-CTI relationship with an average CTD = 160 ms and CTI = 270 ms. This effect can be emphasized by the cycle-length distribution for soft and hard substrate rigidities, respectively (see Fig. 3 D). Tissue that is cultured on soft substrates (red bars) exhibited a lower CL distribution than that of tissues cultured on hard substrates (green bars). The CL standard deviation (SD) of each rigidity shows the same trend (see Fig. S3 B). Tissue that is cultured on soft substrates exhibit lower CL SD than that of tissues cultured on hard substrates.

Figure 3.

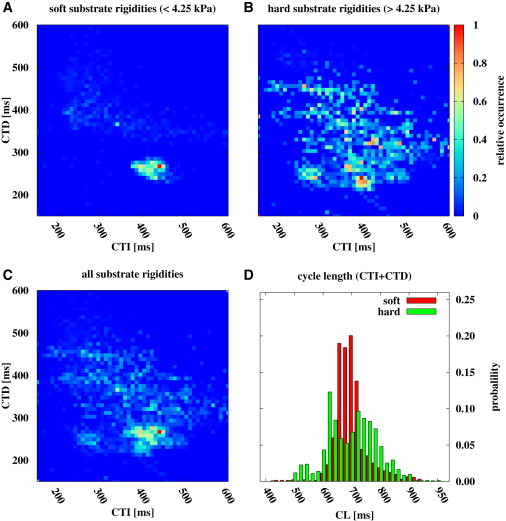
Normalized histogram of CTD and CTI of each wave shows stabilization when the substrate rigidity goes below the cell rigidity. (A) Relative CTD-CTI occurrence for soft substrates with rigidities <4.25 kPa. (B) Shows relative CTD-CTI occurrence for hard substrates with rigidities >4.25 kPa. (C) Shows relative CTD-CTI occurrence for all substrates. (D) Histogram of cycle length (CL = CTD + CTI) distribution for soft (red) and hard substrates (green) with an average CL of (437 ± 35) ms and (437 ± 55) ms, respectively.

We next focus on the role and effect of wave conduction in tissues cultured on gels with rigidities close to 4 kPa (six gel rigidities from 2.3 kPa to 5.4 kPa, and glass). We performed independent measurements of conduction speed for an equally large collection of samples (n = 31). We obtained the restitution properties of each sample by electric high-frequency stimulation at the edge of the tissue (T = 700 ms – 250 ms) (see Fig. 1). Under the experimental conditions in this study at room temperature, cardiac tissue exhibited strong calcium transient alternans (Fig. 4 A), which led to alternating wave propagation at high-frequency entrained waves (31,32). We extracted the CTD and CTI of each wave at an intensity level of 50% as performed previously (see also Fig. S2 A) to investigate wave-to-wave interaction (Fig. 4 B). Depending on the activation time of the wave, CTD varied linearly whereas the pacing period T remained constant for higher pacing periods (T = CTD + CTI) (33). If we define the variation of CTI, Γ, as a generic function of the pacing period, T, we can determine the critical pacing period, T_c, by

$$\Gamma =\alpha \exp \left(-\beta \left(T-T_c\right)\right)+{\Gamma }_0,$$ (2)

where Γ₀ is the average variance of CTI, and α and β are parameters. Thus, we could quantify T_c for each tissue preparation as a function of substrate rigidity (Fig. 4 D). The advantage of using this approach is that T_c can be estimated more precisely when located between subsequent measurements. We found that T_c is increased at a substrate rigidity of ∼4 ± 1 kPa. Analyzing the conduction velocities with calcium transient amplitude in a manner similar to that used in previous studies (31,34,35) leads to comparable T_c with an increase at a substrate rigidity of 4 kPa; however, the SD showed much larger deviations (see Fig. S2). This result corresponds well with the independent result obtained for the spontaneous target wave activity, where the highest activity was also found at ∼4 kPa. Although we found that cytosolic calcium alternans is elevated toward larger periods when the substrate rigidity and cell rigidity matches, we could not observe any significant change in the conduction velocity when the tissue is entrained with the pacing period of 700 ms.

Figure 4.

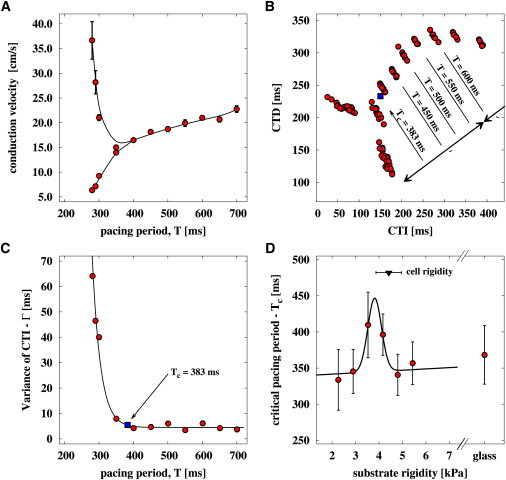
Calcium transient alternans of high-frequency-paced cardiac tissue shows a peak at substrate rigidity of 4 kPa. (A–C) Typical data obtained from cultured cell tissue at a substrate rigidity of 3.5 kPa. (A) Restitution curve showing calcium transient alternans induced at a pacing period of ∼400 ms. (B) CTD versus CTI plot of waves (red circles) observed with an estimated critical pacing period T_c (blue square). (C) T_c is estimated by considering the variance of CTI. (D) Mean T_c versus substrate rigidity. A local maximum is observed at ∼4 kPa, which is consistent with the cell rigidity of 4.4 ± 0.6 kPa determined by AFM indentation measurements on glass substrates.

Numerical simulations on the mechanical resonance between cells and substrate

A generic numerical model of FitzHugh-Nagumo type was adapted to simulate the essential of the dynamical feature of interaction between cells and substrate (36,37). The FitzHugh-Nagumo equations were numerically solved by a Runge-Kutta fourth-order explicit integration scheme considering dx = 0.1, dt = 0.2, and D = 0.01 for a one-dimensional array,

$$\dot{u}=D{\partial }_{xx}u+\left[u\left(u-1\right)\left(\alpha -u\right)-v\right]+I_n+I_c,$$ (3)

$$\dot{v}=\epsilon \left(\beta u-\gamma v-\eta \right),$$ (4)

where u and v are the activator and inhibitor, respectively, and I_n is Gaussian noise with SD 0.017 (38) to induce a more natural environment that may cause wave failure, α = 0.1, β = 0.5, γ = 1.0, and ɛ = 0.01. Excitable and oscillatory cells are distinct by the parameter η either 0.0 or 0.1, respectively, where the first 10 units are set to be oscillatory, mimicking a natural pacemaker. Further, we introduce a nondiffusive coupling term, I_c, to mimic the basic function of stress-activated ion-channels; it is considered as a monotonically decaying, arbitrarily defined function of the distance between neighboring cells. Thus, we define I_c as

$$I_c\left(u_x\right)=\Theta \left(u_x>u_{th}\right)\times \sum _i^{i\ne x}\left[u_i+f\left(E_s,E_c\right)\right],$$ (5)

with

$$f\left(E_s,E_c\right)=c_1\exp \left(-\frac{\left|i-x\right|-1}{c_2+\left|E_c^2{\left(E_c^2+\left|E_s^2-E_c^2\right|\right)}^{-1}-c_3\right|}\right),$$ (6)

where Θ is a Heaviside step-function, which triggers coupling of neighboring cells only if the cell is in the excited state, and contracts. E_s is the substrate rigidity and E_c is the cell rigidity. Parameters are set arbitrary to c₁ = 0.002, c₂ = 0.1, and c₃ = 0.3. No-flux boundary conditions are assumed.

Equation 6 is defined having two characteristics. When the elastic moduli (rigidities) E_s and E_c are equal, the coupling is strongest, therefore, independent of elastic moduli because Eq. 6 reduces to

$$f=c_1\exp \left(-\frac{\left|i-x\right|-1}{c_2+c_3}\right),$$ (7)

so that the parameters c_1,2,3 define the strength of coupling. On the other hand, the denominator shows a strong asymmetry for smaller and larger E_s, respectively, due to the choice of the quadratic elasticities.

Fig. 5 shows, exemplarily, in respect to the undisturbed system (Fig. 5 A), the influence of noise (Fig. 5 B) and long-range coupling (Fig. 5 C) for 100-unit lattices, respectively. The influence of noise leads to failure of wave propagation in the excitable part of lattices, whereas the coupling decreases failure probability of waves, resulting in a more stable wave train. In Fig. 5 D, we show the power spectrum, depending on rigidity, to evaluate the underlying relation between substrate rigidity and the frequency of wave train, which reproduces the experimental trend (Fig. 2 F). The power spectra were analyzed in the same manner as it was explained for the experimental data. To begin, the power spectra were obtained from a single recorded space unit in the excitable region and then normalized to the maximum of all power spectra. In the simulation, the cell rigidity was set to 4 kPa.

Figure 5.

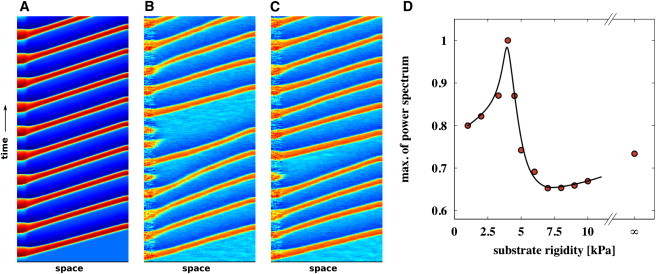
Influence of rigidity matching in a one-dimensional array of computed cells. (A) Idealized system with I_n = I_c = 0. (B) System with no coupling I_c = 0 and Gaussian noise I_n ≠ 0. The influence of noise leads to failure of wave propagation in the excitable part of lattices. (C) System with coupling I_c ≠ 0 and Gaussian noise I_n ≠ 0. The influence of coupling leads to stabilization of the conduction system and less propagation failure are observed. (D) Maximum of power spectrum depending on substrate rigidity in numerical simulations that assumes coupling I_c ≠ 0 and Gaussian noise I_n ≠ 0.

Discussion

Enhancement of the stability of the target-wave activity and an increase in the critical period of calcium transient alternans were observed at the same substrate rigidity (corresponding to a cell rigidity of 4.4 ± 0.6 kPa) as that obtained from measuring the cell rigidity by the AFM indentation method (25,39,40) in control tissue on glass coverslips on the fourth day of culture (i.e., observation day, with three samples at three different locations). The cell rigidity obtained by this method is in good agreement with the obtained result, and confirms independently that cardiac cells exhibit an optimized and more stable state of spontaneous wave activity when the substrate rigidity matches or is lower than the cell rigidity. Thus, the cell rigidity can be interpreted as a critical point of stability, because an increase of the substrate rigidity yields to a decrease in stability so that spontaneous activity becomes erratic, as Fig. 2 E and Fig. 3 suggest.

Our results indicate that the rigidity of the extracellular environment of cells plays a significant role in determining cardiac conduction dynamics. The interaction of biomechanical and cell physiological activity exhibits a resonance effect when the rigidity of the extracellular matrix is equal to the rigidity of cardiac cell tissue. We observed an increase in the stability of target waves that led to stabilization of the main entrained activation frequency in the system when the substrate rigidity matches or is lower than the cell rigidity, which also indicates an effect on the intracellular activity (41). Further, we found that the critical period of calcium transient alternans increases when cell rigidity is equal or less than the substrate rigidity, because it is induced at a longer pacing period, than is associated with a more diseased state, such as heart failure (42). However, although calcium transient alternans is induced at a longer pacing period, it does not lead to a diseased state, but a change in tissue properties considering cardiac tissue. Thus, together with the finding of the stabilization of spontaneous wave activity, we can speak of a stabilization of cardiac conduction.

The observed resonance effect between tissue and substrate can be explained by the changes induced in cell morphology during tissue maturation due to the difference in adhesion area (9), and thus also in the cohesion area between cells. Although speculative, we believe that this may regulate the intracellular morphology of cells by adjusting the actin skeleton and gap-junction density between cells. Thus, the interaction between force actuation and conduction may regulate to the extent to which cell functionality is optimized when cell rigidity is equal to or less than the substrate rigidity. The mechanical interaction between cell and substrate is considered to play a dominant role on the excitable system, resulting in stabilized spontaneous wave activity for lower rigidities (see Figs. 2 F and 3 D) and induced calcium alternans at larger pacing periods (see Fig. 4 D). A simple theoretical model is discussed that reproduces the essential feature of the experimental results (Fig. 5). We believe that by additionally introducing cell orientation, the resonant effect may increase so that the conduction system will improve toward the quality seen in the in vivo systems.

Here, we provide insights into the stability of spontaneous target wave activity and calcium transient alternans in high frequency-paced tissue, which are determined by biomechanical interactions between cells and the extracellular environment that dynamically modulate the physiological tissue behavior in living cells. Our results suggest that the quality of in vitro studies on cardiac tissue culture can be dramatically improved so that they are more similar to those performed in vivo by adjusting the substrate rigidity—so that the extracellular matrix successfully mimics the extracellular environment of cardiac tissue (5,7,43,44).

Our results should contribute to in vitro studies on the cardiac system. Although the underlying cell-physiological mechanism and the intracellular cell morphology in confluent cardiac tissue remain to be elucidated, our results support the hypotheses that decreased rigidity preserves not only stem cells (7) but also enhances cell development by altering the cell morphology (9), resulting in cytoskeletal rearrangement and altered signaling. Our results suggest that mimicking the extracellular environment in in vitro cultures can cause the tissue culture to more closely approximate native cell functionality, and may help improve reengineering heart tissues for regeneration of diseased hearts with the use of extracellular matrix proteins such as Matrigels (45).