Abstract
Mechanical force applied along a disulfide bond alters its rate of reduction. We here aimed at quantifying the direct effect of force onto the chemical reactivity of a sulfur-sulfur bond in contrast to indirect, e.g., steric or mechanistic, influences. To this end, we evaluated the dependency of a disulfide bond's redox potential on a pulling force applied along the system. Our QM/MM simulations of cystine as a model system take conformational dynamics and explicit solvation into account and show that redox potentials increase over the whole range of forces probed here (30–3320 pN), and thus even in the absence of a significant disulfide bond elongation (<500 pN). Instead, at low forces, dihedrals and angles, as the softer degrees of freedom are stretched, contribute to the destabilization of the oxidized state. We find physiological forces to be likely to tune the disulfide's redox potentials to an extent similar to the tuning within proteins by point mutations.
Introduction
Similar to thermal or light energy, mechanical force can change chemical reactivity. An example for this kind of mechanochemistry is the force-dependency of disulfide bond reduction. Generally, a pulling force accelerates the reduction of a disulfide by a chemical reducing agent (1,2). Divergence from this simple enhancement of reactivity by mechanical work has also been observed. Namely, the reduction of a protein disulfide bond with thioredoxin was found to decelerate at low forces (<200 pN) (3), and redox reactions by metal ions as reducing agents were found to be largely insensitive to forces (4). Hydroxide anions, in turn, show a decrease in susceptibility toward the mechanical force at large forces (>500 pN) (5). Hence, the acceleration of disulfide bond reduction strongly depends on the reducing agent. The observed differences between reducing agents were ascribed to changes in the overall reaction mechanism (3–5).
However, Kucharski et al. (6) recently concluded that strain does not alter a disulfide's chemistry directly in the first place. They claim that mechanical force increases reactivity only indirectly by steric effects. More specifically, force solely deforms the molecule such that the reducing agent can more readily access the disulfide bond. To reconcile these findings, we here asked the fundamental question: does mechanical force alter the redox potential of a disulfide bond?
A redox potential measures the chemical stability of the bond, and as such is independent from the reducing agent, reaction mechanism, or steric hindrance. Also, in the particular case of mechanical force, we can directly infer changes in the reactivity of the disulfide bond from the shift in redox potential by mechanical force, as kinetics and thermodynamics are directly related. The reason is that, within the assumption that mechanical force tilts the energy landscape along the reaction coordinate x by F·x (7), the shifts in the product and transition state free energy with respect to the reactant free energy are linearly proportional. Therefore, a stabilization of the product with respect to the reactant by mechanical force also involves an acceleration of the reaction by lowering the activation energy. Thus, within the framework of the Bell model, the redox potential is directly related to the relative reactivity of a bond and allows the validation of our calculations by experimental measurements of force-dependent reaction rates.
Previous theoretical studies have given detailed insight into the reduction and cleavage of disulfide bonds in the absence of mechanical force (8–10). Rickard et al. (11) could show that the electron affinity of partly optimized structures rises when elongating the disulfide bond. Iozzi et al. (12) also recently presented a study showing that forces in the range of 100–400 pN promote reduction of a disulfide bond. The conclusions presented in these studies all result from restrained optimizations performed in vacuo.
The relevant experiments to compare to, however, are performed in water at ambient conditions. For direct comparison, we here aimed at mimicking the force spectroscopy experiments (1,2,4,5) as closely as possible. We subjected the disulfide-bond-containing molecule to a constant pulling force that is applied on the terminal N and C atom, respectively (Fig. 1). Our molecular dynamics (MD) simulations take free dynamics and solvation into account. We solvated our protein model system in explicit water and simulated at room temperature and 1 bar. This is of particular importance, because experiments have shown a strong impact of solvent on the disulfide mechanochemistry (2). Our hybrid quantum and molecular mechanical (QM/MM) calculations indeed showed a strong increase in redox potential, i.e., a higher reactivity, with pulling force. Unexpectedly, elongation of the disulfide bond itself sets in later than the destabilization of the system. Low forces (up to ∼500 pN) stretch the angles and dihedrals enclosing the disulfide bond rather than the bond itself. Still, a change in redox potential was observed within this range of small forces. Apparently, chemical destabilization of the system arises from any minor change in the conformation near the reaction center.
Figure 1.
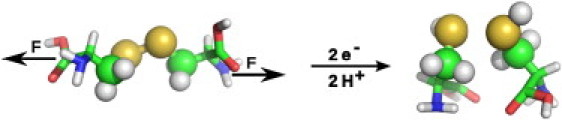
Scheme of cystine reduction by addition of each two hydrogens and electrons under a constant mechanical force acting on the terminal atoms, C and N, respectively, as indicated. (Spheres) QM atoms.
Methods
Calculating redox potentials
The redox potential can be calculated from the reaction free energy, ΔG—i.e., the difference between the free energy of the disulfide-bonded oxidized state, Gox, and the reduced state, Gred, that results from the addition of each two hydrogens and electrons (Fig. 1). The relative change in redox potential due to the mechanical force F, ΔE0redox(F), then is given by the difference between the reaction free energies at force F, ΔG(F), and at zero force, ΔG(F = 0), following Nernst's equation,
| (1) |
where Fc is the Faraday constant.
Full disulfide bond reduction includes the addition of two electrons and two protons, and results in a product with two thiols, i.e., with a broken sulfur-sulfur bond (Fig. 1). Such an open state is force-independent, as the pulling force, acting on two individual molecules in opposite directions, no longer causes a restoring force. Therefore, Gred is force-independent. In principle, for estimating the redox potential of a disulfide bond, other product states can be considered alternatively, namely a radical anion resulting from the addition of one electron, and a monoprotonated state. However, for those reaction intermediates, we find them to spontaneously open the sulfur-sulfur bond at ambient conditions, even in the absence of force (see Results). Thus, the force-independent reduced state cancels out in Eq. 1, and we calculated the force-dependent redox potential, ΔE0redox(F), directly from the energy difference between the oxidized state at force F, G(F), and zero force, G(F = 0). As another consequence of the force-independent product state, the redox potential calculations are unaffected by any assumption of the protonation state of the product.
We approximated the free energy by the electronic energy of the quantum mechanically treated region (see Fig. 1), EQM. Due to the electronic embedding into the classically treated environment, EQM includes the electrostatic interaction with the solvent and the rest of the cystine. It is a time average obtained from picosecond scale MD simulations, thereby capturing the thermal fluctuations of the system. We note that choosing the full QM/MM energy, which also includes the interaction energy within the MM system, was unfeasible. The high fluctuations of the interwater nonbonded interaction (in the 1000 kJ/mol range) impeded a reliable estimation of time-averaged energies. Using Eq. 1, we obtained ΔE0redox(F) for forces up to F = 3320 pN from QM/MM MD simulations totaling >2.0 ns of simulation time.
Simulation setup
All molecular dynamics (MD) simulations were carried out using the GROMACS 4.0.5 package (13). For the hybrid QM/MM calculations, we used GROMACS 4.0.5 interfaced with Gaussian 03 (14,15).
A cystine, created with the Molecular Operating Environment software (MOE 2008.10; Chemical Computing Group, Montreal, Quebec, Canada), was solvated in a box of explicit water of TIP4P (16). The box was large enough to allow a 1.5-nm distance in x and y directions. We used a larger length of 8 nm in z direction, along which the molecule will be subjected to a pulling force (see below), to prevent interactions with itself in periodic boundary conditions. A salt concentration of 0.1 mol/L was chosen, resulting in 2370 water molecules and four ions of each sodium and chloride. Cystine was chosen as a simple model system for disulfides in proteins. The disulfide bond, the adjacent methylene groups, and two link atoms were treated with QM, and the remainder with MM, as shown in Fig. 1.
Simulation details
To begin, the system was energy-minimized with a pure molecular mechanical description, using the steepest descent algorithm. We used the OPLS-AA force field (17) for all MM calculations. Next, we performed a pure MM MD simulation, where the system was heated to 300 K, using the Berendsen thermostat (18) over 20 ps at a timestep of 2 fs. The time constant of temperature coupling was chosen as 0.1 ps and the pressure was kept at 1 bar via isotropic coupling with the Parrinello-Rahman barostat (19), with a time constant of 1.0 ps. Thus, we work with an NpT ensemble for this study. The LINCS constraint (20) was used on all bonds. Nonbonded interactions were calculated within a cut-off of 1 nm. Electrostatic interactions beyond 1 nm were treated with particle-mesh Ewald (21) with a grid spacing of 0.12 nm.
The next step was a 10-ns MD simulation for equilibration, here using the Nosé-Hoover thermostat (22,23) with a coupling constant of 0.4 ps for temperature coupling. Forces and velocities were taken from the heating simulation.
From the equilibration, 10 configurations were chosen between 2 and 10 ns for subsequent QM/MM simulations without force. A QM/MM energy minimization was performed, using the steepest descent algorithm. An interface between GROMACS 4.0.5 (13) and Gaussian 03 (14) was used for these simulations, with the QM system electronically embedded into the MM-system (15). The QM system was treated with MP2/6-31+G∗ (24) as suggested by Bergès et al. (25) and included 10 atoms: the two sulfur atoms, both CH2 groups and the link atoms between Cα and Cβ. In restraint optimizations of cystine in vacuo, the MP2/6-31+G∗ method produces a Morse-potential for disulfide bond elongation in close agreement with the results of a coupled-cluster level of theory (see Fig. S1 in the Supporting Material), and thus can be expected to yield reliable energies for the redox potential calculations carried out here.
For all QM/MM calculations, the MM region was treated as described above. LINCS constraints were only applied to bonds involving hydrogen, and the timestep was changed to 0.5 fs. The Berendsen thermostat and barostat (18) were applied. Other simulation parameters were the same as for pure MM MD simulations. As conformations are sampled at 300 K, we did not use any zero point energy or thermal corrections. The applied electronic embedding took solvation effects into account.
Ten simulations, each 20 ps in length, were performed without applying any force. For evaluation of these zero-force simulations, only data for t >10 ps were used. Simulations at forces up to 498 pN were performed starting from a randomly chosen set of coordinates and velocities of the zero-force QM/MM simulations. For any force larger than 498 pN, the structure and velocities were read in from the MD simulation at the next-smaller force. Thereby, we did not introduce large errors into the simulation by suddenly applying a large force to a structure equilibrated at zero force. We applied the constant force onto the terminal N and C atoms in z direction, i.e., in the longest dimension of our simulation box. To check for convergence, we performed additional simulations at F = 166, 332, and 498 pN, which started from structures sampled at 830 pN instead of 0 pN. We did not observe any significant differences between these force-quench and force-jump protocols in terms of geometries and energies after 5 ps, and concluded that the 15-ps timescale was sufficient for full relaxation to the respective force. Overall, we performed 15 simulations each at F = 30, 50, 100, 166, 332, 498, and 830 pN and 5 simulations at F = 664, 1162, 1660, 2490, and 3320 pN, each lasting 15 ps, resulting in an overall simulation time of >2 ns.
Results
The reduced state
A redox potential measures the energy difference between the reduced and oxidized state. In this article, we are interested in the change of redox potential upon force application. Applying a range of mechanical forces to the oxidized state to calculate its force-dependent energy is straightforward, as the disulfide bond can withstand forces up to 3320 pN on the picosecond scale. The question arises: can the reduced state withstand mechanical forces, or does it open the sulfur-sulfur bond?
Simple electron addition to a disulfide bond, the primary reaction mostly chosen to study redox reactions quantum-mechanically (8–10), results in a radical anion, which was previously found to maintain a chemical bond between the sulfur atoms in QM calculations of minimized structures in vacuo (11).
As a start to estimating the force-induced stability change of the reduced state, we performed QM/MM calculations of the radical anion at ambient conditions, in explicit solvent, and in the absence of force. These simulations were set up in a way equivalent to simulations in the oxidized state: The same configurations from the pure classical MD simulations that were used for QM/MM minimization in the oxidized state were chosen and minimized with one additional electron in the QM-region (charge −1, multiplicity 2). Then, five independent QM/MM simulations were started, at the same conditions used for the oxidized state, again with a charge of −1 and a multiplicity of 2. We observed a dissociation of the disulfide bond within the first 40 ps for four out of five simulations of the reduced state (see Fig. S2). Thus, in contrast to previous findings for the same system at 0 K in vacuo, the open state is the equilibrium state of the radical anion in water at ambient conditions, even in the absence of force.
The protonated radical, resulting from the addition of one electron and one proton, can be considered as another feasible product state of the reduction reaction. Previous estimates for the pKa of a disulfide radical anion range from 6 to 10 (26,27), and strongly depend on the chemical surrounding. This is similarly the case for fully reduced cysteine residues; whereas proteins predominantly contain protonated cysteines, the catalytic cysteine in thioredoxins, for example, has been clearly shown to be deprotonated (28). We used a number of methods to check whether the protonated reduced state, as another possible product state, was closed and thus, force-dependent. Pure QM optimizations showed a closed state only for semiempirical methods (AM1 and PM3), whereas further refinement (UB3LYP, UMP2) showed that the bond dissociated upon optimization. This was further confirmed by a QM/MM energy minimization at the MP2/6-31+G∗ level of theory, which again led to dissociation (see Table S2 in the Supporting Material). These findings suggest that the addition of a proton to the radical anion does also not stabilize the reduced state any further, as we observe spontaneous bond lengthening in both QM and QM/MM optimizations for this uncharged radical species.
Obviously, the doubly protonated reduced state, consisting of two molecules of cystine, does not feature a bond between the sulfur atoms, and as a consequence its energy is independent of force. We conclude that irrespective of its precise nature and protonation, the product state is force-independent, and it is fair to estimate force-altered redox potentials solely based on the oxidized state. Thus, in the following, we only consider the closed, oxidized state, the cystine molecule.
Redox potentials
We here investigated the impact of mechanical force on the redox potential of the disulfide bond in cystine solvated in water from MD simulations. To this end, we applied mechanical forces in the range of 0–3320 pN to the N- and C-termini of cystine. The changes in redox potential as a function of force are shown in Fig. 2. As expected, we observed an overall increase in redox potential with mechanical force. In other words, stretching forces acting on the molecule enhance the electron affinity of the disulfide bond by destabilizing the molecule. However, this pronounced increase in redox potential is only found for forces >166 pN. Forces <100 pN, instead, show the opposite trend. Surprisingly, they stabilize the system slightly and thus decrease the redox potential, as shown in the inset of Fig. 2. Counterintuitively, this involves a shortening of the disulfide bond at low force (see further below).
Figure 2.
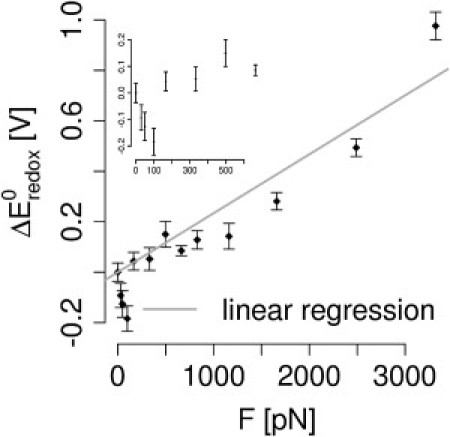
Mechanical force changes the redox potential toward higher reduction potentials. From our linear regression (solid line), we estimated the distance on the reaction coordinate between reactant and product, Δxr,p. The redox potential ΔE0redox continuously increases with force, except for small forces (see main text). (Error bars) Mean ± SE obtained from the average values over each trajectory at a given force.
Assuming force to tilt the energy landscape linearly by F·x, one can obtain the distance between the reactant and product state along the reaction coordinate, Δxr,p. This is also the basic assumption of the Bell model (7), which relates mechanical force to kinetic rates, whereas we here infer force-induced thermodynamic changes. From a linear fit to our force-dependent redox potential data, we estimate Δxr,p, the distance between reactant and product state, to be 0.37 Å over the entire range of forces probed here. Due to the nonlinear dependency of ΔE0redox on force (Fig. 2), we obtain a smaller Δxr,p of 0.25 nm for forces up to 830 pN (Table 1).
Table 1.
Estimated Δxr,p from linear regression and experimentally measured Δxr,ts
How does our estimated Δxr,p compare to experimental data? Force-clamp experiments allow measuring the distance between the reactant and the transition state, Δxr,ts. Such an experiment performed on a titin immunoglobulin domain yielded a Δxr,ts of 0.34 Å (1). Other thiol-containing reducing agents resulted in Δxr,ts between 0.23 and 0.35 nm (2,3) (compare Table 1). Overall, the experimental and calculated values for the distance of the reactant to the transition and product state, respectively, largely overlap—semiquantitatively validating our results.
Structural changes
The observed overall increase of the disulfide's electron affinity can involve the deformation of various degrees of freedom of the system near the bond. We next analyzed the structural features of cystine under a stretching force that is likely to cause the increase in redox potential and thus the enhanced tendency for sulfur-sulfur bond scission. As expected, the destabilization of the system by the applied mechanical force, as measured by ΔEQM, overall involves a lengthening of the disulfide bond (Fig. 3 a). Within the force range probed here, the bond elongates by up to 0.02 nm, which corresponds to roughly 10% of the initial length, within the oxidized state. However, our QM/MM calculations show that at low forces <500 pN, the disulfide bond length does not increase steadily (black curve in Fig. 3 b), even though the end-to-end length between the cystine's termini increases (blue curve). We find that low to intermediate forces up to 500 pN lengthen and destabilize the oxidized state significantly without considerably stretching the disulfide bond. Instead, unexpectedly, we even observe a slight shortening of the disulfide bond in the regime of small force application (from 0 pN to 30 pN).
Figure 3.
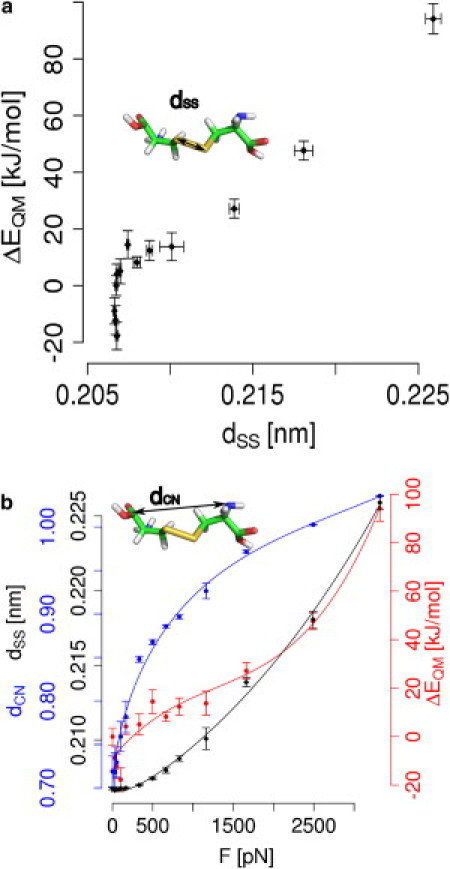
Mechanical force changes the redox potential of cystine by shifting the conformational equilibrium to larger bond lengths, angles, and dihedrals. (a) Both the energy of cystine, ΔEQM, and the elongation of the sulfur-sulfur bond, dSS, rise with mechanical force. However, at forces <500 pN, the destabilization of the cystine does not involve any significant bond lengthening. (b) In addition to the lengthening of the sulfur-sulfur bond (black), force leads to a lengthening of the whole molecule, measured by the distance between the termini, dCN (blue). Taken together, these changes in softer and stiffer degrees of freedom cause the energy ΔEQM (red) to rise over the entire range of forces. In all figures, the energy and redox potential obtained at F = 0 pN served as a reference. (Lines) Guides to the eye.
The lengthening of the disulfide bond is significant only at forces >500 pN (Fig. 3 b), and thus can explain the observed rise in redox potential only partly. Apparently, other degrees of freedom that contribute to the stability and thereby to the redox potential of cystine are affected by mechanical force. Indeed, at forces <500 pN, the overall length of the cystine molecule, measured by dCN, increases (Fig. 3 b). This lengthening at low forces is caused by changes in the dihedrals and angles in proximity to the disulfide bond (Fig. 4). The dihedral angle enclosing the disulfide bond is the degree of freedom that starts changing first. Without any mechanical force applied externally, it samples angles at ∼80°. Though flexible, as evidenced by the large error bars, the dihedral angle expands already upon application of the smallest force probed here, namely 30 pN, to ∼115°. At forces of 1160 pN and higher, the average dihedral angle is ∼170°. As the maximum extension is already reached, forces >1160 pN do not increase the dihedral angle any further.
Figure 4.
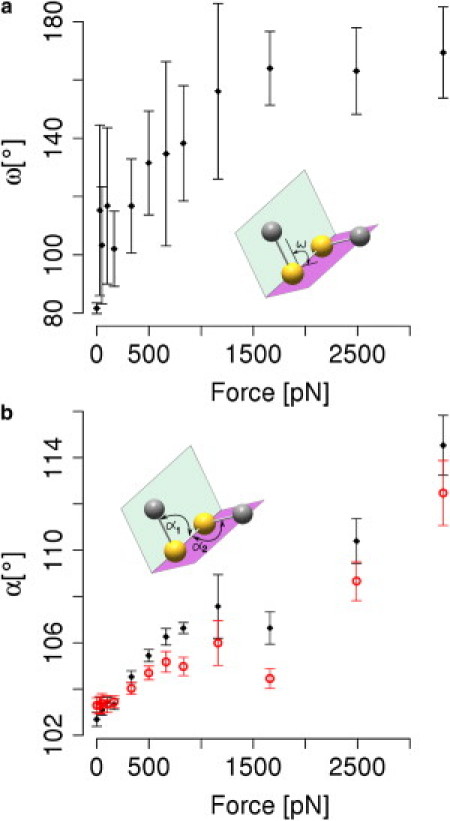
Changes of softer degrees of freedom of cystine, i.e., angles and dihedrals, by mechanical force. (a) Dihedral angles ω between the cystine side chain atoms Cβ-S-S-Cβ (see inset) increase already at forces as small as 50 pN, and open up to ∼170°. Other dihedrals show similar tendencies (not shown). (b) Angles α1 and α2 between Cβ-S-S and S-S-Cβ, respectively, show changes over nearly the whole force range (from F >320 pN).
An analogous picture was found for the two CSS angles enclosing the disulfide bond. Increasing the force from zero to 1000 pN enlarges the angle from 103 to ∼105°. For forces >1160 pN—that is where dihedrals are already extended to be nearly planar—angles are continuously being stretched up to 114°. In a simplistic view, we can infer a sequence of events upon stretching a disulfide bond from this analysis. This is to say, cystine elongates first by extending soft dihedrals all the way up to nearly 180°, secondly by stretching angles, and lastly by elongating the comparably stiff sulfur-sulfur connection itself. The high force-sensitivity of angles and even more so for dihedrals implies that the extension of the overall cystine molecule at low forces (Fig. 3 b) can be primarily attributed to the stretching of dihedrals and angles, leaving the disulfide bond largely unchanged.
As already implied, fully releasing the force from 50 pN to 0 pN elongates the disulfide bond marginally by ∼10−3 Å (see Fig. 3), thereby destabilizing the cystine and leading to a rise in ΔE0redox (as shown in the inset in Fig. 2). Apparently, low forces act on degrees of freedoms orthogonal to the disulfide bond length. This counterintuitive behavior is likely to be cystine-specific, because it was not observed for a larger protein (titin I27) (29). To ensure that the bond shortening we observed is not an artifact of the QM/MM calculations, we performed pure QM optimizations on a cystine, where we enlarged the dihedral angle stepwise. The disulfide bond shows a minimum in bond length not in the fully optimized structure, but at a torsion that is 10° larger than the one found in the minimized structure (see Fig. S3).
Discussion
We here employed molecular dynamics simulations of cystine at ambient conditions to assess the effect of mechanical force on disulfide reduction. By quantifying the redox potential, our study allows conclusions independent from the reducing agent and reduction mechanism. We find that a pulling force, even at forces as small as a few 100 pN, directly affects the redox potential, i.e., the chemistry of the disulfide bond. This major result of our study, the thermodynamic destabilization of the oxidized state by force, can be directly related to the force-altered kinetics of single-molecule force experiments. As mentioned in Methods, the increase in redox potential entails a lowering in the activation barrier for reduction, as the free energy landscape is steadily tilted by force according to the Bell or other refined models (see the linear fit to ΔE0redox according to Bell in Fig. 2) (7,30). Our results thus can explain the enhanced reactivity observed in various recent force spectroscopy experiments and in calculations (1–5,29). Other factors such as substrate accessibility or changes in the reaction mechanism can additionally alter the reaction rates. However, as we here show, mechanical force does destabilize the oxidized system directly, which is sufficient to explain the experimental rate enhancement by force. In this light, the mechanical insensitivity of disulfides in strained ring structures (6) is surprising and might possibly be caused by several compensating effects that are subject to further investigations.
Remarkably, lower and medium forces (between 50 and 830 pN) primarily affect the softer degrees of freedom, namely angles and dihedrals, whereas the disulfide bond remains unstretched or even becomes shortened. Only at high forces (beyond ∼500 pN), stretching of the disulfide bond itself sets in. Both effects jointly lead to a steady destabilization of the system and thus an increase in redox potential throughout the whole range of forces (30–3320 pN) probed here. At 3320 pN, the maximum force investigated here, we found the disulfide bond to stretch by 0.2 Å and dihedrals to fully open (i.e., close to 180°). We compared these findings for the isolated cystine to a cystine in a mutant of I27, a titin immunoglobulin domain, under different stretching forces. Again, the disulfide bond shows a slow increase in bond length upon stretching, whereas angles and dihedrals enlarge already significantly in the low force regime (results not shown). Also, angles and dihedrals in titin expand up to 180°, in a similar way as discussed for cystine (compare to Li and Gräter (29)). Thus, our major findings are largely independent from the system comprising the sulfur-sulfur bond. The decrease in disulfide bond length, however, seems to be specific for cystine. How this shortening of disulfide bond length at low forces is related to catch-binding (1,31) could not yet be understood, and remains to be explored.
As opposed to our results, the COGEF study recently presented by Iozzi et al. (12) predicts the bond to stretch by 0.35 Å until the rupture point—which is found for ∼3500 pN—but the dihedrals enlarge to no greater than 120°. The major differences between the two approaches is that we take solvation and dynamic fluctuations at room temperature into account, whereas Iozzi's study was performed in vacuo using optimization, i.e., by comparing minimized structures. Apparently, these different conditions cause very different degrees of freedom to be affected by mechanical force. In other words, the dynamics at ambient conditions allow the structure to relax differently compared to the relaxation taking place at 0 K in vacuo as is the case for the COGEF approach. We note that the different levels of theory used by Iozzi et al. (12) (B3LYP) and by us (MP2) is unlikely to give rise to the discrepancies, as they yield similar bond lengths, and only differ in their electron affinity for sulfur-sulfur systems (25).
Comparison to experiments
How are the changes in redox potential upon force application related to previous experimental findings? We above have quantified the sensitivity of our redox system toward a mechanical force, in other words the extent to which the energy landscape is tilted by a given force, in terms of Δxr,p, the distance between reactant and product state along the reaction coordinate (Table 1). The force-sensitivity of the redox potential, measured by Δxr,p, is of a magnitude similar to the force dependency of the redox reactivity probed in experiments in terms of Δxr,ts. We can conclude that our QM/MM calculations are in line with previous force spectroscopy experiments. They suggest that the whole redox reaction is as susceptible to the mechanical force as the transition barrier. The structural interpretation of Δx, then, implies the transition state highly resembles the product state.
The above analysis of our force-dependent redox potential calculations is based on the simple assumption that force tilts the energy linearly along the reaction coordinate, as originally proposed by Bell (7). However, other advanced nonlinear models have been put forward and have proven useful (30) to interpret force-altered reaction rates probed experimentally. Devising a nonlinear model for estimating force-dependent redox potentials for the disulfide bond, i.e., a Morse potential, might further improve the accuracy of our analysis, but that is outside the scope of this study.
Comparison to redox changes by chemical environment
How does the observed force-sensitivity of the disulfide bond redox potential compare to the variation in redox potential of this bond in different chemical environments? Our calculations estimated a force of ∼300 pN to increase the redox potential by ∼50 mV, whereas an external force as high as ∼1000 pN increases the redox potential by ∼140 mV. On average over the whole force range, we obtain from Δxr,p a force-sensitivity of 0.23 mV/pN. In living organisms, we usually find redox potentials in the range of 200–300 mV, i.e., variations <100 mV. Fig. 5 shows some examples of thioredoxin mutations and their redox potentials (32–34). A single point mutation changes the redox potential by no more than 32 mV. As another example, engineered disulfide-bonded GFP mutants feature redox potentials differing by no more than 10–20 mV (35). Such an alteration of redox potential would require a pulling force of several tens of picoNewtons.
Figure 5.
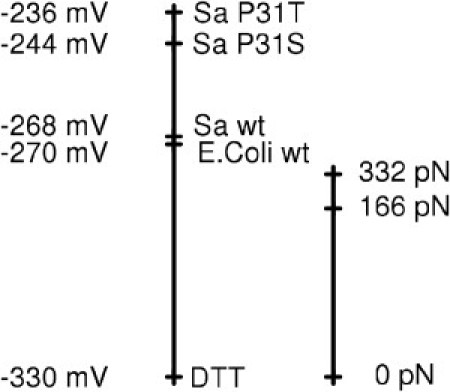
Redox potentials in biological systems in comparison to redox potentials induced by mechanical force. (Left) Measured redox potentials for chemical and biological reducing agents, namely DTT (33), Escherichia coli thioredoxin (34), and Staphylococcus aureus thioredoxin, including two mutants (32). (Right) Shifts in redox potential for cystine from our QM/MM calculations, shown at the same scale. Force-altered redox potentials cover a similar range to those sampled within different molecules and mutants.
As demonstrated by this comparison (Fig. 5), a change in redox potential can be similarly achieved by either a change in the biochemical neighborhood, e.g., a mutation, or a mechanical force in the 100 pN range. The question then arises: is a mechanical force of this magnitude likely to act on a disulfide bond in the living cell?
Titin immunoglobulin domains have been shown to unfold at forces in the range of 150–300 pN (36). Another example for a biological system experiencing mechanical force is the fibronectin/integrin cluster. Its bond strength is estimated to lie between 30 and 100 pN (37). In general, forces on a single molecule in living organisms are estimated to be a few picoNewtons or a few tens of picoNewtons large (38), and thus are able to tune redox potentials significantly.
Conclusion
In conclusion, force can alter the redox biochemistry in the cell to an extent comparable to single point mutations in redox reactive proteins. We expect our approach, by including conformational sampling and explicit solvation, to reliably predict the correct tendencies in ΔE0redox upon force application. A more thorough treatment based on free energy calculations (39,40) and taking proton uptake into account might, in future, help to make quantitative estimates of force-altered redox potentials.
Acknowledgments
The authors acknowledge fruitful discussions with Peter Comba, Bodo Martin, Agnieszka Bronowska, and Matthias Ullmann.
Financial support by the Klaus Tschira Foundation, by the Deutsche Forschungsgemeinschaft (“Mechanochemistry”), and the Excellence Initiative (Global Networks, Heidelberg University) is gratefully acknowledged.
Footnotes
This is an Open Access article distributed under the terms of the Creative Commons-Attribution Noncommercial License (http://creativecommons.org/licenses/by-nc/2.0/), which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Supporting Material
References
- 1.Wiita A.P., Ainavarapu S.R.K., Fernandez J.M. Force-dependent chemical kinetics of disulfide bond reduction observed with single-molecule techniques. Proc. Natl. Acad. Sci. USA. 2006;103:7222–7227. doi: 10.1073/pnas.0511035103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Koti Ainavarapu S.R., Wiita A.P., Fernandez J.M. Single-molecule force spectroscopy measurements of bond elongation during a bimolecular reaction. J. Am. Chem. Soc. 2008;130:6479–6487. doi: 10.1021/ja800180u. [DOI] [PubMed] [Google Scholar]
- 3.Wiita A.P., Perez-Jimenez R., Fernandez J.M. Probing the chemistry of thioredoxin catalysis with force. Nature. 2007;450:124–127. doi: 10.1038/nature06231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Perez-Jimenez R., Li J., Fernandez J.M. Diversity of chemical mechanisms in thioredoxin catalysis revealed by single-molecule force spectroscopy. Nat. Struct. Mol. Biol. 2009;16:890–896. doi: 10.1038/nsmb.1627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Garcia-Manyes S., Liang J., Fernández J.M. Force-activated reactivity switch in a bimolecular chemical reaction. Nat. Chem. 2009;1:236–242. doi: 10.1038/nchem.207. [DOI] [PubMed] [Google Scholar]
- 6.Kucharski T.J., Huang Z., Boulatov R. Kinetics of thiol/disulfide exchange correlate weakly with the restoring force in the disulfide moiety. Angew. Chem. Int. Ed. Engl. 2009;48:7040–7043. doi: 10.1002/anie.200901511. [DOI] [PubMed] [Google Scholar]
- 7.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 8.Houée-Levin C., Bergès J. Single electron localization on the cystine/cysteine couple: sulfur or carbon? Research Chem. Int. 2009;35:421–430. [Google Scholar]
- 9.Sawicka A., Skurski P., Simons J. Excess electron attachment to disulfide-bridged l,l-cystine. An ab initio study. J. Phys. Chem. A. 2004;108:4261–4268. [Google Scholar]
- 10.Uggerud E. Electron capture dissociation of the disulfide bond—a quantum chemical model study. Int. J. Mass Spectrom. 2004;234:45–50. [Google Scholar]
- 11.Rickard G.A., Bergès J., Rauk A. Ab initio and QM/MM study of electron addition on the disulfide bond in thioredoxin. J. Phys. Chem. B. 2008;112:5774–5787. doi: 10.1021/jp710917t. [DOI] [PubMed] [Google Scholar]
- 12.Iozzi M.F., Helgaker T., Uggerud E. Influence of external force on properties and reactivity of disulfide bonds. J. Phys. Chem. A. 2011;115:2308–2315. doi: 10.1021/jp109428g. [DOI] [PubMed] [Google Scholar]
- 13.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 14.Frisch M.J., Trucks G.W., Pople J.A. Gaussian; Wallingford, CT: 2004. [Google Scholar]
- 15.Groenhof G., Lensink M.F., Mark A.E. Signal transduction in the photoactive yellow protein. I. Photon absorption and the isomerization of the chromophore. Proteins. 2002;48:202–211. doi: 10.1002/prot.10136. [DOI] [PubMed] [Google Scholar]
- 16.Jorgensen W.L., Chandrasekhar J., Klein R.W. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 17.Jorgensen W.L., Maxwell D.S., Tirado-Rives J. Development and testing of the OPLS All-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996;118:11225–11236. [Google Scholar]
- 18.Berendsen H.J.C., Postma J.P.M., Haak J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- 19.Parrinello M., Rahman A. Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 1981;52:7182–7190. [Google Scholar]
- 20.Hess B., Bekker H., Fraaije J.G.E.M. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. [Google Scholar]
- 21.Darden T., York D., Pedersen L. Particle mesh Ewald: an N-log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 22.Nosé S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984;52:255–268. [Google Scholar]
- 23.Hoover W.G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 24.Moller C., Plesset M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934;46:618–622. [Google Scholar]
- 25.Bergès J., Rickards G., Houée-Levin C. QM/MM study of electron addition on protein disulfide bonds. Chem. Phys. Lett. 2006;421:63–67. [Google Scholar]
- 26.Faraggi M., Klapper M.H., Dorfman L.M. Fast reaction kinetics of one-electron transfer in proteins. The histidyl radical. Mode of electron migration. J. Phys. Chem. 1978;82:508–512. [Google Scholar]
- 27.Mezyk P.S., Armstrong D.A. Disulfide anion radical equilibria: effects of -NH3+, -CO2−, -NHC(O)− and -CH3 groups. J. Chem. Soc., Perkin Trans. 2. 1999:1411–1420. [Google Scholar]
- 28.Lmoumène C.E.H., Conte D., Houée-Levin C. Redox properties of protein disulfide bond in oxidized thioredoxin and lysozyme: a pulse radiolysis study. Biochemistry. 2000;39:9295–9301. doi: 10.1021/bi000468e. [DOI] [PubMed] [Google Scholar]
- 29.Li W., Gräter F. Atomistic evidence of how force dynamically regulates thiol/disulfide exchange. J. Am. Chem. Soc. 2010;132:16790–16795. doi: 10.1021/ja104763q. [DOI] [PubMed] [Google Scholar]
- 30.Dudko O.K., Hummer G., Szabo A. Intrinsic rates and activation free energies from single-molecule pulling experiments. Phys. Rev. Lett. 2006;96:108101–108104. doi: 10.1103/PhysRevLett.96.108101. [DOI] [PubMed] [Google Scholar]
- 31.Yuriy Pereverzev O.P. Deformation model for thioredoxin catalysis of disulfide bond dissociation by force. Cell. Mol. Bioeng. 2009;2:255–263. [Google Scholar]
- 32.Roos G., Garcia-Pino A., Messens J. The conserved active site proline determines the reducing power of Staphylococcus aureus thioredoxin. J. Mol. Biol. 2007;368:800–811. doi: 10.1016/j.jmb.2007.02.045. [DOI] [PubMed] [Google Scholar]
- 33.Cleland W.W. Dithiothreitol, a new protective reagent for SH groups. Biochemistry. 1964;3:480–482. doi: 10.1021/bi00892a002. [DOI] [PubMed] [Google Scholar]
- 34.Quan S., Schneider I., Bardwell J.C. The CXXC motif is more than a redox rheostat. J. Biol. Chem. 2007;282:28823–28833. doi: 10.1074/jbc.M705291200. [DOI] [PubMed] [Google Scholar]
- 35.Hanson G.T., Aggeler R., Remington S.J. Investigating mitochondrial redox potential with redox-sensitive green fluorescent protein indicators. J. Biol. Chem. 2004;279:13044–13053. doi: 10.1074/jbc.M312846200. [DOI] [PubMed] [Google Scholar]
- 36.Rief M., Gautel M., Gaub H.E. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 1997;276:1109–1112. doi: 10.1126/science.276.5315.1109. [DOI] [PubMed] [Google Scholar]
- 37.Lehenkari P.P., Horton M.A. Single integrin molecule adhesion forces in intact cells measured by atomic force microscopy. Biochem. Biophys. Res. Commun. 1999;259:645–650. doi: 10.1006/bbrc.1999.0827. [DOI] [PubMed] [Google Scholar]
- 38.Huang H., Kamm R.D., Lee R.T. Cell mechanics and mechanotransduction: pathways, probes, and physiology. Am. J. Physiol. Cell Physiol. 2004;287:C1–C11. doi: 10.1152/ajpcell.00559.2003. [DOI] [PubMed] [Google Scholar]
- 39.Formaneck M.S., Li G., Cui Q. Calculation accurate redox potentials in enzymes with a combined QM/MM free energy perturbation approach. J. Theor. Comput. Chem. 2002;1:53–67. [Google Scholar]
- 40.Sattelle B.M., Sutcliffe M.J. Calculating chemically accurate redox potentials for engineered flavoproteins from classical molecular dynamics free energy simulations. J. Phys. Chem. A. 2008;112:13053–13057. doi: 10.1021/jp803859j. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


