Chain Length Determines the Folding Rates of RNA

Abstract

We show that the folding rates (k_Fs) of RNA are determined by N, the number of nucleotides. By assuming that the distribution of free-energy barriers separating the folded and the unfolded states is Gaussian, which follows from central limit theorem arguments and polymer physics concepts, we show that $k_F\approx k_0\exp \left(-\alpha N^{0.5}\right)$. Remarkably, the theory fits experimental rates spanning over 7 orders of magnitude with $k_0\sim 1.0{\left(\mu \text{s}\right)}^{-1}$. Our finding suggests that the speed limit of RNA folding is ∼1 ms, just as it is in the folding of globular proteins.

RNA molecules are evolved biopolymers whose folding has attracted a great deal of attention (1–3) because of the crucial role they play in a number of cellular functions. The slightly branched polymeric nature of RNA implies that the shapes, relaxation dynamics, and even their folding rates must depend on N. In support of this assertion, it has been shown that the radius of gyration of the folded states, obtained with the use of data available in the Protein Data Bank, scales as $R_g\sim 5.5N^{\nu }$ Å, where the Flory exponent ν varies from 0.33 to 0.40 (4–6). Although this result is expected from the perspective of polymer physics, it is surprising from the viewpoint of structural biology because one might argue that the sequence and complexity of secondary and tertiary structure organization could lead to substantial deviations from the predictions based on Flory-like theory. Here, we show that the folding rates, k_Fs, of RNA are also primarily determined by N, thus adding to the growing evidence that it is possible to understand RNA folding by using polymer physics principles.

Theoretical Considerations

Theoretical arguments based on the dynamics of activated transitions in disordered systems suggest that

$$k_F=k_0\exp \left(-\alpha N^{\beta }\right),$$ (1)

where β should be 0.5 (7). The rationale for this finding hinges on the observation that favorable basepairing interactions and the hydrophobic nature of the bases tend to collapse RNA, whereas the charged phosphate residues are better accommodated by extended structures. Thus, the distribution of activation free energy, $\Delta G_{UF}^{‡}/k_{\text{B}}T$, between the folded and unfolded states is a sum of favorable and unfavorable terms. We expect from central limit theorem that the distribution of $\Delta G_{UF}^{‡}/k_{\text{B}}T$ should be roughly Gaussian with dispersion $\langle {\left(\Delta G_{UF}^{‡}\right)}^2\rangle \sim N$. Thus, $\Delta G_{UF}^{‡}/k_{\text{B}}T\sim N^{\beta }$with β = 1/2.

We analyzed the available experimental data (see Table 1 for a list of RNA molecules) on RNA folding rates by assuming that $\Delta G_{UF}^{‡}$ grows as N^β with β as a free parameter. The theoretical value for β is 0.5. The folding rates of RNA spanning over 7 orders of magnitude is well fit using $\log k_F=\log k_0-\alpha N^{\beta }$ with a correlation coefficient of 0.98 (Fig. 1). The fit yields $k_0^{-1}=0.87$ μs, α = 0.91, and β ≈ 0.46. In the inset we show the fit obtained by fixing β = 0.5. Apart from the moderate differences in the $k_0^{-1}$ values, the theoretical prediction and the numerical fits are in agreement, which demonstrates that the major determining factor in determining RNA folding rates is N.

Table 1.

RNA length versus folding rate

RNA	N	kf (sec-1)
GCUUCGGC (16)	8	6.7 × 104	Tetraloop hairpin
GCUUCGGC (16)	8	27.2 × 104	Tetraloop hairpin
GGUUCGCC (16)	8	1.3 × 104	Tetraloop hairpin
GGUUCGCC (16)	8	4.7 × 104	Tetraloop hairpin
GGACUUUUGUCC (16)	12	6.1 × 104	Tetraloop hairpin
GGACUUCGGUCC (16)	12	4.5 × 104	Tetraloop hairpin
A6C6U6 (17)	18	3.4 × 104	Tetraloop hairpin
Extra arm of tRNAser (yeast) (18)	21	1 × 105	tRNA
pG half of tRNAPhe (yeast) (18)	36	9 × 103	tRNA
CCA half of tRNAPhe (yeast) (18)	39	8.5 × 103	tRNA
CCA half of tRNAPhe (wheat) (18)	39	8 × 103	tRNA
tRNAPhe (yeast) (19)	76	5.3 × 102	tRNA
tRNAAla (yeast) (18)	77	9 × 102	tRNA
Y4 hairpin (20)	14	5.75 × 104	Hairpin (5 × 2 + 4)
Y9 hairpin (20)	19	2.29 × 104	Hairpin (5 × 2 + 9)
Y19 hairpin (20)	29	8.70 × 102	Hairpin (5 × 2 + 19)
Y34 hairpin (20)	44	6.03 × 102	Hairpin (5 × 2 + 34)
VPK pseudoknot (21)	34	9.09 × 102	Pseudoknot
Hairpin ribozyme (four-way junction) (22,23)	125	6	Natural form of hairpin ribozyme
P5abc (24)	72	50	Group I intron T. ribozyme
P4-P6 domain(Tetrahymena ribozyme) (24)	160	2	Group I intron T. ribozyme
Azoarcus ribozyme (23,25)	205	7 ∼ 14
B. subtilis RNase P RNA catalytic domain (26)	225	6.5 ± 0.2
Ca.L-11 ribozyme (27)	368	0.03
E. coli RNase P RNA (28)	377	0.011 ± 0.001
B. subtilis RNase P RNA (28)	409	0.008 ± 0.002
Tetrahymena ribozyme (23,29)	414	0.013	Group I intron T. ribozyme

Figure 1.

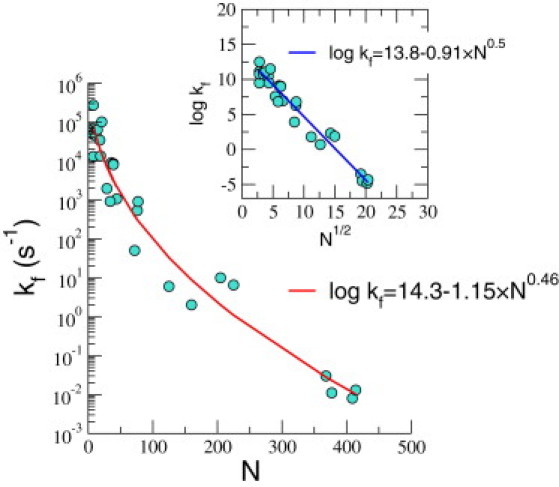
Dependence of the folding rates of RNA on N. The circles are experimental data and the line is the fit obtained using $\log k_F=\log k_0-\alpha N^{\beta }$, with β used as an adjustable parameter. Inset shows the fit obtained by fixing β to the predicted theoretical value of 0.5.

It is known that RNAs, such as Tetrahymena ribozyme, fold by multiple pathways that are succinctly described by the kinetic partitioning mechanism (8). According to this mechanism, a fraction, Φ, of molecules reaches the native states rapidly and the remaining fraction is trapped in an ensemble of misfolded intermediates. For Tetrahymena ribozyme Φ ∼ 0.1 (9). The N dependence given by Eq. 1 holds for the majority of molecules that fold to the native state from the compact intermediates, which form rapidly under folding conditions (10).

Conclusions

Our findings indicate that the inverse of the prefactor, $k_0^{-1}={\tau }_0\approx 0.87$ μs, is almost 6 orders of magnitude larger than the transition-state theory estimate of h / k_BT ≈ 0.16 ps. The value of τ₀, which coincides with the typical basepairing time (11), is the speed limit for RNA folding. Of interest, general arguments based on the kinetics of loop formation have been used to predict that the speed limit for protein folding is also ∼1 ms (12–14). It remains to be ascertained whether the common folding speed limit for proteins and RNA is due to evolutionary pressure on the folding of evolved sequences. It is worth pointing out that Dill et al. (15) recently showed that the rates and stabilities of protein folding depend only on the number of amino acids, which in turn places strict constraints on their functions in the cellular context. Taken together, these studies show that despite the complexity of protein and RNA folding, it is possible that only a few variables determine their global properties. This suggests that certain simple principles may determine biological functions.