A Small Post-Translocation Energy Bias Aids Nucleotide Selection in T7 RNA Polymerase Transcription

Abstract

The RNA polymerase (RNAP) of bacteriophage T7 is a single subunit enzyme that can transcribe DNA to RNA in the absence of additional protein factors. In this work, we present a model of T7 RNAP translocation during elongation. Based on structural information and experimental data from single-molecule force measurements, we show that a small component of facilitated translocation or power stroke coexists with the Brownian-ratchet-driven motions, and plays a crucial role in nucleotide selection at pre-insertion. The facilitated translocation is carried out by the conserved Tyr⁶³⁹ that moves its side chain into the active site, pushing aside the 3′-end of the RNA, and forming a locally stabilized post-translocation intermediate. Pre-insertion of an incoming nucleotide into this stabilized intermediate state ensures that Tyr⁶³⁹ closely participates in selecting correct nucleotides. A similar translocation mechanism has been suggested for multi-subunit RNAPs involving the bridge-helix bending. Nevertheless, the bent bridge-helix sterically prohibits nucleotide binding in the post-transolocation intermediate analog; moreover, the analog is not stabilized unless an inhibitory protein factor binds to the enzyme. Using our scheme, we also compared the efficiencies of different strategies for nucleotide selection, and examined effects of facilitated translocation on forward tracking.

Introduction

During gene transcription (1), RNA polymerases (RNAPs) act as molecular motors (2,3). They move processively along double-stranded (ds) DNA to synthesize a complementary RNA strand from the template DNA strand. The free energy fueling RNAP elongation comes from binding and incorporating nucleotides for RNA synthesis. RNAPs come in two molecular architectures: the single subunit RNAPs from certain viral and mitochondrial species (4), and the multi-subunit RNAPs from bacteria, eukaryotes, and archaea (5,6). The single subunit RNAPs share many biochemical properties with the more common multi-subunit RNAPs, the most essential of which is their two-magnesium ion catalysis mechanism that employs both RNA and DNA polymerases (7,8). However, there appear to be no structural or sequence similarities between the single and multi-subunit RNAPs. Instead, the single subunit RNAPs resemble, in both sequence and structure, the Family I DNA polymerases (DNAPs) (9,10).

The RNAP from bacteriophage T7 is a prototype single subunit RNAP (11–13). It can carry out all transcriptional functions, from initiation and elongation to termination, without additional protein partners. The molecular architecture of the T7 RNAP resembles the hand-like configuration of DNAPs (13,14), with the active site for nucleotide incorporation located on the palm of the hand. Among the single subunit RNAPs and some of DNAPs, the highly conserved O-helix from the fingers subdomain abuts the active site (see Fig. 1, a and b). The O-helix, along with the fingers subdomain, moves between open and closed conformations during each nucleotide addition or elongation cycle. Due to their small size and self-sufficiency, T7 RNAPs are widely used for synthesizing specific transcripts. This RNAP makes an ideal model system to study the transcriptional process in its simplest form and it has been investigated extensively in structural (15–18) and biochemical studies (19–22), and in single-molecule measurements as well (23–26).

Figure 1.

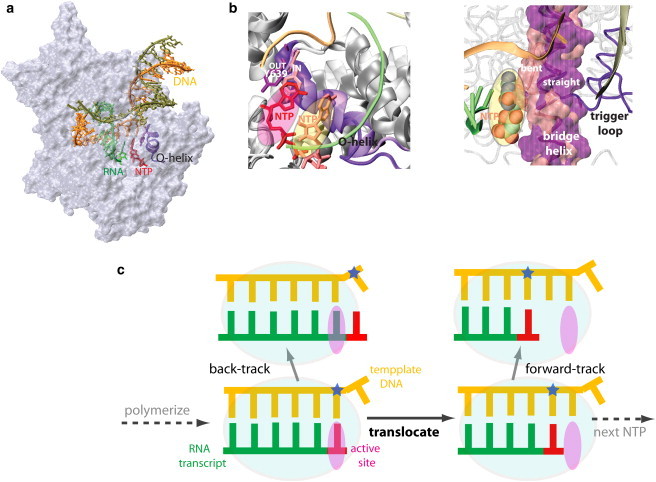
RNAP elongation complex and essential structural elements for translocation. (a) T7 RNAP (PDB:1S76) in the substrate insertion state (16). (Red) The newly inserted NTP. (Purple and magenta) Highly conserved O-helix and Tyr⁶³⁹ abutting the active site, respectively. (Tan) Nontemplate DNA strand. (Orange) Template DNA strand. (Green) RNA transcript. (b) (Left panel) Close view around the active site of T7 RNAP at both substrate insertion (16) and pre-insertion configurations (PDB:1S0V) (17). The O-helix is in its closed (purple, insertion) and open (purple transparent, pre-insertion) conformations, with the Tyr⁶³⁹ side chain OUT (magenta, insertion) and IN (pink, pre-insertion) the active site (red transparent oval), respectively. A nucleotide (red) is inserted into the active site, with another nucleotide (orange) shown in the pre-insertion site (orange transparent oval). Neither IN nor OUT Tyr⁶³⁹ poses steric hindrance to the pre-inserted nucleotide (orange), whereas the OUT Tyr⁶³⁹ stays farther from the pre-insertion site than the IN. (Right panel) Close view around the active site of a multi-subunit RNAP (Pol II) at pre-insertion (PDB: 1Y77) (44). The pre-insertion site (orange transparent oval) is occupied by a nucleotide (in vdW spheres), with the bridge helix (magenta transparent surface with backbone trace) straight. A bent configuration of the bridge helix (pink transparent surface with backbone trace) is also shown, taken from a bacterial RNAP (PDB:1IW7) (55). The bent region of the bridge helix has steric clashes with the pre-insertion nucleotide. (Purple) Nearby trigger loop. The above molecular modeling and images are generated using VMD (56). (c) Schematic representation of the DNA-RNA hybrid around the active site, before and after RNAP translocation. The template DNA strand (orange) is on top, and the RNA transcript (green) on the bottom. In addition to the normal translocation step, the forward and backward tracking configurations are also shown. The newly inserted nucleotide (red) is next to the 3′-end of the RNA; (blue star) the template DNA nucleotide that will pair with the newly inserted nucleotide.

During transcription elongation of RNAP, each nucleotide addition cycle can be viewed as taking place in two stages: polymerization and translocation. In the polymerization stage, a new RNA 3′-end is generated from an incoming NTP by phosphoryl transfer and pyrophosphate (PPi) dissociation. In the translocation stage, RNAP moves 1-nt forward on the dsDNA, breaking 1-bp downstream and reannealing 1-bp upstream. At the same time, the 3′-end of the RNA moves along with its template DNA, vacating the active site for the next incoming NTP (see Fig. 1 c). Concurrently, the 5′-end of the RNA is released 1-nt from the DNA-RNA hybrid, resulting in a dynamically growing RNA transcript. In addition to normal elongation and translocation, multi-subunit RNAPs can track either forward or backward (see Fig. 1 c). In forward-tracking (or hypertranslocation), the RNAP hops forward without synthesizing RNA. This can shorten the DNA-RNA hybrid and may lead to termination (22,27). In back-tracking, the 3′-end RNA is extruded (opposite to that in normal translocation) into an exit channel as the RNAP moves backward along the dsDNA (28–31). Back-tracking, however, has not been detected in T7 RNAP.

Most experimental evidence suggests that RNAPs use a Brownian-ratchet mechanism of translocation (32–34) wherein the RNAP fluctuates back and forth equally fast (Brownian) until the incoming NTP binds, preventing backward movement (the ratchet), producing a net forward motion (20,24,35,36). Interestingly, single-molecule force measurements of T7 RNAP showed that there is a slight free energy bias (∼1.3 k_BT) toward the post-translocated state compared with the pre-translocated state (24). However, experiments still favor a Brownian ratchet mechanism of translocation over a power-stroke mechanism—the latter requiring a significant free energy drop to drive translocation coupled with the chemical transition (37). Controversially, high-resolution structural studies of T7 RNAP intimate a power-stroke translocation mechanism in which PPi release triggers a rotational pivoting of the O-helix from the closed to open conformation, directly driving the RNAP translocation (13,16).

In this work, we examine the translocation mechanism more closely to resolve these conflicting views. The translocation dynamics take place on a millisecond timescale, too fast to be examined thoroughly in experiments but still much too slow for atomistic molecular dynamics simulations, which are limited to nano- to microseconds. To address this difficulty, we construct a semi-phenomenological model of RNAP elongation combining single-molecule force measurements (24,25) with information from structural studies (16,17). To accomplish this, we regard published high-resolution structures as highly populated intermediate states in the enzymatic cycle. There are, however, more sparsely populated intermediate states that are unlikely to be captured by crystallography. This viewpoint allows us to extrapolate contemporary experimental knowledge to finer timescales, and to provide guidance for further detailed structure-dynamics studies.

To focus on elongation-translocation, we dissect translocation into two parallel paths as follows. The RNAP can either translocate without a free energy bias (as in pure Brownian motion) or the translocation can be locally biased (or facilitated) via pushing by the side chain of Tyr⁶³⁹ that resides on the C-terminal of the O-helix. Tyr⁶³⁹ is highly conserved and is essential for selecting rNTP over dNTP (38). In building the model, we utilize the same set of high-resolution structures from which the power-stroke mechanism was proposed (16). We nevertheless assume that PPi release precedes translocation, and that the O-helix opens partially upon PPi release. These assumptions are supported by recent molecular dynamics simulation studies on DNA polymerase I that is structurally homologous to T7 RNAP (39).

Importantly, the parallel-path scheme introduces an essential degree of freedom that links the two paths (Brownian and facilitated), i.e., fluctuation of the Tyr⁶³⁹ side chain IN and OUT of the active site. This degree of freedom is important for both translocation and transcription fidelity. Under this scheme, the facilitated path terminates in a locally stabilized post-translocated intermediate wherein Tyr⁶³⁹ stays close to the pre-insertion site (i.e., IN). In this position, Tyr⁶³⁹ can screen incoming nucleotides, thus ensuring transcription fidelity. Without this energy stabilization or bias, Tyr⁶³⁹ would frequently fluctuate (i.e., OUT) far from the pre-insertion site, impairing nucleotide selection and hence transcription fidelity.

Another important property of the parallel-path scheme is that it provides a common representation of the translocation-elongation kinetics for both single and multi-subunit RNAPs. Our model of T7 RNAP translocation is similar in some respects to the two-pawl-ratchet model previously proposed for a bacterial multi-subunit RNAP (36). In Fig. 1 b, we show molecular views of the essential structural elements involved in translocation/elongation for both the single subunit T7 RNAP (left) and the multi-subunit RNAP (right). In the multi-subunit RNAPs (40,41), the bridge-helix alternates between bent and straight configurations (36,42), similar to Tyr⁶³⁹ IN and OUT, respectively. The bending of the bridge-helix also appears to assist RNAP translocation, as suggested for Tyr⁶³⁹. Moreover, in the multi-subunit RNAPs the trigger loop folds and unfolds during each cycle, similar to the O-helix closing and opening in T7 RNAP. Hence, the two types of polymerases can carry out analogous functions by different structural elements. We show that, under the common parallel-path scheme, the two systems show comparable—but different—reaction topologies.

Below we first calibrate the model with single-molecule force measurements and then address steady-state properties of T7 RNAP elongation. Details on how we constructed the model shown in Fig. 2 can be found in the Supporting Material. The focus of our work is to explain the functional role of facilitated translocation as the RNAP ratchets along DNA during elongation. Our model also shows how efficient nucleotide selection can be achieved during the elongation cycle, and examines whether facilitated translocation affects forward tracking. The model also suggests that the functional role of translocation is somewhat different for multi-subunit RNAPs.

Figure 2.

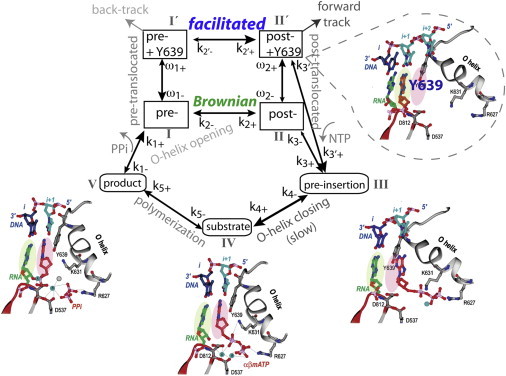
T7 RNAP translocation-elongation cycle, with a facilitated translocation path in parallel with the diffusive (Brownian) path. The scheme is constructed using high-resolution structural information (16,17), and is kinetically calibrated with single-molecule force measurements (24,25). To illustrate the process, we have adopted structural images from Fig. 3 of Yin and Steitz (16), including a stabilized post-translocated state (II′), the pre-insertion state (III), the substrate /insertion state (IV), and the product state (V). The kinetic rate parameters are labeled and their numeric values are listed in Table S1 in the Supporting Material, with some of them adopted from measurements in Anand and Patel (21). The energetics between translocation intermediates are defined as: γ ≡ E_II − E_I ∼ 0 (Brownian; fluctuating around zero under DNA sequence effects), α ≡ E_I′ − E_I ∼1 k_BT (thermal fluctuation level), and β ≡ E_I − E_II′ > 0 (fitted to ∼2 k_BT). Accordingly, for the Brownian translocation (I ↔ II), k₂₋ = k₂₊e^γ/kBT; for the facilitated translocation path (I′ ↔ II′), k_2′− = k_2′+e^{−(α+β)/kBT}. Fluctuations of the Tyr⁶³⁹ side chain IN and OUT of the active site happen between I and I′ or II and II′: ω₁₊ = ω₁₋e^−α//kBT at pre-translocation, and ω₂₊ = ω₂₋e^(β+γ)/kBT at post-translocation. During elongation, the O-helix closing from NTP pre-insertion to insertion (III → IV) is assumed slow (21).

Model and Results

Fitting elongation rates with single-molecule measurements

To calibrate our model, we fit numerical simulations of our model with single-molecule force measurement data for T7 RNAP elongation (24,25). The measurements were taken at different NTP concentrations, against a mechanical force 5 ≤ F ≤ 15 pN opposing forward translocation of RNAP. The experimental data had been fitted to a simplified three-state scheme, composed of pre-translocated, post-translocated, and NTP-loaded states. The fitting gave a maximum elongation rate (v_max) ∼130 nt/s. It also indicated a ∼1.3 k_BT free energy bias during translocation to the post-translocated state (24).

Using the kinetic scheme shown in Fig. 2, we can also fit the force measurement data, as shown in Fig. 3 a (see the Supporting Material for technical details). The most essential feature of the model, compared with the simpler scheme used for fitting experiments (24), is that the translocation is now split into two parallel paths. The path (I → II) with the Tyr⁶³⁹ side chain positioned out of the active site (OUT) is assumed to be diffusive so that the RNAP can move forward and backward equally fast. The frequency of the movements is >∼10³ s⁻¹ so that at high NTP concentrations, translocation takes place much faster than the O-helix closing that happens at ∼10² s⁻¹. At high NTP concentrations, the O-helix closing is assumed to be the rate-limiting step. Thus, even though the load force slows down translocation, it may not much affect the overall elongation rate. Along the alternate pathway (I′ → II′), however, the Tyr⁶³⁹ side chain inserts into the active site (IN) at the beginning (I′), pushing the 3′ end of the RNA out of the active site by the end (II′). Hence, Tyr⁶³⁹ directly assists the movement of the RNA-DNA hybrid. According to our fitting, the free energy bias along I′ →II′ is ∼3 k_BT (see Table S1 in the Supporting Material: $E_{I^{\prime }}-E_{I{I}^{\prime }}=\alpha +\beta$, with α assumed ∼1 k_BT and β fitted ∼2 k_BT). Consequently, the two parallel paths give an overall energy bias toward the post-translocated state by an amount between 0 and 3 k_BT, consistent with the ∼1.3 k_BT bias inferred from the experiments (24,25) (according to the standard errors of the measured elongation rates, the overall energy bias would vary around 1 ∼2 k_BT, see the Supporting Material).

Figure 3.

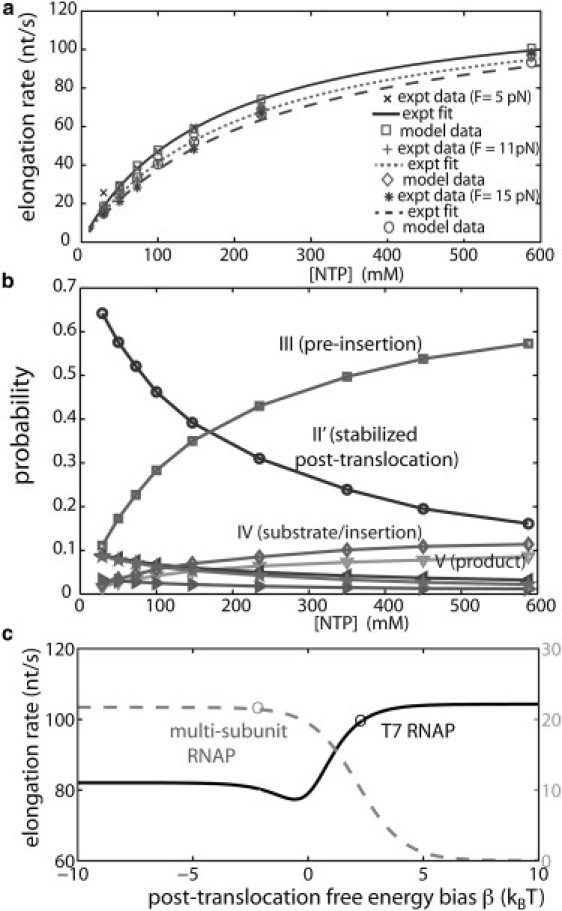
Steady-state properties of T7 RNAP elongation obtained from the model. (a) Elongation rates calculated at different NTP concentrations and load forces, F = 5 (data at top), 11 (middle), and 15 pN (bottom), compared with single-molecule experimental data measured at these conditions (24,25) as well as with fitting curves for the experimental data (24). The standard deviations of the simulated data are small (∼1 nt/s for 100 s trajectories) and are not shown. (b) Probability distributions of intermediate states in the elongation cycles at different NTP concentration. The states are indexed as in Fig. 2, from top to bottom (at the high [NTP]): III (□), II′ (○), IV (⋄), V (▿), I (◃), II (☆), and I′ (▹). Among them the more populated states III, II′, IV, and V had all been crystallized (16,17). The pre-insertion state (III) and the stabilized post-translocated state (II′) are dominantly populated at high and low NTP concentrations, respectively. (c) Elongation rates versus the post-translocation free energy bias (β ≡ E_I − E_II^′) for T7 RNAP (dark solid curve, left axis) and the multi-subunit RNAPs (gray dashed curve, right axis), as demonstrated in Eqs. S6 and S7 in the Supporting Material (at [NTP] = 588 μM). For T7 RNAP, β is fitted to ∼2 k_BT (circle), and the elongation rate is close to saturation at this condition. For the multi-subunit RNAP case, presumably, β ∼ −2 k_BT (circles); for illustration, v_max ∼ 30 nt/s is used. One can see that increasing β for the multi-subunit RNAPs (stabilizing II′) can quickly reduce the elongation rate.

Steady-state probability distributions of elongation intermediates

We obtained the steady-state probability distributions for all intermediate states in the elongation cycle by simulating RNAP elongation for a long time (100 s for each trajectory), or equivalently by solving the master equation (see the Supporting Material). The probabilities at various NTP concentrations for these intermediate states are shown in Fig. 3 b.

At high NTP concentrations (588 μM by default to compare with experimental data), the RNAP elongates fast (∼100 nt/s). Under this condition the most populated state is the pre-insertion state III (P_III ∼ 57%). Those states that are moderately populated include: the stabilized post-translocated state II′ with Tyr⁶³⁹ IN (P_II′ ∼ 16%), the NTP insertion or substrate state IV (P_IV ∼11%), and the product state V (P_V ∼ 9%). Other intermediates are only marginally populated: the pre-translocated states I or I′ (P_I ∼ 3% and P_I^′ ∼ 1%) and the nonstabilized post-translocated state II with the Tyr⁶³⁹ OUT (P_II ∼ 2%). Indeed, those more populated intermediates (II′, III, IV, and V in Fig. 2) had all been crystallized in the previous structural studies of T7 RNAP (16,17). This consistently shows that the captured structures are almost always those abundantly populated intermediates.

In particular, the pre-insertion state III populates most at high NTP concentrations. By contrast, the stabilized NTP insertion state IV is populated much less. The is due to the slow transition III → IV and the fast transition IV → V, such that the populations leave III slowly while passing through IV quickly. This property allows sufficient time for nucleotide selection upon pre-insertion (at III). Note that the stabilized NTP insertion state IV can become the most populated state if a noncatalytic analog of NTP is provided (16,17) (as IV → V inhibited).

Importantly, our results always show that P_II′ > P_II at post-translocation (see Fig. 3 b), which is essential for maintaining transcription fidelity. Because the Tyr⁶³⁹ side chain fluctuates IN and OUT rapidly (>10⁴ s⁻¹), II′ and II intermediates stay close to local equilibrium. By fitting the single-molecule experimental data we obtained the free energy difference between II and II′ (or I and II′, because E_II − E_II′ ∼ E_I − E_II′ ≡ β) ∼2 k_BT > 0, giving a population bias of P_II′/ P_II ∼ 7–8. This explains why the post-translocation structure II′ with Tyr⁶³⁹ IN was detected and crystallized (16), but not the structure II with Tyr⁶³⁹ OUT (see Fig. 2).

In the pre-insertion state III, the Tyr⁶³⁹ side chain was also captured IN rather than OUT (16,17). From the structural comparisons shown in Fig. 1 b (left), we note that the Tyr⁶³⁹ side chain is close to the pre-insertion site when it is IN the active site (II′), whereas the side chain stays far from the pre-insertion site when it is OUT (II). Hence, the performance of nucleotide selection by Tyr⁶³⁹ at the pre-insertion site relies strongly on whether it populates more in the II′ or II state, or on the population bias P_II′ > P_II. When P_II′ ≤ P_II (i.e., without the post-translocation energy bias), the pre-inserted nucleotide would not be screened well because Tyr⁶³⁹ frequently stays (OUT) far from the pre-insertion site.

Comparing the ratcheting scheme with multi-subunit RNAPs

As mentioned earlier, using the parallel-path scheme allows us to describe the translocation-elongation kinetics for single and multi-subunit RNAPs in a unified way. The IN and OUT configurations of Tyr⁶³⁹ in the single subunit T7 RNAP correspond to the bent and straight configurations, respectively, of the bridge-helix in the multi-subunit RNAP (36,42,43). Moreover, the closing and opening of the O-helix in T7 RNAP correspond, respectively, to folding and unfolding of the trigger loop in the multi-subunit RNAPs.

There are distinctive features, however, that vary between the two ratcheting schemes (see Fig. S1 in the Supporting Material):

First, our structural examination of T7 RNAP reveals that binding or pre-insertion of an incoming nucleotide can take place without steric hindrance whether the Tyr⁶³⁹ side chain is IN (II′) or OUT (II) of the active site (see Fig. 1 b and Fig. 2, and see Fig. S1 a). Whereas for the multi-subunit RNAP, the nucleotide pre-insertion seems to take place only when the bridge-helix is straight (II) (see Fig. S1 b). The bending region of the bridge-helix (pink surface) has steric clashes with the pre-inserted nucleotide (van der Waals spheres inside the yellow oval), as demonstrated in Fig. 1 b, right.

Second, the configuration II′ is more stabilized than II as we have found for T7 RNAP, likely due to stacking of the side chain of Tyr⁶³⁹ with the end base pair of the RNA-DNA hybrid. Whereas in the multi-subunit RNAP, there is no evidence that the bent configuration of the bridge-helix (II′) is more stabilized than the straight one (II). In fact, a post-translocated state with the bridge-helix straight (II) was captured structurally (43,44), implying that II is likely more stabilized than II′ in the multi-subunit RNAP. A high-energy translocation intermediate captured in complex with an inhibitor is consistent with this idea (45).

In Eqs. S6 and S7 in the Supporting Material, we derive approximate formulas for the elongation rates of both types of RNAPs. Correspondingly, Fig. 3 c shows the curves of elongation rate, v versus the post-translocation free energy bias, β (or β + γ in general when γ ≡ E_II − E_I ≠ 0) for each type of the RNAPs. For T7 RNAP, we see that increasing the post-translocation free energy bias β beyond 2 k_BT does not improve the elongation rate much (e.g., <5% increase) as the rate is already close to its saturation value. On the other hand, in comparison to a pure Brownian ratchet, the 3 k_BT (α + β) free energy bias along I′ → II′, or an overall ∼1.3 k_BT for both paths, does improve the elongation rate somewhat (e.g., ∼14% increase).

For multi-subunit RNAPs, however, it is likely that β < 0 (E_II′ > E_II; see Brueckner et al. (43) and Fig. 1 b in that work as well), with the bridge-helix more stabilized in the straight (II) than the bent (II′) configuration at post-translocation. In this case, the elongation rate still stays close to its saturation. Remarkably, the elongation rate can be significantly reduced when the bent configuration (II′) of the bridge-helix becomes more stabilized than the straight conformation (II) by binding some inhibitory factor such that β > 0 (E_II > E_II′; see Fig. 3 c).

Efficient nucleotide selection before stable insertion

Because T7 RNAP lacks a proof-reading mechanism, accurate nucleotide selection is crucial for transcription fidelity. For a wild-type T7 RNAP, experiments estimated that transcriptional errors occur at an average frequency ∼10⁻⁴ (46). If there were only one checkpoint for nucleotide selection in T7 RNAP, a free energy difference between wrong and right nucleotides at this checkpoint would be ΔE ∼ − k_BT ln(10⁻⁴) ∼10 k_BT to achieve this accuracy. Such a large energy disparity can hardly be maintained in a fluctuating protein cavity such as the active site of T7 RNAP. The site is not buried deeply inside the protein, and cocrystallized water molecules are observed close to the site (16) and the water molecules would smear the energy difference between the right and wrong nucleotides (47). Therefore, T7 RNAP would likely have two or more steps, or checkpoints, dedicated to its nucleotide selection.

Using our elongation scheme, we compared the energy efficiencies of several individual selection mechanisms, i.e., the error rates of elongation under different selection methods, using a constant energy penalty for differentiating between right and wrong nucleotides (see the Supporting Material for details). We find that selection methods (No. 1 and No. 2) that take place before the rate-limiting step (nucleotide insertion III → IV) are more efficient than (No. 3 and No. 4) that take place after. For example, using an energy of ∼5 k_BT to reject the wrong nucleotide upon pre-insertion (No. 1) or to inhibit its insertion rate (No. 2) can achieve an error rate ∼10⁻², whereas using the same amount of energy to reject the wrong nucleotide right after insertion (No. 3) or to inhibit the chemical reaction rate (No. 4) gives an error rate ∼10⁻¹ (see Table S2). The property is closely related to where the rate-limiting transition is located in the elongation cycle. If one makes the chemical transition IV → V rate-limiting, then selections (Nos. 1–3) that take place before IV → V become similarly efficient, whereas the one after (No. 4) is still the least efficient. This happens because a rate-limiting forward transition presumably crosses a large activation barrier that can further hinder the backward transition. The hindered backward transition makes releasing the wrong nucleotide difficult.

Our results also show that, when there is no selection against wrong nucleotides at pre-insertion, or if the selection at pre-insertion costs an energy only at the thermal fluctuation level (1–2 k_BT), the elongation rate becomes quite low. For example, the rate drops below 30 nt/s when single selection happens but not at pre-insertion (selections Nos. 2–4, see Table S2), which is much lower than the error-free rate ∼100 nt/s. These results suggest that the pre-insertion step is the most crucial checkpoint in T7 RNAP for achieving efficient nucleotide selection as well as maintaining a sufficiently high elongation rate.

Forward tracking with facilitated translocation

In addition to studying the effect of facilitated translocation on the nucleotide selection at pre-insertion, we also examined whether the facilitated translocation affects forward tracking. We assume that in the stabilized post-translocated state II′, T7 RNAP can randomly switch between regular elongation and forward tracking, i.e., moving forward without synthesizing RNA (illustrated in Fig. 1 c). Consequently, the RNA-DNA hybrid shortens and association between RNAP and the DNA weakens. Forward tracking likely takes place frequently at terminator regions causing intrinsic termination (22,27).

We examined the probability of T7 RNAP forward tracking around two terminator regions: one is T-ϕ, a late terminator found in the T7 genome (48), and the other is a threonine (thr) attenuator in Escherichia coli (49). To take into account sequence dependence during translocation (see the Supporting Material), we evaluated the free energy difference between the post (II) and pre-translocated states (I), γ, by a sum of energies calculated from unzipping/zipping of downstream/upstream of the dsDNA and RNA-DNA hybrid (50). Similarly we evaluated β by the translocation energy difference plus an additional energy contribution from Tyr⁶³⁹ stabilization at II′. We found that the forward tracking can take place at high efficiency at the terminator and at a very low efficiency at nonterminator regions, if one allows the forward rate to decrease exponentially with the stabilization energy of the RNA-DNA hybrid upstream. The forward tracking efficiency was determined by counting the number of extensive forward tracking events (beyond 3 nt) for every 100 trial events.

We then compared the forward-tracking efficiency (with the facilitated path I′ ↔ II′) with that of a pure Brownian ratchet scheme (without the facilitated path I′ ↔ II′). We found that the forward tracking efficiencies are almost identical in both cases. For example, when the Brownian ratchet case is tuned with 48 ± 3% forward tracking efficiency at the thr attenuator, the efficiency is 51 ± 5%, and further increase of the post-translocation energy bias (β + γ) hardly improves the efficiency (∼53 ± 5% maximum). In all these cases, the forward tracking efficiency at the nonterminator region remains at the same low value (∼2% for equally long regions). Similar trends were found also for the T-ϕ terminator. Hence, compared with the pure Brownian translocation case, the facilitated translocation in T7 RNAP does not enhance the likelihood of forward tracking. Note that the forward tracking may not be the mechanism for intrinsic termination (51,52), so the conclusion does not extend in general to termination.

Discussion

A large translocation free energy bias is not an advantage for sequence detection

In our model, T7 RNAP translocation is driven largely—but not completely—by a Brownian ratchet mechanism. Each translocation step involves changes in DNA and RNA structures that depend on sequence stabilities. Therefore, translocation can be utilized by RNAP to sense and respond to sequence signals along dsDNA. When there is no structural element or energy output from RNAP to assist in translocation, its movements are diffusive. The RNAP moves forward and backward equally fast until an incoming NTP binds to prevent the backward movements. Because the RNAP itself does not induce a free energy bias along the translocation path, sequence variations on the DNA can readily be detected, and RNAP can respond to the variation by slowing down, tracking forward or backward. By contrast, a large translocation energy bias can reduce the activation barrier and accelerate the forward movements, while it can mask relatively small energy differences arising from different DNA sequences. In addition, the translocation is not rate-limiting during the elongation cycle, so a large translocation energy bias can hardly improve the overall elongation rate. In our translocation-elongation model of T7 RNAP, for example, the sequence signal is encoded in the translocation energy γ that affects the elongation rate (see Eq. S6 in the Supporting Material). When the post-translocation free energy bias (β + γ) becomes large, the elongation rate increases to saturation independent of the sequence signal (γ). In multi-subunit RNAPs, a large post-translocation free energy bias simply stalls the elongation (see Eq. S7 in the Supporting Material and Fig. 3 c). Hence, a large translocation energy bias of RNAP does not improve elongation rate nor confer an advantage for sequence detection during transcription elongation.

A small post-translocation free energy bias in T7 RNAP aids in transcription fidelity

Our analysis of T7 RNAP data shows that a small free energy bias that stabilizes the post-translocated intermediate can aid in nucleotide selection at pre-insertion, without interfering with sequence detection.

Using experimental data from single-molecule force measurements (24,25), we identified a post-translocation free energy bias of ∼2 k_BT imposed by the RNAP. The structural elements that achieve this bias include, but are not necessarily limited to, Tyr⁶³⁹ at the C-terminal end of the O-helix (see Fig. 1). The translocation can take place without a free energy bias (i.e., via Brownian path I → II in Fig. 2), during which the 3′-end of the RNA moves out of the active site without assistance (with the Tyr⁶³⁹ side chain OUT). Alternatively, the side chain of Tyr⁶³⁹ could squeeze IN the active site at the pre-translocated state when the active site is still occupied by the 3′-end of the RNA. Because the 3′-end of the RNA appears quite flexible (53), the squeezing (I → I′) costs but a small amount of free energy (e.g., ∼1 k_BT). The unstable intermediate (I′) can be easily driven by ∼3 k_BT free energy bias toward a more stabilized post-translocated configuration (II′), in which the 3′-end of the RNA is pushed out of the active site, leaving only the side-chain Tyr⁶³⁹ in occupancy. Indeed, this stabilized intermediate (II′) had been captured in high-resolution structural studies (16), and led to the suggestion that PPi release powers the translocation mechanism. Our studies indicate, however, that the intermediate (II′) results from the small power stroke exerted by Tyr⁶³⁹, not from PPi release. In the post-translocated state, II′ is stabilized by the Tyr⁶³⁹ side chain stacking with the base pair at the end of the RNA-DNA hybrid (see Fig. 2). Due to the side-chain fluctuation, there also exists a nonstabilized, and therefore lowly populated post-translocated state II, in which Tyr⁶³⁹ is OUT. Because the energy changes among the translocation intermediates (I, I′, II′, and II) are small, the translocation mechanism appears to be largely a Brownian ratchet.

Although the post-translocation energy bias appears quite small, there is still a way to distinguish the biased translocation from the pure Brownian case. At high NTP concentrations, the post-translocated intermediate II′ is moderately populated during the elongation cycle. Its population grows as NTP concentration decreases, and becomes dominant at very low NTP concentrations (see Fig. 3 b). By comparison, in the pure Brownian ratchet scheme, both the pre-translocated (I) and the post-translocated states (II) become dominant and equally populated (∼50% each) at low NTP concentrations. Hence, to test whether the translocation is purely Brownian or slightly biased, one should examine whether there exist two equally populated conformations (Brownian) or one dominant conformation (biased) at very low NTP concentrations, close to equilibrium. Because sequence effects can locally bias state populations and interfere with accurate measurements, experimental tests should be conducted when RNAP transcribes homogeneous DNA sequences.

Taking into account both translocation paths, the overall free energy bias of translocation is ∼1.3 k_BT (24). This small post-translocation energy bias can actually slightly improve the elongation rate compared to a pure Brownian ratchet, whereas further increasing the energy bias improves the elongation rate very little (see Fig. 3 c). Thus, the major role of the facilitated translocation in T7 RNAP is not to improve the elongation rate, it is to bring about a locally stabilized post-translocated intermediate (II′) before NTP pre-insertion. In this intermediate state, the Tyr⁶³⁹ side chain inserts IN next to the pre-insertion site; its hydroxyl group can subsequently coordinate with a magnesium ion such as to discriminate between ribo- versus deoxy-ribo nucleotides (17) when the nucleotide pre-inserts. As the side chain of Tyr⁶³⁹ is OUT, its hydroxyl group moves farther (∼6 Å; see Fig. 1 b) away from the pre-insertion site and cannot participate in nucleotide selection. In brief, by consuming only a small amount of energy to stabilize the Tyr⁶³⁹ side chain IN the active site, T7 RNAP can guarantee an ∼80∼90% chance of keeping the tyrosine abutting the pre-insertion site for nucleotide selection.

Our studies point out that there are two reasons why the pre-insertion is the most crucial checkpoint of nucleotide selection. First, it appears energetically more efficient to reject the wrong nucleotide before its slow insertion than afterward. This property depends on where the rate-limiting step is located in the nucleotide addition cycle: selection before the rate-limiting transition always seems more efficient than selection after. Second, to maintain both high fidelity (low error rate) and sufficiently high elongation rate, it is necessary to have an energy above the thermal fluctuation level to filter out the incorrect nucleotide at pre-insertion. Exactly how—and by how much—Tyr⁶³⁹ and other structural elements contribute to nucleotide selection awaits further studies.

In our further examination, forward tracking is allowed during elongation via the stabilized post-translocated intermediate (II′). The forward tracking seems to happen at high efficiencies at the terminator sequences. However, we have not identified any substantial effect that the facilitated translocation brings to the forward tracking compared to pure Brownian ratchet translocation (with forward tracking via II). Indeed, increasing the post-translocation energy bias along the facilitated path hardly affects the II′ population in T7 RNAP. However, this property does not necessarily hold for multi-subunit RNAPs as increasing the post-translocation bias does substantially increase the population of II′ as well as inhibit RNAP elongation.

What about translocation and ratcheting in the multi-subunit RNAPs?

In comparison with the single subunit T7 RNAP, we suggest a slightly different ratcheting scheme under our parallel-path scheme for the multi-subunit RNAPs (see Fig. S1). In the multi-subunit RNAPs, bending and straightening of the bridge helix are analogous to IN and OUT fluctuations of the Tyr⁶³⁹ side chain in T7 RNAP. In this alternative ratcheting scheme, however, there are two essential features that distinguish the multi-subunit RNAPs from T7 RNAP:

First, pre-insertion of nucleotide can only happen when the bridge helix is straight (II → III allowed), but not when it is bent (II′ → III forbidden). This is because the bent bridge helix sterically occludes the pre-insertion site (see Fig. 1 b, right). In T7 RNAP, by contrast, the nucleotide can pre-insert at either IN (II′) or OUT (II) configuration of Tyr⁶³⁹ without steric hindrance.

Second, the bridge helix bent configuration in the post-translocated state (II′) does not appear to be stabilized as is the corresponding IN configuration of Tyr⁶³⁹ in T7 RNAP. Indeed, the bent configuration seems to be less stable than the straight configuration of the bridge helix in the post-translocated state because crystal structures of both the post-translocated state (II) and the pre-insertion state (III) of the multi-subunit RNAP were caught with the straight form of the bridge helix (43,44). Whereas in T7 RNAP, it is Tyr⁶³⁹ IN that was structurally captured (II′ and III) but not OUT (16).

Nevertheless, the bent configuration of the bridge helix has been structurally identified when an inhibitory factor was bound to the multi-subunit RNAP. Previously, a toxin-bound translocation intermediate (α-amanitin) was structurally resolved (45). The bridge helix is bent in this structure with the trigger loop in a wedged conformation. The captured structure is likely a stabilized form of a high-energy intermediate in translocation. This intermediate corresponds nicely to II′ in our model (Fig. 2). According to our interpretation, the post-translocation bias β + γ (≡ E_II− E_II′) < 0 is originally set for the multi-subunit RNAP, while the toxin stabilizes the II′ intermediate such that β + γ > 0 (as in T7 RNAP). However, because the II′ configuration cannot bind incoming nucleotide in the multi-subunit RNAP, it competes with the nucleotide for the binding (pre-insertion) site. In multi-subunit RNAPs, only a few k_BT stabilization of II′ can lower the effective concentration of NTP significantly and cause a large drop of the elongation rate (see Fig. 3 c). Therefore, II′ appears to be a target intermediate state for inhibitory factors of elongation in the multi-subunit RNAPs: once the factor stabilizes the state (i.e., by increasing the post-translocation free energy bias), the elongation activity is greatly reduced. Notably, in recent high-resolution studies of a multi-subunit RNAP from a bacterial species (54), a ratcheted state has been identified that is in complex with a transcription inhibitor (Gfh1). This inhibitor protein occludes the channel for NTP entry into the active site. The bridge helix is kinked in the ratcheted state. Accordingly, this structure appears to be a stabilized form of II′ as well. Once II′ becomes more stabilized than the other post-translocated intermediate II (bridge helix straight), II′ dominantly populates at low NTP concentration.

In summary, we have dissected the ratchet mechanism of T7 RNAP during its transcription elongation. A small post-translocation free energy bias (∼2 k_BT) is identified and its functional role is proposed: The energy bias creates a locally stabilized post-translocated intermediate in which the highly conserved Tyr⁶³⁹ stays close to the pre-insertion site for nucleotide selection. Without this post-translocation energy bias (equivalently, local stabilization) the tyrosine side chain frequently moves away from the pre-insertion site so that nucleotide selection is less effective, lowering transcription fidelity. Further studies will be necessary to determine if other structural elements participate in nucleotide selection at pre-insertion, how subsequent nucleotide selection proceeds, and whether a similar property exists for other single subunit polymerases.

Remarkably, one can identify analogous functional elements and build an analogous but distinct ratcheting scheme for the multi-subunit RNAPs. The variations of structural features of the RNAPs lead to different reaction topologies. The post-translocation intermediate with the bent bridge-helix does not allow NTP binding. Nor is it destabilized unless some inhibitory factor binds and enhances the post-translocation energy bias. Hence, bending of the bridge-helix, in addition to coordinating backtracking, appears to support inhibitory control (36).