Abstract
Many human neurodegenerative diseases are associated with the aggregation of insoluble amyloid-like fibrous proteins. However, the processes by which the randomly diffused monomer peptides aggregate into the highly regulated amyloid fibril structures are largely unknown. We proposed a residue-level coarse-grained variational model for the investigation of the aggregation pathway for a small assembly of amyloid proteins, the peptide GNNQQNY from yeast prion protein Sup35. By examining the free energy surface, we identified the residue-level sequential pathways for double parallel and antiparallel β-peptides, which show that the central dry polar zipper structure is the major folding core in both cases. The critical nucleus size is determined to be three peptides for the homogeneous nucleation process, whereas the zig-zag growth pattern appears most favorably for heterogeneous nucleation. Consistent with the dock-and-lock mechanism, the aggregation process of free peptides to the fibril core was found to be highly cooperative. The quantitative validation with the computational simulations and experimental data demonstrated the usefulness of the proposed model in understanding the general mechanism of the amyloid fibril system.
Introduction
The abnormal accumulation of amyloid proteins in tissues and organs can result in the occurrence of more than 20 different neurodegenerative and nonneuropathic disorder diseases, including Alzheimer's disease, Parkinson's disease, type II diabetes, and transmissible spongiform encephalopathies (1). Despite the significant efforts on the investigation of the diseases, there has been no effective treatment for preventing or even slowing down the progress of amyloidoses (2,3). Recently, two most promising treatments for the Alzheimer's disease, latrepirdine (Dimebon; Pfizer, Groton, CT) and tarenflurbil (Flurizan; Myriad Genetics, Salt Lake City, UT), turned out to be ineffective in phase-3 trials (4). As a key toward the improvement of the pathology of amyloid-related diseases, a better understanding of the detailed mechanisms of amyloid fibrillogenesis is urgently needed.
To explore the mechanisms of amyloid fiber formation, enormous efforts have been made from the experimental, computational, and theoretical aspects. Among these studies, theoretical approach has its unique advantage in providing quantitative analytical results and explicit insights into the mechanisms of amyloid fiber formation. For instance, Jarrett and Lansbury (5) proposed a nucleation-dependent polymerization model that distinctly characterized the lag time, critical concentration, and seeding of amyloid aggregation. Watzky et al. (6) and Morris et al. (7) developed a two-step kinetic model and showed that a wide range of amyloid aggregations can be fit with the minimalistic model of nucleation and autocatalytic growth. Knowles et al. (8) demonstrated that general features of fibril aggregation procedures, including nucleation, elongation, and fragmentation, can be well described by the analytical solution of the master equation of the time evolution of filament concentration.
Hong et al. (9) recently proposed a more comprehensive mathematical dissection of the kinetic procedure of amyloid fiber formation and a tentative classification of amyloid proteins based on their characteristic scaling exponents. The authors also developed a simple lattice-gas model to explore basic statistical properties of the amyloid fiber system (10). However, most theoretical approaches were based on a macroscopic description of the amyloid fiber formation procedure, which deals with the statistical average of massive fibrils rather than individual peptide or a small assembly of peptides. As a consequence, they cannot provide detailed molecular-level insights into the aggregation intermediates and pathways of oligomers and protofibrils, which are believed to be a key to understanding the origin of amyloidoses and the toxicity of amyloid proteins (11,12).
To address these issues, in this article we propose a variational model to investigate the aggregation pathway of amyloid fibrils at a residue-level resolution. The theoretical framework of this model was first introduced by Portman et al. (13–15) for the study of the protein folding problem, which demonstrated its usefulness in constructing the free energy surface of globular proteins (13–17). Later, Qi and Portman (18) implemented the model in the calculation of protein folding rates and the classification of folding patterns of two-state proteins (19). The essence of the variational model is to determine the folding pathway from unfolded to folded states by varying the constraints on each residue from small to large number, continuously.
Analogous to protein folding, the aggregation process of amyloid proteins can be considered as a transition between two distinguished states (the denatured state with amyloid proteins randomly diffused in the solution and the condensed state with amyloid proteins regularly packed into fibrils). This can be explicitly characterized through the fluctuation magnitude of each residue according to its average position (in the denatured state, the residue fluctuation is large; whereas in the condensed state, it is relatively small), and thus by the conjugated residue constraints (in other words, we choose the constraint parameters on each residue as the reaction coordinates). This argument builds up the theoretical foundation for using the variational model to calculate the free energy surface of amyloid fibrils, by which the aggregation pathway can be determined from the kinetics of residue contact formation. Conceptually in the variational model, for each state we are dealing with the statistical average of an ensemble of structures rather than single unique conformation. These structures may share substantial diversity, but they are characterized through the same residue constraints and thus can convert into each other within the given residue fluctuations.
Here, we choose a small fibril assembly (hexamer in this case) of the peptide GNNQQNY from the yeast prion protein Sup35 as the model system, whose crystal structure was recently solved by Nelson et al. (20), as shown in Fig. 1. A typical cross-β spine structure with this short peptide may share common characteristics of amyloid fibers, making it an ideal model system to study the general mechanism involved in fibril aggregations. Plenty of numerical and experimental studies conducted on this peptide (20–24) also facilitate the examination of our model calculations by the comparison with the existing data.
Figure 1.
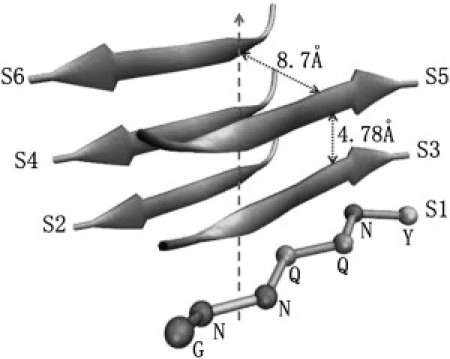
Typical crystal structure of hexamer made up by the peptide GNNQQNY. The β-strands are oriented perpendicular to the fibril axis (dashed line). The distance between two neighbor strands in the parallel β-sheet is 4.78 Å, and the distance between two antiparallel β-strands is 8.7 Å. The index for each peptide is enumerated as S1, S2, S3, S4, S5, and S6.
Methods
We first briefly outline the general variational theory for a single peptide chain (14,15). An extension to the multiple chains, which is correlated to amyloid fibril systems, is then described.
Variational model for single peptide
In a residue-level coarse-grained variational model, single polypeptide is specified by a collection of Cα atoms along the sequence. The Hamiltonian of the peptide (HS) is constituted by two parts:
| (1) |
The Hchain represents the backbone potential of a collapsed polymeric chain,
| (2) |
where represents the coordinate vector of ith Cα atom, β = 1/(kBT) is the Boltzmann factor, a = 3.8 Å is the average distance between two adjacent Cα atoms, and B is conjugated to the radius of gyration of the chain and controls the collapse degree of the polypeptide chain through a confining harmonic potential. We set B = 10−3 as in Portman et al. (14). The position correlation matrix
| (3) |
is obtained through the freely rotating chain model with stiffness g = cos(θ) for a fixed angle θ between adjacent covalent bonds. KR is the Rouse matrix for the nearest-neighbor harmonic chain, and Δ represents the effect of chain boundaries.
The interactions between nonlocal residues (Hintra) are modeled by a summation of pairwise potentials between contact residues,
| (4) |
where εij is the strength of contact interaction, depending on the chemical natures of residues i and j, which we choose as Miyazawa-Jernigan energy parameters in the unit of kBT (25). The pairwise contact potential can be further approximated by a sum of three Gaussian terms,
| (5) |
where parameters γk and αk represent the strengths and ranges of short-, intermediate-, and long-range interactions respectively. Here we set (αs, γs; αi, γi; αl, γl) = (3, 25; 0.54, 9; 0.27, −6) according to Portman et al. (14), which produces a Lennard-Jones like potential with the normalized minimum at r0 = 6.3 Å (see Fig. 2).
Figure 2.
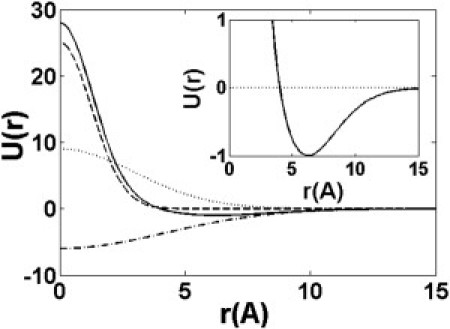
Pairwise residue-residue contact potential as a function of residue distance. (Dashed line) Short-range repulsive interaction; (dotted line) intermediate-range interaction; (dash-dotted line) long-range attractive interaction; (solid line) total contact potential. (Inset) Zoomed-in potential well.
To calculate the partition function, a reference Hamiltonian is introduced in the variational model to approximate the native free energy surface around the reference state by a harmonic potential well, which is written as
| (6) |
where is the position of the ith Cα atom in the native structure. The value Ci represents the strength of the harmonic constraint, which is conjugated to the fluctuation of ith residue.
Now the variational free energy surface of single peptide can be parameterized through the constraint parameters {Ci} as
| (7) |
with being the partition function of the reference Hamiltonian, and denoting the statistical average taken with respect to H0.
Substituting the expressions for HS and H0 gives the variational energy
| (8) |
and entropy
| (9) |
where
is the covariance matrix for the thermal fluctuation of residues. provides the relative displacement of residue fluctuations, and describes the average position of ith Cα atom in the reference chain.
Variational model for multiple chains
For a fibril system constituted by multiple amyloid peptides, the total Hamiltonian involves three parts: in addition to the backbone interaction and intrachain interaction within a single peptide, the interchain interaction between different peptides should also be taken into consideration (10), i.e.,
| (10) |
where Hichain and Hiintra represent the backbone potential and the intrachain interaction for ith peptide, and Hijinter represents the interchain interaction between peptide i and peptide j.
Analogous to the intrachain interaction, the interchain interaction could be approximated by a summation of pairwise potentials between two different residues in two different peptides, i.e.,
| (11) |
where index p denotes the pth residue in peptide i, and index q denotes the qth residue in peptide j. In our calculations, intrachain interactions will be limited to the nonlocal residues i and j with |i – j| ≥ 3, whereas interchain interactions are defined between contact residues within neighboring parallel and antiparallel peptides.
By following the same procedure we can calculate the variational free energy for multiple chains. However, if all chains are identical, which is valid in most applications, the fibril system can be assumed as a translational invariant when the peptide number is large enough (M → ∞). Under that condition, the constraints on each peptide are equal; so are the fluctuations (so what we considered here is the uniformly collective modes for fluctuations). The position correlation matrix ΓM and covariance matrix GM for multiple peptides can be decomposed into the direct products of ΓS and GS for a single peptide, i.e.,
| (12) |
and
| (13) |
This will lead to equations for variational energy E and entropy S similar to that in Eqs. 8 and 9, except for replacing ΓS by ΓM, and GS by GM. With the mean-field approximation, we can formulate a many-body problem into the study of single peptides, which will greatly facilitate the research on real amyloid fibers that may contain thousands of peptides.
Determination of aggregation pathway
In the above sections, through the variational approach, we formulated the problem of amyloid fiber formation into the study of a free energy functional as a set of constraint parameters {C}. We especially focus on the conformational transition between two distinguished states: one is a high entropic denatured state with all {C} setting as zero (denoted as {CU}), the other is the stable aggregated state with {C} corresponding to the lowest free energy (denoted as {CN}). By continuously tuning the constraint parameters from {CU} to {CN}, the fibrillation pathway (characterized by the free energy surface) between the initial denatured state and the final condensed state is completed constructed.
In reality, as the dimensionality of the free energy surface is very high (equal to the length of peptide), an explicit exploration of all local minima and saddle points seems almost impossible. In this study, to simplify the calculation, we take a sequential search of the aggregation pathway on the free-energy surface with the assumption that a residue (or residue pair) can be either completely aggregated or not aggregated at all at each aggregation step (in other words, a residue cannot be partially aggregated).
The explicit procedure is as follows. In Step 1, we identify the condensed state ({C = CN}) with minimum free energy for the homogenous system. In Step 2, we set tunable {C} for one residue (or residue pair) and {C = 0} for the rest residues. Then choose the one with the lowest free energy barrier height between {C = 0} and {C = CN} from all possible cases as the first aggregation step. If there is no free energy barrier, as in the uphill or downhill cases, we take the free energy value at {CN}. In Step 3, we fix {C = CN} for the residue (or residue pair) identified in Step 2, and repeat the procedure in Step 2 for the rest residues until all of them are constrained at {C = CN}.
Results
Despite the generality of the constructed variational model for multiple-chain aggregation, we will focus the application on a small fibril assembly of the peptide GNNQQNY from the yeast prion protein Sup35 whose structure was recently solved (Fig. 1) (20). A systematic investigation on this model system will help illustrate the detail procedure of how to construct the free energy surface, how to identify the most probable aggregation pathway, and how to determine the fibrillation temperature and the critical nucleus size, etc. Although the short chain length of GNNQQNY does not fulfill the Gaussian chain approximation that was taken for the calculation of backbone potential, it has been shown that the derivation is not large even when the chain length is <10 (26,27). Our data of quantitative comparisons with computational simulations and experimental data also demonstrated that the Gaussian approximation should not be a critical effect for the modeling of fibril aggregation, and can be partly compensated by a choice of smaller constraint parameters.
Parallel β-peptides are the major units for GNNQQNY aggregation
The highly regular cross-β spine structure is generally regarded as the central part of amyloid fiber (20). However, whether the parallel or antiparallel β-peptides make the major contribution to the stability of fibril structure is still controversial (23,28).
For the peptide GNNQQNY, we calculated the free energy surface of single peptides and double parallel and antiparallel β-peptides with homogeneous parameters {Ci = C} for all residues at T = 1 (see Fig. 3), where Ci represents the strength of the harmonic constraint put on the ith residue in our variational model (see Eq. 6).
Figure 3.
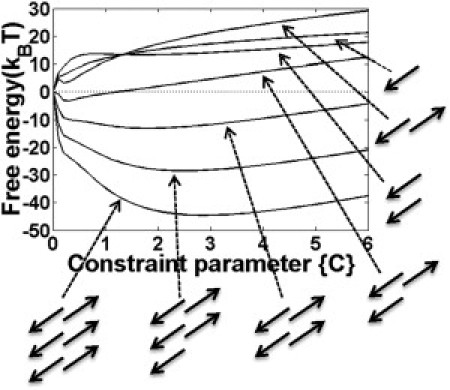
Free energy surface for oligomers with size varying from one to six peptides at T = 1. The constraint parameters {Ci} for each residue are set equal.
Clearly, the single GNNQQNY peptide favors the coil structure at room temperature (29). For double peptides, when the constraint parameter is small (C < 1.3), the free energy barrier for the parallel form is larger than the antiparallel, which means the initial formation of loose contacts between antiparallel peptides is relatively easier and faster. However, as the constraint gets strong enough, the free energy for double antiparallel β-peptides becomes much higher than the parallel (∼8 kBT at C = 2.9). Similar results were also reported by molecular dynamic (MD) simulations in that the parallel β-sheet is more stable than the antiparallel structure for the GNNQQNY dimer (28,30). Therefore, we believe the parallel β-peptides make the major contribution to the stability of fibril structure.
Asn2-Gln4-Asn6 provides a common folding core for both parallel and antiparallel peptides
According to the search procedure we introduced in Methods, we further examine the sequential folding pathway for double parallel and antiparallel β-peptides by varying the constraints on each residue pair separately. For easy counting, we labeled two corresponding partner residues as 1–7, i.e., G1G1, N2N2, N3N3, Q4Q4, Q5Q5, N6N6, and Y7Y7 for parallel peptides, and G1Y7, N2N6, N3Q5, Q4Q4, Q5N3, N6N2, and Y7G1 for antiparallel peptides.
A summary of our illustrated sequential folding pathways for double parallel and antiparallel β-peptides is shown in Fig. 4. Although the detailed sequential folding pathways for double parallel and antiparallel β-peptides are not exactly the same, they share some dramatic features in common, i.e.:
-
1.
The folding of both structures starts from the middle residue pairing Q4Q4, which probably is a direct consequence of the sequential symmetry of peptide GNNQQNY in chemical nature.
-
2.
Free energy barriers for central residue pairs (NNQQN) are very small in both cases, so that the formation of the central complementary structure is a highly cooperative process in dynamics, and the sequence Asn2-Gln4-Asn6 may serve as a common folding core for both parallel and antiparallel β-sheets (21).
-
3.
Edge residue pairs form at last (31,32).
Figure 4.
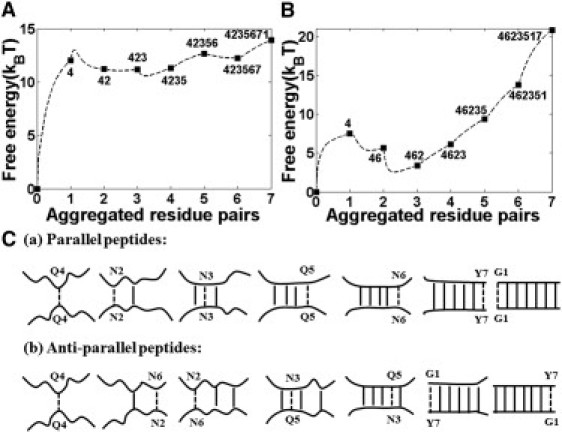
Sequential aggregation pathways are plotted through the free energy surface (dashed lines) versus number of aggregated residue pairs at T = 1. (A) Aggregation pathway for double parallel peptides as 4-2-3-5-6-7-1. (B) Aggregation pathway for double antiparallel peptides as 4-6-2-3-5-1-7. (C) Illustration of sequential aggregation pathways. (Dashed lines) Newly formed aggregated residue pairs; (solid lines) previously formed aggregated residue pairs.
The dominant importance of sequence N2-Q4-N6 for GNNQQNY fibrillation uncovered by our variational model is consistent with the all-atom MD simulations (22,33) and experimental observations (20). These have showed that the dry polar steric zipper structure through van der Waals interactions between complementary side chains provides a major contribution to stabilize the antiparallel β-sheet, whereas the interstrand hydrogen bonds and aromatic stacking are the driving forces to associate parallel β-sheet in an in-register fashion.
This pathway result is consistent with the recent atomic simulation for the parallel GNNQQNY dimer by Reddy et al. (24). The authors showed that the folding of N2N2 and N3N3 residue pairs happens at almost the same time, whereas the contact between N7N7 forms much later. This is consistent with our result. However, as no direct trajectory for the Q4Q4 residue pair was provided by the author, the role of the stacking of Glu4 still requires further clarification. The late formation of edge residue pairs could also be learned from the different interaction energy of residue pairs (29). The calculation in parallel peptides showed that the interaction energies for edge residue pairs G1G1 and Y7Y7 increase as two peptides move closer, whereas the interaction energies decrease for other central residue pairs. Thus, the formation of central residue pairs should be much easier than edge residue pairs. Further evidence comes from the calculation of root mean-square position fluctuations of Cα atoms. As shown in Fig. 5, the position fluctuations of edge residues Gly1 and Tyr7 are much larger than central residues under the same constraint parameters, which were attributed to the +1 and −1 charges associated with them (24). The low fluctuations in the middle indicate that much of the stability of the dimer is provided when the hydrogen bonds formed between the two strands at the central residues.
Figure 5.
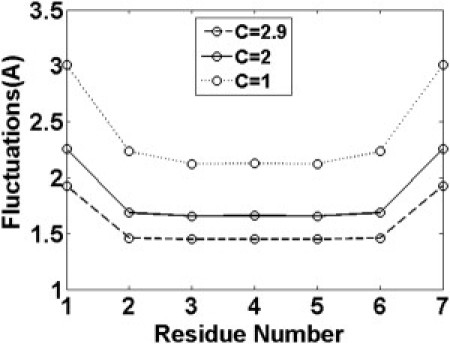
Root mean-square position fluctuations of backbone residues in hexamer as a function of constraint parameters.
Critical nucleus size for GNNQQNY aggregation is 3
To interpret the aggregation mechanism of amyloid fiber, classical nucleation theory was often borrowed (5,28,29), which suggested that the formation of amyloid fiber starts with an initial energetically unfavorable nucleation process, with free monomers aggregated homogeneously or heterogeneously into some nuclei. Once these nuclei reach certain critical size, they can spontaneously grow into long mature fibrils by sequential monomer addition at both ends, which is usually referred as the “elongation process” (30). Thus, the critical nucleus size serves as an important quantity to characterize the nucleation stage, and is directly related to the intrinsic chemical nature of amyloid proteins and the fibrillation conditions.
To explore this problem, we first studied the homogeneous nucleation process of 1–6 peptides with equal constraint parameters {Ci = C} on all residues at T = 1 (see Fig. 3). As we can see, the free energy for the monomer and dimer (either parallel or antiparallel) is always positive. For the trimer, the free energy is negative only when the constraint is very small, and it turns positive when C > 1.2. For bigger oligomers with size >3, their free energies keep negative for reasonable constraint parameters (C > 7.6). The corresponding minimum free energies for different oligomers can be determined as F(N = 3) = −3.19 kBT at C = 0.3; F(N = 4) = −13.13 kBT at C = 1.8; F(N = 5) = −28.51 kBT at C = 2.5; and F(N = 6) = −44.60 kBT at C = 2.9. Therefore we believe the trimer acts as the critical nucleus in the homogeneous nucleation process of GNNQQNY peptides. Similar conclusions have also been reported by Nelson (20) and Zheng et al. (22).
The thermal stability of oligomers in different sizes could be learned from the aggregation temperature (as illustrated through the trimer in Fig. 6), which is defined as the point at which the minimum free energy of the system equals to zero. Below this temperature, the free energy of the condensed state becomes negative, and the monomers can spontaneously aggregate into oligomers. Through systematic exploration, we found the aggregation temperature increases with oligomer size, i.e., T∗ = 1.12 for trimer; T∗ = 1.27 for tetramer; T∗ = 1.36 for pentamer; and T∗ = 1.43 for hexamer. Therefore, larger oligomers appear more stable than smaller ones. The aggregation temperature that we determined for the trimer system is close to the results (T∗ ∼ 1.2) obtained by Cecchini et al. (33) through replica-exchange MD simulation, which corresponds to the maximum fluctuations in the radius of gyration.
Figure 6.
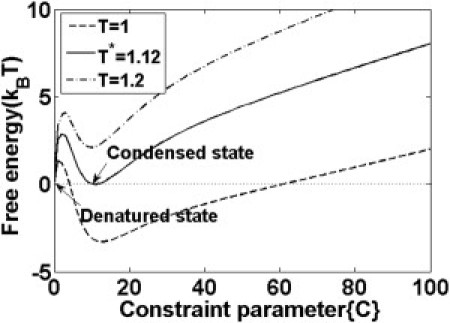
Free energy surface for a trimer at different temperatures. The constraint parameters {Ci} for each residue are set equal.
We further explored the sequential nucleation process of the oligomers—a heterogeneous nucleation procedure where peptides nucleate one by one in contrary to the homogeneous nucleation. Through the tree plot in Fig. 7, we listed all possible sequential nucleation pathways for a hexamer by simultaneously changing the constraints on single peptides while keeping the rest of the peptides at the condensed state (C = 2.9 corresponding to the minimum free energy in the homogenous system). Then the occurrence probability of the ith path is given by
where Pij ∝ exp(−βΔFij), and ΔFij is the free energy barrier height for step j in the path i. As we can see in Fig. 7, the first three steps are critical for the heterogeneous nucleation. The relative occurrence probabilities for the paths of S1-S3-S2, S1-S3-S5, S1-S2-S3, S1-S3-S4, and S1-S2-S4 are 1:0.45:0.03:0.02:0.02. Thus, the zig-zag form (S1-S3-S2) and the parallel-sheet form (S1-S3-S5) are the two most favorable patterns for trimer formation. Similar results were also observed by Zhang et al. (34) in MD simulations that showed that new strands might prefer to extend in a parallel arrangement to form oligomers. After critical steps, the free energy surfaces for most paths become downhill. And the differences between each path are subtle. This also helps us to reach a conclusion that the critical nucleus size for GNNQQNY is 3.
Figure 7.
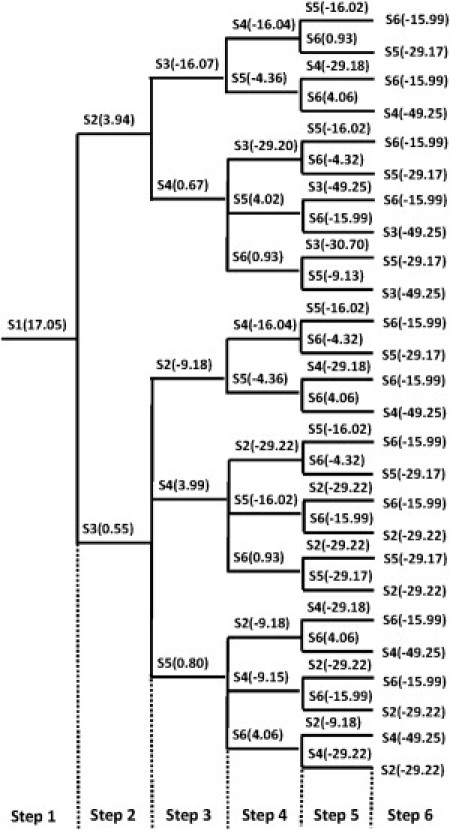
Tree plot for all possible sequential nucleation patterns of a hexamer. S1–S6 corresponds to the peptide number assigned in Fig. 2. (Brackets) Values denote the free energy barrier heights (or the free energy difference between the condensed state and the denatured state if the free energy surface is downhill) at each nucleation step.
Aggregation of free monomer to fibril is a highly cooperative process
To explore how fiber elongation spontaneously proceeds after the nucleation stage, we constructed the aggregation pathway for individual free peptides attaching onto existing fibril. We took hexamer as a reference system, in which five peptides are fixed at the condensed state with C = 2.9 (corresponding to the minimum free energy in the homogenous system), whereas the C values for residues in the sixth peptide are freely tunable.
Through the calculated sequential aggregation pathway (Fig. 8), an overall downhill free energy surface was observed, which indicates that the process of monomer attaching onto the existing fibril is a highly cooperative process. From Fig. 8, the initial attachments of residues Gln4, Asn6, and Gly1 are relatively easy according to the downhill free-energy surface, which is probably due to the strong orientation force between hydrophilic residues induced by existing fibril structures. Starting from the contact of residue Asn2, the attachments of Asn3, Gln5, and Tyr7 cause a slight increase in free energy, corresponding to the optimization of β-strand registers (21). The final stabilization of Tyr7 suggested that the π-π stacking of aromatic residues plays an important role in stabilizing the oligomer structure rather than giving directionality for β-strand alignment (31,32,34).
Figure 8.
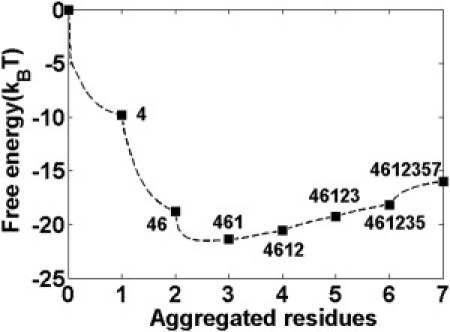
Sequential aggregation pathway for a single free monomer attaching to an existing pentamer, which is plotted through the free energy surface (dashed line) versus the number of aggregated residues at T = 1. The residue aggregation order is shown as 4-6-1-2-3-5-7.
The above analysis coincides with the general picture of dock-and-lock mechanism proposed by Reddy et al. (35), which suggests that fiber aggregation starts with a relatively easy dock step and finishes in a more difficult lock procedure of the remaining residues. However, in our model, the docking starts from central hydrophilic residues (Gln4 and Asn6) based on the minimization of free energy; whereas in Reddy's simulations, they arbitrarily chose Gly1 to start with (35).
Discussions
The focus of this work is on constructing a microscopic thermodynamic theory that can provide quantitative insights of the amyloid fiber formation process only from the peptide sequence and the fiber crystal structure. Based on the residue-level variational modeling approach, we performed a systematic investigation of the aggregation pathways of oligomers formed by peptide GNNQQNY from the yeast prion protein Sup35. Our analytical results demonstrated that: 1), the central dry polar zipper structure is the major folding core for both double parallel and antiparallel β-peptides; 2), trimer acts as the critical nucleus in the homogeneous nucleation process of GNNQQNY peptides; 3), the heterogeneous nucleation prefers the zig-zag growth pattern; and 4), the aggregation of free peptides to existing fibrils is a highly cooperative process, consistent with the dock-and-lock procedure.
Despite the generality of the theoretical framework and detailed calculations of this work, there are several issues remaining to be addressed.
First, in dealing with the free energy calculation of fiber systems, some approximations were taken to make the model analytically treatable, such as the Gaussian chain approximation for backbone potential, the pairwise contact potential for intrachain and interchain interactions, and the harmonic approximation for the native free energy surface around the reference state. Thus our predicted free energy surface can be shifted away from the real fibril systems. Though our quantitative comparisons with the computational and experimental data demonstrate that these approximations may not have a major impact on the effective modeling of the fibrillation process, where many can be partly compensated by the choice of different constraint parameters, it is not clear to us to what extent these approximations can robustly hold.
Second, the determination of most probable pathways for fiber aggregation is a crucial step in our model application. Due to the high dimensionality of the free energy surface, an explicit exploration of all local minima and saddle points is not possible. In this article, we adopted a sequential search by assuming that each residue can only take two discrete states (aggregated or not aggregated). In reality, those partially aggregated states should be taken into consideration for a comprehensive study. For this purpose, we perform a completely different study based on the method of free energy steepest descent, which searches the local free energy minimum (rather than the minimal free energy barrier in the sequential search) and allows the partial aggregation of residues. The details are provided in the Supporting Material, which show that the basic predictions of two different searching methods are in qualitative agreement. However, a quantitative relationship between the exact aggregation pathway and the one based on the on-or-off mechanism is yet to be explored.
Third, in addition to the data we have provided, additional quantitative comparisons with computational and experimental studies could be performed, which include: 1), the aggregation temperature for oligomers with different size, 2), root mean-square position fluctuations of residues (or Cα atoms) in the fibril, and 3), aggregation order of residues in the fiber, etc. A critical test is concerned with the elucidation of the amino-acid sequence dependence in amyloid fibril formation. It is known that point mutations on certain key residues can dramatically change the stabilities of the fibril structures under physiological conditions. For instance, the study by Abedini et al. (36) showed that even a single point mutation can convert the highly amyloidogenic human islet amyloid polypeptide into a potent fibrilization inhibitor. The exploration of these issues would significantly enhance the usefulness of our model and also improve our understanding with a residue-level description of the amyloid fibril systems. Related work is under progress.
Acknowledgments
The authors thank Dr. John Portman for discussions.
X.Q. is grateful for the support from Techera Inc. This work is supported in part by the Alfred P. Sloan Foundation, the National Science Foundation (Career Award 1027394), the National Institute of General Medical Sciences (GM083107 and GM084222), and Tsinghua University Initiative Scientific Research Program (2010THZ02-1).
Supporting Material
References
- 1.Chiti F., Dobson C.M. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006;75:333–366. doi: 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- 2.Skovronsky D.M., Lee V.M., Trojanowski J.Q. Neurodegenerative diseases: new concepts of pathogenesis and their therapeutic implications. Annu. Rev. Pathol. 2006;1:151–170. doi: 10.1146/annurev.pathol.1.110304.100113. [DOI] [PubMed] [Google Scholar]
- 3.Frieden C. Protein aggregation processes: in search of the mechanism. Protein Sci. 2007;16:2334–2344. doi: 10.1110/ps.073164107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Alzheimer's Association. 2010. Changing the trajectory of Alzheimer's diseases: a national imperative. www.alz.org.
- 5.Jarrett J.T., Lansbury P.T., Jr. Seeding “one-dimensional crystallization” of amyloid: a pathogenic mechanism in Alzheimer's disease and scrapie? Cell. 1993;73:1055–1058. doi: 10.1016/0092-8674(93)90635-4. [DOI] [PubMed] [Google Scholar]
- 6.Watzky M.A., Morris A.M., Finke R.G. Fitting yeast and mammalian prion aggregation kinetic data with the Finke-Watzky two-step model of nucleation and autocatalytic growth. Biochemistry. 2008;47:10790–10800. doi: 10.1021/bi800726m. [DOI] [PubMed] [Google Scholar]
- 7.Morris A.M., Watzky M.A., Finke R.G. Fitting neurological protein aggregation kinetic data via a 2-step, minimal/“Ockham's razor” model: the Finke-Watzky mechanism of nucleation followed by autocatalytic surface growth. Biochemistry. 2008;47:2413–2427. doi: 10.1021/bi701899y. [DOI] [PubMed] [Google Scholar]
- 8.Knowles T.P., Waudby C.A., Dobson C.M. An analytical solution to the kinetics of breakable filament assembly. Science. 2009;326:1533–1537. doi: 10.1126/science.1178250. [DOI] [PubMed] [Google Scholar]
- 9.Hong L., Qi X., Zhang Y. Dissecting the kinetic process of amyloid fiber formation through asymptotic analysis. J. Phys. Chem. B. 2011 doi: 10.1021/jp205702u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hong L., Qi X.H., Zhang Y. A lattice-gas model for amyloid fibril aggregation. Epl. Europhys Lett. 2011;94:68006. doi: 10.1209/0295-5075/94/68006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wetzel R. Kinetics and thermodynamics of amyloid fibril assembly. Acc. Chem. Res. 2006;39:671–679. doi: 10.1021/ar050069h. [DOI] [PubMed] [Google Scholar]
- 12.Shankar G.M., Li S., Selkoe D.J. Amyloid-β protein dimmers isolated directly from Alzheimer's brains impair synaptic plasticity and memory. Nat. Med. 2008;14:837–842. doi: 10.1038/nm1782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Portman J., Takada S., Wolynes P. Variational theory for site resolved protein folding free energy surfaces. Phys. Rev. Lett. 1998;81:5237–5240. [Google Scholar]
- 14.Portman J., Takada S., Wolynes P. Microscopic theory of protein folding rates. I. Fine structure of the free energy profile and folding routes from a variational approach. J. Chem. Phys. 2001;114:5069–5081. [Google Scholar]
- 15.Portman J., Takada S., Wolynes P. Microscopic theory of protein folding rates. II. Local reaction coordinates and chain dynamics. J. Chem. Phys. 2001;114:5082–5096. [Google Scholar]
- 16.Shen T., Hofmann C.P., Wolynes P.G. Scanning malleable transition state ensembles: comparing theory and experiment for folding protein U1A. Biochemistry. 2005;44:6433–6439. doi: 10.1021/bi0500170. [DOI] [PubMed] [Google Scholar]
- 17.Zong C., Wilson C.J., Wittung-Stafshede P. Phi-value analysis of apo-azurin folding: comparison between experiment and theory. Biochemistry. 2006;45:6458–6466. doi: 10.1021/bi060025w. [DOI] [PubMed] [Google Scholar]
- 18.Qi X., Portman J.J. Excluded volume, local structural cooperativity, and the polymer physics of protein folding rates. Proc. Natl. Acad. Sci. USA. 2007;104:10841–10846. doi: 10.1073/pnas.0609321104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Qi X., Portman J.J. Capillarity-like growth of protein folding nuclei. Proc. Natl. Acad. Sci. USA. 2008;105:11164–11169. doi: 10.1073/pnas.0711527105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nelson R., Sawaya M.R., Eisenberg D. Structure of the cross-β spine of amyloid-like fibrils. Nature. 2005;435:773–778. doi: 10.1038/nature03680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Strodel B., Whittleston C.S., Wales D.J. Thermodynamics and kinetics of aggregation for the GNNQQNY peptide. J. Am. Chem. Soc. 2007;129:16005–16014. doi: 10.1021/ja075346p. [DOI] [PubMed] [Google Scholar]
- 22.Zheng J., Ma B., Nussinov R. Structural stability and dynamics of an amyloid-forming peptide GNNQQNY from the yeast prion sup-35. Biophys. J. 2006;91:824–833. doi: 10.1529/biophysj.106.083246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Vitagliano L., Esposito L., De Simone A. Stability of single sheet GNNQQNY aggregates analyzed by replica exchange molecular dynamics: antiparallel versus parallel association. Biochem. Biophys. Res. Commun. 2008;377:1036–1041. doi: 10.1016/j.bbrc.2008.10.039. [DOI] [PubMed] [Google Scholar]
- 24.Reddy A.S., Chopra M., de Pablo J.J. GNNQQNY—investigation of early steps during amyloid formation. Biophys. J. 2010;98:1038–1045. doi: 10.1016/j.bpj.2009.10.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Miyazawa S., Jernigan R.L. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol. 1996;256:623–644. doi: 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- 26.Bois, J. 2002. Rudiments of polymer physics. http://www.citeulike.org/user/norris/article/2086610.
- 27.Flory P.J. Cornell University Press; Ithaca, NY: 1953. Principles of Polymer Chemistry. [Google Scholar]
- 28.Gsponer J., Haberthür U., Caflisch A. The role of side-chain interactions in the early steps of aggregation: molecular dynamics simulations of an amyloid-forming peptide from the yeast prion Sup35. Proc. Natl. Acad. Sci. USA. 2003;100:5154–5159. doi: 10.1073/pnas.0835307100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lipfert J., Franklin J., Doniach S. Protein misfolding and amyloid formation for the peptide GNNQQNY from yeast prion protein Sup35: simulation by reaction path annealing. J. Mol. Biol. 2005;349:648–658. doi: 10.1016/j.jmb.2005.03.083. [DOI] [PubMed] [Google Scholar]
- 30.Meli M., Morra G., Colombo G. Investigating the mechanism of peptide aggregation: insights from mixed Monte Carlo-molecular dynamics simulations. Biophys. J. 2008;94:4414–4426. doi: 10.1529/biophysj.107.121061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Azriel R., Gazit E. Analysis of the minimal amyloid-forming fragment of the islet amyloid polypeptide. An experimental support for the key role of the phenylalanine residue in amyloid formation. J. Biol. Chem. 2001;276:34156–34161. doi: 10.1074/jbc.M102883200. [DOI] [PubMed] [Google Scholar]
- 32.Harper J.D., Lansbury P.T., Jr. Models of amyloid seeding in Alzheimer's disease and scrapie: mechanistic truths and physiological consequences of the time-dependent solubility of amyloid proteins. Annu. Rev. Biochem. 1997;66:385–407. doi: 10.1146/annurev.biochem.66.1.385. [DOI] [PubMed] [Google Scholar]
- 33.Cecchini M., Rao F., Caflisch A. Replica exchange molecular dynamics simulations of amyloid peptide aggregation. J. Chem. Phys. 2004;121:10748–10756. doi: 10.1063/1.1809588. [DOI] [PubMed] [Google Scholar]
- 34.Zhang Z., Chen H., Lai L. Molecular dynamics simulations on the oligomer-formation process of the GNNQQNY peptide from yeast prion protein Sup35. Biophys. J. 2007;93:1484–1492. doi: 10.1529/biophysj.106.100537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Reddy G., Straub J.E., Thirumalai D. Dynamics of locking of peptides onto growing amyloid fibrils. Proc. Natl. Acad. Sci. USA. 2009;106:11948–11953. doi: 10.1073/pnas.0902473106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Abedini A., Meng F., Raleigh D.P. A single-point mutation converts the highly amyloidogenic human islet amyloid polypeptide into a potent fibrilization inhibitor. J. Am. Chem. Soc. 2007;129:11300–11301. doi: 10.1021/ja072157y. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


