Neurotech for Neuroscience: Unifying Concepts, Organizing Principles, and Emerging Tools

Abstract

The ability to tackle analysis of the brain at multiple levels simultaneously is emerging from rapid methodological developments. The classical research strategies of “measure,” “model,” and “make” are being applied to the exploration of nervous system function. These include novel conceptual and theoretical approaches, creative use of mathematical modeling, and attempts to build brain-like devices and systems, as well as other developments including instrumentation and statistical modeling (not covered here). Increasingly, these efforts require teams of scientists from a variety of traditional scientific disciplines to work together. The potential of such efforts for understanding directed motor movement, emergence of cognitive function from neuronal activity, and development of neuromimetic computers are described by a team that includes individuals experienced in behavior and neuroscience, mathematics, and engineering. Funding agencies, including the National Science Foundation, explore the potential of these changing frontiers of research for developing research policies and long-term planning.

Introduction

“And so these [women and] men of Indostan

Disputed loud and long

Each in his own opinion

Exceedingly stiff and strong

Though each was partly in the right

And all were partly in the wrong!”

The Blind Men and the Elephant, by American poet John Godfrey Saxe, is based on an ancient Indian fable and remains timely in providing a view of the daunting task of scientists trying to understand the nervous system.

Fundamental shifts in our history of thinking about the brain, emerging from major technological and conceptual developments, will enable a revolutionary change in the kinds of questions that can be asked and the kinds of answers that can be achieved. These include new directions in the scope and scale of experimental investigations such that it is becoming possible to start to measure brain structure, chemistry, and activity simultaneously at many locations with high specificity and spatial/temporal resolution, instead of doing one- or few-at-a-time measurements. Furthermore, advances in theoretical understanding make it possible to formulate comprehensive multiscale models that are simultaneously bottom-up and top-down and include relevant dynamics at different spatial and temporal scales.

Major aspects of neuroscience research are shifting directions. This is a consequence, in part of increasing interest in neuroscience among experts from diverse disciplines, each bringing unique perspectives and methodologies. Scientists traditionally trained in mathematics, computer science, engineering, as well as biology and psychology study how brains compute. Behavioral scientists want to understand the neural basis of language, cognition, and emotion. Physicists seek to understand general principles of nervous system organization. The origin of thought and memory is being sought by those trained in chemistry; biologists study the evolution of simple neural systems into complex systems. Increasingly, successful research strategies in neuroscience require that engineers, biologists, and mathematicians among other scientists work together on challenges that extend from molecules to whole organisms, on systems that are dynamic and nonlinear. Of course, the tendency toward intellectual and empirical dominance of teams in producing new, high-impact knowledge has been the trend not only in neuroscience but also in other domains of knowledge, including the arts and humanities (Wuchty et al., 2007). Some of the contributing factors for the importance of teamwork include the high cost of neuroscientific research, scale and complexity of the field, the explosion of information, and the tendency toward increasing specialization. Although key insights and individual genius will always be treasured, participation in research teams is escalating in importance. In neuroscience, the interplay of empirical experimental studies of the brain with mathematical and engineering tools brings new opportunities to create deeper knowledge of nervous system function. Changes of this scope require that the federal agencies, such as the National Science Foundation, develop and support opportunities that can advance research, education, and training to promote transformational developments across the disciplines and at the frontiers of science.

With regard to neuroscience, there is a broad consensus that the use of previously unattainable, non-invasive, multimodal measurement tools with high temporal, spatial, and chemical resolution will increasingly reveal the underlying design characteristics of living systems. Such design characteristics tell scientists and engineers how living systems solve problems of form and function and are leading to the development of strategies for optimizing the use of convergent methods to understand the brain and nervous systems.

This paper describes the ideas and methods discussed by some of the participants in the symposium Neurotech for Neuroscience: Unifying Concepts, Organizing Principles, and Emerging Tools at the 2007 Society for Neuroscience meeting. True to the interdisciplinary nature of the questions asked and answers sought, the contributors represent departments of neuroscience, mathematics, and bioengineering. The research strategies used are multimodal and include “measuring,” “modeling,” and “making” studies of neural systems (Fig. 1). For each scientist, the program of research requires the incorporation of knowledge from disciplines outside of their own and often entails collaborative teams. Grillner describes progress in understanding cellular biophysical properties to the generation of rhythms associated with locomotion, Kopell links cellular biophysical properties to the generation of rhythms associated with cognitive states in the central nervous system, and Boahen describes simulation technology that promises to make the supercomputer-level performance required to scale-up the models Grillner and Kopell describe more accessible.

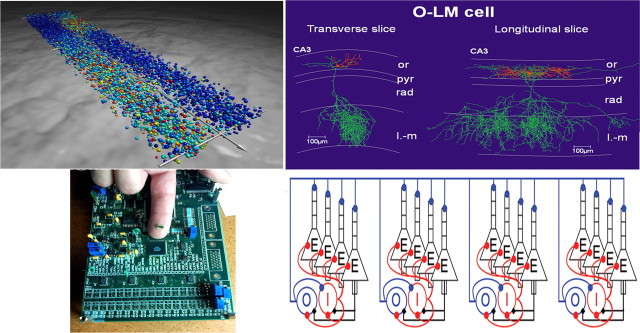
Figure 1.

Top left, Full-scale network simulation of the network coordinating locomotion in the lamprey–intersegmental coordination in a complete spinal cord. This large-scale network model consists of approximately the correct number of excitatory interneurons and commissural inhibitory interneurons (10,000 Hodgkin-Huxley, 5-compartment models) along the entire spinal cord. The model neurons express the different subtypes of ion channels found experimentally. The excitatory synaptic interaction is via AMPA and NMDA receptors and the inhibition via glycine Cl⁻ channels. The wave of activity is transmitted from rostral to caudal, with the left and right sides alternating. Red dots represent actively spiking neurons, yellow ones are depolarized but are not firing, and blue dots are inhibited cells. The network extends from the rostral (bottom right) to the caudal (top left; segment 100) aspect. Segment 50 is indicated with a hatched line, and the perspective is thus compressed caudally. Top right, Biocytin-labeled O-LM interneuron in transverse and longitudinal slices of CA3 hippocampus. Note the longer extension in the longitudinal slice. Bottom right, The network is an abstraction used for numerical simulations to explain how these interneurons, which fire at a theta (4–12 Hz) frequency, can coordinate spatially separated cell assemblies firing at the higher gamma band frequencies. Such analyses permit exploration of emergent properties of interacting neurons and networks of neurons (Tort et al., 2007). Bottom left, A neuromorphic chip (designed by John Arthur, Stanford University, Stanford, CA) that models 1024 pyramidal cells and 256 interneurons in the hippocampus. The chip is housed in a black plastic package and mounted on a printed circuit board. or, Stratum oriens; pyr4, stratum pyramidale; rad, stratum radiation; l-m, stratum lacunosum-moleculare.

Measuring the computational logic of networks in motion

With the development of more powerful computers and effective software, it has become possible, for the first time, to model large neuronal networks with biophysically detailed neurons and synaptic properties that approach the numbers and complexity found in living nervous systems, whether at a cortical or subcortical level. This type of full-scale model now becomes a powerful analytical tool. We will illustrate this below with the modeling used to analyze and reproduce the networks coordinating locomotion, posture, and steering in the lamprey model system. We will describe simulations with fairly complex multicompartment Hodgkin–Huxley neurons that faithfully reproduce the activity of their biological counterparts. In this case, ∼10,000 such neurons have been simulated with altogether ∼500,000 synapses that approach the numbers found in the biological systems (Grillner et al., 2007). Very recently, with the same software, a neocortical simulation of 22 million neurons in layer 2/3 and 11 billion synapses has been performed (Djurfeldt et al., 2007) on the IBM Blue gene supercomputer. This approaches the number found in these layers of the mouse neocortex.

This technological development opens up new important possibilities to use neuroinformatics tools, for both modeling and data basing different aspects of the function of the nervous system (Bjaalie and Grillner, 2007). The development of this type of critical neuroscience infrastructure has been initiated by the Allen Institute for Brain Science (www.brain-map.org) and the International Neuroinformatics Coordinating Facility (www.incf.org), an initiative of the Organisation for Economic Co-operation and Development (Global Science Forum), a joint effort of several European countries, Japan, and the United States. Other efforts to share information and data can be found on the Society for Neuroscience website (http://www.sfn.org/index.cfm?pagename=PublicResources&section=aboutNeuroscience).

The vertebrate motor infrastructure

Vertebrate motor behavior is impressive and can be adapted to the instantaneous demands of an ever changing environment. How is this achieved? At the disposal of each species, there is a set of adaptable motor programs that can be recruited to solve a variety of standard tasks. We have termed these motor programs, together with the structures that determine when each motor program should be called into action, the motor infrastructure (Grillner, 2003). Fortunately, the design and structure of these control systems appear to be evolutionarily conserved to a large degree; this applies from the level of the lamprey nervous system to that of mammals, including humans. The lamprey diverged from the main vertebrate line ∼530 million years ago. What is common today between lampreys and mammals must have been available already at that time. The general “bauplan” of the vertebrate nervous system is common from the forebrain to the brainstem–spinal cord level. This applies to a surprising degree also to the detailed cellular and synaptic organization of, for instance, the basal ganglia, tectum, and the brainstem–spinal cord motor structures that control different aspects of vertebrate motor behavior.

An important question is how the different motor programs and selection mechanisms operate at the cellular and network level. Different experimental and computational model systems are required depending on the type of process explored. For fine control of hand and finger movements, primate models may be a first choice, but simpler vertebrate models may provide a better alternative for the neural control of the general motor repertoire common to many vertebrates, such as goal-directed locomotion, including steering, posture, eye and orientation movements, and so forth. In these model systems, the chances of unraveling the basic design of these neuronal networks [central pattern generator (CPG) networks] are greater. To achieve this, we need to identify the different neurons within the networks, their cellular properties, and types of synaptic interaction.

At the cellular level, this type of integrated knowledge is in itself difficult to obtain experimentally. Furthermore, in most cases, it is not sufficient to evaluate critically whether or not the experimental findings can account for the behavior under consideration. This is because, in each case, a great number of dynamically interacting processes take place at multiple levels, within both each neuron and the network itself. Our brains have difficulty handling or are simply unable to handle this level of complexity. Modeling, based on a detailed knowledge of the network components, provides an indispensable tool for evaluating different possible interpretations of the experimental results obtained. Modeling is useful for exploring the neuronal bases of behavior, ranging from directly observable motor responses to less directly observable inferred cognitive processes (see below). Fortunately, the same cellular and molecular building blocks of networks may serve in circuits having widely different functions, for instance in the spinal cord and in neocortex (Grillner et al., 2005b; Yuste et al., 2005).

Intrinsic function of networks in motion, with special reference to goal-directed locomotion

By focusing on the knowledge gained in the lamprey model through an interactive process between experiments and modeling (Grillner, 2003, 2006), we have achieved a detailed cellular and molecular understanding of the networks generating locomotor movements. These include steering, the control of body orientation (posture), and also the neural mechanisms by which the behavior is selected. The emphasis here is on the modeling of the different components of the neural systems underlying goal-directed locomotion, with reference to detailed experimental evidence. The overall aim is to account for this complex set of behaviors, based on an understanding of the intrinsic cellular mechanisms determining the operation of the different neuronal networks. The different subsystems involved in the control of goal-directed locomotion are represented in Figure 2A and have been analyzed experimentally and through modeling.

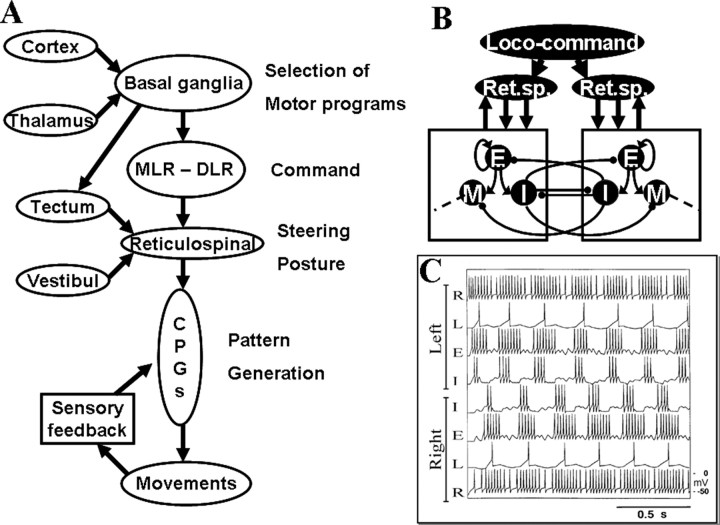
Figure 2.

Subsystems involved in the control of goal-directed locomotion. A, Selection of a motor program is performed in the basal ganglia, which receive inputs from the cortex (pallium) and the thalamus. The basal ganglia output stage (pallidum) inhibits command centers in the DLR and MLR during resting conditions. Through a well controlled inhibition of pallidal regions, the spinal CPG for locomotion can be activated via the reticulospinal (RS) neurons. In the brainstem, information is further integrated based on visual, sensory, and vestibular inputs to control both steering and posture. In all vertebrates, the spinal cord CPG neurons are modulated by local sensory feedback. Generation of locomotor activity in the spinal cord. B, The CPG network is activated from the locomotor regions via reticulospinal neurons (Ret.sp.) in the brainstem. Excitatory interneurons (E) excite all types of interneurons, including other excitatory interneurons. The inhibitory glycinergic interneurons (I) provide inhibition to the contralateral side and are also responsible for the left–right alternation seen during normal swimming. M indicates motoneurons. Some phasic feedback modulation (both glutamatergic and glycinergic) from the spinal cord network back to the brainstem also occurs. C, Activation of the spinal CPG by reticulospinal neurons (R). Neurons can drive the local network activity and cause a left–right alternating pattern over the experimentally observed frequency range in the simulations. L, Lateral interneurons.

Selection of motor programs

At a higher level of organization, there are neuronal mechanisms that select which CPG is to be turned on at any given moment (Fig. 2A). The basal ganglia play an important role in this contextual control (Hikosaka et al., 2000; Grillner et al., 2005). Under resting conditions, the output layer of the basal ganglia (pallidum) keeps the different CPG networks and thalamocortical neurons under tonic inhibition. For a behavior to be elicited, the particular CPG (or its input) needs to be disinhibited. Striatal neurons (input layer of the basal ganglia) can achieve this by inhibiting the cells within pallidum that are responsible for inhibiting the particular CPG. The striatal neurons, in turn, can be activated from either neocortex (pallium in lower vertebrates) or directly from thalamus. The responsiveness of striatal neurons to activation can be markedly facilitated by the dopaminergic input. A deficient dopamine innervation produces severe Parkinson-like hypokinetic symptoms in all vertebrates investigated from lamprey to humans (Grillner et al., 2005a), whereas enhanced levels of dopamine results in inadvertent initiation of movements (hyperkinesias). The striatal microcircuitry underlying the decision and selection processes for the control of the locomotor CPGs is modeled based on current experiments.

Command systems for locomotion

Two command systems for locomotion, the mesencephalic (MLR) and diencephalic (DLR) motor regions have been defined and are present in all vertebrates investigated. They are under tonic inhibitory control from the basal ganglia output nuclei, and they can be brought into action by a disinhibition resulting from striatal inhibition of the pallidal subpopulation. MLR and DLR act via a symmetric activation of reticulospinal neurons in the lower brainstem that turn on the spinal locomotor CPGs (Fig. 2B).

The intrinsic operation of the spinal CPGs coordinating the locomotor synergy

Segmental and intersegmental networks constituting the CPG are located at the spinal level. For mammals, there is one CPG for each limb. The limb CPGs can interact in different patterns to generate the different gaits as in walk and gallop. Each CPG contains the necessary timing information to activate the different motoneurons in the appropriate sequence to produce the propulsive movements. During swimming, as in the lamprey and other lower vertebrates, an undulatory wave is propagated along the body with a phase lag between the activation of each segment (Ijspeert et al., 2007).

The segmental burst generating network in the lamprey contains excitatory interneurons (EINs) that provide excitation within the pool of interneurons. The burst-generating network is turned on by glutamatergic excitation [AMPA, NMDA, and mGluRs (metabotropic glutamate receptors)] from the supraspinal command system. This drive signal excites the pool of excitatory interneurons, which also provides excitation to other interneurons within the pool (Fig. 2B). The burst is terminated primarily by intrinsic membrane properties. The Ca²⁺ level increase during activity attributable to NMDA receptors and voltage-dependent Ca²⁺ channels, and this Ca²⁺ in turn activates calcium-dependent K⁺ channels (K_Ca), which provides a hyperpolarization of the interneurons and thereby a termination of the burst (Fig. 3B). After a recovery phase, a new burst can be generated. The alternating pattern between the left and right side of each segment is provided by reciprocal inhibitory connections between pools of excitatory interneurons on the two sides (Fig. 2B,C). A sensory control system, sensing the locomotor movements, helps to compensate for external perturbations by a feedback action on the spinal CPGs.

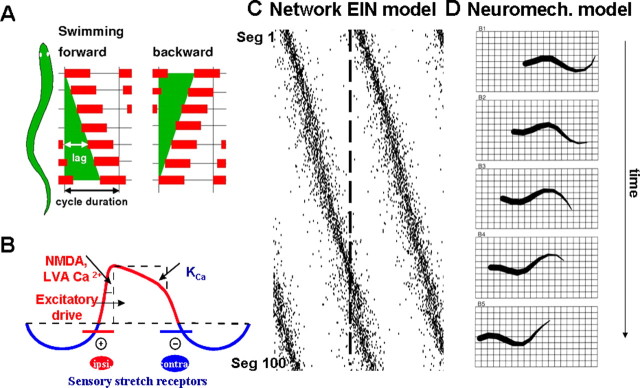
Figure 3.

Lamprey spinal cord intersegmental coordination. A, During swimming, a mechanical wave activating the muscles is transmitted along the spinal cord. When the animal moves forward, there is a lag between consecutive segments in the spinal cord. This lag is always a certain proportion of the cycle duration (i.e., a constant phase lag). It can be reversed into a wave that is propagated from tail to head, as during backward swimming. A rostral-to-caudal lag is also seen in the isolated spinal cord preparation. This pattern can be reversed if, for example, extra excitation is added to the caudal spinal cord. B, Ionic membrane and synaptic events important during activation within the CPG network. Slower processes can cause spike frequency adaptation, like Ca²⁺ accumulation during ongoing spiking and resulting activation of K_Ca. LVA, Low-voltage activated; Ipsi, ipsilateral; Contra, contralateral. C, Raster plots of the rostrocaudal activation of each of the 3000 EIN neurons in the model hemicord network (corresponding to 100 segments) during spontaneously forming forward swimming. Seg, Segment. D, The model lamprey swimming in water is simulated using a neuromechanical model of the muscles activated by the output from local CPG neurons.

The neural mechanisms generating a distributed flexible phase coupling for both rostral and caudal swimming (Fig. 3A) have been analyzed extensively through modeling with a realistic number of complex “Hodgkin–Huxley neurons” and synapses (Kotaleski et al., 1999; Kozlov et al., 2001). A hemisegmental “biophysically realistic” model network, including the established intersegmental connectivity, has been extended in the rostral and caudal direction with up to 100 segments and the EINs arranged with rostrocaudal connectivity as mentioned above (Fig. 3C). Such a network can be made to display a constant phase lag along the spinal cord, similar to that found in the isolated hemicord. If instead the entire spinal cord is modeled with two such extended EIN networks in parallel along with reciprocal inhibitory coupling at the segmental level, the two sides will be alternating at each segment. In addition, there will be a phase lag along the simulated spinal cord (Fig. 1, top left; full-scale simulation seen in Fig. 3C). The network can generate the phase lag for both forward and backward swimming by simply modifying the excitability in the rostral or caudal part of the spinal cord. A simplified version of such a network has also been used to control a neuromechanical model of the lamprey (Fig. 3D). It can simulate swimming movements in the water and can turn in three dimensions, as established experimentally (Grillner 2003). Finally, swimming has also been implemented in lamprey- or salamander-like aquatic robots based on the same principles (Grillner et al., 2007; Ijspeert et al., 2007).

Neural mechanisms underlying steering

Steering commands are superimposed on the basic locomotor activity and will bias the control signals, so as to steer the movements to the left or right side or to other orientations. Such commands are achieved through an asymmetric activation of reticulospinal neurons on the left and right side, particularly involving the middle and posterior rhombencephalic reticular nuclei. This results in longer and more intense bursts on the side toward which a turning response occurs. The basic brainstem circuitry for turning is thus comparatively simple and has been modeled based on detailed experimentation (Kozlov et al., 2001). The above results illustrate the basic neural machinery for turning but do not in themselves unravel the mechanisms by which the animal itself performs goal-directed steering toward a particular object or prey. The tectum (superior colliculus) is an important structure in the latter context. It receives input from the eye, which is organized in a retinotopic manner. It also provides a sensory map that is aligned to a motor map, which can elicit eye movements to a target, orientation movements of the body. It also allows for locomotion (Saitoh et al., 2007), seemingly swimming toward an object that gave rise to the activation of retina. The tectal circuitry in interaction with the basal ganglia presumably is responsible for this action (Fig. 2).

Control of body orientation during movements: posture

During locomotion, the body moves with the dorsal side up, regardless of perturbations. This “postural” control system for orientation of the body in the gravity field depends on bilateral vestibular input that detects any deviation from the appropriate orientation of the head, whether tilt to the left or right or changes in pitch angle during locomotion. The vestibular input is mediated via interneurons to the reticulospinal neurons in the rhombencephalon, so that a tilt to the left leads to an enhanced activity of reticulospinal neurons on the right side of the brainstem, and this elicits a correction of the body position (Deliagina et al., 2006). In both modeling work (Kozlov et al., 2001) and in an experimental hybrid system (immobilized lamprey), the recorded tilt-elicited signals in reticulospinal neurons have been used to elicit body corrections via an external motor, which was indeed quite effective (Zelenin et al., 2000). The lamprey is not able to stabilize its body orientation without the vestibular system. The visual system, however, can also provide input to the reticulospinal neurons and thereby stabilize positions with a certain degree of tilt, termed the dorsal light response.

In aquatic animals, vestibular signals are sufficient to control body orientation, but, for land-living tetrapods or bipeds, other sensors also contribute importantly (Deliagina et al., 2006). Furthermore, brainstem centers controlling posture and muscle tone receive input from the pallidal output nuclei of the basal ganglia (Grillner et al., 2005a).

From experiments and modeling to a physical implementation of a swimming “artifact”

The current knowledge of how the lamprey model coordinates locomotion, steering, eye movements and the control of body orientation has evolved through an interaction between different types of experiments and modeling. To further explore the function of this control system, we are currently in the process of developing a swimming artifact with the general properties of the lamprey together with Paolo Dario and colleagues (Grillner et al., 2007). This artifact has a reduced number of segments (currently only five). In each segment/myotome, it has four actuators with muscle-like properties, two on each side of the “body.” The arrangements of the four actuators can generate left/right alternation but also an enhanced activation of either the dorsal or the ventral actuators that will bias the swimming movements for steering to an upward or downward direction. It swims with laterally directed undulatory movements and is able to steer toward different targets.

The lamprey robot is being further developed to adapt to the environment, select different patterns of motor behavior, swim in both the forward and backward direction, and avoid obstacles in a predictable manner. The control system will follow closely that which is established experimentally. In addition to being an important research tool, this eel-like artifact may become a model for swimming robots that should be able to subserve a number of different engineering tasks. The long-term goal is that it will be possible to program the artifact to home to a specific area or to track an object.

In summary, the organization of the vertebrate motor system from lamprey to primates is to a large extent conserved throughout phylogeny. Because of the relative simplicity of the lamprey nervous system, it has been possible to address the neuronal mechanisms underlying goal-directed motor control and to develop general principles for goal-directed behavior in vertebrates. Computational approaches are essential tools for analyzing the dynamically interacting processes at the cellular and network levels that underlie motor behavior. As discussed by Nancy Kopell in the next section, the most appropriate analysis shifts when the behavior of interest must be inferred and is not directly observable, as are motor movements. All neurons, however, whether in cortex or the spinal cord, express a palette of ion channels that give them their particular properties, and this also holds true for the types of synapses they establish. Neurons in different networks are not identical but the building blocks are the same, and therefore knowledge can often be generalized (Grillner et al., 2005b).

Brain rhythms as a scaffold among levels of organization

Although it is undeniably true that there has been an explosion of techniques in neuroscience, we each still see the field as an analog of the blind men and the elephant: we see little pieces of what everyone acknowledges to be a huge entity. For many, however, an overarching question is the relationship between brain and cognition. There is a huge amount of work at each of these poles, but our ability to use information about the biophysical building blocks of the brain to get insight into cognition is still in its infancy. A strategy to build conceptual bridges between those poles that makes use of the spectral content of the electrical activity produced by the brain is (Buzsaki, 2006). The study of neural rhythms provides a framework for correlating the results of investigations from genetics through behavior. The strategy used depends heavily on modeling and mathematical analysis along with empirical experiments making use of new engineering techniques.

Questions and connections

The attempt to formulate and answer specific questions using this strategy is a very large program that is still in its infancy, but the framework is there, and there are enough preliminary projects to see how the program can work. A few examples can illustrate some of the questions central to the strategy and the connections that they illuminate. The examples each give partial answers and act as a kind of proof of principle. The central questions are as follows.

What produces the various spectral bands (and combinations of them) in different neuromodulatory environments?

Answers to this question via modeling connect the anatomy and physiology of cells and networks to dynamical mechanisms underlying the rhythms.

How does the brain make use of rhythms? For which functions and in what ways?

These are major questions whose answers provide one kind of connection between physiology/dynamics and cognition.

What are the behavioral consequences of pathologies in rhythms?

To date, every mental disorder appears to be associated with pathologies in rhythms of the nervous system (Phillips and Silverstein, 2003; Uhlhaas and Singer, 2006), and every psychotropic drug changes these rhythms (Whittington et al., 2000a). A study of how rhythms change in mental disorders is a way to connect underlying genetic and biophysical pathologies with changes in function.

Classical rhythms and their discontents

The electrical activity of the nervous system has been parsed into spectral bands for approximately the past three-quarters of a century. There is now a large and rapidly expanding literature that describes the spectral content of electrical activity in different cognitive states, in different tasks, and in different parts of the brain (Engel et al., 2001; Tallon-Baudry, 2004). These studies also document how spectral content can change over the process of learning (Ravel et al., 2003). Finally, many studies have documented how spectral content differs from controls in a variety of mental disorders (Phillips and Silverstein, 2003; Uhlhaas and Singer, 2006). This work establishes that neural rhythms are markers for cognitive state, in ways that are subtle; however, they do not establish the more compelling claim that the brain makes use of these rhythms for a variety of functions. How might that be explored?

The current frequency delineation is crude. One problem is that it may differ from animal to animal or from task to task in the same animal. Neural rhythms, as measured non-invasively by EEG or MEG (magnetoencephalogram), do not address mechanisms, either biophysical or dynamical, for the frequency content that is seen. Such studies cannot answer the question of whether activity in the same spectral range but different parts of the nervous system have the “same” features and similarly for activity found in different tasks. Indeed, these questions are not even well posed at this level.

Rhythms and biophysics: gamma

Here is where applied math, in particular dynamical systems, makes its entrance. It starts by asking about the dynamical and biophysical properties of given parts of the spectral activity, such as the gamma frequency band. By this is meant which types of cells are involved, what are the patterns of activity in each of classes of cells, and what kinds of parameters are critical for emergence of stable population activity in a given frequency range. This is generally better investigated in vitro, with all the usual and important caveats about the translation from in vitro to in vivo.

Work in a variety of different slice preparations, mostly in rodents, has shown that local circuits from hippocampus, neocortex, entorhinal cortex, amygdala, and cerebellum have the ability to form many of the classical rhythms, and that there are multiple ways in which a given tissue slice can produce that spectral band. The gamma frequency (30–90 Hz) has been most studied, and at least three different versions of gamma have been found: a rhythm created entirely by inhibitory cells in slices with blockers of ionotropic excitation and metabotropic activation of interneurons (ING); a gamma involving both pyramidal cells and interneurons (PING), produced by initial tetanic stimulation of the slice at higher frequencies and characterized by a high firing rate of all the participating cells; and a “persistent” or “weak” gamma that is created pharmacologically using kainate and/or carbachol in the bath, characterized by low firing rates of the pyramidal cells and 20–40 Hz rates of the interneurons (Whittington et al., 2000b).

Gamma rhythms and function: is the gamma rhythm just an index to behavior?

A large literature connects the appearance of gamma rhythms to attention, awareness, working memory, and other cognitive states (von Stein and Sarnthein, 2000; Engel and Singer, 2001; Womelsdorf and Fries, 2007). There are also links between gamma rhythms and particular biophysical processes, especially the kinetics of GABAergic cells (Whittington and Traub, 2003; Bartos et al., 2007). What is missing from those studies is an explanation for why it is “gamma” rather than any other possible dynamical marker that appears in the characteristic states associated with that rhythm. Such an explanation should create a connection between the biophysics of gamma and the functions of gamma. Two case studies that make such connections are discussed below.

The first is a study by Olufsen et al. (2003), showing a connection between the PING form of gamma and cell assemblies. In this gamma, pyramidal cells fire, causing interneurons [notably parvalbumin-positive (PV⁺) basket cells] to fire, which then temporarily suppress the firing of the pyramidal cells. The firing starts when the inhibition decreases, making the period of this gamma rhythm dependent on the excitability of the pyramidal cells and the amplitude and kinetics of the GABA_A pulse. Although many papers using the idea of cell assemblies have invoked the involvement of gamma rhythms (Singer et al., 1990; Engel et al., 1997; Harris et al., 2003), it was not clear why the biophysical properties of the gamma rhythms should be especially useful. The Olufsen et al. modeling work showed that an essential property of the PING form of gamma is that it is shaped by inhibition, and the GABA_A decay time is the slowest relevant timescale in the network. (For example, some slower currents that are active in the cells between spikes may be turned off because of the voltage range in which gamma is active; the membrane time is small because there is a large flow of transmembrane current during this rhythm.) As a consequence, there is essentially no cellular memory from one cycle to another; a pyramidal cell that receives tonic excitation will either fire on essentially every gamma cycle or not fire at all, depending on the level of input. Thus, the gamma rhythm is perfectly suited to the creation of cell assemblies: subsets of cells that are temporarily synchronous. The Olufsen et al. study also showed that the addition of other currents (such as the M-current) could destroy the ability of the network to produce both gamma rhythms and cell assemblies. Thus, changes in membrane properties attributable to neuromodulation or pathology can have a significant effect on function.

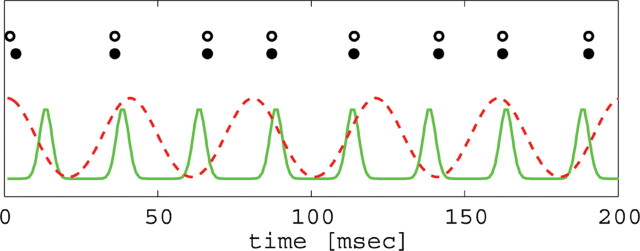
The second study relates the dynamical and biophysical properties of gamma to selective attention. Borgers and colleagues (Borgers et al., 2005; Borgers and Kopell, 2007) consider recent data showing that cell firing is more coherent in the presence of attention (Fries et al., 2001; Bichot et al., 2005; Womelsdorf and Fries, 2006). They examined the effect of coherent and less coherent input onto a microcircuit of one pyramidal cell and one basket cell. They showed that coherent input locks with the target circuit, and this creates inhibition to the target pyramidal cell that effectively locks out the less coherent input, even if the latter is somewhat larger in amplitude (Fig. 4). The effect depends on the coherent input being in a range of gamma frequencies, because the GABA_A signal from one cycle of the input provides inhibition until the next gamma cycle, by the nature of the gamma rhythm. The work shows that, rather than just being a correlate of function (Womelsdorf and Fries, 2007), the specific biophysical properties of gamma (e.g., its relationship to the timescale of inhibitory decay) contribute to how the function is performed.

Figure 4.

Target network (black, excitatory; white, inhibitory) responds at same frequency as coherent input (solid line), even in the presence of less coherent distractor input (dotted line) firing at a different frequency (higher or lower).

Dynamics and biophysics: the interaction of gamma and theta rhythms

Gamma rhythms often occur in vivo in the presence of other rhythms, notably the theta rhythm (4–12 Hz) (Bragin et al., 1995; Chrobak and Buzsaki 1998). One question is how the gamma and theta rhythms interact: do they occur in separate networks or one network? If the latter is true, is it possible to modulate the gamma rhythms separately from the theta rhythms? That question can be approached by relating biophysical and anatomical facts to the dynamics of gamma and theta. This kind of connection permits understanding of how pathologies in rhythms can be related to aberrations in intrinsic and synaptic currents, which can themselves occur when there are pathologies in genes that code for membrane channels (Whittington et al., 2000b; Benes and Berretta, 2001).

Very approximately, rhythms in the 30–90 Hz frequency range occur as an interaction between pyramidal cells and PV⁺ interneurons, in which the pyramidal cells excite the interneurons, which then inhibit the pyramidal cells for a period of time that depends on the decay time of the inhibition and the excitability of the pyramidal cells. [Variations on this theme include gamma pacemaker cells in the neocortex (Gray and McCormick, 1996), inhibition of axonal plexus activity (Traub et al., 2002), and activity in entirely inhibitory networks (Whittington et al., 1995).]

The 30–90 Hz gamma rhythm is a network phenomenon dependent on inhibitory currents. In contrast, the theta rhythm can be produced by individual cells (Klink and Alonso, 1993; Dickson et al., 2000; Saraga et al., 2003), although a coherent population rhythm depends on connectivity (Netoff et al., 2005; Rotstein et al., 2006). In all cases, the rhythm depends on intrinsic currents that do not seem to be important for the gamma rhythm. These include the hyperpolarization-activated h-current, the persistent sodium current, and the M-current and/or the A-current (Klink and Alonso, 1997; Acker et al., 2003; Saraga et al., 2003).

In vitro work (Gloveli et al., 2005) has shown that brain slices of the CA3 part of the hippocampus in the transverse direction give rise to gamma oscillations (with low concentrations of kainate in the artificial CSF); if the slice is in the longitudinal axis, the same artificial CSF gives rise to a predominantly theta rhythm. A slice made in an in-between angle shows the nesting of gamma and theta rhythms, as seen in vivo. Mathematical modeling (Gloveli et al., 2005) has suggested that the gamma rhythm comes from the interaction of pyramidal cells and PV⁺ interneurons, whereas the theta rhythm comes from an interaction of the PV⁺ cells and oriens-lacunosum moleculare (O-LM) interneurons (Fig. 1, right). The power of each rhythm in the slice depends on the strength of the effects of the O-LM cells on the other cell types, which is modulated by the angle of the slice, because the O-LM cells extend further in the longitudinal direction. The same modeling shows how the O-LM and pyramidal cells compete for control of the basket cells, allowing for flexible modulation of the rhythms by any modulators that separately change the outputs or synaptic currents of the O-LM and pyramidal cells. More recent modeling (Tort et al., 2007) shows how the O-LM cells, which project to the distal dendrites of the pyramidal cells, can synchronize assemblies of cells firing at gamma frequencies, although those O-LM cells fire at a much lower frequency. This sheds light on how inputs from the entorhinal cortex to the distal dendrites can be coordinated.

Gamma, beta, and schizophrenia

The final example uses rhythms to connect pathologies at the level of cells to pathologies in sensory processing. As discussed above, the gamma rhythm is believed to be important for attention, and there are similar studies about other rhythms and other cognitive states (Tallon-Baudry et al., 1999; Palva and Palva, 2007). Together, they start making a case for the hypothesis that neural rhythms are important, perhaps even essential, to normal cognitive function. This line of thought makes it compelling to study the changes in rhythms in specific mental disorders, to see what they might say about both the behavioral symptoms and the underlying pathophysiology of the disease. One situation in which this has been done is in schizophrenia (SZ), a disease in which the sufferers often have auditory hallucinations as well as attention deficits (Phillips and Silverstein, 2003). The symptoms of SZ are very broad, and changes in tissue structures are found throughout the brain. A major challenge is to connect at least some of the physical changes to some of the behavioral changes.

Some studies are suggesting that there are problems with primary sensory processing (Wilson et al., 2007). For example, patients with SZ respond differently to auditory inputs consisting of click trains at 20, 30, or 40 Hz. In EEG studies (Kwon et al., 1999) and EMG studies (Vierling-Claassen et al., 2006), it was found that the control subjects respond to 40 Hz click trains with 40 Hz electrical activity in the primary auditory region. Patients with schizophrenia, however, respond to the same inputs with a significant 20 Hz component. Similarly, with 20 Hz click train, the controls respond with mixed 40/20 Hz output, and the patients with schizophrenia respond with a larger amount of 20 Hz (Kwon et al., 1999; Vierling-Claassen et al., 2006).

One very promising new approach to SZ has been the discovery (Lewis et al., 2004) that there is damage in postmortem tissue to the PV⁺ inhibitory chandelier cells of the prefrontal cortex. In that tissue, and possibly other more widespread throughout the brain in SZ patients, the loss and damage of the relevant inhibitory cells lead to lower amounts of two essential products. One is GAD-67, a synthesizing enzyme of the inhibitory neuromodulator GABA, and the other is GAT-1, a transporter of GABA. The loss of the former suggests that people with schizophrenia may, at least in some parts of their brain, have less inhibition from the deficit of GABA, but the loss of the transporter can change the kinetics of the GABA response, prolonging the effective time of inhibition (Overstreet and Westbrook, 2003). The question is, can this alone account for the above aberration in primary auditory processing?

Here is where modeling can help, using dynamical systems describing networks of neurons in the primary auditory cortex. The reduction of GABA synthesis is modeled by a lower inhibitory effect on other cells, and the change in the transporter is modeled as increasing the time it takes for the inhibitory effect to decay. The modeling is done both in detailed representations of a piece of cortex (although not as detailed as by, for example, Traub et al., 2005) but also with a much reduced model whose analysis provides clarity about the dynamical mechanisms underlying the switch from the gamma to the beta rhythm (Kopell, 2005). Both versions reproduce the experimental results. This does not yet account for why specific biophysical deficits should lead to symptoms such as auditory hallucinations, but it does allow one to connect the deficits with changes in dynamics known to be associated with the formation of cell assemblies and cortical communication.

Scientific strategies

The case studies discussed above illustrate some connections: between anatomy/physiology of cells and dynamical mechanisms of rhythms (gamma/theta interaction); between physiology/dynamics and behavior (attention); and between pathologies of synapses and mental disorder, via rhythms (schizophrenia). These few examples are but the tip of a large emerging literature considering many other spectral bands, in many parts of the nervous system (Tallon-Baudry et al., 2005; DeCoteau et al., 2007; Palva and Palva, 2007). To fully exploit this strategy will require taking advantage of advances in imaging methods and other new technology, analysis of neural data, and neural dynamics, as well as new experiments on the relationship of neural rhythms to behavior. Of particular interest is the growing ability to measure responses from large numbers of electrodes (Tsytsarev et al., 2006) to achieve fine spatial resolution of temporal activity and coherence. Similarly, the new ability to image simultaneously from EEG and fMRI allows both spatial and temporal resolution of dynamics in human subjects, as well as opening up the study of how hemodynamics may alter neurodynamics (Lachaux et al., 2007). Understanding the implications embedded in the avalanche of these data will require new statistical methods (Kass et al., 2005), possibly guided by dynamical systems models. Thus, the study of brain rhythms relates to and requires a large number of new techniques just now being developed; as these mature, we can expect that the “scaffold” of brain rhythms will become increasingly useful for relating different levels of organization.

The modeling techniques used in the above examples are similar in spirit to those described by Grillner's delineation of motor patterns, using biophysically based nonlinear differential equations to describe electrical activity. One difference in scientific approach comes from the fact that the function of the swimming CPG is well understood, and so questions concerning the cellular basis of such function arrive well posed. In contrast, the roles of dynamics in cognition are mysterious, and the strategy used is to tease that out by concurrently studying the origin of the neural dynamics and how the underlying physiology affects the processing of neural signals. This gives insight into how processes at one level become integrated to give rise to processes at another whose function is not well understood; dynamical systems modeling provides a very flexible platform to pursue this challenge.

Although progress has been made linking cellular biophysics to the generation of rhythms in the central as well as the peripheral nervous systems, the task of linking rhythms to cognition still remains. Although we have succeeded in putting more of the pieces together, we are still missing the complete picture, as with the blind men and the elephant. On one hand, we can manipulate and measure a limited number of quantities in our experiments. For instance, we cannot simultaneously access the electrical activity of all the cells of all the lamprey segmental networks and characterize their changes over time. On the other hand, we can include only a subset of the details uncovered experimentally in our models. For instance, we limit their scope to a particular subsystem (e.g., the hippocampus) and focus on the role of a particular biophysical mechanism (e.g., the kinetics of GABAergic cells). Scaling up these models without sacrificing detail requires us to build more powerful simulation platforms, as well as to generate sufficient data to constrain such large-scale models by building high-throughput brain probes. Boahen addresses the former issue when he describes a simulation technology with the potential to deliver flexible supercomputer performance on a manageable budget.

Emulating the brain in silicon

As described in the preceding sections, simulations permit inclusion of molecular-level details while replicating system-level behavior, thereby providing insight into how processes at lower levels become integrated to give rise to processes at higher levels. To date, however, simulations large enough to accommodate multiple cortical areas, yet detailed enough to include distinct cellular properties, remain impractical. For instance, a model built by Lansner and his colleagues with 8 million neurons connected by 4 billion synapses run 4750 times slower than real time on a 2048-processor Blue Gene rack (Djurfeldt et al., 2005). It took 1 h, 20 min to simulate 1 s of the behavior of the model, yet a model of this size corresponds to just 4% (50 mm²) of macaque V1. Simulating an entire cortical area in real time, not to mention multiple cortical areas, will remain outside the realm of the fastest supercomputers for the foreseeable future.

Various hardware solutions are being explored to satisfy the need for more powerful, and affordable, simulation platforms. Impressive speedups have been achieved with graphical processing units (GPUs) and field-programmable gate arrays (FPGAs). Sporting 128 general-purpose processors on a single chip, GPUs have been programmed to run neural simulations 100 times faster than a personal computer (Paul Rhodes, personal communication). Sporting 100,000 individually configurable logic gates on a single chip, FPGAs have been configured to run neural simulations 2000 times faster than a personal computer (Guerrero-Rivera et al., 2006). Although rivaling the performance of the 2048-processor Blue Gene rack in the latter case, at a fraction of the cost, this performance is several orders of magnitude short of what is needed to simulate multiple cortical areas in real time.

In this final component of our symposium, we highlight a radical approach to computation that has the potential to perform real-time cortex-scale simulations. The fundamental component of this neuromorphic chip is not a logic gate, like in a digital computer, but a silicon neuron: an analog electronic circuit of transistors that mimic the ion-channel repertoire of a real neuron. The cellular properties of these silicon neurons and network connectivity are configurable, akin to the logic gates of an FPGA. To emphasize that this is a physical instantiation of a neural model that operates in real time, we will use the term “emulate” as opposed to simulate. This technology, developed over the past two decades, yields a hitherto unimagined level of efficiency that makes beyond-Blue-Gene performance affordable on a Beowulf-cluster budget.

Breakthroughs in neuromorphic engineering

Neuromorphic chips were pioneered by Carver Mead in the late 80s, when he developed the first silicon retina at California Institute of Technology (Mead, 1989). Extrapolating the doubling in computer performance that was occurring every 18 months (Moore's Law), Mead predicted correctly in 1990 that present-day computers would use 10 million times more energy (per instruction) than the brain uses (per synaptic activation) (Mead, 1990). In other words, a computer that executes one instruction every time the brain fires a synapse would consume 100 MW! He sought to close this gap by building microelectronic circuits based on the brain. Inspired by graded synaptic transmission in the retina, Mead investigated operating transistors in a graded manner (analog), a radical departure from their on–off operation in (digital) computers. He showed that analog required far fewer transistors than digital, resulting in substantial energy savings.

Neuromorphic chips have had limited utility as simulation platforms, however, because they are hardwired to perform a specific function. For instance, the transistors in Mead's silicon retina, which he developed with Misha Mahowald, are wired together in accord with the synaptic organization of the retina. This reflects neuromorphic engineers' historical focus on applications in autonomous robots and prosthetic implants, in which efficiency and size come first. When seeking support for a hypothesis through simulation, however, one has to perform controls (rule out alternative hypotheses), replicate experimental manipulations (block a specific channel or cut a certain connection), implement existing models (for input or benchmarks), and explore mechanisms (what is necessary and sufficient). This is not possible when the chip is hardwired.

A second shortcoming prevented neuromorphic chips from serving as simulation platforms: the physiological properties of their silicon neurons were fixed. For instance, in the ganglion cells of the silicon retina, a clever arrangement of transistors sensed the voltage of a node in the electronic circuit and fed back a current that mimicked the spike-generating action of sodium ion channels. These transistors could not, however, be used to model another type of ion-channel, for example, to generate a calcium spike. That would require designing an appropriate arrangement of transistors and fabricating a new chip, a severe impediment to modeling, because the design-fabricate-test cycle takes several months.

In recent years, neuromorphic engineers have overcome both shortcomings by combining the real-time operation of analog with the programmability of digital to reap the best of both worlds. Instead of hardwiring silicon neurons together, they and their synaptic targets are assigned unique addresses. Every time a spike occurs, the chip outputs the address of that neuron (Mahowald, 1994). This address points to a memory location (RAM) that holds the address of the synaptic target. When this address is fed back into the chip, a postsynaptic potential is triggered at the target; assigning multiple memory locations to a neuron makes multiple synaptic targets (divergence) possible (Elias, 1993). These “softwires” may be rerouted simply by overwriting the look-up table of RAM. Encoding, translating, and decoding an address happens fast enough to route several million spikes per second, allowing 1 million connections to be made among 1000 silicon neurons. In contrast, FPGAs use tracts of metal wires to connect their logic gates together through programmable switches, severely limiting the number of connections each gate can have (typically four); their analog counterparts (field-programmable analog arrays) face similar wiring constraints (Hall et al., 2005).

To make cellular properties programmable as well, neuromorphic engineers developed an analog electronic equivalent of the Hodgkin–Huxley model, the gold standard for ion-channel populations (Hynna and Boahen, 2006). The sigmoid activation curve and bell-shaped time-constant curve of this electronic circuit may be adjusted (after it is fabricated) to match any particular ion-channel type, making it possible to model various types of neurons with the same chip. The circuit can accommodate the observed range of voltage levels and timescales, as does the Hodgkin–Huxley model. For ligand- or calcium-gated ion channels, charge on a capacitor is used to represent neurotransmitter in the synaptic cleft or calcium inside the cell; a modified version of the circuit achieves this. As few as eight transistors can model an entire ion-channel population, making it possible to fabricate millions of these silicon models on one chip. This design is the first to capture the voltage dependence of the temporal dynamics of the ion channel, while at the same time using fewer transistors than previous neuromorphic models that do not possess these nonlinear dynamics (Mahowald and Douglas, 1991; Simoni et al., 2004; Farquhar and Hasler, 2005; Saighi et al., 2005). Exploiting parallels in the thermodynamic behavior of ion channels and transistors, originally recognized by Carver Mead (1989), made this possible.

With the ability to model various types of ion channels as well as arbitrary patterns of synaptic connections, the stage is now set for using neuromorphic chips as a simulation platform. Choosing to use analog to emulate ion-channel activity and to use digital to realize neuronal connectivity, however, imposes significant tradeoffs that must be tailored to suit the scientific goals in mind.

Tradeoffs in neuromorphic simulation platforms

Analog computation imposes an upper limit on the number of distinct ion-channel populations that can be emulated (parallel operation), unlike digital processors, which simply take longer to run bigger simulations (serial operation). The desired number of ion-channel populations depends on how many neurons are modeled, on the subcellular compartments of each neuron, and on the types of ion channels each compartment expresses. Compartments may range from one, for interneurons that are electrotonically compact, to 1000, for pyramidal cells with different voltages in each terminal dendrite. Each compartment may have anywhere from one type of ion channel, for the passive (cable-like) dendrites of interneurons, to 10, for the active dendrites of pyramidal cells. Hence, a single cell may have anywhere from 1 to 10,000 distinct ion-channel populations, each handled by a dedicated analog electronic circuit, millions of which may fit on a chip. Thus, the number of neurons modeled drops from millions to hundreds as the number of compartments or ion-channel types goes up.

Digital communication imposes an upper limit on the number of synapses that can be activated per second (serial operation). The desired rate depends on how many neurons are modeled, on the number of synapses each one makes, and on the number of spikes it fires per second. Cortical cells make thousands of connections and can fire several spikes per second. Modeling 1000 cells requires on the order of 10 million synaptic activations per second (1000 cells × 1000 synapses/cell × 10 spikes/seconds, round numbers), a rate that has already been achieved (Boahen, 2004). With the same activation rate, more cells could be modeled by distributing them across multiple neuromorphic chips that encode, translate, and decode addresses in parallel. Furthermore, the number of connections could be increased by using local (on-chip) wiring to elicit postsynaptic potentials at neighboring locations (mimicking an axonal arbor). Both schemes have been demonstrated (Fig. 5) (Choi et al., 2005).

Figure 5.

A multichip model of orientation hypercolumns. Four Gabor chips (top), each with a 64 × 128 array of silicon neurons, receive spikes from a silicon retina, encoded as addresses that are decoded to retinotopic locations, in which postsynaptic potentials are elicited such that alternating stripes of On and Off ganglion cells drive each neuron. Receptive fields of neurons at the center of each array are shown on the bottom (black, on; white, off). Other neurons are tuned to the same orientation but to different visual locations. For details, see Choi et al. (2005).

Neuromorphic engineers are currently exploring how best to tailor the tradeoff between cell count and compartments per cell and that between cell count and connections per cell to achieve the goal of simulating multiple cortical areas in real time. With respect to the first tradeoff, the interactions between inputs delivered to different cortical layers have been replicated in a two-compartment pyramidal-cell model (Larkum et al., 2004). Furthermore, varying how strongly these compartments are coupled replicates firing patterns of various pyramidal cell types (Mainen and Sejnowski, 1996). With respect to the second tradeoff, axonal ramifications have been found to be patchy, indicating a preponderance of local connections, as expected from the map-like organization of cortical areas (Amir et al., 1993). Based on these studies, engineers favor using minimal cell models to maximize cell count and using local wiring to maximize connectivity, as described in the next section. In contrast, the Blue Brain project, with its complementary focus on modeling a single cortical column, uses thousands of compartments per cell (Markram, 2006).a

Modeling the cortex with neuromorphic chips

In a neuromorphic simulation platform currently under construction (in the Boahen laboratory), the cell layers of the cortex, which are stacked one atop the other, are mapped onto 16 identical chips, tiled in a 4 × 4 grid on a paper-back-sized circuit board, hence the name Neurogrid (Fig. 6). Each chip, or Neurocore, models 65,536 two-compartment cells, tiled in a 256 × 256 array. Thus, Neurogrid will have a total of just over 1 million silicon neurons. Their spikes are relayed from chip to chip by sending an address that specifies which chip, which row, and which column a neuron resides in every time it spikes (Merolla et al., 2007). By encoding, translating, and decoding these addresses in parallelb and implementing patchy arbors with on-chip wiring,c 6 billion synaptic connections may be maded, 680,000 times more than a previous silicon cortex (Deiss et al., 1999).

Figure 6.

Neurogrid, a platform for cortical simulations. Cortical cell layers (left) are mapped onto chips (right) with arrays of silicon neurons. Silicon analogs of the Hodgkin–Huxley model emulate the repertoire of ion channels of each cell type. Spikes are relayed from chip to chip, routed using information stored in on- and off-chip RAM, which specify targets of vertical and horizontal projections (black and purple), respectively. Cable-like on-chip wiring (with adjustable electrotonic spread) models the local arbor of a projection (brown). A version of Neurogrid with a 4 × 4 grid of chips, each with a 256 × 256 array of two-compartment cells, is currently being built.

User-programmable lookup tables stored in RAM allow software-like flexibility. These tables identify where spikes should be delivered and specify the anatomical (e.g., basal/apical) and physiological (e.g., excitatory/inhibitory) properties (Lin et al., 2006) of each connection. A common set of ion-channel parameters is also specified for all cells on the same chip. Thus, Neurogrid can accommodate as many distinct cell types as it has Neurocores. It is possible to have a unique set of parameters for each cell, or even each compartment, by storing this information on floating gates, which provide compact nonvolatile memory, an approach being pursued in another project (Farquhar et al., 2006). The user enters anatomical and physiological properties using a graphical user interface and views simulation results in real time on an interactive display. She or he can select a single cell in the network and plot its firing pattern, observe the activity of an entire layer, or examine any level of complexity in between.

When it is completed in 2 years, Neurogrid will emulate 1 million neurons in the cortex in real time, rivaling 200 Blue Gene racks.e Based on its similarity to GRAPE-6, an affordable supercomputer with 32 chips mounted on a desktop-sized circuit board that has transformed astrophysics (Normile, 2001), Neurogrid will cost $60,000 (estimated) to produce in large quantities, <¹/₁₀₀₀ the cost of the 200 Blue Gene racks. Larger versions of Neurogrid could be built by expanding the chip size, by expanding the grid size, or by squeezing more silicon neurons on a chip. Doing all three should make it possible to scale up the current design to 64 million neurons in the next few years.

A transformative technology?

The digital technique used to simulate neural activity has not changed since Hodgkin and Huxley pioneered ion-channel modeling in the 1950s. Since then, progress has come incrementally, from the doubling in computer performance every 18 months (Moore's Law). However, performance has plateaued in recent years, putting real-time cortex-scale simulations outside the realm of the fastest supercomputers for the foreseeable future. Fortuitously, the analog technique developed by neuromorphic engineers over the past two decades has now matured, with the recently developed ability to program various types of ion channels as well as arbitrary patterns of synaptic connections.

How will the availability of affordable supercomputers capable of performing real-time cortex-scale simulations impact neuroscience? One of the biggest stumbling blocks to understanding the cortex is feedback. Virtually every cortical area projects back to the areas that feed it, making these feedback projections approximately half the total, yet they remain mysterious. The preponderance of feedback poses several conundrums. Why is the brain stable, yet plastic? Why is noise, which is rife,f not amplified? Answers to the first question would yield insight into epilepsy (Cossart et al., 2005); answers to the second question would yield insight into schizophrenia (Winterer and Weinberger, 2004). Shedding light on these fundamental questions calls for simulations large enough to include interactions between multiple cortical areas yet detailed enough to account for distinct cellular properties, which give rise to the rhythms that appear to modulate corticocortical interactions dynamically (Womelsdorf et al., 2007). Neuromorphic platforms promise to perform such large-scale simulations affordably.

Promise of interdisciplinary neuroscience research

Scientists and engineers, like the subjects in The Blind Men and the Elephant, have as a goal “that each by observation might satisfy his [or her] mind.” The progress of science has often been hastened by communicating and applying findings and insights, tools and techniques from one discipline to new questions and to new experimental paradigms. In this article, experimenters with significantly different research interests and methodologies point to emerging opportunities in neuroscience to measure, model, and make exciting new tools, technologies, and concepts from multiple disciplines. Progress in understanding emergent properties of nervous systems of the type they envision will require that scientists, mathematicians, and engineers work together in an environment conducive to the integration of education, training, and research across the disciplines and at the frontiers of science. Such progress must be actively encouraged and fostered. One strategy used by the National Science Foundation has been to host workshops to mine the knowledge at the frontiers and to look ahead to the next generation of breakthroughs. Meeting participants saw broad areas of opportunities for exploring grand challenges of mind and brain; they saw mutual scientific benefit between brain sciences and the physical and mathematical sciences, computer science, and engineering. These included possibilities for developments in instrumentation and measurement, data analysis, statistical modeling, and informatics, conceptual and theoretical approaches, building brain-like devices and the longer-term goal of understanding how cognition emerges from the physical matter of the brain (see http://www.nsf.gov/od/oia/activities/neuroscience/). The promise is that here, as in other endeavors, investigators from many disciplines will strive to understand how organisms sense and adapt to changing environments, how they control movement, how they can think, and what makes them resilient and robust, durable, and flexible. Discovery will be hastened by each of us groping a piece of Saxe's elephant while attending to what the rest are seeing and hearing.