A State Space Transformation Can Yield Identifiable Models for Tracer Kinetic Studies with Enrichment Data

Abstract

Tracer studies are analyzed almost universally by multicompartmental models where the state variables are tracer amounts or activities in the different pools. The model parameters are rate constants, defined naturally by expressing fluxes as fractions of the source pools. We consider an alternative state space with tracer enrichments or specific activities as the state variables, with the rate constants redefined by expressing fluxes as fractions of the destination pools. Although the redefinition may seem unphysiological, the commonly computed fractional synthetic rate actually expresses synthetic flux as a fraction of the product mass (destination pool). We show that, for a variety of structures, provided the structure is linear and stationary, the model in the enrichment state space has fewer parameters than that in the activities state space, and is hence better both to study identifiability and to estimate parameters. The superiority of enrichment modeling is shown for structures where activity model unidentifiability is caused by multiple exit pathways; on the other hand, with a single exit pathway but with multiple untraced entry pathways, activity modeling is shown to be superior. With the present-day emphasis on mass isotopes, the tracer in human studies is often of a precursor, labeling most or all entry pathways. It is shown that for these tracer studies, models in the activities state space are always unidentifiable when there are multiple exit pathways, even if the enrichment in every pool is observed; on the other hand, the corresponding models in the enrichment state space have fewer parameters and are more often identifiable. Our results suggest that studies with labeled precursors are modeled best with enrichments.

1. Introduction

Many biological systems are studied by introducing a tracer, typically as a bolus or as a primed constant infusion, and following the tracer appearance and disappearance in one or more chemical species. The data are typically tracer enrichment (abundance, atoms percent excess) or specific radioactivity, e.g., d₃-leucine as tracer and data on d₃-leucine enrichment in plasma leucine and in circulating apolipoproteins. Tracer kinetics are studied typically by linear, stationary models. Hearon (1963), and later Bright (1973), pointed out that, when pool masses are constant, state variables can be the total tracer amounts (expressed in mass units, activities, etc.) in the pools, or the tracer concentrations (expressed as enrichments, specific activities, etc.) in the pools. However, modeling has been performed almost universally in terms of activities (Berman and Schoenfeld, 1956; Shipley and Clark, 1972; Rescigno and Michels, 1973; DiStefano 3rd, 1983; Chapman and Godfrey, 1985; Cobelli et al., 1987, 2000; García-Meseguer et al., 2003), and for good reason: the coefficients in the differential equations for activities are rate constants that express mass fluxes as fractions of the source pools, a natural definition in the context of the common assumption of first-order kinetics. This is not the case with enrichment modeling, where some coefficients do not have the same natural physical interpretation.

We focused instead on the fact that in most human tracer studies, measurements are of tracer enrichments or specific activities (SA), and looked at tracer kinetics models in the state space of enrichments compared to models in the state space of activities. We present both activity and enrichment (or SA) formulations for tracer studies and show that, for certain commonly encountered model structures, enrichment modeling has fewer parameters, and hence is better suited with respect to identifiability and parameter estimation. We find that there is an advantage, especially where there is direct removal of material from multiple pools, to modeling enrichments and not activities.

Enrichment and activity modeling are first compared in four simple, illustrative structures: the simple situation of calculating the fractional synthetic rate (FSR) in a single pool, then a simple two-pool cascade structure with direct material removal from both pools and tracer introduced as an exogenous bolus into the first pool or endogenously via a precursor, and finally a two-pool exchange structure with multiple outflows. Enrichment modeling is shown to be superior in each example—it leads to simpler formulations and fewer parameters, and consequently to identifiability when the commonly used activity models are unidentifiable.

The two-pool structures are followed by general n-pool structures, first for exogenous tracer studies, and then for endogenous tracer studies, which generalize FSR modeling. Finally, a duality is proved between activity and enrichment models to explain why one approach is better for certain structures and the other for others.

2. Preliminaries and notation

2.1. Definitions

The words “system,” “structure,” and “model” are used synonymously in the literature on identifiability of pool models, as seen in the seminal paper of Bellman and Åström (1970) as well as in the major review by Cobelli and DiStefano 3rd (1980). We believe it is useful to distinguish among (1) a biological system, (2) a structure with pools and pathways used to represent the system, and (3) a mathematical model for tracer kinetics when a tracer is introduced into the system. Thus, a pool structure abstracts the system into a set of interconnected pools and is completely described by a diagram, with no equations; the model contains the mathematical relationships needed to describe the structure.

We consider multicompartmental structures, i.e., structures made up of a number of compartments or pools, the material within each of which is assumed to behave identically (homogeneous). Tracer activity refers to the amount of tracer, typically expressed in units of mass or of radioactivity. Activity modeling refers to modeling (writing differential and algebraic equations for) tracer activities in different structural pools. Enrichment is expressed as the amount of tracer divided by the total of tracer and tracee. We use enrichment modeling to refer to modeling enrichments or equivalent quantities—tracer abundance in the form of atoms percent excess or a fraction, tracer-to-tracee ratio where appropriate, specific radioactivity in a study with a radiolabel. Activity modeling refers to the usual formulation of differential equations for the tracer amount, quantity or activity. Following the definition of local identifiability by Bellman and Åström (1970) and later by Chapman and Godfrey (1985), and dropping the word “local” for brevity, a model is identifiable if error-free data lead to a unique solution (or a finite number of solutions) for all the parameters in the model equations; a model is unidentifiable if one or more parameters are unidentifiable, i.e., have an infinity of possible values consistent with error-free data.

We consider a biological system that can be abstracted by a linear, stationary structure of n pools. Linear means that mass fluxes are linearly proportional to (i.e., a constant multiplied by) pool masses so that linear differential equations can describe the changes with time of tracer quantities in different pools. Stationary means the biological system is in a steady state and pool masses are not changing with time so that the differential equations for tracer quantities have only constant coefficients. The quantity or mass (tracer+tracee) of the ith pool is Q_i, and the quantity or activity of tracer q_i (t), and the tracer enrichment or SA is y_i (t) = q_i (t)/Q_i. Q_i is assumed to be constant, either because the tracer is radioactive, and hence of negligible mass or, in case of a stable isotope, the tracer enters the system via synthetic pathways unaffected by the introduction of the isotope (Garlick et al., 1994; Ramakrishnan, 2006). Some systems with mass isotopes have been modeled by considering the amount of tracee to be constant (Cobelli et al., 1987), especially in glucose kinetics (Basu et al., 2003). The results of the present paper will apply to those systems provided Q_i stands for the quantity or mass of tracee alone in the ith pool, and y_i (t) stands for the tracer-to-tracee ratio. Q_i may be unknown.

Tracer is introduced in one of two ways: as a bolus into one or more pools (e.g., if introduced into pool 1, q₁(0) = q₁₀, possibly unknown), or into a precursor structure with the tracer concentration of the immediate precursor known as a function of time, w(t). More generally, w(t) can be a vector in case of multiple immediate precursor pools; while we assume a scalar w(t) for simplicity of presentation, the results would hold for a vector w(t). The mass fluxes are F_ij into pool i from pool j, with the additional understanding of F_i0 as the direct inflow or synthesis into pool i, F_0j as the direct outflow or catabolism from pool j, and F_ii as the total flux through the ith pool (equal to the sum of all the individual fluxes into the ith pool, as well as to the sum of all the fluxes out of the ith pool).

Rate constants are defined conventionally as fluxes divided by source pool masses:

$$k_{ij}=F_{ij}/Q_j,k_{ii}=F_{ii}/Q_i$$ (1)

For convenience, which will become apparent presently, we also define

$$k_{i0}=F_{i0}/Q_i$$ (2)

The rate constant k_i0 is termed the fractional synthetic rate (FSR) in protein turnover.

An alternative, seldom used (Hearon, 1963), definition for rate constants is as fluxes divided by the destination pool masses:

$$r_{ij}=F_{ij}/Q_i,r_{ii}=F_{ii}/Q_i$$ (3)

with the additional definition for the fractional catabolic rates (FCR):

$$r_{0j}=F_{0j}/Q_j$$ (4)

It may be noted that k_ij expresses each flux as a fraction of its source pool mass so that the flux out of a pool, F_ij, is k_ij times Q_j, analogous to and consistent with first order reaction kinetics and mass diffusion models where the mass transport is proportional to the source mass. On the other hand, r_ij expresses the flux from j to i as a fraction of the destination pool mass and thus has no natural physical meaning. It is for this reason that modeling with k’s is nearly universal while modeling with r’s is virtually nonexistent (Rubinow and Winzer, 1971; Ramakrishnan et al., 1981, 1984; Anderson, 1983; Ramakrishnan, 1984).

The parameters k_ij and r_ij are strongly related. It is easily seen that

$$\begin{array}{l}{k}_{ii}=r_{ii},k_{i0}=r_{i0},k_{0i}=r_{0i}\\ k_{ij}=r_{ij}{Q}_i/Q_j,k_{ij}{k}_{ji}=r_{ij}{r}_{ji}\end{array}$$ (5)

The total flux out of the ith pool (= k_ii Q_i) must equal the total of all the fluxes from the ith pool to the other pools and to the outside (= k_ji Q_i summed over j):

$$k_{ii}=\sum _{\begin{array}{l}j=0\\ j\ne i\end{array}}^n{k}_{ji}$$ (6)

Also, the total flux into the ith pool (= r_ii Q_i) must equal the total of all the fluxes into the ith pool from the other pools and from the outside (= r_ij Q_i summed over j):

$$r_{ii}=\sum _{\begin{array}{l}j=0\\ j\ne i\end{array}}^n{r}_{ij}$$ (7)

Since k_ii = r_ii, it follows that

$$k_{ii}=\sum _{\begin{array}{l}j=0\\ j\ne i\end{array}}^n{k}_{ji}=r_{ii}=\sum _{\begin{array}{l}j=0\\ j\ne i\end{array}}^n{r}_{ij}$$ (8)

Also, writing Eq. (7) in terms of the k-parameters, and Eq. (6) in terms of the r-parameters, yields two more relationships:

$$k_{ii}{Q}_i=\sum _{\begin{array}{l}j=0\\ j\ne i\end{array}}^n{k}_{ij}{Q}_j$$ (9)

$$r_{ii}{Q}_i=\sum _{\begin{array}{l}j=0\\ j\ne i\end{array}}^n{r}_{ji}{Q}_j$$ (10)

Data are typically measurements of enrichments. The measurements may be made in single structure pools. Often, however, if the measurement technique cannot separate material in structural pools that occupy the same physical space, the measurement is of the weighted mean enrichment in multiple structure pools. For instance, Demant et al. (1996) consider model structures for apolipoprotein B in which each measurement typically is of the enrichment in two or three structural pools. [If tracer concentration in some unit volume is measured, e.g., dpm/ml plasma, we assume that it can be converted to SA on dividing by tracee concentration in the same unit volume.] We define an index set J_m that points to the pools whose enrichment is z_m(t). For instance, if z₂ is the enrichment in pool 4, then J₂ = {4} and z₂ = y₂; if z₆ is the combined enrichment in pools 5, 7, 8, 10, then J₆ = {5, 7, 8, 10} and $z_6=\frac{Q_5{y}_5+Q_7{y}_7+Q_8{y}_8+Q_{10}{y}_{10}}{Q_5+Q_7+Q_8+Q_{10}}$. We also define the masses of these responses:

$$M_m=\sum _{j\in J_m}{Q}_j$$ (11)

2.2. Two alternative models for the same structure

The differential equations for tracer kinetics in a pool structure can be written for q(t), the tracer activities in the pools, or for y(t), the tracer enrichments (or SA) in the pools. It is to be noted that there are two models for the same structure. The models are equivalent in that they describe the same biological processes and the same assumptions; a pictorial representation of the structure with pools and arrows would be the same for the enrichment and activity models. But the models are different in their state variables and model parameters so that the differential equations and the model solutions take different forms, which as we see below, can lead to one model being identifiable while the other is not. Each model describes a different state space, much as a change of variable in calculus.

We begin by noting that, by the assumptions of stationarity, linear relationships among the pool masses can be derived from flux balances for the ith pool:

$$0=F_{i0}+\sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^n{F}_{ij}-F_{ii}=k_{i0}{Q}_i+\sum _{\begin{array}{l}j=1\\ j\ne 1\end{array}}^n{k}_{ij}{Q}_j-k_{ii}{Q}_i$$ (12)

for the ith pool. We note that Eq. (9) above follows from this equation, which is referred to as the Q-model or as the tracee model (Pont et al., 1998).

The activity model differential equations are written readily (Cobelli and DiStefano 3rd, 1980). The rate of change in tracer activity in the ith pool is given by

$$\frac{{dq}_i(t)}{dt}=S_{i}w(t)+\sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^n{k}_{ij}{q}_j(t)-k_{ii}{q}_i(t)$$ (13)

The first term on the right side is tracer entry from the precursor into the ith pool; the second term is tracer entry from the other pools into the ith pool; the last term is tracer leaving the ith pool, going to other pools or to the outside. The quantity S_i is the synthetic flux into the ith pool from the precursor with enrichment w(t); S_i equals F_i0 = k_i0Q_i if all flux into the ith pool is labeled. The parallel to the steady-state equation (12) is apparent, making clear once again why activity modeling is natural.

For the enrichment model, the rate of change in tracer enrichment in the ith pool is derived from Eq. (13) (Ramakrishnan et al., 1984) by a change of variable q_j (t) = y_j (t)Q_j, using the relationships k_ij Q_j = r_ij Q_i from Eq. (5), and noting that, since the structure is stationary, Q_i ’s are constant:

$$\frac{{dy}_i(t)}{dt}=s_{i}w(t)+\sum _{\begin{array}{l}j=1\\ j\ne i\end{array}}^n{r}_{ij}{y}_j(t)-r_{ii}{y}_i(t)$$ (14)

The quantity s_i is S_i /Q_i, the fractional synthetic flux into the ith pool with enrichment w(t), equaling r_i0 if all flux into the i th pool is labeled.

The activities model is written readily in matrix-vector notation (Cobelli and DiStefano 3rd, 1980):

$$\frac{dq(t)}{dt}=Kq(t)+Sw(t),q(0)=q_o,\text{observe}z(t)=Cq(t)$$ (15)

where the matrix K, vector S, and matrix C are given by

$$\begin{array}{l}{K}_{ii}=-k_{ii},K_{ij}=k_{ij}\text{for}i\ne j,\\ S_i\text{is}\text{the}\text{labeled}\text{synthetic}\text{flux}\text{into}\text{the}i\text{th}\text{pool},\\ =k_{i0}{Q}_i\text{if}\text{all}\text{flux}\text{into}i\text{th}\text{pool}\text{is}\text{labeled},\\ C_{ij}=\{\begin{array}{ll}1/M_i\hfill & \text{if}j\in J_i\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\end{array}$$ (16)

The activities model is termed the q-model.

The enrichment model in matrix-vector notation is as below:

$$\frac{dy(t)}{dt}=Ry(t)+sw(t),y(0)=y_o,\text{observe}z(t)=Dy(t)$$ (17)

where the matrix R, vector s, and matrix D are given by

$$\begin{array}{l}{R}_{ii}=-r_{ii},R_{ij}=r_{ij}\text{for}i\ne j,\\ s_i=S_i/Q_i\\ =r_{i0}(\text{FSR}\text{of}\text{the}i\text{th}\text{pool})\text{if}\text{all}\text{flux}\text{into}\text{the}i\text{th}\text{pool}\text{is}\text{labeled}\\ D_{ij}=\{\begin{array}{ll}{Q}_j/M_i\hfill & \text{if}j\in J_i\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\end{array}$$ (18)

The enrichment model is termed the y-model.

Either model can be derived from the other by noting that

$$q(t)=Py(t)\text{where}P\text{is}\text{diagonal}\text{with}{P}_{ii}=Q_i,\text{i}.\text{e}.,P=\text{diag}(Q)$$ (19)

The state spaces for q(t) and y(t) are differentiable vector spaces of n-tuples of functions of time, isomorphic to each other. Equation (19) defines the transformation between the two state spaces.

It follows from Eqs. (5), (16), and (18) (as shown in Anderson, 1983, Section 9) that

$$K={\mathit{PRP}}^{-1},\text{and}S=Ps$$ (20)

Often, each response is the enrichment in a single pool, obviating the need for index sets J: If the mth response is the enrichment in the j th pool,

$$\begin{array}{l}{C}_{mj}=1/Q_j,D_{mj}=1\\ C_{mi}=D_{mi}=0\text{for}i\ne j\end{array}$$ (21)

The differential equation coefficients in a q-model (for activities) are k’s, rate constants in terms of source pool masses, while those in a y-model (for enrichments) are r ’s, rate constants in terms of destination pool masses. As noted above, a rate constant in terms of the source pool mass has a natural physical meaning, explaining why tracer kinetics models are almost always in terms of total activities, even though the data are generally of enrichments or specific activities.

3. Four simple illustrations of superiority of enrichment modeling

3.1. Modeling fractional synthetic rate

Consider the usual method of estimating an organ-specific protein synthetic rate constant or the fractional synthetic rate (FSR) of a particular protein (Zilversmit, 1960; Zak et al., 1979), modeled by a single pool, as shown in Fig. 1. The precursor is shown by a square, instead of the usual circle for a pool, to indicate that it is used as a forcing function known from precursor enrichment data, and that it is not necessarily a single pool. Note that, in this case, the parameter of interest itself is flux divided by the destination pool mass. The q-model is a single differential equation:

$$\frac{dq}{dt}=-kq+Sw,q(0)=0,w(t)\text{known},\text{observe}z(t)=q(t)/Q$$ (22)

Fig. 1.

A simple one-pool structure for a product of interest, with the tracer entering by a synthetic pathway from a precursor whose enrichment, w(t), is known. The precursor is denoted by a square to indicate an arbitrary model structure for the precursor. The synthetic rate is S, the mass of the product pool is Q, the tracer activity or amount in the product pool is q(t), the tracer enrichment or specific activity in the product pool is y(t), and the fractional synthetic (or catabolic) rate is k.

There are three parameters, k, S, Q. One is eliminated easily since S = kQ:

$$\begin{array}{l}\frac{dq}{dt}=k(Qw-q),q(0)=0,\\ w(t)\text{known},\text{observe}z(t)=q(t)/Q\end{array}$$ (23)

However, it is not actually possible to estimate Q from the data. This is easily seen with the y-model for the enrichment:

$$\frac{dy}{dt}=k(w-y),y(0)=0,w(t)\text{known},\text{observe}y(t)$$ (24)

A single parameter, k, is identifiable. This point is obscured by the formulation in the q-model.

This example is quite trivial as the q-model’s unidentifiability is manageable: Q can be set to an arbitrary value and k estimated from the enrichment data. The point to note is that the q-model unidentifiability is not apparent from Eq. (23). In the three examples that follow, setting a mass arbitrarily is not enough to make the k rate constants in the activity state space identifiable.

The generalized models for FSR are analyzed in Section 4.2 under Endogenous Tracer Studies.

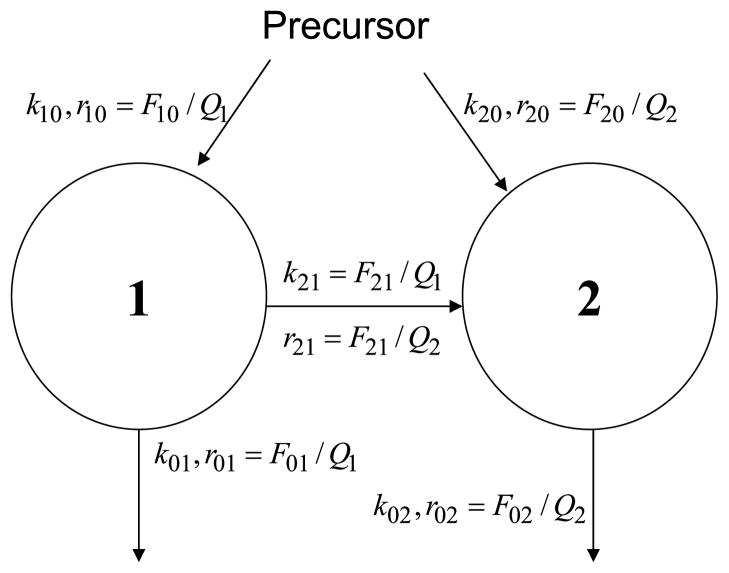
3.2. A two-pool cascade with entry and removal from both pools

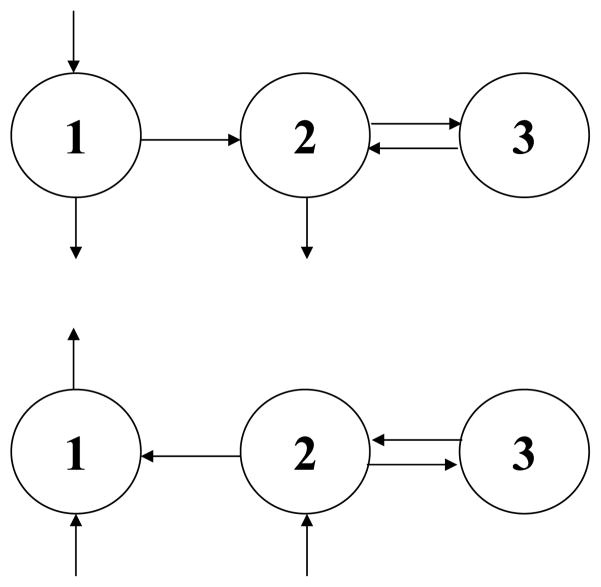
Consider the simple two-pool structure in Fig. 2, a great simplification of complex structures such as the delipidation cascade of very low density lipoproteins (VLDL) to intermediate density lipoproteins (IDL) (Packard et al., 2000; Barrett et al., 2006). Assume a known bolus tracer injection u into pool 1 at time zero, and enrichments in both pools observed. The y-model for enrichments involves two differential equations:

$$\begin{array}{l}\frac{{dy}_1}{dt}=-r_{11}{y}_1,y_1(0)=\frac{u}{Q_1}\\ \frac{{dy}_2}{dt}=r_{21}{y}_1-r_{22}{y}_2,y_2(0)=0\\ \text{Observe}{y}_1(t),y_2(t)\end{array}$$ (25)

Fig. 2.

A two-pool cascade structure with precursor feeding both pools and material exit from both pools. Two experimental designs are considered in the text, one with a bolus tracer injection into pool 1, and the other with a labeled precursor at constant enrichment as in Fig. 1. With data available on enrichments in both pools, the activity model is unidentifiable, but the enrichment model is identifiable. Next to each arrow is a definition for the corresponding rate constant in the activity model (k’s) and in the enrichment model (r’s).

The y-model has four parameters—three rate constants (r₁₁, r₂₁, r₂₂) and one mass (Q₁). The differential equations (25) are easily solved:

$$\begin{array}{l}{y}_1(t)=\frac{u}{Q_1}{e}^{-r_{11}t}\\ y_2(t)=\frac{{ur}_{21}}{Q_1}\frac{e^{-r_{22}t}-e^{-r_{11}t}}{r_{11}-r_{22}}\end{array}$$ (26)

It is readily seen that all four parameters can be estimated from the data: the two exponential rate constants are r₁₁ and r₂₂; the coefficient for y₁(t) leads to Q₁; the coefficients for y₂(t), equal in magnitude, lead to r₂₁.

The q-model for activities also involves two differential equations:

$$\begin{array}{l}\frac{{dq}_1}{dt}=-k_{11}{q}_1,q_1(0)=u\\ \frac{{dq}_2}{dt}=k_{21}{q}_1-k_{22}{q}_2,q_2(0)=0\\ \text{Observe}{y}_1(t)=\frac{q_1(t)}{Q_1},y_2(t)=\frac{q_2(t)}{Q_2}\end{array}$$ (27)

The activity model has five parameters, one more than the enrichment model—three rate constants (k₁₁, k₂₁, k₂₂) and two masses (Q₁, Q₂). But Eqs. (26) for the enrichments, which are observed, contain only four parameters—two exponential rate constants and two coefficients. Therefore, the activity model is unidentifiable while the enrichment model is identifiable. And the unidentifiability of the activity model is not obvious.

Further, unlike in the first example with FSR, it is not apparent how to deal with the unidentifiability. From Eqs. (5), we know that k₁₁ = r₁₁, k₂₂ = r₂₂. Therefore, from the analytical solutions in Eqs. (26), three parameters (k₁₁, k₂₂, Q₁) are identifiable, but what about k₂₁ and Q₂? How are they related to r₂₁, which is identifiable, and to the other parameters?

With the help of the results from the enrichment model, we can investigate k₂₁ and Q₂, the two unidentifiable parameters of the activity model, and determine what values they can assume consistent with the data. From Eqs. (5), we know that

$$\begin{array}{l}{k}_{21}{Q}_1=r_{21}{Q}_2,\text{but}{k}_{21}=k_{11}-k_{01}\\ \text{Therefore},k_{01}=k_{11}-r_{21}{Q}_2/Q_1\end{array}$$ (28)

The mass ratio Q₂/Q₁ and k₀₁, both unidentifiable, have a negative linear relationship involving r₂₁, an identifiable enrichment model parameter, as shown in Fig. 3.

Fig. 3.

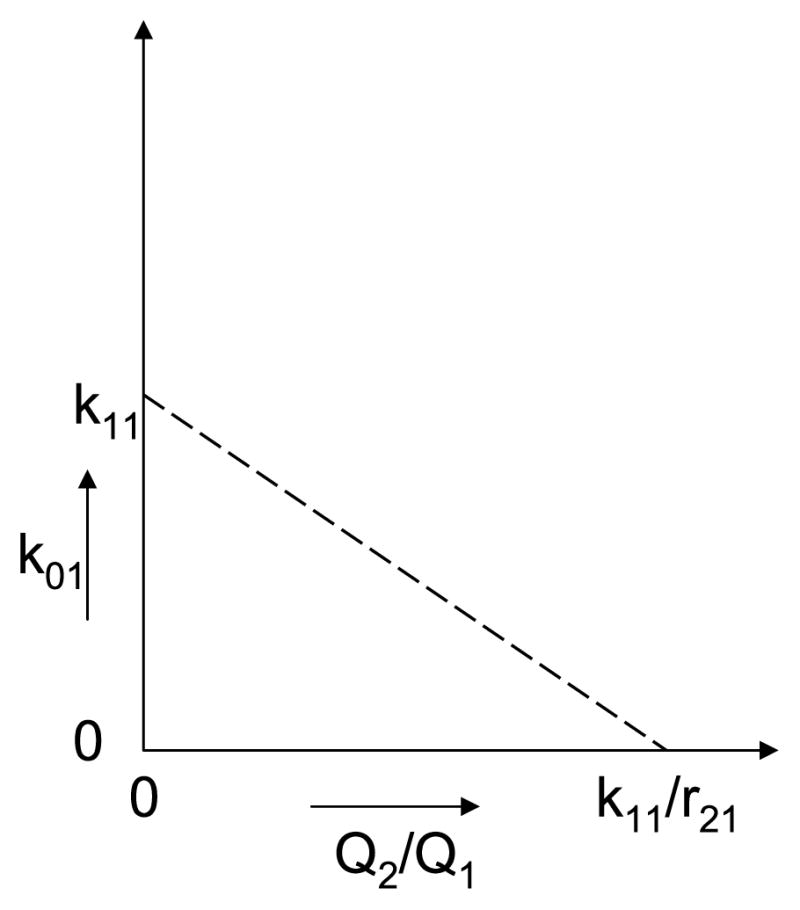
For the structure in Fig. 2, the dashed line shows how two unidentifiable parameters, the direct removal rate constant from pool 1 and the ratio of the two pool masses, can vary together. The removal rate constant, k₀₁, can take any value between 0 and k₁₁, while the mass ratio Q₂/Q₁ goes from a high of k₁₁/r₂₁ down to zero.

Thus, even if activity model parameters are of interest, we can first fit the data with enrichment modeling and estimate the identifiable Q₁, r₁₁, r₂₁, and r₂₂, three of which are activity model parameters as well, and then use Eqs. (5) to obtain a relationship between Q₂/Q₁ and k₀₁, the direct removal rate constant, as in Fig. 3. The activity model, on the other hand, is unidentifiable, so some simplification (e.g., setting k₀₁ = 0) is necessary even to fit the data. In contrast, no simplifying assumption is needed in the state space of enrichments.

3.3. Two-pool cascade with tracer entry from precursor

Consider again the two-pool structure in Fig. 2 but, instead of a bolus tracer injection into pool 1, tracer enters both pools from a precursor at constant enrichment, c, and enrichments in both pools are observed. Lipoprotein kinetics are typically studied by a primed constant infusion of a labeled amino acid so that the precursor enrichment may be assumed to be constant (Nagashima et al., 2005; Tremblay et al., 2006). The y-model for enrichments again involves two differential equations:

$$\begin{array}{l}\frac{{dy}_1}{dt}=r_{11}(c-y_1),y_1(0)=0\\ \frac{{dy}_2}{dt}=(r_{22}-r_{21})c+r_{21}{y}_1-r_{22}{y}_2,y_2(0)=0\\ \text{Observe}{y}_1(t),y_2(t)\end{array}$$ (29)

The y-model has three parameters—the rate constants r₁₁, r₂₁, r₂₂. The differential equations (29) are easily solved:

$$\begin{array}{l}{y}_1(t)=c(1-e^{-r_{11}t})\\ y_2(t)=c+\frac{{cr}_{21}}{r_{11}-r_{22}}{e}^{-r_{11}t}-\frac{c(r_{11}-r_{22}+r_{21})}{r_{11}-r_{22}}{e}^{-r_{22}t}\end{array}$$ (30)

The three rate constants (and, if needed, the precursor enrichment c) can be estimated by fitting the model to enrichment data from the two pools.

The q-model for activities also involves two differential equations:

$$\begin{array}{l}\frac{{dq}_1}{dt}=k_{11}(Q_{1}c-q_1),q_1(0)=0\\ \frac{{dq}_2}{dt}=(k_{22}{Q}_2-k_{21}{Q}_1)c+k_{21}{q}_1-k_{22}{q}_2,q_2(0)=0\\ \text{Observe}{y}_1(t)=\frac{q_1(t)}{Q_1},y_2(t)=\frac{q_2(t)}{Q_2}\end{array}$$ (31)

The activity model has five parameters, two more than the enrichment model—three rate constants (k₁₁, k₂₁, k₂₂) and two masses (Q₁, Q₂). We know from Eqs. (30) that only three parameters can be estimated from the data—three rate constants. Therefore, the activity model is unidentifiable while the enrichment model is identifiable.

Once again, it is not obvious how to deal with the unidentifiability of the activity model. From Eqs. (5), we know that k₁₁ = r₁₁, k₂₂ = r₂₂. Therefore, two parameters (k₁₁, k₂₂) are identifiable, but in order to estimate them, an identifiable model is needed; the enrichment model can be used for this purpose. We can analyze the other three using the results from the previous two examples. From the first example, with FSR, Q₁ is unidentifiable but can be set to an arbitrary value. From the second example, the mass ratio Q₂/Q₁ and k₀₁, both unidentifiable, have a negative linear relationship involving r₂₁, an identifiable enrichment model parameter, as shown in Fig. 3. As in the previous example, the choice of state space determines the identifiability of the tracer kinetics model.

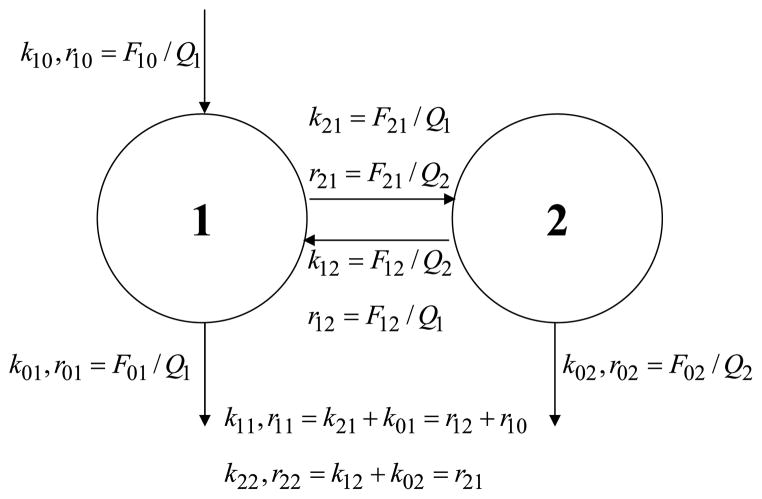
3.4. Two-pool exchange structure with removal from both pools

Consider the simple two-pool structure in Fig. 4. Assume a known bolus tracer injection u into pool 1 at time zero, and pool 1 enrichment observed. The y-model for enrichments involves two differential equations:

$$\begin{array}{l}\frac{{dy}_1}{dt}=-r_{11}{y}_1+r_{12}{y}_2,y_1(0)=\frac{u}{Q_1}\\ \frac{{dy}_2}{dt}=r_{22}(y_1-y_2),y_2(0)=0\\ \text{Observe}{y}_1(t)\end{array}$$ (32)

Fig. 4.

A simple two-pool exchange structure with tracee input into pool 1 alone but with removal from both pools. A bolus injection of tracer is made into pool 1, and the enrichment in pool 1 is observed. The activity model is unidentifiable, but the enrichment model is identifiable. Next to each arrow is a definition for the corresponding rate constant in the activity model (k’s) and in the enrichment model (r’s).

The y-model has four parameters—three rate constants (r₁₁, r₁₂, r₂₂) and one mass (Q₁). The solution is given by

$$\begin{array}{l}{y}_1(t)=\frac{u}{Q_1}\frac{({\lambda }_1-r_{22})e^{-{\lambda }_{1}t}+(r_{22}-{\lambda }_2)e^{-{\lambda }_{2}t}}{{\lambda }_1-{\lambda }_2}\\ \text{where}{\lambda }_1,{\lambda }_2=\frac{r_{11}+r_{22}}{2}\pm \frac{\sqrt{{(r_{11}+r_{22})}^2-4r_{01}{r}_{22}}}{2}\end{array}$$ (33)

It can be shown easily that the four parameters can be estimated from the two eigenvalues (λ₁ and λ₂) and the two exponential coefficients in y₁(t). The y-model is identifiable.

The q-model for activities also involves two differential equations:

$$\begin{array}{l}\frac{{dq}_1}{dt}=-k_{11}{q}_1+k_{12}{q}_2,q_1(0)=u\\ \frac{{dq}_2}{dt}=k_{21}{q}_1-k_{22}{q}_2,q_2(0)=0\\ \text{Observe}{y}_1(t)=\frac{q_1(t)}{Q_1}\end{array}$$ (34)

The activity model has five parameters, one more than the enrichment model—four rate constants (k₁₁, k₁₂, k₂₁, k₂₂) as opposed to three in the enrichment model, and one mass (Q₁). We know from Eq. (33) for the enrichment in pool 1 that only four parameters can be estimated from the data—two exponential rate constants and two coefficients. Therefore, the activity model is unidentifiable.

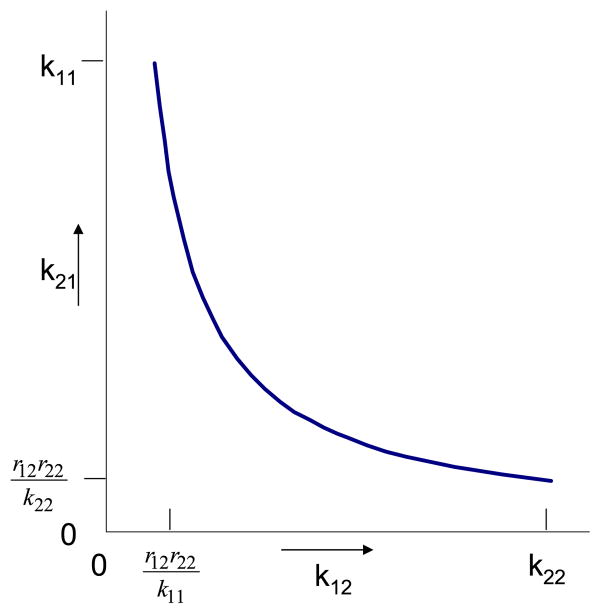
As in the previous examples, the identifiable enrichment model can be used to study the unidentifiable activity model. From Eqs. (5), we know that k₁₁ = r₁₁, k₂₂ = r₂₂. Therefore, three parameters (k₁₁, k₂₂, Q₁) are identifiable in the activity model. As for the other two, we know from Eqs. (5) that k₁₂k₂₁ = r₁₂r₂₁ = r₁₂r₂₂. This means that we can only estimate the product of the two exchange rate constants k₁₂ and k₂₁. Each has an upper bound: k₁₂ ≤ k₂₂; k₂₁ ≤ k₁₁. Since the product is fixed, each has a lower bound as well:

$$\frac{r_{12}{r}_{22}}{k_{11}}\le k_{12}\le k_{22},\frac{r_{12}{r}_{22}}{k_{22}}\le k_{21}\le k_{11}$$ (35)

The relationship between k₁₂ and k₂₁ is displayed in Fig. 5, a rectangular hyperbola. The product of the two unidentifiable activity model parameters, k₁₂ and k₂₁, equals the product of two identifiable enrichment model parameters r₁₂ and r₂₂.

Fig. 5.

For the structure in Fig. 4, the curve, a rectangular hyperbola, shows how k₁₂ and k₂₁, two unidentifiable parameters in the activity model, vary together. Their product is fixed (equal to the product r₁₂r₂₂). The smallest and largest values possible for each are indicated on the axes.

4. Enrichment and activity modeling compared in multicompartmental structures

We next consider some general n-pool structures where analytical solutions are not available but the relative merits of working in the q-space versus the y-space can be determined. Exogenous tracer studies are followed by endogenous tracer studies and then by a duality.

4.1. Modeling exogenous tracer studies

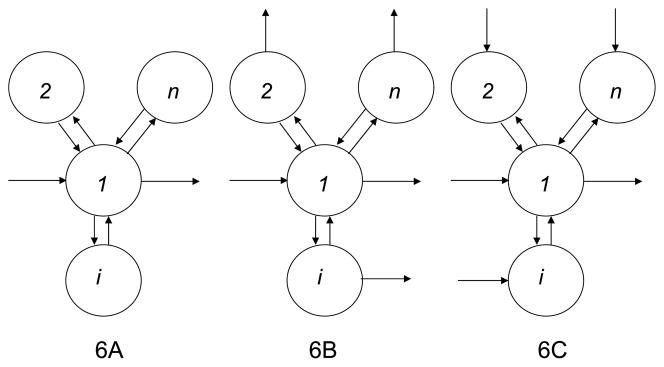
We contrast q- and y-modeling with mammillary structures; catenary and other structures will be shown to yield similar results. A mammillary structure, seen in Fig. 6, has a central pool that exchanges material directly with each of the other pools with no direct material flux between any other pools; a catenary structure is one that can be visualized on a line with each pool exchanging material directly only with the pool immediately to the left or to the right (Hart 1955, 1965). Consider an n-pool mammillary structure with a bolus injection of tracer into the central pool and the tracer enrichment (or specific activity) in that pool observed. In this case, w(t) is zero. The q-model becomes:

$$\begin{array}{l}\frac{dq(t)}{dt}=Kq(t),q(0)=\left[\begin{array}{c}\hfill q_o\hfill \\ \hfill 0\hfill \\ \hfill \cdots \hfill \\ \hfill 0\hfill \end{array}\right],\text{observe}z(t)=q_1(t)/Q_1\\ \text{where}{K}_{ii}=-k_{ii},K_{i1}=k_{i1},K_{1i}=k_{1i}\\ K_{ij}=0\text{for}i,j>1,i\ne j\end{array}$$ (36)

Fig. 6.

An n-pool mammillary structure studied by a bolus tracer injection into the central pool 1, and tracer enrichment measured in the same pool. Three possibilities are shown for material entry and exit in the peripheral pools 2, …, i, …, n. Figure 6A has all entry and exit solely in the central pool. Figure 6B has possible exit from all the pools but entry solely into the central pool. Figure 6C has possible entry into all the pools but exit solely from the central pool.

Alternatively, the y-model is

$$\begin{array}{l}\frac{dy(t)}{dt}=Ry(t),y(0)=\left[\begin{array}{c}\hfill y_o\hfill \\ \hfill 0\hfill \\ \hfill \cdots \hfill \\ \hfill 0\hfill \end{array}\right],\text{observe}z(t)=y_1(t)\\ \text{where}{R}_{ii}=-r_{ii},R_{i1}=r_{i1},R_{1i}=r_{1i}\\ R_{ij}=0\text{for}i,j>1,i\ne j\end{array}$$ (37)

The system matrices for the q-model and for the y-model, respectively, are

$$\left[\begin{array}{ccccccc}& k_{01}& k_{02}& \cdots & k_{0i}& \cdots & k_{0n}\\ k_{10}{Q}_1& -k_{11}& k_{12}& \cdots & k_{1i}& \cdots & k_{1n}\\ k_{20}{Q}_2& k_{21}& -k_{22}& \cdots & 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ k_{i0}{Q}_i& k_{i1}& 0& \cdots & -k_{ii}& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ k_{n0}{Q}_n& k_{n1}& 0& \cdots & 0& \cdots & -k_{nn}\end{array}\right]$$ (38)

$$\left[\begin{array}{ccccccc}& r_{01}& r_{02}& \cdots & r_{0i}& \cdots & r_{0n}\\ r_{10}& -r_{11}& r_{12}& \cdots & r_{1i}& \cdots & r_{1n}\\ r_{20}& r_{21}& -r_{22}& \cdots & 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ r_{i0}& r_{i1}& 0& \cdots & -r_{ii}& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ r_{n0}& r_{n1}& 0& \cdots & 0& \cdots & -r_{nn}\end{array}\right]$$ (39)

The matrices K and R have each been augmented by a column on the left to indicate pathways from the outside, and by a row at the top to indicate pathways to the outside. [This formulation extends the notation of Chapman and Godfrey (1985) who used an augmented row to account for fluxes to the outside.] Equations (5) provide relationships between K and R. With n pools, z(t) can be expressed by a sum of n exponentials, which means 2n parameters are identifiable.

We begin with the simplest flux configuration and proceed to more complex structures.

4.1.1. All tracee input and output in central pool

First, suppose that all tracee entry is into the central pool 1 (i.e., k_i0 = r_i0 = 0 for i > 1), and all removal is from that pool as well (i.e., k_0i = r_0i = 0 for i > 1), as shown in Fig. 6A. Applying Eq. (6) leads to k_ii = k_1i for i > 1, while Eq. (7) leads to r_ii = r_i1 for i > 1.

The system matrices for the q-model and for the y-model, respectively, are

$$\left[\begin{array}{ccccccc}& k_{01}& 0& \cdots & 0& \cdots & 0\\ k_{10}{Q}_1& -k_{11}& k_{22}& \cdots & k_{ii}& \cdots & k_{nn}\\ 0& k_{21}& -k_{22}& \cdots & 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& k_{i1}& 0& \cdots & -k_{ii}& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& k_{n1}& 0& \cdots & 0& \cdots & -k_{nn}\end{array}\right]$$ (40)

$$\left[\begin{array}{ccccccc}& r_{01}& 0& \cdots & 0& \cdots & 0\\ r_{10}& -r_{11}& r_{12}& \cdots & r_{1i}& \cdots & r_{1n}\\ 0& r_{22}& -r_{22}& \cdots & 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& r_{ii}& 0& \cdots & -r_{ii}& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& r_{nn}& 0& \cdots & 0& \cdots & -r_{nn}\end{array}\right]$$ (41)

For the q-model, there are 2n parameters—Q₁, k₁₁, and k_ii, k_i1 for i > 1. For the y-model, as well, there are 2n parameters—y₀, r₁₁, and r_ii, r_1i for i > 1. Thus, both models satisfy a necessary condition for the model to be identifiable. Cobelli et al. (1979) have shown that the q-model is identifiable; the y-model is identifiable from applying Eqs. (5):

$$r_{ii}=k_{ii},r_{10}=r_{01}=k_{01},r_{1i}=k_{i1}$$ (42)

4.1.2. All tracee input into central pool

We next consider a structure with outflows possible from all pools but entry only into the central pool, as shown in Fig. 6B. This means that while r_ii = r_i1 for i > 1 as in the simpler case, k_ii = k_0i + k_1i ≥ k_1i for i > 1. The system matrices for the q-model and for the y-model, respectively, are

$$\left[\begin{array}{ccccccc}& k_{01}& k_{02}& \cdots & k_{0i}& \cdots & k_{0n}\\ k_{10}{Q}_1& -k_{11}& k_{12}& \cdots & k_{1i}& \cdots & k_{1n}\\ 0& k_{21}& -k_{22}& \cdots & 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& k_{i1}& 0& \cdots & -k_{ii}& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& k_{n1}& 0& \cdots & 0& \cdots & -k_{nn}\end{array}\right]$$ (43)

$$\left[\begin{array}{ccccccc}& r_{01}& r_{02}& \cdots & r_{0i}& \cdots & r_{0n}\\ r_{10}& -r_{11}& r_{12}& \cdots & r_{1i}& \cdots & r_{1n}\\ 0& r_{22}& -r_{22}& \cdots & 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& r_{ii}& 0& \cdots & -r_{ii}& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0& r_{nn}& 0& \cdots & 0& \cdots & -r_{nn}\end{array}\right]$$ (44)

The y-model is identical to the simpler case in Fig. 6A with all tracee output from the central pool because r_0i ’s do not appear in the differential equations; not so for the q-model in which the presence of k_0i ’s makes it impossible to eliminate the k_1i ’s unlike in the simpler case. While the y-model still has only 2n parameters (y₀, r₁₁, and r_ii, r_1i for i > 1), the q-model has 3n − 1 parameters—Q₁, k₁₁, and k_ii, k_1i, k_i1 for i > 1. Again, we note that k_ii = r_ii from Eqs. (5), but k_1i = F_1i /Q_i, k_i1 = F_i1/Q₁, while r_1i = F_1i /Q₁, r_ii = F_i1/Q_i, and so the q-model has 2n − 2 unidentifiable parameters with the only constraints being k_1i k_i1 = r_1i r_ii. Each k_1i can assume a range of values ≤ k_ii with a corresponding value for k_i1.

DiStefano 3rd (1983) has derived bounds for the q-model parameters, but the identifi-ability of the y-model when all tracee input is into the central pool appears to be a novel result here.

4.1.3. All tracee output from central pool

We next consider a structure with entry possible into all pools but outflow only from the central pool, as shown in Fig. 6C. The system matrices for the q-model and for the y-model, respectively, are

$$\left[\begin{array}{ccccccc}& k_{01}& 0& \cdots & 0& \cdots & 0\\ k_{10}{Q}_1& -k_{11}& k_{22}& \cdots & k_{ii}& \cdots & k_{nn}\\ k_{20}{Q}_2& k_{21}& -k_{22}& \cdots & 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ k_{i0}{Q}_i& k_{i1}& 0& \cdots & -k_{ii}& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ k_{n0}{Q}_n& k_{n1}& 0& \cdots & 0& \cdots & -k_{nn}\end{array}\right]$$ (45)

$$\left[\begin{array}{ccccccc}& r_{01}& 0& \cdots & 0& \cdots & 0\\ r_{10}& -r_{11}& r_{12}& \cdots & r_{1i}& \cdots & r_{1n}\\ r_{20}& r_{21}& -r_{22}& \cdots & 0& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ r_{i0}& r_{i1}& 0& \cdots & -r_{ii}& \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ r_{n0}& r_{n1}& 0& \cdots & 0& \cdots & -r_{nn}\end{array}\right]$$ (46)

In this case, the q-model is identical to the simpler case in Fig. 6A with all tracee input into the central pool because k_i0’s do not appear in the differential equations; not so for the y-model in which the presence of r_i0’s makes it impossible to eliminate the r_i1’s unlike in the simpler case. The q-model has only 2n parameters (Q₁, k₁₁, and k_ii, k_i1 for i > 1), while the y-model has 3n − 1 parameters (y₀, r₁₁, and r_ii, r_1i, r_i1 for i > 1) with 2n − 2 unidentifiable parameters with the only constraints being k_ii k_i1 = r_1i r_i1. So, q-modeling is to be preferred in this case.

4.1.4. Catenary structures

The results are similar with general catenary structures. We assume tracer injection and observation in one of the two terminal pools, termed pool 1 for convenience. The system matrices K and R are tridiagonal: nonzero elements of the system matrix are on the diagonal, superdiagonal and subdiagonal for a total of 3n − 2, the same as in the mammillary structure. When all tracee input and outflow are in pool 1, each diagonal element other than the first can be expressed in terms of other elements—in the q-model, equal to the negative sum of the other elements in its column (as output from each pool goes only to other pools and not to the outside); and, in the y-model, equal to the negative sum of the other elements in its row (as tracee input into each pool comes only from other pools):

$$\begin{array}{l}{k}_{ii}=k_{i-1,i}+k_{i+1,i},r_{ii}=r_{i,i-1}+r_{i,i+1}\text{for}1<i<n\\ k_{nn}=k_{n-1,n},r_{nn}=r_{n,n-1}\end{array}$$ (47)

This decreases the number of distinct nonzero elements in the system matrix to 2n − 1 with both the q-model and the y-model. Both models are identifiable.

When all tracee input is into pool 1 but outflow is from multiple pools, the system matrix for the y-model is the same as with the simpler configuration but not for the q-model. And when all tracee outflow is from pool 1 but input is into multiple pools, the system matrix for the q-model is the same as with the simpler configuration but not for the y-model. Thus, the results for catenary structures parallel those for mammillary structures.

4.1.5. General pool structures

Considering a more general mammillary or catenary structure, with tracee input as well as outflow in multiple pools, it can be seen that both the q-model and the y-model have more than 2n and up to 3n − 1 parameters because neither the k_ii ’s nor the r_ii ’s can all be eliminated; neither is superior.

The above results for mammillary and catenary structures can be extended to arbitrarily general structures as follows. If a pool has tracee outflow to the outside, it is not possible to use Eq. (6) to express an element in that column in K in terms of the others, and so there is one more unknown parameter in K. On the other hand, if a pool has tracee inflow from the outside, it is not possible to use Eq. (7) to express an element in that row in R in terms of the others, and so there is one more unknown parameter in R. Thus, for exogenous tracers, enrichment modeling is superior when there are multiple exit pathways while activity modeling is superior with multiple unlabeled entry pathways. The results are different with endogenous labeling as shown in the next section.

4.2. Modeling endogenous tracer studies

We now consider experiments where most or all entry pathways are labeled by the use of a labeled precursor. With an endogenous tracer, if all synthetic pathways are labeled, s_i = r_i0 = k_i0 for all i. The precursor enrichment w(t) can be constant in a primed constant infusion study; in general, w(t) is a time-varying function assumed to be known. We consider a general n-pool structure with arbitrary connectivity with the enrichment in every pool observed. This is a generalization of the structure shown in Fig. 2 and analyzed in Section 3.3, as well as of the one-pool structure in Fig. 1 analyzed in Section 3.1. The q-model is as follows:

$$\left[\begin{array}{ccccccc}& k_{01}& k_{02}& \cdots & k_{0i}& \cdots & k_{0n}\\ k_{10}{Q}_1& -k_{11}& k_{12}& \cdots & k_{1i}& \cdots & k_{1n}\\ k_{20}{Q}_2& k_{21}& -k_{22}& \cdots & k_{2i}& \cdots & k_{2n}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ k_{i0}{Q}_i& k_{i1}& k_{i2}& \cdots & -k_{ii}& \cdots & k_{in}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ k_{n0}{Q}_n& k_{n1}& k_{n2}& \cdots & k_{ni}& \cdots & -k_{nn}\end{array}\right],\text{observe}z(t)=P^{-1}q(t)$$ (48)

In the system matrix above, the k_i0 can be eliminated by applying Eqs. (9). The k_0i do not appear in the model differential equations but, if any k_0i is zero, the corresponding k_ii can be set to the sum of the other k_ji ’s in that column by applying Eqs. (6); if k_0i is nonzero because of a clearance pathway out of pool i, the corresponding k_ii is an unknown parameter. The nQ_i ’s appear in the differential equations as well as in P to calculate the observed z(t). The number of unknown parameters to be estimated from the data is the number of nonzero off-diagonal elements (equal to m_a, the number of pathways among the pools) in K plus the number of pools n, plus m_c, the number of nonzero entries in the top row for clearance pathways, or m_a + n + m_c. This number is reduced if the Q_i ’s are not of interest. At least one Q_i can be set to an arbitrary value such as 1. If the matrix K can be partitioned into m_d disconnected blocks (i.e., no flux between blocks, i.e., i, j in different blocks implies k_ij = k_{j i} = 0), m_d of the masses can be set arbitrarily. Thus, the number of unknown parameters is m_a + n + m_c − m_d. We note that, since each block must have at least one outflow element in the top row, m_c ≥ m_d. If m_d > 1, the structure graph is not connected (Rescigno and Segre, 1964).

The y-model is as follows:

$$\left[\begin{array}{ccccccc}& r_{01}& r_{02}& \cdots & r_{0i}& \cdots & r_{0n}\\ r_{10}& -r_{11}& r_{12}& \cdots & r_{1i}& \cdots & r_{1n}\\ r_{20}& r_{21}& -r_{22}& \cdots & r_{2i}& \cdots & r_{2n}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ r_{i0}& r_{i1}& r_{i2}& \cdots & -r_{ii}& \cdots & r_{in}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ r_{n0}& r_{n1}& r_{n2}& \cdots & r_{ni}& \cdots & -r_{nn}\end{array}\right],\text{observe}z(t)=y(t)$$ (49)

In the system matrix above, the r_i0 can be eliminated as equal to ${\sum }_{j=1}^n-r_{ij}$. The removal rate constants r_0i do not appear in the model differential equations. The number of unknown parameters to be estimated from the data is just the number of nonzero elements in R, which is m_a + n.

Thus, the q-model has m_a + n + m_c − m_d parameters while the y-model has only m_a + n. Since the information content is the same, the number of parameters that can be uniquely identified cannot exceed m_a + n. If m_c = m_d, then the activity model is identifiable if the enrichment model is; the structure in Fig. 1, analyzed in Section 3.1, is an example, where the activity model is identifiable except for Q. However, with multiple exit pathways, m_c > m_d, and activity modeling results in an unidentifiable model, with more parameters than can be identified from the data. As an example, for the structure shown in Fig. 2 and analyzed in Section 3.3, n = 2, m_a = 1, and m_c = 2, so that, as shown in Section 3.3, the q-model with m_a + m_c + n = 5 parameters (k₁₁, k₂₁, k₂₂, Q₁, Q₂), only one (m_d = 1) of which (Q₁) can be set arbitrarily, is unidentifiable, while the y-model with only m_a + n = 3 parameters (r₁₁, r₂₁, r₂₂) is identifiable.

4.3. Duality in flux balances between modeling activities and enrichments

Pool model parameters are masses and rate constants. Flux balances around the pools provide relationships among the parameters, which can be used to decrease their number by expressing some parameters in terms of the others, as in Section 4.2 to analyze endogenous tracer studies. Here, we manipulate the flux balances for a general pool structure and show a duality between modeling activities and modeling enrichments.

The flux balances are simple to state: for each pool, the total of all the individual fluxes into that pool must equal the total flux out of that pool and, in turn, the total of all the individual fluxes from that pool.

With the matrix K for rate constants in modeling activities, using the relationships between K_ij and k_ij in Eqs. (16), we can rewrite Eqs. (9) for the total of the individual fluxes into the ith pool in matrix-vector notation as follows:

$$KQ+Pf=0$$ (50)

where Q is the vector of pool masses; P is a diagonal matrix whose iith element is Q_i, i.e., P = diag(Q); and f is the vector of outside entry rate constants (f_i = k_i0 = r_i0).

Equation (6) for the total of the individual fluxes from the ith pool to the other pools and to the outside becomes:

$$K^{T}u+g=0$$ (51)

where K^T is the transpose of K; u is a vector whose every element is 1; and g is the vector of removal rate constants (g_i = k_0i = r_0i).

Proceeding similarly with the matrix R for rate constants in modeling enrichments, using the relationships between R_ij and r_ij in Eqs. (18), we can rewrite Eq. (7) for the total of the individual fluxes into the ith pool in matrix-vector notation as follows:

$$Ru+f=0$$ (52)

Equation (10) for the total of the individual fluxes from the ith pool to the other pools and to the outside becomes:

$$R^{T}Q+Pg=0$$ (53)

where R^T is the transpose of R; and the other symbols are as explained for Eqs. (50) and (51).

Equations (50)–(51) and (52)–(53) are quite distinct. However, there is a structural similarity between Eqs. (50) and (53), and between (51) and (52).

Consider a dual of a structure, obtained by reversing every pathway. An entry from the outside to the ith pool becomes a path to the outside from the ith pool; a path to the outside becomes an entry in from the outside; a flux from pool j to pool i becomes a flux from pool i to pool j. Denoting the parameters of the dual structure by the prime symbol (′), Eqs. (50)–(51) become for the dual q-model:

$$K^{\prime }Q+P{f}^{\prime }=0,{K^{\prime }}^{T}u+g^{\prime }=0$$ (54)

But since, by definition:

$$K^{\prime }=K^T,R^{\prime }=R^T,f^{\prime }=g,g^{\prime }=f$$ (55)

we get, substituting these equalities into Eqs. (54) for the dual structure:

$$K^{T}Q+Pg=0,Ku+f=0$$ (56)

which are identical to Eqs. (52)–(53) for the original structure with R.

Likewise, substituting the equalities in (55) into Eqs. (52)–(53) for the dual y-model, we get

$$R^{T}u+g=0,RQ+Pf=0$$ (57)

which are identical to Eqs. (50)–(51) for the original structure with K.

Thus, the flux balances for the dual q-model and for the original y-model are identical. Likewise, the flux balances are identical for the dual y-model and for the original q-model.

4.3.1. An illustration of duality

As an illustration, consider the three-pool structure in Fig. 7A. The flux balances for the activities model lead to:

$$\begin{array}{l}{k}_{11}=k_{01}+k_{21},k_{22}=k_{02}+k_{32},k_{33}=k_{23},\\ k_{11}=k_{10},k_{22}{Q}_2=k_{21}{Q}_1+k_{23}{Q}_3,k_{33}{Q}_3=k_{32}{Q}_2\end{array}$$ (58)

Fig. 7.

An example of duality as defined here: each structure is obtained from the other by reversing all the pathways. The flux balances for an activities model are the same as those for the enrichment model of its dual, and vice versa.

Next, consider the dual structure in Fig. 7B; note that every path in this figure is the opposite of a corresponding path in Fig. 7A. The flux balances for the enrichment model leads to:

$$\begin{array}{l}{r}_{11}=r_{10}+r_{12},r_{22}=r_{20}+r_{23},r_{33}=r_{32}\\ r_{11}=r_{01},r_{22}{Q}_2=r_{12}{Q}_1+r_{32}{Q}_3,r_{33}{Q}_3=r_{23}{Q}_2\end{array}$$ (59)

Equations (58) and (59) can each be obtained from the other by interchanging “r” and “k,” and reversing all subscripts (i.e., “ij” by “ji”). A similar duality can be shown between the flux balances for the enrichment model for Fig. 7A and the activities model for Fig. 7B.

This duality helps to explain the differences between Figs. 6B and 6C. We saw that enrichment modeling was superior for the structure in Fig. 6B, while activity modeling was superior for the structure in Fig. 6C. The two structures are duals of each other. This means that the flux equations for the activities model for Fig. 6B are identical to those for the enrichment model for Fig. 6C. Thus, since the activities model is unidentifiable for Fig. 6B, the enrichment model is similarly unidentifiable for Fig. 6C.

5. Discussion

5.1. Paradox of identifiable and unidentifiable models for same structure

It may appear paradoxical that a biological system, with a specific configuration of pools and pathways and a specific tracer injection/observation study design, can have an unidentifiable as well as an identifiable model. In each of the four examples in Section 3, the structure being modeled was the same, shown in Figs. 1, 2, and 4, but the activity model was unidentifiable while the enrichment model was identifiable. The reason is that the same structure can be modeled in two different state spaces—the space of activities as state variables or the space of enrichments as state variables. Each state space induces a distinct parameter space. The dimensionality of the two parameter spaces may be different, depending on the pathways among the structure pools and the study design (how the tracer is introduced, which enrichments are observed).

We have shown in Section 4.2 that, particularly with endogenous tracer studies, which are widely used, enrichment modeling is to be preferred because the dimensionality of its parameter space is smaller.

Another way to understand this is that following the definition of Cobelli and DiStefano 3rd (1980), the identifiability of a model is determined by just those parameters that appear in the differential and observation equations and initial conditions. Parameters that do not appear thus, and there may be many such, do not influence the identifiability of the model. Thus, in the first example, in Section 3.1, the enrichment model in Eq. (24) has just one parameter, the rate constant k. It is not that the pool mass Q and flux S are not system parameters, but they do not appear in the enrichment model and so their unidentifiability does not affect the enrichment model’s identifiability. On the other hand, the activity model, in Eq. (23), contains the pool mass Q as well and is, therefore, unidentifiable. Similarly, for either of the two examples in Fig. 2, analyzed in Sections 3.2 and 3.3, the enrichment model is identifiable though the direct removal rate constant r₀₁ is unidentifiable; this is because r₀₁ does not appear in the enrichment model given by Eqs. (25) or (29).

It should be noted here that what we propose is not reparameterization. Rather, the state space is transformed, in a manner analogous to change of variable in calculus, so the model is in a completely different state space, which in turn induces a different parameter space of possibly different dimensionality.

5.2. Limitations of enrichment modeling

The most important limitation of enrichment modeling is that it relies on the stationarity assumption to replace the conventional k parameters with the r parameters. In Eqs. (5), which express the relationships between the k and r parameters, k_ij equals r_ij multiplied by the ratio of two pool masses. In a stationary structure, the pool masses, and consequently their ratios, do not change with time and so the r_ij parameters are constant and enrichment modeling is useful. However, if the structure is nonstationary, the pool masses, as well as their ratios, may be changing with time, which means the r_ij parameters are changing with time even if the k_ij parameters are constant with time, which makes enrichment modeling using r_ij not useful. Linearity is also required but this assumption is likely to be satisfied in tracer studies: even if the tracee system is nonlinear, the differential equations for the tracer are linear.

Also, as shown in Sections 4.1.3 and 4.1.5, with exogenous tracers and multiple unlabeled inputs into the structure, activity modeling can have fewer parameters and may be the preferred approach. This is much less common with the increasing use of mass isotopes and the use of labeled precursors to achieve endogenous labeling, which means most if not all input pathways are labeled.

The obvious fact should also be noted that any parameters that are unidentifiable in the activity model remain unidentifiable with enrichment modeling. When the focus of interest is an unidentifiable k parameter, enrichment modeling can first fit the observed data and estimate the identifiable r parameters, and the numerical values used to construct useful relationships for the unidentifiable k parameters of interest. This approach was illustrated in Section 3.2 with Fig. 3 for the structure in Fig. 2, and in Section 3.4 with Fig. 5 for the structure in Fig. 4.

5.3. Relationship to earlier work in pool model identifiability

An important paper by DiStefano 3rd (1983) introduced the idea of quasi-identifiability. The main example of an unidentifiable model in that paper was a mammillary model with tracer input into the central pool and exit pathways from all the pools—the model shown here in Fig. 6B, except that DiStefano’s model is more general in not specifying tracee input, thus allowing for tracee input into multiple pools, not just in the central pool as in Fig. 6B. The author derived the transfer function, solved for the k parameters in terms of the system eigenvalues and transfer function coefficients in order to determine what combinations of the k parameters are identifiable, and constructed bounds on the others. The algebraic expressions are quite complicated. We have shown here that, when the modeling is done with enrichments, the elements of the matrix R are identifiable when all tracee input is into the central pool. The other parameters, the removal rate constants r_0i and the mass ratios Q_i /Q₁ are indeed unidentifiable, but their bounds can be derived in a manner similar to what was done here for the structure in Fig. 2, as shown in Fig. 3. Neither DiStefano nor Cobelli and Toffolo (1984), who commented critically, noted that the structure could be analyzed in a much simpler fashion by enrichment modeling if all tracee could be assumed to enter the central pool.

DiStefano’s work on quasi-identifiability was followed by papers from his group on algorithms for the identifiable parameter combinations and parameter bounds of unidentifiable mammillary structures (Landaw et al., 1984) of the type shown in Fig. 6B here, and similarly for catenary structures (Chen et al., 1985; DiStefano 3rd et al., 1988), and later on the effects of measurement errors (Lindell et al., 1988) and fixing some rate constants (Vicini et al., 2000) on these parameter bounds. Chau (1985) considered more general bolus-introduction and observation situations in mammillary structures of the type in Fig. 6B. Cobelli and coworkers (Cobelli et al., 1984; Ferrannini et al., 1985; Gastaldelli et al., 1997) studied glucose kinetics and developed relationships among unidentifiable parameters in three-pool mammillary structures with all tracee input into the central pool. The examples given in the glucose papers can all be studied much more easily by enrichment modeling since the models are identifiable in the enrichment state space.

5.4. Utility in parameter estimation

Going beyond identifiability analysis, the knowledge that certain combinations of rate constants in an activity model are identifiable is not helpful when the aim is to estimate parameters for a given study, because a model has to be identifiable for an iterative estimation algorithm to work well. Vajda (1984), Cobelli and Toffolo (1987), and Vajda et al. (1989) suggested constructing “submodels,” typically obtained by setting some of the outflows (k_0i) to zero so that the model is made identifiable. Parameter estimates of the identifiable submodels are used to construct bounds on the parameters of the original unidentifiable model. In contrast, with the state space transformation approach proposed here, the tracer enrichment data can be fitted by an identifiable enrichment model, and the resulting parameter estimates for the elements of R used in Eqs. (5) to calculate identifiable rate constants, and to develop bounds for the unidentifiable rate constants, in the activity model, as illustrated in Section 2 and in Figs. 3 and 5. This approach is not feasible in the activity state space, as seen in the many papers referenced above. It is to be noted that enrichment modeling is quite different from, say, fitting enrichment data by sums of exponentials.

5.5. Impact of pool mass measurements

If all pool masses are known through measurements, activity and enrichment models are equivalent: if one is identifiable, so is the other; if one is not, the other is not as well. In all four examples in Section 3, the activity model would be identifiable if all the pool masses were known. Even in such structures, it may be of interest to know which parameters are identifiable without the mass data, and which require mass measurements. We have considered this question elsewhere (Ramakrishnan and Ramakrishnan, 2008). Enrichment modeling can help answer the question, as in the examples considered here.

5.6. Prior use of enrichment modeling

Rubinow and Winzer (1971) described both activity and concentration models and used the equivalents of the rate constants r_ij defined here, noting that it “represents the rate of transport of material from the jth compartment to the ith compartment, per unit amount of material in the ith compartment. Such a quantity is not of particular physical or physiological interest, but it is mathematically convenient.” Bright (1973) allowed for the state equations to be in terms of activities or enrichments, with the corresponding equivalents of k_ij and r_ij defined here. Perl et al. (1975), while modeling indicator kinetics, mentioned that the analog with tracers would be specific activities. Hearon (1974) used the analog of the R matrix here to prove a result in open linear systems. Anderson (1983, Section 25) derived the y-model and used it to study catenary structures. Jacquez (1985a) worked out a number of examples with specific-activity modeling but using the k-rate constants and mass ratios. A review of the literature since Hearon’s (1963) early observation on the equivalence of activity and enrichment modeling turns up no other publication with enrichment modeling in tracer kinetics outside of our group at Columbia University (Ramakrishnan et al., 1981, 1984; Ramakrishnan, 1984; Arad et al., 1990; Berglund et al., 1998; Nagashima et al., 2005). The use of activity models has been so universal that even authors who have studied identifiability questions and made major contributions (Jacquez, 1985b; Berman et al., 1962; DiStefano 3rd, 1983; Chapman and Godfrey, 1985; Jacquez and Simon, 1993; Eisenfeld, 1996) have not looked at enrichment modeling as an alternative approach to the problem, including in a book devoted to identifiability (Walter, 1987) or in a journal volume concerned with the work of Bellman (Jacquez, 1985a).

5.7. Relationship to pharmacokinetics

A major distinction in pharmacokinetics is that, unlike in tracer kinetics, there is no tracee. Activity modeling is easily extended to pharmacokinetics since the quantity of a drug in a pool is analogous to the quantity of a tracer in a pool. Rate constants are defined simply as fractions of the amount of drug in the source pool, and Eq. (6) relates k_ii to k_{j i} ; the equation can be derived, without recourse to any tracee, from a balance between the drug flux leaving the ith pool (= k_ii q_i) and the total of all the drug fluxes from the ith pool to the other pools and to the outside (= k_ji q_i summed over j). State equations are similar to Eqs. (15) except for S.

The analog of enrichment modeling in pharmacokinetics is to model drug concentrations, but the r-parameters are not useful. Since there is no tracee and consequently no tracee steady state, Eq. (7) relating r_ii to r_ij does not hold. Without this equation, there is no simplification and the matrix R will always have more parameters than the matrix K. Thus, Evans et al. (2004) modeled drug concentrations in cell studies with k-rate constants and volume ratios.

While it is risky to speculate on the development of ideas, it seems to us that one reason for researchers not pursuing enrichment modeling in tracer kinetics may be that pharmacokinetics was a major area of modeling. Early books on kinetics covered drugs as well as tracers (Jacquez, 1985b; Rescigno and Segre, 1966; Shipley and Clark, 1972). Models were written for the tracer; arrows in figures denoted tracer fluxes. Unlabeled tracee fluxes into the structure were not even shown since they did not appear in differential equations for the tracer (Brown and Godfrey, 1978; Cobelli and DiStefano 3rd, 1980; Chapman and Godfrey, 1985).

5.8. Nature of observations and choice of model

Anderson (1983, Section 9) remarked: “In the first and probably most common type of experiment, the concentration of tracer in one or more compartments is followed and sampled over time. Thus, it is preferable to have our basic tracer model in a form involving tracer concentrations rather than amounts.” So, tracer enrichments should be the natural choice as state variables in order to keep the modeling straightforward, with the minimum number of parameters needed to solve for the observed variables. The commonly used state variables are total tracer quantities. The differential equations involve pool masses in tracer entry expressions and also in calculating the observed enrichments from the total tracer quantities. As a consequence, total activity modeling involves more parameters, making the model unidentifiable and estimation more complex. By modeling enrichments directly, studying identifiability is facilitated.

The main reason for total activity modeling is that the rate constants have a natural physical meaning. But we have seen that the rate constants from enrichment modeling are related to those from activity modeling through mass ratios, as given in Eqs. (5). In particular, as shown there, fractional catabolic rates (FCR), fractional synthetic rates (FSR) and pool turnover rate constants, which are the rate constants of greatest biological relevance, are the same with either type of model:

$$k_{0i}=r_{0i},k_{i0}=r_{i0},k_{ii}=r_{ii}$$

Further, Eqs. (5) express the other k parameters in terms of the identifiable r parameters and mass ratios.

It may also be noted that, with the increasing use of precursor tracers, FSR’s are routinely estimated and reported in the protein literature; FSR is a rate constant expressing a synthetic or input flux as a fraction of the destination pool. Thus, rate constants as defined in enrichment models are in fact considered to have physical meaning.

5.9. Conclusion

A number of general linear, stationary structures were analyzed here. When there are multiple exit pathways, the q-model for total activities has many more parameters, whether the tracer is introduced as an exogenous bolus or by endogenous labeling through a precursor. The only situation in the linear, stationary setting where q-modeling has fewer parameters, and is the preferred approach, is with an exogenous tracer and multiple unlabeled tracee entry pathways. Tracer methodology in humans increasingly makes use of mass isotopes and highly sensitive mass spectrometry so that there are now hardly any radiotracer studies in humans. Mass isotopes are often introduced in a precursor—amino acids to study proteins, for example. The resulting structures are of the type described above under endogenous modeling, where most or all the entry pathways are labeled. It was seen that total activity modeling offers no benefit—enrichment modeling has fewer parameters and is to be preferred. SAAM, a popular modeling program, does only total activity modeling and finds the structure in Fig. 2 to be unidentifiable.

To conclude, when the data to be fitted are of enrichments, and especially when the activity model is unidentifiable for the chosen model structure, it may be helpful to write the model with enrichments as the state variables, defining rate constants as fluxes divided by the masses of destination pools. This unconventional definition facilitates modeling enrichment data from linear, stationary structures.

Abbreviations

F

flux

f

vector of rate constants for entry from outside

FCR

fractional catabolic rate

FSR

fractional synthetic rate

g

vector of rate constants for exit to outside

K,R

system matrix of rate constants

k,r

rate constant

P

diagonal matrix of pool masses

Q

total mass or activity of tracer+tracee

q

mass or activity of tracer

q-model

model for tracer activities or amounts

S

synthetic flux

s

synthetic rate constant

t

time

u

a vector whose every element is 1

w

precursor enrichment

y

tracer enrichment

y-model

model for tracer enrichments or specific activities

z

observed tracer enrichment