Intrinsic contribution of the 2′-hydroxyl to RNA conformational heterogeneity

Abstract

Canonical duplex RNA assumes only the A-form conformation at the secondary structure level while, in contrast, a wide range of non-canonical, tertiary conformations of RNA occur. Here, we show how the 2′-hydroxyl controls RNA conformational properties. Quantum mechanical (QM) calculations reveal that the orientation of the 2′-hydroxyl significantly alters the intrinsic flexibility of the phosphodiester backbone, favoring the A-form in duplex RNA when it is in the base orientation and facilitating sampling of a wide range of non-canonical, tertiary structures when it is in the O3′ orientation. Influencing the orientation of the 2′-hydroxyl are interactions with the environment as evidenced by crystallographic survey data, indicating the 2′-hydroxyl to sample more of the O3′ orientation in non-canonical RNA structures. These results indicate that the 2′-hydroxyl acts as a “switch” both limiting the conformation of RNA to the A-form at the secondary structure level, while allowing RNA to sample a wide range of non-canonical tertiary conformations.

Introduction

Awareness of the “RNA world” is expanding due to the continual identification of novel RNA molecules involved in a wide range of biological phenomena^1–3. Understanding the structure-function relationship is essential as many RNAs require distinct tertiary structures for their biological functions that often, as in the case of riboswitches⁴ or ribozymes⁵, involve significant changes in tertiary structure⁶. The range of tertiary structures sampled by RNA is significantly larger than with DNA, although at the secondary structure level the opposite is true, with RNA assuming primarily the A-form and DNA assuming the A, B and Z forms, amongst others⁷. Accordingly, a detailed understanding of the role of the 2′-hydroxyl in the structural heterogeneity of RNA is key to understanding the differences in the conformational properties of RNA and DNA.

The conformational flexibility of a molecule is dictated by a combination of its intrinsic or mechanical energy and interactions with the surrounding environment. In the case of oligonucleotides, the conformational properties are largely defined by the five backbone dihedral degrees of freedom (α: P-O5′, β: O5′-C5′, γ: C5′-C4′, ε: C3′-O3′, and ζ: O3′-P), sugar puckering, and the glycosidic linkage, χ, connecting the sugar to the base⁷. The conformation of RNA is additionally defined by the C2′-O2′ dihedral. In the present work, we use quantum mechanical (QM) methods to investigate how the presence of the 2′-hydroxyl influences the intrinsic conformational flexibility of the phosphodiester backbone. This knowledge is then combined with crystallographic survey data on RNA, from which a model of how interactions of the 2′-hydroxyl with the environment allow for changes in the orientation of that moiety, thereby impacting the intrinsic conformational properties of the phosphodiester backbone. This model, supported by additional QM calculations, allows for an understanding of how the 2′-hydroxyl acts as a conformational switch leading to the diminished heterogeneity of duplex RNA as compared to duplex DNA, while allowing access to wider range of non-canonical, tertiary conformations.

Methods

QM calculations were performed on R3PS (Fig. 1), a small molecule representative of the phosphodiester backbone in RNA, which is analogous to T3PS, a model compound for the phosphodiester backbone of DNA that lacks the 2′-hydroxyl moieties used in our previous study⁸. Data from that previous study are included in the present study to facilitate comparison of the intrinsic conformational flexibility of RNA versus DNA. The initial geometries for R3PS were generated using the program CHARMM⁹ with the additive CHARMM27 all-atom nucleic acid force field^10,11. Potential energy surfaces for the compounds were obtained via QM optimization at the MP2/6-31+G(d) level using the Gaussian03 package¹² followed by single point energy calculations at the RIMP2/cc-pVTZ level using the program QCHEM¹³.

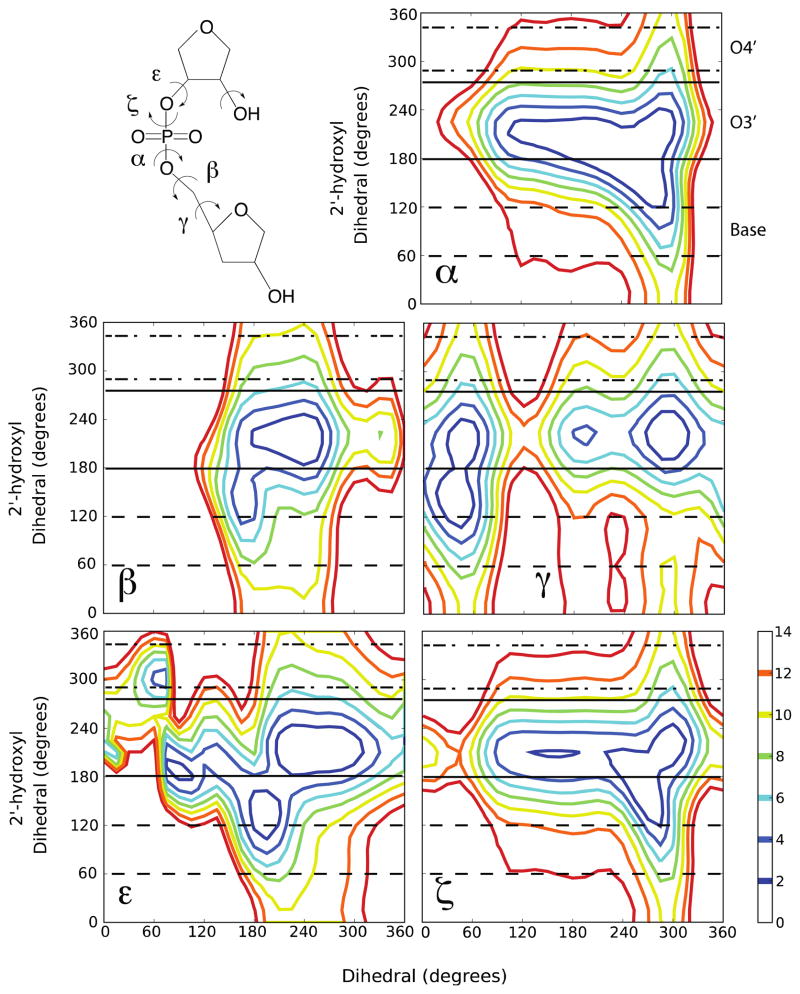
Figure 1.

Model compound, R3PS, used in the QM calculations and the 2D QM potential energy surfaces (phosphodiester α, β, γ, ε, or ζ torsions vs. 2′-hydroxyl) for R3PS obtained at the MP2/6-31+G(d)//RIMP2/cc-pVTZ level of theory. The energy scale is in kcal/mol. [The 2′-hydroxyl dihedral is defined as C1′-C2′-O2′-H2′ and the 2′-OH three orientations ranges are as follows: base (60° to 120° - dashed lines), O3′ (190° to 270° - solid lines) and O4′ (280° to 330° - dot-dashed lines).]

Previously, for T3PS a series of one-dimensional backbone dihedral energy scans were performed. The target dihedral was scanned in increments of 15° and all degrees of freedom were allowed to relax except for the dihedrals that define the A, B_I and B_II forms of DNA (Supplementary Table S1). The dihedral constraints were defined based on previous research^14–17 and selected to sample energy surfaces of the target dihedrals consistent with the A, B_I, or B_II forms of DNA. For RNA, two-dimensional (2D) QM scans were performed, where one dimension was the target backbone dihedral and the second dimension was the 2′-hydroxyl dihedral (defined as C1′-C2′-O2′-H2′). QM calculations were performed in a manner similar to those used for T3PS in terms of the degree increments and dihedral constraints with the addition of a 2′-hydroxyl constraint.

Survey data was obtained from the Protein Databank (PDB)¹⁸. The survey results were extracted from DNA and RNA crystallographic structures at a resolution ≤ 2.5 Å (Supplementary Tables S2 and S3). The selected structures do not contain DNA/RNA hybrids, protein, ligands, or chemical modifications. The probability distributions for the backbone torsions and the sugar pucker were calculated from the survey data using MDAnalysis¹⁹. A total of 80 DNA structures (975 nucleotides) and 60 RNA structures (801 nucleotides) were used, where the canonical RNA regions were defined as a WC base-paired duplex region with a minimal length of four nucleotides and the non-canonical RNA regions were defined as those regions not fitting the canonical description. The procedure yielded 405 canonical and 396 non-canonical nucleotides.

3D probability distributions of water oxygens around RNA nucleotides were calculated by aligning the sugar (C1′, C2′, C3′, C4′, and O4′ atoms) of each nucleotide to a template structure (Supplementary Fig. S1). Crystallographic water molecules within 5 Å of the nucleotide were then identified. The water oxygen 3D probability distributions for the canonical and non-canonical structures were then generated within MDAnalysis using the density_from_Universe function and a grid spacing of 1 Ź⁹. The 3D probability distributions were normalized relative to the total number of nucleotides used to generate the final probability distributions, such that a probability of 1 indicates that voxel to be occupied for all the nucleotides of the respective class.

To determine if the water position based on the 3D probability distribution results for the non-canonical structures (see results below), additional QM calculations were performed at the MP2/6-31+G(d) level using the Gaussian03 package¹². The calculations used a model compound containing the phosphodiester backbone and a uracil base (NUSU), and a single water molecule. The water molecule was initially oriented donating a hydrogen bond to the 2′-hydroxyl oxygen in the O3′ orientation and the distance between the water H and the O2′ optimized with the remaining degrees of freedom constrained. Once the minimum H…O2′ distance was obtained, a second optimization was performed where all degrees of freedom were allowed to relax, including the 2′-hydroxyl dihedral and water molecule, except for the dihedrals that define the A-form of RNA (Supplementary Table S1).

Results and Discussion

Investigation of the impact of the 2′-hydroxyl orientation on the intrinsic energies of the conformation of the phosphodiester backbone in RNA was initiated via QM calculations on the model compound, R3PS (Fig. 1). Two-dimensional (2D) potential energy surfaces for rotation of the individual phosphodiester dihedrals, α, β, γ, ε, and ζ were obtained versus rotation of the 2′-hydroxyl proton. In the surfaces the four “non-target” dihedral angles and the sugar pucker were constrained to values associated with the A-form of RNA (Supplementary Table S1), as previously described^8,20. All five 2D surfaces (Fig. 1) show broad minima with energies less than 2 kcal/mol, with the γ, ε, and ζ surfaces showing the presence of multiple, distinct minima. In the α and ζ surfaces the low energy regions encompass a backbone range from approximately 120° to 300°. For these backbone torsions, the 2′-hydroxyl assumes two energetically favorable orientations (i.e. < 2 kcal/mol), one at 120° to 150° and the other at 180° to 250°. With β, for both the β torsion and 2′-hydroxyl the intrinsically accessible region is limited to 180° to 240°. γ shows four minima, with three associated with the 2′-hydroxyl in the 190° to 250° range, with a second at γ ~45° with the 2′-hydroxyl in the 120 to 180° range. In the case of ε three conformations are readily accessible: i) ε ~ 75, 2′-OH ~ 180°, ii) ε ~ 180°, 2′-OH ~ 120°, and iii) ε ~ 240, 2′-OH ~ 210°. Overall, the results in Figure 1 indicate that the intrinsic energy of the backbone torsions depends both on the torsion angle itself and the orientation of the 2′-hydroxyl, consistent with previous MD studies^21,22 suggesting that the 2′-hydroxyl orientation influences the overall the structural properties of RNA.

The 2′-hydroxyl can sample three orientations^21,23; the base (60° to 120°), O3′ (190° to 270°) and O4′ (280° to 330°) orientations. Experimentally, the exact orientation of the 2′-hydroxyl in RNA is typically not known due to the inability of X-ray experiments to visualize hydrogens and the exchangeable nature of the proton²⁴. Despite these issues, NMR studies of duplex RNA at low temperatures show that the 2′-hydroxyl samples the O3′ and base orientations, with the base orientation dominating^23–25. The base orientation involves the 2′-hydroxyl proton hydrogen bonding with a water molecule that also hydrogen bonds with the minor groove face of the base moiety^24,26, while the O3′ orientation involves the hydroxyl proton hydrogen bonding with the O3′ atom on the same sugar moiety.

To better visualize the direct impact of the 2′-OH orientation on the energies of the phosphodiester backbone, 1D “slices” were extracted from the 2D energy surfaces. The slices involved the relative energies as a function of the respective phosphodiester backbone dihedral for a range of values for the C1′-C2′-O2′-H2′ dihedral that correspond to the base, O3′ and O4′ orientations, as indicated in Fig. 1. In this process, the lowest energy from the range of C1′-C2′-O2′-H2′ dihedral angles defining the base, O3′ or O4′ 2′-hydroxyl orientation for each 15° increment in the phosphodiester torsion dimension was extracted and used to create the 1D energy surfaces. The three energy surfaces for each dihedral were then offset to the global minimum for the three 2′-hydroxyl 1D surfaces (Fig. 2). The difference between the three 1D energy surfaces for each dihedral are significant, and further suggests a model where changes in the orientation of the 2′-hydroxyl impact the intrinsic conformational flexibility of the phosphodiester backbone.

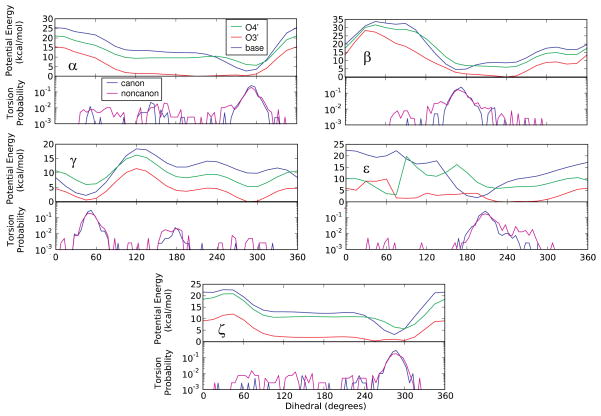
Figure 2.

(Upper panels) 1D QM potential energy surfaces extracted from the 2D surfaces in Figure 1 with the 2′-hydroxyl in the base (60° to 120°), O3′ (190° to 270°) or O4′ (280° to 330°) orientations for the five phosphodiester backbone torsions: α, β, γ, ε, and ζ. (Lower panels) Log scale plots of the probability distributions for the corresponding phosphodiester backbone dihedrals obtained from crystallographic-survey data for canonical and non-canonical RNA regions [Blue: Canonical; Pink: Non-canonical].

To relate the differences in the backbone torsion energy surfaces due to changes in the 2′-hydroxyl orientation to RNA structure, included in the lower panels of Figure 2 are log plot dihedral probability distributions from canonical and non-canonical crystal structures of RNA. Distinct maxima are seen in the distributions for all 5 dihedrals, with those maxima corresponding to the minima in the base orientation 2′-hydroxyl energy surfaces in all cases. In contrast, the energy surfaces for the O3′ 2′-hydroxyl orientation are significantly “flatter” and in certain cases (i.e. α, β, and ε) the minima do not correspond to the maxima in the survey probability distributions. Such flat energy surfaces would allow for a wider range of conformations and conformational transitions of the phosphodiester backbone to be accessible as compared to the surfaces for the base orientation of the 2′-hydroxyl. Consistent with this are the probability distributions for the non-canonical RNA crystal structures in which a larger number of conformations away from the maxima in the five dihedral probability distributions are sampled versus the distributions of the canonical structures. These results support a model where switching of the 2′-hydroxyl from the base to the O3′ orientation leads to a significant increase in the intrinsic conformational flexibility of the phosphodiester backbone, thereby leading to more sampling of torsion angles away from the maxima in non-canonical RNA crystal structures as compared to canonical duplex structures.

The QM results in Figure 2 also show that the 2′-hydroxyl orientation with the lowest intrinsic energy is consistently the O3′ orientation. The favorable intrinsic energy of the O3′ conformation is due to the strong hydrogen bond between the 2′-hydroxyl and the O3′ atom on the negatively charged phosphodiester moiety. However, the base orientation is known to dominate in duplex RNA, as discussed above, stabilized by an interaction of the 2′-hydroxyl with solvent, either water, ions or other molecules²⁷.

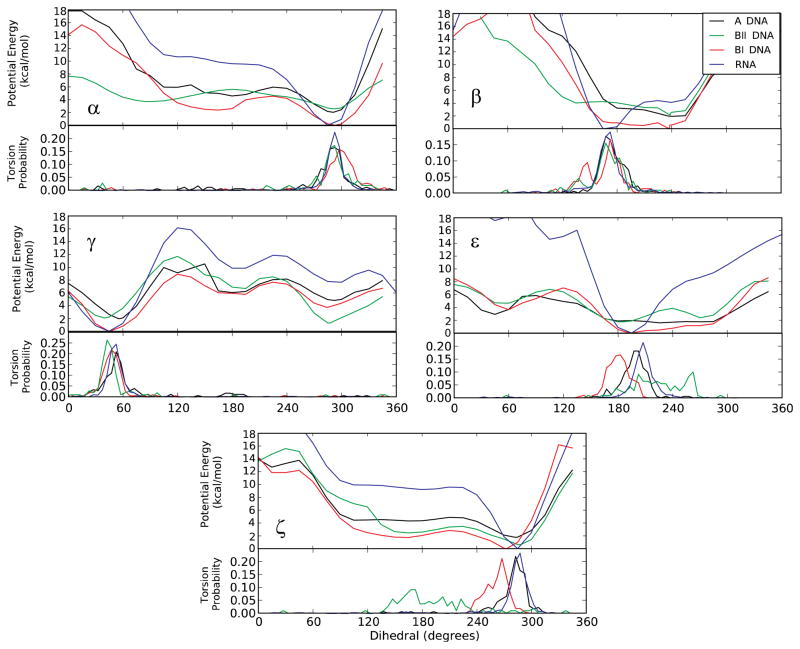
Combined with the QM and survey data (Fig. 2), this leads to a model where solvent stabilization is required for sampling the base orientation of the 2′-hydroxyl, with sampling of the base orientation contributing to intrinsic conformational properties of the phosphodiester backbone that strongly favor the A-form of duplex RNA. As previously shown by us, such intrinsic effects contribute to the conformational properties of duplex DNA⁸. Accordingly, such effects would be anticipated to impact the conformation of duplex RNA, including that duplex RNA is limited to the A-form versus the multiple canonical forms accessible to duplex DNA. This is indeed evident when the potential energy surfaces for R3PS in the base orientation are compared to the QM potential energy surfaces for the analogous DNA model compound, T3PS, obtained from our previous study (Fig. 3). Analysis of Figure 3, which also includes probability distributions from crystal surveys for canonical RNA and the A, B_I and B_II forms of DNA in the lower panels, shows the RNA model compound energy surfaces to have minima that are significantly deeper and narrower than those with the DNA model compound. Thus, when the 2′-hydroxyl interacts with solvent in the minor groove and assumes the base orientation the intrinsic conformational energies of the phosphodiester backbone favor the canonical A-form to a larger extent then occurs with any of the DNA canonical forms. This result indicates that the intrinsic conformational energies of the phosphodiester backbone in combination with the 2′-hydroxyl being in the base orientation contribute to the A-form dominating the conformation of duplex RNA.

Figure 3.

(Upper panels) 1D QM potential energy surfaces and (Lower panels) probability distributions obtained from crystallographic-survey data for five backbone torsions: α, β, γ, ε, and ζ for the three canonical forms of duplex DNA and the canonical form of duplex RNA [Black: A-form DNA, Red: B_I-form DNA, Green: B_II-form DNA, Blue: RNA]. The DNA potential energy surfaces were obtained on the model compound T3PS, as previously described⁸, which is identical to R3PS (Fig. 1) except that the 2′-hydroxyl moieties are omitted.

If the 2′-hydroxyl is limiting the conformational sampling of duplex RNA to just the A-form, then how can that moiety also contribute to the ability of RNA to sample a wide range of non-canonical conformations including conformational changes between canonical and non-canonical conformations? If the interactions of the 2′-hydroxyl with solvent that are stabilizing the base orientation are perturbed, the intrinsically favored O3′orientation may be assumed. Once the O3′orientation occurs the intrinsic conformational energies of the phosphodiester backbone now allows for a larger range of conformations to become accessible, thereby facilitating the sampling of non-canonical conformations. This is consistent with the crystal survey data (Fig. 2) and suggests that in non-canonical conformations the solvation of the 2′-hydroxyl is perturbed as compared to canonical conformations.

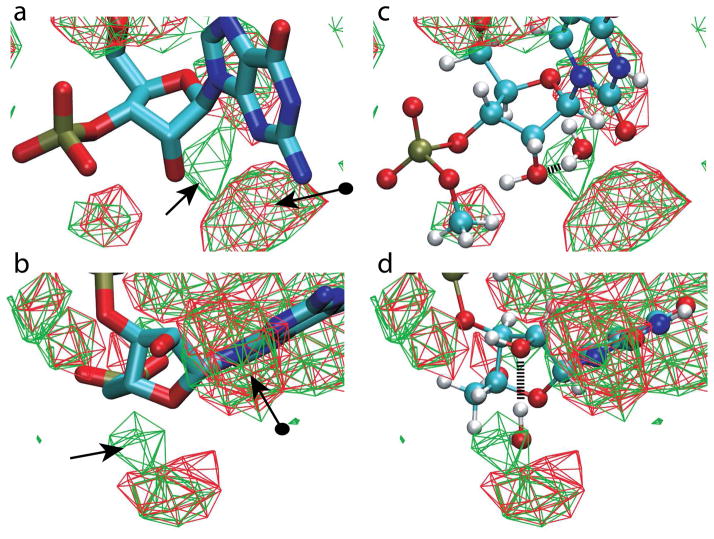
Obtaining experimental evidence for the hypothesis that the 2′-hydroxyl in the O3′ orientation favors non-canonical conformations is difficult given the limitations in experimentally detecting the location of the 2′-hydroxyl proton. To overcome this, we consider that the orientation of the 2′-hydroxyl will affect its ability to hydrogen bond with solvent molecules in its environment, a phenomena which should lead to differences in the distribution of solvent molecules around the O2′ atom in crystal structures. Presented in Figure 4 are 3D probability distributions of the water oxygen from the survey data for canonical and non-canonical RNA nucleotides. Overall, the distributions are similar; however, there is a distinct region of high probability in the non-canonical structures, indicated by the standard arrow in Figure 4a and b, that is not as populated in the canonical structures. This region is suggested to be associated with water hydrogen bonding with the O2′, where the water is acting as a donor when the 2′-hydroxyl is in the O3′orientation. The average distance between this distribution and the O2′ atom is 2.77±0.28 Å, a distance corresponding to a near ideal O…H-O hydrogen bond as judged by the water O…O radial distribution functions obtained from X-ray scattering experiments^28,29.

Figure 4.

3D water oxygen probability distributions around RNA nucleotides from the crystallographic survey. a and b) Approximately orthogonal images of water distributions from canonical (red) and non-canonical (green) RNA structures. Water contour levels are at 33% occupancy and a guanine base is shown for reference although all bases were included in the survey. Standard arrow indicates the higher probability distribution region in the non-canonical nucleotides and the arrow with a sphere on the tail is the distribution associated with water interacting with both the O2′ atom and the minor groove of the base. c and d) Approximately orthogonal images of the uradine nucleotide (model compound NUSU) and the water obtained from the QM calculation overlaid on the water probability distributions from a and b in the identical orientation. The hydrogen bond between the water and the O2′ atom is shown.

Directly adjacent to the distinct region potentially associated with the 2′-hydroxyl in the O3′orientation is a second region which is highly populated in both the canonical and non-canonical forms of RNA. This region, marked with the arrow with the circle tail in Figure 4, is associated with the base orientation of the 2′-hydroxyl. As previously discussed^{21–23,25,26}, in the base orientation the 2′-hydroxyl is acting as a donor in a hydrogen bond with water, with that water also donating a hydrogen bond to the base. This is the interaction that stabilizes the base orientation of the 2′-hydroxyl that dominates in canonical conformations of RNA. It is evident that in non-canonical RNA this region is also highly populated, indicating that 1) the base orientation of the 2′-hydroxyl is also sampled in non-canonical RNA structures or 2) that in the O3′orientation the 2′-hydroxyl O2′ can accept hydrogen bonds from waters located in the unique region sampled in the non-canonical structures as well as the region adjacent to the base sampled significantly in both the non-canonical and canonical structures.

To further test that the water probability distribution in the non-canonical RNA structures is due to hydrogen bonding between water and the 2′-hydroxyl in the O3′orientation we return to QM calculations. These calculations involved placement of a water molecule in an idealized orientation adjacent to a model compound, NUSU, where the water can act as a hydrogen bond donor to the lone pair of the O2′ atom (Supplementary Fig. S2). The orientation between the water and NUSU was then optimized using QM methods with the resulting O…O distance being 2.89 Å and the 2′-hydroxyl dihedral being 214°, indicative of the O3′ orientation. Presented in Figure 4c and d is the optimized water overlaid on the crystal water probability distribution, showing the water to occupy the region of high probability observed in the non-canonical structures. While the water-NUSU QM calculation represent a significant assumption as compared to the complex nature of the solvation of RNA oligonucleotides, the results support the model where the region of a high probability of hydration in non-canonical RNA is associated with water-O2′ hydrogen bonds when the 2′-hydroxyl is in the O3′ orientation.

Consistent with the present model of the role of the orientation of the 2′-hydroxyl on RNA conformational heterogeneity are recent results from empirical force field studies of RNA²². In that study, the dihedral force field parameters that influence the orientation of the 2′-hydroxyl were systematically varied to control the extent of sampling of the O3′ versus base orientations. Molecular dynamics simulations with these parameter sets on a collection of 14 RNA molecules showed that increased sampling of the base orientation while simultaneously decreasing the sampling of the O3′ orientation led to increased stabilization of the RNA as judged by a number of criteria²². These results lend further support to the model where the 2′-hydroxyl orientation impacts the conformational sampling of RNA.

Finally, the presented model is consistent with the impact of methylation of the 2′-hydroxyl on RNA stability²⁵. As is well known, for a given sequence, RNA is significantly more stable than DNA, a phenomenon that is largely attributed with the 2′-hydroxyl stabilizing the water network in the minor groove. This stabilization involves the 2′-hydroxyl in the base orientation donating a hydrogen bond to water with that water then hydrogen bonding to the minor groove side of the respective base, as discussed above. However, the 2′-O-Me modification of RNA leads to increased stability over unmodified RNA even though the crucial hydrogen bond donating capacity of the 2′-hydroxyl is lost. While this has been suggested to be associated with a “clathrate-like H₂O structure^25,30” in the major groove the present model can be used to explain this observation. Simply, replacement of the 2′-hydroxyl proton with a methyl group makes sampling of the O3′ orientation forbidden, thereby further favoring the equilibrium towards the base orientation, leading to intrinsic stabilization of the A-form conformation of the phosphodiester backbone.

A final note concerns the selection of the model compound, R3PS for the present study. While this system has limitations in the context of a model for full RNA and its environment (e.g. the absence of the bases and no treatment of hydration), it was designed specifically for the present study. By omitting the bases and solvent contributions, we are able to focus solely on the intrinsic properties of the phosphodiester backbone and the impact of the 2′-hydroxyl on those properties, in the absence of confounding effects associated with the remainder of the RNA molecule and its environment. Indeed, it is the simplicity of models such as T3PS and R3PS, which may be considered analogous to the alanine dipeptide as a model system of polypeptide conformational properties³¹, that allowed for the identification of the impact of the 2′-hydroxyl on the phosphodiester backbone conformational properties in the presented study.

Conclusions

A combination of QM calculations and survey data of RNA crystal structures have been used to develop a model whereby the 2′-hydroxyl of RNA leads to conformational restriction to the A-form at the secondary structure level, while also contributing to the wide range of RNA non-canonical, tertiary structures. This role as a conformational switch is due to the balance of intrinsic conformational properties of the RNA phosphodiester backbone, as indicated by QM methods, and interactions of the 2′-hydroxyl with the solvent environment. In duplex RNA, solvation of the minor groove leads to the 2′-hydroxyl hydrogen bonding with water, thereby assuming the base orientation, leading to the intrinsic energetics of the phosphodiester backbone favoring the A-form. Alternatively, possibly due to perturbation of the hydration pattern in the minor groove, sampling of the O3′ orientation of the 2′-hydroxyl leads to the intrinsic conformational properties of the backbone allowing for a wider range of conformations to be sampled, consistent with the broad range of non-canonical, tertiary structures of RNA.