Significance analysis and statistical dissection of variably methylated regions

Abstract

It has recently been proposed that variation in DNA methylation at specific genomic locations may play an important role in the development of complex diseases such as cancer. Here, we develop 1- and 2-group multiple testing procedures for identifying and quantifying regions of DNA methylation variability. Our method is the first genome-wide statistical significance calculation for increased or differential variability, as opposed to the traditional approach of testing for mean changes. We apply these procedures to genome-wide methylation data obtained from biological and technical replicates and provide the first statistical proof that variably methylated regions exist and are due to interindividual variation. We also show that differentially variable regions in colon tumor and normal tissue show enrichment of genes regulating gene expression, cell morphogenesis, and development, supporting a biological role for DNA methylation variability in cancer.

1. INTRODUCTION

DNA methylation is a chemical modification of DNA that has been shown to play a critical role in complex diseases such as cancer (Okano and others, 1999; Portela and Esteller, 2010; Feinberg and Tycko, 2004). Although there is substantial evidence that changes in the average level of DNA methylation are meaningful (Lengauer and others, 1997; Cui and others, 2003; Irizarry and others, 2008), an alternative theory has recently been proposed for the relationship between DNA methylation and phenotype. Feinberg and Irizarry (2010) propose that increased biological variability in methylation at specific genomic locations may be highly relevant to common diseases. These variably methylated regions (VMRs) are important for 2 reasons. First, as shown in Feinberg and Irizarry (2010), they identify regions of stochastic epigenetic variation in developmentally important genes. Thus, they indicate a target for flexibility in developmental pathways that was not previously anticipated. Both developmental and evolutionary biologists are interested in testing these regions functionally. Second, as shown in Feinberg and others (2010), VMRs between individuals serve as a new type of molecular fingerprint stable over more than a decade, based on an epigenetic signature. Thus, they are a new target for understanding biological diversity in normal human variation and potentially in disease.

Given the potential importance of regions of DNA methylation variability, it is critical to be able to identify and quantify these regions from genome-wide DNA methylation measurements. Here, we focus on procedures for identifying VMRs from genome-wide microarray measurements of DNA methylation obtained from the CHARM platform (Irizarry and others, 2008). A key question is how to find genomic regions of true biological variability and separate them from intraindividual and technical variation due to the microarray technology. A second question of interest is to identify regions that show differences in variability when comparing biological groups, such as cancer tumors and healthy normal samples.

Here, we take a multiple hypothesis testing approach to both of these important statistical questions. But the multiple testing procedure is complicated by the fact that regions of increased or differential variability are not known in advance. Therefore, our multiple testing procedure will have 2 components: (i) a procedure for identifying candidate variability regions from genome-wide DNA methylation measurements, and (ii) a method for assigning statistical significance to the candidate regions. This general algorithm of discovery followed by significance is relatively uncommon in genomics but has been previously applied in the analysis of functional brain imaging data (Holmes and others, 1996; Nichols and Holmes, 2002). Our approach is the first to use this strategy to scan for regions of increased variability as opposed to searching for mean shifts.

We propose a 1-group multiple testing procedure designed to identify contiguous genomic regions that show significantly more variability than the background level of variation in methylation in the genome (Figure 1(a)), in contrast to regions that demonstrate background variability (Figure 1(c)). In the 1-group case, the biological variability is not associated with a specific outcome, which makes testing variability at any single position in the genome difficult because the background level of variation in methylation measurements is unknown a priori. We also propose a 2-group statistic for finding contiguous genomic regions that show differences in variability between biological groups (Figure 1(b)), in contrast with regions where the variability is close to the same in the 2 groups (Figure 1(d)). There are a number of significance tests that can be applied to detect differences in variability for specific genomic locations (Levene, 1960), (Bresuch and Pagan, 1979). However, a more powerful approach is to take advantage of the spatial arrangement of DNA methylation measurements across the genome.

Fig. 1.

Examples of 1- and 2-group DNA methlyation patterns at VMRs and randomly chosen regions. The top panel of each plot is the DNA methylation for each array, and the bottom panel is the smoothed adjusted MAD or absolute difference in MADs statistic with shading representing statistically significant regions (a) One-group VMR on chromosome 12. (b) Two-group dVMR on chromosome 11 (black lines = cancer and gray lines = normal). (c) One-group randomly chosen region representing background variability in the genome. (d) Two-group randomly chosen region with similar variability across both groups (black lines = cancer and gray lines = normal).

We apply our 1-group procedure to detect regions of variable methylation in 2 human studies of DNA methylation in peripheral blood and spleen tissue. We show that the VMRs detected with our methodology are more variable across individuals than across either (i) technical replicates or (ii) replicates within individuals at different times. This is the first statistically rigorous demonstration that regions of variable methylation exist and are driven by interindividual biological variation not technical or intraindividual variation. We also apply our 2-group approach to detect differentially variably methylated regions (dVMRs) between normal and tumor samples in human colon tissue. A gene ontology analysis indicates that regions of differential variability between cancer and normal samples are enriched for genes involved in the regulation of gene expression, cell morphogenesis, and development suggesting a biological role for variability of DNA methylation in cancer.

2. STATISTICAL MODEL

Novel high throughput technology permits DNA methylation data to be observed at a large number of locations in the genome, called probes. Since our goal is to find regions of unusual variability in methylation, we begin by calculating an adjusted median absolute deviation (MAD) statistic s_i for probe i = 1,…,m at genomic positions g_i, i = 1,…,m (described in detail in Section 4). A key observation is that variability estimates at probes close to each other in the genome are likely to be correlated because the measurements are based on DNA fragments that may cover more than one probe (see supplementary material available at Biostatistics online for a description of the CHARM microarray protocol). We examined regions longer than 100 probes on the CHARM microarray and confirmed that estimates of variability are in fact autocorrelated (Supplementary Figure 1 available at Biostatistics online). We therefore propose the following model for the variation statistics s_i across the genome:

where ρ parameterizes the autocorrelation between nearby probes in the genome and ϵ_i∼F—a symmetric distribution centered at zero. For the calculations that follow, we assume a normal distribution for ϵ_i.

Our model assumes K regions of biological variability above the background level of variation due to the microarray technology. We define R_k as the set of genomic indices corresponding to region k = 1,…,K. Here, R_k corresponds to a contiguous region in the genome, where f(g_i) is a nonzero continuous function. Neither the number K or location R_k of the regions are known in advance. Let ℛ = cup_k=1^KR_k be the set of contiguous regions with nonzero f(g_i) in the genome. We assume that the function f(·) is zero in the complement of ℛ.

Our goal is to develop a procedure that scans the genome, identifies the regions R_k, and calculates the statistical significance of the identified regions. The steps are (i) smooth the variability statistics to capture the behavior of f(·), (ii) generate candidate regions $\hat{R}\ell ;\ell =1,\dots ,L$ based on the smoothed statistics, and (iii) calculate the statistical significance of candidate regions. This approach identifies contiguous regions of biological variability and produces a region level, rather than probe level, measure of statistical significance.

We first generate smoothed estimates $\hat{f}(g_i)$ from the observed s_i using loess. Within each chromosome, we define probe groups so within each group, the probes are no more than 300 base pairs apart, matching the design of the original layout of the original microarray probe groups (Irizarry and others, 2008). There are 36 803 probe groups with a median of 42 probes per group. Within each probe group, we smoothed the probe-specific statistics s_j using a span defined as , where d_max = 300 bp is the maximum distance between probes and bad hbox = 35 bp is the median distance between probes. This span results in smoothing that assigns weight to nearby probes approximately proportional to the genomic distance between the probes. This choice of span therefore allows the smoothing to be comparable across probe groups.

We use a threshold to identify candidate regions with large smoothed statistics. Similar threshold-based approaches have been proposed for functional brain mapping, where spatially contiguous signals are also of interest (Holmes and others, 1996), (Nichols and Holmes, 2002). Candidate regions are defined as any set of contiguous probes such that the smoothed statistics, $\hat{f}(g_i)$, are above a threshold q_t. We set the threshold to be a quantile, $q_t=F_{\hat{f}}^{-1}\left(t\right)$, of the distribution of smoothed statistics $F_{\hat{f}}$. A more stringent threshold results in fewer and narrower candidate regions, while a more liberal threshold is more likely to identify longer, more numerous candidate regions but with lesser magnitude. The result is a set of estimated regions $\hat{R}\ell$, ℓ = 1,…,L.

It is not currently known whether long regions with moderately large signal or shorter regions with very strong signal regions have greater biological significance. Our approach is to weight equally height and width and calculate an area statistic for each candidate region. If we let $\hat{f}(g_i)$ be the smoothed statistic for probe i, then our region-specific area statistic is defined as follows:

3. STATISTICAL SIGNIFICANCE

We perform one hypothesis test for each candidate region identified using the threshold from the previous section ${\widehat{R}}_{\ell }$; ℓ = 1,…,L. Under the global null hypothesis, we assume that the probe-level statistics s_i are drawn from an auto-regressive (1) process with no spatial effect.

We allow for spatial dependence since the biological generating process is likely to produce dependence between probes that are close together on the genome as described in the supplementary material available at Biostatistics online (Irizarry and others, 2008). The alternative hypothesis for each region is that there is a nonzero smooth region-specific function that describes the variation within region R_k:

It is likely that the number of VMRs in the genome is relatively small so that the null hypothesis holds for most of the probes in the genome. In other words, f(·) = 0 for most g_i.

After obtaining observed statistics, the next step is to define the null distribution. We fit the null model to each probe group with greater than 100 probes, to ensure a sufficiently long series for accurate estimation using the Yule–Walker method (Yule, 1927), (Walker, 1931). Then we average the estimates across probe groups to obtain an overall estimate $\widehat{\rho }$. We generate parametric bootstrap null data from the model

where the ϵ_i are drawn from the $N(0,{\widehat{\sigma }}^2)$ with since the adjusted smoothed statistics are approximately normally distributed (Supplementary Figure 2 available at Biostatistics online).

For bootstrap iterations b = 1,…,B, we calculate null candidate regions ${\widehat{R}}_{{\ell }_b}^0$ and statistics A_ℓb⁰;ℓ_b = 1,…,L_b by applying the procedure described in the previous section to the null data s_i⁰. Based on this bootstrap null distribution, we calculate the empirical p-values from the pooled statistics from all null simulations (Storey and Tibshirani, 2003):

Since many candidate regions are generated for each study, it is necessary to correct these p-values for multiple testing. We use the p-values to calculate q-values, the false discovery rate (FDR) analog of p-values, as previously described (Benjamini and Hochberg, 1995), (Storey, 2002). In the simulation section, we show that our procedure empirically controls the FDR, while taking into account both the size and the width of the estimated signal.

The p-values from our procedure quantify the statistical significance of regions directly rather than calculating significance based only on peak height (Schwartzman and others, 2009), (Gavrilov and others, 2009). The p-values are calculated marginally, averaging both height and length. These are correct marginal p-values for the area statistic as discussed in Storey and Tibshirani (2003). Under this model, a long region with moderate variability would be ranked similarly to a short region with very high variability but nearly the same area in line with the biological intuition.

For comparison, we directly applied the peak height significance calculation to our methylation data after normalization. The R code to implement the peak height significance calculation was kindly supplied by Schwartzman and others (personal communication). The algorithm identified a large number of local maxima; many corresponding to likely probe effects (Supplementary Figure 3 available at Biostatistics online). This result suggests that peak height only significance calculation may not be appropriate for CHARM data where long moderate signals are likely of importance. A similar argument suggests that other peak-finding approaches developed for ChIP-seq/chip (Song and others, 2007), (Ji and others, 2008), (Johnson and others, 2006) may also not be appropriate for methylation data, as the structure of the significant peaks is wider and more moderate for methylation data.

4. CHARM DATA PROCESSING

As in many high-dimensional problems, the statistical model and significance calculation depend critically on proper preprocessing. Before presenting the results of our analysis, we describe in detail, the preprocessing pipeline for deriving variability estimates from raw CHARM data. Each step removes a source of potential bias that would have a substantial negative impact on the significance calculations from the formal statistical model.

The CHARM platform produces one raw methylation measurement for each probe on each individual y_ij as described in the supplementary material available at Biostatistics online. Since the CHARM platform is a sensitive and specific technology, it is subject to a number of potential confounding artifacts such as batch effects (Leek and others, 2010). We address potential confounders by applying a modification of surrogate variable analysis (Leek and Storey, 2007), (Leek and Storey, 2008). First, we transform the probe-specific methylation percentages element wise to the logit scale, We form the centered matrix Y^* with element i,j equal to and calculate the singular value decomposition Y^* = UDV^T. Then we identify the number, n_sv, of right singular vectors that are associated with more variation than expected by chance (Leek, 2010). The significant singular vectors are usually associated with the processing date (Supplementary Figure 4 available at Biostatistics online), a common surrogate for technical artifacts. We regress the probe-specific methylation values on the significant singular vectors:

and calculate residuals and transform back to the original scale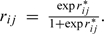

Like many other microarray-based measurements, DNA methylation values are also subject to probe effects (Irizarry and others, 2003). Regions with the same level of methylation may appear to have different methylation values simply because some probes produce larger methylation measurements than others on average. To account for these effects, we subtract the median probe intensity across samples for each probe; the resulting batch and probe-effect corrected estimates, $m_{ij}=r_{ij}-{\stackrel{-}{r}}_{i·}$, are the basis for our downstream analyses of stochastic variability in methylation.

Next, we observed that the methylation profile for a single sample may be very different than the remaining arrays at specific genomic locations. These outlier profiles drive variability estimates in some regions and lead to increased false positives. We therefore estimate variability using the MAD. We transform the MAD statistics to the log scale to obtain a symmetric distribution: mad_i = log(median|m_ij − median(m_·j)|) that is more amenable to auto-regressive models.

Saturation bias is particularly relevant to estimates of variability because measurements from the microarrays are constrained to a fixed range. Regions where the measurements are near the boundaries will appear less variable since they cannot exceed the bounds. The saturation bias can be seen when we plot the probe-specific MADs (mad_i) versus the median microarray intensity across all subjects (Supplementary Figure 5 available at Biostatistics online). When the overall intensity is near the boundary, the probe-specific variability is smaller. To reduce the impact of this bias, we fit a loess curve to the scatterplot of the probe-specific variability and microarray intensity. We subtract the fit from the loess and the residuals from this fit form probe-specific variability statistics: s_i used in our statistical model.

In the 2-group case, we calculate probe MADs within each group s_i^A, s_i^B and fit the loess curves separately to the scatterplots of mad_i^A and mad_i^B versus the microarray intensity measured across all subjects, resulting in probe-specific variability measurements for each group. The probe-specific 2-group variability comparison statistic is the absolute difference in MADs between the 2 groups.

5. RESULTS

We applied our new methods to a simulation study and 3 real DNA methylation experiments using CHARM arrays to evaluate both the statistical and the biological properties of the resulting variable regions. We performed a simulation study to evaluate empirically whether our methods controlled the FDR among the candidate regions and to determine the power of our procedures. We also used 3 different CHARM data sets, encompassing 3 different types of tissue to identify regions of variable methylation in (i) spleen tissue with biological replicates (multiple microarrays from the same tissue sample) to show that methylation variability in these regions was not due to artifacts of the microarray measurements, (ii) peripheral blood samples taken at 2 time points to demonstrate that the variability was due to interpersonal rather than intrapersonal variation, and (iii) colon tumor and normal tissue to identify and characterize regions of differential variability between biological groups.

5.1. Simulation

We generated simulated data sets using this estimated beta distribution of dimension 25 000 probes by 8 arrays (supplementary material available at Biostatistics online). We inserted VMRs using parabolas of varying heights and widths (Supplementary Figure 6 available at Biostatistics online). We applied our 1-group simulation to a data set consisting of 8 arrays described above. We evaluated FDR control and power at region-level FDR cut offs of 1%, 5%, 10%, and 20%. Table 1 shows the average observed FDR and power for at both region-level and probe-level resolution across the 100 simulated samples. The simulation results suggest that our region-specific approach conservatively controls the region-level FDR at various thresholds. Our approach makes no claim about the probe-level FDR, however, the results in Table 1 also suggest that the probe-level FDR is nearly controlled. Null data for the 2-group simulation was generated analogously to the 1-group simulation. These results also suggest that our 2-group approach for regions controls the FDR for commonly used significance levels. Again our results suggest that the region-level FDR is controlled and the probe-level FDR is nearly controlled.

Table 1.

Simulation tables: estimated FDRs and power for one and two groups: “probe” refers to values calculated on individual variable probes and “regions” refers to values calculated for groups of contiguous probes

		Region		Probe
	FDR (%)	Observed FDR	Power	Observed FDR	Power
One group	1	0.011	0.232	0.036	0.227
	5	0.017	0.514	0.051	0.418
	10	0.025	0.663	0.070	0.499
	20	0.053	0.796	0.101	0.562
Two group	1	0.029	0.023	0.092	0.027
	5	0.033	0.067	0.086	0.070
	10	0.076	0.144	0.119	0.138
	20	0.145	0.269	0.193	0.231

5.2. CHARM data analysis

We applied our multiple testing procedures to CHARM data on 3 different tissue types from 3 distinct studies. In 2 of the studies, we applied our 1-group procedure to identify VMRs and evaluate whether the identified regions were due to interindividual biological variation. The first data set was CHARM data from spleen tissue on technical replicates for 5 unique spleens. Four of the spleens were processed on 2 arrays and the fifth was processed on 5 arrays. We used these data to evaluate whether the identified VMRs were due to technical variation. The second data set was CHARM data from peripheral blood samples collected by the Baltimore Longitudinal Study of Aging (BLSA) (National Institute on Aging, 2010). We discovered VMRs in N = 55 individuals at a first visit and evaluated those VMRs in a subset of the individuals (N = 38) in a follow-up sample. We used this study to evaluate whether 1-group VMRs are due to interindividual biological variation or variation within individuals. The last data set was CHARM data from normal and tumor colon tissue (N = 8 in each group). We used this data to identify differences in variability of methylation between the 2 groups.

5.2.1. Spleen—technical replicates.

The 13 spleen arrays were preprocessed as described in the supplementary material available at Biostatistics online. We identified and removed significant batch effects in the first 3 principal components of these data as describe above. We identified variable regions in a subsample of 5 arrays corresponding to unique samples. There were a total of L = 8214 candidate regions identified for the spleen data. Among these candidates, we found 64, 136, 193, and 233 significant VMRs at FDR thresholds of 1%, 5%, 10%, and 15%, respectively. Although we are hesitant to draw biological inference from data generated by 5 samples, we can demonstrate that these VMRs represent biological interindividual variation.

We examined the remaining 8 arrays, consisting of technical replicates for our discovery set. Our hypothesis was that levels of methylation within technical replicates should be more similar than nonreplicates in VMRs. For each VMR, we defined a profile of methylation measurements for each array as the methylation values for all probes within the identified region. Figure 2(a) is a plot of the methylation profiles versus genomic positions for a specific VMR, where technical replicates are the same color. The technical replicate profiles appear to be closer than the biological replicate profiles.

Fig. 2.

VMRs in replicates. (a) Sample of biological replicates in peripheral blood: identical colors come from the same individual, solid lines are from the earlier study visit, and dashed lines come from the later study visit. The solid and dashed lines of the same color are closer together than solid lines of different colors in VMRs, indicating the VMRs are due to interpersonal rather than intrapersonal variation (b) Technical replicates from spleen tissue: identical colors come from the same spleen. The solid and dashed lines of the same color are closer than other pairwise line pairs (solid or dashed), indicated the VMRs are due to biological, rather than technical variation.

To confirm this observation, within each VMR significant at an FDR of 5%, we computed all the pairwise distances between the methylation profiles for the 13 arrays. We calculated the average distance between the biological replicates and then the nonreplicates within each VMR. Of the 136 VMRs significant at FDR < 5%,116(86%) had less average distance between replicates than nonreplicates.

We randomly sampled regions of the genome that were not identified as having increased variability and performed the same average distance procedure. Figure 3(a) shows the boxplot of the difference in average distance between replicates and nonreplicates for VMRs we identified with our procedure and for the randomly selected regions. The boxplots for differences in random regions are approximately centered around zero suggesting that there is no variability above the background rate due to technical noise. However within VMRs, the difference in distances is much larger, suggesting that there is substantial variability above the background rate in these regions.

Fig. 3.

The distribution of euclidean distances between replicates and nonreplicates in VMRs and random regions. Each boxplot is the average distances between replicates minus the average distance between nonreplicates in all VMRs and an equal number of randomly selection genomic regions. (a) Biological peripheral blood replicates: the average distances are much smaller between replicates than nonreplicates within VMRs than random regions. (b) Technical spleen tissue replicates: the average distances are also smaller between replicates than nonreplicates in VMRs.

5.2.2. BLSA—biological replicates.

Next, we analyzed methylation data from N = 109 CHARM arrays from the BLSA study. Fifty five arrays were sampled from individuals at the first timepoint, and 54 arrays were sampled from the second timepoint, with 38 individuals having arrays at both timepoints. We identified VMRs among the arrays sampled at the first timepoint using our 1-group procedure. There were a total of L = 4508 candidate regions identified for the BLSA data, and we identified 881, 1201, 1479, and 1613 significant VMRs at FDR thresholds of 1%, 5%, 10%, and 15%. The increase in power over the spleen data set is likely due to the larger sample size. A gene ontology analysis of genes associated with the regions significant at an FDR threshold of 5% indicated enrichment for genes related to development and morphogenesis (Table 2). Figure 2(b) shows an example plot of a sample of methylation profiles versus genomic position for the BLSA data, where replicate profiles from the same individual are the same color. Here, profiles from biological replicates appear closer together than profiles between individuals.

Table 2.

Significant GO terms among VMRs in the BLSA biological replicates: “GO term” is the gene ontology category name, “p value” shows the statistical significance of enrichment, “set size” is the number of genes in that GO term, and “number of significant” is the number of genes near statistically significant VMRs in the GO set

GO term	p value	Set size	Number of significant
Immune system development	4.10 × 10−8	274	52
Neuron fate commitment	3.57 × 10−7	44	16
RNA biosynthetic process	4.22 × 10−7	1705	202
Spleen development	3.38 × 10−6	17	9
Negative regulation of transcription	4.86 × 10−6	545	78
Pattern specification process	5.08 × 10−6	277	47
Tissue morphogenesis	5.92 × 10−6	238	42
Positive regulation of transcription	8.75 × 10−6	683	92
Negative regulation of RNA metabolic process	9.13 × 10−6	411	62
Positive regulation of RNA metabolic process	9.21 × 10−6	482	70
Epithelium development	1.22 × 10−5	286	47
Leukocyte differentiation	1.29 × 10−5	144	29

We evaluated the VMRs significant at a 5% FDR using the samples from the second time point to confirm that the regions showed an increase in interpersonal variability. We again computed the pairwise distances between the methylation profiles within each variable region. We computed nonreplicate distances only within in the first time point to minimize variation due to environmental variation over time.

The biological replicates appear closer together than distinct individuals, suggesting that the identified VMRs are due to interindividual, rather than intraindividual variation. Figure 3(b) shows that the average distance in variability between replicates and nonreplicates for both the VMRs we identified and random regions. Identified VMRs again show that there is an increase in variability when comparing biological replicates than when comparing within individual variation. In fact, 1143 of the 1201 (95%) VMRs called significant at FDR < 5% had less average distance between individual replicates than across biological samples.

5.2.3. Cancer versus normal.

We identified regions of differential variability between normal and tumor colon tissue using the 2-group procedure described above. There were N = 8 samples in each group. A total of L = 8650 candidate regions identified in the comparison of cancer versus normal. Among these candidates, we found 262, 493, 652, and 894 regions at FDR thresholds of 1%, 5%, 10%, and 15%. A gene ontology analysis (Ashburner and others, 2000) of the genes associated with these regions showed enrichment for regulation of transcription and metabolic processes, tissue morphogenesis, development, and cell fate commitment (conditional P < 0.01 for all categories). These categories are consistent with the pathophysiology of cancer and support the previously postulated role for VMRs in cancer (Feinberg and Irizarry, 2010). 6. Discussion

We have developed the first general-purpose multiple-testing procedure for scanning the genome for variable regions and calculating region-level statistical significance. We used this procedure to identify regions of high DNA methylation variability in 3 different human tissue types: spleen, peripheral blood, and colon. By utilizing both technical replicates (same tissue processed multiple times) and biological replicates (same person across time), we proved that our procedure identifies VMRs that are associated with interindividual variation in DNA methylation rather than intraindividual variation or technical variation. Our simulation results suggested that our multiple testing procedure both controls the FDR and has sufficient power to detect variable regions even in cases where the sample size is relatively low.

We believe our methods may be useful in a range of statistical applications. First, our specific statistical methods may be applied to identify variable regions in other genome-wide measurements, whether from microarray measurements of other DNA modifications such as histone modifications or transcription factor binding or from next-generation sequencing experiments. More generally, our 2-stage multiple testing procedure for identifying candidate regions and calculating their statistical significance may be useful for parameters other than variability, such as mean shifts.

Perhaps more importantly, we have confirmed the existence of statistical significant regions of DNA methylation variability, supporting the hypothesis proposed by Feinberg and Irizarry (2010). We are also the first to show that these regions are truly due to biological variability between individuals rather than intraindividual or technical variation. Our analysis of variation in colon tumor and control samples suggest that proximal genes to VMRs show some enrichment for development, gene expression, and morphogenesis reinforcing the hypothesis that VMRs may play an important role in the development of common disease (Feinberg and Irizarry, 2010). Our analysis opens the door for future research into the potential role of these VMRs in complex disease.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

National Institutes of Health (P50HG003233, R01HG005220).