A robust method using propensity score stratification for correcting verification bias for binary tests

Abstract

Sensitivity and specificity are common measures of the accuracy of a diagnostic test. The usual estimators of these quantities are unbiased if data on the diagnostic test result and the true disease status are obtained from all subjects in an appropriately selected sample. In some studies, verification of the true disease status is performed only for a subset of subjects, possibly depending on the result of the diagnostic test and other characteristics of the subjects. Estimators of sensitivity and specificity based on this subset of subjects are typically biased; this is known as verification bias. Methods have been proposed to correct verification bias under the assumption that the missing data on disease status are missing at random (MAR), that is, the probability of missingness depends on the true (missing) disease status only through the test result and observed covariate information. When some of the covariates are continuous, or the number of covariates is relatively large, the existing methods require parametric models for the probability of disease or the probability of verification (given the test result and covariates), and hence are subject to model misspecification. We propose a new method for correcting verification bias based on the propensity score, defined as the predicted probability of verification given the test result and observed covariates. This is estimated separately for those with positive and negative test results. The new method classifies the verified sample into several subsamples that have homogeneous propensity scores and allows correction for verification bias. Simulation studies demonstrate that the new estimators are more robust to model misspecification than existing methods, but still perform well when the models for the probability of disease and probability of verification are correctly specified.

1. INTRODUCTION

To assess the accuracy of a diagnostic test, knowledge of the true disease status is needed. Usually this is determined by means of a so-called “gold standard” test that always correctly ascertains the true disease status. When a diagnostic test is binary, sensitivity and specificity are frequently used to assess the accuracy of the test. If all subjects given the new diagnostic test have their true disease status verified, sensitivity and specificity can be estimated unbiasedly by simple proportions.

We consider the setting of a cross-sectional cohort study in which a random sample is drawn from the population of interest and the new diagnostic test result and other subject characteristics are measured. In some situations, not all subjects given the new diagnostic test ultimately have the true disease status verified. There are various reasons for this. For example, some gold standard tests are expensive and time consuming, and some are based on invasive procedures such as surgery. In these situations, subjects with negative test results may be less likely to receive a gold standard evaluation than subjects with positive test results. When the decision regarding whether or not to verify the subject's true disease status depends on the test result (and possibly other subject characteristics), naive methods that use only data from disease-verified subjects usually give biased estimates of the test's accuracy; this is called verification bias (Begg and Greenes, 1983).

Let T_i denote the binary test result and let D_i denote the true disease status for the ith subject, i = 1,2,…,n, where T_i = 1 indicates a positive test result, T_i = 0 indicates a negative test result, D_i = 1 indicates that the subject has the disease and D_i = 0 indicates that subject does not have the disease. Only a subset of the subjects have their disease status verified; let V_i = 1 if the ith subject has the true disease status verified, and V_i = 0 otherwise. Let X_i be a vector of observed covariates for the ith subject that may be associated with both D_i and V_i.

Various methods have been developed to deal with the problem of verification bias, most of which assume that the true disease status, if missing, is missing at random (MAR) (Little and Rubin, 2002), that is that the probability of a subject having the disease status verified is purely determined by the test result and the subject's observed characteristics and is conditionally independent of the unknown true disease status. In our notation, V⊥D|(T,X). The decision to verify the subject's true disease status may depend on the true condition of the subject, but the dependence is only through the test result and (possibly) observed covariates. Existing methods for estimating disease prevalence, sensitivity, and specificity in this case are summarized in Table 1, including the naive estimators computed using only information from the verified subjects. The naive estimators are unbiased if the subjects are selected for verification completely at random. Under the less restrictive MAR assumption, the naive estimators are biased.

Table 1.

Existing methods for correcting verification bias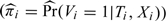

The Begg and Greenes (1983) (BG) estimator and the mean score (MS) estimator (Pepe and others, 1994), (, reilly1995) typically require parametric models for the probability of disease Pr(D|T,X). The inverse probability weighting (IPW) estimator typically requires a parametric model for the probability of disease verification π = Pr(V|T,X). The semiparametric efficient (SP) estimators typically require parametric models for both the probability of disease and the probability of verification, but they are “doubly robust” in that they are consistent if either Pr(D|T,X) or π is estimated consistently (Robins and others, 1994), (, robins1995). Asymptotic variance formulas have been developed for all of these estimators based on estimating equations; see Alonzo and Pepe (2005) for a unified treatment.

When X is high dimensional or includes continuous variables, nonparametric estimation of Pr(D|T,X) and Pr(V|T,X) becomes more challenging, which is why parametric models are typically used to estimate these quantities. The validity of these parametric models affects the behavior of the estimators. Existing methods are not robust to model misspecification, except that the SP estimators are doubly robust in the sense discussed above.

In this paper, we propose a new method for correcting verification bias based on the propensity score, defined as the predicted probability of verification given the test result and observed covariates. The new method stratifies the verified sample into several subsamples that have homogeneous propensity scores and allows correction for verification bias within each subsample. Parametric models may still be used to estimate the propensity scores, but since the estimated propensity scores are only used for the purpose of stratification, the estimators of sensitivity and specificity are less sensitive to model misspecification. We develop the new estimators and their asymptotic properties in Section 2. Simulation studies comparing the new method with existing methods are presented in Section 3, followed by an example in Section 4 in which the competing methods are illustrated using data from a study of depression in elderly primary care patients. The paper concludes with a discussion in Section 5.

2. A ROBUST METHOD FOR CORRECTING VERIFICATION BIAS FOR BINARY TESTS

2.1. Development of the new estimators

The derivation of the BG estimators was based on Bayes' theorem:

Recognizing that the probability of disease can depend on a set of covariates X as well as the test result T, one can express the positive and negative predictive values of the test as

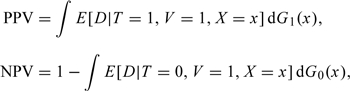(2.1)

respectively, where G_t(x) is the cumulative distribution function of X for subjects with T = t, t = 0,1. Note that the presence of V = 1 in these expressions is justified by the MAR assumption. It follows that the disease prevalence and the sensitivity and specificity of the test can be expressed as:

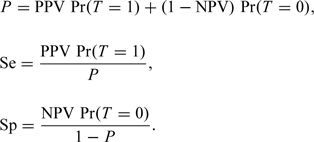(2.2)

The extended BG estimators (Alonzo and Pepe, 2005) incorporate parametric estimation of E[D_i|T_i,V_i = 1,X_i] using, say, a logistic regression model, use of the empirical distribution functions to nonparametrically estimate G_t(x), t = 0,1, and use of the indicator functions I(T_i = t) to estimate Pr(T_i = t), t = 0,1.

A potential concern with the BG (and other) estimators is model misspecification. Instead of using a parametric model to estimate E[D|T,V = 1,X], one could try to estimate this quantity nonparametrically. This is difficult when the dimension of X is high and it contains continuous variables. We propose to reduce the dimension of X by replacing it with the propensity score e_t(X) = Pr(V = 1|T = t,X), 0 < e_t(X) < 1, t = 0,1. This is justified by the following theorem (Theorem 3 in Rosenbaum and Rubin, 1983):

THEOREM 1 If D⊥V|(T,X) for any T and X, then D⊥V|e(X) for any e(X), where e(X) = Pr(V = 1|T,X), 0 < e(X) < 1.

The condition that D⊥V|(T,X) for any T and X is known as the “strongly ignorable” condition (Rosenbaum and Rubin, 1983) which, in our case, is exactly the same as the MAR assumption.

Propensity scores provide data reduction because they adequately capture all relevant covariate information in a single variable. The propensity score is unknown and is typically estimated using a logistic regression model or discriminant analysis. This model can include a large number of covariates since the goal is to provide an adequate summary of the covariate information rather than to construct a parsimonious model that would perform well in predicting verification for future subjects.

Let F_t(e) be the cumulative distribution function of e_t(X), t = 0,1. Then PPV and NPV can be expressed as in the following theorem:

THEOREM 2 PPV and NPV can be expressed as follows:

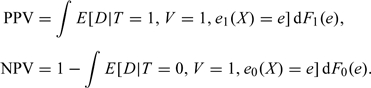(2.3)

Proof. E[D|T = 1] = E[E[D|T = 1,e₁(X)]] = E[E[D|T = 1,V = 1,e₁(X)]]. Also, 1 − E[D|T = 0] = 1 − E[E[D|T = 0,e₀(X)]] = 1 − E[E[D|T = 0,V = 1,e₀(X)]].∥

To estimate the prevalence, sensitivity, and specificity, one needs to estimate the integrals in Theorem 2. One approach to estimating these integrals after having estimated the propensity scores is to categorize the propensity score into, say, 5–10 categories (D'Agostino, 1998), estimate ΔF₁(e) (or ΔF₀(e)) by the proportion of subjects whose estimated propensity score falls in the interval, estimate E[D|T = 1,V = 1,e₁] (or E[D|T = 0,V = 1,e₀]) by the proportion of diseased subjects among the verified subjects with T = 1 (or T = 0) and with an estimated propensity score falling in that interval, and sum across the categories. We call this method “PS” (propensity score stratification).

Suppose that among n subjects in the study, there are n₁ subjects with positive test results and n₀ subjects with negative test results. The n_t subjects are stratified into K classes, C_t,1,C_t,2,…,C_t,K, based on the propensity scores e_t = e_t(X), t = 0,1. Note that the number of strata when T = 0 and T = 1 can be different, but to simplify the notation we assume that they are the same. Let e_t,i = Pr(V_i = 1|T = t,X_i) for i = 1,2,…,n_t be the propensity score for the ith subject in the group with T = t, t = 0,1. We assume a logistic model for V_i with a parameter vector α_t, with separate models for subjects with T = 0 and T = 1:

(2.4)

Let q_t,k, k = 1,2,…,K − 1, be the kth quantile of the distribution of e_t. Then the kth stratum C_t,k consists of those subjects with q_{t,k − 1} < e_t,i ≤ q_t,k, where q_t,0 = 0 and q_t,K = 1. It is assumed that the classes are chosen so that Pr(e_t∈C_t,k) > 0 for t = 0,1 and k = 1,2,…,K. Suppose that there are n_t,k subjects with T = t falling in the kth class and m_t,k subjects with T = t and V = 1 falling in the kth class for t = 0,1. Then the proposed estimators for PPV and NPV can be expressed as:

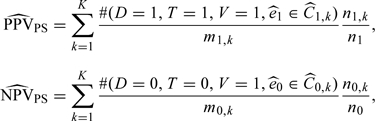(2.5)

where ${\hat{e}}_t$ is the estimated propensity score and ${\widehat{C}}_{t,k}$ are the strata classified according to the empirical quantiles of propensity scores, t = 0,1.

Let φ = Pr(T = 1) with $\hat{\phi }=n_1/n$. Then the disease prevalence, sensitivity, and specificity of the test can be estimated by

(2.6)

The main purpose of stratification here is to categorize the covariate information contained in X instead of assuming a functional form for the relationship between D and X, which may lead to model misspecification. Stratification based directly on X is difficult when X is high-dimensional; therefore, the propensity score provides a helpful tool for dimension reduction and bias reduction in this setting. Although parametric models were used to estimate the propensity scores, the values of the estimated propensity scores are only used to stratify the subjects into different subgroups. Any monotone transformation of the propensity score will not change the stratification, and thus will not change the estimates. For all of these reasons, it is expected that our proposed method will be more robust than methods that require the use of parametric models. Our simulation study presented in the next section verifies this. The type of model misspecification that our method is designed to avoid, however, is misspecification of the functional form of the relationship between D and X. It is not expected to be robust to misspecification of the model in terms of omitted covariates.

The stratification approach is closely related to the method of Begg and Greenes (1983) except the subjects are stratified using the propensity scores instead of the set of covariates X. In fact, if C_1,k (and C_0,k) has only one actual propensity score for each k, as in the case of a single finite pattern covariate, then ${\widehat{\text{Se}}}_{PS}$ and ${\widehat{\text{Sp}}}_{PS}$ are exactly the same as the BG estimators with categorical covariates and are consistent estimators.

The stratification approach in general cannot completely remove the bias, but can greatly reduce it (Rosenbaum and Rubin, 1984, D'Agostino, 1998). On the other hand, for a large sample, if we increase the number of strata, bias may be further reduced.

2.2. Asymptotic properties of the new estimators

Following Lunceford and Davidian (2004), the asymptotic distributions of the estimators ${\widehat{\text{PPV}}}_{\text{PS}}$ and ${\widehat{\text{NPV}}}_{\text{PS}}$ can be derived by representing them as solutions to sets of estimating equations and appealing to the theory of M-estimation (Stefanski and Boos, 2002). The asymptotic distributions of the estimators of interest, ${\widehat{\text{Se}}}_{PS}$ and ${\widehat{\text{Sp}}}_{\text{PS}}$, may then be derived by applying the delta method. As will be shown below, the variance of the resulting asymptotic distribution has a very complicated form and is difficult to estimate. A more useful result can be obtained by assuming that the propensity scores e_t,i and the quantiles of the distribution of the propensity score, q_t,k, are known, t = 0,1, i = 1,2,…,n_t, k = 1,2,…,K − 1. Under these assumptions, the following theorem gives the asymptotic joint distribution for ${\hat{P}}_{\text{PS}}$, ${\widehat{\text{Se}}}_{PS}$, and ${\widehat{\text{Sp}}}_{PS}$.

THEOREM 3. Let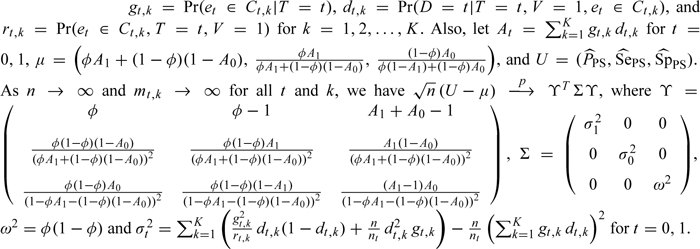

The proof of Theorem 3 is given in Section A1 of the Appendix (supplementary material available at Biostatistics online).

The estimators ${\hat{P}}_{\text{PS}}$, ${\widehat{\text{Se}}}_{PS}$, and ${\widehat{\text{Sp}}}_{PS}$ are not consistent. However, if the number of strata K→∞ and max_{1 ≤ k ≤ K}{q_t,k − q_{t,k − 1}}→0, where q_{t,k − 1} and q_t,k are the two end points of the class defined by C_t,k, then, as we show in Section A2 of the Appendix (supplementary material available at Biostatistics online), ${\hat{P}}_{\text{PS}}$, ${\widehat{\text{Se}}}_{PS}$, and ${\widehat{\text{Sp}}}_{PS}$ are consistent estimators of the disease prevalence, sensitivity and specificity, respectively, given that the number of verified subjects in each stratum m_t,k→∞.

In practice, the propensity scores e_t,i and the quantiles of the distribution of the propensity score, q_t,k, t = 0,1, i = 1,2,…,n_t, k = 1,2,…,K − 1, are not known and the variance of the asymptotic distribution should take into account the sampling variability of their estimates. The asymptotic distributions of ${\widehat{\text{Se}}}_{PS}$ and ${\widehat{\text{Sp}}}_{PS}$ that account for the sampling variability of the estimates are derived in Section A3 of the Appendix (supplementary material available at Biostatistics online).

The variances Σ_t in Lemma 3 in Section A3 of the Appendix (supplementary material available at Biostatistics online) are too difficult to estimate to make them useful in practice. As Lunceford and Davidian (2004) note, it is usual practice to treat the strata as fixed and independent and to estimate the parameter of interest within each stratum, then average across strata. In our case, this would yield the estimator 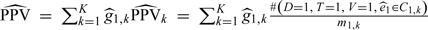for PPV (and a similar estimator for NPV), where 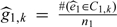. Note that the ${\hat{g}}_{t,k}$ and m_t,k (number of verified subjects in C_t,k) are treated as fixed, t = 0,1, k = 1,2,…,K. The variances would thus only consider the variability of and would be estimated as 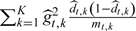, where .

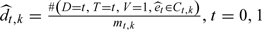The variances σ_t² in Lemma 1 in Section A1 of the Appendix (supplementary material available at Biostatistics online) can be seen as a compromise between the correct (but difficult to estimate) variances in Lemma 3 and the naive variances usually estimated in practice. The naive variances and σ_t² are both less than the correct variances, but the latter are closer to the correct variances; the differences between the two variances can be shown to be 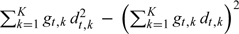, which are always positive. The bootstrap is another option for variance estimation. If the propensity scores and the quantiles of the distributions of the propensity scores are estimated, the responses D_i within each stratum and between strata will not be independent because the stratification is based on the estimated propensity scores, which are obtained from a common model (Du, 1998). In our simulations, we adopt the bootstrap procedure of Tu and Zhou (2002) in this setting; the details are provided in Section A4 of the Appendix (supplementary material available at Biostatistics online).

3. SIMULATION STUDY

In this section, simulation studies are used to compare the new method with existing approaches with respect to bias and variance. From Section 2, the BG and MS methods require a parametric model for D|(T,X), the IPW method requires a parametric model for V|(T,X), and the SP method requires both models. Hence in the simulation studies, we consider four scenarios: (i) the models for D|(T,X) and V|(T,X) are both correctly specified, (ii) the model for D|(T,X) is misspecified but the model for V|(T,X) is correctly specified, (iii) the model for D|(T,X) is correctly specified but the model for V|(T,X) is misspecified, and (iv) the models for D|(T,X) and V|(T,X) are both misspecified. In practice, it is often a challenge to correctly specify a model for D|(T,X). On the other hand, as addressed in Alonzo and others (2003), it is often the case that the verification mechanism is well understood or can be controlled by the investigators; hence, it is more likely that the model for V|(T,X) is correctly specified. Therefore, comparisons among the competing methods in scenarios (ii) and (iv) may be particularly important.

As in Alonzo and others (2003), we consider the disease to arise from two underlying continuous disease processes, which remain subclinical until some function of the processes exceeds some threshold, at which point the disease becomes apparent. In particular, two independent random variables Z₁∼N(0,0.5) and Z₂∼N(0,0.5) were generated, and the disease indicator D was specified as D = I[g(Z₁,Z₂) > r₁]. Thus, by varying g(Z₁,Z₂) one can consider different disease processes, and by varying r₁ one can consider different disease prevalences.

The diagnostic test result was assumed to be determined by an underlying continuous latent variable L that is related to D through Z₁ and Z₂: L = α₁Z₁ + β₁Z₂ + ε₁, where ε₁∼N(0,0.25) and is independent of Z₁ and Z₂. The binary test result T was determined as T = I[L > r₂], with the threshold r₂ determining the sensitivity and specificity of the test. Similarly, two covariates were chosen such that they relate to the two separate components of the disease process: X₁ = α₂Z₁ + ε₂ , and X₂ = β₂Z₂ + ε₃, where ε₂ and ε₃ are independent N(0,0.25) random variables (and also independent of Z₁,Z₂, and ε₁). By varying α₁, α₂, β₁, and β₂, one can vary the extent to which the test result and the covariates capture the different components of the underlying disease process, as well as the correlations between the test result and the covariates. The values also affect the discriminatory abilities of T, X₁, and X₂ with respect to D. Finally, the verification probability h(T,X₁,X₂) was chosen to be a specified function of T, X₁, and X₂ in keeping with the MAR assumption. In the following simulation studies, the PS method used 10 strata for classification.

(A) Models for D|(T,X) and V|(T,X) are both correctly specified.

Let g(Z₁,Z₂) = Z₁ + Z₂ and h(T,X₁,X₂) = δ₁ + δ₂T + (1 − δ₁ − δ₂)I[X₁ ≥ c₁]I[X₂ ≥ c₂], where 0 ≤ δ₁,δ₂ < 1 and δ₁ + δ₂ < 1. A generalized linear model for D given T, X₁, and X₂ with probit link is close to the true model (Alonzo and Pepe, 2005).

In this case, the verification probabilities are 1.0 for those subjects with T = 1,X₁ ≥ c₁, and X₂ ≥ c₂;1 − δ₂ for those subjects with T = 0,X₁ ≥ c₁, and X₂ ≥ c₂;δ₁ + δ₂ for those subjects with T = 1 and either X₁ < c₁ or X₂ < c₂; and δ₁ otherwise. Under the true model, the verification probabilities can be estimated using a logistic regression with V as the response and T and I[X₁ ≥ c₁]I[X₂ ≥ c₂] as the predictors.

The thresholds r₁ and r₂ were chosen to make the disease prevalence 0.10 and the specificity 0.80, respectively. We consider different values of α₁ and β₁ for T = I[α₁Z₁ + β₁Z₂ + ε₁ > r₂] and set α₂ = β₂ = 1; we fix δ₁ = 0.2,δ₂ = 0.5, and choose c₁ and c₂ to be the 80th percentiles of the distributions of X₁ and X₂, respectively.

Table 2 presents estimates of the disease prevalence, sensitivity, and specificity of the test across 1000 realizations of the simulation with a sample size of 1000. The mean asymptotic variance (averaged over 1000 realizations) and the simulation variances are also presented. The asymptotic variance for the PS method was estimated using the asymptotic variance formula in Theorem 3, and for the existing methods the asymptotic variances were estimated based on the methods suggested in Alonzo and Pepe (2005). For comparison, the results for the simple estimators using the complete data (“Full”), that is with all cases verified, are also presented. Results for all methods discussed are given in the rows, while results for the different values of (α₁,β₁) considered are provided in the columns. From the simulation results, it is clear that all of the methods except for the naive estimators perform very well if both parametric models for D|(T,X) and V|(T,X) are correctly specified. The estimated variances from the asymptotic variance formulae are very close to their corresponding simulation variances. The variances presented in the three sections of the table indicate that the BG and MS estimators are typically more efficient than the SP, IPW, and PS estimators, in agreement with Alonzo and Pepe (2005). Similar results were obtained when δ₁ and δ₂ were varied.

Table 2.

Mean estimated disease prevalence, sensitivity, and specificity (mean asymptotic variance, simulation variance in 10⁻⁴ units) from 1000 realizations with different values of α₁ and β₁ when the sample size is 1000. Models for disease and verification are correctly specified

	(α1, β1)
Method	(0.7, 0.7)	(0.5, 0.5)	(1, 0)	(0, 0)
Prevalence
True value	0.10	0.10	0.10	0.10
Full†	0.10 (0.90, 0.90)	0.10 (0.89, 0.82)	0.10 (0.90, 0.87)	0.10 (0.90, 0.90)
Naive	0.21 (4.80, 4.89)	0.20 (4.61, 4.35)	0.18 (4.42, 4.59)	0.12 (3.44, 3.29)
BG	0.10 (1.33, 1.40)	0.10 (1.51, 1.52)	0.10 (1.73, 1.84)	0.10 (2.34, 2.28)
MS	0.10 (1.33, 1.40)	0.10 (1.52, 1.52)	0.10 (1.74, 1.85)	0.10 (2.35, 2.28)
IPW	0.10 (1.44, 1.46)	0.10 (1.73, 1.63)	0.10 (2.13, 2.16)	0.10 (3.21, 3.16)
SP	0.10 (1.39, 1.44)	0.10 (1.61, 1.60)	0.10 (1.86, 1.93)	0.10 (2.56, 2.45)
PS	0.10 (1.47, 1.48)	0.10 (1.75, 1.67)	0.10 (2.16, 2.20)	0.10 (3.21, 3.16)
Sensitivity
True value	0.89	0.78	0.65	0.20
Full†	0.89 (9.8, 9.7)	0.78 (17.2, 17.4)	0.65 (22.7, 24.2)	0.20 (15.9, 16.6)
Naive	0.96 (5.2, 5.5)	0.91 (11.7, 12.7)	0.85 (21.5, 22.8)	0.40 (63.0, 66.7)
BG	0.89 (30.0, 36.0)	0.79 (46.5, 54.5)	0.65 (53.8, 63.2)	0.20 (24.4, 27.3)
MS	0.89 (30.5, 36.1)	0.79 (46.9, 54.5)	0.65 (54.2, 63.2)	0.20 (24.7, 27.3)
IPW	0.90 (34.7, 39.5)	0.80 (56.6, 65.1)	0.67 (69.4, 79.4)	0.21 (31.3, 34.9)
SP	0.89 (33.8, 39.8)	0.79 (51.4, 60.0)	0.65 (58.9, 68.3)	0.20 (25.9, 28.5)
PS	0.89 (34.9, 40.4)	0.79 (56.0, 65.1)	0.66 (67.7, 77.7)	0.20 (29.9, 33.2)
Specificity
True value	0.80	0.80	0.80	0.80
Full†	0.80 (1.77, 1.85)	0.80 (1.78, 1.68)	0.80 (1.78, 1.79)	0.80 (1.78, 1.77)
Naive	0.53 (9.11, 9.66)	0.53 (9.08, 8.78)	0.53 (9.06, 8.98)	0.54 (9.08, 9.64)
BG	0.80 (1.90, 2.01)	0.80 (1.89, 1.82)	0.80 (1.89, 1.87)	0.80 (1.88, 1.85)
MS	0.80 (1.90, 2.01)	0.80 (1.90, 1.82)	0.80 (1.90, 1.87)	0.80 (1.88, 1.85)
IPW	0.80 (1.94, 2.04)	0.80 (1.93, 1.90)	0.80 (1.94, 1.93)	0.80 (1.93, 1.88)
SP	0.80 (1.91, 2.02)	0.80 (1.91, 1.85)	0.80 (1.91, 1.88)	0.80 (1.89, 1.85)
PS	0.80 (1.95, 2.06)	0.80 (1.95, 1.92)	0.80 (1.96, 1.95)	0.80 (1.94, 1.89)

^†Estimator based on complete data.

BG, Begg and Greenes estimator; MS, Mean Score estimator; IPW, Inverse Probability Weighting estimator; SP, Semi-parametric Efficient estimator; PS, Propensity Score Stratification estimator.

(B) Only the model for D|(T,X) is misspecified.

Let g(Z₁,Z₂) = exp(Z₁Z₂),T = I[Z₁Z₂ + ε₁ > r₂] and let h(T,X₁,X₂) be defined as in (A). Here r₁ and r₂ were chosen to make the disease prevalence 0.105 and the specificity 0.65, respectively. In this case, if we use a generalized linear model for D given T, X₁, and X₂, with logit link, this model is misspecified. As in (A), the verification probabilities are 1.0 for those subjects with T = 1,X₁ ≥ c₁[tnqit]and[/tnqit]X₂ ≥ c₂;1 − δ₂ for those subjects with T = 0,X₁ ≥ c₁, and X₂ ≥ c₂;δ₁ + δ₂ for those subjects with T = 1 and either X₁ < c₁[tnqit]or[/tnqit]X₂ < c₂; and δ₁ otherwise. The verification probabilities can be reasonably estimated using a logistic regression with V as the response and T and I[X₁ ≥ c₁]I[X₂ ≥ c₂] as the predictors.

We fix α₂ = β₂ = 1, and δ₁ = 0.05, but allow δ₂ to have different values from 0 to 0.8. It should be noted that small values of both δ₁ and δ₂ indicate a strong dependence of V on X₁ and X₂ (but not on T); a small value of δ₁ but larger value of δ₂ indicates a stronger dependence of V on T (but not on X₁ and X₂) such that a greater number of subjects with a positive test will have their disease status verified; and a large value of δ₁ indicates little dependence of V on either T, X₁ or X₂. We consider the case where the thresholds c₁ and c₂ are the 80th percentiles of the distributions of X₁ and X₂, respectively.

We compare the estimates of the disease prevalence, sensitivity, specificity, and their mean square errors (MSEs) among the different methods. The MSE, estimated by summing the square of the bias of the estimate and the simulation variance, serves as a summary index of overall performance. The estimates of the disease prevalence, sensitivity, specificity, and their MSEs with varying δ₂ are presented in Figures A1, A2, and A3 in the Appendix (supplementary material available at Biostatistics online) when the thresholds c₁ and c₂ are the 80th percentiles of the distributions of X₁ and X₂, respectively. As shown in Figures A1(a), A2(a), and A3(a) (supplementary material available at Biostatistics online), the BG and MS estimators are noticeably biased. Although the SP approach requires a model for disease, it still yields good estimates due to its “doubly robust” property. Since the verification model is correctly specified, as expected, the IPW and PS methods yield good estimates. The MSEs presented in Figures A1(b), A2(b), and A3(b) (supplementary material available at Biostatistics online) indicate that the BG and MS estimators tend to have larger MSEs in most cases, mainly due to their larger bias. In terms of bias and MSE, the PS, IPW, and SP methods are very comparable for estimating the disease prevalence and sensitivity. This is not true for estimating specificity, as shown in Figure A3(b) (supplementary material available at Biostatistics online) where the IPW estimator has a larger MSE than the other estimators. Similar results hold when δ₂ is fixed but δ₁ is varied when only the model for D|(T,X) is misspecified.

(C) Only the model for V|(T,X) is misspecified.

Let g(Z₁,Z₂),T, and h(T,X₁,X₂) be defined as in (A). As in (A), a generalized linear model for D given T, X₁, and X₂ with probit link is considered as the true model. The verification probabilities are estimated from a logistic regression model with V as the response and T and (continuous) X₁ and X₂ as predictors. This model is clearly misspecified. We also fix α₂ = β₂ = 1 and δ₁ = 0.05, and c₁ and c₂ are the 80th percentiles of the distributions of X₁ and X₂, respectively. The value of δ₂ is also allowed to range from 0 to 0.8.

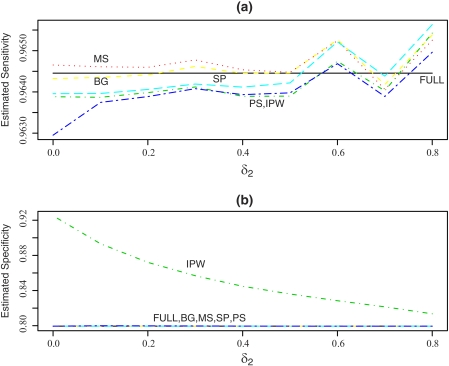
We again compare the estimates of the disease prevalence, sensitivity, specificity, and their MSEs among the competing methods. The estimates of the disease prevalence, sensitivity, specificity, and their MSEs with varying δ₂ are presented in Figure 1 and Figures A4 and A5 in the Appendix (supplementary material available at Biostatistics online). As expected, the BG, MS, and SP estimators perform very well in terms of bias and MSE. The IPW and PS estimators depend only on the model for V|(T,X) and are not expected to perform as well in this case. The PS estimators perform much better than the IPW estimators for estimating disease prevalence and specificity, but the IPW estimator is better than the PS estimator for sensitivity.

Fig. 1.

Mean estimated sensitivity and specificity from 1000 realizations with δ₁ = 0.05 when the sample size is 1000 and c₁ and c₂ are the 80th percentiles of the distributions of X₁ and X₂. Only the model for V|(T,X) is misspecified. BG, Begg and Greenes estimator; FULL, estimator based on complete data; MS, Mean Score estimator; IPW, Inverse Probability Weighting estimator; SP, Semi-parametric Efficient estimator; PS, Propensity Score Stratification estimator.

(D) Models for D|(T,X) and V|(T,X) are both misspecified.

Let g(Z₁,Z₂), T, and h(T,X₁,X₂) be defined as in (B). We again use a generalized linear model for D given T, X₁, and X₂ with logit link; this model is misspecified. The verification probabilities are estimated from a logistic regression model with V as the response and T and (continuous) X₁ and X₂ as predictors. This model is also clearly misspecified. We also fix α₂ = β₂ = 1 and δ₁ = 0.05. The value of δ₂ is allowed to range from 0 to 0.8. We again consider the case where the thresholds c₁ and c₂ are fixed to be the 80th percentiles of the distributions of X₁ and X₂, respectively.

Figure 2 and Figures A6 and A7 in the Appendix (supplementary material available at Biostatistics online) present estimates of the disease prevalence, sensitivity, and specificity of the test and their MSEs across 1000 realizations of the simulation with a sample size of 1000. As shown in Figures 2 and A6(a) (supplementary material available at Biostatistics online), the estimates derived from the PS method are uniformly less biased than those for the other methods. Also, as shown in Figures A6(b) and A7 (supplementary material available at Biostatistics online), the PS method has better overall performance in terms of MSE. Although the SP method is doubly robust, it performs poorly when the disease and verification models are both misspecified. The results presented here indicate that the proposed PS method is more robust to model misspecification in this case. Similar results hold when δ₂ is fixed but δ₁ is varied in this situation.

Fig. 2.

Mean estimated sensitivity and specificity from 1000 realizations with δ₁ = 0.05 when the sample size is 1000 and c₁ and c₂ are the 80th percentiles of the distributions of X₁ and X₂. Both models for D|(T,X) and V|(T,X) are misspecified. BG, Begg and Greenes estimator; FULL, estimator based on complete data; MS, Mean Score estimator; IPW, Inverse Probability Weighting estimator; SP, Semi-parametric Efficient estimator; PS, Propensity Score Stratification estimator.

Simulation results for all cases for a smaller sample size (n = 500) are presented in Table A1 and Figures A8–A16 in the Appendix (supplementary material available at Biostatistics online). The relative performance of the competing estimators is very similar to that for n = 1000.

4. STUDY OF DEPRESSION IN ELDERLY PRIMARY CARE PATIENTS

We illustrate our proposed methodology using data from a longitudinal study of depression in elderly patients (age ≥ 65) recruited from primary care practices in Monroe County, New York. At the intake evaluation, 708 patients underwent a comprehensive diagnostic assessment for depression using the Structured Clinical Interview for DSM-IV (SCID), an intensive examiner-based assessment that can be considered as a practical gold standard for this purpose (Spitzer and others, 1994). Depression was defined based on the SCID as major or minor depression, actively symptomatic (i.e. either current or partially remitted); 249 patients were classified as having depression and 459 patients were classified as not having depression. Other information collected as part of this study included the Hamilton Depression Rating Scale (HAM-D), a 24-item observer-rated scale designed to measure the severity of depressive symptoms (Williams, 1988). In this example, the utility of the HAM-D as a screening marker for the diagnosis of depression will be evaluated. The HAM-D takes approximately 15–20 min to administer compared to 1–3 h for the SCID.

Data for both the SCID and the HAM-D were collected from all participating patients in this study; therefore, we used randomly selected subsets of these data that resemble data that would be obtained from a two-phase design. In these subsets, HAM-D results are available for all patients, but SCID diagnoses are available only for certain patients randomly selected according to the following mechanism:

(4.1)

where the CIRS is the total score on the Cumulative Illness Rating Scale, a reliable and valid measure of medical burden that quantifies the amount of pathology in each organ system (Linn and others, 1968). Thus, the verification mechanism preferentially selects patients who have a HAM-D score > 7 or patients under the age of 75 with a relatively high cumulative illness burden. Using this mechanism, approximately 46% of patients, on average, would be selected for SCID verification of the depression diagnosis.

We consider estimation of the sensitivity and specificity of the HAM-D > 7 for screening for depression and treat age, gender, years of education, and CIRS total score as covariates (i.e. D = SCID diagnosis,T = I[HAM-D > 7] and X = [age, gender, years of education, CIRS total score] in terms of previous notation). Sensitivity and specificity were estimated using the naive, BG, MS, IPW, and SP methods as well as the new method based on propensity score stratification (PS) with five strata. Since the full data are available (in addition to the selected subsets), the estimators in the setting of verification bias can be compared to the “full data” estimators, which are not subject to this bias.

The BG, MS, and SP estimators require a model for Pr(D|T,X). A logistic regression model was used for this purpose assuming linear relationships between log odds of depression and age, years of education, and CIRS total score. Although the true model in this case is not known, it is likely that there is some degree of model misspecification present. The IPW and SP estimators require a model for Pr(V|T,X). Again a logistic regression model was used for this purpose assuming linear relationships between log odds of verification and age, years of education, and CIRS total score. According to the true verification mechanism described above, this model for verification is clearly misspecified.

Table 3 presents estimates of the disease prevalence, sensitivity, and specificity of the HAM-D averaged across 1000 simulated realizations of the process of selecting subsets of data from a two-phase design. The means of bootstrap variances with 100 bootstrap replications are also presented in the table. Since the true model for the verification probabilities is known, the estimates for the IPW, SP, and PS methods using the verification probabilities estimated from the true model are also presented for comparison (indicated by ‡ in Table 3). When the true model for verification is used, the IPW, SP, and PS yield very good estimates, as expected. When the verification model is misspecified, the PS estimators yield estimates that are very close to the full data estimates, although their variances are slightly larger than those for the BG, MS, and SP estimators. The BG, MS, SP, and IPW estimators are slightly more biased. As expected, the naive estimators are badly biased.

Table 3.

Mean estimated disease prevalence, sensitivity and specificity (mean bootstrap variance in 10⁻³ units) across 1000 realizations in the depression study example

	Estimation
Method	Prevalence	Sensitivity	Specificity
Full†	0.35	0.82	0.69
Naive	0.48 (0.92)	0.95 (0.28)	0.36 (1.10)
BG	0.33 (0.65)	0.85 (1.81)	0.68 (0.67)
MS	0.33 (0.65)	0.85 (1.81)	0.68 (0.67)
IPW	0.33 (0.78)	0.84 (2.46)	0.69 (0.78)
IPW‡	0.34 (0.87)	0.82 (2.40)	0.68 (0.73)
SP	0.33 (0.79)	0.84 (2.41)	0.68 (0.70)
SP‡	0.35 (0.84)	0.82 (2.30)	0.68 (0.73)
PS	0.34 (0.68)	0.82 (2.06)	0.68 (0.67)
	§(0.81)	§(3.00)	§(0.65)
PS‡	0.34 (0.87)	0.82 (2.40)	0.68 (0.73)
	§(0.82)	§(3.10)	§(0.65)

^†Estimator based on complete data.

^‡Pr(V|T, X) estimated using the true model (4.1).

^§Variance for the PS estimator based on the asymptotic distribution (Theorem 3).

BG, Begg and Greenes estimator; MS, Mean Score estimator; IPW, Inverse Probability Weighting estimator; SP, Semi-parametric Efficient estimator; PS, Propensity Score Stratification estimator.

5. DISCUSSION

Existing methods for correcting verification bias require estimation of Pr(D|T,X), Pr(V|T,X), or both. For cases in which X is continuous or high dimensional, nonparametric estimation of these quantities is more challenging and parametric models are commonly used for this purpose. Misspecification of these models can have an adverse impact on the performance of the existing estimators, as was evident in our simulation studies. Alonzo and Pepe (2005) found that the SP estimator performed well when only one of the models (disease or verification) was misspecified due to its doubly robust property, but their studies, as well as ours, showed that it performed as poorly as the IPW estimator when both models were misspecified. The BG and MS estimators seemed to perform better than the SP and IPW methods in this case but still had significant bias. Our proposed PS estimator demonstrated excellent robustness to misspecification of both models. The PS estimators will be most useful in cases where the verification mechanism is unknown and the functional form of the relationship between D and X is unclear. The PS estimators are not designed to be robust to model misspecification due to omitted covariates, but our simulation study suggests that even in this case they perform well relative to competing methods. The robustness of the PS estimator comes at the price of reduced efficiency when the models for disease and verification are correctly specified, as would be expected.

When the probabilities of selection for verification are very small for some subjects, the IPW and SP methods yield very unstable estimates of sensitivity and specificity, and the SP estimates may even fall out of the [0,1] range. By using wider intervals at the lower end of the propensity score scale for stratification, the PS method will yield more stable estimates; however, in such cases, the bias may increase if the variation in propensity scores within the stratum is large. On the other hand, the BG and MS methods do not require specification of a model for verification, but rely on proper modeling of the relationship between disease and the test results and covariates. Correct specification of this model may be difficult, particularly in settings involving many covariates.

When using the PS method, the practitioner has to decide on the number of strata (K) to form based on the estimated propensity score. In the context of propensity score stratification, Rosenbaum and Rubin (1984) demonstrated that using five strata would remove >90% of the bias due to the covariates in most cases. In practice, between 5 and 10 strata are typically used, but it is difficult to recommend a rule-of-thumb for the best choice in our context because it depends not only on the sample size but also on the prevalence of the disease and on the number of verified cases. Our limited simulation studies indicate that, as expected, there is a bias variance trade-off when having more strata (reduced bias but increased variability) versus fewer strata (increased bias but reduced variability).

Variations on the PS estimator could be developed. For example, to estimate the integrals in (2.3), we can estimate F_t(e) nonparametrically using the empirical distribution function, and then estimate E[D|T = t,V = 1,e_t(x) = e],t = 0,1, using a generalized additive model (Hastie and Tibshirani, 1990). A special case of this, when the latter quantity is estimated using a generalized linear model, is propensity score regression. Our investigation of this method showed that it lacked robustness because it requires specification of a parametric model. The use of generalized additive models in this setting, however, may be useful.

SUPPLEMENTARY MATERIAL

Supplementary material is available at http://biostatistics.oxfordjournals.org.

FUNDING

National Institutes of Health (1 UL1 RR024160-01 to M.P.M.).