Characterizing Longitudinal Patterns of Physical Activity in Mid-Adulthood Using Latent Class Analysis: Results From a Prospective Cohort Study

Abstract

The authors aimed to describe how longitudinal patterns of physical activity during mid-adulthood (ages 31–53 years) can be characterized using latent class analysis in a population-based birth cohort study, the Medical Research Council’s 1946 National Survey of Health and Development. Three different types of physical activity—walking, cycling, and leisure-time physical activity—were analyzed separately using self-reported data collected from questionnaires between 1977 and 1999; 3,847 study members were included in the analysis for one or more types of activity. Patterns of activity differed by sex, so stratified analyses were conducted. Two walking latent classes were identified representing low (52.8% of males in the cohort, 33.5% of females) and high (47.2%, 66.5%) levels of activity. Similar low (91.4%, 82.1%) and high (8.6%, 17.9%) classes were found for cycling, while 3 classes were identified for leisure-time physical activity: “low activity” (46.2%, 48.2%), “sports and leisure activity” (31.0%, 35.3%), and “gardening and do-it-yourself activities” (22.8%, 16.5%). The classes were reasonably or very well separated, with the exception of walking in females. Latent class analysis was found to be a useful tool for characterizing longitudinal patterns of physical activity, even when the measurement instrument differs slightly across ages, which added value in comparison with observed activity at a single age.

The beneficial effects of regular physical activity on health and well-being are well established (1), and promoting a physically active lifestyle is now considered a major element of public health policies. However, most studies to date have had limited information on the types of physical activity undertaken throughout adult life. Identification of longitudinal patterns of physical activity across adulthood may allow better understanding of the role of type, timing, and duration of physical activity in later health and well-being.

The measurement of physical activity has proven to be a challenge, partly because of the multidimensional nature of movement and also because of the limitations of self-reported data. Both objective measurement of the different dimensions of motion (type, duration, intensity) and subjective reporting of activity are prone to errors (2). However, the use of questionnaires to capture physical activity behavior may provide insights into habitual physical activity patterns.

The United Kingdom Medical Research Council’s National Survey of Health and Development (NSHD), also known as the 1946 British birth cohort, is a population-based birth cohort study that provides a unique opportunity to investigate longitudinal patterns of physical activity in a national sample of over 3,800 men and women (3). As with most longitudinal studies, the nature of the physical activity data available in the NSHD presents an additional methodological challenge, in that different versions of the questionnaire were used in different waves. One statistical approach that can be useful in the reduction of complex, correlated data such as these is latent class analysis (LCA).

Our aim in this paper is to describe how longitudinal patterns of physical activity can be characterized using LCA and to assess their added value in comparison with observed activity at a single age, using data from mid-adulthood (ages 31–53 years) collected in the NSHD.

MATERIALS AND METHODS

Participants

The sample comprised participants in the NSHD, a social-class-stratified sample of all singleton births occurring to married parents in England, Scotland, and Wales during 1 week in March 1946. The study began with 5,362 subjects (2,814 men), and the cohort has been followed up on many occasions since birth, with information being collected from a variety of sources. The average follow-up response rate during the period of the present study (ages 31–53 years) was 84% (3), and comparisons with census data showed that persons remaining in the cohort at age 53 years were broadly representative of native-born adults living in England, Scotland, and Wales at that time (4).

Measures

In the NSHD, self-reported information about physical activity has been collected to differing extents during several sweeps of data collection. At ages 31 and 43 years (in 1977 and 1989, respectively), a number of questions were asked about specific types of physical activity, and at age 36 years (in 1982) more detailed information was collected (5), with study participants being asked about the frequency and duration of participation in many different activities during the preceding month, based on the Minnesota Leisure Time Physical Activity Questionnaire (6). At age 53 years (in 1999), a more general question was asked regarding sports, vigorous leisure activities, and exercises.

In the present analysis, we focused on 3 different types of self-reported physical activity: walking, cycling, and leisure-time physical activity (LTPA). Three-level categorical variables were derived from the questionnaire responses, which can be generally considered as 1) no activity or virtually no activity, 2) less active, and 3) most active.

Participants responded to questions on walking at ages 36 and 43 years only. The following 3-level categorical variables were derived on the basis of reported frequency, duration, or distance of activity: time spent walking during the day at age 36 years; time spent walking to work at age 36 years; time spent walking for pleasure at age 36 years; and distance walked on an average weekday at age 43 years.

Participants were asked about cycling only at ages 31, 36, and 43 years, with a single 3-level categorical variable being derived at each age based on the frequency, duration, or distance of activity.

LTPA was defined as all other activities undertaken in participants’ spare time, with data available at ages 36, 43, and 53 years. At age 36 years, responses to questions based on the Minnesota Leisure Time Physical Activity Questionnaire were used to derive variables for gardening (a combination of 10 different activities), “do-it-yourself” (DIY) activities (14 activities, including building, decorating, moving heavy objects, and woodwork), and sports and leisure activities (29 activities). For each activity, the corresponding metabolic equivalent of task was first identified using the compendium of Ainsworth et al. (7). These metabolic equivalents were multiplied by the reported amount of time spent performing that activity during the previous month; these data were then summed across the activity type (e.g., gardening). From these total values, the 3-level categorical variables were derived. At age 43 years, participants were asked specific questions about 5 different regular activities: vigorous housework or cleaning; heavy gardening; heavy building or DIY; sports or vigorous leisure activities; and other activity. Variables were derived for each activity using the amount of time the study participant reported having spent in that activity. At age 53 years, a single variable was derived based on the number of occasions the study participant reported having taken part in sports, vigorous leisure activities, or exercise in his/her spare time during the previous 4 weeks.

The resultant derived variables are shown in Web Table 1, which appears on the Journal’s Web site (http://aje.oxfordjournals.org/).

Because the data collection took place over several months during each follow-up, we investigated the effect of seasonal influences on the distributions of the above variables.

Statistical analyses

LCA is a multivariate regression model that describes the relations between a set of observed dependent variables (“latent class indicators”), in this case the reported physical activity levels, and an unobserved categorical latent variable, each level of which is referred to as a “latent class.” For ordered categorical latent class indicators, as in the present application, the relations are characterized by a set of logistic regression equations (8). LCA assumes conditional independence of variables within each latent class. The latent class indicators may be cross-sectional, longitudinal, or a combination of both. When longitudinal, the resultant latent classes are often referred to as latent profiles, which identify subgroups that have similar patterns of change in behavior over time. The objective is usually to identify the latent class indicators that best distinguish between classes and to categorize people into their most likely classes given their observed responses (9). This approach has been used previously in NSHD analyses to derive longitudinal profiles of childhood enuresis (10), social functioning (11), adolescent and adult mental health (12), and midlife urinary incontinence (13).

LCA was conducted on each type of physical activity separately. The expectation-maximization algorithm (14) was used to allow the inclusion of all subjects with at least 1 measure of a given type of physical activity. The expectation-maximization algorithm relies on the assumption that data are missing at random (15). For comparison, we also fitted LCA models using only subjects with complete data. Sample weights were used in each LCA model to allow for the study design of NSHD. Bootstrap standard errors of the model parameter estimates were obtained using 3,000 bootstrap samples. To ensure that a true (rather than local) maximum likelihood solution had been reached, we used 100, 1,000, or 10,000 random start values (as necessary) to fit each model.

To assess whether it was necessary to conduct the analyses separately by sex, we compared male-female multigroup LCA models with and without constraining the parameters to be the same in both sexes. Model fits were compared using the likelihood ratio test (LRT), with the sizes of the latent classes also being considered. Class sizes were calculated on the basis of the estimated posterior class membership probabilities (the probability of a subject’s belonging to a given class conditional on his or her observed response values).

We used a variety of different tools to decide how many classes were required, since no single approach is commonly accepted (9). The standard LRT is not valid in the LCA setting, so we used the Lo-Mendell-Rubin adjusted LRT (16) and 3 information criteria: Akaike’s Information Criterion (17), Schwarz’s Bayesian Information Criterion (BIC) (18), and the sample-size-adjusted BIC (19). The Lo-Mendell-Rubin adjusted LRT tests the model that has T classes against the model with T − 1 classes, with a significant P value indicating that the T-class model provides a better fit to the data. Models that best combine goodness of fit and parsimony are indicated by minimum values of the information criteria. The entropy, relative sizes, and meaningful interpretation of the latent classes were also considered. Entropy is a summary statistic based on the posterior class membership probabilities that evaluates the quality of the classification in terms of the separation of the latent classes. The values of entropy range from 0 to 1, with scores close to 1 indicating clear classifications (8).

As well as conducting the analysis outlined above in the entire sample of subjects, we randomly split the sample into 2 equal-sized subsamples that were analyzed using the same approach as an internal test of validity.

To assess whether the longitudinal latent variables were capturing any additional information over reported activity at a single age, we compared the associations between 3 variables representing reported activity (chosen a priori as the most “representative”) and the remaining reported variables within the same type of physical activity with the associations between the latent variables and each reported physical activity variable using (multinomial) logistic regression, weighted by the estimated posterior class membership probabilities. The 3 chosen variables were 1) distance walked on an average weekday at age 43 years, 2) cycling at age 36 years, and 3) LTPA at age 53 years.

The LCA was conducted using Mplus 6 (20), and other analyses were conducted using Stata 11 (21). All tests of statistical significance were 2-sided. Annotated Mplus code is provided in the Web Appendix.

RESULTS

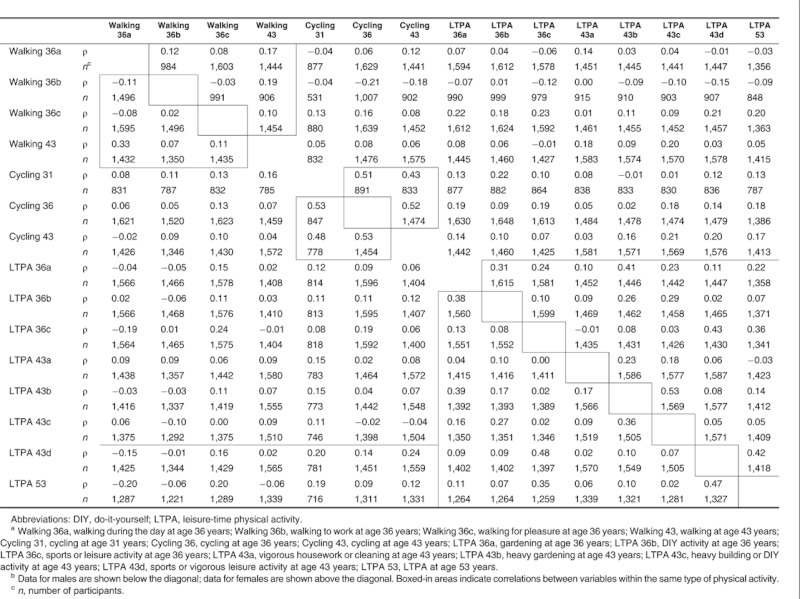
Table 1 shows the polychoric correlations (correlations between ordinal variables) between physical activity variables for males and females. Correlations between variables in different types of physical activity were generally moderate to low, with higher correlations between variables within the same type of activity.

Table 1.

Polychoric Correlations (ρ) Between Physical Activity Variables^a in the National Survey of Health and Development, United Kingdom, 1977–1999^b

The distributions of the physical activity variables for each type, stratified by sex, are shown in Web Table 1. For the majority of variables, there was strong (P < 0.001) evidence of a difference between males and females.

At each age, the physical activity data were collected mainly during the summer and autumn. At age 36 years, 94.1% of data were collected between April and October; at age 43 years, 91.3% were collected between June and November; and at age 53 years, 96.3% were collected between May and November. Only at age 43 years was there more than a handful of subjects with data collected during the winter months. There was some evidence that during winter months there was a reduction in time spent walking for pleasure at age 36 years (P = 0.003 by chi-squared test) and engaging in 5 of the LTPA activities (all P’s ≤ 0.004). Observed differences in activity levels between seasons other than winter were less marked.

LCA models with and without the parameters constrained to be the same in both sexes were compared. Table 2 shows the results for walking, which illustrate the approach. Allowing parameters to differ between males and females always provided a significantly better model fit when fit was assessed using the LRT. For models with 2 and 3 classes, constraining the parameters to be the same for males and females resulted in single-sex classes, providing compelling evidence that sex-specific classes were required.

Table 2.

Latent Class Analysis Fit Statistics for Walking, Comparing Models With the Parameters Constrained to Be the Same Between the Sexes With Those Without Such a Constraint, National Survey of Health and Development (n = 3,587), United Kingdom, 1982–1989

	No. of Latent Classes
	1	2	3
Parameters Allowed to Differ Between Males and Females
No. of parameters	17	35	53
Log likelihood	−14,610.7	−14,510.0	−14,480.0
Smallest class percentagea
Males	100.0	47.2	16.8
Females	100.0	33.5	7.8
Parameters Constrained to Be the Same for Males and Females
No. of parameters	9	19	29
Log likelihood	−14,739.1	−14,610.7	−14,527.0
Smallest class percentagea
Males	100.0	0.0	0.0
Females	100.0	0.0	1.1
Overall	100.0	49.7	20.9
Difference in no. of parameters	8	16	24
Likelihood ratio test
Statistic	256.8	201.4	94.0
P value	<0.001	<0.001	<0.001

^aBased on estimated posterior class membership probabilities.

The corresponding results for cycling and LTPA are given in Web Tables 2 and 3. In both cases, allowing parameters to differ between males and females always provided a significantly better fit to the data, so sex-specific latent classes were used.

Models with different numbers of classes were then compared. Table 3 shows the results for walking. In males, the Lo-Mendell-Rubin adjusted LRT indicated that the 2-class model provided a significantly better fit to the data than the 1-class model (P = 0.002), but the introduction of a third class did not result in further improvement (P = 0.34). The 2-class model provided the best fit (i.e., the lowest values) according to Schwarz’s BIC and the sample-size-adjusted BIC, and the 3-class model provided the best fit according to Akaike’s Information Criterion. On the balance of evidence, the 2-class model was used. In females, the same pattern of results was observed and the 2-class model was again used, though the entropy (0.371) was low.

Table 3.

Latent Class Analysis Fit Statistics for Walking Models, National Survey of Health and Development, United Kingdom, 1982–1989

	Sex and No. of Latent Classes
	Males (n = 1,797)			Females (n = 1,790)
	1	2	3	1	2	3
No. of parameters	8	17	26	8	17	26
Log likelihood	−6,129.9	−6,082.8	−6,065.4	−5,994.1	−5,940.5	−5,931.0
Information criteriaa
Akaike’s Information Criterion	12,275.9	12,199.7	12,182.8	12,004.2	11,915.0	11,913.9
Schwarz’s BIC	12,319.8	12,293.1	12,325.6	12,048.1	12,008.3	12,056.6
Sample-size-adjusted BIC	12,294.4	12,239.1	12,243.0	12,022.7	11,954.3	11,974.0
χ2 goodness-of-fit tests
Degrees of freedom	72	63	54	72	63	54
Pearson χ2 test
Statistic	149.1	82.8	51.5	184.5	85.2	64.1
P value	<0.001	0.05	0.57	<0.001	0.03	0.16
LRT χ2
Statistic	160.7	90.7	64.4	166.2	85.7	70.9
P value	<0.001	0.01	0.16	<0.001	0.03	0.06
Smallest class percentageb	100.0	47.2	16.8	100.0	33.5	25.2
Entropy	1.000	0.659	0.500	1.000	0.371	0.556
T classes vs. T − 1 classes
Difference in no. of parameters		9	9		9	9
Lo-Mendell-Rubin adjusted LRT
Statistic		92.8	34.4		150.8	62.1
P value		0.002	0.34		0.003	0.37

Abbreviations: BIC, Bayesian Information Criterion; LRT, likelihood ratio test.

^aMinimum information criterion values are shown in italic type.

^bBased on estimated posterior class membership probabilities.

The results for cycling and LTPA are given in Web Tables 4 and 5. Though findings again were not unanimous, the results suggested using 2-class models for cycling and 3-class models for LTPA.

Table 4 shows the class-specific response probabilities (the probability of observing each level of each indicator variable given membership in a certain class) for the walking models, with classes ordered by decreasing size, and Figure 1 shows circle plots in which the area of each circle is proportional to the probability of observing that level of the variable. In males, subjects in class A (52.8% of study members using estimated posterior class membership probabilities) reported almost entirely low rates of walking during the day at age 36 years, while in class B (47.2%), subjects reported middle or high rates. There was also some difference in walking at age 43 years, with subjects in class B being more likely to report high rates. Class A can thus be considered “low during the day/low” and class B “high during the day/high.” In females there was a more general, though not extreme, shift from higher rates of walking in class A (66.5%) to lower rates in class B (33.5%). The classes can therefore be considered “high” and “low.” The higher-activity class is thus the slightly smaller class in males but the larger class in females.

Table 4.

Class-Specific Response Probabilities for the Walking Latent Class Analysis Models, National Survey of Health and Development, United Kingdom, 1982–1989

	Males (n = 1,797)				Females (n = 1,790)
	Class A (52.8%a)		Class B (47.2%)		Class A (66.5%)		Class B (33.5%)
	Estimate	SEb	Estimate	SE	Estimate	SE	Estimate	SE
Time spent walking during the day at age 36 years
Less than half of the time	0.802	0.104	0.000	0.063	0.174	0.043	0.528	0.066
At least half of the time	0.198	0.082	0.465	0.064	0.342	0.030	0.394	0.040
Practically all of the time	0.000	0.044	0.535	0.074	0.484	0.050	0.077	0.068
Time spent walking to work at age 36 years, minutes
<5	0.797	0.019	0.834	0.021	0.538	0.045	0.871	0.060
5–15	0.150	0.016	0.129	0.019	0.397	0.056	0.028	0.047
≥16	0.053	0.009	0.038	0.009	0.065	0.023	0.101	0.028
Time spent walking for pleasure in the last month at age 36 years, hours
0	0.328	0.022	0.403	0.030	0.342	0.024	0.325	0.032
1–6	0.357	0.022	0.297	0.030	0.264	0.024	0.468	0.047
>6	0.315	0.022	0.300	0.028	0.394	0.030	0.207	0.043
Distance walked on an average weekday at age 43 years, miles (km)
≤0.5 (≤0.8)	0.368	0.035	0.198	0.051	0.275	0.045	0.543	0.052
>0.5–2.5 (>0.8–4.0)	0.469	0.025	0.404	0.038	0.536	0.033	0.437	0.041
>2.5 (>4.0)	0.163	0.041	0.397	0.076	0.188	0.027	0.020	0.026

Abbreviation: SE, standard error.

^aBased on estimated posterior class membership probabilities.

^bBootstrap standard errors based on 3,000 resamples.

Figure 1.

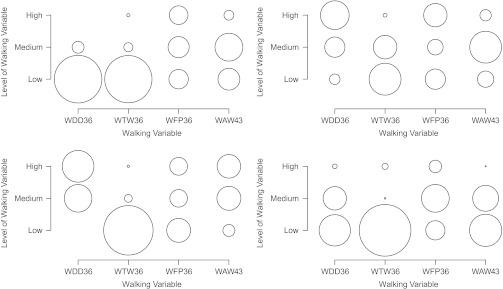
Circle plots of the probability of a positive response in each walking latent class among males (left; n = 1,797; 52.8% in class A, 47.2% in class B) and females (right; n = 1,790; 66.5% in class A, 33.5% in class B), National Survey of Health and Development, United Kingdom, 1982–1989. Upper panels show class A; lower panels show class B. WDD36, amount of time spent walking during the day at age 36 years; WTW36, amount of time spent walking to work at age 36 years; WFP36, amount of time spent walking for pleasure at age 36 years; WAW43, distance walked on an average weekday at age 43 years.

Figure 2 shows a plot of cycling score versus age in each latent class. The score is calculated by summing the products of the class-specific response probability and the corresponding level of cycling (coded 0, 1, or 2) within each class-age combination. In both sexes, there was a larger class (class A: males 91.4%; females 82.1%) with a score close to zero at each age and a smaller class (class B: males 8.6%; females 17.9%) with a much higher score, especially in males. Thus, in both sexes the classes can be considered “low” and “high.”

Figure 2.

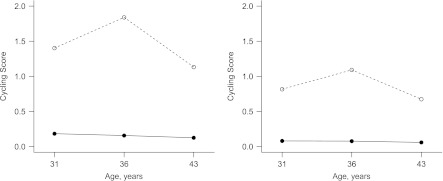
Plot of cycling score (range, 0–2) against age for each cycling latent class in males (left; n = 1,904; 91.4% in class A, 8.6% in class B) and females (right; n = 1,872; 82.1% in class A, 17.9% in class B), National Survey of Health and Development, United Kingdom, 1977–1989. Solid lines, class A; dashed lines, class B.

Figures 3 and 4 are bar plots showing the probability of observing each level of each variable within the latent classes of LTPA for males and females, respectively. The characteristics of the classes were similar in males and females, with the largest class (class A: males 46.2%, females 48.2%) being characterized by low levels of all of the variables, meaning it can be considered “low.” The second-largest class (class B: males 31.0%, females 35.3%) was characterized by high levels of sports or leisure activity at ages 36 and 43 years and thus can be considered “sports and leisure activity.” The smallest class (class C: males 22.8%, females 16.5%) was characterized by relatively high levels of gardening and DIY at ages 36 and 43 years and thus can be considered “gardening and DIY.”

Figure 3.

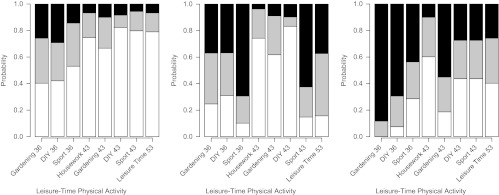
Bar plots of the probability of a positive response for each leisure-time physical activity variable (e.g., gardening at age 36 years) for each latent class (n = 1,848; class A (left), 46.2%; class B (center), 31.0%; class C (right), 22.8%) among males, National Survey of Health and Development, United Kingdom, 1982–1999. White bars, inactive; gray bars, less active; black bars, most active. DIY, do-it-yourself.

Figure 4.

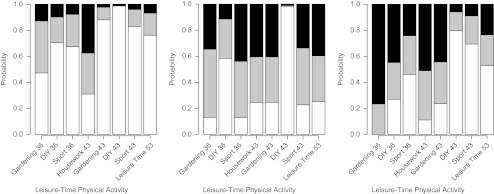
Bar plots of the probability of a positive response for each leisure-time physical activity variable (e.g., gardening at age 36 years) for each latent class (n = 1,823; class A (left), 48.2%; class B (center), 35.5%; class C (right), 16.5%) among females, National Survey of Health and Development, United Kingdom, 1982–1999. White bars, inactive; gray bars, less active; black bars, most active. DIY, do-it-yourself.

Web Table 6 shows the probability of belonging to each latent class conditional on a given most likely latent class (the “separation” of the classes). For example, the first row for walking suggests that males whose most likely latent class is class A had a probability of 0.919 of actually being in class A and a probability of 0.081 of instead being in class B. Classification accuracy is thus signified by high diagonal and low off-diagonal elements in the assignment matrix. The assignment probabilities and entropy values (see Table 3 and Web Tables 4 and 5) suggest that the classes were reasonably well or very well separated, with the exception of walking in females (entropy 0.371).

In the internal validity analysis (results not shown), there was strong evidence in both of the randomly assigned 50% subsamples that sex-specific latent classes were required for all 3 types of physical activity. The number of classes required in each type was again not clear-cut, but on the balance of evidence the same number of classes as in the full sample was used. The proportion of subjects in each class was similar to that in the full sample, and class-specific response probabilities also generally differed little. Even in cases where there was some discrepancy, the interpretation of the classes remained essentially the same. Overall, this suggested strong internal validity of the results using the full sample.

The associations between the latent variable and the observed physical activity variables were always stronger than the associations between the representative reported physical activity variable and the remaining reported variables (results not shown). For cycling, the high correlations (“tracking”) between the observed variables at different ages meant that the differences in the strengths of the associations were relatively small, so the use of longitudinal latent variables added little. For walking and (particularly) LTPA, the associations with the latent variables were much stronger. For example, the LTPA latent variable was strongly associated with vigorous housework or cleaning at age 43 years (P < 0.001 in both males and females), but LTPA at age 53 years was not (males: P = 0.51; females: P = 0.24). The longitudinal latent variables thus captured features of the data which were not captured by the single observed variables.

DISCUSSION

We used an LCA approach to identify latent classes in 3 types of physical activity over 22 years during adulthood. The models generally fitted the data well, the classes were well-separated (with the exception of walking in females), and interpretation of the classes was straightforward. The use of longitudinal latent classes was found to capture additional information over reported activity at a single age.

Males and females were seen to differ in two ways: the sizes and characteristics of the classes (as evidenced by the necessity for sex-specific classes) and the clarity of the separation of the classes (as evidenced by the lower entropy values for walking and cycling in females). Both of these issues could be explained by either true sex differences in physical activity or sex differences in the way the questions were perceived and reported.

Male-female differences in levels of physical activity have been acknowledged in children and adolescents (22, 23), in adults (24), and in later life (25), with males being consistently more active than females. In the present analysis, the higher activity classes for walking and cycling were both estimated to be larger in females than in males. However, the stratified analysis means that the latent classes are not directly comparable between the sexes. In addition, physical activity was mainly considered in terms of frequency or duration, and males may have exercised over greater distances than females and/or with greater intensity for a given frequency or duration. Sex differences could also be partly due to reporting bias—for example, through the overreporting of activities traditionally associated with one’s sex—in order to adhere to a perceived societal norm.

Previous studies examining types of physical activity have often used different classifications (26) or evaluated more specific outcomes (27), making direct comparison difficult. Kuh and Cooper (5) examined physical activity cross-sectionally at age 36 years in the NSHD. They used the same data as were used in the present analysis and derived 4 variables corresponding to “physical activity during the working day,” “sports and recreation activities,” “cycling and walking,” and “heavy gardening and DIY.” We compared Kuh and Cooper’s variables with our longitudinal latent classes and found that those corresponding to similar types of activities were highly correlated. Because our classes cover more than a single time point yet retain similar information, this suggests that our approach is a parsimonious way of summarizing the data.

There was much strength to this analysis. The sample used in the study was large and representative of the population of England, Scotland, and Wales over this period (4), the response rate was high, and a range of different physical activities were examined. The inclusion of sample weights in the LCA models ensured that the sampling structure of the NSHD was correctly accounted for.

The use of the expectation-maximization algorithm in the LCA allowed the inclusion of all subjects with at least 1 measure of physical activity within a given type. Although subjects with no physical activity data could not be included in that part of the analysis, the number of subjects included in at least 1 type of physical activity (n = 3,847) was close to the maximum that could be expected given attrition from the initial NSHD sample. While the validity of the assumption of missingness at random is difficult to assess, analyses were repeated using the subset of subjects with complete data, and results were very similar. The analysis of randomly assigned 50% subsamples additionally suggested strong internal validity of the results obtained using the full sample.

A particular strength of LCA is the flexibility with which it can handle purely longitudinal data (as in the case of cycling) or a mixture of longitudinal and cross-sectional data (walking and LTPA), as well as variables measured on different scales at different time points, within the same modeling framework. These complexities mean that other approaches which have been used to examine physical activity trends over time, such as multilevel modeling (28), would not have been appropriate.

The latent classes of physical activity can be simply incorporated into future analyses either as predictors or as outcomes by weighting models by the estimated posterior class membership probabilities. Fractions of a given subject may thus be allocated to different classes, meaning that analyses correctly adjust for the uncertainty in class membership.

However, there were also limitations. Data availability in the NSHD determined at what ages and to what extent we could examine the different types of physical activity. We could not derive classes that examined changing activity levels within individuals, because changes in the questions over time meant that the same type of activity was often reported in different ways (e.g., in terms of frequency, duration, or distance) at different ages. Therefore, we need to be careful not to overinterpret the longitudinal features of the classes.

The data on physical activity were obtained from questionnaires, which may be prone to nondifferential measurement error (29). The retrospectively self-reported nature of the physical activity measures may have led to recall bias, potentially differentially through social desirability and social approval influencing the responses (30). These potential misclassifications may have attenuated differences between classes, reducing entropy.

Physical activity data were not collected at the same time of year for each study member at each age, which may have led to misclassification due to seasonal variability in activity levels (31). However, because data were rarely collected in winter and activity levels were found to be largely similar between the remaining seasons, the validity of the results should be fairly robust. In any future analyses using the physical activity latent classes, it will also be possible to adjust for the season or month of data collection. Additionally, secular trends in types of physical activity may have changed somewhat since 1977–1999, when these data were collected.

Although the separation of the classes was generally clear, this was not the case for walking in females. Entropy values were higher in the complete-case analysis for all types of physical activity, particularly for walking in females (0.537 vs. 0.371), indicating that the increased sample size came at the expense of reduced separation.

In conclusion, LCA is a useful tool for characterizing longitudinal patterns of physical activity, even when the measurement instrument differs slightly across ages. We found evidence of clearly separated latent classes in different types of physical activity in this large, population-based, prospective study. Further research is needed to link these physical activity classes with health outcomes in later life.

Glossary

Abbreviations

BIC

Bayesian Information Criterion

DIY

do-it-yourself

LCA

latent class analysis

LRT

likelihood ratio test

LTPA

leisure-time physical activity

NSHD

National Survey of Health and Development