New Insights into the Genetics of in Vivo Induction of Maternal Haploids, the Backbone of Doubled Haploid Technology in Maize

Abstract

Haploids and doubled haploid (DH) inbred lines have become an invaluable tool for maize genetic research and hybrid breeding, but the genetic basis of in vivo induction of maternal haploids is still unknown. This is the first study reporting comparative quantitative trait locus (QTL) analyses of this trait in maize. We determined haploid induction rates (HIR) in testcrosses of a total of 1061 progenies of four segregating populations involving two temperate haploid inducers, UH400 (HIR = 8%) and CAUHOI (HIR = 2%), one temperate and two tropical inbreds with HIR = 0%, and up to three generations per population. Mean HIR of the populations ranged from 0.6 to 5.2% and strongly deviated from the midparent values. One QTL (qhir1) explaining up to $\widehat{p}=66\%$ of the genetic variance was detected in bin 1.04 in the three populations involving a noninducer parent and the HIR-enhancing allele was contributed by UH400. Segregation ratios of loci in bin 1.04 were highly distorted against the UH400 allele in these three populations, suggesting that transmission failure of the inducer gamete and haploid induction ability are related phenomena. In the CAUHOI × UH400 population, seven QTL were identified on five chromosomes, with qhir8 on chromosome 9 having $\widehat{p}>20\%$ in three generations of this cross. The large-effect QTL qhir1 and qhir8 will likely become fixed quickly during inducer development due to strong selection pressure applied for high HIR. Hence, marker-based pyramiding of small-effect and/or modifier QTL influencing qhir1 and qhir8 may help to further increase HIR in maize. We propose a conceptual genetic framework for inheritance of haploid induction ability, which is also applicable to other dichotomous traits requiring progeny testing, and discuss the implications of our results for haploid inducer development.

IN VIVO induction of maternal haploids in maize has paved the way for large-scale production of doubled haploid (DH) inbred lines, which today form the backbone of the global hybrid maize industry. Traditionally, the maize plants’ cross-breeding nature required recurrent self-pollinations for 6–10 generations to obtain sufficiently homozygous inbred lines (Hallauer et al. 2010). Application of DH technology reduces the time for inbred development by more than half compared to the traditional method and additionally provides several quantitative genetic, operational, logistical, and economic advantages (Nei 1963; Schmidt 2003; Melchinger et al. 2005; Seitz 2005; Smith et al. 2008; Chang and Coe 2009; Geiger 2009). By using haploid inducer genotypes as pollinators in crosses with source germplasm, ears obtained carry a proportion of seeds containing haploid embryos of maternal origin. Subsequent treatment of haploids with mitotic inhibitors facilitates chromosome duplication resulting in diploid and completely homozygous inbred lines (see Prigge and Melchinger 2012 for a detailed description of DH production).

Modern maize inducers have haploid induction rates (HIR) of about 8% on average (e.g., Röber et al. 2005; Prigge et al. 2011). The genetic mechanisms underlying in vivo induction of maternal haploids in maize are not yet fully understood. The two major hypotheses for possible mechanisms are: (i) failure of fertilization of the egg cell and subsequent parthenogenetic development of the reduced egg into a haploid embryo (Sarkar and Coe 1966; Chalyk et al. 2003; Barret et al. 2008), and (ii) normal fertilization followed by elimination of inducer chromosomes (Fischer 2004; Zhang et al. 2008; Li et al. 2009). Further, Kato (1997) suggested that the aberrant fertilization mechanisms leading to haploidy may be related to mechanisms leading to heterofertilization.

Continuous variation of segregating populations developed from inducer by noninducer crosses suggests that HIR is a quantitative trait (Lashermes and Beckert 1988). The first exploratory quantitative trait locus (QTL) mapping study, conducted with RFLP markers in an F₃ population involving Stock6 (HIR = 2.3%; Coe 1959) as inducer parent, provided evidence for two QTL for HIR on chromosomes 1 and 2, together explaining 17.9% of the phenotypic variance (Deimling et al. 1997). Barret et al. (2008) used marker segregation ratio distortion analyses in small samples from the two phenotypic extremes of a segregating population developed from a cross between a noninducer and an inducer line and also identified a locus on chromosome 1 associated with HIR.

None of the most recently developed haploid inducers with high HIR have been subjected to genome-wide QTL analysis yet. Further, QTL must be examined for stable expression in different germplasm because high congruency of QTL in different genetic backgrounds is desirable to facilitate marker-assisted introgression approaches. Therefore, we conducted comparative QTL analyses for HIR in four populations involving two inducers, UH400 and CAUHOI. Our objectives were to (1) study the inheritance of in vivo haploid induction ability and its association with segregation distortion and embryo abortion rate (EAR), (2) estimate the number, genomic positions, and genetic effects of QTL associated with HIR and EAR, and (3) discuss possible mechanisms underlying in vivo haploid induction in monocots as well as implications of the results for fine mapping and improving HIR in maize.

Materials and Methods

Genetic materials

Four mapping populations involving haploid inducer inbred UH400 as pollinator with two temperate (CAUHOI, 1680) and two tropical (CML395, CML495) inbreds as female parents were generated (Table 1). UH400 was developed at the University of Hohenheim, Germany, and has a HIR of ∼8% averaged across several tropical (Prigge et al. 2011) and temperate (W. Schipprack, personal communication) environments. It carries the dominantly inherited marker gene R1-nj conferring a purple coloration of the scutellum and the aleurone of seeds (Nanda and Chase 1966; Neuffer et al. 1997), which can be used as embryo and endosperm marker, respectively, to identify putative haploid seeds. CAUHOI is a haploid inducer developed by China Agricultural University with high kernel oil content (78 g kg⁻¹) and a HIR of ∼2% (Li et al. 2009). Inbreds 1680 (developed by China Agricultural University) as well as CML395 and CML495 (both developed by the International Maize and Wheat Improvement Center, CIMMYT) have no induction ability but excellent agronomic characteristics.

Table 1 . Number of families (N_F) and marker loci (N_L) used for QTL analyses in the four populations and various generations; the average number of seeds (N_S) used to determine the haploid induction rates (HIR); and the corresponding estimates of the genetic variance components (${\mathit{\sigma }}_g^2$), repeatabilities (w²), means, and ranges for HIR.

Population–generation	Code	NF	NL	NS	HIR [%]
					${\text{σ}}_{\text{g}}^{\text{2}}$	w2	Mean	Range
CAUHOI × UH400-F2	CAU-F2	185	89	246	8.25**	69	5.2	0.5–15.5
CAUHOI × UH400-F2:3	CAU-F3	161	89	189	1.52**	46	2.3	0.0–8.0
CAUHOI × UH400-F2:4	CAU-F4	124	89	317	3.50**	76	2.4	0.0–10.3
1680 × UH400-F2	1680-F2	124	106	237	6.59**	91	2.8	0.0–15.6
1680 × UH400-F2:3	1680-F3	113	106	264	10.65**	85	2.9	0.0–13.4
CML395 × UH400-F2:3	CML395-F3	171	191	153	0.40**	40	0.6	0.0–5.0
CML495 × UH400-F2:3	CML495-F3	183	183	171	1.88**	88	0.8	0.0–12.9

^**Significant at P < 0.01.

In all four populations, random F₂ plants were selfed to produce F_2:3 lines. In addition, for population CAUHOI × UH400, randomly chosen seeds from self-pollinated ears of F_2:3 lines were bulked and grown as F_2:4 lines. In summary, F₂, F_2:3, and F_2:4 generations were evaluated for HIR in CAUHOI × UH400 (designated CAU-F₂, CAU-F₃, and CAU-F₄, respectively), F₂ and F_2:3 generations in 1680 × UH400 (1680-F₂ and 1680-F₃), and the F_2:3 generation was evaluated in CML395 × UH400 (CML395-F₃) and in CML495 × UH400 (CML495-F₃) (Table 1).

Marker assays and linkage map construction

Genotyping was performed differently for the two temperate (CAU-F₂, 1680-F₂) and the two tropical (CML395-F₂, CML495-F₂) populations following the protocols used at China Agricultural University and CIMMYT, respectively. For CAU-F₂ and 1680-F₂, leaf tissue from the parental lines and the F₂ plants was harvested at the three-leaf stage. Genomic DNA was extracted following the procedures of Porebski et al. (1997). One-hundred eighty-six F₂ individuals of populations CAU-F₂ and 1680-F₂ were genotyped with 90 and 113 polymorphic simple sequence repeat (SSR) markers, respectively, following standard protocols (Ninamango-Cárdenas et al. 2003). The SSRs were selected from the MaizeGDB database (http://www.maizegdb.org; Lawrence et al. 2004) to provide good coverage of the entire genome.

For CML395-F₂ and CML495-F₂, leaf tissue from the parental lines and the F₂ plants was harvested at the 10-leaf stage, placed in glassine bags, and stored at −80° until lyophilization at CIMMYT’s biotechnology facility. Genomic DNA was extracted following standard protocols (CIMMYT 2005). Parents of both populations were screened for polymorphism with the custom GoldenGate assay containing 1536 single nucleotide polymorphism (SNP) markers (Yan et al. 2010). SNP genotyping for the parental screening was performed using the Illumina BeadStation 500 G (Illumina, San Diego, CA) at the Cornell University Life Sciences Core Laboratories Center according to the protocol of Fan et al. (2006) and data were analyzed using the Illumina BeadStudio genotyping software. The genotyping of 220 (CML395-F₂) and 233 (CML495-F₂) F₂ individuals with 324 and 297 polymorphic SNPs, respectively, was conducted by KBioSciences (United Kingdom) using simple-plex, automated high throughput KasPar chemistry assays. Genotypes for all populations are available as Supporting Information, File S1.

The four linkage maps were constructed by Haldane’s mapping function with software JoinMap 3.0 (Van Ooijen and Voorrips 2001). Individuals and loci with >20% missing data were excluded from the analysis. A LOD (log₁₀ of the likelihood odds ratio) value of 3.0 was used as critical threshold to declare linkage between two markers. The order of the mapped SSR markers on each linkage group was confirmed according to the IBM2 2008 Neighbors Map (http://www.maizegdb.org). SNP marker order was confirmed by their absolute physical location on the B73 reference maize sequence (http://www.maizesequence.org) and bin positions were identified from the sequence. As some markers were very close (<1.01 cM) to each other, they were combined into a “synthetic” marker resulting in a reduced number of loci used for QTL analysis (Table 1). Further, we tested expected allele frequencies of p = 0.5 of the UH400 allele with a standard χ² goodness-of-fit test and declared segregation distortion when loci significantly (P < 0.05) deviated from the expectation.

Assessment of haploid induction and embryo abortion rates

The mapping populations were grown in completely randomized designs at the experimental stations of China Agricultural University near Beijing (China) in summer 2008 (CAU-F₂ and 1680-F₂) and 2009 (CAU-F₄ and 1680-F₃), and in Hainan province (China) in winter 2008/2009 (CAU-F₃), as well as at CIMMYT’s experimental station in Tlaltizapan (Mexico) in summer 2009 (CML395-F₃ and CML495-F₃). Field plots consisted of 11 plants in each experiment.

Determination of HIR was conducted on the basis of two haploid identification systems. For the CAU and 1680 mapping populations, the R1-nj color marker inherited from the inducer parent UH400 was scored on testcross seeds harvested from the nonpigmented Chinese hybrid ZD958 after pollination with the mapping populations. Three to five plants of ZD958 were pollinated with either pollen of individual F₂ plants (CAU-F₂ and 1680-F₂) or bulked pollen of a minimum of five plants per family (CAU-F₃, 1680-F₃, and CAU-F₄). Testcross seed with purple endosperm (indicating a regular triploid endosperm resulting from successful fertilization with inducer pollen) but colorless embryo (indicating a haploid embryo of ZD958 origin) were designated as putative haploid seed following Prigge and Melchinger (2012). To verify the effectiveness of the R1-nj color marker and to account for putative misclassifications (Röber et al. 2005; Prigge et al. 2011), all haploids detected by the above method were grown near Beijing in summer 2010 and visually scored for plant type before flowering; haploid plants had shorter statures, thin stalks, and erect and narrow leaves. For 1680-F₂ and 1680-F₃, we additionally determined the EAR as the proportion of completely collapsed testcross seeds exhibiting embryoless pericarps.

For the CML mapping populations, a single cross obtained by crossing two temperate inbred lines carrying the recessive mutation liguleless was used as tester (hereafter referred to as lglg tester). The specific genetic source (lg1 vs. lg2) is unknown for this germplasm. The lglg tester allows clear distinction between haploid and diploid seedlings because haploids are characterized by absence of the ligule and auricle combined with an upright-positioned leaf enveloping the shoot (Neuffer et al. 1997). All lglg tester plants were emasculated to avoid self-contamination. Bulked pollen of a minimum of five plants per F₃ family was used to pollinate a minimum of eight lglg tester plants. All testcross seeds were grown in the greenhouse until the four-leaf stage and were visually rated for the liguleless phenotype, an indication of haploidy.

For all populations, each testcross ear was shelled separately. Three testcross ears per family were selected on the basis of the highest total number of testcross seeds to determine HIR (in all populations) and EAR (in 1680-F₂ and 1680-F₃). Repeatabilities (w²) for HIR and EAR were calculated with the statistical software PLABSTAT (Utz 2004) taking the values of the three individual ears as three replicates in a completely randomized design. Combining the three ears, HIR and EAR were computed for each family as the proportion of putative haploid and embryoless testcross seeds, respectively, detected in the total testcross progeny monitored. Parent–offspring regression was performed with CAU-F₂, CAU-F₃, CAU-F₄, 1680-F₂, and 1680-F₃ and the regression coefficient was used as an estimator of the narrow-sense heritability (h²) for HIR and EAR of the corresponding populations.

QTL analyses

Analyses of QTL for HIR and EAR were performed with software PlabQTL (Utz and Melchinger 1996) using composite interval mapping (CIM; Jansen and Stam 1994; Zeng 1994) and a multiple regression procedure (Haley and Knott 1992). The appropriate number of marker cofactors and the appropriate genetic models were chosen on the basis of the smallest values of the modified Bayesian Information Criterion (mBIC, Baierl et al. 2006). Using the mBIC as significance criterion, we did not detect significant first-order epistatic interactions in any of the populations. Minimized mBIC were obtained for a model including additive and dominance effects for all populations except CAU-F₂ and CML495-F₃ for HIR as well as 1680-F₂ and 1680-F₃ for EAR, where no significant dominance effects were detected. Critical LOD thresholds were determined empirically with 1000 random permutations (Churchill and Doerge 1994) for each generation, population, and trait. LOD thresholds corresponding to genome-wide error rates of α = 0.25 were employed for CIM, which is common for explorative QTL analyses (Beavis 1998). The support intervals with a LOD fall-off of 1.0 were expressed as a position on the chromosome. The proportion of the genetic variance $\left({\text{σ}}_{\text{g}}^{\text{2}}\right)$ explained by the model was estimated as $\widehat{p}=R_{\text{adj}}^2/w^2,$ where $R_{\text{adj}}^2$ is the adjusted proportion of phenotypic variance explained by the model and w² is the repeatability of the trait. The proportion of ${\text{σ}}_{\text{g}}^{\text{2}}$ explained by individual QTL was estimated as ${\widehat{p}}_{\text{part}}=R_{\text{part}}^2/w^2$, where $R_{\text{part}}^2$ is the proportion of phenotypic variance explained by that QTL. All values of ${\widehat{p}}_{\text{part}}$ were normalized to sum to $\widehat{p}.$ For those loci showing significant dominance effects, we calculated the dominance ratio (d/|a|) of the estimated dominance effect over the absolute value of the estimated additive effect.

Further, to account for the special features of the phenotypic distributions of HIR in QTL mapping, we used the two-part model developed by Broman (2003) implemented in the software R/QTL (Broman and Sen 2009) in addition to CIM. This model combines the analysis of the binary trait (i.e., z_i = 1 vs. z_i = 0, corresponding to HIR > 0% vs. HIR = 0%, respectively, of inducer F₂ plant or F_2:3/F_2:4 family i) with standard interval mapping for those having z_i = 1. For plants/families with haploid induction ability (i.e., z_i = 1) and genotype g (AA, AB, or BB) at marker locus m in the parental F₂ plant, the square root HIR is assumed to follow a normal distribution with mean μ_g and standard deviation σ (Broman 2003). As HIR is determined on the basis of the testcross progeny of i, the phenotype of each testcross seed ij can be coded by an indicator variable z_ij, with z_ij = 1 if seed ij is haploid or z_ij = 0 otherwise. Further, π_g = Pr(z_i = 1|m_i = g) denotes the conditional probability of obtaining z_i = 1, if the genotype of the parental F₂ plant i at marker locus m is g, whereas μ_g = E(z_ij|m_i = g, z_i = 1) denotes the conditional expectation for testcross seed ij within the progeny of inducer i with HIR > 0%, if the genotype of the parental F₂ plant i at marker locus m is g. Separate LOD scores were calculated to test whether the three genotype classes g have the same probability π_g of inducing haploidy (i.e., z_i = 1) and/or whether those families with z_i = 1 have the same sample means μ_g (corresponding to HIR) according to three hypotheses (Broman 2003): (1) LOD(π) to test whether π_AA = π_AB = π_BB; (2) LOD(μ) to test whether μ_AA = μ_AB = μ_BB; and (3) LOD(πμ) to test the combined hypothesis that both the π_g and μ_g were equal. The corresponding critical LOD thresholds for the two-part model were determined empirically with 1000 random permutations.

Results

Haploid induction and embryo abortion rates

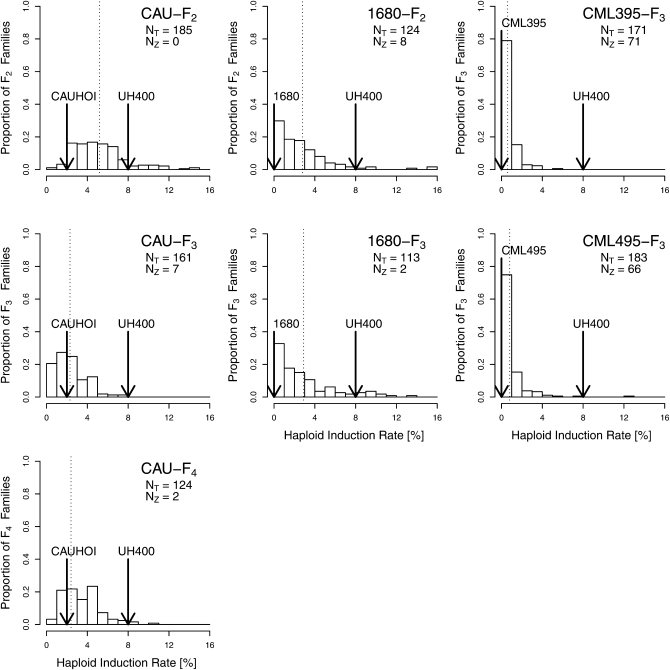
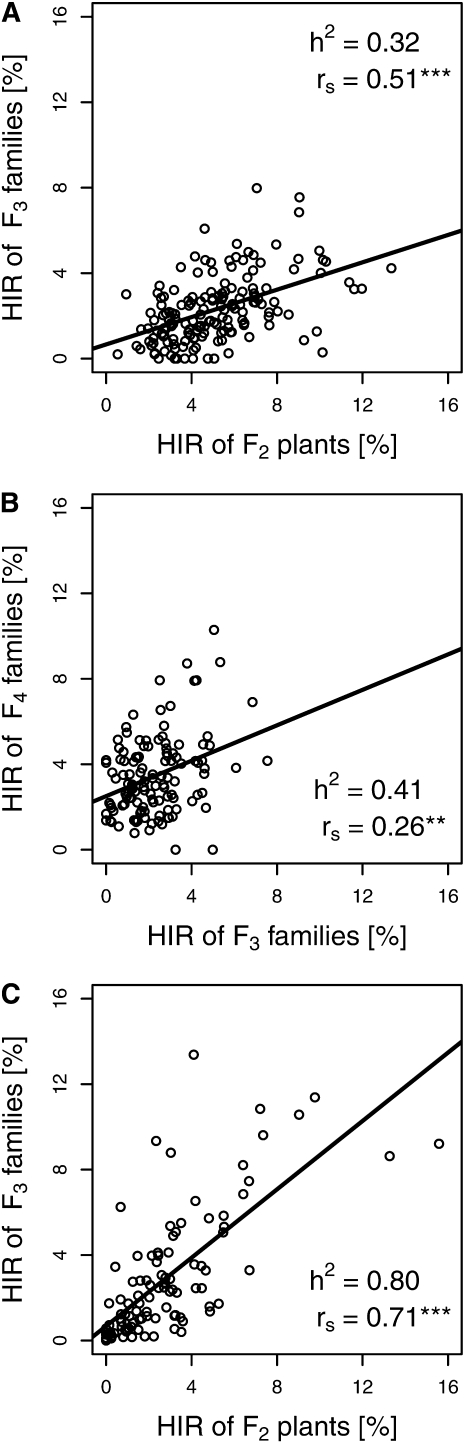
The average number of testcross seeds used for determination of HIR was lowest in CML395-F₃ (153) and highest in CAU-F₄ (317; Table 1) and ranged from 50 to 640 for individual families. Genotypic variances for HIR were significant (P < 0.01) in all populations. Repeatabilities (w²) were intermediate for CML395-F₃ and CAU-F₃ and high for all other populations. Mean HIR were highest in CAU-F₂ and lowest in the two CML populations and HIR ranged from 0 to 15.6% for individual families (Table 1 and Figure 1). Distributions of HIR were strongly skewed toward low values in populations where noninducers (1680, CML395, CML495) were used as parents. Population means deviated significantly (P < 0.001, Wilcoxon signed rank test) from the midparent values toward lower values in all but the CAU-F₂ population. CML395-F₃ and CML495-F₃ harbored a larger number of families with HIR = 0% than the other populations. Heritability estimates for HIR obtained from parent–offspring regression (Figure 2) were lower for the CAU population (h² = 0.32 and 0.41) than for the 1680 population (h² = 0.80). Spearman’s rank correlations were higher for HIR between F₂ and F₃ generations in both the CAU (r_s = 0.51***) and the 1680 (r_s = 0.71***) populations than for HIR between F₃ and F₄ generations of the CAU population (r_s = 0.26**).

Figure 1 .

Distribution of haploid induction rates (HIR) assessed in different generations of four populations: F₂, F₃, and F₄ of CAUHOI × UH400 (CAU-F₂, CAU-F₃, CAU-F₄), F₂ and F₃ of 1680 × UH400 (1680-F₂ and 1680-F₃), F₃ of CML395 × UH400 (CML395-F₃), and F₃ of CML495 × UH400 (CML495-F₃). N_T, total number of families phenotyped. N_Z, number of families with HIR = 0%. Arrows indicate the parental HIR. Dashed lines represent the population mean.

Figure 2 .

Relationship between HIR obtained in (A) CAU-F₂ and CAU-F₃, (B) CAU-F₃ and CAU-F₄, and (C) 1680-F₂ and 1680-F₃ generations. h² denotes the heritability estimate and r_s denotes Spearman’s rank correlation coefficient. Significant at (**) P < 0.01 and (***) P < 0.001.

Significant ${\text{σ}}_{\text{g}}^{\text{2}}$ and high w² were estimated for EAR in 1680-F₂ and 1680-F₃ (Table 3). Mean EAR was higher in 1680-F₃ than in 1680-F₂ and the range of EAR was also wider in 1680-F₃. Heritability of EAR was 0.77 on the basis of parent–offspring regression (Figure S1) and Spearman’s rank correlation between EAR in F₂ and F₃ generations was 0.36 (P < 0.001). Moderate correlations existed between EAR and HIR of 1680-F₂ (r_s = 0.63***) and 1680-F₃ (r_s = 0.53***).

Table 3 . Summary of results from phenotypic and QTL analyses of embryo abortion rate (EAR) in F₂ and F₃ generations of 1680 × UH400.

Parameter	Unit	1680-F2	1680-F3
Phenotypic results
No. of families	No.	132	116
No. of SSR loci	No.	106	106
Average number of testcross seeds	No.	344	399
Genetic variance $\left({\mathit{\sigma }}_{\text{g}}^2\right)$	%	0.68**	1.31**
Repeatability (w2)	%	68	73
Mean	%	0.81	1.11
Range	%	0–6.70	0–11.10
QTL results
Chromosome	–	1	1
Position (Support interval)	cM	52 (50–56)	60 (56–66)
Flanking markers	–	bnlg2180, umc1917	umc1811, umc1770
LOD	–	8.19	3.19
Proportion of genetic variance explained $\left(\widehat{p}\right)$	%	34.13	14.18
Additive effect	%	0.97**	0.97**
Name	–	qear1	qear1

^**Significant at P < 0.01.

Linkage maps and segregation distortion

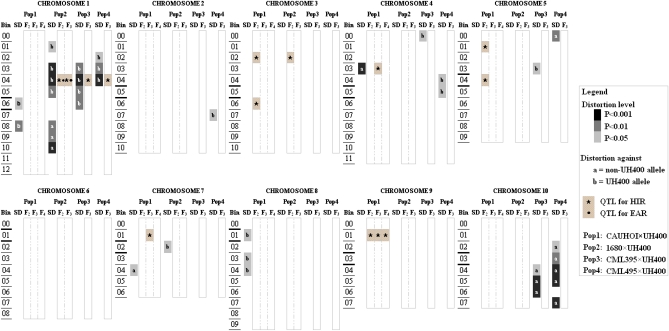
The length of the four genetic linkage maps ranged from 1353 to 1630 cM and the average marker intervals were 4.8 cM in CML395-F₂, 5.2 cM in CML495-F₂, 13.1 cM in 1680-F₂, and 20.4 cM in CAU-F₂ (data not shown). Significant deviations from expected allele frequencies were observed in all populations (Figure 3). Most notably, strong (P < 0.001) distortion occurred against the UH400 allele in bin 1.04 in 1680-F₂, CML395-F₂, and CML495-F₂, and in a varying number of adjacent bins depending on the population. Chromosome 4 was affected in three of the four populations (although distortion happened against different alleles), while chromosome 7 was affected by segregation distortion only in CAU-F₂ and 1680-F₂ and chromosomes 5 and 10 were affected only in CML395-F₂ and CML495-F₂. Across the four populations, distortion was observed against the UH400 allele in 17 bins and against the non-UH400 allele in 11 bins.

Figure 3 .

Chromosomal positions, direction, and magnitude of segregation distortion (column SD) in four F₂ populations as well as positions of QTL for haploid induction rate (HIR, *) and embryo abortion rate (EAR, •) detected in generation F_n of the populations. Bin assignment is based on the IBM2 2008 neighbors reference map (http://maizegdb.org). The centromeric bin is shown between thick lines.

QTL analyses

Five QTL for HIR were detected with CIM in CAU-F₂ on chromosomes 3, 5, and 9 explaining together $\widehat{p}\hspace{0.17em}\text{=}\hspace{0.17em}\text{71\%}$ of the genetic variance (Table 2 and Figure 3). In CAU-F₃ three QTL were detected on chromosomes 4, 7, and 9 with $\widehat{p}\hspace{0.17em}\text{=}\hspace{0.17em}\text{64\%,}$ while in CAU-F₄ one QTL was detected on chromosome 9 (qhir8; $\widehat{p}\hspace{0.17em}\text{=}\hspace{0.17em}\text{20\%}$). The HIR-enhancing allele was always contributed by UH400 except for qhir5 in bin 5.01 of CAU-F₂.

Table 2 . Chromosomal bin locations and positions (Pos.), support intervals (SI), flanking marker names, and characterization of quantitative trait loci (QTL) for in vivo haploid induction rate (HIR) assessed in four populations involving haploid inducer UH400.

Chr. bina	Pos. (cM)	SI (cM)	Flanking markerb	LOD	Typec	${\widehat{p}}_{\text{part}}$d	Effecte	d/af	Name
CAU-F2g
3.02	30	24–32	umc1886–bnlg1523	5.83	a	9.39	0.93**	NA	qhir2
3.06	90	78–106	bnlg1601–umc2169	5.40	a	8.20	1.11**	NA	qhir3
5.01	28	18–32	umc1097–phi024	7.32	a	11.33	−1.01**	NA	qhir5
5.04	122	114–128	umc1332–umc1155	9.54	a	17.44	1.55**	NA	qhir6
9.01	14	10–26	bnlg1272–umc1040	19.76	a	24.13	1.82**	NA	qhir8
						$\widehat{p}$: 71.49
CAU-F3
4.03	34	16–50	umc2082–umc2039	3.23	a	15.46	0.72**	NA	qhir4
7.01	64	58–78	phi057–umc2142	3.66	a	17.43	0.63**	NA	qhir7
9.01	8	0–18	bnlg1272–umc1040	6.81	a	31.04	0.96**	NA	qhir8
						$\widehat{p}$: 63.93
CAU-F4
9.01	4	0–12	bnlg1272–umc1040	5.80	a	12.27	1.07**	−1.17	qhir8
					d	8.09	−1.25**
						$\widehat{p}$: 20.36
1680-F2
1.04	56	54–60	umc1917-umc2390	28.07	a	51.61	4.33**	−0.44	qhir1
					d	14.80	−1.89**
3.02	30	22–38	bnlg1325–umc1886	2.85	a	4.86	−0.68**	NA	qhir2
						$\widehat{p}$: 71.27
1680-F3
1.04	58	54–60	umc2390–umc1811	19.21	a	53.04	4.03**	−0.37	qhir1
					d	9.20	−1.50**
						$\widehat{p}$: 62.24
CML395-F3
1.04	90	72–98	PHM5306–PHM9418	3.67	a	8.05	0.28**	−1.71	qhir1
					d	11.44	−0.48**
						$\widehat{p}$: 19.49
CML495-F3
1.04	78	72–88	PZA02550–PHM5306	5.27	a	8.95	0.66**	NA	qhir1
						$\widehat{p}$: 8.95

^**Significant at P < 0.01.

^aBold type bins: the QTL was identified with both composite interval mapping (CIM) as well as the two-part model; nonbold type bins: QTL was identified with CIM.

^bThe marker closest to the position of the putative QTL is italicized.

^ca, additive; d, dominance.

^dPortion of the genotypic variance explained by a specific QTL and summing up to the total proportion $\left(\widehat{p}\right)$ of the genotypic variance explained by the model including all QTL in a population–generation combination.

^ePositive values indicate that UH400 contributed the favorable allele.

^fDominance ratio of the estimated dominance effect over the estimated additive effect. NA = not applicable due to nonsignificant dominance effects.

^gFor codes of populations, see Table 1.

In 1680-F₂ and 1680-F₃, a major QTL (qhir1; ${\widehat{p}}_{\text{part}}\hspace{0.17em}\text{=}\hspace{0.17em}$63–66%) for HIR was detected on chromosome 1 (bin 1.04) and the favorable allele was contributed by UH400 in both generations. Furthermore, a minor QTL on chromosome 3 (qhir2) was detected in 1680-F₂ resulting in $\widehat{p}\hspace{0.17em}\text{=}\hspace{0.17em}\text{71\%}$ for 1680-F₂ and the favorable allele at qhir2 was contributed by the noninducer parent 1680. One QTL for EAR (qear1) was detected on chromosome 1 (bin 1.04) in 1680-F₂ $\left(\widehat{p}\hspace{0.17em}\text{=}\hspace{0.17em}\text{38\%}\right)$ and 1680-F₃ ($\widehat{p}\hspace{0.17em}\text{=}\hspace{0.17em}\text{14\%;}$ Table 3). qear1 shared one flanking marker each with qhir1 in 1680-F₂ (umc1917) and 1680-F₃ (umc1811). The EAR-enhancing allele was from UH400.

In CML395-F₃ and CML495-F₃, qhir1 was detected in bin 1.04 explaining $\widehat{p}\hspace{0.17em}\text{=}\hspace{0.17em}\text{20}$ and 9%, respectively. In both CML populations, SNP PHM5306 flanked qhir1 and the favorable allele was contributed by UH400. On the basis of the physical positions of flanking SNPs (Table 2), the delimited physical interval for qhir1 was about 40 Mbp (data not shown).

Significant dominance effects were revealed for qhir8 in CAU-F₄ as well as for qhir1 in 1680-F₂, 1680-F₃, and CML395-F₃ (Table 2). At these loci, the dominance ratio ranged from −0.37 to −1.71 indicating weak to strong recessive gene action adopting the nomenclature suggested by Stuber et al. (1987). Individuals homozygous for the UH400 allele at the nearest flanking marker (see Table 2) to qhir1 always showed HIR > 0% in 1680-F₂, while about one-third of the individuals of this genotype class showed HIR = 0% in CML495-F₃ (Figure 4).

Figure 4 .

Box-whisker plots of HIR of the three marker genotypes at the closest markers flanking the quantitative trait locus qhir1 detected on chromosome 1 (bin 1.04) in populations 1680-F₂ (left) and CML495-F₃ (right). A represents the noninducer allele (1680 or CML495) and B the inducer allele (UH400). Individual observations are indicated as circles and jittered along the x-axis to avoid overplotting.

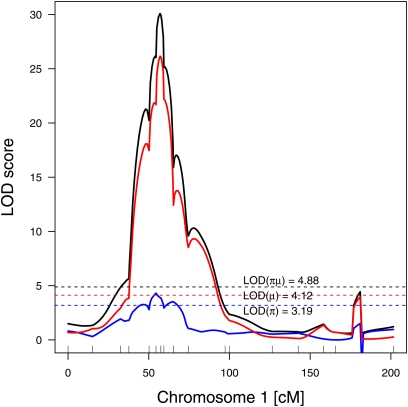
Using the two-part model approach on HIR data, we confirmed qhir2, qhir6, and qhir8 for CAU-F₂; qhir4, qhir7, and qhir8 for CAU-F₃; and qhir8 for CAU-F₄ (Table 2). Furthermore, qhir1 of 1680-F₂, 1680-F₃ and CML495-F₃ was confirmed with this method. All QTL identified with the two-part model affected only the mean HIR of the nonnull phenotypes, except for qhir1 in 1680-F₂ (Figure 5), which additionally affected the probability of occurrence of nonnull phenotypes.

Figure 5 .

LOD profile of chromosome 1 of population 1680-F₂ for interval mapping of the square root transformed HIR data using the two-part model. Separate LOD scores were calculated to test whether the three genotype classes g (AA, AB, BB) of inducer i have the same probability π_g of inducing haploidy (i.e., z_i = 1) and whether those inducers with z_i = 1 have the same sample mean μ_g according to three hypotheses (Broman 2003): LOD(π) (blue) to test whether π_AA = π_AB = π_BB; LOD(μ) (red) to test whether μ_AA = μ_AB = μ_BB; and LOD(πμ) (black) to test the combined hypothesis that both the π_g and μ_g were equal. Dashed lines represent empirically determined significance thresholds (α = 0.05) for the three LOD curves.

Discussion

Conceptual genetic framework for inheritance of haploid induction ability

Results of our study and others (Lashermes and Beckert 1988; Barret et al. 2008) showed that (1) the phenotypic distributions of HIR obtained with segregating populations are mostly skewed and (2) a large proportion of null phenotypes is observed. This suggests that the properties of haploid induction ability differ from those of most agronomic traits, which display continuous phenotypic variation that usually approximates a Gaussian distribution.

Haploid induction ability of maize inducer genotypes is considered to be a pollen characteristic, because pollen of inducers under evaluation is used to pollinate a tester and expression of haploidy is assessed on the testcross seed. Under this premise, the genotype of the inducer as such does not matter, but only its gametic array transmitted through the pollen. Hence, dominance effects should be absent for HIR because testcross genotypic values follow a simple additive model in the absence of epistasis (Bernardo 2002). However, segregation distortion as detected in our study at four QTL in three populations can potentially mimic dominance, because if gene frequencies in the gametic arrays produced by heterozygous F₂ individuals and even more so of their selfing progenies in generations F₃ and F₄ deviate from 0.5, this causes a deviation from the additive genetic model for testcross progeny. Nevertheless, it cannot be ruled out entirely that haploid induction ability is not only a property of the pollen itself but also influenced by its parental genotype, similar to factors causing sporophytic self-incompatibility in plants (e.g., Hiscock and Tabah 2003), in which case our observation would reflect dominance between HIR-affecting alleles.

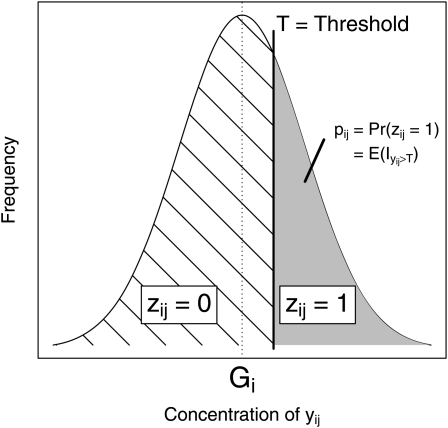
Genetic analysis of haploid induction ability is complicated further by the dichotomous nature of the trait. In the testcross progeny of inducer genotype i the phenotype of each testcross seed ij is coded by the indicator variable z_ij, with z_ij = 1 if ij is haploid or z_ij = 0 otherwise. For our conceptual framework, we assume that the phenotype z_ij is determined by the concentration y_ij of the unobservable genetic factor(s) X (e.g., expression level of gene(s) or concentration of metabolite(s)) in the pollen grain triggering the development of testcross seed ij. We suppose that y_ij displays a quantitative distribution and decompose it according to the model commonly employed in quantitative genetics: y_ij = G_i + ε_ij, where G_i refers to the genotypic value of genotype i (i.e., G_i = E(y_ij|i)) for factor X and ε_ij reflects the experimental noise as well as genetic segregation in case of a heterozygous inducer genotype. This situation is depicted schematically in Figure 6. If y_ij exceeds a certain threshold T, the phenotype of seed ij will be haploid. Consequently, $z_{ij}=I_{[y_{ij}>T]}$, which takes z_ij = 1 if y_ij > T and z_ij = 0 if y_ij ≤ T, links the distribution of the unobservable variable y_ij with the phenotype z_ij. Thus, genotype i induces haploidy in testcross seed ij with a true probability of p_i such that Pr(z_ij = 1) = p_i, and it follows that Pr(z_ij = 0) = 1 – p_i. Hence, the expectation of z_ij is E(z_ij) = p_i and its variance is var(z_ij) = p_i(1 – p_i). The genetic factor(s) X affecting p_i are unknown, but once identified (e.g., through gene expression studies with near-isogenic lines) they could potentially be measured on a continuous scale and the inheritance could be studied directly.

Figure 6 .

Scheme of the quantitative distribution of concentration y_ij of the unobservable factor X empowering male gametes of genotype i to induce haploidy in testcross seed ij. G_i represents the genotypic value of inducer i for factor X. If y_ij passes the threshold T, and then haploidy is induced in ij and the indicator variable takes z_ij = 1; otherwise ij becomes diploid (z_ij = 0).

In summary, we propose that the trait haploid induction ability is a threshold character under polygenic control, yet leading to dichotomous expression (haploid vs. diploid) on the level of the individual testcross seed. Prominent examples of threshold characters include disease susceptibility (affected vs. not affected) in plants or litter size in large mammals (single vs. twin births; Falconer and Mackay 1996). Further, the two common assumptions for genetic analysis, i.e., normality of residuals and homoscedasticity, are not fully met for haploid induction ability. Composite interval mapping (Jansen and Stam 1994; Zeng 1994) and alternative approaches such as nonparametric tests (Kruglyak and Lander 1995) or two-part model tests (Broman 2003) are expected to work well for nonnormally distributed data as long as critical LOD scores are determined via permutation tests from the original data set. However, heteroscedasticity of error variances remains an unsolved problem and warrants further research.

Heritability of HIR

Between-family heritability estimates for HIR (represented by h² estimates from parent–offspring regression) were lower than within-family heritability estimates (represented by repeatabilities w² estimated from HIR of three ears per family). Since parents and offspring were not evaluated in the same environments, genotype-by-environment interactions for HIR may have reduced h² estimates. Further, the discrepancy between h² and w² can be explained by natural selection disfavoring the haploidy-inducing gametes during selfing as suggested by the observed segregation distortion. From an evolutionary point of view, a higher proportion of haploids in the progeny caused by high HIR of the pollinator would result in fitness disadvantages, because haploid maize plants are less vigorous, often male sterile, and, therefore, generally less likely to produce offspring than diploid maize plants (Chase 1952; Chalyk 1994), which explains the counteracting force of natural selection. The latter may also explain the difficulties encountered during maintenance of inducers reported by maize breeders.

Surprisingly, h² for HIR estimated from regression of the 1680 generations was twice as high as those estimated from regression of the CAU generations or the estimate Deimling et al. (1997) (h² = 0.44) reported for HIR. Since h² is a population parameter (Falconer and Mackay 1996), the different germplasm base explains this discrepancy. Further, from our conceptual genetic framework it follows that h² for HIR estimated from a segregating population such as F₂ or F₃ depends on the genotypic variance for the probability parameter p_i as well as on the sample size N_i of the testcross progeny used for determining HIR of inducer genotype i. Consequently, estimation of h² remains difficult because (1) phenotyping of HIR in multilocation experiments on various testers is extremely laborious, and (2) heteroscedasticity as well as the associated segregation distortion complicate quantitative genetic analyses including estimation of h², so novel biometric approaches are urgently needed.

Agreement between conceptual genetic framework and QTL results

To the best of our knowledge, this is the first study that used multiple populations and generations to identify QTL responsible for HIR. A common approach for comparison of QTL locations across populations is using joint linkage analysis as proposed by Blanc et al. (2006), but this was not possible because of a lack of common markers between the four populations. Yet, simple addition of LOD curves from CIM runs of individual populations revealed that only qhir1 was significant across both CML populations (see Figure S3 and Figure S4), while no joint QTL was significant for the two Chinese populations (data not shown). Further, a variable degree of segregation distortion in different populations complicates joint analysis. Therefore, we refrained from joint linkage analysis and compared QTL across populations using the “bin concept,” which is well established in the literature (e.g., Gardiner et al. 1993; Schön et al. 2010).

The number of QTL and the magnitude of QTL effects obtained for HIR in the present study varied depending on populations and generations. There was a clear trend, however, for qhir1 in bin 1.04 having a major effect on HIR in populations involving noninducer genotypes as females (1680, CML395, and CML495). Previous studies have also identified this chromosomal region to segregate in populations involving only one inducer parent (Deimling et al. 1997; Barret et al. 2008). In contrast, no QTL was detected in bin 1.04 in CAU-F₂, CAU-F₃, and CAU-F₄, which were derived from a cross of the two haploid inducers CAUHOI and UH400. Most likely, the CAU generations are not segregating for qhir1 because the favorable allele is fixed in the parents, which provides a simple biological explanation for the incongruency of QTL. In fact, further analysis of the bin 1.04 region with 16 markers that were all polymorphic between inducer line UH400 and noninducer line 1680 revealed monomorphism between inducers UH400 and CAUHOI (Figure S2). As large-effect QTL are subjected to strong selection pressure, qhir1 has likely become fixed quickly when selection for high HIR occurred during the development of UH400 and CAUHOI. Further, the two inducers may be identical by descent in this chromosomal region due to derivation from the same original inducer source, Stock6 (Coe 1959).

QTL detection frequencies obtained with 200 runs of fivefold cross-validation (Utz et al. 2000) were 95–100% for the large effect QTL in bins 1.04 (qhir1) for each of the populations except CAU, and 9.01 (qhir8) for the CAU populations in this study. This explains why these QTL were detected in more than one population and/or all generations of the respective population and underlines their significance for HIR. In contrast, QTL detection frequencies ranged from 23 to 80% for QTL with smaller effects and, accordingly, none of the minor QTL except qhir2 was detected in more than one population. The power of simultaneous detection of QTL in different experiments is obtained by multiplication and, therefore, low congruency of minor QTL across experiments meets expectations and has also been reported previously (Melchinger et al. 1998; Mihaljevic et al. 2004).

The use of cofactors in CIM has been shown to increase power of QTL detection (Jansen and Stam 1994; Zeng 1994). Analyses with the two-part model did not confirm all of the QTL identified with CIM. Higher critical LOD thresholds were employed for this model and the minor QTL identified with CIM (qhir3 and qhir5) fell short of the critical LOD during two-part analyses due to lower power for QTL detection (Broman 2003).

The two-part analyses also revealed that qhir1 in 1680-F₂ significantly affected the chance of whether genotypes have HIR > 0%, while the remaining QTL affected only the genotype means once HIR > 0%. Hence, we speculate that qhir1 acts as a key modulator for HIR; i.e., genes located in bin 1.04 trigger genetic processes that enable passing of the threshold outlined in our conceptual genetic framework. In this case, introgression of qhir1 would equip any germplasm with haploid induction ability. However, in the two CML populations not all individuals homozygous for the inducer allele at the flanking markers of qhir1 showed HIR > 0%, a phenomenon known as incomplete penetrance (e.g., Barret et al. 2008; Eldar et al. 2009; Gaudet et al. 2010), while complete penetrance was observed in 1680-F₂ and 1680-F₃. Yet, genotypes at the actual QTL position are unknown and denser marker coverage would be necessary to more conclusively infer about penetrance.

The QTL qhir1 explained a much larger proportion of the genetic variance in 1680-F₂ and 1680-F₃ than in CML395-F₂ and CML495-F₂, possibly due to incomplete penetrance. This discrepancy can be attributed to different testers and the associated haploid identification systems employed for the different mapping populations (Kebede et al. 2011; Prigge et al. 2011). Further, the presence of different modifier genes (Allard 1999) acting as enhancers or suppressors of major genes in different germplasm sources as well as QTL by genetic background interactions (Pumphreys et al. 2007) may be responsible. Future studies should employ different testers (such as liguleless, glossy, R1-nj) and near-isogenic lines developed from crosses of inbreds with contrasting HIR to focus on modifier QTL regions in greater detail and investigate putative epistatic interactions. Our results suggest that populations developed from crossing two inducers will be particularly helpful in revealing QTL other than qhir1.

Effects of segregation distortion

Distorted allele frequencies were observed in all populations indicating the presence of segregation distortion loci (SDL) that cause linked markers to deviate from expected Mendelian segregation patterns due to gametic or zygotic selection (Xu 2008). It is expected that recombination frequencies and, consequently, marker positions during linkage map construction will not be affected by segregation distortion if only one SDL is present in a distorted region and codominant markers such as SSRs or SNPs are used (Lorieux et al. 1995; Lu et al. 2002). The total map lengths estimated for our F₂ populations were comparable to those reported in previous studies with F₂ populations (e.g., Melchinger et al. 1998; Mihaljevic et al. 2004). Further, both marker order as well as bin positions have been confirmed for all markers on the basis of published IBM2 2008 Neighbors Map or physical locations. Thus, our QTL results should be robust and reliable as far as the flanking markers and chromosomal bins are concerned.

In fact, had SDL been excluded from analysis, qhir1 would have been missed in our study. This confirms previous results indicating that genomic regions exhibiting strong segregation distortion are equally or even more likely to contain QTL (e.g., Wang et al. 2005). The strong distortion against the UH400 marker allele observed in the region of qhir1 in three populations of this study supports the putative association between HIR and transmission failure of the inducer gamete suggested by Barret et al. (2008). Perhaps the same or tightly linked loci are responsible for both causing segregation distortion as well as triggering induction of haploidy.

Under the assumption that qhir1 is responsible for the observed segregation distortion in bin 1.04, this relationship could potentially be exploited for fine mapping of qhir1. By saturating this QTL region with SNPs and identifying those SNPs with maximum segregation distortion, fine mapping of the QTL may be achieved without the need of elaborate designs in a simple large-size F₂ population. Schneeberger and Weigel (2011) proposed a similar approach using next-generation sequencing technology for mutation mapping in Arabidopsis.

Putative candidate genes for haploid induction ability

Identification of candidate genes for haploid induction ability is premature because the underlying biological mechanisms are still unknown. Considering that limited pollen production capacities and protogyny have been observed for inducers (data not shown; W. Schipprack, personal communication), weak or partial male sterility may be involved in haploid induction. Particularly relevant are mutants producing pollen that does not always lead to complete fertilization of egg and central cells. Almost 50 male sterility genes (ms; Neuffer et al. 1997) are known. For example, mutants carrying ms12, which is located on chromosome 1, show partial male sterility, probably depending on the genetic background (Albertsen and Phillips 1981).

Further, defective kernel mutations (dek; Neuffer et al. 1997) map to similar chromosomal regions as QTL identified in our study in bins 1.04 (dek32), 3.02 (dek5, dek24), 3.06 (dek17), 4.03 (dek11), 5.01 (dek18), 5.04 (dek9, dek26, dek27, dek33), and 9.01 (dek12). These mutations are characterized by a variation of degenerated embryo and endosperm tissues. Several mutants such as carriers of dek12, dek32, and dek33 show completely collapsed kernels appearing as embryoless pericarps without any starch deposition (Sheridan and Neuffer 1980). This phenotype was employed to determine EAR in our study. Significant variation for EAR was detected and EAR estimates of >10% were observed, which is more than expected in normal crosses. The joint presence of qhir1 and qear1 in bin 1.04 as well as the highly significant rank correlations between HIR and EAR in 1680-F₂ and 1680-F₃, suggest a possible relationship with inducer properties. However, further genetic mapping or gene expression studies will be necessary to study the involvement of dek loci in HIR. Examining the genotypes of endosperm and embryo via comparative seed and leaf DNA-based analyses (Gao et al. 2011) may be helpful to study the fertilization process(es) inducing haploidy and to better understand the biological basis of in vivo haploid induction in maize.

In Arabidopsis thaliana, Ravi and Chan (2010) report the production of haploid plants by crossing the source germplasm with a mutant carrying a genetic alteration of the centromeric histone CENH3. In our study, no QTL for HIR was detected in bin 6.06, which harbors CENH3 of maize (Zhong et al. 2002). This indicates that in vivo induction of haploidy in maize is not governed by the mechanism reported by Ravi and Chan (2010), although such centromere-mediated genome elimination may also work in maize to produce haploids. Nonetheless, in vivo induction of haploidy may be fundamentally different in mono- and dicots and maize could serve as a model species for studying this phenomenon in monocots.

Implications for haploid inducer development

Transgressive segregants were identified in all populations except CML395-F₃ and also noninducer parents contributed HIR-enhancing alleles, indicating that inducers with increased HIR can be generated through targeted parental recombination and selection. To reduce the laborious and time-consuming task of phenotypic selection for HIR, marker-based approaches such as genomic selection are suitable for increasing the frequency of favorable alleles for HIR in inducer development programs. This seems particularly relevant if haploid induction ability is indeed governed by one or few major genes influenced by several modifier genes (Allard 1999), as major genes will quickly become fixed, and gain from selection will then depend entirely on small-effect modifier genes, which will be extremely difficult to select for phenotypically.

In addition, targeted introgression of relevant QTL into adapted and agronomically superior noninducer germplasm will enable the development of custom-made inducers that can be employed for efficient DH line production in various breeding programs and agroecologies. qhir1 represents an interesting chromosomal region for map-based cloning and the required fine mapping can be achieved by developing near-isogenic lines. However, incomplete penetrance observed for this QTL in CML395-F₂ and CML495-F₂ suggests that the relationship between genotype and phenotype is not that reliable in all genetic backgrounds. Thus, phenotyping of marker-selected inducers still seems necessary as a final evaluation step.