Optimization of light source parameters in the photodynamic therapy of heterogeneous prostate

Abstract

The three-dimensional (3D) heterogeneous distributions of optical properties in a patient prostate can now be measured in vivo. Such data can be used to obtain a more accurate light fluence kernel. (For specified sources and points, the kernel gives the fluence delivered to a point by a source of unit strength). In turn, the kernel can be used to solve the inverse problem that determines the source strengths needed to deliver a prescribed PDT dose distribution (light fluence) within the prostate (assuming uniform drug concentration). We have developed and tested computational procedures to use the new heterogeneous data to optimize delivered light fluence. New problems arise, however, in quickly obtaining an accurate kernel following the insertion of interstitial light sources and data acquisition. (1) The light-fluence kernel must be calculated in 3D and separately for each light source, which increases kernel size. (2) An accurate kernel for light scattering in a heterogeneous medium requires ray tracing and volume partitioning, thus significant calculation time. To address these problems, two different kernels were examined and compared for speed of creation and accuracy of dose. Kernels derived more quickly involve simpler algorithms. Our goal is to achieve optimal dose planning with patient-specific heterogeneous optical data applied through accurate kernels, all within clinical times. The optimization process is restricted to accepting the given (interstitially-inserted) sources, and determining the best source strengths with which to obtain a prescribed dose. The Cimmino feasibility algorithm is used for this purpose. The dose distribution and source weights obtained for each kernel are analyzed. In clinical use, optimization will also be performed prior to source insertion to obtain initial source positions, source lengths, and source weights, but with the assumption of homogeneous optical properties. For this reason, we compare the results from heterogeneous optical data with those obtained from average homogeneous optical properties. The optimized treatment plans are also compared with the reference clinical plan, defined as the plan with sources of equal strength, distributed regularly in space, which delivers a mean value of prescribed fluence at detector locations within the treatment region. The study suggests that comprehensive optimization of source parameters (i.e., strengths, lengths, and locations) is feasible, thus allowing acceptable dose coverage in a heterogeneous prostate PDT within the time constraints of the PDT procedure.

INTRODUCTION

Photodynamic therapy (PDT) is a treatment modality using light of an appropriate wavelength in the presence of oxygen to activate a photosensitizing drug which then causes localized cell death or tissue necrosis (Dougherty et al. 1998). Using a surface illumination technique, PDT has been used to treat superficial tumors, including those of skin, lung, esophagus, and bladder (Hsi et al. 1999). Interstitial light delivery is considered as an efficient illumination scheme for PDT to treat large bulky tumors in solid organs (e.g. prostate), whereby optical fibers are placed directly into the bulky tumors or organs.

Since tumors of the prostate are often confined to the prostate itself, brachytherapy techniques used for the placement of radioactive seed implants can be adapted for the placement of interstitial optical fibers (D’Amico et al. 1996). Several preclinical studies have evaluated the feasibility of delivering PDT to prostate via the interstitial approach (Lee et al. 1997, Chang et al. 1996, Chang et al. 1997, Chen et al. 1997 and Zhu et al. 2003). Based on our preclinical study in canines (Hsi et al. 2001), we have initiated a protocol for motexafin lutetium (MLu)-mediated interstitial PDT of the prostate in patients at the University of Pennsylvania (Stripp et al. 2004, Zhu et al. 2005a, and Zhu et al. 2005b, Du et al. 2006, and Verigos et al. 2006).

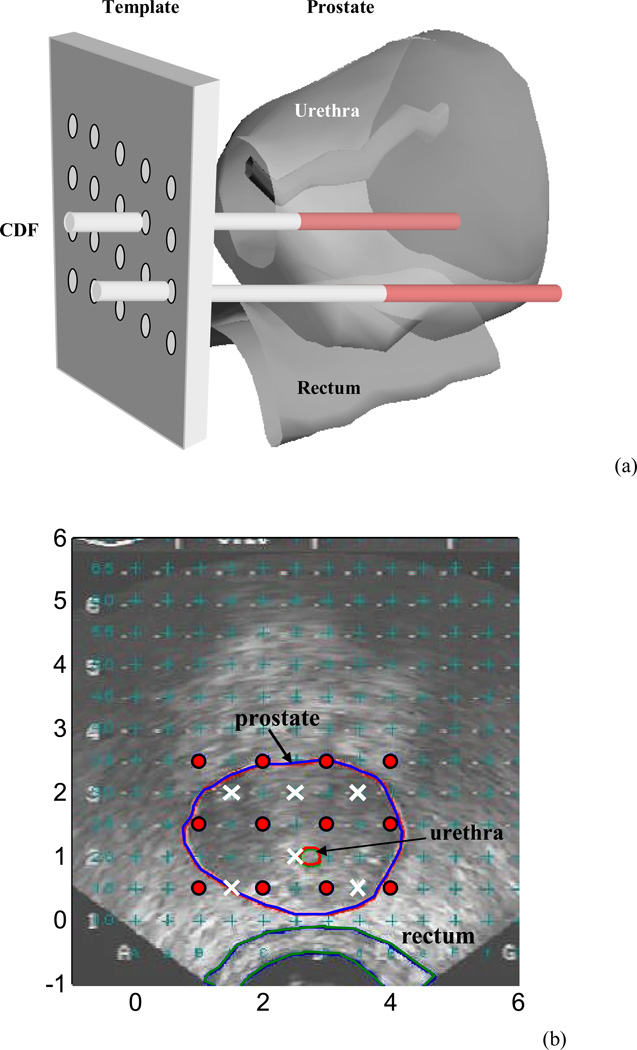
In the current prostate PDT protocol (Fig. 1(a)), we use cylindrical diffusing fibers (CDF) as light sources; these have active lengths of 1–5 cm and are aligned parallel within the prostate 1 cm apart. A reference clinical plan (RCP) is thus defined as a plan that uses (1) sources of equal strength and equal spaced loading of 1 cm , with the length of the CDF at each base position set to extend the full length of the prostate, and (2) a treatment time (typically 20 – 40 minutes) for each prostate quadrant determined from the prescribed total light dose and the observed mean light fluence rate at the middle of the quadrant (see Fig. 1b and marked as “x”). Light fluence distribution was predicted by calculation using uniform source strength (e.g., 150 mW/cm), assuming that the prostate was homogeneous.

Figure 1.

(a) Schematic of prostate PDT. CDF: Cylindrical diffusing fibers. (b) Transrectal ultrasound image. Isotropic detectors (“×”) were located at a distance between 0.5 – 1.1 cm from the light source (“”).

To improve treatment planning, we developed procedures based on the Cimmino feasibility algorithm, to optimize source parameters (e.g., position, length, and strength) for a homogeneous prostate (Altschuler et al. 2005). The study showed that for homogeneous tissue the optimized plans had better coverage of the prostate and sparing of the urethra and rectum than did the standard plan. The Cimmino feasibility algorithm (Censor et al. 1988 and Benzi M 2004) is an iterative linear algorithm that was first applied to radiotherapy inverse problems by Censor and Altschuler et al. (Powlis et al. 1989, Censor et al. 2001, and Benzi 2004). The algorithm always converges and, if the prescribed dose constraints are not all satisfied, it reverts to the least-squares solution (Censor et al. 2001).

Our recent development of optical property measurement allows us to measure three dimensional (3D) optical properties in vivo in a patient prostate (Zhu et al., 2005a). Measurements have shown that human prostates are optically heterogeneous (Zhu et al. 2005b), which indicates that any optimization procedure may need to account for that heterogeneity.

In this study, we tested an optimization procedure for an optically heterogeneous prostate. In the previous study for homogeneous tissue, a universal kernel sufficed to calculate light fluence; that kernel required just a few constants to specify tissue optical properties and used only source-detector distances and source strength as input. In the current optimization, a light fluence matrix is pre-calculated for a 3D heterogeneous tissue domain for each possible linear source at each allowed location. The matrix is different for each patient because of the patient-specific optical heterogeneity. Two new kernels were tested. Optimization results from these different kernels were compared.

MATERIALS AND METHODS

1. Prostate PDT and clinic plan

In prostate PDT, a built-in template with a 0.5-cm grid was used, which was attached to a transrectal ultrasound unit to project the locations of possible light sources relative to the prostate (Fig. 1(a)). The CDF sources were parallel and spaced 1 cm apart and the length of the CDF at a particular position within the prostate was selected to cover the full length of the prostate. The light power per unit length was less than or equal to 150 mW/cm for each CDF. For practical reasons, clinical application often required that the prostate be divided into four quadrants and that isotropic detectors be used to measure the in vivo light fluence rate in each quadrant (Fig. 1(b)).

Before treatment, the light fluence rate distribution and the treatment time were predicted with a calculation using the average optical properties (µ_a = 0.3 cm−1 and µ_s' = 14 cm−1) measured in patients treated previously (Zhu TC et al 2005a). During treatment, based on the in vivo measurement of light fluence rates, a clinical plan was created in real time, which determined the treatment on-time of the sources in each quadrant. The treatment time was determined by taking the ratio of the prescribed light fluence (J/cm²) and half of the maximum fluence rate (W/cm²) measured in the quadrant. This value is approximately equal to the mean light fluence rate measured in the track of the detector catheter.

We measured the optical properties inside the prostate using a motorized probe and a point-by-point procedure with 5×5×5 mm³ resolution (Zhu et al. 2005b). Briefly, a point source was introduced into the prostate gland using the same catheters used for PDT treatment. Multiple detectors around the point source through parallel catheters at distances between 0.5 – 0.7 cm were introduced to measure the light fluence rate around the point source. An analytical model was used to fit the data to extract the absorption and scattering coefficients assuming homogeneous optical properties with a 5×5×5 mm³ voxel of interest. The details of the methodology are described elsewhere (Zhu et al. 2005b).

The spacing for the clinical plan (1 cm) was based on a preclinical canine animal study (Hsi et al. 2001), which showed necrosis depth of about 1 cm around a cylindrical diffusing fiber for Mlu-mediated PDT. The prostate volumes in patients were delineated using a trans-rectal ultrasound (TRUS) imaging by an urologist. The same TRUS was used for imaging guidance for the prostate PDT of the actual plan.

2. Models for light fluence calculation

The transport of near-infrared light in biological tissue is often described by the diffusion equation (Schweiger et al. 1995),

$$-\nabla \cdot (D(\mathbf{r})\nabla \varphi )+{\mu }_a(\mathbf{r})\varphi =S,$$ (1)

where the diffusion coefficient D=1/(3 µ_s') (µ_s' is the reduced scattering coefficient), µ_a is the absorption coefficient, and S is the source power (in units of mW or W). With the diffusion approximation, the light fluence rate φ at a distance r from a point source can be expressed as (Jacques 1998)

$$\varphi =\frac{S.{\mu }_{\mathit{\text{eff}}}^2}{4\pi r\cdot {\mu }_a}\cdot e^{-{\mu }_{\mathit{\text{eff}}}\cdot r}=\frac{3S{\mu }_s\text{'}}{4\pi r}\cdot e^{-{\mu }_{\mathit{\text{eff}}}\cdot r},$$ (2)

where S is the power of the point source (mW); φ(r) is the the fluence rate (mW/cm²); the quantity ${\mu }_{\mathit{\text{eff}}}=\sqrt{3\cdot {\mu }_a\cdot {\mu }_s\text{'}}$ (Jacques 1998) is the effective attenuation coefficient in tissues, applicable over a wider range of µ_a and µ_s' than the traditional definition ${\mu }_{\mathit{\text{eff}}}=\sqrt{3\cdot {\mu }_a\cdot ({\mu }_s\text{'}+{\mu }_a)}$ (Nakai 1997). The PDT dose is defined as the product of light fluence and photosensitizer concentration. For simplicity, we use the light fluence (fluence rate × exposure time, φ·t) for the PDT dose throughout the paper, assuming uniform drug concentration. We applied two different kernels to calculate light fluences, which were then used for the optimizations.

2.1 Heterogeneous test kernel 1

A heterogeneous kernel was developed by extending the homogeneous kernel (Eq. 2), by taking into account optical heterogeneities around the light source. We assume that the optical heterogeneities around a light source dominate the light fluence distribution.

$$\varphi =\frac{3S{\mu }_s\text{'}(0)}{4\pi r}\cdot e^{-{\mu }_{\mathit{\text{eff}}}(0)r},$$ (3)

where µ_s'(0) and µ_eff(0) are the reduced scattering coefficient and the effective attenuation coefficient at the source location (r = 0), respectively. Considering that a linear source is composed of multiple point sources (segments), the light fluence rate for a linear source can be expressed as a superposition of the solution for a point source, i.e.,

$$\varphi ={\displaystyle \sum _{i=1}\frac{3{\mu }_s\text{'}\cdot s\cdot \mathrm{\Delta }{x}_i\cdot e^{-{\mu }_{\mathit{\text{eff}}}{r}_i}}{4\pi r_i},}$$ (4)

where s is the source strength of each segment along the linear source, Δx_i is the division along the direction parallel to the orientation of the linear source, and r_i is the distance between the ith source segment and the detector. The summation in Eq. 4 is over all the segments composing the linear source. The fluence rate at a point in a prostate is the summation of the fluence rates generated by each linear source.

2.2 Heterogeneous test kernel 2

A more rigorous kernel was developed based on the assumption of a spherical-shell distribution of optical properties (Li and Zhu 2007). For a point source located at r=0, optical properties are assumed to be homogeneous in each shell surrounding the source and are different from shell to shell. Light fluence rates in each shell are expressed as

$${\varphi }_i=\frac{C{\mu }_{s,i}\text{'}}{4\pi r}(p_i{e}^{-{\mu }_{\mathit{\text{eff}},i}r}+q_i{e}^{{\mu }_{\mathit{\text{eff}},i}r}),(r_{i-1}<r<r_i),$$ (5)

and in the last shell,

$${\phi }_{N+1}=C\frac{p_{N+1}{\mu }_{s,N+1}\text{'}}{4\pi r}\cdot e^{-{\mu }_{\mathit{\text{eff}},N+1}r},(r_N<r<\infty ).$$ (6)

The coefficients C, p_i, q_i are obtained using the boundary conditions between two shells and the energy conservation in the volume. For i=N+1 (i.e., the outmost shell), r_N+1 = ∞ and q_N+1 = 0. In the study, we assume p_N+1 = 1 and calculate the light fluence rate in the Nth shell.

For arbitrary 3D distribution of optical properties, we expanded the expressions for the light fluence rate to keep the forms the same as those expressed above; optical properties along a ray line between a source and a detector were used, i.e., µ_eff(r) was replaced by µ_eff(r,θ,φ). The model was applied to linear sources by considering a linear source to be composed of multiple point sources.

2.3 FEM forward calculation

An FEM model (Li et al. 2006) was taken as the gold standard relative to the two test kernels and was used for forward light fluence calculation to compare the optimization results of the two kernels. The FEM calculation was implemented using COMSOL Multiphysics (COMSOL Inc., Burlington, MA). The CDFs were modeled as linear sources using weak forms. Meshes were generated in a 3D prostate geometry, which was partitioned into tetrahedrons and the boundary was partitioned into triangular elements. The elements were Lagrange quadratic. Finer meshes (0.1 mm) were generated near linear sources to ensure calculation accuracy. A tissue-tissue boundary condition with a refractive-index match was applied at the boundary between the prostate and the outside medium. In all the calculations, the entire exterior of the prostate is considered to have the same optical properties as the boundaries.

3. Determining source strengths with the Cimmino feasibility algorithm

In the study, we tested the optimization of source strengths in a heterogeneous prostate, which is the “simple” inverse problem of PDT (Altschuler et al. 2005). The optimization is to find individual source strengths that collectively deliver a prescribed dose to the target (prostate) without exceeding specified maximum dose values for the target and non-target regions (urethra, rectum, and unspecified background), when given all the source locations and source lengths. The Cimmino feasibility algorithm is used to determine directly a “best” solution for the simple inverse problem, which is similar to that used in the previous homogeneous optimization (Altschuler et al. 2005). Although the study is focused on the test of the “simple” inverse problem of PDT, it can be easily extended to solve the “general” inverse problem (Altschuler et al. 2005), which is to find not only the source strengths but the source locations and lengths as well, to best satisfy the dose prescription.

The Cimmino feasibility algorithm was chosen because it is relatively fast, easy to constrain to positive source strengths (the positive J-tant), allows importance weighting of the volumes, and converges to a unique least squares compromise solution when not every constraint can be satisfied (De Pierro et al. 1985).

The discretized simple inverse problem can be written as

$$b_i^{\text{min}}\le {\displaystyle \sum _j{A}_{\mathit{\text{ij}}}{x}_j\le b_i^{\text{max}}}(i=1,\dots ,I;j=1,\dots ,J)$$ (7)

or in matrix form as

$${\mathbf{b}}^{\mathbf{\text{min}}}\le \mathbf{\text{Ax}}\le {\mathbf{b}}^{\mathbf{\text{max}}}$$ (8)

where I is the number of voxels (or constraint points); b^max and b^min are the dose bounds on the voxels; J is the number of light sources; a component of matrix A denoted A_ij gives the dose absorbed at voxel i per unit strength of light source j. A positive lower bound prescribes a minimum dose for a target (prostate) voxel; it is zero for non-target voxels. An upper bound on dose is provided for every voxel. The goal is to find the vector x of source strengths that satisfies the inequality constraints of the expression (8).

The matrix A is a pre-calculated 2-D light fluence table (or kernel) for sources of all allowed lengths. In this study, for simplicity, the matrix is calculated for sources of fixed lengths, which are geometrically pruned based on the prostate geometry. The dose at a point due to a particular light source is obtained by calculating with kernel 1 and kernel 2, which account for optical heterogeneity. The dose at any point is found by summing the dose contributions of all the sources. In the previous study, a universal kernel was used based on the homogeneous assumption. Differently, the light fluence matrix A here is calculated for each individual source and for each patient. Since the tissue around each linear source is now heterogeneous, the fluence delivered by a source to each point cannot make use of a kernel with azimuthal symmetry.

The template currently being used for source insertion is a plate with a square array of 13 × 13 = 169 holes (slots for linear light sources) spaced 0.5 cm apart (Fig. 1). For the benchmark patient, only 12 of the 169 template slots are used for sources. In the study, we tested the optimization of strengths of 12 sources, which were separated by 1 cm. The arrangement is similar to that in the treatments.

RESULTS AND DISCUSSIONS

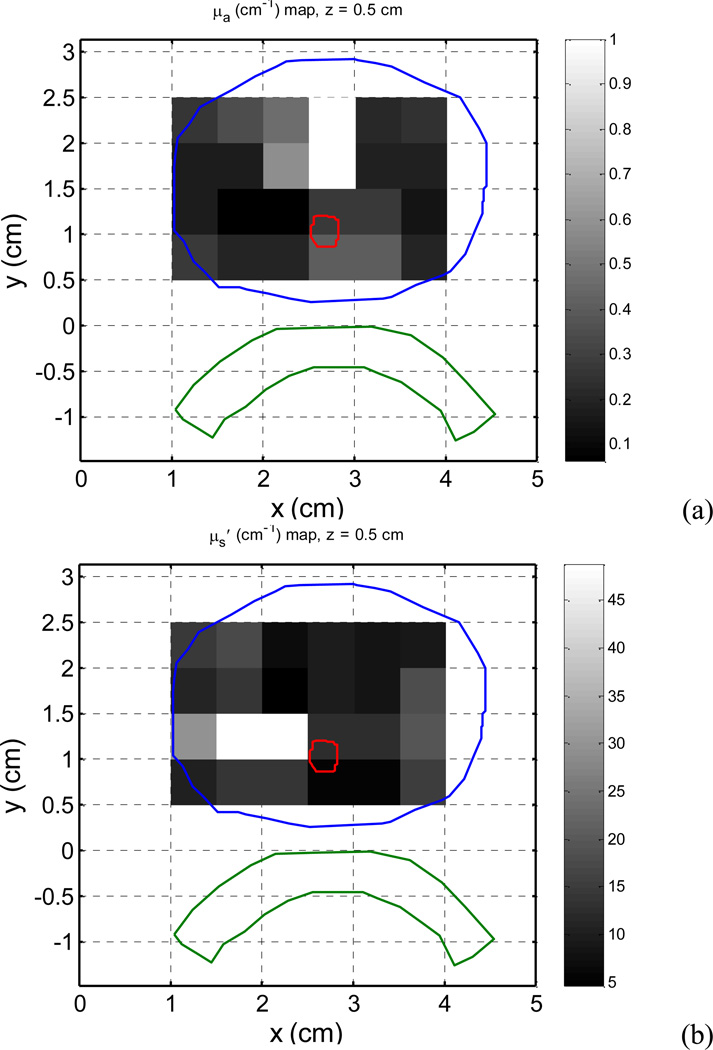
The study used the optical properties measured in a patient prostate during PDT. Figure 2 shows the optical property distributions (optical absorption µ_a and scattering µ_s' coefficients) in one slice, which are superimposed on the prostate contour. Significant heterogeneities are observed. In the slice, the optical absorption coefficient varies from 0.1–1 cm−1, and the optical scattering coefficient varies from 5–45 cm−1.

Figure 2.

Optical properties measured in a patient prostate are superposed on the prostate contour. (a) Optical absorption coefficient µ_a. (b) Optical scattering coefficient µ_s'.

In our previous study, for which in vivo optical properties were unavailable, a pre-plan was created on the assumption of a homogeneous prostate, i.e., µ_a = 0.3 cm−1 and µ_s' = 14 cm−1. Now with actual (measured) optical properties on hand, we can reevaluate two plans created previously. One plan had the same strength for all the sources and the other had individual source strengths obtained by Cimmino optimization (Table 1). With the assumption of homogeneous optical properties, the two plans showed good fluence coverage on the prostate. Had those source strengths been used for an actual heterogeneous prostate, the light distribution would not have been what was expected. Figure 3 shows the actual light fluence distributions (100 J/cm² isodose lines), which would have been delivered by those source strengths to the true heterogeneous prostate. Thus for these two plans we took the source strengths derived on the assumption of homogeneous optical properties and calculated the flux distribution the patient would have actually received if those source strengths had been used (by calculating fluence with the FEM kernel obtained from measured optical properties). For both plans, the upper region of the prostate is not well covered because there is greater absorption there (Fig. 2). Interestingly, the coverage of the source-optimized plan is worse than that of the uniform-strength plan. This result shows that knowledge of the heterogeneity of optical properties is essential information without which any optimization may be useless.

Table 1.

Summary of the source strengths of different plans. In the heterogeneous Cimmino plans of 35 sources, only the source strengths of the 12 sources, which correspond to those in the 12-source plans, i.e., at the same locations, are listed. For kernel 2 with 35 sources, only 19 of the 35 sources have non-zero weights as determined by Cimmino algorithm.

Source index	Source strength (J/cm)
	Uniform strengths (12 sources)	Homo Cimmino (12 sources)	Clinic plan (RCP) (12 sources)	Heter Cimmino (12 sources, kernel 1)	Heter Cimmino (12 sources, kernel 2)	Heter Cimmino (35 sources, kernel 1)	Heter Cimmino (35 sources, kernel 2)
1	127	83	210	153	270	8	0
2	127	81	210	351	543	140	172
3	127	70	206	321	441	62	0
4	127	83	206	171	40	53	99
5	127	65	210	47	130	18	43
6	127	83	210	134	240	30	8
7	127	89	206	250	120	70	265
8	127	68	206	163	725	24	422
9	127	56	78	51	136	27	62
10	127	58	78	56	110	16	52
11	127	68	110	140	143	36	43
12	127	49	110	81	0	28	36

Figure 3.

Comparison of 100% isodose lines of the reference clinical plan (RCP) (dotted line) and the homogeneous Cimmino optimized plan (solid line). Homogeneous optical properties (µ_a = 0.3 cm−1 and µ_s' = 14 cm−1) are assumed to generate the optimal plans. The isodose lines were calculated with the FEM model using heterogeneous optical properties (as illustrated in Fig. 2) Source locations are marked by “”.

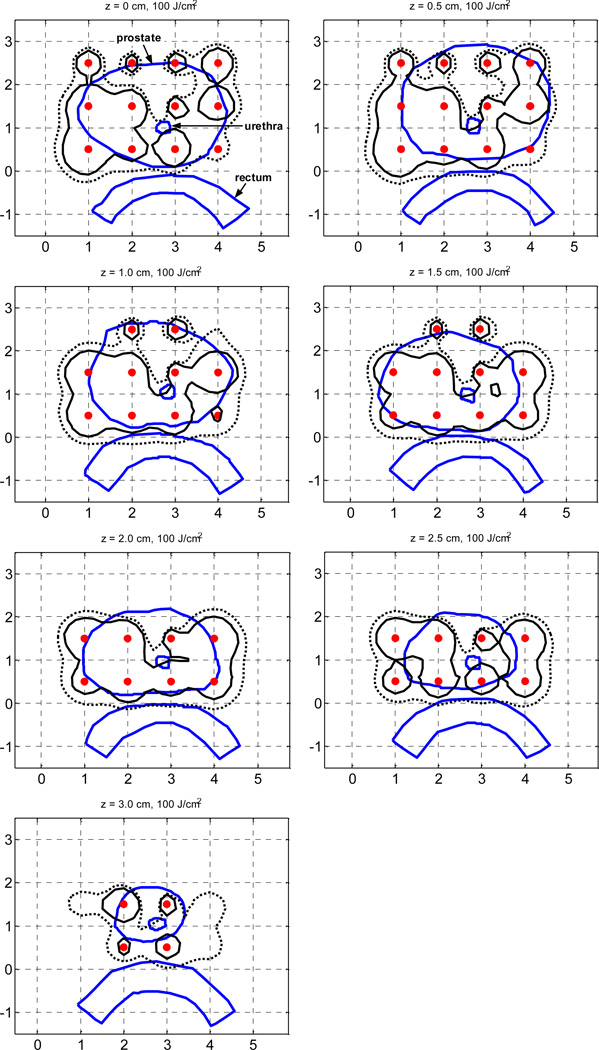
The Cimmino optimized plans for the heterogeneous prostate based on kernel 1 and kernel 2 are compared in Fig. 4. The RCP is also shown. All light fluence rates were calculated with the FEM model. In the clinical planning, the treatment on-time of each source, which is a measure of source strength, was determined from the light fluence rate in each quadrant, in a similar way to that used in treatment. Compared with Fig. 3, the Cimmino optimized plans for the heterogeneous prostate show improved coverage of the prostate. The plan using kernel 2 is better than that using kernel 1. The coverage of the RCP is close to those of the Cimmino optimized plans. Due to significant heterogeneity, a small portion in the upper region is still not covered in the plans. Optimization of source strengths only cannot provide substantial improvement on the light fluence coverage if the heterogeneity is dramatic. To improve the coverage, more light sources are needed in the opaque region.

Figure 4.

Comparison of the 100% isodose lines of the two heterogeneous Cimmino optimized plans and those of the reference clinical plan (RCP). The heterogeneous Cimmino optimized plan, which used kernel 1 to calculate the light fluence matrix, is indicated by a dotted line. The plan which used kernel 2 is indicated by a solid line. The RCP is indicated by a dot-dash line. All forward calculations used FEM model and the source locations are marked by “”.

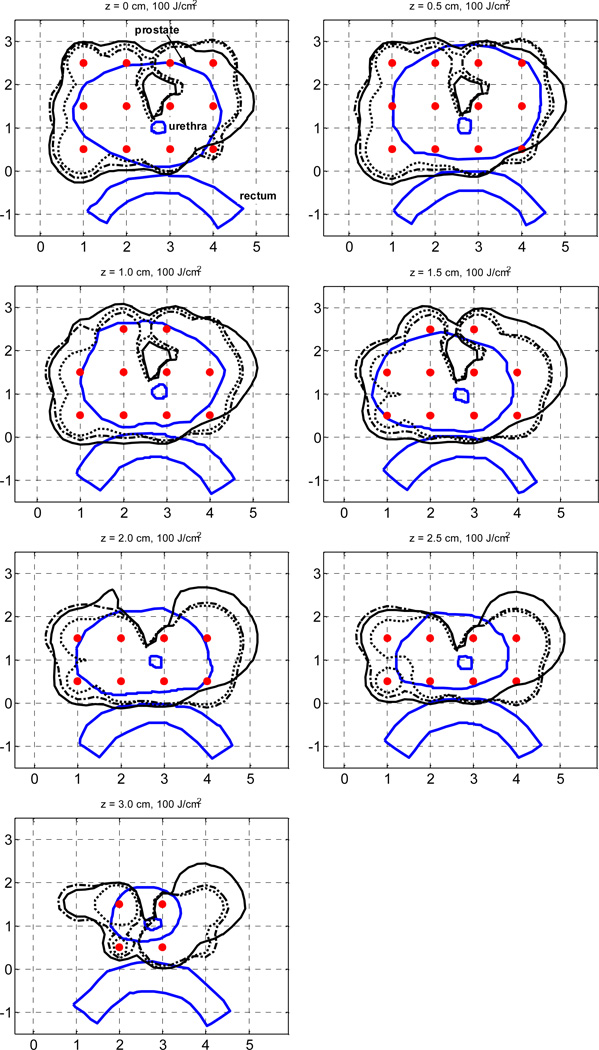
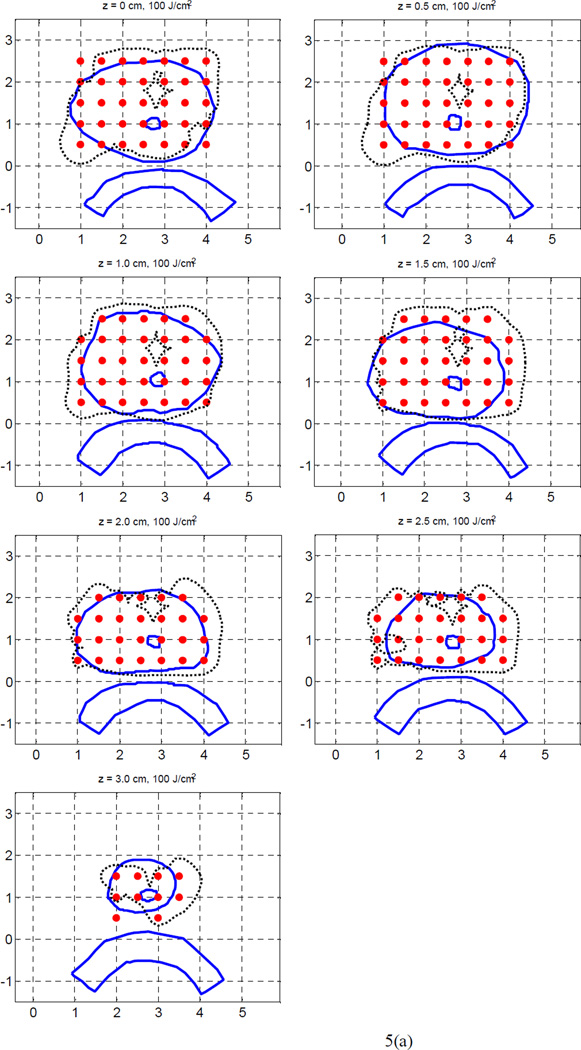
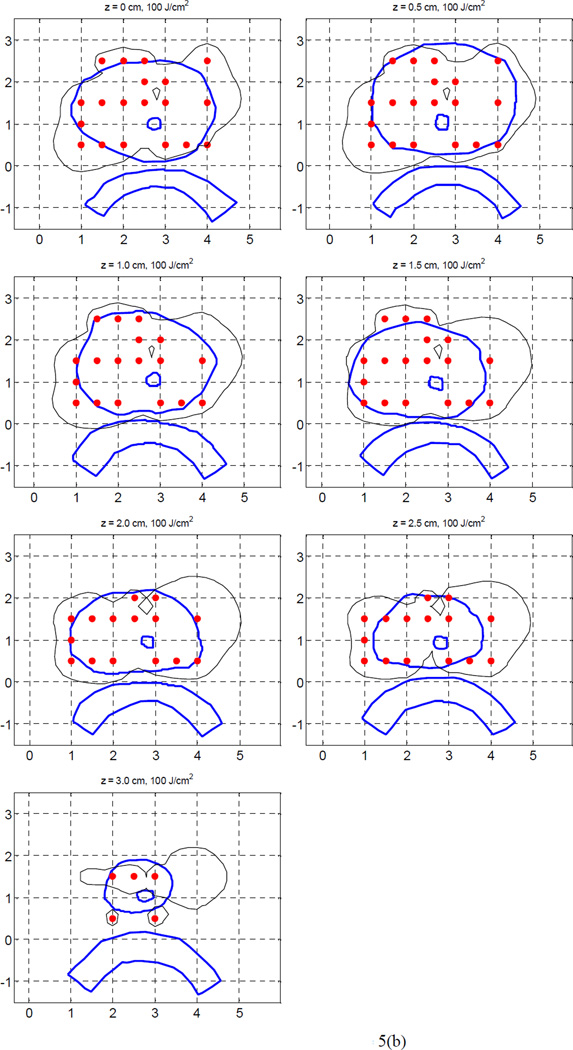
We examined the case of 35 sources, which covered the prostate with a spacing of 0.5 cm. Figure 5(a) shows the 100% isodose distributions of the Cimmino optimized plans, which used kernel 1 and kernel 2, respectively, for the light fluence matrix calculation. As expected, the light fluence coverage in the upper region of the prostate is improved in both plans because there are more light sources located in the region. The plan using kernel 2 has better coverage in the upper region than the plan using kernel 1. The result indicates that kernel 2 produces better coverage of the prostate than kernel 1. Although 35 sources were allowed for optimization, 16 sources were weighted zero when the Cimmino algorithm was used with kernel 2, so that only 19 sources were applied in the plan. The source strengths obtained with kernel 2 differ significantly from those obtained with kernel 1. Our previous study (Li and Zhu 2008) indicates that kernel 2 agrees well with the FEM model.

Figure 5.

100% isodose lines of the heterogeneous Cimmino plans for 35 sources, (a) using kernel 1 (a), and (b) using kernel 2, respectively. Only 19 sources had non-zero weights in (b).

Table 2 shows the time required to perform the Cimmino optimization. There is no significant time difference between the optimizations using light fluence matrices generated with kernels 1 and 2. Typically, the optimizations took ~37 s and ~140 s for 12-source and 35-source plans, respectively.. The generation of the light fluence matrix using kernel 1 took ~30 s. However, the calculation of the light fluence matrix with kernel 2 currently takes much longer than with kernel 1. Efforts are being taken to improve the speed. Since kernel 1 is not as accurate as kernel 2, there is a tradeoff between the calculation speed and the accuracy.

Table 2.

Time (seconds) required for the Cimmino Optimization for various conditions for heterogeneous prostate optical properties.

Kernel	Time required for optimization (seconds)
	12-source plan	35–source plan
Kernel 1	37	137
Kernel 2	37	148

The 100% isodose lines in Figs. 2– 5 suggest that the urethra is receiving 100% of the prescribed dose. This is despite of the fact that we are not placing any light sources directly on the urethra. There are multiple variables that would affect PDT dose to the urethra, including light fluence and drug concentration. We did not measure MLu uptake in the urethra but speculate that it is likely that the urethra did receive some PDT dose because several patients had Grade I–II urinary urgency and one case of a urethral-rectal fistula was observed.

In regions of high absorption the light fluence can only reach a very short distance from a light source. In this case, changing the intensity of the light sources is no longer enough to cover the treatment tissue. One has to physically place light sources in regions to be treated. This is demonstrated by comparing plans using 35 light sources, which can more adequately cover the prostate gland (Fig. 4) than that using the 12 sources (Fig. 5). Our experience suggests that the spacing of the light sources has to be about the same as the penetration of the light fluence rate. For the patient shown in this study, the penetration depth is less than 0.5 cm in the high absorption region. As a result, one may want to consider using more light sources in high-absorption regions to improve the coverage of the prostate gland.

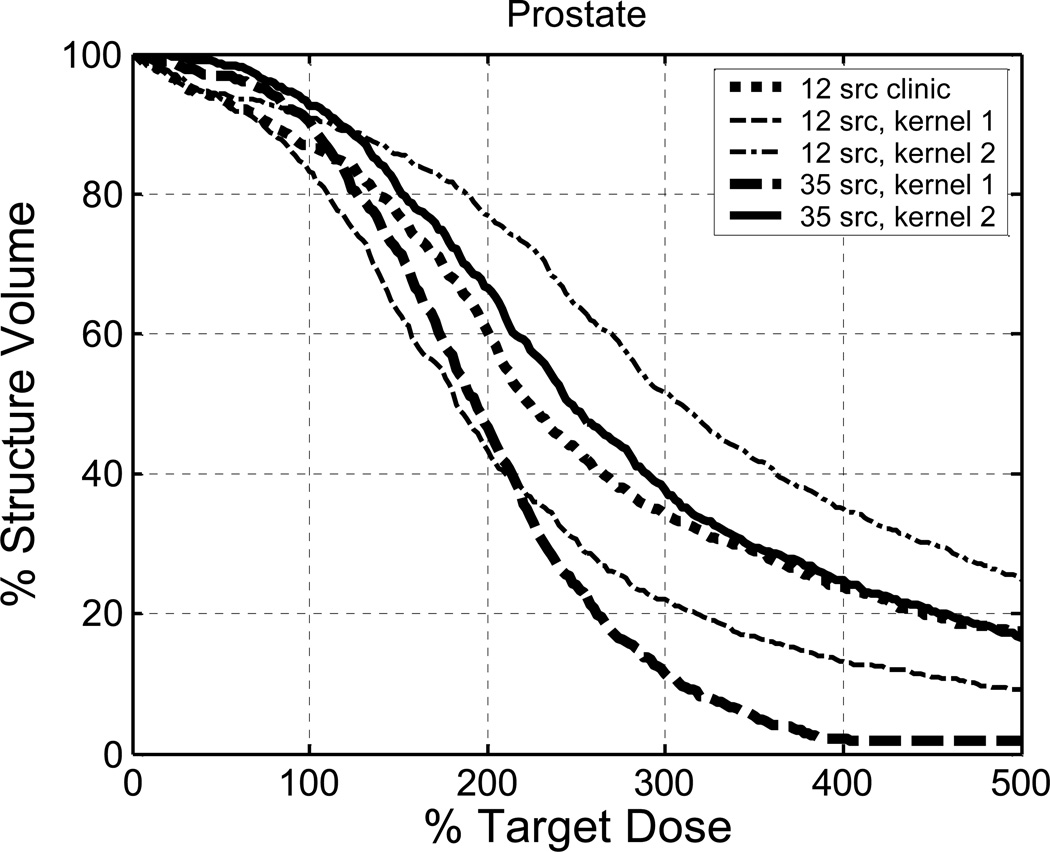
Figure 6 shows the dose volume histograms (DVHs). The DVH is defined as the percent of the volume receiving at least the dose shown on the abscissa. (The dose of the abscissa of Fig. 6 is expressed as a percentage of the prescribed dose to the prostate). The coverage of the prostate (i.e., the coverage of the 100% light fluence) improves in the following sequence: 12-source heterogeneous Cimmino plan using kernel 1, RCP (12 sources), 12-source heterogeneous Cimmino plan using kernel 2, 35-source heterogeneous Cimmino plan using kernel 1, and 35-source (actually, 19-source) heterogeneous Cimmino using kernel 2. The results indicate that knowledge of the optical properties is important for treatment planning. If the optical properties are known, the Cimmino optimization of source strengths, which takes into account optical heterogeneity, can greatly improve the light fluence coverage. In the case that heterogeneity is significant, more sources are needed to cover the highly opaque region. If the optical properties are unknown, use of the measured light fluence rate for clinical planning is a practical strategy to deal with tissue heterogeneity in prostate PDT. If both the optical properties and the light fluence rate measurement are unavailable, it would be safer to use a uniform-strength plan rather than a homogeneous Cimmino optimized plan, because individually-derived source strengths may amplify errors in the absence of information. It is seen that the overdose becomes significant if the source strengths are raised too much (e.g., the case of the 12-source kernel 2). The situation could be improved by adding sources in the opaque region to boost the local light fluence to that region.

Figure 6.

Comparison of the prostate DVH of the reference clinical plan (RCP) (12 sources), the heterogeneous Cimmino plan using kernel 1 (12 sources), the heterogeneous Cimmino plan using kernel 2 (12 sources), the heterogeneous Cimmino plan using kernel 1 (35 sources), the heterogeneous Cimmino plan using kernel 2 (35 sources planned, 19 sources actually used).

CONCLUSIONS

The study shows that knowledge of the optical properties is critical for prostate PDT planning and that it is feasible to improve dose coverage in a heterogeneous prostate by optimizing light source intensities with the Cimmino feasibility algorithm. There is a tradeoff between the time needed to calculate a dose kernel and its accuracy. At least one kernel for real-time (in vivo) optimization with measured heterogeneous optical properties has been demonstrated.

It is implied that further improvement in dose coverage is possible through comprehensive optimization of source parameters (i.e., strengths, lengths, and locations).