Abstract
Light fluence delivered to the tumor volume is an important dosimetry quantity in photodynamic therapy (PDT). The in vivo measurements in 4 patients showed that light fluence rates varied significantly in a prostate during PDT. The maximum and the mean fluence rates in a quadrant varied from 74 to 777 mW/cm2 and from 45 to 385 mW/cm2, respectively, among 13 quadrants of 4 patients’ prostates. To determine three-dimensional (3D) light fluence rate distribution in a heterogeneous prostate, a kernel model was developed. The accuracy of the model was examined with a finite-element-method (FEM) model calculation, a phantom measurement, and the in vivo measurements. The kernel model calculations showed good agreements with the FEM model calculation and the measurements. The maximum and the mean deviations of the kernel model calculation from the in vivo measurements in the 4 patients were 23% and 4%, respectively. The kernel model, which is based on an analytic expression of a point source in a spherical symmetrical heterogeneity, has the advantage of fast calculation and is suitable for real time PDT treatment planning.
Keywords: photodynamic therapy, light fluence rate, prostate, heterogeneity, kernel model, finite element method model, cylindrical diffusing fiber
1. INTRODUCTION
Photodynamic therapy (Dougherty et al. 1998) is a treatment modality employing light of a certain wavelength in the presence of oxygen to activate a photosensitizer which then causes localized cell death and tissue necrosis. The efficacy of photodynamic therapy (PDT) depends upon multiple factors including light fluence, photosensitizer concentration, and tissue oxygen level (Wilson et al. 1997).
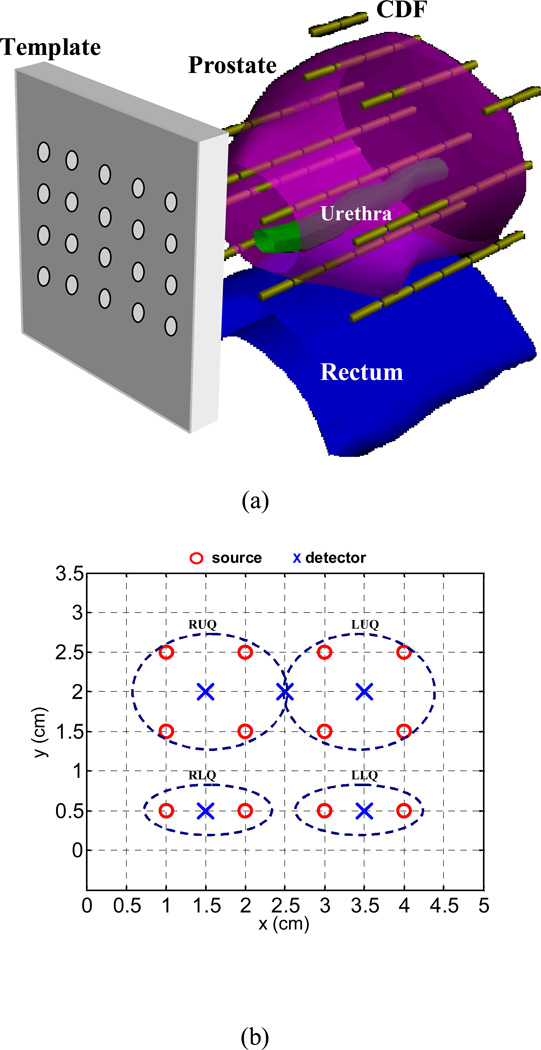
Interstitial light delivery (Arnfield et al. 1989, Whitehurst et al. 1993, Fenning et al. 1994, Chang et al. 1996, Lee et al. 1997, Nathan et al. 2002) has been applied as an efficient illumination scheme for PDT to treat large bulky tumors in solid organs such as prostate, whereby optical fibers are placed directly into the organs. Based on a preclinical study in canines (Zhu et al. 2003), we have initiated a protocol for motexafin lutetium (MLu)-mediated interstitial PDT of the prostate in patients at the University of Pennsylvania (Stripp et al. 2004, Zhu et al. 2005a, Zhu et al. 2005b, Du et al. 2006, Verigos et al. 2006). Laser at a wavelength of 732 nm is used to activate MLu. In the prostate PDT, cylindrical diffusing fibers (CDFs) with active lengths between 1 and 5 cm were used as light sources (Fig. 1(a)). Transparent catheters were inserted in parallel into the prostate with the guidance of a transrectal ultrasound (TRUS) unit through a template. The CDFs were placed in the catheters, with sufficient lengths to cover the prostate geometry. During the treatment, light fluence rates were measured at a few selected locations in the patient prostates.
Figure 1.
(a) Schematic of prostate PDT. CDF: cylindrical diffusing fiber. (b) Template with source and detector arrangement. RUQ, LUQ, RLQ, and LLQ indicate four quadrants in a treatment. The coordinate units are cm. The detectors, except the one between RUQ and LUQ, which is used for blood flow measurement, are used to measure light fluence rates in each quadrant.
The in-vivo measurement is limited in that it only measures light fluence rates at limited points (or linear arrays) rather than in a full three-dimensional (3D) volume. It is therefore necessary to have an accurate algorithm to calculate 3D light fluence rates. We have made the hypothesis that it is a given that the 3D distribution of the optical properties in prostate gland are known, e.g., one can determine the optical properties using diffuse optical tomography. Under this condition, the major concern is to develop an accurate algorithm for light fluence rate calculation. And it is desired that the algorithm can perform a fast calculation, which can be used for real-time inverse planning to optimize light fluence rate distribution during treatment.
The purposes of the study are two fold. The first is to determine the variation of light fluence rates in heterogeneous prostate during PDT, which is an important dosimetry quantity. The second objective is to develop an algorithm (method) and compare the difference between the measurements and calculations using the proposed method.
To calculate light fluence rates generated by a CDF, Dickey et al. (2004) had proposed a model, which simulated the source as a Huygens radiator. The model was tested with measurements in a homogeneous liquid phantom. In our previous study (Zhu et al. 2003), we had applied a homogeneous kernel model to calculate light fluence rates in prostate PDT. The model was based on the analytic solution of the diffusion equation for a point source in an infinite homogeneous medium (Jacques 1998). Although little variation of light fluence rates and optical properties were observed during prostate PDT (Zhu et al. 2005b, Chen et al. 1997), the human study (Zhu et al. 2005b) has shown that optical properties are heterogeneous in a prostate, which indicates that to accurately predict light fluence distribution in a prostate, optical heterogeneity needs to be taken into account.
Finite-element method (FEM) can deal with heterogeneity and irregular geometries. However, the calculation is not fast enough for real time treatment planning for prostate PDT. In the study, we developed a heterogeneous kernel model, which has the capability of dealing with optical heterogeneity. The model, which is based on an analytic expression for a point source in a spherically symmetrical heterogeneity, is fast in calculation. The calculation accuracy was examined with a FEM model, a phantom experiment, and in vivo measurements in patients.
2. METHODS
2.1 In vivo light fluence rate measurement
Light fluence rates in patients were measured using isotropic detectors (CardioFocus, Inc., West Yarmouth, MA) during PDT. Figure 1(b) shows a typical arrangement of light sources and detectors in a treatment geometry, in which the prostate was divided into four quadrants (or regions): right upper quadrant (RUQ), left upper quadrant (LUQ), right lower quadrant (RLQ), and left lower quadrant (LLQ). A detector was located at the center of each quadrant and was scanned in the catheter along the z direction, which was parallel to the CDFs. One-dimensional (1D) light fluence rate distributions along each track were obtained. The detector between RUQ and LUQ was used for blood flow measurement. The light power per unit length of the CDF usually was less than or equal to 150 mW/cm. The emission profile of each CDF was measured in air before application.
2.2 Heterogeneous kernel model
The transport of near-infrared light in biological tissue is often described by the diffusion equation (Schweiger et al. 1995)
| (1) |
where ϕ is the light fluence rate, D (=1/(3µs')) is the diffusion coefficient, S0 is the isotropic source distribution and µs' is the reduced scattering coefficient. For heterogeneous medium, D and µa are spatially dependent. The light transport in a prostate during PDT can be described using the diffusion equation. For homogeneous medium, Eq. 1 can be solved analytically for a point source (Jacques et al. 1998, Zhu et al. 2003):
| (2) |
where S is the source power (mW or W). The quantity (Nakai 1997) is used to replace the standard expression for the effective attenuation coefficient in tissues, and r is the distance between source and detector.
The heterogeneous kernel model was expressed here for a point source, for spherical-shell distribution of optical properties. The model can be extended for CDF and arbitrary optical property distribution. For a point source located at r=0, optical properties are assumed to be homogeneous in each shell surrounding the source and are different from shell to shell. Light fluence rates in each shell are expressed as
| (3) |
| (4) |
and
| (5) |
in the last shell. Boundary conditions between two shells are applied, which include fluence continuity and flux continuity (Schweiger et al. 1995)
| (6) |
| (7) |
In addition, the total energy released by the light source is conserved:
| (8) |
That is, the energy absorbed in the medium is equal to the source power S. The boundary conditions (Eqs. 6 and 7) are used to determine the iterative relationship (Eqs. 9 and 10) for the coefficients pi and qi. The coefficient C (Eqs. 11–12) is derived using Eq. 8. The expressions for pi, qi, and C are,
| (9) |
| (10) |
| (11) |
where
| (12) |
For i=N+1 (i.e., the outmost shell), rN+1=∞ and qN+1=0. In the study, we assumed pN+1=1 and calculated the light fluence rate in the ith (i<N+1) shell. For homogeneous optical properties, the fluence rate expression (Eqs. 3–12) becomes Eq. (2).
For arbitrary 3D distribution of optical properties, we expanded the expressions for light fluence rate to keep the forms to be the same as those expressed in Eqs. 3–5 and Eqs. 9–12, and optical properties on the ray line between the source and the detector were used, i.e., µeff(r) was replaced by µeff(r,θ,ϕ). The solution derived for a point source was extended for a CDF source by considering that a CDF was composed of multiple point sources. The fluence rate at a point was a summation of fluence rates generated by each point source.
A FEM model was applied to examine the kernel model, which was taken as the gold standard in the comparison. The FEM model was implemented using Comsol Multiphysics software (Comsol Inc., Burlington, MA). Based on a previous study (Li and Zhu 2005), we think a tissue-tissue boundary with refractive-index match is a reasonable boundary condition for the prostate and the outside medium. In the FEM model, the prostate geometry was surrounded with a large cylindrical layer simulating the outside medium (tissue). Meshes were generated in the 3D geometry, which was partitioned into tetrahedrons in the volume and triangular elements on the boundary. The elements were Langrange quadratic. Finer meshes (0.1 mm) were generated near CDFs to ensure calculation accuracy.
3. RESULTS AND DISCUSSION
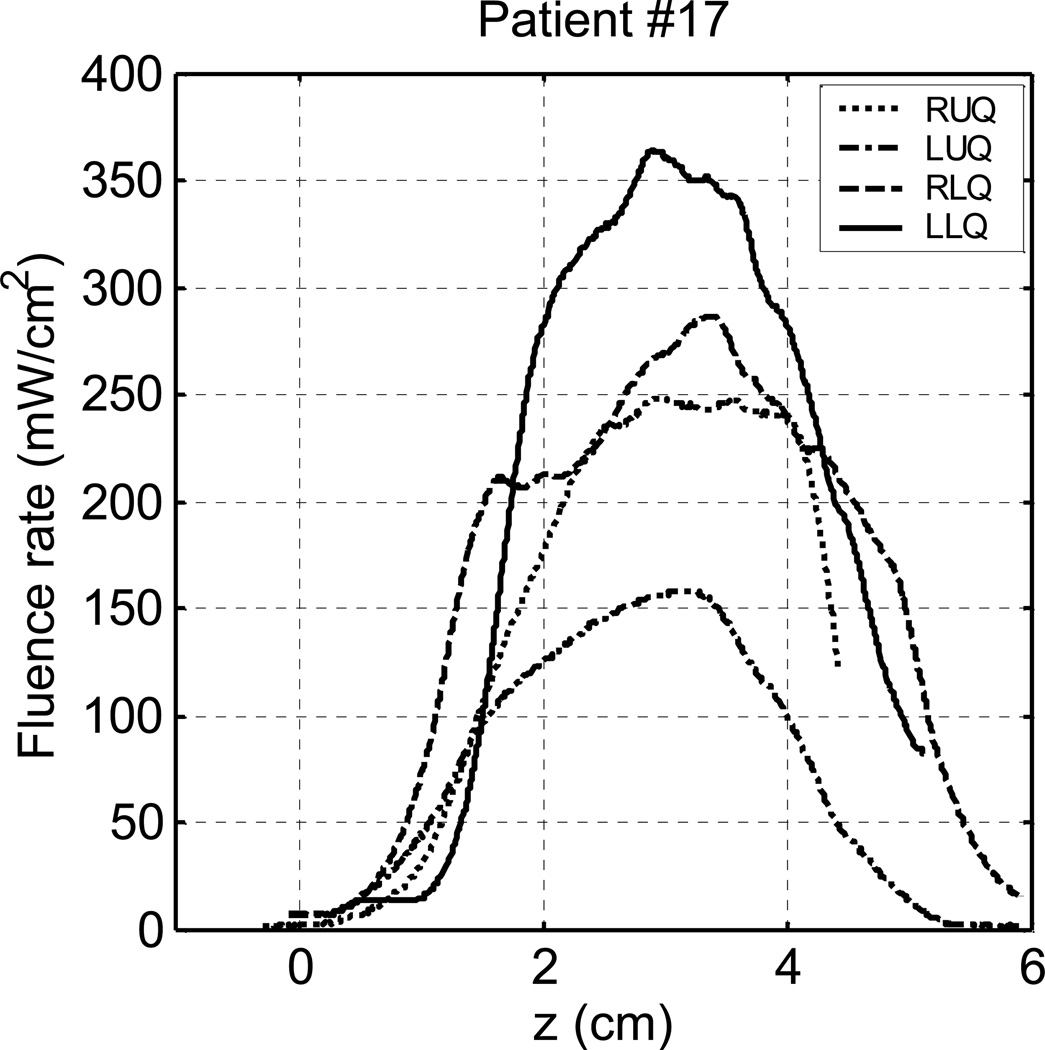
Figure 2 shows 1D light fluence rate distributions measured in vivo in 4 quadrants of a patient (#17) prostate. The light fluence rates in RUQ were not recorded completely. The source lengths and light fluence rates in each quadrant are summarized in Table 1. All the sources had the same light power per length of 150 mW/cm. The measured fluence rate distributions were different from quadrant to quadrant. The peak fluence rates in LUQ, RLQ, and LLQ were 158 mW/cm2, 285 mW/cm2, and 363 mW/cm2, respectively. The source arrangement and source powers were similar for RLQ and LLQ in the treatment. We attribute the difference in the fluence rate distribution to the effect of optical heterogeneity. We measured light fluence rates in 4 patients (totally 13 quadrants). The fluence rate distributions were found to be different from quadrant to quadrant in every patient. In one patient, the peak fluence rate of a quadrant was 3 times larger than that of another quadrant. The peak fluence rates and the mean fluence rates in 13 quadrants varied from 74 to 777 mW/cm2, and from 45 to 385 mW/cm2, respectively. The measurements indicate that light fluence could be significantly different at different locations in a patient prostate and it is important to obtain 3D light fluence rate distribution in a prostate.
Figure 2.
In vivo light fluence rates measured in 4 quadrants of a patient prostate during PDT.
Table 1.
Summary of source lengths and measured light fluence rates in each quadrant in patient #17. All the sources have the same light power per length of 150 mW/cm.
| Quadrant | Source length in each quadrant (cm) | Light fluence rates in each quadrant (mW/cm2) |
|||||
|---|---|---|---|---|---|---|---|
| Source 1 | Source 2 | Source 3 | Source 4 | Minimum | Maximum | Mean | |
| RUQ | 3 | 3 | 3 | 4 | 1 | 248 | 141 |
| LUQ | 3 | 3 | 4 | 3 | 1 | 158 | 74 |
| RLQ | 3 | 4 | _____ | _____ | 6 | 285 | 159 |
| LLQ | 4 | 3 | _____ | _____ | 14 | 363 | 213 |
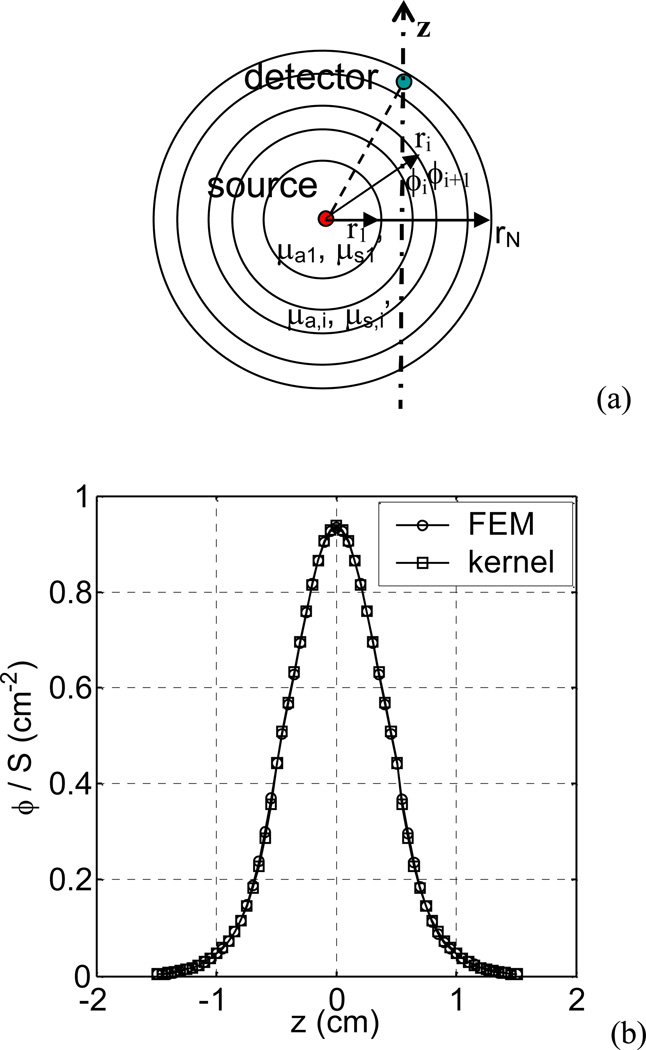
The heterogeneous kernel model was examined firstly for a point source. A spherical shell distribution of optical properties was used (Fig 3(a)). The optical properties were set arbitrarily from shell to shell: µa=0.3, 0.1, 0.8, and 0.7 cm−1, and µs’ =14, 5, 8, and 10 cm−1, in the shell of r=0.3, 0.7, 1.1, and 4 cm, respectively. Figure 3(b) shows the comparison of the light fluence rates calculated using the kernel model and the FEM model, respectively. The light fluence rates were along a line 0.5 cm away from the point source. The fluence rates calculated using the kernel model agree with those calculated using the FEM model with the mean percentage deviation of 2%. The model was also tested using other optical property settings and similar results were obtained (the comparisons are not shown). This study verifies that the model for a point source in a spherical shell distribution of optical properties is correct.
Figure 3.
(a) Schematics of spherical shell optical property distribution for the kernel model. (b) Comparison of light fluence rates calculated using the kernel model and the FEM model, respectively, for a point source with a spherical shell distribution of optical properties (µa=0.3, 0.1, 0.8, and 0.7 cm−1, µs’ =14, 5, 8, and 10 cm−1, in the shells of r=0.3, 0.7, 1.1, and 4 cm, respectively). The fluence rate distributions are along a line 0.5 cm away from the source.
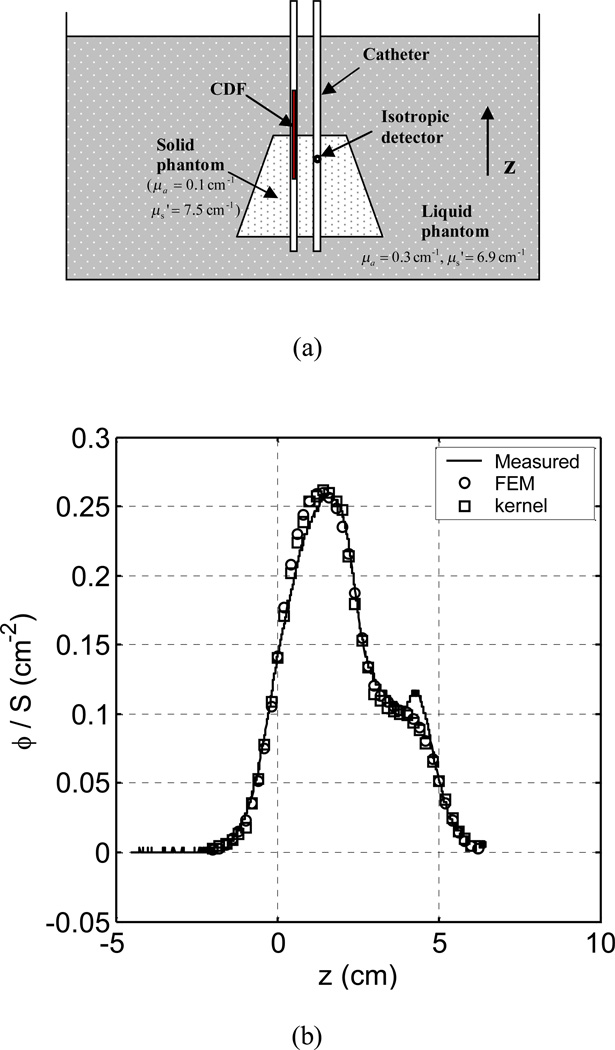
A phantom experiment was then carried out to test the model for a CDF source in a heterogeneous medium. Figure 4(a) shows the schematic of the experiment, which simulated a prostate PDT. A solid cone-shape phantom (µa = 0.1 cm−1 and µs' = 7.5 cm−1) simulating a prostate was immersed in a liquid phantom (µa = 0.3 cm−1 and µs' = 6.9 cm−1). The top and the bottom surfaces of the solid phantom were 3 cm and 4.5 cm in diameter, respectively. The height was 4 cm. The liquid phantom was much larger than the solid phantom, which behaved like an infinite medium. A 5-cm CDF was placed in a catheter, which was half in the solid phantom and half in the liquid phantom. The two phantoms composed a heterogeneous medium. An isotropic detector was scanned in a catheter 0.7 cm away from the source. Figure 4(b) shows the comparison of measured and calculated light fluence rates. The kernel model calculation agrees with the FEM calculation and both of them have good agreement with the measurement: the mean percentage deviation of the FEM calculation from the measurement and that of the kernel calculation are both 6%. The phantom study demonstrates that the kernel model is capable of predicting light fluence rates generated by a CDF in a heterogeneous medium. The phantom used in the test was a simple geometry. A more challenging test would have included asymmetric heterogeneities within the cone. To test the kernel model with complex heterogeneity, we applied the model to calculate 3D light fluence rate distribution in patient prostates.
Figure 4.
(a) Schematics of light fluence rate measurement in a heterogeneous phantom, which was composed of a solid cone-shape phantom (µa = 0.1 cm−1 µs' and = 7.5 cm−1) and liquid phantom (µa = 0.3 cm−1 and µs' = 6.9 cm−1). The top and the bottom surfaces of the cone-shape solid phantom were 3 cm and 4.5 cm in diameter, respectively, and the height was 4 cm. A 5-cm cylindrical diffusing fiber (CDF) was half in the solid phantom and half in the liquid phantom, which was located between z=0 and z=5 cm. (b) Comparison of measured fluence rates and those calculated using the FEM model and the kernel model, respectively. The light fluence rate distribution is in the z direction, i.e., along the catheter.
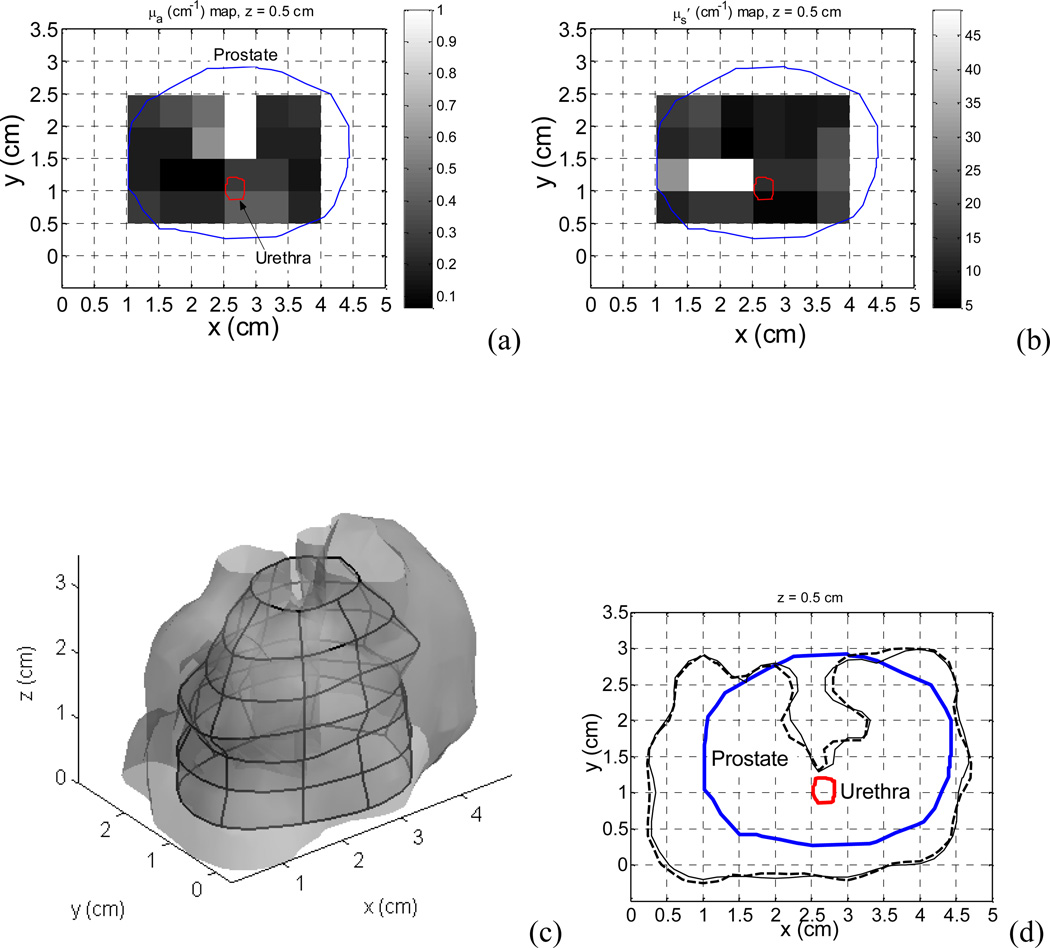
We had measured 3D optical properties in a patient prostate during PDT. The measurements were performed using a point source (Zhu et al. 2005b) on a 0.5×0.5 cm2 grid template at 0.5 cm spacing. The optical properties were assumed to be homogeneous in each 0.5×0.5×0.5 cm3 voxel. Figure 5(a) and (b) show the absorption coefficient map and the scattering coefficient map measured in the patient in the plane of z=0.5 cm, respectively. The measured optical properties were used in the calculation and the optical properties of the medium outside of the prostate were assumed to be the same as those on the prostate boundary. The source arrangement and source strengths used in the calculation were the same as those in the treatment. Figure 5(c) shows a calculated isodose (100 mW/cm2) surface, which is superimposed on the prostate geometry. Figure 5(d) shows the comparison of the isodose lines of 100 mW/cm2 in one of the planes (z=0.5 cm). The solid line and the dashed line are the isodose lines calculated using the FEM model and the kernel model, respectively. The kernel calculation agrees well with the FEM calculation: the mean deviation of the coordinates of the kernel isodose line from those of the FEM isodose line is 0.2 cm. Both of the fluence rate distributions show the effect of the optical heterogeneity in the prostate, i.e., significant absorption in the upper region of the prostate. The fluence rates vary remarkably in the prostate. In the plane, the fluence rate is over 100 mW/cm2 in the majority of the prostate while it is only ~23 mW/cm2 in the upper region.
Figure 5.
Heterogeneous optical properties measured in a patient prostate in the plane of z=0.5 cm. (a) Optical absorption coefficient map. (b) Scattering coefficient map. (c) Isodose (100 mW/cm2) surface calculated using the kernel model. The surface is superimposed on the prostate geometry. (d) Comparison of isodose (100 mW/cm2) lines calculated using the kernel model (dashed line) and the FEM model (solid line), respectively.
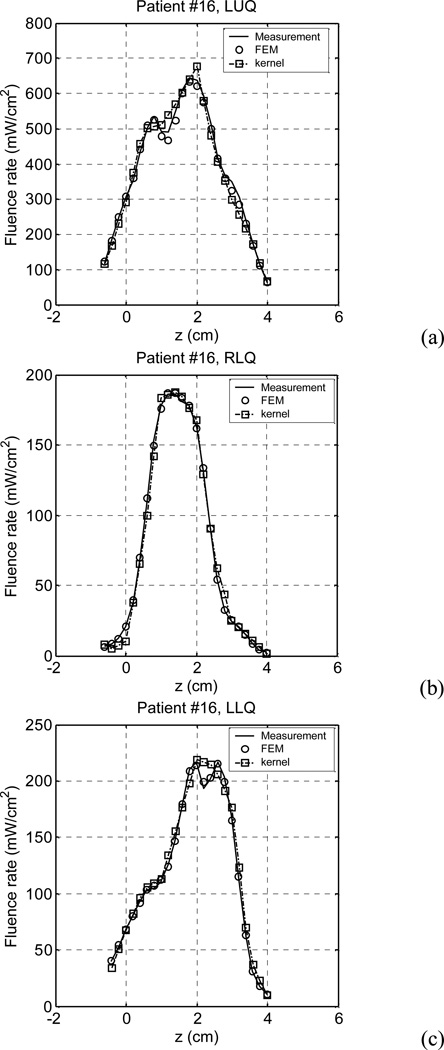
A further study was carried out to check if the kernel model could accurately predict light fluence rates in clinical cases, i.e., check if the kernel model calculation would agree with in vivo light fluence rate measurements. Light fluence rates measured in 4 patients (totally 13 quadrants) were studied. Due to the lack of 3D optical properties, we tried an inverse process to obtain optical properties for the kernel model calculation to compare with the in vivo measurements. Initial optical properties (µa =0.3 cm−1 and µs'=14 cm−1) were assumed, which were the average optical properties measured in 14 patients’ prostates (Zhu et al. 2005b), and a calculation was carried out iteratively, with the same source arrangements and source strengths as those in the treatment. In each iteration step, the optical properties were adjusted to make the calculated light fluence rates match the measurement. The optical scattering coefficient was assumed to be 14 cm−1, and the absorption coefficient was searched using the FEM calculation, which was varied along the z direction. Optimal optical properties (µa) were obtained when the deviations of the calculation and the measurement were less than 2% (Dimofte at al. 2008). We found that one can use any µs' and still fit the light fluence rate curve. The maximum difference in extrapolated µa is within 20%. With the optimal optical properties, light fluence rates were calculated using the kernel model. Figure 6 shows the comparison of the measurement, the FEM calculation, and the kernel calculation in a patient (#16). In the patient, light fluence rates were measured only in 3 quadrants (LUQ, RLQ, and LLQ). The comparisons show that the kernel calculation and the FEM calculation results are very close to the measurements.
Figure 6.
Comparison of measurement, FEM calculation, and kernel calculation in three quadrants of a patient (#16) prostate: (a) LUQ, (b) RLQ, and (c) LLQ. The calculations used the optimal optical properties which were obtained by a search process.
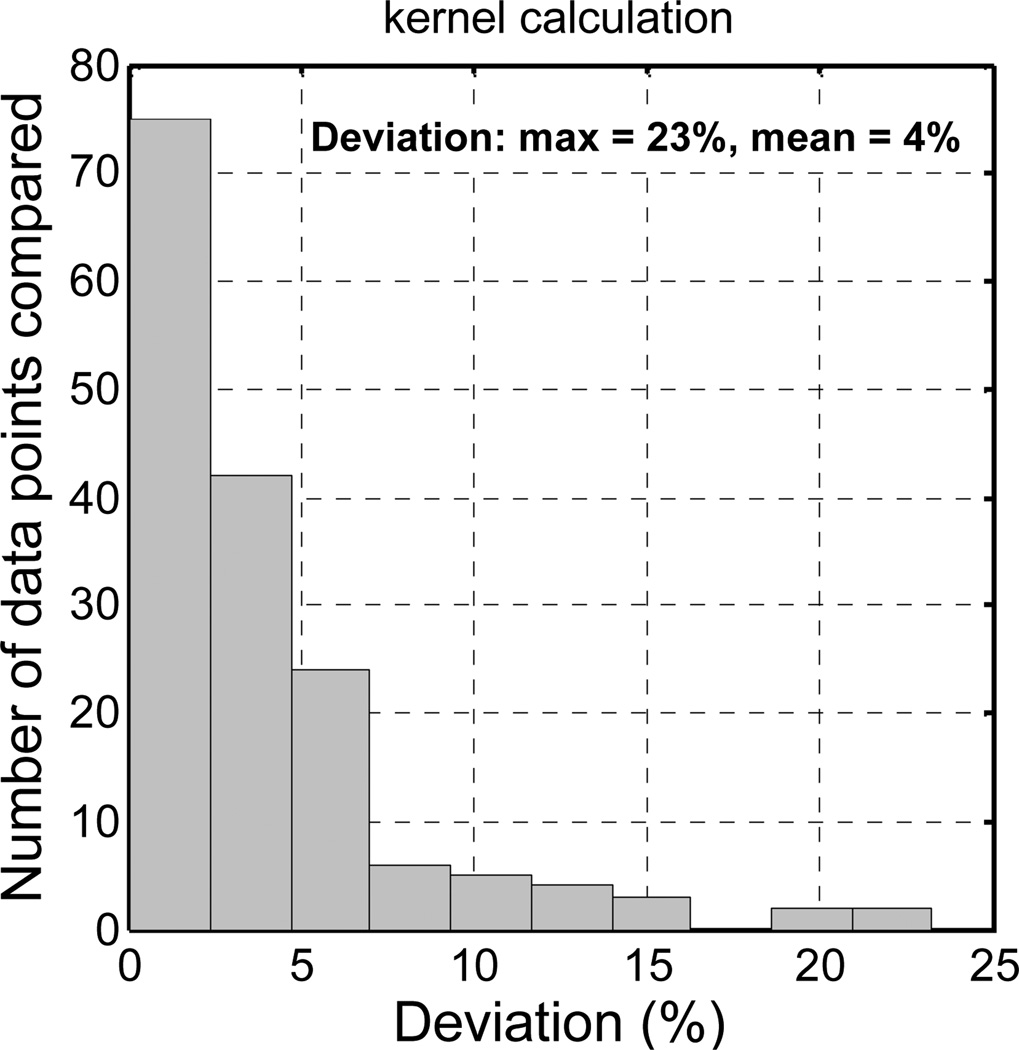
Similar calculations were performed in 13 quadrants of 4 patients’ prostates. Deviations of the calculated fluence rates from the measurements were calculated, by taking the absolute value of the percentage difference at each data point, i.e., deviation = abs (calculation -measurement) / measurement. Figure 7 shows histogram of the deviations of light fluence rates calculated using the kernel model. Because the deviation (i.e., the ratio) at the tail of the fluence rate distribution may have large errors, data in those regions were excluded in the deviation calculation. The fluence rates which had magnitudes larger than the half maximum in the quadrant were counted. The maximum deviation and the mean deviation of the kernel calculation were 23% and 4%, respectively. These are the statistical results of 163 data points. The results indicate that if actual optical properties are known, the kernel model can give good predication of light fluence rates in a prostate during PDT. Although the kernel model calculation is not as accurate as the FEM model calculation which has mean deviation of 1%, it is faster in calculation. The calculations in Fig. 5 took ~10 seconds and ~180 seconds on a PC with a 2.4 GHz CPU, for the kernel model and the FEM model, respectively. The kernel model is promising for real-time treatment planning.
Figure 7.
Histogram of the deviations of fluence rates calculated using the kernel model from those measured in 13 quadrants of 4 patients. The calculation used the fluence-rate data points which had magnitudes larger than the half of the maximum in each quadrant.
4. CONCLUSIONS
In vivo measurements showed significant difference of light fluence rate distributions in patient prostates during PDT, which indicate that it is important to obtain light fluence rates at any point in a prostate volume. The heterogeneous kernel model showed the capability of calculating 3D light fluence rate distribution in a heterogeneous prostate. The calculation accuracy was close to that of the FEM model. The statistics based on the comparisons among 13 quadrants of 4 patients’ prostates showed that the maximum and the mean deviations of the kernel model calculation from the in vivo measurements were 23% and 4%, respectively. The kernel model, which is fast in calculation, can be applied for real-time treatment planning.
ACKNOWLEDGMENT
This work is supported by grants from Department of Defense (DOD) DAMD17-03-1-0132 and National institute of health (NIH) P01 CA87971 and R01 CA109456.
References
- Arnfield MR, Tulip J, Chetner M, McPhee MS. Optical dosimetry for interstitial photodynamic therapy. Med. Phys. 1989;16:602–608. doi: 10.1118/1.596361. [DOI] [PubMed] [Google Scholar]
- Chang SC, Buonaccorsi G, MacRobert A, Bown SG. Interstitial and transurethral photodynamic therapy of the canine prostate using meso-tetra-(m-hydroxyphenyl) chlorin. Int. J. Cancer. 1996;67:555–562. doi: 10.1002/(SICI)1097-0215(19960807)67:4<555::AID-IJC15>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- Chen Q, Wilson BC, Shetty SD, Patterson MS, Cerny JC, Hetzel FW. Changes in vivo optical properties and light distributions in normal canine prostate during photodynamic therapy. Radiat. Res. 1997;147:86–91. doi: 10.2307/3579447. [DOI] [PubMed] [Google Scholar]
- Dickey DJ, Partridge K, Moore RB, Tulip J. Light dosimetry for multiple cylindrical diffusing sources for use in photodynamic therapy. Phys. Med. Biol. 2004;49:3197–3208. doi: 10.1088/0031-9155/49/14/013. [DOI] [PubMed] [Google Scholar]
- Dimofte A, Finlay JC, Li J, Zhu TC. Determination of optical properties in a heterogeneous turbid media using a cylindrical diffusing fiber. Proc. SPIE. 2008;6845 doi: 10.1088/0031-9155/57/19/6025. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dougherty TJ, Gomer CJ, Henderson BW, Jori G, Kessel D, Korbelik M, Moan J, Peng Q. Photodynamic therapy. J. Natl. Cancer Inst. 1998;90:889–905. doi: 10.1093/jnci/90.12.889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du KL, Mick R, Busch TM, Zhu TC, Finlay JC, Yu G, Yodh AG, Malkowicz SB, Smith D, Whittington R, Stripp D, Hahn SM. Preliminary results of interstitial motexafin lutetium-mediated PDT for prostate cancer. Lasers Surg. Med. 2006;38:427–434. doi: 10.1002/lsm.20341. [DOI] [PubMed] [Google Scholar]
- Fenning MC, Brown DQ, Chapman JD. Photodosimetry of interstitial light delivery to solid tumors. Med. Phys. 1994;21:1149–1156. doi: 10.1118/1.597342. [DOI] [PubMed] [Google Scholar]
- Jacques SL. Light distributions from point, line and plane sources for photochemical reactions and fluorescence in turbid biological tissues. Photochem. Photobiol. 1998;67:23–32. [PubMed] [Google Scholar]
- Lee LK, Whitehurst C, Chen Q, Pantelides ML, Hetzel FW, Moore JV. Interstitial photodynamic therapy in the canine prostate. Br. J. Urol. 1997;80:898–902. doi: 10.1046/j.1464-410x.1997.00460.x. [DOI] [PubMed] [Google Scholar]
- Li J, Zhu TC. Finite-element modeling of light fluence distribution in prostate during photodynamic therapy. Proc. COMSOL Multiphysics Conference 2005. 2005:57–62. [Google Scholar]
- Nakai T, Nishimura G, Yamamoto K, Tamura M. Expression of optical diffusion coefficient in high-absorption turbid media. Phys. Med. Biol. 1997;42:2541–2549. doi: 10.1088/0031-9155/42/12/017. [DOI] [PubMed] [Google Scholar]
- Nathan TR, Whitelaw DE, Chang SC, Lees WR, Ripley PM, Payne H, Jones L, Parkinson MC, Emberton M, Gillams AR, Mundy AR, Bown SG. Photodynamic therapy for prostate cancer recurrence after radiotherapy: a phase I study. J. Urol. 2002;168:1427–1432. doi: 10.1016/S0022-5347(05)64466-7. [DOI] [PubMed] [Google Scholar]
- Schweiger M, Arridge SR, Hiraoka M, Delpy DT. The finite element method for the propagation of light in scattering media: boundary and source conditions. Med. Phys. 1995;22:1779–1792. doi: 10.1118/1.597634. [DOI] [PubMed] [Google Scholar]
- Stripp DCH, Mick R, Zhu TC, Whittington R, Smith D, Dimofte A, Finlay J, Miles J, Busch TM, Shin D, Kachur A, Tochner ZA, Malkowicz SB, Glatstein E, Hahn SM. Phase I trial of motexafin lutetium-mediated interstitial photodynamic therapy in patients with locally recurrent prostate cancer. Proc. SPIE. 2004;5315:88–99. doi: 10.1615/jenvironpatholtoxicoloncol.v25.i1-2.230. [DOI] [PubMed] [Google Scholar]
- Verigos K, Stripp DCH, Mick R, Zhu TC, Whittington R, Smith D, Dimofte A, Finlay J, Busch TM, Tochner ZA, Malkowicz SB, Glatstein E, Hahn SM. Updated results of a phase I trial of motexafin lutetium-mediated interstitial photodynamic therapy in patients with locally recurrent prostate cancer. J. Environ. Pathol. Toxicol. Oncol. 2006;25:373–387. doi: 10.1615/jenvironpatholtoxicoloncol.v25.i1-2.230. [DOI] [PubMed] [Google Scholar]
- Wilson BC, Patterson MS, Lilge L. Implicit and explicit dosimetry in photodynamic therapy: a new paradigm. Lasers Med. Sci. 1997;12:182–199. doi: 10.1007/BF02765099. [DOI] [PubMed] [Google Scholar]
- Whitehurst C, Pantelides ML, Moore JV, Blacklock NJ. Optimization of multifiber light delivery for the photodynamic therapy of localized prostate cancer. Photochem. Photobiol. 1993;58:589–593. doi: 10.1111/j.1751-1097.1993.tb04937.x. [DOI] [PubMed] [Google Scholar]
- Zhu TC, Finlay JC, Hahn JSM. Determination of the distribution of light, optical properties, drug concentration, and tissue oxygenation in-vivo in human prostate during motexafin lutetium-mediated photodynamic therapy. J. Photochem. Photobiol. B Biology. 2005a;79:231–241. doi: 10.1016/j.jphotobiol.2004.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu TC, Dimofte A, Finlay JC, Stripp D, Busch T, Miles J, Whittington R, Malkowicz SB, Tochner Z, Glatstein E, Hahn SM. Optical properties of human prostate at 732nm measured in vivo during motexafin lutetium-mediated photodynamic therapy. Photochem. Photobiol. 2005b;81:96–105. doi: 10.1562/2004-06-25-RA-216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu TC, Hahn SM, Kapatkin AS, Dimofte A, Rodriguez CE, Vulcan TG, Glatstein TE, Hsi RA. In vivo optical properties of normal canine prostate at 732 nm using motexafin lutetiummediated photodynamic therapy. Photochem. Photobiol. 2003;77:81–88. doi: 10.1562/0031-8655(2003)077<0081:ivopon>2.0.co;2. [DOI] [PubMed] [Google Scholar]