Constant-speed vibrational signaling along polyethyleneglycol chain up to 60-Å distance

Abstract

A series of azido-PEG-succinimide ester oligomers with a number of repeating PEG units of 0, 4, 8, and 12 (azPEG0, 4, 8, and 12) was investigated using a relaxation-assisted two-dimensional infrared (RA 2DIR) spectroscopy method. The RA 2DIR method relies on the energy transport in molecules and is capable of correlating the frequencies of vibrational modes separated by large through-bond distances. Excitation of the azido group in the compounds at ca. 2,100 cm^-1 generates an excess energy which propagates in the molecule as well as dissipates into the solvent. We discovered that a part of the excess energy propagates ballistically via the covalent backbone of the molecules with a constant speed of ca. 550 m/s. The transport is described as a propagation of a vibrational wavepacket having a mean-free-path length of 10–15 Å. The discovery has the potential for developing new efficient signal transduction strategies for molecular electronics and biochemistry. It also permits extending the distances accessible in RA 2DIR structural measurements up to ca. 60 Å.

Understanding the energy transport dynamics on a molecular scale is vital for a variety of fields including molecular electronics, nanoscience, and biochemistry. A fast developing molecular electronic field utilizes signaling based on charge transport in molecular assemblies; it is conceivable that signaling mechanisms based on energy transduction could be useful if molecular systems featuring efficient energy transport are discovered. Efficient energy dissipation is important for devices of different dimensions ranging from molecular scale—for example, molecular junctions (1)—to macroscopic, such as, for example, optical limiters. Chemical reactions, including charge transfer processes can be influenced substantially by the excess vibrational energy; understanding of the energy transport properties can lead to a control of such reactions (2).

Two-dimensional infrared (2DIR) spectroscopy (3–5), in particular the relaxation-assisted 2DIR (RA 2DIR) method (6–8), permits measuring energy transport on a molecular scale. The method relies on the energy transport from the initially excited vibrational mode to the probed mode (a reporter mode); the excess energy transferred to the vicinity of the reporter mode causes a change of its frequency, which results in appearance of the RA 2DIR cross-peak (Fig. 1). Efficient energy transport via covalent bonds resulting in large cross-peak enhancements was observed for the through-bond distances of up to 23 Å (9). The energy transport between ligands in transition-metal complexes has been shown to be efficient as well, demonstrating a 27-fold cross-peak amplification using RA 2DIR (10–12).

Fig. 1.

Cartoon representation of various cross-peak contributions between the initially excited (stars) and probed (boxes) infrared labels. The areas bearing excess energy in each diagram are colored in red.

The energy transport via strong bonds, covalent, coordination, etc., is the dominant energy transport channel at the early time delays after excitation (Fig. 1B). The energy transport to the solvent (13–15) and between the solvent molecules completes the thermal equilibration in the system (Fig. 1C). For example, thermal equilibration in the sample of 0.1 M concentration in chloroform following excitation of IR labels in the sample at ca. 2,100 cm^-1 results in a temperature increase in the solution by ca. 0.1 °C (Fig. 1C) (9); the characteristic time of the thermalization was found to be ca. 19 ps (9). Because most vibrational modes respond to a temperature change with a shift of their central frequencies, the temperature increase and the equilibration dynamics can be measured via RA 2DIR spectroscopy as an evolution of the cross-peak amplitude as a function of the delay between the excitation and probing IR pulses, the waiting time. If the initially excited IR mode and the reporter mode reside on the same molecule and the through-bond interlabel distance is small (< 23 Å), the through-bond energy transfer mechanism is much more efficient than the through-solvent energy transport. However, it could be reversed at larger interlabel distances as the size of the excessively excited part of the molecule increases with the energy transport advancement resulting in more efficient cooling to the solvent. It could be difficult to separate the contributions of the two pathways experimentally.

There are two limits for the energy transport: One is described by a diffusion-like heat conduction equation; another assumes a vibrational wavepacket propagation via phonons and results in a ballistic energy transport. Both regimes can be found for energy transport in macroscopic and mesoscopic samples in the condensed phase; the ballistic transport requires delocalized vibrational states in the sample and can be observed for transport distances less than or comparable to the mean-free-path length of the wavepacket (16, 17). Both acoustic and optical phonons can transfer energy ballistically; while the dispersion relations for acoustic phonons favor a wavepacket propagation with limited broadening, those for optical phonons are more complex (18).

Different energy transport regimes in molecules have been studied theoretically (1, 17, 19–21) and experimentally. Diffusive energy transport was observed in many molecular systems including 3₁₀ helices of different sizes with vibrational (22) and electronic (23) initial excitation and a range of model compounds (6, 8, 10, 24, 25). Ballistic energy transport in long-chain stretched hydrocarbons exposed to ca. 800-K transient temperature gradient was found by Dlott and coworkers in self-assembled monolayers of alkanes at a gold surface (26, 27). A ballistic contribution to energy transport was reported for single-wall carbon nanotubes (28) and for several other systems (29–31).

In this paper we use RA 2DIR spectroscopy to investigate the energy transport and dissipation in a series of PEG oligomers featuring an azido moiety and succinimide ester at two ends of the oligomer. The cross-peaks among N ≡ N and several other stretching modes, including three C = O, and C-N-C modes were measured and analyzed. We discovered an efficient long-range through-bond energy transport along the PEG oligomer chains that occurs with a constant speed.

Results and Discussion

Molecular System.

A series of four compounds was investigated featuring an azido and succinimide ester end moieties connected via a PEG oligomer chain with a number of repeating units (n) of 0, 4, 8, and 12 (azPEGn). Note that the azPEG0 compound has three bridging carbon atoms (Fig. 2A). The chain length, taken as the through-bond distance between the nitrogen atom of the azido group attached to the chain and the carbon atom of the ester, equals 6.1, 22.1, 39.7, and 57.2 Å with the number of the bridging backbone atoms of 3, 14, 26, and 38 for n = 0, 4, 8, and 12, respectively. All four compounds can be mixed with chloroform in any proportions and are expected to be fully solvated. The concentration of all compounds was ca. 80 mM, which corresponds to a solvent-to-solute mole fraction of ca. 150. No strong specific attraction of the end groups is expected based on the chemical nature of the groups. The statistical mean square end-to-end distance in a theta solvent where polymer coils act like ideal chains, 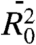, can be estimated using a random flight chains model with restricted bond angles, ϕ, Eq. 1.

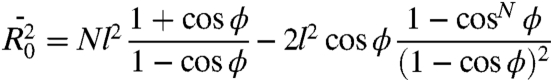[1]

Here N is the number of bonds in the polymer, l is the mean bond length taken as a mean of the existing C-C (1.53 Å) and C-O (1.43 Å) bonds, and ϕ equals 70.5°. The polymer expansion factor, α, characterizing the solvent-polymer interaction, determines the root-mean-square end-to-end distance in the solvent, 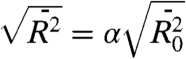. For small PEG oligomers in chloroform at room temperature α was found to be ca. 1.15 (32), which results in the root-mean-square end-to-end distances of ca. 4.5, 9.0, 12.2, and 14.7 Å for the four compounds in chloroform. Thus, all four compounds in chloroform assume a random coil conformation with a broad distribution of the head-to-tail distances. Note that chloroform was found to be one of the best solvents for PEG compared to water, DMSO, THF, and methanol (32). The Mark–Houwink exponent for PEG in chloroform a ∼ 0.68 is the largest among these solvents; the value suggests that the oligomers in chloroform adopt a partially extended but still mostly coiled conformation (32).

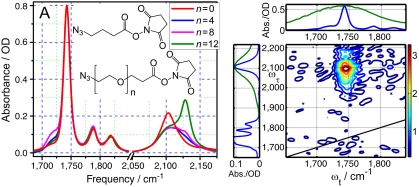
Fig. 2.

(A) Linear absorption spectra of the four compounds shown in the inset. (B) 2DIR spectrum of azPEG4 measured at T = 60 ps.

RA 2DIR Measurements.

Dual-frequency RA 2DIR measurements were performed for the four compounds focusing on the cross-peaks between the N ≡ N stretching mode (2,107 cm^-1) of the azido group and the C = O stretching modes of the succinimide ester (Fig. 2B), as well as between the N ≡ N stretching and the C-N-C asymmetric stretching (1,207 cm^-1) modes of succinimide. The three C = O groups of succinimide ester form a very characteristic coupling pattern: The strongest peak found at the low-frequency side (1,742 cm^-1) belong purely to an asymmetric stretch of the two carbonyls of the succinimide moiety, while the other two peaks (1,778 and 1,819 cm^-1) have almost equal contributions (in-phase and out-of-phase) from the symmetric stretch of succinimide and the C = O stretch of the ester (9).

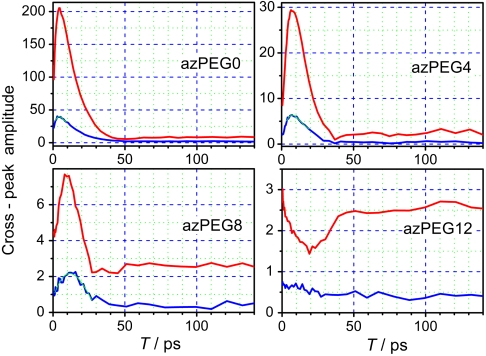
The waiting-time, T, dependencies of the N ≡ N/1,742 cm^-1 cross-peak amplitude for the four compounds are shown in Fig. 3. The dependencies share many similarities: The cross-peak amplitude at T = 0 is substantial in all four compounds, reporting on the direct N ≡ N/1,742 cm^-1 coupling. The cross-peaks increase with time (except for azPEG12) due to the RA 2DIR contribution (Fig. 1B). The cross-peak enhancement, which is the ratio of the cross-peak amplitude at the maximum and at T = 0, depends on how efficiently the excess energy is transported from the azido group to the succinimide ester moiety. Excitation of the modes at the succinimide moiety results in a shift of the reporter mode (1,742 cm^-1) frequency due to anharmonic coupling of those modes with the reporter. The smaller values of the cross-peak amplitude at the maximum found for the longer compounds indicate that a smaller amount of excess energy reached the succinimide moiety there.

Fig. 3.

Waiting-time dependencies for the N ≡ N/1,742 cm^-1 (red) and N ≡ N/1,778 cm^-1 (blue) cross-peaks for the four compounds indicated. The best fits with the asymmetric bell-shaped function, y = y₀ + A^∗ exp(- exp(-z) - z + 1), where z = (x - x_c)/w, are shown for the N ≡ N/1,778 cm^-1 cross-peaks with thin lines (cyan).

The cross-peak amplitudes at T = 0 confirm the coiled conformation of the compounds: Despite a very large through-bond distance between the IR labels in azPEG4-12, the direct coupling is substantial and the amplification factor is small. Negligible direct couplings and very large amplification factors are expected for fully extended azPEG4-12 structures. Because of the large through-bond distances, the through-space transition dipole–transition dipole coupling is expected to dominate at T = 0 for the azPEG4-12 compounds. Despite large transition dipoles of the N ≡ N and 1,742 cm^-1 modes (0.29 and 0.41 D), only a subensemble of molecules having small end-to-end distances is contributing to the cross-peak at T = 0. The through-space interaction of N ≡ N and 1,742 cm^-1 modes estimated using the point-dipole approximation (12) results in the experimentally accessible N ≡ N/1,742 cm^-1 anharmonicity of 0.01 cm^-1 when the groups are separated by ca. 5.5 Å. Note that the cross-peak amplitude at T = 0 decreases steeply with an increase of the chain length (Fig. 3).

Energy Transport.

In all compounds except azPEG12 the cross-peaks grow with the waiting time T, reach a maximum, and then decay to a plateau, not to a zero amplitude. At the delay times of the plateau (> 50 ps), the excess energy introduced by the N ≡ N excitation is fully equilibrated over the excitation region (Fig. 1C) (9). The temperature increase, although only ca. 0.1 °C, (9) causes a shift of the 1,742 cm^-1 mode frequency, which is easily detectable in all four compounds. While both the RA 2DIR cross-peaks and the cross-peaks at the plateau are caused by the excess energy transported to the succinimide region, there are two major differences between them. First, the relaxation-assisted contribution occurs predominantly via through-bond energy transport, which permits correlating the frequencies of the two labels of the same molecule (Fig. 1B). On the contrary, at the plateau the excess energy is fully equilibrated and the frequencies of all CO modes in the excitation region will be affected resulting in a loss of a pairwise (N ≡ N/C = O) correlation (Fig. 1C). Note that only about 20% of all azido groups are excited by the IR pulses (k₁ and k₂). The second difference is in the nature of the influence of the excess energy on the CO mode frequency. The RA cross-peaks are dominated by the intramolecular mode couplings; the through-bond excitation of a mode strongly coupled to the reporter mode shifts the frequency of the reporter by the value of their anharmonicity. At the plateau, the excessively excited intramolecular modes and the heated solvent both affect the CO mode frequency.

For smaller compounds such as azPEG0 and azPEG4 the energy transport is dominated by the through-bond energy transport—the cross-peak amplitudes at the maximum exceed greatly those at the plateau (Fig. 3). For azPEG8, however, the cross-peak amplitude at the maximum is only ca. threefold larger than that at the plateau, and the maximum occurs at larger time delays (T^max = 9.5 ± 0.5 ps); a substantial thermal contribution is expected at such delays and at such small amplitudes, which is expected to affect the retrieved T_max values (vide infra). Nevertheless, the through-bond contribution is dominant for azPEG8, which permits correlating the frequencies of the excited (N ≡ N) and probed (C = O) modes of the same molecule.

The T-dependence in azPEG12, albeit an unusual shape, is easily understandable: The direct through-space N ≡ N/C = O coupling results in the cross-peak at T = 0, which reduces with time due to relaxation of the IR-active N ≡ N mode into other modes with smaller transition dipole. The cross-peak decay is complicated as the modes populated from the N ≡ N relaxation are also IR-active and contribute to the cross-peak via through-space coupling with C = O. Some excess energy is expected to arrive to the succinimide site at ca. 15–20 ps via the through-bond transport; this process is, however, hidden beneath the cross-peak originated from the overall heating of the sample. The latter reaches a plateau at ca. 50 ps, as expected (9). Thus, the overall heating of the sample hides the through-bond energy transfer contribution in azPEG12.

A monotonic correlation of the T_max value and the through-bond interlabel distance (Fig. 4) suggests a dominant role of the through-bond energy transport in the azPEG0, 4, 8 compounds. Indeed, for small molecules the through-bond transport was found to be much more efficient than the energy dissipation to the solvent (7, 9). However, as the energy transport proceeds, the excessively excited part of the molecule becomes larger and larger, which favors the dissipation process to the solvent. Note that a linear dependence of the energy transport time on the chain length is expected for the through-solvent transport because the transport time is proportional to the square of the end-to-end distance, which, in turn, is proportional to the square root of the chain length. Because both through-bond and via solvent transfer processes are present, how can one tell them apart? The through-bond energy transport contribution dominates the cross-peak for azPEG0 and azPEG4, as apparent from a large ratio of the cross-peak amplitude at the maximum and that at the plateau (24 and 12, respectively). For azPEG8 and azPEG12, however, it is difficult to rule out the influence of the heating through the solvent because the cross-peak amplitude at the maximum is only marginally larger than that at the plateau (3.1 and 1.3, respectively). In azPEG12 the thermal contribution is so substantial that the intramolecular component to the cross-peak is completely hidden—no maximum associated with the through-bond energy transport is seen for the N ≡ N/1,724 cm^-1 cross-peak. Similar tendencies are found for the N ≡ N/1,778 cm^-1 cross-peak (Fig. 3): The plateau is substantial for azPEG8, while for azPEG12 it dominates the signal hiding the through-bond transport contribution (Fig. 3). Notice that a small through-bond peak can be seen for azPEG12 at ca. 12 ps, but its relative contribution is small preventing its accurate T_max determination.

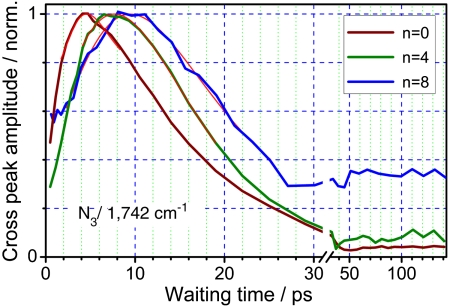
Fig. 4.

Normalized waiting-time dependencies for the N ≡ N/1,742 cm^-1 cross-peak for azPEG0, 4, and 8. The best fits are shown with thin red lines.

Several factors affect the T_max values, such as the through-space coupling strength, the through-bond and via solvent energy transfer efficiencies, and the nature of the energy accepting modes shifting the reporter-mode frequency. For example, the through-space coupling contribution affects the shape of the T-dependence kinetics, especially for the data with small T_max values (azPEG0 and 4). A detailed analysis of the cross-peak T-dynamics is required to address the issue, which will be given in another publication. Such detailed analysis is even more important for the azPEG8 data, which are affected substantially by the thermal contribution (except for N ≡ N/1,819 cm^-1). For example, the lower T_max value for azPEG8 obtained from the N ≡ N/1,742 cm^-1 peak is due to a cancelation effect between the RA 2DIR through-bond contribution, which red-shifts the C = O frequency, and the thermal contribution causing its blue shift; a characteristic dip at ca. 35 ps is an indication of this cancellation (Fig. 3) (9).

Cross-Peaks Among N ≡ N and 1,819 cm^-1 Modes.

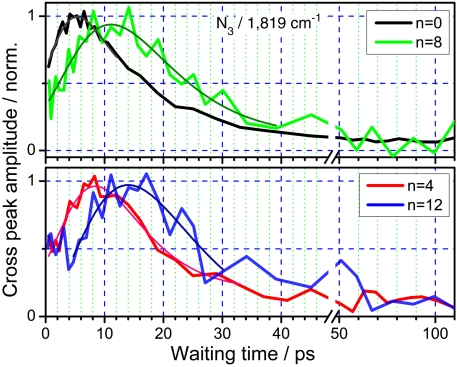
Interestingly, the cross-peak involving the CO transition at 1,819 cm^-1 shows different waiting-time dynamics. This CO transition was found to be very insensitive to temperature. The temperature sensitivity of its central frequency, evaluated at room temperature for azPEG4 in chloroform, is -0.003 ± 0.002 cm^-1/K, which is ca. 20-fold smaller than that for the 1,742 cm^-1 peak (+0.057 ± 0.004 cm^-1/K) (9). Indeed, the N ≡ N/1,819 cm^-1 cross-peaks in all four compounds show negligible plateaus at large T values. As a result, clear maxima are found in the T dependencies for this cross-peak for all four compounds, including azPEG12 (Fig. 5). For all four compounds the N ≡ N/1,819 cm^-1 cross-peak is dominated by the through-bond energy transport, as no cross-peak is expected (and none observed) for the equilibrium temperature increase. In other words, populating the low-frequency modes at the succinimide moiety with a close to thermal distribution should cause essentially no frequency shift of the 1,819 cm^-1 mode and, as a result, no cross-peak. Only if the higher frequency modes at succinimide are excited, resulting in an energy distribution being far from the thermal equilibrium, the central frequency of the 1,819 cm^-1 mode will be affected and the cross-peak will appear.

Fig. 5.

Normalized waiting-time dependencies for the N ≡ N/1,819 cm^-1 cross-peak for azPEG0, 4, 8, and 12. The best fits are shown with thin lines.

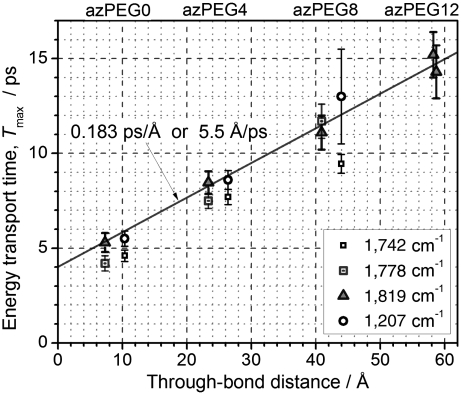
The maxima in the T-dependencies for all cross-peaks were determined by fitting the data with an asymmetric bell-shaped function (see Fig. 3 caption) in the vicinity of the peak (Fig. 3, 4, 5). The through-bond distances were calculated from the central nitrogen atom of the azido moiety to the carbon atom of the ester for modes at 1,778 and 1,819 cm^-1 and to the nitrogen atom of succinimide for modes at 1,742 and 1,207 cm^-1, because the latter modes are located solely at the succinimide moiety; this results in ca. 2.78-Å larger distances to them. Fig. 6 shows how T_max depends on the through-bond distance. The data obtained from different cross-peaks are labeled with different symbols. As discussed, the data for the N ≡ N/1,819 cm^-1 cross-peak are available for the largest distance range, and they contain the smallest contribution from the equilibrium sample heating. The direct coupling contribution for this peak is also the smallest due to the small transition dipole of the 1,819 cm^-1 mode, which results in sampling a smaller part of the end-to-end distribution. The points for the N ≡ N/1,819 cm^-1 cross-peaks were fitted with a linear function resulting in a slope of 0.183 ± 0.008 ps/Å and an intercept of 4.0 ± 0.3 ps (Fig. 6).

Fig. 6.

Energy transport time, T_max, as a function of through-bond distance. The distances were calculated from the central nitrogen atom of the azido moiety to the carbon atom of the ester for modes at 1,778 and 1,819 cm^-1 and to the nitrogen atom of succinimide for modes at 1,742 and 1,207 cm^-1.

Cross-Peaks Among N ≡ N and 1,207 cm^-1 Modes.

Additional data are provided by the N ≡ N/1,207 cm^-1 cross-peak. The peak at 1,207 cm^-1, common to all compounds, is due to the C-N-C asymmetric stretching motion at the succinimide ring. Unfortunately the CNC stretching mode frequency also showed a substantial sensitivity to temperature, which results in a large plateau, affecting the waiting-time dependencies. The thermal contribution to the signals is substantial already for azPEG4, where the plateau amounts at ca. 45% of the cross-peak amplitude at the maximum. If the purely thermal (equilibrium) contribution to the cross-peak dynamics is known it can be subtracted from the overall T-dependence to obtain a pure through-bond dynamics. The pure thermal cross-peak dynamics was approximated by that found for the mixture of two nonaggregating compounds, N,N-dimethyl-nicotinamide and methyl 4-azidobutanoate, where the N₃/amide-I cross-peak was reaching a plateau exponentially with a characteristic time of 18.7 ps. The pure through-bond energy transport dynamics was isolated for azPEG4 and azPEG8 by subtracting a function exponentially growing with 18.7 ps from zero amplitude to the amplitude of the cross-peak at the plateau. The corrected T_max values are shown in Fig. 6 and in Table 1. Interestingly, the N ≡ N/CNC cross-peak data also indicate an essentially constant-speed energy transport. The slope of the T_max vs. distance is found to be slightly larger than that for the N ≡ N/1,819 cm^-1 cross-peak, but the error introduced by assuming that the purely thermal response in PEGs is the same as that in the system with randomly distributed partners is difficult to evaluate, which is particularly important for T_max in azPEG8.

Table 1.

T_max values (in ps) for azPEG n compounds measured for four cross-peaks

	azPEG0	azPEG4	azPEG8	azPEG12
NN/1742	4.6 ± 0.3	7.7 ± 0.4	9.5 ± 0.5
NN/1778	4.2 ± 0.4	7.5 ± 0.4	11.7 ± 0.9
NN/1819	5.3 ± 0.5	8.5 ± 0.6	11.1 ± 0.9	15.2 ± 1.2*
NN/1207	5.5 ± 0.4	8.6 ± 0.5	16.4/13†

^*Another measurement gave 14.3 ± 1.4 ps.

^†Corrected value (see text).

Transport Mechanism.

Due to a weak thermal sensitivity of the 1,819 cm^-1 mode, essentially no thermal contribution is seen for the NN/1819 cross-peak. Energy dissipation to the solvent occurs via small vibrational quanta, which results in a fast local thermalization. As the local equilibrium is reached quickly, the mode at 1,819 cm^-1 does not respond with a frequency shift and therefore does not generate a cross-peak. The NN/1,819 cross-peak, therefore, reports selectively on the through-bond energy transport process. These data, even though noisier, were used for the linear fit in Fig. 6. Note that the points for other cross-peaks for azPEG0 and 4 (Fig. 6), generally follow the same trend; interestingly, they cluster into a repeating pattern.

A constant-speed regime of the energy transfer suggests a ballistic transport mechanism, where the energy is transferred as a vibrational wavepacket. In ordered samples (crystals) such wavepackets involve a linear combination of a number of states that are closely spaced in frequency (a band) and delocalized over a substantial part of the sample (phonons). The bands are formed by exciton coupling of a large number of the local states found in the repeating units of the sample. The PEG oligomer bridge consists of repeating units and has several exciton bands, each formed by a number of states delocalized over a substantial part of the whole chain. Such bands involve C-C and C-O-C stretching and CH₂ bending and scissoring delocalized motions. The transfer process starts with relaxation of the highly localized N ≡ N mode into the bands of the chain. Because a spatial overlap is required for such process to occur and the states in the band are delocalized over the large portion of the chain, a linear combination of the states in the band is excited so that the nonzero vibrational motion is localized in the vicinity of the azido group—such linear combination is called a wavepacket. The wavepacket then propagates along the PEG chain in accord with the dispersion relations characteristic for the wavepacket involved and governed by the time-dependent Schrödinger equation. Such propagation is characterized by momentum conservation, which is the reason for a constant-speed wavepacket propagation. While propagating, the wavepacket can scatter and relax. The scattering process may either preserve the momentum or change it; the relaxation causes transfers of the energy into other modes in the chain. With an increase of the disorder in the system causing fluctuations of the site frequencies, the delocalization size of the vibrational states will decrease and may not span over the whole chain. This case can be characterized by a wavepacket with a shorter mean-free-path length. In the limit of a very short delocalization length, equal for example to one PEG unit, the energy transport is described as a hopping between the neighboring localized states. Because the jumps forward and backward have similar probabilities the process will be diffusive. The DFT calculations performed with azPEG4 in vacuum and in the chloroform solvent, described by a continuum polarized model, showed that the vibrational states are fully delocalized over the whole chain.

The Y-intercept of 4.0 ± 0.3 ps in Fig. 6 in much larger than the N ≡ N mode lifetime of 1.4 ps. The difference (2.6 ps) can be interpreted as the time needed to generate a wavepacket; the process is governed by anharmonic mode couplings. Note that this delay has a common nature with a substantial temperature gradients at the boundary observed in stationary energy transport experiments (19).

The ballistic energy transfer speed of 950 m/s, found in long-chain stretched hydrocarbons by Dlott and coworkers under large temperature gradient conditions,(26) is ca. 2.4 times slower than the speed of sound in polyethylene, governed by acoustic phonons; the authors attributed the wavepacket to optical phonons (26). Interestingly, the ratio of the speed of sound in pure PEG 400 (1,595 m/s) (33) to the energy transfer speed found in this work is similar (approximately 2.9). Notice that the group velocity of the optical phonons is expected to differ substantially depending on the types of modes involved in the transfer (18).

The experiments described here have several characteristic features that are different from the previous studies. First, the ballistic energy transport is found in response to introduction of a very small excess energy (2,100 cm^-1 per molecule), which suggests that the wavepacket formation in this system is very efficient. A small number of degrees of freedom at the azido group might be the reason of the high efficiency. Second, the vibrational wavepacket is generated at optical-phonon frequencies, because the acoustic phonons are not expected to generate the cross-peak. Third, the ballistic energy transport is found in solution at room temperature; the energy dissipation to the solvent is substantial, which leads to a substantial scattering of the wavepacket. Despite the losses, the ballistic component of the energy transport is found to be clearly detectable, currently for distances up to ca. 60 Å. Accurate measurements of the absolute cross-peak amplitudes for different compounds are required for precise evaluation of the mean-free-path length of the wavepacket. The mean-free-path length was coarsely estimated to be 10–15 Å, based on about two orders of magnitude drop of the cross-peak amplitude for azPEG12 compared to that for azPEG0. The efficiency of the through-bond ballistic transport is expected to increase dramatically if the level of disorder in the sample is decreased and/or the temperature is lowered (30). It is currently unclear how the mean-free-path length and the transport speed depend on the coiling level of the chain and its disorder extent. Nevertheless, even at current level of disorder in the system, these compounds offer a signaling mechanism that is fast (550 m/s), long-range (up to 60 Å), uses (consumes) very small amount of energy (ca. 2,100 cm^-1), and can be directed to a desired target, not necessarily along a straight line. Implications for signal transduction in molecular electronics could be envisioned.

Conclusions

A careful selection of the IR reporters used in the RA 2DIR measurements permitted observing separately two paths of energy transport, through-bond and via solvent. A linear correlation of the through-bond transport time with distance is experimentally discovered. The results are based on the data obtained for several mode pairs, which were found to report similar (linear) dependencies. The energy transport is described as a ballistic propagation of a vibrational wavepacket along the oligomer chain. In addition to finding an efficient energy transport mechanism that suggests novel ways of using molecules for signal transduction, the results permit correlating the vibrational frequencies in molecules via RA 2DIR for groups separated by unprecedented 60-Å distances.

Experimental Details.

The 2DIR measurements were performed using a dual-frequency three-pulse photon echo method with heterodyned detection (10, 34, 35). The (ω_NN, ω_NN, ω_CO) pulse sequence was used in the 2DIR measurements with heterodyning at the ω_CO frequencies. The delays between the three pulses, the dephasing time τ and the waiting-time T, and the delay between the third-order signal and the local oscillator, t, were controlled with interferometric precision of < 0.05 fs (10). The energies of each of the IR pulses interacting with the sample were ca. 0.9–1.2 μJ. For the RA 2DIR measurements the τ delay was kept at 0 or 200 fs, while the T and t delays were scanned; the beam polarizations were kept at the magic angle. The cross-peak amplitude at each T delay was determined by integrating the ω_t absolute-value peak in the vicinity of its maximum and subtracting the integrated and normalized background. The compounds were purchased from Quanta BioDesign and were used as received. All experiments were performed in chloroform (Fisher, 99.9%) at room temperature, 23.5 ± 0.6 °C, in a CaF₂ sample cell with a 50-μm pathlength.