On achieving high accuracy and reliability in the calculation of relative protein–ligand binding affinities

Abstract

We apply a free energy perturbation simulation method, free energy perturbation/replica exchange with solute tempering, to two modifications of protein–ligand complexes that lead to significant conformational changes, the first in the protein and the second in the ligand. The approach is shown to facilitate sampling in these challenging cases where high free energy barriers separate the initial and final conformations and leads to superior convergence of the free energy as demonstrated both by consistency of the results (independence from the starting conformation) and agreement with experimental binding affinity data. The second case, consisting of two neutral thrombin ligands that are taken from a recent medicinal chemistry program for this interesting pharmaceutical target, is of particular significance in that it demonstrates that good results can be obtained for large, complex ligands, as opposed to relatively simple model systems. To achieve quantitative agreement with experiment in the thrombin case, a next generation force field, Optimized Potentials for Liquid Simulations 2.0, is required, which provides superior charges and torsional parameters as compared to earlier alternatives.

Biological processes often depend on protein–ligand binding so that accurate prediction of protein–ligand binding affinities is of central importance in structural based drug design (1–4). Among the existing methods used to calculate these binding affinities in explicit solvent, free energy perturbation (FEP) simulations provide one of the most rigorous simulation techniques. Usually FEP is applied in the lead optimization stage of structure based drug design and is used to rank-order a series of congeneric ligands to choose the most potent ones for further investigation (1–4).

Despite the potentially large impact that FEP could have on structure based drug design projects, practical applications in an industrial context have been limited over the past decade. High accuracy and reliability in the methodology are required to make productive decisions about compound modification during late stage lead optimization, but neither has yet been demonstrated by existing implementations. Two types of challenges stand in the way of developing FEP into a true engineering platform for drug candidate optimization. Firstly, converging explicit solvent simulations to the desired precision is far from trivial, even with the immense computing power that is currently available using low cost multiprocessor clusters or cloud computing platforms of various types. Secondly, errors in the potential energy models must be reduced to the point where they lead to errors in a converged calculation that are smaller than the desired errors in relative binding affinities compared to experiment. In our estimation these errors are on the order of 0.5–1.0 kcal/mole mean unsigned error for a typical late stage lead optimization effort in a drug discovery project. While the present article focuses primarily upon a unique algorithm design to address the sampling challenge, we also provide an example, taken from the recent medicinal chemistry literature, illustrating that existing energy models, although substantially improved over the past 20 years via extensive effort in a number of research groups (5–9), require further refinement if the demanding target accuracy specified above is to be achieved.

FEP provides an in-principle rigorous method to calculate protein–ligand binding affinities within the limitations of the potential energy model as long as the simulation time is long enough that all the important regions in phase space are sampled. In practice, however, problems arise when there are large structural reorganizations in the protein or in the ligand upon the formation of the binding complex or upon the alchemical transformation from one ligand to another (1, 3, 4). In these cases, there can be large energy barriers separating the different conformations and the ligand or the protein may remain kinetically trapped in the starting configuration for a very long time during brute-force FEP/MD simulations. The incomplete sampling of the configuration space results in the computed binding free energies being dependent on the starting protein or ligand configurations, thus giving rise to the well-known quasi-nonergodicity problem in FEP. The slow structural reorganizations, even at a single side chain level (10, 11), or some key solvent molecules in the binding pocket (12–14), can affect the calculated binding affinities to a significant degree.

Recently, many groups have made efforts to reduce or eliminate the quasi-nonergodicity problem in FEP. In 2007, Mobley et al. proposed the “confine-and-release protocol” (10), using umbrella sampling to calculate the potential of mean force (PMF) along the prior known slow degree of freedom. However, this method requires prior knowledge of the slow degrees of freedom, making it difficult to use for more complicated real systems. In 2010, the Roux group designed the 2-dimensional replica exchange method (REM) to compute absolute binding free energies of ligands, (11) with one REM on the Hamiltonian space for alchemical transformation, and the other REM on the sidechains surrounding the binding pocket that were assumed to include all the slow degrees of freedom without prior knowledge. However, the number of parallel replicas required in this method is very large.

In this article, we introduce a very efficient protocol called free energy perturbation/replica exchange with solute tempering (FEP/REST), which combines the recently developed enhanced sampling method REST (15–17) into normal FEP to deal with the structural reorganization problem and use it to calculate relative protein–ligand binding affinities in some troublesome cases. The method assumes that the slow degrees of freedom are located within a close neighborhood of the bound ligand without prior knowledge. The computational cost of this method is comparable with normal FEP, and it can be very easily generalized to more complicated systems of pharmaceutical interest. We apply this method on two systems; (a) the L99A mutant of the T4 lysozyme (T4L/L99A), (18, 19) a popular model system with an engineered nonpolar binding pocket where the structural reorganization happens in the protein, and (b) thrombin (Factor IIa),(20, 21, 22) an important drug target in the coagulation cascade where the structural reorganization happens in the ligand. (See Fig. 1.) In both cases, the relative binding affinities calculated using FEP/REST agree with experiment within the error bars independent of starting conformation of the protein or the ligand, whereas normal FEP fails to characterize the effects of structural reorganization and thus gives incorrect free energies. In the latter case, we show that use of an upgraded force field model is essential in achieving the accuracy targets delineated above.

Fig. 1.

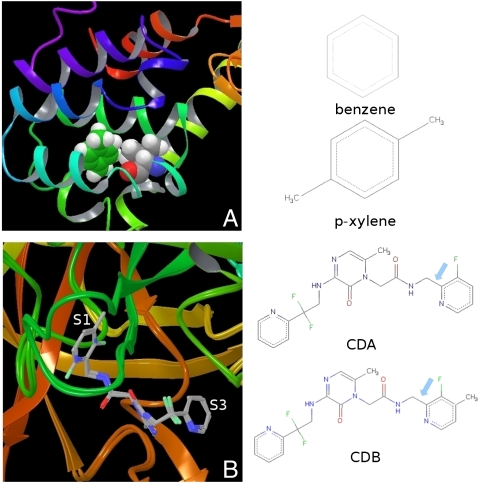
A The nonpolar binding pocket of T4L/L99A with p-xylene bound. The key residue Val111 and p-xylene are displayed in van der Waals (VDW) mode. The structures of the two ligands, benzene and p-xylene, for the relative binding affinity calculation are given on the right. B The binding pocket of thrombin with the ligands CDA and CDB superimposed. With the addition of the methyl group on the P1 pyridine ring of ligand CDB, the ring flips. In the binding complex of thrombin/CDA, the fluorine atom on the P1 pyridine points out of the S1 pocket (F-out conformation), whereas the fluorine atom points into the S1 pocket (F-in conformation) in the thrombin/CDB binding complex. The structures of the two ligands CDA and CDB for relative binding affinity calculation are given on the right with the dihedral involved in the flipping of the P1 pyridine ring (N-C-C-C) indicated by an arrow.

Results

Upon alchemical transformation from one ligand to another, structural reorganization might occur in the protein or in the ligand. In this article, we study two systems, the T4L/L99A and thrombin, using both normal FEP method and the FEP/REST protocol as described in the methods section. Many aromatic molecules can bind to the nonpolar binding pocket of T4L/L99A and experimental binding affinity data are available for comparison (19). Despite the rigidity of the protein and the simplicity of the nonpolar pocket, accurate prediction of the relative binding affinities for the ligands has proved challenging for methods ranging from rapid virtual screening and MM-GBSA to more rigorous FEP methods (3, 4, 23, 24). The difficulty arises from the key residue Val111 surrounding the binding pocket: in the binding complex of small ligands like benzene and toluene, the Val111 stays in the “trans” conformation as in the apoprotein; in the binding complex of larger ligands like p-xylene and o-xylene, the Val111 changes its rotameric states from the trans conformation (χ ≈ -180) to the “gauche” conformation (χ ≈ -60) (Fig. 1A), which is usually called an induced fit effect (10, 11, 18). Thrombin, a serine protease, is a very important drug target in the coagulation cascade for many thromboembolic diseases such as deep vein thrombosis, myocardial infarction, and pulmonary embolism (20, 21, 22). With the discovery of a neutral P1 substitute of the native substrates, a new generation of more potent inhibitors were designed with high levels of bioavailability and good pharmacokinetic properties, among which 2-(6-chloro-3-{[2,2-difluoro-2(2-pyridinyl)ethyl]amino}-2-oxo-1(2H)-pyrazinyl)-N-[(2-fluoro-6-pyridinyl)methyl]acetamide (CDA) and 2-(6-chloro-3-{[2,2-difluoro-2(2-pyridinyl)ethyl]amino}-2-oxo-1(2H)-pyrazinyl)-N-[(2-fluoro-3-methyl-6-pyridinyl)methyl]acetamide (CDB) are representative (20, 22). In the binding complexes of CDA and CDB, the structures of the protein are essentially the same. However, with the addition of a methyl group on the P1 pyridine ring next to the fluorine atom, the ring flips (22). This is shown in Fig. 1B where the two binding complexes are superimposed. While the fluorine atom on the P1 pyridine ring is pointing out of the S1 pocket in ligand CDA (denoted as “F-out” conformation), it is pointing into the S1 pocket in ligand CDB (denoted as “F-in” conformation). Both the reorienting of Val111 and the flipping of the pyridine ring are sufficiently slow that they are trapped in the initial conformation on the time scale of typical FEP simulation.

The estimated relative binding affinities of p-xylene with respect to benzene binding to T4L/L99A calculated using normal FEP, lambda hopping FEP (replica exchange between neighboring lambda windows), (11, 25) and FEP/REST starting from different conformations of the protein (trans vs. gauche of Val111) are given in Table 1. With a 2 ns simulation, the normal FEP predicted relative binding affinities depend on the starting conformation and neither of them is within the error bars to the experimental result (19). Starting from the trans conformation, the predicted binding affinity is more positive than experimental result (0.95 vs. 0.52 kcal/mol); starting from the gauche conformation, the predicted binding affinity is less positive than experimental result (0.30 vs. 0.52 kcal/mol). Using lambda hopping, the predicted binding affinities are a little closer to the experimental value than normal FEP, but a similar discrepancy as with normal FEP was found. By comparison, the estimated binding affinities determined by FEP/REST for the same 2 ns simulation time are independent of the starting conformations, and are very close to the experimental result.

Table 1.

Predicted relative binding affinities of p-xylene to T4L/L99A compared with benzene using various methods

Starting conformation	Method	ΔG in complex	ΔΔG
	FEP	−3.31 ± 0.10	0.95 ± 0.15
Trans	λ-hopping	−3.36 ± 0.10	0.90 ± 0.15
	FEP/REST	−3.78 ± 0.10	0.48 ± 0.15
	FEP	−3.96 ± 0.10	0.30 ± 0.15
Gauche	λ-hopping	−3.83 ± 0.10	0.43 ± 0.15
	FEP/REST	−3.77 ± 0.10	0.49 ± 0.15
Exp			0.52 ± 0.09

Free energies in kcal/mol; ΔG in solvent is -4.26 ± 0.05 kcal/mol.

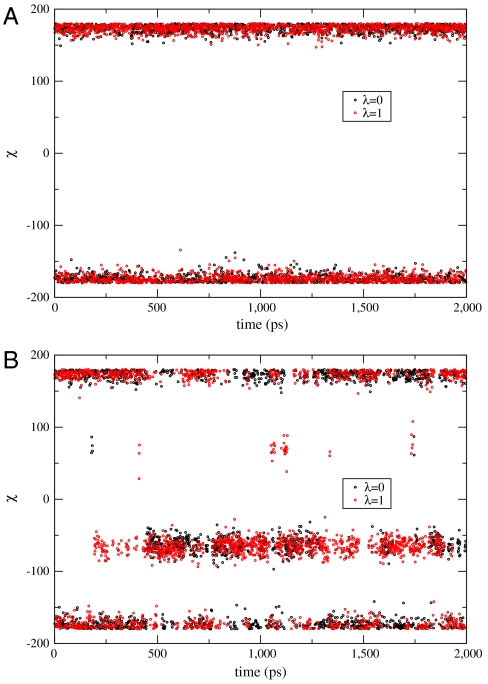
The side chain dihedral angle of Val111 (N-CA-CB-CG1) for the initial lambda window (binding complex of benzene) and the final lambda window (binding complex of p-xylene) as a function of simulation time starting from the trans conformation using normal FEP and FEP/REST are given in Fig. 2. It is clear that, starting from the trans conformation, the Val111 was trapped in that conformation during a 2 ns simulation in normal FEP. By comparison, using FEP/REST, for the same 2 ns simulation time the Val111 was able to make many transitions between the different rotameric states, and although the initial state favors the trans conformation, the final state favors the gauche conformation after a short equilibration time, in agreement with experimental results (18). Similar kinetic trapping in normal FEP and enhanced sampling in FEP/REST are observed starting from the gauche conformation of Val111.

Fig. 2.

The Val111 side chain dihedral angle (N-CA-CB-CG1) as a function of simulation time for the initial and final lambda windows. Initial lambda window corresponds to the T4L/L99A/benzene binding complex, and the final lambda window corresponds to the T4L/L99A/p-xylene binding complex. A Results from normal FEP simulation starting from the trans conformation. The Val111 was trapped in the trans conformation through the 2 ns simulation time. B Results from FEP/REST simulation starting from the trans conformation. After a short equilibration time, the Val111 transits between the trans and gauche conformation with a dominating gauche conformation for the final state and a dominating trans conformation for the initial state, in agreement with experiment. Similar enhanced sampling was observed using FEP/REST starting from the gauche conformation.

We determined the probabilities for the initial and final states being in the trans, gauche+, and gauche- conformations and calculated the free energy to confine the binding complex in each of these conformations using FEP/REST. For the binding complex of benzene (initial state), the probability of the trans conformation is 0.6, of the gauche+ conformation is 0.4, but because the free energy of the remaining gauche- conformation is very high, its probability is very close to 0. For the binding complex of p-xylene (final state) the probability of the gauche conformation is 0.75 and of the trans conformation is 0.24, in agreement with previous results using umbrella sampling (0.76, 0.23, 0.002) or 2-dimensional replica exchange with a boosting potential (0.73, 0.16, 0.11) (10, 11). In normal FEP calculations, the protein was found to be “virtually” confined in the starting trans or gauche conformation, and we can correct their free energies by adding the “confine-and-release” free energies for each conformation according to the confine-and-release protocol proposed by Mobley et al. (10). We thus add (0.90 + 0.30 - 0.85 = 0.35 kcal/mol) for the trans conformation, and (0.30 + 0.54 - 0.17 = 0.67 kcal/mol) for the gauche conformation, finding that the corrected results fall within the error bars of experimental value. This validates that the error of normal FEP is due to incomplete sampling of conformational space.

We used the FEP and FEP/REST protocols to calculate the relative binding affinity of ligands CDB and CDA to thrombin, using the Optimized Potentials for Liquid Simulations (OPLS) 2005 force field for the ligands, (7, 9) starting from different conformations of the ligand (denoted by F-in or F-out, respectively). The results from 3 ns simulations are given in Table 2. The structures of the ligands are much more complicated than the T4L/L99A case, and the error bars for these free energy results are larger. Similar to the T4L/L99A system, the calculated binding affinities using normal FEP depend on the starting conformation of the ligands, and neither of them comes close to the experimental value (22). Using FEP/REST, the calculated binding affinities are within error bars of each other, independent of the starting conformation. From the simulated trajectories, we observed that the P1 pyridine ring was trapped in the starting conformation using normal FEP, whereas it flipped many times using FEP/REST, indicating the efficiency of enhanced sampling. However, none of these calculated free energies are within error bars of the experimental value.

Table 2.

Predicted relative binding affinities of ligand CDB to thrombin compared with ligand CDA using OPLS 2005 force field for the ligands

Starting conformation	Method	ΔG in complex	ΔΔG
	FEP	2.04 ± 0.20	−0.14 ± 0.30
F-out	FEP/REST	0.50 ± 0.20	−1.68 ± 0.30
	FEP	0.32 ± 0.20	−1.86 ± 0.30
F-in	FEP/REST	0.70 ± 0.20	−1.48 ± 0.30
Exp			−0.85

Free energies in kcal/mol; ΔG in solvent is 2.18 ± 0.10 kcal/mol. F-in/F-out means the fluorine atoms on the P1 pyridine ring pointing into or out of the P1 pocket of thrombin.

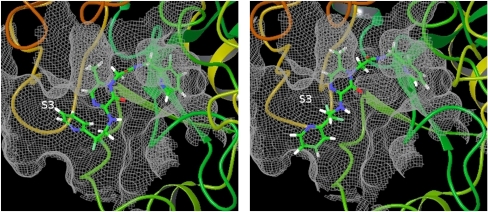
Upon closer investigation of the FEP/REST simulated trajectories using the OPLS 2005 force field for the ligands, we found another important conformation of the ligand different from the two conformations identified in the crystal structures. The correct binding pose of ligand CDA from the crystal structure and the erroneous conformation from the simulation are given in Fig. 3. In the correct binding pose, the P3 pyridine ring of the ligand is in the S3 pocket of the protein whereas in the erroneous conformation the P3 pyridine ring moves out of the S3 pocket pointing into solvent. The S3 pocket is a hydrophobic pocket and the P3 pyridine ring binds to the S3 pocket through hydrophobic interaction and edge-to-face σ - π interaction between P3 aryl group and Trp215 (22). However, in the OPLS 2005 force field, there are large partial charges on the atoms of the pyridine ring (as large as −0.68 on the nitrogen atom), so the P3 pyridine ring incorrectly prefers to point into solvent. (SI Text) In addition, the distribution of the dihedral angle involved in the flipping of P1 pyridine ring (N-C-C-C labeled in Fig. 1) also has an erroneous state that might be due to the incorrect dihedral angle terms in the OPLS 2005 force field (See SI Text). These investigations point out the deficiency of the OPLS 2005 force field and lead us to use an improved version of force field for the ligands, OPLS 2.0, which assigns the partial charges and the bonded interaction terms through high accuracy quantum mechanics calculation. The major differences between the OPLS 2005 and OPLS 2.0 force fields are the different partial charges on the atoms of the pyridine ring and the different torsional angle terms. (See detailed comparison in SI Text)

Fig. 3.

The correct binding pose from the crystal structure (Left) and the erroneous conformation (Right) observed in simulation using the OPLS 2005 force field for the ligands. In the correct binding pose, the P3 pyridine ring points into the S3 pocket of thrombin whereas the P3 pyridine ring moves out of the S3 pocket and points into solvent in the erroneous conformation.

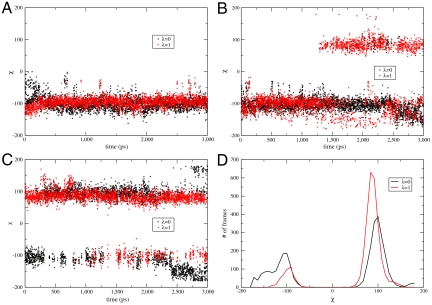
The calculated relative binding affinities using the OPLS 2.0 force field for the ligands from normal FEP and FEP/REST are given in Table 3. Significantly improved results are obtained compared with those obtained from the OPLS 2005 force field. Using normal FEP, the calculated binding affinities depend on the starting conformation, with an error of about 0.6 kcal/mol compared with experimental result starting from the F-out conformation. By comparison, the FEP/REST predicted results are within the error bar of the experimental value independent of the starting conformation of the ligand. The dihedral angle involved in the flipping of the pyridine ring ( N-C-C-C labeled in Fig. 1) as a function of simulation time for the initial and final states using normal FEP and FEP/REST starting from the F-out conformation (χ ≈ -100) are given in Fig. 4A and B. It is clear that the ligand was trapped in that conformation using normal FEP whereas it flipped between the F-out (χ ≈ -100) and F-in (χ ≈ 90) conformations many times after an initial equilibration time using FEP/REST. A similar enhanced sampling effect was observed using FEP/REST starting from the F-in conformation.

Table 3.

Predicted relative binding affinities of ligand CDB to thrombin compared with ligand CDA using OPLS 2.0 force field for the ligands

Starting conformation	Method	ΔG in complex	ΔΔG
	FEP	1.09 ± 0.20	−0.21 ± 0.30
F-out	FEP/REST	0.12 ± 0.22	−1.18 ± 0.32
	FEP	0.07 ± 0.20	−1.23 ± 0.30
F-in	FEP/REST	0.31 ± 0.21	−0.99 ± 0.31
F-in/out	FEP/REST	0.30 ± 0.15	−1.00 ± 0.25
F-out/in	FEP/REST	0.52 ± 0.15	−0.78 ± 0.25
F-in/out	FEP/REST(res)	1.22 ± 0.10	−0.08 ± 0.20
F-out/in	FEP/REST(res)	1.44 ± 0.10	0.14 ± 0.20
Exp			−0.85

Free energies in kcal/mol; ΔG in solvent is 1.30 ± 0.10 kcal/mol. F-in/out means the first half lambda windows start from the conformation with the fluorine atoms on the P1 pyridine ring pointing into the P1 pocket of thrombin and the last half lambda windows start from the conformation with the fluorine atoms on the P1 pyridine ring pointing out of the P1 pocket. The reversed starting conformations were used for F-out/in. FEP/REST(res) means FEP/REST simulation with the protein heavy atoms harmonically restrained to the initial position (corresponding to the crystal structure).

Fig. 4.

The distribution of the dihedral angle involved in the flipping of P1 pyridine ring (N-C-C-C labeled in Fig. 1) for the initial and final lambda windows using OPLS 2.0 force field for the ligands. A The dihedral angle as a function of simulation time using normal FEP starting from the F-out conformation (χ ≈ -100). The ligands were trapped in that conformation through the 3 ns simulation time. B The dihedral angle as a function of simulation time using FEP/REST starting from the F-out conformation (χ ≈ -100). After the equilibration stage, the pyridine ring transits between the F-in (χ ≈ 90) and F-out (χ ≈ -100) conformations. C The dihedral angle as a function of simulation time using FEP/REST with the first half lambda windows starting from F-out conformation and the last half lambda windows starting from F-in conformation. The equilibration time was much shorter compared with B. D The distribution of the two conformations for the initial and final states. The binding complex of thrombin/CDB (λ = 1) favors the F-in (χ ≈ 90) conformation in agreement with crystal structure, whereas the binding complex of thrombin/CDA (λ = 0) has almost equal probability for the two conformations. This slight discrepancy with experimental crystal structure might be due to the different physical conditions in simulation and in experiment (in solution vs. in crystal). Details are given in SI Text.

The flipping of the pyridine ring in the thrombin system occurs more slowly than the transitions between rotameric states in the T4L/L99A system, and more intermediate lambda windows were needed to help converge its free energy, thus it takes a much longer time (about 1.5 ns) to equilibrate the two F-in and F-out conformations. To shorten the simulation time to get close to equilibrium, we performed two additional FEP/REST simulations; (a) one with the first half of the lambda windows starting from F-in conformation and the last half of the lambda windows starting from F-out conformation (denoted as “F-in/out” in Table 3), and (b) the other with an inverted starting conformation for each lambda window (denoted as “F-out/in”). The calculated relative binding affinities from these two simulations (Table 3) are within the error bar of the experimental result independent of whether starting conformations (a) or (b) are used. The dihedral angle involved in the flipping of the pyridine ring is given as a function of simulation time for the initial and final lambda windows in Fig. 4C. Indeed, the time required to get close to equilibrium was much shorter than what was found from a single conformation for each lambda window and, importantly, higher precision results were obtained. Thus when the binding poses for the two ligands are known a priori, it will be more efficient to start the FEP/REST simulation with each lambda window starting from different conformations. It should be pointed out that the final equilibrium distribution and the free energy are independent of the starting conformation for each replica as long as there are a sufficient number of conformational transitions in the middle lambda window in FEP/REST. Using different starting conformations for different replicas, as opposed to the same starting conformations, can shorten the simulation time for getting close to equilibrium within the same error bars. This is because the time scale for a transition from one conformation to another in MD is much longer than the time scale for the exchange of two conformations between neighboring replicas. We note that the time required to truly equilibrate is the same for any starting configuration except if we started with the equilibrium distribution. The fact that the calculated free energies using different replica starting conformations (F-in, F-out, F-in/out, F-out/in) are within the error bars of each other indicates that a 3 ns simulation time is sufficiently long enough to equilibrate the generalized ensemble in this case *.

In the FEP/REST simulations, we also calculated the probabilities for the initial and final states being in the two conformations (F-in vs F-out) that are displayed in Fig. 4D (with a bin width of 5°). For the final state (binding complex of CDB), the F-in conformation is the major conformation, in agreement with the experimental crystal structure; however, for the initial state (binding complex of CDA), the two conformations have almost equal probability in contrast to the experimental crystal structure where it was found to be in the F-out conformation. This discrepancy might be due to the different physical conditions in experiment (crystal) and in simulation (in solution). To confirm this argument, we performed another two FEP/REST simulations with the protein heavy atoms harmonically restrained to the initial position (corresponding to the crystal structure) starting from different ligand conformations for each lambda window. The trajectories from these simulations confirm that the F-out conformation is a major conformation for the initial state and the F-in conformation is a major conformation for the final state when the protein heavy atoms are restrained (see SI Text), validating the hypothesis that the solution environment may shift the relative population of the two conformations from what is found in the solid. Interestingly, the calculated relative binding affinities from the two simulations with protein heavy atoms restrained (Table 3) converge to the same value but different from experimental result by about 0.8 kal/mol, indicating a 0.8 kcal/mol difference in protein restrain free energy for the two binding complexes.

Discussions and Conclusions

The results reported comprise only a few test cases. However, the performance of the algorithm is encouraging with regard to overcoming problems due to significant configurational changes, in either the protein or ligand, upon ligand modification. The FEP/REST methodology in both examples facilitates rapid interconversion between the phase space region separated by barriers in normal FEP, at a relatively low computational cost and with the only assumption that the slow degrees of freedom are within a localized region surrounding the binding pocket. If these properties are shown to hold for a larger, diverse set of test cases, this will represent a significant advance in the convergence of FEP simulations. Other groups have succeeded in the T4L/L99A case, but as pointed out above, at a substantially higher computational cost. The thrombin example is no longer a toy problem, but represents the sort of modification made on a routine basis on complex ligands in late stage drug discovery projects. The striking success of FEP/REST in this case offers hope that it will be applicable, in its current form, to real-world problems as well as model systems. The efficient sampling of FEP/REST allows us to observe that one is free to play with the Hamiltonian of intermediate states in FEP as long as the correct physical states are achieved at the end-points. It is also worth noting that both the 2-dimensional replica exchange method (11) and FEP/REST in their current forms enhance the sampling only of the localized region around the ligands, which might not be sufficient for treating delocalized conformational changes (allosteric regulation). A possible procedure to treat this problem is the following: (1) include a larger “hot” region in a first round FEP/REST simulation and find those key residues responsible for the allosteric regulation; (2) run a second round FEP/REST just including those key residues in the hot region.

Three other points are worthy of discussion. Firstly, the improved results obtained with OPLS 2.0, as opposed to OPLS 2005, were achieved without any specific parameter adjustment based on the experimental FEP data. Rather, much more extensive fitting to basic quantum mechanical data for charges and torsional parameters yields a superior force field that can be expected to display similarly enhanced results for other ligands and receptors. For ligands relevant to medicinal chemistry efforts, it is likely that improvements in both sampling and the potential energy model are needed to approach agreement with high quality experimental data on a routine basis.

Secondly, our results suggest that FEP/REST methods can be substantially improved in efficiency and reliability if the end-points of the calculation (i.e, the cocrystallized structures that would be obtained experimentally for the two ligands) are known. Often, one endpoint is available from experiment (the lead compound that is being modified in the lead optimization process). The other endpoint can then be generated via conformational search calculations using induced fit docking (IFD) algorithms (26), which are typically much less expensive than the FEP simulation itself. In some challenging cases the IFD calculation will generate a small number (typically two to three) alternatives for the endpoint; here, FEP/REST can be used to select between these alternatives with improved accuracy, while at the same time using the truncated list of alternatives to reduce FEP/REST calculation time, and focus FEP/REST sampling on relevant phase space regions.

Finally, the differences between results obtained with crystal packing as compared to free solution are of significant interest, although a large dataset will have to be investigated to draw firm conclusions. One would not expect crystal packing to lead to very large changes in structure or binding affinity in an active site cavity (which typically is recessed and hence has few direct contacts with neighboring protein molecules of the crystal) except in unusual cases, and our results are consistent with this intuition. However, a nontrivial effect, big enough to be relevant to the potency targets in drug discovery projects, is observable, and the better agreement of the solution calculation with experiment (performed in solution) confirms that the computational estimation of the effect is likely to be a good estimate.

Methods

FEP/REST.

The incomplete sampling of configurational space in normal FEP results from the large energy barriers separating the relevant conformational states. Our strategy to solve the quasi-nonergodicity problem is to combine enhanced sampling techniques into FEP.

Recently, our group proposed REST in which, through Hamiltonian scaling, only a small region of interest of the system is effectively “heated up” while the rest of the system stays “cold” (15). In this way, a small number of replicas are sufficient to maintain the sampling efficiency, in contrast to the large number of replicas needed in the usual temperature replica exchange. Here, we are using a more recently developed version of REST (called REST2) where the effective temperature of the hot region is achieved at the Hamiltonian level through scaling the potential energy terms of the hot region (16).

We combine REST with FEP through 1-dimensional replica exchange protocol demonstrated in Fig. 5. We call this method FEP/REST. In FEP/REST, along the alchemical transformation from the initial lambda window to the final lambda window, the effective temperature of the hot region (the region we are interested in, usually including the ligand and the protein residues surrounding the binding pocket) is gradually increased from T₀ for the initial lambda window to T_h for the middle lambda window, and then gradually decreased from T_h for the middle lambda window back to T₀ for the final lambda window. The effective temperature of the hot region is achieved by scaling the Hamiltonian, and exchange of configurations between neighboring lambda windows is attempted using the Hamiltonian Replica Exchange Method (HREM) (27). (All of the replicas are run at the same temperature, and the velocities and kinetic energies of all of the atoms whose interactions are scaled remain always in contact with a single heat bath at this same temperature.) In this way, enhanced sampling is achieved through the scaled potential energy of the hot region at intermediate lambda windows, (16) and through replica exchange the initial and final lambda windows can sample the different conformations. The potential energies of the initial and final states reach the physical states, and the sum of free energy difference between all neighboring lambda windows gives the relative binding affinity between the two ligands. The intermediate accessory states not only help to bridge the different phase space regions for the initial and final states as in normal FEP but also helps the sampling of different conformational states through the scaled potential energy of the hot region. This method can be easily applied to complicated real systems of medicinal interest.

Fig. 5.

One-dimensional replica exchange protocol combining REST into FEP. Each box represents a lambda window with the input parameters given by λ, the thermodynamic coupling parameter, and T , the effective temperature of the hot region. The double arrow symbols indicate attempts to exchange configurations between neighboring replicas.

Details of the Simulations.

The proper choice of the hot region and the criteria for optimizing the temperature profile to be used in FEP/REST are discussed in the SI Text. In the two systems studied in this article, we know the slow degrees of freedom, so only the residue Val111 or the P1 pyridine ring was included in the hot region. In general, if there is no prior knowledge about the slow degrees of freedom, a proper choice of hot region would include the ligand and the protein residues surrounding the ligand because usually the structural reorganization involves the ligand and the protein residues surrounding the binding pocket.

The details in the FEP/REST simulation protocols, including the starting structures of the simulation, the length of the simulation, the lambda values and scaling factors of the hot region for each lambda window, and how the data are analyzed are given in the SI Text. The bonded interactions involving the dummy atoms are treated differently in this article to avoid singularities and instabilities, with the details given in the SI Text. This problem is not appreciated in the literature on FEP.