A procedure to determine the planar integral spot dose values of proton pencil beam spots

Abstract

Purpose: Planar integral spot dose (PISD) of proton pencil beam spots (PPBSs) is a required input parameter for beam modeling in some treatment planning systems used in proton therapy clinics. The measurement of PISD by using commercially available large area ionization chambers, like the PTW Bragg peak chamber (BPC), can have large uncertainties due to the size limitation of these chambers. This paper reports the results of our study of a novel method to determine PISD values from the measured lateral dose profiles and peak dose of the PPBS.

Methods: The PISDs of 72.5, 89.6, 146.9, 181.1, and 221.8 MeV energy PPBSs were determined by area integration of their planar dose distributions at different depths in water. The lateral relative dose profiles of the PPBSs at selected depths were measured by using small volume ion chambers and were investigated for their angular anisotropies using Kodak XV films. The peak spot dose along the beam’s central axis (D₀) was determined by placing a small volume ion chamber at the center of a broad field created by the superposition of spots at different locations. This method allows eliminating positioning uncertainties and the detector size effect that could occur when measuring it in single PPBS. The PISD was then calculated by integrating the measured lateral relative dose profiles for two different upper limits of integration and then multiplying it with corresponding D₀. The first limit of integration was set to radius of the BPC, namely 4.08 cm, giving PISD_RBPC. The second limit was set to a value of the radial distance where the profile dose falls below 0.1% of the peak giving the PISD_full. The calculated values of PISD_RBPC obtained from area integration method were compared with the BPC measured values. Long tail dose correction factors (LTDCFs) were determined from the ratio of PISD_full/PISD_RBPC at different depths for PPBSs of different energies.

Results: The spot profiles were found to have angular anisotropy. This anisotropy in PPBS dose distribution could be accounted in a reasonable approximate manner by taking the average of PISD values obtained using the in-line and cross-line profiles. The PISD_RBPC values fall within 3.5% of those measured by BPC. Due to inherent dosimetry challenges associated with PPBS dosimetry, which can lead to large experimental uncertainties, such an agreement is considered to be satisfactory for validation purposes. The PISD_full values show differences ranging from 1 to 11% from BPC measured values, which are mainly due to the size limitation of the BPC to account for the dose in the long tail regions of the spots extending beyond its 4.08 cm radius. The dose in long tail regions occur both for high energy beams such as 221.8 MeV PPBS due to the contributions of nuclear interactions products in the medium, and for low energy PPBS because of their larger spot sizes. The calculated LTDCF values agree within 1% with those determined by the Monte Carlo (MC) simulations.

Conclusions: The area integration method to compute the PISD from PPBS lateral dose profiles is found to be useful both to determine the correction factors for the values measured by the BPC and to validate the results from MC simulations.

INTRODUCTION

A magnetically scanned spot pencil proton beam line of the Hitachi ProBeat machine (Hitachi, Ltd., Tokyo, Japan), which has the ability to deliver highly conformal radiation therapy in the form of intensity-modulated proton therapy, has recently been commissioned for clinical use at The University of Texas M. D. Anderson Cancer Center Proton Therapy Center in Houston (PTCH). The desired dose delivery is achieved by placing proton pencil beam spots (PPBSs) of suitable energies at various locations in a target volume of the patient without the use of any beam shaping device.^{1, 2} The clinical commissioning of the dose delivery system of the PPBS at PTCH has been described in details elsewhere.^{3, 4}

The dose distribution of the individual PPBS are the building blocks for creating the desired broad field dose distribution. The accuracy of calculation of the broad beam dose distribution depends on the precise modeling of the incident spot and its subsequent interaction in the media of interest. Many treatment planning systems (TPSs) use analytical functions, such as a Gaussian to define the fluence profiles of PPBS and model the interaction of the protons in the medium analytically.^{5, 6} The most important input data for beam configuration of PPBS in some of the TPSs like the Varian Eclipse (Varian Medical Systems, Palo Alto, CA), are the incident lateral fluence profiles and the planar integral spot doses (PISDs) ($\mathrm{in}\frac{\mathit{Gy}\hspace{1em}{\mathit{mm}}^2}{\mathit{MU}}$) at different depths in water.

Because of the large number of discrete beam energies available, and the difficulty associated with precise dosimetry of narrow pencil beams, Monte Carlo (MC) simulation was used to generate the required profiles and percentage planar integral spot dose (PPISD) values at different depths (Refs. ^{4, 7}) for configuring the PTCH scanning beam in Eclipse TPS. The accuracy of the MC simulation was validated by comparing the calculated dose distribution with measured data using ion chambers.^{4, 7} The MC simulation can only give the relative dose values or dose per proton. To meet the TPS requirements, the relative dose from MC simulation has to be converted to Gy mm²/MU. A PTW Bragg peak chamber (BPC) (model 34070-0024) with an active sensitive radius of 4.08 cm was used to measure the PISD value at a depth of 2 cm in water for each of the 94 discrete energies of the PTCH beamline. The 2 cm depth was chosen because of its location in the plateau region of the depth dose curve for the PPBS. Because of the finite size of the chamber, some dose in the long tail region of the spot’s lateral profile, also known as low dose envelope,⁸ may not be accounted for. To overcome this limitation, the BPC-measured PISD value was scaled using a chamber size correction factor obtained from the ratio of the MC simulation results for PISD values for a virtual chamber with a 20 cm radius and another with 4.08 cm radius. Although the accuracy of this input beam data was verified by measuring the predicted point doses of broad fields created by superposition of PPBSs, it is beneficial to have a method for determining PISD values that is completely independent of MC simulation. Precise determination of the PISD requires a good understanding of the characteristics of the lateral profiles of PPBS for different energies, especially in their low dose envelopes. Sawakuchi et al. have described the characteristics of PPBS profiles in the low dose envelope regions for the PTCH beams in their recent paper⁸ and have demonstrated that lateral profiles can be measured with reasonable accuracy with small ion chambers. Experimental determination of the PISD of PPBS still remains a challenge. New techniques and devices need to be explored to overcome this challenge. In this work, we present a technique for the determination of PISD values based on measured in-line and cross-line lateral relative dose profiles and spot peak dose values at various depths in water. Additionally, we present results of PPBS peak dose measurements at various depths in water using a technique developed for dosimetry of narrow x-ray stereotactic radiosurgery beams.⁹ This paper gives the details of the computation and validation procedures for this alternative method to determine the PISD of the PPBS that is independent of MC simulation.

MATERIALS AND METHODS

Planar integral spot dose computation

If the planar dose distribution of the PPBS is known at any depth d, PISD can be obtained from two-dimensional integration

$$\mathit{PISD}(d)\hspace{0.17em}=\hspace{0.17em}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{\infty }{\int }}\mathrm{D}(\mathrm{r},\theta ,\mathrm{d})\hspace{0.17em}\mathrm{r}\hspace{0.17em}\mathrm{dr}\hspace{0.17em}\mathrm{d}\theta \hspace{0.17em}=\hspace{0.17em}{\mathrm{D}}_{\mathrm{o}}(d)\hspace{0.17em}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{\infty }{\int }}\mathrm{f}(\mathrm{d},\mathrm{r},\theta )\hspace{0.17em}\mathrm{r}\hspace{0.17em}\mathrm{dr}\hspace{0.17em}\mathrm{d}\theta ,$$ (1)

where D(r,θ,d) = D₀(d) f(d,r,θ), D₀(d) being the peak PPBS dose measured at its central axis at depth d, and f(d,r,θ) being the relative dose at any location in the transverse plane at this depth. If the spot has an isotropic dose distribution, Eq. 1 simplifies to

$$\mathit{PISD}(d)=D_o(d)2\pi {\int }_0^{\infty }f(d,r)r\hspace{1em}\mathit{dr},$$ (2)

where f(d, r) is the radial relative dose profile function.Only a single line profile would be required to compute PISD (d)using Eq. 2. In case of angular anisotropy in planar dose distribution, the PISD can be approximated by using method of averages as

$$\mathrm{PISD}\left(\mathrm{d}\right)\hspace{0.17em}=\hspace{0.17em}2\pi D_0(d)\hspace{0.17em}\frac{{\displaystyle \sum _{j=1,N}{\displaystyle \underset{0}{\overset{\infty }{\int }}{f}_j(d,r)\hspace{0.17em}r\hspace{0.17em}\mathit{dr}}}}{N},$$ (3)

where $2\pi D_0(d)\hspace{1em}\sum _{j=1,N}{\int }_0^{\infty }{f}_j(d,r)\mathit{rdr}$ is the sum of integral dose measured from each line profile $f_j$ collected along different angles θ at depth d, and N is the number of angular scans used for averaging.

The calculation of PISD also requires the value of D₀ of PPBS. The D₀ of single PPBS can be measured by a calibrated ion chamber, but may not be accurate both due to chamber positioning uncertainties in the measurement and detector volume averaging effect. Alternatively, one can derive the value of D₀ by combining PPBSs at various locations to produce a broad field and then measuring the dose at its center using a procedure recently proposed for measuring dose output of narrow x-ray beams used in stereotactic radiosurgery.⁹ The point of measurement is located in a flat region of this broad field, where the second gradient of the dose in the volume of the detector is zero and the detector size would not affect the measured D₀.

Suppose that N spots are programmed to be located at known distances from the central spot. An ion chamber positioned at the central spot and depth d will measure the cumulative dose D_c from these N spots for this location

$${\mathrm{D}}_{\mathrm{c}}(\mathrm{d})={\mathrm{D}}_0(\mathrm{d})\sum _{j=1,N}{\mathrm{F}}_{\mathrm{j}}.$$ (4)

where F_j is the relative contribution of jth spot to the dose measured at the central axis of the broad beam at depth d. F_j is determined from the measured relative lateral dose profile, f, of the PPBS and will depend on the location of its center from the point of measurement. Thus, F_j = C_jf(d, R_j, Θ_j), where R_j and Θ_j are the polar coordinates of jth spot with the origin of the coordinate system located at the point of measurement and C_j is the ratio of the peak dose of the jth spot to that of the central spot in the transverse plane at depth d. For an isotropic PPBS dose distribution, F_j will depend on the distance of the PPBS from the central axis. C_j in principle can be different from the value of one due to the difference in radiological path length of the jth spot as compared to the central spot. The differences in the radiological path length for a spot located at 7.9 cm off-axis on a plane at a depth of 30 cm is estimated to be 0.1 cm with a nominal virtual source distance of 253 cm for our scanning beam nozzle. Although, the differences in the PPBS peak dose due to such small differences in the radiological path length are expected to be rather small (for example, it is much less than 0.5% in the proximal high gradient region of the Bragg peak for 221.8 MeV PPBS), it is included in the calculation of the contribution of individual spots in the broad beam to the measured point dose at the field center. The value of D₀ is determined by dividing the measured D_c by the value of the sum in the right-hand side of Eq. 4, assuming knowledge of C_jf(R_j, Θ_j).

Measurements

The technique for measurement of profiles needed for the calculation of the PISD is described in an earlier paper⁸ by Sawakuchi et al. and is briefly described below for quick reference. We used a water tank (PTW MP3) and 3D scanning and control systems (MEPHYSTO MC² software, PTW, Freiberg, Germany) and small cylindrical ion chambers, PTW PinPoint (model 31014, sensitive volume 0.015 cm³) to measure the PPBS in-line and cross-line lateral dose profiles. A fixed reference PTW PinPoint chamber (model 31016 sensitive volume 0.016 cm³) was used during the scans. The profile measurements are done by integrating the charge collected by the moving chamber (field chamber) for a fixed time at the desired locations. In order to avoid the effect of dose rate fluctuation, a reference chamber, which is kept at a fixed location some distance away from the scanning line, is used to record the integrated charge for the same fixed duration at that location. The ratio of the integral charges of the field chamber and the reference chamber at the fixed location then becomes dose rate independent and is used as the relative dose profile data. The surface of the water in the tank was placed at the isocenter plane, which stands at a distance of 38 cm from the gantry nozzle. A new set of in-line and cross-line lateral dose profiles were measured at two different depths for the 72.5 MeV and at three different depths for the 89.6, 146.9, 181.1, and 221.8 MeV PPBSs.

Lateral relative dose profile scans were extended until the values in the tail did not show any observable change. In order to place the data in a very fine grid for the numerical integration, the profiles were interpolated using cubic spline fit with number of interpolated points kept at 10 000. The maximum radial distance from the central axis to truncate the profiles was chosen as the distance at which the relative dose value falls below 0.1% of the peak value. For example, this distance was found to be 9 cm for the lowest energy (72.5 MeV) PPBS.

Computation of PISD using Eq. 3 would require measured lateral dose profiles along different radial directions in the plane of interest. It is difficult and time consuming to acquire these angular dose profile scans with ion chamber and was not attempted. The use of only cross-line and in-line lateral dose profiles in Eq. 3 (with N = 2) may also lead to PISD values close to that obtained with the use of many angular scans. This hypothesis was tested by using lateral relative dose profiles from film dosimetry to compute PISD with multiple angular profiles from the dose distribution in the films and comparing it with that obtained using only in-line and cross-line profiles obtained from the same film.

We measured PPBS lateral relative dose profiles for energies (72.5, 89.6, 146.9, 181.1, and 221.8 MeV) at a depth of 2 cm using Kodak XV films (Eastman Kodak, Rochester, NY) placed in plastic water phantom. The films were scanned in a VIDAR scanner (VIDAR Systems Corporation, Hendon, VA) using the OmniPro-Accept 6.4A software (Scanditronix/Wellhoeffer, Bartlett, TN). A calibration curve to convert film optical density (OD) to proton beam dose was generated by irradiating films inside plastic water phantom to nine different dose values ranging from 2 to 120 cGy in a 10 × 10 cm field of passively scattered proton beams with incident energies of 250, 200, and 120 MeV at the center of a 10 cm SOBP. Although, the OD to dose calibration curves show some noticeable differences with beam energies, the transverse relative dose profiles of fields of different energies are seen to be unaffected by the energy dependence of the calibration curves. Additionally, the suitability of using these films for PPBS relative dose profile measurements was confirmed by comparing the in-line and cross-line profiles from film with those measured by ion chamber at 2 cm depth. Film dosimetry was then used to obtain lateral relative dose profiles at angles of 0 (cross-line), 20, 40, 60, and 90 (in-line) degrees. The in-line and profiles at other angles (will be termed as angular dose profiles) were compared with the cross-line profile to evaluate the magnitude of the angular anisotropy of PPBS planar dose distribution.

The D₀ of PPBSs was measured using two different techniques. First method involved making measurements using a PTW Advanced Markus parallel plate chamber (model TN 34045) with a known Co-60 dose to water calibration factor determined by our Accredited Dosimetry Calibration Laboratory (ADCL) in a water tank and exposing it to the PPBS for a fixed MU. Because of the difficulty in precisely aligning the chamber with the central axis of the beam, the peak dose was found by searching for the maximum dose reading in the neighborhood of the apparent central axis of the beam. To overcome the chamber size effect in the Markus Chamber measurement of D₀ of single PPBS, we created a 10 × 10 cm² broad field by placing monoenergetic PPBSs in a transverse plane with an interspot spacing of 5 mm and measured the cumulative dose from their superposition. This cumulative dose was then used to calculate the D₀ value using Eq. 4. As mentioned earlier, this approach is similar to a recently published method used for determining the dose output of narrow photon fields.⁹ The results from the first method were used as a reference to check that the value of D₀ obtained by second method is indeed larger compared to the single point measurement at the spot central axis of a single PPBS. This is intuitively expected due to the absence of detector volume averaging at the center of a broad field.

Computing average values of PISD

The adequacy of using the average PISD values from orthogonal axis profiles was evaluated by computing the limited dose averaging factor (LDAF) from the ratio of average PISD values from x (cross-line), y (in-line) profiles, and the average PISD values from various angular scans and the cross-line and in-line profiles. The LDAF can be expressed as

$$\mathit{LDAF}=\frac{(D_x+D_y)/2}{\raisebox{1ex}{${\displaystyle \sum _{i=1}^N{D}_i}$}\!\left/ \!\raisebox{-1ex}{$N$}\right.}.$$ (5)

The D_x, D_y, and D_i in the above equation are PISD [(Gy mm²/MU)] calculated using the cross-line, in-line, and angular dose profiles of PPBS from film measurements, respectively, in Eq. 2. The LDAF values were then calculated using these D_is in Eq. 5, with N = 5, which include D_x and D_y.

PISD measurement with Bragg peak chamber and determination of long tail dose correction factor

PISD obtained from measured profiles using our area integration method were compared with those measured using a plane-parallel ion chamber, PTW BPC (model TN 34070, SN 0024) with an active volume of 10.5 cm³ (4.08 cm radius and 0.2 cm thickness) to validate the accuracy of the proposed procedure. Since the International Atomic Energy Agency (IAEA) Technical Report Series No. 398 (TRS 398) protocol¹⁰ does not provide the beam quality correction factor for the BPC, it was thus cross calibrated against an ADCL calibrated Farmer chamber (PTW 310013) using a broad passively scattered proton beam field. For comparison purpose, the limit of integration in Eq. 2 was set to a 4.08 cm radius to match the chamber’s radius to compute the PISD, which is termed as PISD_RBPC. The PISD values were also computed by setting the limit of integration in Eq. 2 to a value of the radial distance where the profile dose falls below 0.1% of the peak (for example, 9 cm for 72.5 MeV PPBS) giving the PISD_full. A convergence study showed that the PISD value remained essentially unchanged with further increase in the upper limit of integration due to small relative dose values beyond the 0.1% of peak dose. PISD_full was compared with BPC measured PISD to quantify the effect of chamber size in measuring the contribution of long tail region of the lateral dose profile or low dose envelope of the PPBS. Long tail dose correction factors (LTDCFs) were determined from the ratio of PISD_full/PISD_RBPC at different depths for PPBSs of different energies.

Monte Carlo simulations

As described earlier and in the paper by Gillin et al.,⁴ the relative PISD data from validated MC model of the ProBeat scanning beam nozzle were converted to the required PISD in Gy mm²/MU by using the BPC measured PISD at a shallow depth of 2 cm with appropriate correction for the chamber size limitation. The correction factors, which are conceptually similar to the LTDCF described earlier, are taken from the MC simulation and were computed from the ratio of PISDs for virtual chambers of radii of 20 and 4.08 cm. The details of the MC model of the scanning beam nozzle and its validation are described in another publication.⁷ Due to low signal to noise ratio, it is difficult to measure the relative dose profiles extending to 20 cm radial distance. Therefore, the calculated LTDCFs from our area integration of experimentally measured lateral dose profiles of PPBS method are compared with those from MC Simulations for a virtual chamber of 9 cm radius, which is also the upper limit for integration in Eq. 2 for the widest PPBS with 72.5 MeV energy in our study.

RESULTS AND DISCUSSION

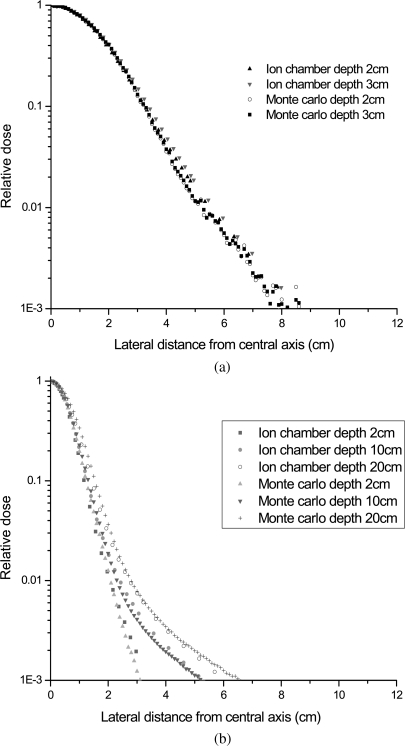
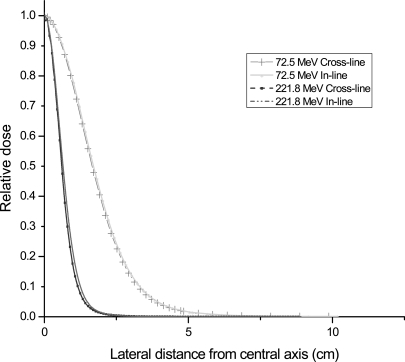
Typical cross-line relative dose profiles for the lowest energy 72.5 MeV and the highest energy 221.8 MeV PPBSs measured at shallow and relatively deeper depths in water by ion chamber are shown in Figs. 1a, 1b, respectively. These profiles have also been compared with the results from Monte Carlo simulation to confirm the quality of the measured data. The ion chamber measured profiles were interpolated by a cubic spline fit. It is evident from these figures that long tail dose of the profiles extend well beyond the radius of the BPC both for low energy beams even at shallow depths and for high energy beams at relatively deeper depths. Figure 2 shows the comparison between the in-line and cross-line ion chamber measured lateral relative dose profiles for the lowest energy 72.5 MeV and highest energy 221.8 MeV PPBSs at 2 cm depth in water, respectively. As can be seen from Fig. 2, the high energy PPBS has relatively larger asymmetrical planar dose distribution. As discussed in the paper⁸ by Sawakuchi et al., low energy spots have long low dose tail regions, and the high energy PPBS have sharp dose gradients in the peak regions of the profile.

Figure 1.

Comparison of: (a) ion chamber measured and Monte Carlo simulated cross-line relative dose profiles at two depths for 72.5 MeV PPBS and (b) ion Chamber measured and Monte Carlo simulated cross-line relative dose profiles at three different depths for 221.8 MeV PPBS.

Figure 2.

Comparison of in-line and cross-line lateral relative dose profiles for 72.5 MeV PPBS and 221.8 MeV PPBS at 2 cm depth measured using ion chamber.

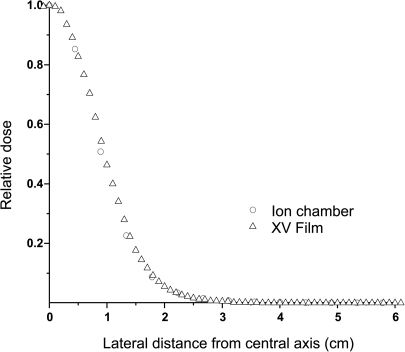
Figure 3 shows the comparison between the film and ion chamber measured lateral relative dose profiles of 146.9 MeV PPBS at a depth of 2 cm. The good agreement seen between the two demonstrates the suitability of films for making qualitative measurements of lateral relative dose profiles for PPBS. The small difference observed between the film and ion chamber measured profiles can be attributed to the detector size effect in the ion chamber measurements and to the uncertainties inherent in film dosimetry. The comparison of angular profiles from film dosimetry was used only to assess the degree of anisotropy in spot dose distribution and to devise a feasible procedure to account for the anisotropy effect in the determination of PISD using the ion chamber dose profile data. The magnitude of observed difference between the film and ion chamber data are rather small and the quality of the angular scans is considered as good as can be expected from film dosimetry to be used for the estimation of the magnitude of the LDAF calculated using Eq. 5.

Figure 3.

Comparison between the ion chamber and film measured lateral relative dose profiles of 146.9 MeV PPBS at a 2 cm water equivalent depth.

The D₀ values measured using the two methods described in Sec. 2 are presented in Table TABLE I.. As expected, there are differences between the ion chamber measured D₀ values for single PPBS, and those measured at the center of the broad field. The D₀ values obtained from single spot measurements were found to be lower compared to the values measured in the broad beam. This can be attributed both to the chamber size effect and the uncertainties associated with alignment and positioning of ion chambers in the peak dose location of a single PPBS. For the chamber used in this measurement, its absorbed dose to water calibration factor was obtained from ADCL, which carries standard calibration uncertainties. Additionally, the chamber positioning errors also contribute to the uncertainties in our measurements. These uncertainties were estimated by making a set of five repeat measurements for each of the energies reported in this work. While the lateral displacements of ±1 mm in the chamber location did not seem to affect values of Do, the depth-displacement error of ±1mm of the chamber do seem to effect the Do values for PPBSs of all the energies studied in this work. The estimated uncertainties associated with our measurements of peak spot dose values are given in Table TABLE I.. Since values of D₀ determined from the dose measurement at the center of broad fields is much less affected by the above two effects, they will be much more accurate, and were used for the calculation of PISD using Eq. 3.

Table 1.

Peak spot dose in cGy/MU at different depths for PPBSs of five different energies measured by ion chamber (IC) by placing it both at the peak of the single PPBS and the center of a 10 × 10 cm² broad field. Spot spacing of 5 mm was used in creating the broad field. The nominal range corresponds to the depth of 90% Bragg peak dose location.

Energy (MeV)/nominal range (cm)	Depth (cm)	D0 from IC at peak of single spot (cGy/MU)	D0 from IC in 10 × 10 cm2 field (cGy/MU)	Overall uncertainty ±(%)
72.5/4.0	2	5.60	5.85	1.90
72.5/4.0	3	7.18	7.42	4.38
89.6/6.0	2	7.31	7.74	0.73
89.6/6.0	3	8.02	8.08	1.03
89.6/6.0	4	9.17	9.27	1.94
146.9/14.9	2	16.33	17.26	0.18
146.9/14.9	7	17.33	18.20	0.31
146.9/14.9	12	21.24	21.25	1.17
181.1/21.5	2	21.78	22.55	0.23
181.1/21.5	4	21.61	22.33	0.10
181.1/21.5	19	26.13	27.90	1.35
221.8/30.6	2	31.58	33.83	0.15
221.8/30.6	10	29.52	31.24	0.10
221.8/30.6	20	24.74	26.05	0.14

The LDAF values for PPBSs of different energies are given in Table TABLE II. and are within 0.99 and 1.01. Thus, the average value of PISD obtained using the in-line and cross-line dose profiles of PPBS can be considered to be within 1% from its value from full treatment of angular anisotropy of the dose distribution. Profiles from film measurements were used only to qualitatively assess the extent of the effect of angular anisotropy of PPBS planar dose distribution on its PISD calculation, and to demonstrate that use of the average of PISD values determined from in-line and cross-line lateral dose profiles to account for this anisotropy is a reasonable approximation.

Table 2.

Limited dose averaging factor (LDAF) obtained from the ratio of the average PISD calculated using PPBS lateral relative dose profiles along the two principal axes and those at different angles measured using Kodak XV film at 2 cm depth.

Energy of PPBS (MeV)	LDAF
72.5	0.99
89.6	1.00
146.9	0.99
181.1	1.01
221.8	0.99

The PISD_RBPC and PISD_full values, which were computed using the ion chamber measured in-line and cross-line relative dose profile functions and D₀ values from dose measurement by ion chamber in a broad field, are given in Table TABLE III.. The accuracy of our computational procedure was assessed by comparing the calculated PISD_RBPC against the BPC measured values. As can be seen from Table TABLE III., there is a good agreement between these two values, with the maximum difference being 3.4%. Some of the differences may be attributed to various uncertainties associated with the measurements of lateral relative dose profiles, point dose by Markus Chamber and PISD by BPC. Major sources of errors that could possibly exist in our measurements and methods are: (a) determination of peak dose values of PPBS, (b) uncertainties in the lateral relative dose profile measurements due to water tank scanning system setup variability, (c) chamber positioning uncertainties along the depth direction, and (d) calibration uncertainties such as: Chamber Co-60 dose to water calibration factor from ADCL and beam quality factor determination for the BPC by cross calibration. For most of these identified sources, separate sets of measurements were made to determine the standard deviation of the calculated values of PISD due to the variability in the measured values of different contributing components. It is found that the uncertainties in Markus Chamber measured peak spot doses and BPC measured PISD are both energy and depth dependent. Hence, the uncertainties in their results were obtained for different energies and different depths by making set of 15 repeat measurements. However, uncertainty in the area integral of relative dose profile function in Eq. 2 turns out to be only energy dependent and remains invariant of depth of measurement. Therefore, the precision of measurement of lateral relative dose profiles was estimated by making a set of five repeat measurements at a depth of 2 cm for different energies. The standard laboratory calibration uncertainties were obtained following the IAEA TRS 398 protocol guidelines¹⁰ and are estimated to be around 3%. The overall uncertainties in our measurements were computed as a quadrature sum of individual uncertainties discussed above. The overall uncertainties both in our method of computing PISD from lateral dose profile function integration and in the measurements of PISD by BPC are given in Table TABLE III..

Table 3.

Comparison of PISD values from the present area integration of planar PPBS dose method (PISD_full and PISD_RBPC) with those from measurement with BPC (PISD_BPC). All PISD values are in units of Gy mm²/MU. The PISD_full is calculated by setting the upper limit of integration for radius in Eq. 2 to a value where the relative dose value is less than the 0.1% of the PPBS peak dose. The upper limit in Eq. 2 was set to 4.08 cm, which corresponds to the radius of BPC, to calculate the PISD_RBPC.

Energy (MeV)	Depth (cm)	PISDfull (a)	PISDRPBC (b)	Overall uncertainty ±(%) in calculated values	PISDBPC (c)	Overall uncertainty ±(%) in BPC measured values	% difference (1-b/c)	% difference (1-a/b)	% difference (1-a/c)
72.5	2	87.16	79.06	3.7	77.3	3.5	2.3	10.2	12.8
72.5	3	117.29	106.05	5.4	103.98	5.1	2.0	10.6	12.8
89.6	2	77.56	73.36	3.3	71.39	3.1	2.7	5.7	8.6
89.6	3	86.62	81.90	3.3	79.28	3.2	3.3	5.8	9.2
89.6	4	101.01	95.44	3.7	92.46	3.5	3.2	5.8	9.2
146.9	2	72.21	71.10	4.7	69.34	3.0	2.5	1.6	4.1
146.9	7	84.00	82.43	4.7	80.51	3.0	2.4	1.9	4.3
146.9	12	115.98	113.36	4.8	110.00	3.2	3.1	2.3	5.4
181.1	2	70.20	69.67	5.3	67.96	3.0	2.5	0.8	3.3
181.1	4	74.04	73.12	5.3	71.29	3.0	2.6	1.3	3.9
181.1	19	130.24	127.06	5.5	122.84	3.3	3.4	2.5	6.0
221.8	2	70.82	70.02	5.4	67.83	3.0	3.2	1.1	4.4
221.8	10	80.04	75.59	5.4	74.30	3.0	1.7	5.8	7.7
221.8	20	89.52	84.78	5.4	83.51	3.0	1.5	5.6	7.2

As expected, the values of PISD_full are larger than both the PISD_RBPC and BPC measured PISD values due to the contribution of the low dose envelope region of the lateral dose profiles of PPBS. For lower energy beams (i.e., 72.5 and 89.6 MeV) at all depths and for high energy beams at deeper depths in water, the spots were relatively wide and the low dose tail regions of the profile extended beyond the 4.08-cm distance from the peak. As discussed earlier, the contribution of the low dose envelope of PPBS is not properly included in the PISD measured by BPC due to its size limitation.

The calculated values of LTDCF, which is the ratio of PISD_full/PISD_RBPC, are given in Table TABLE IV. along with the values from Monte Carlo simulation using a 9 cm radius virtual chamber for comparison. The LTDCF values are seen to be energy and depth dependent. This is expected because the PPBS lateral dose profiles become narrower with an increase in the energy, with exceptions at certain depths where there are nuclear contributions affecting the long tail regions.^{7, 8} Since the LTDCF is the ratio of two PISDs, the D₀ value is not required to calculate them. Hence, it is more accurate to compute LTDCF than computing PISD itself. It is necessary to point out that in case of high energy PPBS at intermediate depths, e.g., for 221.8 MeV PPBS at a depth of 20 cm, the LTDCF can easily go up to 6% due to the contribution from the secondary particles produced from the nuclear interactions taking place in the medium.⁷ LTDCFs obtained from measured profile integration method agree within 1% with MC simulation generated LTDCFs for a 9 cm radius virtual chamber. The difference between the measured and MC simulation data can be attributed both to the uncertainties in the present calculation procedure and to that in the MC simulation. For the beam commissioning purposes, LTDCFs from the present area integration of planar dose procedure can be used to obtain detector size effect corrected PISD of PPBS from the BPC measurements, especially for low energy PPBS, where nuclear interaction contributions are not important. Currently, our beam configuration of the PPBS in the TPS is based on the MC simulated PISD data for a 20 cm radius virtual chamber. This contribution may not be accurately measured with ion chamber due to low signal to noise ratio in the tail region of the lateral profiles extending out to 20 cm. However, the profile data up to 9 cm distance from the PPBS center is found to be adequate to validate the accuracy of MC simulation model and the TPS input data for PISD.

Table 4.

Calculated LTDCF from the present area integration of planar PPBS dose method and comparison with Monte Carlo simulated values for a virtual chamber of 9 cm radius.

Energy (MeV)	Depth (cm)	LTDCF (a)	LTDCF MC (b)	% difference (1-a/b)
72.5	2	1.103	1.094	0.82
72.5	3	1.106	1.095	1.00
89.6	2	1.057	1.052	0.48
89.6	3	1.058	1.053	0.47
89.6	4	1.058	1.054	0.38
146.9	2	1.020	1.021	−0.10
146.9	7	1.020	1.029	−0.87
146.9	12	1.020	1.029	−0.87
181.1	2	1.010	1.008	0.20
181.1	4	1.010	1.013	−0.30
181.1	19	1.030	1.026	0.39
221.8	2	1.010	1.007	0.30
221.8	10	1.060	1.050	0.95
221.8	20	1.060	1.065	−0.47

The LTDCF for the size limitation of the BPC arises because of the long low dose tails of the PPBS profile that may extend beyond its active volume. These long tails occur due to two factors: (1) size of the incident spot and (2) the contribution of the nuclear interaction products in the medium, which is also known as the halo dose. In this work, measured profile integration method is used to determine the LTDCFs for BPC measured PISD and to compare them with those from Monte Carlo simulation. An alternative method to determine the long tail dose contribution from the nuclear halo component was used by Pedroni et al.⁵ In their approach, an extra Gaussian function for the nuclear halo component was added to the Gaussian function representing the primary pencil beam in its empirical dose distribution function. The values of two parameters, one for the relative contribution of the nuclear halo to integral dose and the other for the width of the Gaussian function, were determined by matching the dose measured at the center of concentric square fields of different sizes at various depths with the calculated dose from the superposition of pencil beams represented by the empirical dose function for the same square fields. The values of the relative fraction for the nuclear halo contribution (f_NI) to integral dose for the 214 MeV beam at 20 cm depth determined by Pedroni et al. (Fig. 6 of Ref. 5) is about 14%, which is much larger than the LTDCF values 6% that we have computed for the 221.8 MeV at 20 cm depth. Since the nuclear halo dose contribution is shown to increase with proton beam energy, the value of f_NI for the 221.8 MeV beam would be more than 14%, if determined by the method of Pedroni et al.⁵ From the qualitative comparison of the values of f_NI from Pedroni et al.⁵ and the LTDCF from the present study for other energies, it is safe to state that their f_NI values are larger than the missing fraction of long tail dose contribution in our BPC measured PISD. The differences can be attributed mainly to the differences in the physical quantity that is measured. The f_NI is an adjustable parameter in the empirical dose function that gives fractional contribution of the second Gaussian representing nuclear halo component relative to contribution of the Gaussian function representing the primary proton beam. Any inadequacy in the Gaussian representation of either the primary or nuclear halo component is expected to severely affect the values of f_NI, which are determined by fitting the calculated dose to measured dose at the center of broad fields created by the superposition of pencil beams represented by the empirical Gaussian function. The LTDCF calculated in the present work provides a correction factor to the measured PISD by the BPC for its size limitation. The PISD measured by the BPC also includes contribution of the part of the nuclear halo of the PPBS contained within its active volume. Thus, the LTDCF determined in our work does not represent the entire nuclear halo contribution, only the missing fraction from the BPC measured PISD. The f_NI in the method of Pedroni et al.⁵ is intended to quantify the entire nuclear halo fraction, which is expected to be larger than the fractional missing contribution represented by our LTDCF. The LTDCF is useful to correct the BPC measured PISD without any specific separation of primary and nuclear halo contributions. On the other hand, the method of Pedroni et al.⁵ would be useful if a separation of primary and nuclear halo component is intended in modeling the PPBS. Both the f_NI and LTDCF can also be determined by Monte Carlo simulation.^{7, 11, 12} Monte Carlo simulation results can be validated by measurements using the procedure of Pedroni et al.⁵ for f_NI and by the procedure described in this paper for LTDCF. Our procedure for the computation of PISD from measured PPBS profiles and peak PPBS dose using Eqs. 1, 2, 3 is not nozzle or beam specific; however, results of its application presented in this paper are specific to the scanning beam nozzle at PTCH.

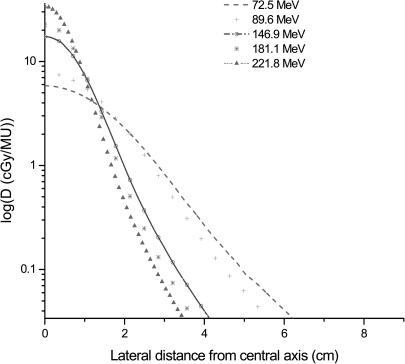
Relative dose profiles provide useful information about the PPBS. However, availability of a library of these profiles in absolute dose values would be useful for validating beam configurations in TPS. Figure 4 shows the in-line profiles in cGy/MU at 2cm depths for the PPBS energies measured in this work. These lateral absolute dose profiles were obtained by multiplying the normalized relative dose profiles with the peak dose (D₀) measured at the central axis using the broad beam method.

Figure 4.

In-line lateral dose (cGy/MU) profiles of PPBSs of different energies measured at 2 cm depth.

The values of PISD_full from the current procedure at 2 cm depth for the PPBS energies investigated in this study are compared with the MC generated data that are currently used in our Eclipse TPS in Table TABLE V.. As mentioned earlier, the PISD values for the TPS were measured using BPC, which were then scaled by LTDCFs obtained using MC simulations. As Table TABLE V. shows, the differences can be as much as 4%. These differences are within the estimated uncertainties (Table TABLE III.) in the determination of PISD using the area integration of the measured profiles. Additionally, there are two other sources that can contribute to these discrepancies. First, for lower energy PPBS, the MC simulated PISD values are for a virtual chamber size of 20 cm and it is not experimentally feasible to measure the dose in the tail regions of the lateral profile beyond a certain distance from the central axis due to low signal to noise ratio. Hence, the PISD from the current area integration method could have missed a small amount of extra dose from the extended tail regions, thereby leading to a lower value. Second, for higher energy PPBSs with small spot sizes, there can be a detector size effect in the measured lateral relative dose profile used in the computation of PISD. The detector size effect on lateral profiles was studied using an analytical deconvolution procedure. The measured profiles were fitted to a linear combination of Gaussian functions and were deconvolved with Gaussian detector response function. The results^{7, 13} showed that the detector size has a rather small effect on the Gaussian like lateral profiles of PPBS measured with small ion chambers. Because the analytical procedure has its limitations due to the approximations involved in the fitting procedure and unknown nature of the detector response function, we did not use the results to make corrections to the values reported in Table TABLE V., rather these were used to understand the possible sources of the observed difference. The PISDs determined by the area integration method are not meant for use as input for the TPS because of large uncertainties associated with these values as shown in Table TABLE III.. Validation of beam configuration in TPS requires comparison of calculated and measured dose in broad fields created by the superposition of PPBSs. Use of input data with large uncertainties would obviously lead to unacceptable large differences (more than customary 2% or 2 mm for clinical treatment fields) in the TPS predicted and measured dose distribution for clinical broad treatment fields. However, they would be highly useful for checking the sanity of data from BPC measurement and for validating the accuracy of the Monte Carlo simulation model and PISD data from this simulation. The level of precision that is achievable by using the measured profiles with a small PTW pinpoint chamber is considered to be acceptable for quality assurance check of the PISD input data for the TPS, which are usually obtained from a combination of Monte Carlo simulation and BPC measurement.

Table 5.

Comparison of calculated PISD values (PISD_full) in (Gy mm²/MU) from the present area integration of planar PPBS dose method with the currently commissioned values in Eclipse TPS at PTCH at 2 cm depths in water. PISD full values are obtained by setting the limit of integration to an off-axis distance in the PPBS profile where the relative dose value is 0.1% of its peak value in Eq. 2, and the TPS PISD values were obtained from Monte Carlo simulation for a 20 cm radius virtual chamber.

Energy (MeV)	Currently commissioned TPS PISD (a)	PISDfull (b)	% difference (1-b/a)
72.5	88.03	87.16	−1.0%
89.6	79.48	77.56	−2.4%
146.9	70.28	72.21	2.7%
181.1	68.80	70.20	2.0%
221.8	68.02	70.82	4.0%

Accuracy of the dose calculation in the TPS will depend on the precision of the input PISD data to configure the PPBS model. Results from both the Monte Carlo simulations and the current profile integration method show that BPC measured PISD is not precise enough to be used as input for the TPS. For example, differences as much as 7% were seen between the TPS calculated dose/MU when uncorrected PISD data from BPC measurement were used for beam configuration as compared to the data corrected with LTDCF for a sample prostate treatment field. The average differences between the TPS calculated and measured point doses in prostatic treatment fields of a group of 249 patients have been found¹⁴ to be within 1% after the use of LTDCF corrected PISD as input data for our Eclipse TPS. Thus, the determination of LTDCF is an important aspect of TPS commissioning process. The proposed profile area integration method will be useful to provide these factors both to correct the BPC measured data and to validate the accuracy of the Monte Carlo simulation model and results, if used for generating the TPS input beam data.

CONCLUSIONS

Within experimental uncertainties, the values of PISD_RBPC for PPBS obtained from the technique described in this paper are found to be in good agreement with those measured with the BPC. For low energy PPBS, where the finite radius of the BPC can restrict its ability to measure the dose of the entire spot, the proposed lateral dose profile integration method, which is based on measured PPBS dosimetry data, can provide the needed LTDCF for its finite size. However, the procedure has limited use for high energy spots where measurement of dose in the long tail region of the profile has high level of uncertainty. It should be noted that the accuracy of the results strongly depends on the quality of lateral relative dose profiles and the accuracy of the measured PPBS peak dose values. Despite these limitations, this technique can be a useful validation tool both for the Monte Carlo simulation results, and for the sanity check of the BPC measured PISD data.