On determining the extent of side-pool synthesis in a three-pool model for whole body cholesterol kinetics

Abstract

Whole body cholesterol turnover is well described by a three-pool model. This model has eight unknown parameters: three masses, three synthesis rates, and two inter-compartmental exchange rates. Only six parameters can be estimated by fitting the model to the plasma specific radioactivity-time curve which results from the intravenous injection of labeled cholesterol. Additional information is obtained if a precursor of cholesterol, labeled with a different isotope, is also injected. Equations are derived to enable the calculation of all eight model parameters from the two sum-of-exponentials equations that are fitted to the two tracer curves. The characteristics of a satisfactory precursor are discussed.

Pool models are widely used in studying whole body cholesterol kinetics in humans. Two-pool models have been used to analyze turnover data from studies of ten-to-twelve weeks duration (1,2). When studies were carried out for 30 to 40 weeks, a three-pool model was found necessary (and sufficient) to fit the turnover data (3,4). Plasma specific radioactivity data following [¹⁴C]cholesterol injection were obtained in 54 subjects (5). Fifteen subjects were normals, 10 were hypercholesterolemic, 21 were hypertriglyceridemic, and 8 had both hypercholesterolemia and hypertriglyceridemia; 21 had a familial form of hyperlipidemia. In every subject in this heterogeneous population, the three-pool model gave the best fit to the data.

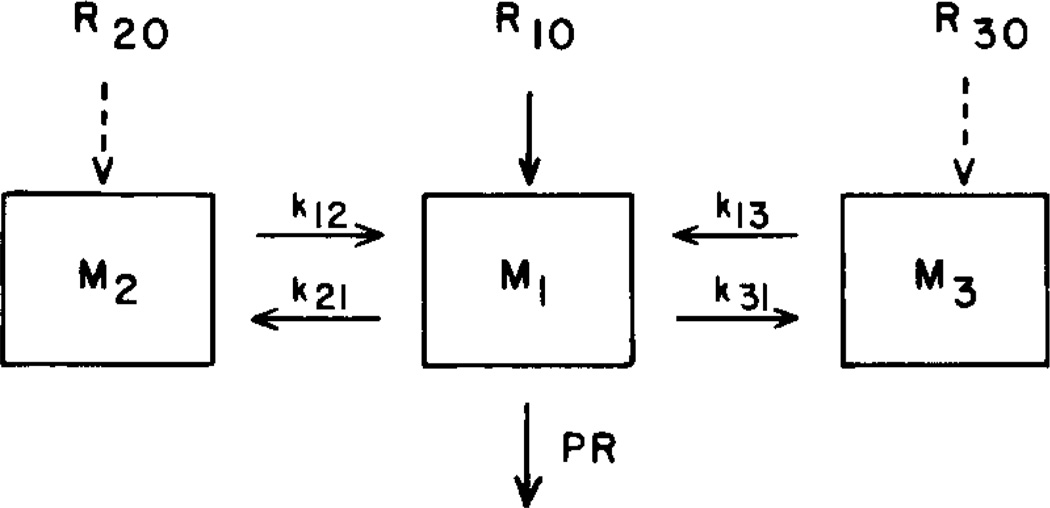
A mammillary model structure, shown in Fig. 1, with a central pool exchanging with two side pools, is usually assumed. The central pool includes plasma; injection and sampling are assumed to be in this pool. Synthesis of cholesterol may take place in each of the three pools, while degradation is assumed to be entirely in the central pool (3–5).

Fig. 1.

Three-pool model with the possibility of side-pool synthesis (R₂₀ and R₃₀) but a single output (PR).

The three-pool model has a number of unknown parameters: three masses, M₁, M₂, M₃; four turnover rate constants, k₁₂, k₂₁, k₁₃, k₃₁; four synthetic/degradation rates, R₀₁, R_.0, R₂₀, R₃₀. (R₀₁ is the total degradation rate, R_.0 is the total endogenous synthesis rate, R₂₀ and R₃₀ are the endogenous synthesis rates into pools 2 and 3, respectively.) Total body production rate, PR (which equals the total degradation rate, R₀₁), is the sum of endogenous synthesis plus absorption of exogenous cholesterol. Absorption rate of exogenous cholesterol is measured independently or assumed; in either case, it is not an unknown parameter of the model. Since the total inflow into each pool must equal the total outflow from that pool, it is possible to compute three of the above unknown parameters when the others are known. Thus,

$$\begin{array}{c}{\mathrm{M}}_2=\frac{{\mathrm{R}}_{20}+{\mathrm{k}}_{21}{\mathrm{M}}_1}{{\mathrm{k}}_{12}}\hfill \\ {\mathrm{M}}_3=\frac{{\mathrm{R}}_{30}+{\mathrm{k}}_{31}{\mathrm{M}}_1}{{\mathrm{k}}_{13}}\hfill \\ {\mathrm{R}}_{.0}={\mathrm{R}}_{01}-\text{absorption rate of exogenous cholesterol}.\hfill \end{array}$$ Eq. 1

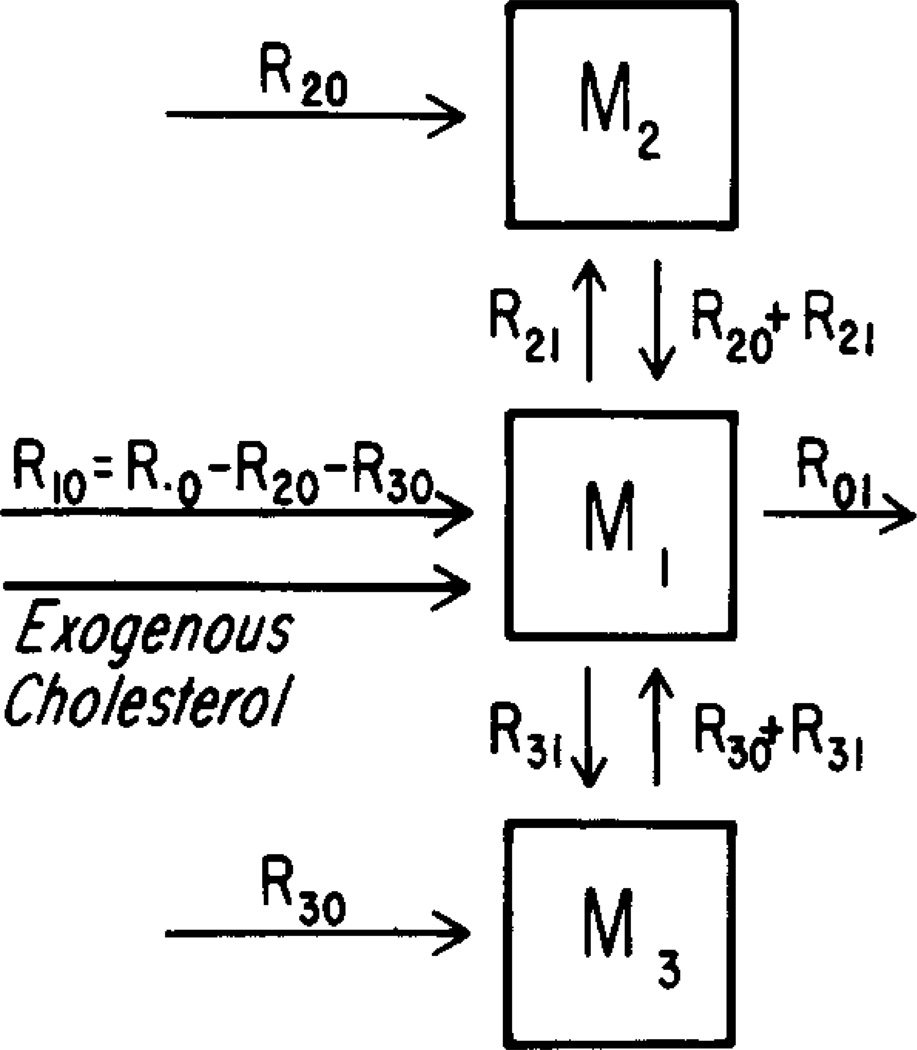
Fig. 2 shows the model in terms of fluxes instead of turnover rates. This model has eight unknown parameters: the masses of the three pools (M₁, M₂, M₃), the total production rate (R₀₁), the rates of synthesis in the two side pools (R₂₀, R₃₀), and the two flow rates from the central pool to the side pools (R₂₁, R₃₁).

Fig. 2.

A three-pool mammillary model for cholesterol turnover. M₁, M₂, and M₃, are masses of cholesterol (g) in pools 1, 2, and 3, respectively; R’s are cholesterol mass flow rates (g/day); R_.0 is the total endogenous cholesterol synthesis rate; R₁₀, R₂₀, and R₃₀, are endogenous synthesis rates into pools 1, 2, and 3, respectively.

In this paper, mathematical expressions are derived that permit the determination of all eight model parameters when the appropriate studies are carried out.

When the three-pool model is fitted to the plasma cholesterol specific activity-time curve (following the injection of labeled cholesterol), only six of the eight unknown parameters can be estimated uniquely. This is because the equation for the specific activity-time curve is a sum of three exponentials, which has only six parameters. It is shown below that M₁, R₀₁, R₂₁, R₃₁, (R₂₀ + R₂₁)/M₂ and (R₃₀ + R₃₁)/M₃ can be determined uniquely from a study in which only labeled cholesterol is injected. Since two of the eight model parameters cannot be determined, the masses of the side pools (pools 2 and 3) cannot be defined uniquely. This ambiguity, in which masses and synthesis rates of the side pools cannot be determined uniquely, may be termed nonuniqueness. Nonuniqueness of general pool models has been studied (6, 7). The study of nonuniqueness comes under the general subject of identifiability (8).

In our previous work, this nonuniqueness has been recognized, and ranges of possible values have been calculated for the side pool masses, M₂ and M₃, and for the side pool synthetic rates, R₂₀ and R₃₀ (3–5). Using this approach, we recently reported the results of an extensive analysis of data obtained from long-term plasma decay curves in 54 subjects (5). In this population, the minimum and maximum values for M₂ (mean ± SD) were determined to be 18.3 ± 8.6 g and 33.2 ± 14.4 g, respectively. The minimum and maximum values for M₃ (mean ± SD) were 39.4 ± 14.0 g and 111.7 ± 47.5 g, respectively. The true values for M₂ and M₃ must lie between these lower and upper limiting values. We were also able to develop and validate regression equations relating the minimum value of M₃ to body weight and serum cholesterol concentration or to excess weight and cholesterol level times body weight.

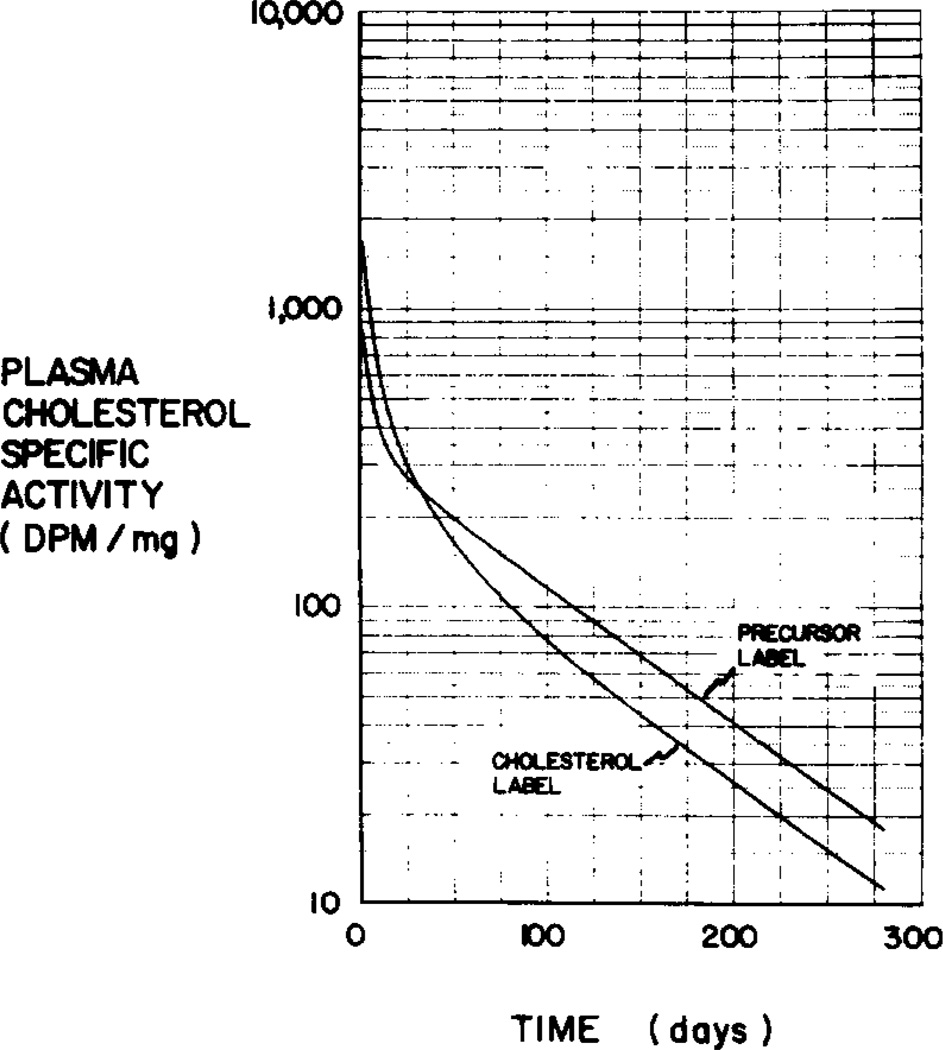
A somewhat different approach was taken by Kekki, Miettinen, and Wahlström (9) who attempted to resolve the indeterminacy by injecting a labeled precursor of cholesterol and subsequently determining plasma cholesterol specific activity. Theoretically, in such an approach, the appropriate labeled precursor (with a different isotope from that used to label cholesterol) traces all newly formed cholesterol and hence may enter the model in all three pools at time zero, while labeled cholesterol enters only the central pool, pool 1. If there is no side-pool synthesis (i.e., no synthesis into pools other than pool l), the precursor enters only the central pool and the resulting plasma specific activity curve will be the same as the curve resulting from labeled cholesterol injection. If, however, there is significant side-pool synthesis, the plasma cholesterol specific activity curves resulting from the two tracers would be different. Fig. 3 shows simulated specific activity curves for the two tracers, assuming that half of the total body synthesis of cholesterol occurs in pool 1 and half in pool 3. Thus, injection of a suitable precursor theoretically permits determination of the extent of side-pool synthesis if the appropriate mathematical equations are derived. In the derivation which follows, equations are derived for the analysis of results that would be obtained after injection of labeled cholesterol alone, after injection of a labeled precursor of cholesterol alone and, finally, after injection of both tracers.

Fig. 3.

Illustrative curves from cholesterol and precursor labels.

Model derivation

The model, as shown in Fig. 2, has eight unknown parameters: M₁, M₂, M₃, R₀₁, R₂₀, R₃₀, R₂₁, R₃₁. If y₁, y₂, and y₃ are tracer specific activities (dpm/mg cholesterol) in pools 1, 2, and 3, respectively, their changes with time following a bolus injection of tracer are described by the differential equations (written in matrix-vector notation):

$$\text{dy}/\text{dt}=\text{Ag}$$ Eq. 2

$$\mathrm{y}=\left[\begin{array}{c}\hfill {\mathrm{y}}_1\hfill \\ \hfill {\mathrm{y}}_2\hfill \\ \hfill {\mathrm{y}}_3\hfill \end{array}\right]\text{\hspace{1em}and\hspace{1em}}\mathrm{A}=\left[\begin{array}{ccc}\hfill -({\mathrm{R}}_{01}+{\mathrm{R}}_{21}+{\mathrm{R}}_{31})/{\mathrm{M}}_1\hfill & \hfill ({\mathrm{R}}_{20}+{\mathrm{R}}_{21})/{\mathrm{M}}_1\hfill & \hfill ({\mathrm{R}}_{30}+{\mathrm{R}}_{31})/{\mathrm{M}}_1\hfill \\ \hfill {\mathrm{R}}_{21}/{\mathrm{M}}_2\hfill & \hfill -({\mathrm{R}}_{20}+{\mathrm{R}}_{21})/{\mathrm{M}}_2\hfill & \hfill 0\hfill \\ \hfill {\mathrm{R}}_{31}/{\mathrm{M}}_3\hfill & \hfill 0\hfill & \hfill -({\mathrm{R}}_{30}+{\mathrm{R}}_{31})/{\mathrm{M}}_3\hfill \end{array}\right]$$

To solve these equations for y₁, specific activities at time zero, i.e., the initial conditions, y₁(0), y₂(0), and y₃(0), must be known. When labeled cholesterol is injected, y₁(0) is the dose of radioactive cholesterol injected divided by M₁, and y₂(0) and y₃(0) are zero. If, however, a labeled precursor of cholesterol, whose incorporation into cholesterol is rapid relative to cholesterol turnover, is injected, then the initial specific activities are non-zero in the pools that receive cholesterol synthesized from the injected precursor.

The mathematical analysis is fairly complicated since the Equations 2 are differential equations in three variables; there is no simple solution. However, a well-known mathematical technique called Laplace transformation (10) changes the differential equations into linear algebraic equations (with no derivatives), which can be solved much more easily. The transformation replaces y as a function of time with Y as a function of s, which is the independent variable in the Laplace domain. Transforming Equations 2 by the Laplace transform,

$$\begin{array}{ccc}{\mathrm{Y}}_{\mathrm{i}}(\mathrm{s})={\displaystyle {\int }_0^{\mathrm{\infty }}}{\mathrm{y}}_{\mathrm{i}}(\mathrm{t}){\mathrm{e}}^{-\text{st}}\text{dt},\hfill & \text{leads to}\hfill & \text{sY}(\mathrm{s})-\mathrm{y}(0)=\text{AY}(\mathrm{s}).\hfill \end{array}$$ Eq. 3

Here, s is the complex frequency in the Laplace domain which replaces t in the equations. This matrix-vector equation can then be solved for Y₁(s), the Laplace transform of y₁(t), the specific activity in pool 1 following a bolus injection of either labeled cholesterol or a labeled precursor of cholesterol.

Analysis of specific activity data arising from injection of labeled cholesterol

In this case, all the injected tracer, c (dpm), is initially in the central pool. So, y₁(0) = c/M₁, y₂(0) = y₃(0) = 0. Using these values, Equation 3 is solved for Y₁, denoted Y_c, to indicate that it applies to the specific activity data arising from cholesterol injection.

$${\mathrm{Y}}_{\mathrm{c}}=\mathrm{c}\frac{{\mathrm{s}}^2/{\mathrm{M}}_1+\mathrm{s}({\mathrm{k}}_{22}+{\mathrm{k}}_{33})/{\mathrm{M}}_1+{\mathrm{k}}_{22}{\mathrm{k}}_{33}/{\mathrm{M}}_1}{{\mathrm{s}}^3+{\mathrm{s}}^2[{\mathrm{k}}_{22}+{\mathrm{k}}_{33}+\frac{{\mathrm{R}}_{01}+{\mathrm{R}}_{21}+{\mathrm{R}}_{31}}{{\mathrm{M}}_1}]+\mathrm{s}[{\mathrm{k}}_{22}{\mathrm{k}}_{33}+\frac{{\mathrm{k}}_{22}({\mathrm{R}}_{01}+{\mathrm{R}}_{31})+{\mathrm{k}}_{33}({\mathrm{R}}_{01}+{\mathrm{R}}_{21})}{{\mathrm{M}}_1}]+\frac{{\mathrm{k}}_{22}{\mathrm{k}}_{33}{\mathrm{R}}_{01}}{{\mathrm{M}}_1}}$$ Eq. 4

where k₂₂ = (R₂₀ + R₂₁)/M₂, and k₃₃ = (R₃₀ + R₃₁)/M₃.

Suppose the data are fitted by a sum of three exponentials:

$${\mathrm{y}}_{\mathrm{c}}={\mathrm{A}}_1{\mathrm{e}}^{-{\alpha }_1\mathrm{t}}+{\mathrm{A}}_2{\mathrm{e}}^{-{\alpha }_2\mathrm{t}}+{\mathrm{A}}_3{\mathrm{e}}^{-{\alpha }_3\mathrm{t}}$$

Then, applying the Laplace transformation to this equation yields the following:

$${\mathrm{Y}}_{\mathrm{c}}=\frac{{\mathrm{A}}_1}{\mathrm{s}+{\alpha }_1}+\frac{{\mathrm{A}}_2}{\mathrm{s}+{\alpha }_2}+\frac{{\mathrm{A}}_3}{\mathrm{s}+{\alpha }_3}=\frac{{\mathrm{s}}^2({\mathrm{A}}_1+{\mathrm{A}}_2+{\mathrm{A}}_3)+\mathrm{s}({\mathrm{A}}_1{\alpha }_2+{\mathrm{A}}_1{\alpha }_3+{\mathrm{A}}_2{\alpha }_1+{\mathrm{A}}_2{\alpha }_3+{\mathrm{A}}_3{\alpha }_1+{\mathrm{A}}_3{\alpha }_2)+{\mathrm{A}}_1{\alpha }_2{\alpha }_3+{\mathrm{A}}_2{\alpha }_3{\alpha }_1+{\mathrm{A}}_3{\alpha }_1{\alpha }_2}{{\mathrm{s}}^3+{\mathrm{s}}^2({\alpha }_1+{\alpha }_2+{\alpha }_3)+\mathrm{s}({\alpha }_1{\alpha }_2+{\alpha }_2{\alpha }_3+{\alpha }_3{\alpha }_1)+{\alpha }_1{\alpha }_2{\alpha }_3}=\frac{{\mathrm{s}}^2{\mathrm{a}}_2+{\text{sa}}_1+{\mathrm{a}}_0}{{\mathrm{s}}^3+{\mathrm{s}}^2{\mathrm{d}}_2+{\text{sd}}_1+{\mathrm{d}}_0},\text{written concisely}.$$ Eq. 5

Since Equations 4 and 5 both describe Y_c, a₂, in the numerator of Equation 5 equals the coefficient of s² in the numerator of Equation 4; similarly for a₁, a₀, d₂, d₁, and d₀. Thus, six equations are obtained, which can be solved for the following six model parameters in terms of the exponential parameters A₁ and α₁:

$$\begin{array}{cc}{\mathrm{M}}_1=\mathrm{c}/{\mathrm{a}}_2\hfill & {\mathrm{R}}_{21}=\frac{[{\mathrm{M}}_1({\mathrm{k}}_{22}{\mathrm{d}}_2-{\mathrm{k}}_{22}{\mathrm{a}}_1/{\mathrm{a}}_2-{\mathrm{d}}_1+{\mathrm{a}}_0/{\mathrm{a}}_2)+{\mathrm{k}}_{33}{\mathrm{R}}_{01}]}{({\mathrm{k}}_{22}-{\mathrm{k}}_{33})}\hfill \\ {\mathrm{R}}_{01}={\text{cd}}_0/{\mathrm{a}}_0\hfill & \hfill \\ {\mathrm{k}}_{22}=[{\mathrm{a}}_1+\sqrt{{{\mathrm{a}}_1}^2-4{\mathrm{a}}_0{\mathrm{a}}_2]/2{\mathrm{a}}_2}\hfill & \hfill \\ {\mathrm{k}}_{33}={\mathrm{a}}_1/{\mathrm{a}}_2-{\mathrm{k}}_{22}\hfill & {\mathrm{R}}_{31}=\frac{[{\mathrm{M}}_1({\mathrm{k}}_{33}{\mathrm{a}}_1/{\mathrm{a}}_2-{\mathrm{k}}_{33}{\mathrm{d}}_2+{\mathrm{d}}_1+{\mathrm{a}}_0/{\mathrm{a}}_2)-{\mathrm{k}}_{22}\mathrm{R}]}{({\mathrm{k}}_{22}-{\mathrm{k}}_{33})}\hfill \end{array}$$ Eq. 6

These are equivalent to the formulation reported previously (3).

Analysis of specific activity data arising from injection of labeled precursor of cholesterol

In this case, the injected tracer, p (dpm), is initially in the precursor pool. For the sake of simplicity, the injected precursor is assumed to be incorporated rapidly into cholesterol. (If the precursor cannot be assumed to be completely converted to cholesterol instantaneously, the result is modified as described later.) Hence the initial conditions are: y₁(0) = pf₁/M₁, y₂(0) = pf₂/M₂, y₃(0) = pf₃/M₃, where f₁, f₂, and f₃ are the fractions of precursor incorporated into the three cholesterol pools. Note that f₁, + f₂ + f₃ = 1. If these fractions are proportional to the corresponding synthesis rates, then each fraction equals the fractional endogenous synthesis in that pool (see Fig. 2):

$${\mathrm{F}}_1=({\mathrm{R}}_{.0}-{\mathrm{R}}_{20}-{\mathrm{R}}_{30})/{\mathrm{R}}_{.0,}{\mathrm{f}}_2={\mathrm{R}}_{20}/R_{.0,}{\mathrm{f}}_3={\mathrm{R}}_{30}/{\mathrm{R}}_{.0}.$$

The fractions must be proportional to the synthesis rates or else the estimation of f₁, f₂, and f₃ from the data will not lead to the estimation of synthesis rates. Assuming that f₁, f₂, and f₃ are fractional synthesis rates, we can solve for Y₁(s) as Y_p:

$${\mathrm{Y}}_{\mathrm{p}}=\mathrm{p}\frac{{\mathrm{s}}^2({\mathrm{R}}_{.0}-{\mathrm{R}}_{20}-{\mathrm{R}}_{30})/{\mathrm{R}}_{.0}{\mathrm{M}}_1+\mathrm{s}[{\mathrm{k}}_{22}({\mathrm{R}}_{.0}-{\mathrm{R}}_{30})+{\mathrm{k}}_{33}({\mathrm{R}}_{.0}-{\mathrm{R}}_{20})]/{\mathrm{M}}_1{\mathrm{R}}_{.0}+{\mathrm{k}}_{22}{\mathrm{k}}_{33}/{\mathrm{M}}_1}{\mathrm{D}}$$ Eq. 7

where D is the same as the denominator of Equation 4.

If conversion of precursor to cholesterol is not rapid, p is replaced by the transform of the specific activity-time function for the precursor, multiplied by the flux from the precursor to cholesterol.

For the three-pool model, the specific activity data arising from injection of a labeled precursor of cholesterol can be fitted by a sum of three exponentials:

$${\mathrm{y}}_{\mathrm{p}}={\mathrm{B}}_1{\mathrm{e}}^{-\alpha 1\mathrm{t}}+{\mathrm{B}}_2{\mathrm{e}}^{-\alpha 2t}+{\mathrm{B}}_3{\mathrm{e}}^{-\alpha 3\mathrm{t}}$$

where the exponential rate constants α₁, α₂, and α₃ are the same as for y_c, but B₁, B₂, and B₃ have a different interpretation.

Applying the Laplace transformation to this equation yields the following:

$${\mathrm{Y}}_{\mathrm{p}}=\frac{{\mathrm{s}}^2({\mathrm{B}}_1+{\mathrm{B}}_2+{\mathrm{B}}_3)+\mathrm{s}({\mathrm{B}}_1{\alpha }_2+{\mathrm{B}}_1{\alpha }_3+{\mathrm{B}}_2{\alpha }_1+{\mathrm{B}}_2{\alpha }_3+{\mathrm{B}}_3{\alpha }_1+{\mathrm{B}}_3{\alpha }_2)+{\mathrm{B}}_1{\alpha }_2{\alpha }_3+{\mathrm{B}}_2{\alpha }_3{\alpha }_1+{\mathrm{B}}_3{\alpha }_1{\alpha }_2}{{\mathrm{s}}^3+{\mathrm{s}}^2({\alpha }_1+{\alpha }_2+{\alpha }_3)+\mathrm{s}({\alpha }_1{\alpha }_2+{\alpha }_2{\alpha }_3+{\alpha }_3{\alpha }_1)+{\alpha }_1{\alpha }_2{\alpha }_3}=\frac{{\mathrm{s}}^2{\mathrm{b}}_2+{\text{sb}}_1+{\mathrm{b}}_0}{{\mathrm{s}}^3+{\mathrm{s}}^2{\mathrm{d}}_2+{\text{sd}}_1+{\mathrm{d}}_0},\text{written concisely}.$$ Eq. 8

Proceeding in a manner analogous to Y_c, b₂, equals the coefficient of s² in the numerator of Equation 7; similarly for b₁, b₀, d₂, d₁, and d₀. Again, six equations are obtained, three of which are the same as for Y_c since the denominators are the same.

Thus, the model is not identifiable (it is nonunique) if either labeled cholesterol or a labeled precursor is injected alone, since only six out of eight parameters can be determined by either set of data. However, if both are injected and two curves obtained, the ambiguity can be resolved, since there are now nine exponential parameters for only eight model parameters. Besides the six expressions given in Equation 6, two of the three additional equations from 7 and 8 can be used for this purpose. The solution of these, along with Equations 6, yields the following:

$$\begin{array}{c}{\mathrm{R}}_{30}={\mathrm{R}}_{.0}[{\mathrm{k}}_{22}+({\mathrm{b}}_2{\mathrm{k}}_{33}-{\mathrm{b}}_1){\mathrm{a}}_0/{\mathrm{b}}_0{\mathrm{a}}_2]/({\mathrm{k}}_{22}-{\mathrm{k}}_{33})\hfill \\ {\mathrm{R}}_{20}={\mathrm{R}}_{.0}-{\mathrm{R}}_{30}-{\mathrm{R}}_{.0}{\mathrm{b}}_2{\mathrm{a}}_0/{\mathrm{b}}_0{\mathrm{a}}_2\hfill \\ {\mathrm{M}}_2=({\mathrm{R}}_{20}+{\mathrm{R}}_{21})/{\mathrm{k}}_{22}\hfill \\ {\mathrm{M}}_3=({\mathrm{R}}_{30}+{\mathrm{R}}_{31})/{\mathrm{k}}_{33}\hfill \end{array}$$ Eq. 9

where R_.0 equals R₀₁, minus exogenous cholesterol absorption rate.

A numerical example

The specific activity curves in Fig. 3 were generated by simulation using the average model parameters for 54 subjects reported by Goodman et al. (5), and assuming 50% of endogenous synthesis to take place in pool 3. The use of the equations derived above can be illustrated by fitting the curves in Fig. 3 by sums of exponentials and then computing then model parameters.

The plasma specific activity of [¹⁴C]cholesterol (dpm/mg cholesterol) is fitted by a sum of three exponentials,

$$1116.5{\mathrm{e}}^{-0.1791\mathrm{t}}+414{\mathrm{e}}^{-0.04368\mathrm{t}}+180{\mathrm{e}}^{-0.00969\mathrm{t}}$$

and the plasma specific activity of [³H]cholesterol is fitted by a sum of three exponentials with the same rate constants:

$$497.4{\mathrm{e}}^{-0.1791\mathrm{t}}+67.31{\mathrm{e}}^{-0.04368\mathrm{t}}+290.6{\mathrm{e}}^{-0.00969\mathrm{t}}$$

The [¹⁴C]cholesterol activity arises from the injection of 20 µCi of [¹⁴C]cholesterol at time zero. The [³H]cholesterol activity arises from the injection of a ³H-labeled cholesterol precursor that is converted rapidly to 20 µCi of cholesterol. The exogenous cholesterol absorbed is 0.2 g/day.

In terms of the symbols used above, α₁ = 0.1791, α₂ = 0.04368, α₃ = 0.00969, A₁ = 1116.5, A₂ = 414, A₃ = 180, B₁ = 497.4, B₂ = 67.31, B₃ = 290.6.

The quantities a₂, a₁, a₀, d₂, d₁, and d₀ are computed from the relations in Equation 5; b₂, b₁, and b₀ are computed from the relations in Equation 8. These quantities are used to compute the model parameters using Equations 6 and 9. The results are as follows: M₁ = 25954 mg, R₀₁ = 1294 mg/d, k₂₂ = 0.0864/d, k₃₃ = 0.0176/d, R₂₁ = 1326.7 mg/d, R₃₁ = 714.3 mg/d, R₃₀ = 547 mg/d, R₂₀ = 0 mg/d, M₂ = 15355 mg, M₃ = 71665 mg.

Thus all the parameters of the three-pool model are estimated from two tracer curves.

Discussion

Equations 6 and 9 together contain expressions for all the parameters of the three-pool model for cholesterol turnover. It may be seen that the expressions above do not involve p, the amount of precursor injected. The quantity p has been eliminated using the fact that the areas under the specific activity-time curves are the same for the two tracers when normalized to the injected dose, since all degradation is from the pool whose specific activity is being observed (6). Thus a₀/cd₀, and b₀/pd₀, both equal l/R₀₁; so, p = cb₀/a₀. This elimination means that the precursor used need not be completely converted to cholesterol; it is also not necessary to know the exact amount injected.

There is one report in the literature (9) in which labeled precursors of cholesterol were used to explore body cholesterol turnover, and side-pool synthesis, in humans. In this work, Kekki et al. (9) injected seven subjects with cholesterol precursors, and examined plasma cholesterol specific radioactivity for varying periods thereafter. In two studies, the subjects were given labeled cholesterol and labeled mevalonate simultaneously. Unfortunately the two studies were of very short duration (42 and 64 days) while at least 140 days, and preferably 200–280 days, are necessary to be able to fit a three-pool model.

In five other studies, they used two precursors: labeled water and labeled mevalonate. In deriving Equation 7 above, it has been noted that the quantity p represents the dynamics of the precursor. For a precursor such as mevalonate whose incorporation into cholesterol is rapid, p is simply the amount of injected tracer converted to cholesterol. For a precursor such as water, p is replaced by the transform of the water specific activity time curve multiplied by the rate of conversion to cholesterol. Thus, the transforms for the two tracers differ only by a multiplicative factor unconnected with cholesterol kinetics. Hence, injection of two precursors does not lead to more information about cholesterol kinetics than injection of one alone (except in the sense of repeat measurements). As has been pointed out above, the injection of a precursor alone is insufficient to estimate all the model parameters; it is necessary to inject labeled cholesterol as well. Therefore, in the five studies in which Kekki et al. (9) injected two precursors, it is not possible to estimate the side-pool synthesis uniquely.

Due to the relatively short duration of their studies (approximately 8 weeks), Kekki et al. (9) used a two-pool model. The results discussed above hold for a two-pool model as well. The two-pool model has five unknown parameters (M₁, M₂, PR, R₂₀, and R₂₁). Kekki et al. (9) injected labeled mevalonate, which introduced a sixth unknown parameter—the fraction of dose incorporated into cholesterol. They carried out sterol balances concurrently which provided an estimate of production rate, PR, leaving five unknown parameters to be estimated from the plasma specific radioactivity data. But a sum of two exponentials has only four coefficients. Thus the injection of labeled mevalonate alone is not sufficient to estimate all the model parameters. The injection of labeled water leads to one additional (fifth) exponential parameter (the multiplicative factor referred to above) but introduces a seventh unknown parameter—the fraction of hydrogen in endogenous synthesis arising from the body water pool. Thus the injection of the second precursor does not help resolve the model ambiguity. Also, since the number of unknown parameters is just one more than what can be determined uniquely by their combined kinetic and sterol balance studies, it is sufficient to fix just one parameter and estimate the rest. The fixed parameter can be varied over its biologically possible values and the other parameters of the model estimated. In this way, it is possible to estimate ranges of possible values for the model parameters that are not uniquely determined from a single injection in a manner similar to what has been done for the three-pool model following the injection of labeled cholesterol (3–5). However, Kekki et al. (9) fixed two parameters: M₁ and the fraction of endogenous synthesis labeled (the fraction of endogenous synthesis that arises from the pool into which the precursor is injected; in the case of hydrogen, it is the fraction of the number of hydrogen atoms in cholesterol that are derived from water as compared with other sources). They then computed parameters that gave the best fit to the data at each of four combinations of values for the two fixed parameters. The combination that gave the best fit to the data was judged the most likely. This procedure was thought to resolve the nonuniqueness but, in fact, there were not enough data to resolve the nonuniqueness. If the authors had fixed one of the parameters instead of two, they would have obtained the same best fit at any value chosen for the fixed parameter. By fixing two parameters, it is even likely that the best fit obtained is not the best possible fit. Thus it appears that the data of Kekki et al. from precursor injections are insufficient to estimate side-pool synthesis. Instead, both labeled precursor and labeled cholesterol must be injected in order to resolve the model ambiguity.

It was assumed in the analysis of labeled precursor results that the fractions of precursor incorporated into the three pools (f₁, f₂, and f₃) are proportional to the corresponding synthesis rates. What is directly estimated from the data are not the relative synthesis rates in the three pools but rather the relative rates of incorporation of the precursor into the three pools. Berman (11) has described this problem in his discussion of model development for lipoprotein kinetics. Thus for a labeled precursor to be useful it must be incorporated at each synthetic site at a rate proportional to the rate of synthesis at that site.

In order to fulfill this criterion, the proximate precursor of cholesterol should have the same specific activity at all sites of synthesis. Others (12) have considered various conditions that could affect the specific activity of the precursor in different tissues such as rate of penetration of cell membranes, dilution with endogenous, unlabeled substrate, etc. Acetate does not meet these requirements (12). Although cholesterol synthesis in humans has been estimated by isotope kinetics of squalene after administration of labeled mevalonate (13), it is extremely unlikely that a method could be developed whereby administered labeled squalene itself would enter cells of all tissues that synthesize cholesterol at the same rate. Labeled octanoate has been shown to provide valid estimates of the absolute rates of cholesterol synthesis in both hepatic and extrahepatic tissues in studies in vitro (12). The possibility that octanoate might meet the requirements described here for in vivo studies would, however, require investigation and validation. Mevalonate has been widely used as a biosynthetic precursor for both qualitative and quantitative studies of cholesterol synthesis. Recent studies in both rats (14) and humans (15) have, however, demonstrated that plasma mevalonate is preferentially metabolized by the kidneys, particularly in females (15). The rat studies (14) indicate that, on the average, 64% of the total conversion of labeled plasma mevalonate to sterol occurs in the kidney. Thus the specific activity may be expected to be much higher in the kidneys than at other synthetic sites. The extent to which this problem might limit the usefulness of mevalonate as a precursor for the in vivo studies described here needs to be evaluated experimentally.

Tritium-labeled water would be a satisfactory labeled precursor if it can be shown that the number of hydrogen atoms in cholesterol derived from water has the same ratio to the total number of cholesterol hydrogen atoms at all synthetic sites. In other words, it must be shown that hydrogen atoms from water are not used preferentially for cholesterol synthesis in certain, as compared to other, tissues. Evidence that this is indeed the case has been obtained from in vivo studies in rats (16). These studies suggest that [³H]-water distributes rapidly, and is incorporated into cholesterol equally, at all synthetic sites. Unfortunately, since only a very small fraction of labeled water is incorporated into cholesterol, very large amounts of radioactivity must be administered in order to label plasma cholesterol effectively. Thus, Kekki et al. (9) administered 8 mCi of [³H]water to each of their study patients. Although this greatly limits the possible use of [³H]water for human investigation, it should, be possible to use [³H]water comparatively in animal studies to evaluate, and possibly validate, the use of a different precursor (e.g., octanoate, mevalonate) for in vivo studies.

Thus, while the simultaneous injection of labeled cholesterol and a labeled cholesterol precursor can lead to a unique determination of the extent of side-pool synthesis and the side-pool masses of cholesterol, there appears to be no precursor yet shown to satisfy the requirements set out above and to be suited to studies in humans. Until animal studies are able to help choose a satisfactory precursor for definitive studies, we suggest that the most appropriate way to analyze whole-body cholesterol turnover data would be to determine ranges of values for side-pool synthesis and side-pool masses, as has been done previously (3–5).

CONCLUSION

Equations have been derived for calculating all the parameters of a three-pool model following the injection of two tracers: labeled cholesterol and a labeled biosynthetic precursor of cholesterol. These equations can be used if a satisfactory precursor label is used along with a cholesterol label. The one reported study using a precursor suffers from the lack of the simultaneous injection of a cholesterol tracer. There is a need to perform animal studies to establish that an injected precursor is incorporated at each synthetic site in an amount proportional to the rate of synthesis at that site. Until a validated precursor is available, it is not possible to determine the side-pool masses uniquely; however, ranges of the masses can be calculated from plasma decay curves.

Abbreviations

PR

production rate

M₁, M₂, M₃

pool sizes

k

rate constant

R

rate of transfer of cholesterol mass

y

specific activity

Y

Laplace transform of specific activity