Direct Maximization of Protein Identifications from Tandem Mass Spectra

Abstract

The goal of many shotgun proteomics experiments is to determine the protein complement of a complex biological mixture. For many mixtures, most methodological approaches fall significantly short of this goal. Existing solutions to this problem typically subdivide the task into two stages: first identifying a collection of peptides with a low false discovery rate and then inferring from the peptides a corresponding set of proteins. In contrast, we formulate the protein identification problem as a single optimization problem, which we solve using machine learning methods. This approach is motivated by the observation that the peptide and protein level tasks are cooperative, and the solution to each can be improved by using information about the solution to the other. The resulting algorithm directly controls the relevant error rate, can incorporate a wide variety of evidence and, for complex samples, provides 18–34% more protein identifications than the current state of the art approaches.

The problem of identifying proteins from a collection of tandem mass spectra involves assigning spectra to peptides, using either a de novo or database search strategy, and then inferring the protein set from the resulting collection of peptide-spectrum matches (PSMs).¹ In practice, the goal of such an experiment is to identify as many distinct proteins as possible at a specified false discovery rate (FDR). However, most of the previous work in the context of shotgun proteomics analysis has focused on controlling error rates at the level of PSMs or peptides (1–11) rather than the protein level FDR.

This approach creates difficulties for estimating protein level FDRs because the PSM or peptide level error rate may be significantly lower than the protein level error rate, especially in the context of a deeply saturated experiment (12, 13). For example, consider a collection of 1000 spectra that map to 100 distinct peptides with a 1% false discovery rate. This 1% false discovery rate corresponds to 10 incorrectly mapped spectra, each of which is likely to map to a different, incorrect peptide. Thus, the PSM error rate of 1% corresponds to a peptide error rate of 10/110 = 9%. A similar inflation of error rate will occur if we move to the protein level.

In general, when the end goal is to find the optimal solution to a protein level problem, it is conceptually and practically beneficial to directly solve the problem of interest rather than artificially dividing the problem into two separate tasks. The two tasks of protein and peptide level optimization are closely related but are likely to have different optimal solutions. Moreover, many machine learning problems involving several subtasks have been shown to benefit from a top-down approach that solves several subtasks simultaneously, in contrast to solving each of them separately. For example, the handwritten document recognition task involves a variety of intermediate problems including extraction of the field of interest, segmentation into characters, and character recognition. An algorithm that combines all the subtasks into a top-down optimization problem substantially outperforms algorithms that treat these subtasks as distinct modules (14). Similarly, object recognition (on photographs, for example) involves defining a hierarchy of features in the image such as edges, motifs, and objects before training an object classifier. Systems that introduce learning of the features in conjunction with classification give superior results in comparison with methods that involve hand-crafted feature generation before training a classifier (15). Such object recognition “end-to-end” learning systems have been used successfully in diverse tasks ranging from building obstacle avoidance systems for mobile robots (16) to segmentation problems in brain imaging (17, 18). Finally, in natural language processing, determining whether a sentence is grammatically and semantically correct involves several intermediate steps, such as predicting part of speech tags, entity tags, semantic tags, etc. An approach that seeks to optimize all of these tasks simultaneously, while avoiding task-specific engineering, performs as well as or better than all of the individual benchmarks for each subtask (19, 20).

In this work, we demonstrate that inferring proteins from peptide-spectrum matches is another example of a problem that benefits from the top-down approach. We describe a machine learning method to optimize directly the desired quantity, the total number of proteins identified by the experiment. We use a target decoy search strategy, searching each spectrum against a database of real (target) peptides and reversed (decoy) peptides. We then train a supervised learning algorithm to induce a ranking on the combined set of target and decoy proteins, learning the parameters of the model so that the top of the ranked list is enriched with target proteins. Compared with existing methods (21–24), the direct approach offers several advantages. First, by formulating an optimization problem that operates at the protein level, our approach correctly controls the relevant error rate. Second, we exploit the structural properties of the problem to optimize PSM, peptide, and protein level tasks simultaneously, and we demonstrate that these tasks are cooperative such that each task benefits from the solution to the other during optimization. Finally, our approach does not filter any PSMs at any stage of the analysis, with the motivation that even low scoring PSMs can carry information about the presence of a protein when considered in the context of other PSMs belonging to this protein.

EXPERIMENTAL PROCEDURES

Description of the Problem

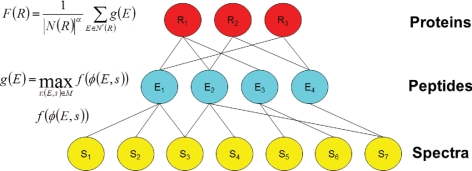
The protein identification problem can be represented as a tripartite graph, with layers corresponding to spectra, peptides, and proteins (Fig. 1). An edge from a spectrum to a peptide indicates that the database search procedure assigned a high score to the peptide. In general, more than one spectrum may be assigned to a single peptide. It is also possible to consider more than one high scoring match for each spectrum, as we do in our analysis. An edge from a peptide to a protein implies that the peptide occurs in the protein. This peptide-to-protein mapping is many-to-many because each protein contains multiple peptides, and each peptide may appear in more than one protein. The input to the problem is the tripartite graph, with a fixed set of features assigned to each peptide-spectrum match. In this work, we represent each PSM using 17 features (Table I) that collectively describe properties of the spectrum and of the peptide, as well as the quality of the match between the observed and theoretical spectra. The desired output is a ranking on proteins, with proteins that are present in the sample appearing near the top of the ranked list.

Fig. 1.

Barista. The tripartite graph represents the protein identification problem, with layers corresponding to spectra (gold), peptides (blue), and proteins (red). Barista computes a parameterized nonlinear function f(·) on each PSM feature vector φ(e,s). The score assigned to a peptide is the maximum PSM score associated with it. The score assigned to a protein is a normalized sum of its peptide scores.

Table I. Features used to represent PSMs.

Each PSM obtained from the search is represented using 17 features. These are the same features used by Percolator, except that three features were removed. These three features—for example, the number of other spectra that match to the same peptide—capture properties of the entire collection of PSMs. We removed them to ensure complete separation between the training set and the test set.

1	XCorr	Cross-correlation between calculated and observed spectra
2	ΔCn	Fractional difference between current and second best XCorr
3	ΔCnL	Fractional difference between current and fifth best XCorr
4	Sp	Preliminary score for peptide versus predicted fragment ion values
5	ln(rSp)	The natural logarithm of the rank of the match based on the Sp score
8	Mass	The observed mass [M + H]+
6	ΔM	The difference in calculated and observed mass
7	abs(ΔM)	The absolute value of the difference in calculated and observed mass
9	ionFrac	The fraction of matched b and y ions
10	ln(NumSp)	The natural logarithm of the number of database peptides within the specified m/z range
11	enzN	Boolean: Is the peptide preceded by an enzymatic (tryptic) site?
12	enzC	Boolean: Does the peptide have an enzymatic (tryptic) C terminus?
13	enzInt	Number of missed internal enzymatic (tryptic) sites
14	pepLen	The length of the matched peptide, in residues
15–17	charge1–3	Three Boolean features indicating the charge state

We solve the protein identification problem using a target decoy training strategy. Decoy databases have been used in shotgun proteomics for two complementary purposes: 1) to provide false discovery rate estimates for peptide identifications (1, 3, 25) and 2) to learn to discriminate between correct and incorrect PSMs produced by a database search algorithm (26–28). In the current work, we produce a decoy database by reversing the amino acids in each target protein. We then merge the target and decoy databases, and we search each spectrum against the combined target decoy database, retaining a fixed number of top scoring peptides for each spectrum. For the purposes of training our ranking function, the target proteins are labeled as positive examples, whereas decoy proteins are labeled as negative examples.

Barista Model

We are given a set of observed spectra S = {s₁,…, s_NS} and a database D of target and decoy proteins against which we perform a database search. The search produces a set of PSMs. Denoting the set of peptides as E = {e₁,…, e_NE}, the PSMs are written as tuples (e_i,s_j) ∈ M, each representing a match of peptide i to spectrum j. Note that, in general, we may opt to retain the single best scoring peptide for each spectrum, or a small constant number of top-ranked PSMs per spectrum. Each of the identified peptides e_k belongs to one or more proteins, leading to a set of proteins R = {r₁,…, r_NR} that cover the set of peptides. Thus, R includes every protein in D that has at least one identified peptide (i.e. the maximal set of proteins that can explain the observed spectra).

For our algorithm, we define a feature representation φ(e,s) ∈ R^d for any given PSM. Our particular choice for this feature representation, which is described in Table I, contains a variety of scores of the quality of the peptide-spectrum match, as well as features that capture properties of the spectrum and properties of the peptide.

The Barista model consists of three score functions, defined with respect to PSMs, peptides, and proteins (Fig. 1).

PSM Score

We define the score of a PSM to be a parameterized function of its feature vector φ(e,s). Previous work, such as PeptideProphet (5) and Percolator (26), used a family of linear functions of the following form,

where w ∈ R^d. We chose a family of nonlinear functions given by two-layer neural networks,

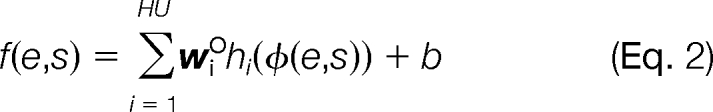where w^O ∈ R^HU are the output layer weights for the hidden units (HU), and h_k(φ(e,s)) is the k^th hidden unit, defined as follows,

where w_k^H ∈ R^d and b_k ∈ R are the weight vector and threshold for the k^th hidden unit. The number of HU is a hyperparameter that can be chosen by cross-validation. This nonlinear function is the improved model used in Q-ranker (27). Throughout this work, we use a fixed value of three hidden units. In preliminary experiments, we observed that three or four hidden units provided approximately the same performance, whereas using five hidden units led to evidence of overfitting.

Peptide Score

Because a single peptide can have several spectra matching to it (several PSMs), we define the score of a peptide as the maximum score assigned to any of its PSMs,

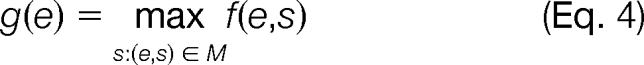where (e,s) ∈ M is the set of PSMs assigned to peptide e. We take the maximum over the PSMs for each peptide because of the argument presented in (21), that many spectra matching the same peptide are not an indication of the correctness of the identification.

Protein Score

Finally, the score of a protein is defined in terms of the scores of the peptides in that protein as follows,

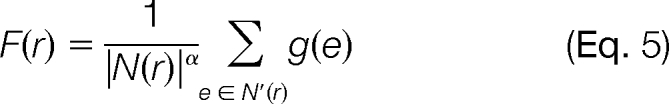where N(r) is the set of predicted peptides in protein r assuming enzymatic cleavages, N′(r) is the set of peptides in the protein r that were observed during the MS/MS experiment, and α is a hyperparameter of the model. The set N(r) is created by virtually digesting the protein database D with the protease used to digest the protein mixture for the mass spectrometry experiment. We require that the predicted peptides have lengths in the range of 6–50 amino acids. We do not allow internal cleavage sites in the peptides, with the motivation that we are trying to create an idealized model, where the digestion went to completion. Alternatively, the normalization factor could be treated as a trainable parameter of the model, although we did not attempt to do so in this work.

Barista uses the predicted number of peptides, rather than the number of observed peptides as a normalization factor, because the predicted peptide number implicitly supplies an additional piece of information: how many peptides appear in the protein but have not been matched by any spectrum. This information allows Barista to penalize longer proteins, which are more likely to receive random matches during the database search procedure.

Setting α = 1 penalizes linearly, whereas setting α < 1 punishes larger sets of peptides to a lesser degree. In our experiments, we use the fixed value α = 0.3, after selecting it in validation experiments (supplemental Fig. 6).

Training the Model

Barista learns a protein score function that performs well on the target decoy training task. For each protein r_i ∈ D, we have a label y_i ∈ ±1, indicating whether it is a target (positive) or decoy (negative). Given our set of proteins R and corresponding labels y, the goal is to choose the parameters w of the discriminant function F(r), yielding Equations 6 and 7.

To find F(r), we search for the function in the family that best fits the empirical data. The quality of the fit is measured using a loss function L(F(r_i), y_i), which quantifies the discrepancy between the values of F(r_i) and the true labels y_i. We train the weights w using stochastic gradient descent with the hinge loss function (29).

During training, the gradients δL(F(ri), y_i)/δw of the loss function are calculated with respect to each weight w, and the weights are updated. After convergence, the final output is a ranked list of proteins, sorted by score. The training procedure is summarized in Algorithm 1. During training, the weights of the neural network that define the PSM score function are optimized, because the PSM score is part of the protein score calculation. These weights are the only adjustable parameters of the learning task.

Algorithm 1 Training Barista
Input: labeled proteins (ri, yi)
repeat
Pick a random protein (ri, yi)
Compute F (ri) given by Equation 1.
if 1 − yF (ri) > 0 then
Make a gradient step to optimize L(F (ri),yi)
end if
until convergence.

Peptide Level and PSM Level Optimization

In this work, we also report results for peptide and PSM level training. For peptide ranking, we use a similar procedure to the protein level training: we pick a peptide example, e_i, and we assign this peptide a label based on the target/decoy labels of the corresponding proteins. We then make a gradient step to optimize the hinge loss function on the peptide level: L_pep(g(e_j), y_j) = max (0,1 − y_jg(e_j)). Similarly, for PSM level training, we optimize the hinge loss function at the PSM level: L_PSM = max (0,1 − y_jf(φ(e_j,s_i))).

Out-of-Sample Testing

In any supervised learning procedure, we must ensure that the data used to train the model is kept apart from the data used to test the model. Therefore, to produce a protein ranking for a given data set, we use a procedure that trains and tests a collection of models. First, we identify connected components in the given tripartite graph, and we subdivide the graph into n approximately equally sized tripartite graphs, ensuring that no edges are eliminated in the process. We then train a model using n − 1 of the subgraphs as a training set and one subgraph as the test set, and we repeat this train/test procedure using each subgraph as one test set. In the end, we merge the scored proteins from the various test sets, yielding a ranking on the entire set of proteins.

The Barista software, which implements this cross-validated train/test procedure, is available as part of the Crux software toolkit (available online).

Reporting Results

When reporting the set of proteins identified by Barista, we eliminate all redundant proteins that are not necessary to explain the spectra, as described in Ref. 23. Specifically, for every protein A, we merge into a single meta-protein all the proteins B_i such that B_i ⊆ A in terms of their observed peptide sets, and we report only A. For degenerate peptides—peptides that appear in several proteins—Barista produces a parsimonious solution, assigning these peptides in a greedy fashion to a single meta-protein that contains it.

In addition, for the purposes of comparison with ProteinProphet, we used the ProteinProphet method to generate all of the plots in the paper. We considered only proteins that received ProteinProphet probability greater than zero, thereby ignoring proteins with probabilities artificially set to zero by the ProteinProphet parsimony procedure. For the resulting set of proteins, we then assigned Barista scores and sorted them based on Barista scores or ProteinProphet probabilities. The Barista scores were assigned based on the parsimony rules above.

Statistical Confidence Estimates

Throughout this work, we use the q value (30) as a statistical confidence measure assigned to each PSM. If we specify a score threshold t and refer to PSMs with scores better than t as accepted PSMs, then the FDR is defined as the percentage of accepted PSMs that are incorrect (i.e. the peptide was not present in the mass spectrometer when the spectrum was produced). The q value is defined as the minimal FDR threshold at which a given PSM is accepted. Note that the q value is a general statistical confidence metric that is unrelated to the Qscore method for evaluating SEQUEST results (1).

We calculate q values by using decoy PSMs (3). Denote the scores of target PSMs f₁, f₂,…, f_mf and the scores of decoy PSMs d₁, d₂,…, d_md. For a given score threshold, t, the number of accepted target PSMs (positives) is P(t) = |{f_i > t; i = 1,…, m_f }| and the number of accepted decoy PSMs (negatives) is N(t) = |{d_i > t; i = 1,…, m_d}|. We can estimate the FDR at a given threshold t as follows.

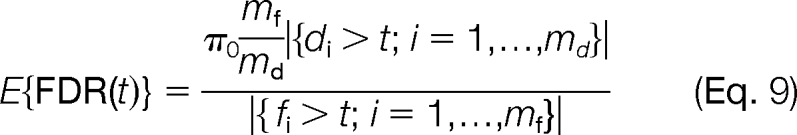The q value assigned to score f_i is then as shown in Equation 10.

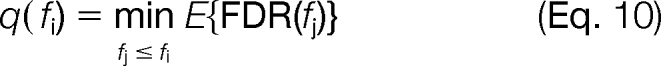Data Sets

We analyzed six different data sets derived from three organisms: yeast, Caenorhabditis elegans, and human. These data sets were previously described in Refs. 26 and 31. For all of the data sets, the peptides were assigned to spectra using the Crux implementation (version 1.3) of the SEQUEST algorithm (32), with partial enzyme specificity, a fixed carbamidomethylation modification of 57 Da to cysteine, no variable amino acid modifications, and mass tolerance for fragment ions of ±3 Da. The cleavage sites for trypsin, chymotrypsin, and elastase were set to KR↓P, FHWYLM↓P, and LVAG↓P, respectively. The search was performed against a concatenated target decoy database for each organism, composed of all available open reading frames and their reversed versions. The top three PSMs were retained for each spectrum for further analysis.

We also repeated the search on four of the data sets—yeast digested with trypsin, C. elegans, and human—with two variable modifications enabled. The modifications included oxidation of methionine (molecular mass, 15.9949 Da) and phosphorylation of S/T/Y (molecular mass, 79.95682 Da).

The first data set consists of spectra acquired from a tryptic digest of an unfractionated yeast lysate and analyzed using a 4-h reverse phase separation. The spectra were searched against a protein database consisting of the predicted open reading frames from Saccharomyces cerevisiae (released February 4, 2004, 6298 proteins). The database search on this data set resulted in 209,115 PSMs, yielding a protein data set of 13,013 proteins total: 6527 targets and 6486 decoys. The next two data sets were derived in a similar fashion from the same yeast lysate but treated using different proteolytic enzymes, elastase, and chymotrypsin. The database search against them resulted in 173,580 and 180,651 PSMs, respectively, and produced data sets of 12,930 proteins (6470 targets and 6460 decoys) and 12,865 proteins (with 6425 targets and 6440 decoys). The fourth data set is derived from a C. elegans lysate digested by trypsin and processed analogously to the tryptic yeast data set. The worm data set was derived from a 24-h MudPIT analysis of C. elegans proteins containing 207,804 spectra, from which 10,000 spectra were randomly sampled. These spectra were searched against a protein database consisting of the predicted open reading frames from C. elegans and common contaminants (Wormpep v160, 27,499 proteins). This set produced 138,297 PSMs, which resulted in the protein set of 40,117, with 20,240 targets and 19,877 decoys. Finally, the fifth and sixth data sets consisted of tryptically digested human tissue lysates, derived from amniotic fluid and gastric asperates. The human protein database consisted of 76,588 proteins, downloaded from online. These spectra received 725,937 and 621,600 PSMs, respectively, which resulted in protein data sets of 139,996 (with 70,055 targets and 69,941 decoys) and 138,524 (with 69,327 targets and 69,197 decoys).

Defining a Gold Standard Based on External Data Sets

For the validation of our results against independent experimental assays, we used protein sets identified by mRNA (33) and protein tagging experiments (34). The following thresholds were applied to the data sets: 1) all 1053 proteins whose mRNA copy count was higher than the average copies/cell counts were considered present according to the microarray experiments, and 2) all 527 proteins detected by both GFP (green fluorescent protein) and TAP (a specific antigen) with intensity above average intensity were considered present according to the protein tagging experiment. The intersection of these sets, consisting of 391 proteins, was used in the validation experiments.

For all of the target proteins in the yeast data sets, a protein was considered a true positive if it was present among the 391 proteins in the validation set and was considered a false positive otherwise. The ranking of proteins was induced based on Barista scores or ProteinProphet probabilities, and the receiver operating characteristic curves were generated based on this ranking. The same set was used to validate the proteins identified only by Barista and only by ProteinProphet presented in supplemental Table 2. In addition, the sets of proteins confirmed by mRNA and tagging experiments were used separately to validate the ranking results of Barista and ProteinProphet in supplemental Fig. 4.

RESULTS AND DISCUSSION

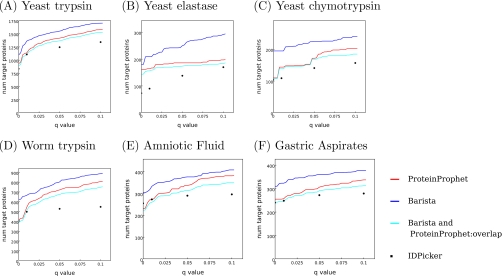
We compared ProteinProphet (21), IDPicker 2.0 (23, 35), and Barista using the six data sets described above. Fig. 2 demonstrates that Barista successfully identifies more target proteins than ProteinProphet and IDPicker across a wide range of false discovery rates and across all six data sets. For example, at an FDR threshold of 1%, Barista identifies 18% more proteins than ProteinProphet (1347 compared with 1138) and 20% more than IDPicker (1347 compared with 1125) for the “yeast trypsin” data set. On the human amniotic fluid and gastric aspirates data sets, Barista identifies 25% and 26% more proteins, respectively, than ProteinProphet (336 compared with 265 and 323 compared with 255) and 25% and 30% more than IDPicker (336 compared with 267 and 323 compared with 248; see supplemental Table 1 for details). ProteinProphet does not support training a model on one data set and then applying the trained model to a separate data set; therefore, to allow a fair comparison of algorithms, the results in Fig. 2 are based on training and testing on the entire data set. However, supplemental Figs. 1 and 2 demonstrate that, even when we split the data into four equal parts and train on only three-quarters of the data, Barista still performs better on the held out test set than ProteinProphet in nearly every case. Furthermore, supplemental Figs. 1 and 2 provide evidence that Barista is not overfitting the training set, because the performance on the test set is similar to the performance on the training set. Finally, we confirmed that enabling variable modifications during search does not affect the relative performance of the methods that we evaluated (see supplemental Fig. 3 for details).

Fig. 2.

Comparison of ProteinProphet, IDPicker, and Barista performance on sample data sets. A–F plot the number of target proteins as a function of q value threshold for three protein identification methods. The cyan series indicates the degree of overlap between proteins identified by Barista and ProteinProphet. All of the results are reported with respect to the set of proteins that received probabilities greater than 0 from ProteinProphet.

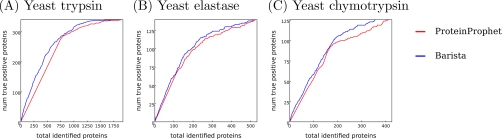
In addition to target decoy validation, we compared the ability of ProteinProphet and Barista to recover proteins that had been identified in log phase growing yeast cells using alternative experimental methods. For this purpose, we gathered a set of 391 proteins whose presence in yeast cells during log phase growth is supported by three independent assays: 1) mRNA counts established by microarray analysis (33), 2) incorporating antigen specific tags into the yeast ORFs and detecting the expression of the resulting protein with an antigen, and 3) incorporating the sequence of green fluorescent protein into the yeast ORFs and detecting the resulting fluorescence (34). For all of the target proteins in the yeast data sets, a protein was considered a true positive if it was present among the 391 proteins in the validation set. Fig. 3 shows that, across the three yeast data sets, the ranked list of proteins in Barista is more highly enriched with these externally validated proteins than that in ProteinProphet.

Fig. 3.

Comparison of ProteinProphet, IDPicker, and Barista against independent experimental assays. All of the results are reported on the set of proteins that received probabilities greater than 0 from ProteinProphet. Each panel plots for Barista and ProteinProphet the number of true positive proteins as a function of the total number of identified proteins, where true positive proteins are those confirmed by alternative experimental methods, as described in the text.

We also used the abundance levels assigned to the proteins measured by Western blot and GFP tagging experiments (34) to investigate the extent to which Barista scores correlate with protein abundance. Supplemental Fig. 4 shows that when target proteins at FDR threshold of 1% are ranked by Barista score, the top of the list is enriched with high abundance proteins.

To better understand the relationship between the proteins identified by ProteinProphet and Barista, we computed the overlap between the sets of proteins identified as true positives by the two methods at a range of false discovery rates (the cyan series in Fig. 2). For all six data sets, ProteinProphet and Barista identify many of the same proteins. We further investigated the composition of the nonoverlapping sets in the yeast data sets identified by ProteinProphet and Barista at FDR threshold of 1% by checking them against the proteins identified by the alternative experimental methods described above. For trypsin-digested yeast, the percentage of nonoverlapping proteins also identified by the alternative experimental methods was 32% for Barista and 11% for ProteinProphet. For elastase, these percentages were 71 and 58%, respectively, and for chymotrypsin, they were 80 and 78%. Thus, on these data sets, the external validation more strongly supports the Barista identifications than the ProteinProphet identifications (see supplemental Table 2 for further details).

Next we investigated proteins identified by ProteinProphet and Barista in the human tissue data sets. A previous study of these data sets (31) determined that amniotic fluid and gastric aspirates collected at birth express essentially the same proteins but that the abundance of a few proteins varies significantly between the two tissues. We focused on a group of homologous proteins containing tubulin β, one of the proteins shown to have significant abundance differences between the gastric aspirates and amniotic fluid. This protein group was identified with high confidence by both ProteinProphet (probability > 0.99) and Barista (FDR < 1%) in the gastric aspirate sample. However, in the amniotic fluid sample, the tubulin β protein was identified with high confidence (FDR < 1%) only by Barista; ProteinProphet assigned this group a low probability of 0.3. Given that the same proteins tend to be present in both samples and given that both methods agree that this protein group is present in one sample, it seems likely that the “present” call in Barista for the amniotic fluid sample is correct.

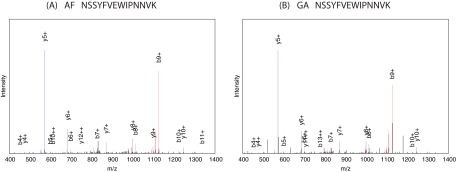
Further investigation of this identification showed that tubulin β was confidently identified by Barista in the amniotic fluid sample based primarily on a single high scoring peptide with amino acid sequence NSSYFVEWIPNNVK. One other peptide received a positive score very close to 0 and therefore made a negligible contribution to the overall protein ranking. The rest of the peptides received negative scores that did not contribute to the overall positive score of the protein. Fig. 4A shows the spectrum that matched to NSSYFVEWIPNNVK. Note that the high intensity y5+ and b9+ peaks result from ions formed from the cleavage N-terminal to proline, which is known to result in high peaks. In addition, this peptide belongs uniquely to the group of homologous proteins containing tubulin β and therefore unambiguously identifies this group.

Fig. 4.

Same peptide contributed to identification of tubulin β in amniotic fluid and gastric aspirates. A, the annotated spectrum that matches the +2 charged peptide NSSYFVEWIPNNVK in the amniotic fluid. B, the annotated spectrum that matches the +2 charged peptide NSSYFVEWIPNNVK in the gastric aspirates. The peaks colored in red are b-ions and the neutral losses associated with the b-ions; the peaks colored in blue are y-ions and the neutral losses associated with the y-ions. However, b-ions and y-ions are annotated. (The high peak near b9+ (at m/z 1126.38) in B occurs at m/z 1127.35, i.e. within the 1-Da range.)

Finally, in further support of this identification, we exploit the fact that tubulin β was confidently identified in gastric aspirates by both ProteinProphet and Barista and that the peptide sequence NSSYFVEWIPNNVK contributed to the identification in this other tissue. We compared the spectra responsible for the peptide sequence identification NSSYFVEWIPNNVK in gastric aspirates (Fig. 4B) and for the same peptide sequence identification in amniotic fluid (Fig. 4A), and verified that these spectra contain most of the major peaks in common. We also include in supplemental Fig. 5 two other confident peptide assignments that permitted the identification of the tubulin β group in gastric aspirates by both ProteinProphet and Barista, thereby confirming the tubulin β identification in gastric aspirates and, by extension, in the amniotic fluid.

Because all but a single identified peptide received either negative scores or scores close to zero in the Barista model, the identification of tubulin β in the amniotic fluid was essentially a single hit, because it was based on one high scoring peptide. This example suggests that Barista is less biased against proteins with a single good identification than ProteinProphet, which penalizes the tubulin β protein group more stringently for the presence of peptides with low probability scores. The validity of this identification by Barista agrees with recent evidence that requiring at least two peptides per protein unnecessarily eliminates many true identifications (36).

In general, basing a protein identification on a single peptide identification can introduce a risk of false positives. Nonetheless, Barista is able to successfully identify some “one-hit wonder” proteins based on a single high scoring peptide because the Barista model normalizes the protein score by the total number of peptides occurring in the protein. Consequently, Barista favors one-hit wonders on proteins of shorter lengths. To give an example, we compared the number and the average lengths of single-hit proteins in the amniotic fluid and in the gastric aspirates that were identified by Barista at FDR threshold 1% with the single-hit proteins identified by ProteinProphet at the same confidence level. For ProteinProphet, which uses only peptides with probability greater than 0.05 for protein identification, the proteins identified based on a single peptide were considered one-hit wonders for the purposes of this comparison. For Barista, which does not discard low quality peptides even if they received negative scores, we count the proteins with a single positively scoring peptide as one-hit wonders. Although Barista identifies slightly more single-hit proteins than ProteinProphet in both amniotic fluid (6% versus 3%) and gastric aspirates (5% versus 3%), the proteins identified by Barista have on average shorter lengths. In the amniotic fluid, the average length of Barista single-hit proteins is 138 in comparison with the average length of 236 of the one-hit wonders identified by the ProteinProphet. Similarly, in the gastric aspirates, the single-hit proteins identified by Barista have an average length of 272, in comparison with the average length of 506 of the single-hit proteins identified by the ProteinProphet. Thus, by normalizing with respect to the total number of peptides in the protein, Barista successfully discards long, single-hit proteins and retains short, single-hit proteins.

Thus far, Barista focused on optimizing a single value: the number of proteins identified from a shotgun proteomics experiment. This approach contrasts with previous applications of machine learning to this task (5, 26, 27, 37, 38), which optimize at the level of PSMs or peptides. In general, focusing on one optimization target or the other will depend on the goal of the proteomics experiment. However, in some applications, it may be desirable to simultaneously achieve high levels of peptide and protein identification. Because the Barista model involves training peptide level and PSM level scoring functions as a part of the protein level optimization, we can measure the performance of Barista separately on the peptide or PSM identification task. Moreover, we can adapt the algorithm to optimize directly on the peptide or PSM levels (see “Experimental Procedures” for details).

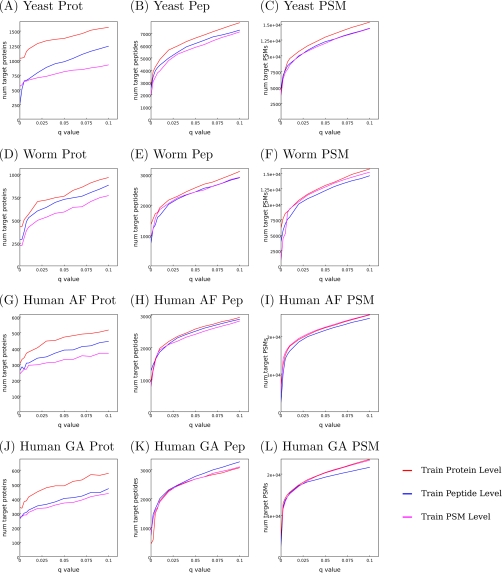
Fig. 5 compares the performance of three variants of Barista, optimizing at the PSM, peptide, or protein level. All three methods are evaluated at the PSM, peptide, and protein levels on the yeast and worm and two human tissue data sets digested with trypsin.

Fig. 5.

Comparison of optimization at the protein, peptide, and PSM levels. Three types of optimization: protein level (red lines), peptide level (blue lines), and PSM level (magenta lines), were performed. The results were measured on the training and testing sets at the protein level (A, D, G, and J), peptide level (B, E, H, and K), and the PSM level (C, F, I, and L). The plots show number of target proteins/peptides/PSMs as a function of q value threshold.

The results demonstrate that performing protein level optimization gives as good results in terms of peptide and PSM identification as the direct peptide level and PSM level optimizations. These results indicate that the protein, peptide, and PSM level optimization tasks are cooperative; hence, the solution to one of the tasks may potentially be improved when given access to information about the solution to the other task. This cooperativity is not particularly surprising because, for example, the protein ranking task introduces higher level information about the scores of all peptides belonging to the same protein. Therefore, even if the goal of the experiment is to optimize peptide identifications, it is feasible to accomplish this task by also optimizing the protein level task.

From a general optimization perspective, the main advantage of the protein level training is that it makes more efficient use of available data. The three optimization tasks—protein, peptide, and PSM level optimization—are closely related but are likely to have different optimal solutions. Fig. 5 (A, D, G, and J) demonstrates that when the end goal is to find the optimal solution to the protein level task, it is clearly beneficial to directly solve the problem of interest.

Many algorithms designed for inferring a set of proteins from a collection of PSMs divide the problem into two stages: assessing the quality of the PSMs and then inferring the protein set (21–24). We claim that subdividing the protein identification problem in this fashion results in a significant loss of information during the second stage of the analysis. For example, typically only a subset of spectra are assigned to a peptide during the peptide identification stage, so information about the unassigned spectra is not available to the protein identification algorithm. Also, if at most one peptide is assigned to each spectrum, and if for a particular spectrum that assignment happens to be incorrect, then information about the second-ranked, possibly correct peptide is not available during the protein identification stage. Finally, if the quality of the match between a peptide and a spectrum is summarized using a single score, such as the probability assigned by PeptideProphet, then detailed information about precisely how the peptide matches the spectrum is lost. In contrast, the machine learning approach described here directly optimizes the number of identified proteins, taking into account all available information to obtain the best possible result.