Common-Mode Differential-Mode (CMDM) Method for Double-Nuclear MR Signal Excitation and Reception at Ultrahigh Fields

Abstract

Double-tuned radio-frequency (RF) coils for heteronuclear mangentic resonance (MR) require sufficient electromagnetic isolation between the two resonators operating at two Larmor frequencies and independent tuning in order to attain highly efficient signal acquisition at each frequency. In this work, a novel method for double-tuned coil design at 7T based on the concept of common-mode differential-mode (CMDM) was developed and tested. Common mode (CM) and differential mode (DM) currents exist within two coupled parallel transmission lines, e.g., microstrip lines, yielding two different current distributions. The electromagnetic (EM) fields of the CM and DM are orthogonal to each other, and thus, the two modes are intrinsically EM decoupled. The modes can be tuned independently to desired frequencies, thus satisfying the requirement of dual-frequency MR applications. To demonstrate the feasibility and efficiency of the proposed CMDM technique, CMDM surface coils and volume coils using microstrip transmission line for ¹H and ¹³C MRI/MRSI were designed, constructed, and tested at 7T. Bench test results showed that the isolations between the two frequency channels of the CMDM surface coil and volume coil were better than −30 and −25 dB, respectively. High quality MR phantom images were also obtained using the CMDM coils. The performance of the CMDM technique was validated through a comparison with the conventional two-pole design method at 7T. The proposed CMDM technique can be also implemented by using other coil techniques such as lumped element method, and can be applied to designing double-tuned parallel imaging coil arrays. Furthermore, if the two resonant modes of a CMDM coil were tuned to the same frequency, the CMDM coil becomes a quadrature coil due to the intrinsic orthogonal field distribution of CM and DM.

I. Introduction

Heteronuclear (e.g., ³¹P [1]–[9], ¹³C [8], [10]–[17], ²³Na [18]–[25], ¹⁹F [26], [27], and ¹⁷O [28]–[30]) MR spectroscopy and spectroscopic imaging has been playing an important role in investigation of metabolism and physiological changes in vivo. Heteronuclear MRS/MRSI has been widely used for noninvasive studies of bioenergetics [6], [8], [9], metabolism [1]–[3], [7], [10], [11], [13], [16], stroke [25], myocardial infarction [4] and cellular physiology [12], [17], drug dynamics and delivery [5], [26], [27] and direct detection of cerebral metabolic rate of oxygen [28]–[30]. However, the low sensitivity of the heteronuclei (mainly due to their low natural abundance) significantly limits performance, especially for in vivo applications. With the advent of ultrahigh field MR [31]–[36] and commercial hyperpolarizers, sensitivity of heteronuclear MR can be significantly improved, resulting in greatly improved noninvasive imaging tools for biomedical research with both higher spatial resolution and higher temporal resolution than previously. In particular, by using the ¹³C hyperpolarization methods with > 50 000 fold sensitivity enhancement in vivo [37]–[41], it becomes possible to observe key cellular bioenergetic processes in vivo by ¹³C MR. A major challenge of implementing heteronuclear MRS/MRSI, particularly at ultrahigh fields, is the design of efficient double-tuned radio-frequency (RF) coils [42]–[49] to optimally detect subtle MR signals from heteronuclei. Heteronuclear MR requires double-tuned RF coils which operate at usually proton Larmor frequency and the lower heteronucleus Larmor frequency. In such double-tuned RF coils, the proton channel is necessary for performing B₀ shimming and anatomic image acquisitions which would be used for correlating the metabolic information collected using the heteronuclear channel. For in vivo heteronuclear MR studies, it is essential for the double-tuned RF coils to have sufficient electromagnetic isolation between the two channels and independent tuning at each frequency, in addition to high quality factors (Q-factors), so that highly efficient acquisitions can be attained. The cross-talk between the two channels is one of the major factors that degrade the capability of detection of the already small signal intensity of heteronuclei in vivo, ultimately reducing the MR sensitivity and thus imaging resolution. The two-pole circuit method is one of important techniques for double-tuned RF coil designs [43]. This method is easy to implement and is particularly suitable for double-tuned surface coil designs. The two-pole circuit is also used to design resonant elements in double-tuned volume coils [50]. Trap circuits [48], [49] and 4-ring schemes [46] have been proposed for double-tuned operation of birdcage type volume coils. The technique of alternately positioning proton and heteronuclear elements has also been employed in designing double-tuned volume coils [47], [51].

In this work, we propose a new method using the common-mode and differential-mode (CMDM) technique to design double-tuned RF coils for heteronuclear MR applications. In a resonator that supports common mode (CM) and differential mode (DM), the EM fields of the two modes are orthogonal to each other and are intrinsically EM decoupled [52], [53]. The resonant frequencies of the common mode and the differential mode can be controlled independently and tuned to the desired values to satisfy the requirement of heteronuclear MR applications. The CMDM resonators can be realized by using many different approaches, such as lumped elements and transmission lines. To validate the proposed CMDM design method, double-tuned CMDM surface coils and volume coils were designed and constructed for ¹³C/¹H MR applications at 7T. All the CMDM coils in this work were realized by using microstrip transmission line method which has been proven to be advantageous for ultrahigh field RF coil designs with high frequency operation capability, high quality factor, reduced radiation losses and improved MR sensitivity [54]–[62]. The resonant frequencies and B₁ field distributions of the double-tuned CMDM surface coils and volume coils at 7T were numerically analyzed using the finite difference time domain (FDTD) algorithm [63]–[66]. Proton images and ¹³C spectroscopic images of a phantom were acquired using the double-tuned CMDM surface coil and volume coil at 7T to investigate the feasibility of the proposed CMDM method for designing double-tuned RF coils for heteronuclear MR applications.

II. Materials and Methods

A. Microstrip CMDM Surface Coil Design

Prior to building the CMDM surface coil, we established a model to numerically analyze the CMDM structure by using the finite-difference time-domain (FDTD) algorithm in terms of the reflection coefficient S₁₁, the transmission coefficient S₁₂, and the resonant frequencies and the magnetic field distributions of the CM and DM. Based on the FDTD simulation results on the capacitance of the termination capacitors, the resonator dimensions and the substrate thickness, the double-tuned CMDM surface coil was designed and constructed for 7T. Bench tests and MR experiments were conducted to fine tune the coil and evaluate its performance.

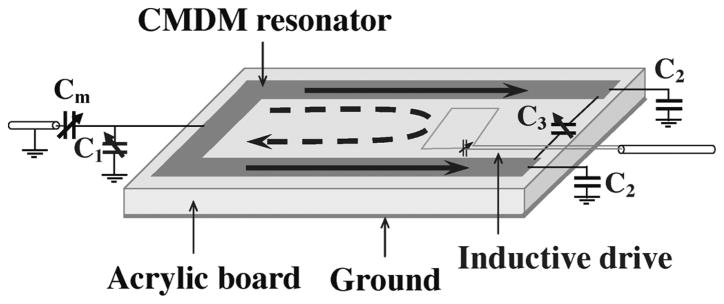
In the simulation, the software XFDTD 6.4 (Remcom, State College, PA) was used to build the model of the double-tuned CMDM surface coil shown in Fig. 1 and to perform all the FDTD numerical calculations. The CMDM coil was modeled as an 89-mm-long and 32-mm-wide split microstrip resonator. The permittivity of the substrate of the microstrip CMDM resonator was set to 2.62, which is the permittivity of the acrylic board used in building the prototypes. The strip conductor with a width of 6.3 mm and ground plane were modeled as a thin copper foil. The two ends of the strip conductor were connected through a variable capacitor (i.e., C₃ in Fig. 1) to support the differential mode. By connecting termination capacitors (i.e., C₁ and C₂ in Fig. 1) at both ends of the microstrip conductors using perfect electric conductors, a CM microstrip resonator with capacitive termination was formed. Besides using the numerical calculation method, the resonant frequency of the common mode of the CMDM coil can also be estimated by using the following analytic equation [57]:

$$f_{\text{re}}=\frac{{(2\pi f_{\text{re}}{Z}_0)}^2{C}_1{C}_2-1}{2\pi Z_0(C_1+C_2)}tan\left(\frac{2\pi l\sqrt{{\epsilon }_{\text{eff}}}}{c}{f}_{\text{re}}\right)$$ (1)

where C₁ and C₂ are the capacitances of the termination capacitors on the microstrip resonator as indicated in Fig. 1. l and ε_eff are the length and effective permittivity of the microstrip resonator. Z₀ is the characteristic impedance of the microstrip resonator. In practice, the frequency tuning for the common mode can be performed by adjusting C₁ and C₂ through variable capacitors.

Fig. 1.

Diagram of the CMDM microstrip single surface coil. The solid line denotes the CM current, while the dashed line denotes the DM current. In this scheme the CM is driven capacitively while the DM is driven inductively.

The coaxial cables for feeding both the CM and DM coils was modeled as a series voltage source with 50 Ω impedance which was connected to each driven port of the CMDM coil. The cell size used for FDTD mesh was 1 mm, which was small enough for satisfying the simulation accuracy. By changing the capacitor values the common mode and differential mode were tuned to ¹H and ¹³C Larmor frequencies at 7T, respectively.

The proposed double-tuned CMDM surface coil was built on a 6.3-mm-thick acrylic board which served as both dielectric substrate and mechanical support. In this microstrip type CMDM surface coil, the strip conductors and the ground planes were made from back-adhesive copper foils (3M, St. Paul, MN). The dimensions of the CMDM surface coil were the same as those used in the simulation setup. To reach the desired resonant frequency for common mode, one end of the CMDM coil was terminated by a variable capacitor (NMAF19HV, Voltronics, Denville, NJ) ranging from 1 to 19 pF which was also used for frequency tuning. Another end of the CMDM coil was terminated by two fixed capacitors with nominal value of 24 pF (ATC, Huntington Station, NY). For the differential mode, a fixed capacitor with nominal value of 30 pF (ATC, Huntington Station, NY) and a variable capacitor (9629, Johanson MFG, Boonton, NJ) ranging from 5 to 20 pF were connected in parallel in the gap of the CMDM coil.

In this study, the common mode and differential mode were driven capacitively and inductively, respectively, as shown in Fig. 1. A variable capacitor (NMAF19HV, Voltronics, Denville, NJ) with a capacitance range from 1 to 19 pF was connected in series to the CMDM microstrip coil to implement impedance match for the common mode. The differential mode was fed by an inductive loop with a variable capacitor (9629, Johanson MFG, Boonton, NJ) ranging from 5 to 20 pF used for impedance match. Bench tests on the coil resonance modes and the isolation between the CM and DM channels were performed by reflection coefficient S₁₁ and transmission coefficient S₂₁ measurements taken on an Agilent E5070B network analyzer.

MR experiments were also conducted to validate the performance of this double-tuned CMDM coil. The ¹H MR imaging and ¹³C spectroscopic imaging experiments of a cylindrical corn oil phantom were performed on a GE 7T whole body MR system (GE Healthcare, Waukesha, WI). For ¹H imaging, the common mode of the CMDM coil was used to collect a set of spin echo (SE) images in axial plane with imaging parameters of TR = 2 s FOV = 9 cm, and number of averages = 1. In the ¹³C spectroscopy experiment, the differential mode of the CMDM coil was used to acquire a set of 16 × 8 2-D ¹³C FIDCSI data with acquisition parameters of TR = 2 s, in-plane resolution = 9 mm × 9 mm slice thickness = 20 mm, and number of averages = 1.

To further validate the CMDM method for double-tuned coil design, we built a conventional double-tuned RF coil based on the two-pole circuit [43] as shown in Fig. 2, and compared it with the proposed CMDM coil in terms of Q-values, isolation between ¹³C and ¹H channels, transmit efficiency and SNR at 7T. The conventional double-tuned two-pole coil was built with the same size as the CMDM coil: the coil was in rectangular shape with dimensions of 89 mm 32 mm. The width of the copper tape used as coil conductors was 6.3 mm. This two-pole circuit was built on a 6.3-mm-thick acrylic board in order to keep the same as what used in the CMDM design. A piece of adhesive backed copper foil (3M, St. Paul, MN) was placed on the other side of the acrylic board to act as the RF shielding. Both bench measurements and MR experiments were performed using the CMDM coil and the two-pole coil with the same parameters and setup. Importantly, the distance between the coil and the sample (water phantom) was kept same during all imaging experiments and bench measurements. The imaging parameters used for the comparison study were as following: pulse sequence = fast gradient echo FOV = 10 cm, slice thickness = 3 mm, slice spacing = 5 mm, TE/TR = 2.2/200 ms, number of averages = 1, matrix size = 128 × 128, and flip angle = 30°.

Fig. 2.

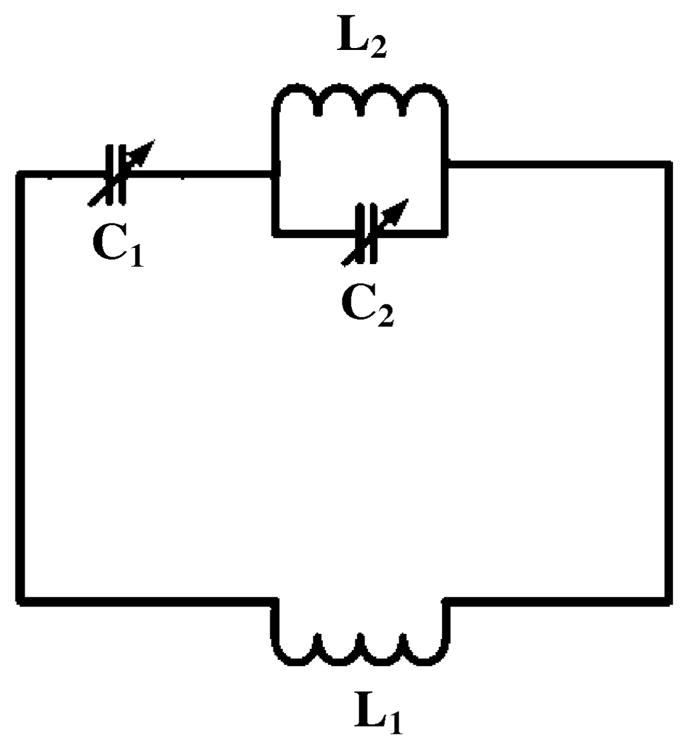
Equivalent circuit of the double-tuned two-pole coil for the comparison study. The trimmer capacitor C1 and C2 are used to perform frequency tuning for two frequencies. L1 is the equivalent inductance of the loop coil.

B. Microstrip CMDM Volume Coil Design

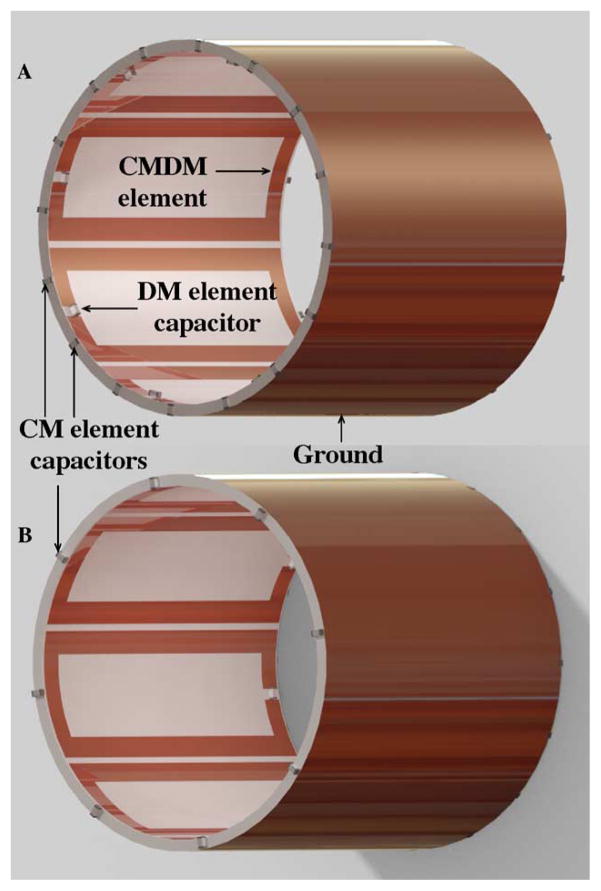
Based on the structure of the CMDM surface coil described above, we built a double-tuned CMDM volume coil for ¹H/¹³C in vivo MR applications at 7T (as shown in Fig. 3) to demonstrate the capability of CMDM technique in designing double-tuned volume coils. An acrylic cylinder with dimensions of 102 mm OD, 95 mm ID, and 102 mm in length was utilized as the dielectric material and mechanical support. This double-tuned CMDM volume coil comprised of eight identical CMDM resonator elements equally spaced along the circumference of the acrylic cylinder with a 1.6-mm separation. The circuit structure of each element was the same as that of the CMDM surface coil described above, but the dimensions of the rectangular element were changed to 102 mm in length and 36 mm in width. In this double-tuned CMDM volume coil, the common mode and differential mode of each element were used to form the volume coil’s ¹H channel and ¹³C channel, respectively. The ground plane of the coil was made of a cylindrical copper foil with 36 μm thickness (3M, St. Paul, Minnesota) on the outer surface of the acrylic cylinder. This continuous ground plane can effectively enhance the coupling among the CMDM microstrip elements and reduce radiation losses [67].

Fig. 3.

Diagram of the double-tuned CMDM microstrip volume coil implemented by using microstrip technology: views from (a) left sides and (b) right side.

The resonant frequency f_vc of the CMDM volume coil can be calculated by using the following equation [57]:

$$f_{\text{ve}}=\frac{1}{\sqrt{1+\frac{1}{L}{\sum }_{i=1}^{N-1}{k}_{1,i+1}cos\left(\frac{2\pi }{N}i\right)}}{f}_{\text{re}}$$ (2)

where k_{1, i+1} is the mutual inductance between the first element and the (i + 1) th elements; f_re denotes the resonant frequency of CM or DM for each CMDM element; N is the number of elements for the volume coil. In this CMDM volume coil design, the magnetic coupling dominated the coupling between the elements, therefore the electric coupling was ignored and only mutual inductance induced voltage from the other resonant elements was considered for the frequency calculation. From (2), it can be seen that the resonant frequency of the volume coil is slightly lower than that of each element due to the mutual coupling among elements.

As in the CMDM surface coil, the ¹H channel of volume coils was driven capacitively and ¹³C channel was driven inductively. To generate circularly polarized B₁ fields, the coil was operated in quadrature driving for both the ¹H and ¹³C channels. In each channel, the two driving elements of the volume coil were 90° apart and fed with a 90° difference in phase.

A network analyzer (Agilent E5070B) was employed for testing the coil resonance modes and performance, including Q-factors and the electromagnetic isolations between the two quadrature ports and also between ¹H and ¹³C channels.

After the bench tests and fine tuning, ¹H MR imaging and ¹³C spectroscopy experiments of a cylindrical corn oil phantom were performed by using the CMDM volume coil with a cylindrical corn oil phantom on the GE 7T whole body MR scanner. A set of fast spin echo (FSE) images in both sagittal and axial planes were acquired with imaging parameters of TR = 2 s, TE = 24 ms, flip angle FA = 90° slice thickness = 5 mm and number of average = 1. An 8 × 8 2-D ¹³C spectroscopic image was also obtained using a FIDCSI sequence with TR = 2 s, number of average = 4, 12 mm in plane and 20-mm-thick slice.

C. Evaluation of B₁ Field Behavior and Performance of the CMDM Structures

The structure of split microstrip resonators that supports common mode and differential mode is different from that of the typical microstrip resonators. To investigate the B₁ field distributions of a double-tuned CMDM volume coil at both frequencies, we did studies using both numerical simulation and MR imaging experiments. In the simulation, we built a numerical model which was exactly the same as the prototype CMDM volume coil described above, and then used the FDTD method to calculate and analyze the B₁ field distribution of both channels. A cylindrical human muscle phantom with permittivity of 58 and conductivity of 0.8 (S/m) was placed in the CMDM volume coil model. The diameter of the phantom was 61 mm which was about 63% of the coil ID. The B₁ field distributions in both axial and sagittal planes were simulated. The standard deviation of B₁ intensity was utilized to quantitatively evaluate the B₁ homogeneity within the phantom area.

The Yee cell size was 1 mm on transverse plane and 3 mm on longitudinal direction and was small enough to satisfy the calculation accuracy. To simulate the B₁ field distribution of the CMDM volume coil model when operating with common mode, current source was placed at the point of C1 (in Fig. 1) for each CMDM resonator and the phase difference between the adjacent elements was 45°. In the simulation of differential mode, the current source was placed at point C3 shown in Fig. 1 for each CMDM resonator and the phase difference between adjacent elements was also 45°. This setting would make the volume coil working at sinusoidal mode to generate homogeneous B₁ field at both frequencies. The stop criteria were that the convergence reached −60 dB or the time period reached 70 cycles which ensured the achievement of the steady state.

In the MR imaging validation, a corn oil phantom was used because it contains both ¹H and ¹³C and also because it has a low permittivity that can avoid the image inhomogeneity problem caused by the “dielectric resonance” effect at ultrahigh fields and can provide the more accurate information on intrinsic B₁ field distributions of the CMDM volume coil. The imaging acquisitions were performed on the General Electric (GE) whole body 7T scanner. With a fast spin echo sequence, ¹H imaging of the cylindrical oil phantom was acquired using the common mode channel of the CMDM volume coil. Relatively long repetition time (TR) of 2 s was employed to reduce the possible saturation effect due to the longer T1 at 7T. Other imaging parameters were TE = 4 ms, flip angle = 90°. To test the ¹³C channel, chemical shift imaging (CSI) was acquired from the same oil phantom using the differential mode channel of the CMDM volume coil. The ¹³C CSI studies were performed to provide information on the B₁ field behavior of the differential mode.

III. Results

A. Microstrip CMDM Surface Coil Design

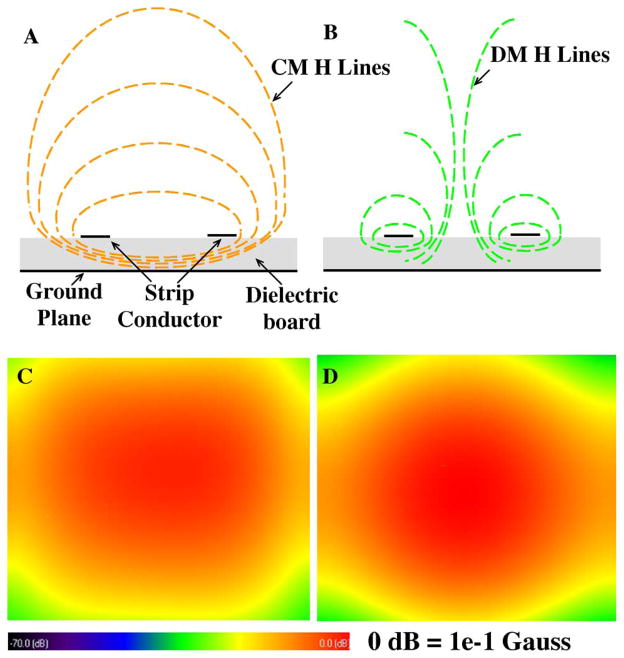
In the FDTD simulation, the waveform source of Gaussian function was used to find proper capacitances for double tuned CMDM microstrip surface coil based on the resonant frequency. The convergence threshold in the calculations was set to −35 dB. Capacitances for the CM working at 298.1 MHz and DM at 75 MHz were identified, which helped to guide the double-tuned CMDM surface coil design for ¹H/¹³C MRSI at 7T. In calculating the B₁ fields, a Sine wave was used and the convergence threshold was set at −40 dB. Simulation results showed that both S₁₁ and S₂₁ were better than −46 dB, indicating an excellent impedance matching and isolation between the ¹H and ¹³C channels which is essential for efficient acquisition of ¹³C and ¹H signals. Fig. 4 shows the two B₁ field distributions of the common mode and differential mode of the CMDM double-tuned surface coil. The two B₁ fields are orthogonal to each other; therefore the two modes are electromagnetically decoupled intrinsically. It was observed that the common mode and differential mode of the proposed CMDM resonator had similar B₁ field distributions, which indicates that both ¹H and ¹³C channels have the similar imaging coverage in unloaded case. When the coil is loaded with a biological sample such as human brain at the ultrahigh field of 7T, the high permittivity of the sample helps improving the field penetration for the proton channel [59].

Fig. 4.

Magnetic field distributions of the (a) common mode and (b) differential mode of the CMDM microstrip double-tuned resonator. FDTD simulated B₁ maps (coronal) of (c) CM at 298.1 MHz and (d) DM at 75 MHz. The B₁ distributions of the common mode and differential mode are similar, helping B₀ shimming for low gamma nuclei.

In the bench tests, the common mode and differential mode were tuned to 298.1 and 75 MHz, respectively, by adjusting the tuning capacitors on the CMDM coil. The S₁₁ measurements demonstrated that the input impedance of ¹H and ¹³C channels were well matched to 50Ω. The isolations between the two frequency channels was measured −30 dB or better in both unloaded and loaded cases, illustrating that the two channels of the prototype CMDM surface coil had excellent isolation for efficient ¹H/¹³C MRI/MRS.

Prior to imaging acquisitions, B₀ field shimming was performed using the CM ¹H channel. ¹H spin echo images and the ¹³C spectroscopic images in the axial plane of a corn oil phantom were then acquired using the double tuned CMDM surface coil. Both the ¹H image and the ¹³C spectroscopic image shown in Fig. 5 verified that the B₁ fields of the common mode and differential mode of the CMDM surface coil have a similar distribution and coverage.

Fig. 5.

(a) ¹H SE image and (b) ¹³C CSI of a corn oil phantom on the axial plane acquired using the CMDM single surface coil at 7T. These MR images show that the common mode and differential mode have similar B₁ distribution.

The comparison study was conducted with the proposed CMDM coil and the double-tuned two-pole coil at the field strength of 7T. The results of the bench tests on the two coils are shown in Table I. The Q-values of the CMDM coil for both ¹H and ¹³C channels are higher than those of the two-pole coil. The electromagnetic isolation between the two nuclear channels in double-tuned coils is a critical factor that influences the coil efficiency. The isolation measured between the two channels of the CMDM coil reached −44 dB or better while that of the two-pole coil was −20 dB, which demonstrates the proposed CMDM coil has an improved electromagnetic isolation between two channels and thus the improved coil efficiency.

TABLE I.

Performance Comparison Between the CMDM Coil and the Two-Pole Coil in Terms of Q-Values and the Electromagnetic Isolation Between Channels in Both Unloaded and Loaded Cases. In All the Measurements, the Coil’s Input Impedance Was Well Matched to the System at 50 Ω

		CMDM		Two-pole
		C13	H1	C13	H1
Unloaded	Q value	300	246	178	185
	S21(dB)	−50	−45	−15	−22
Loaded	Q value	150	52	66	50
	S21(dB)	−44	−44	−13	−21

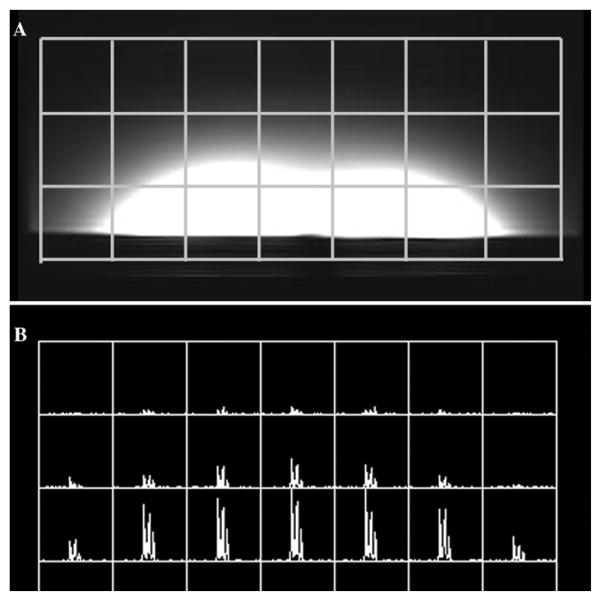
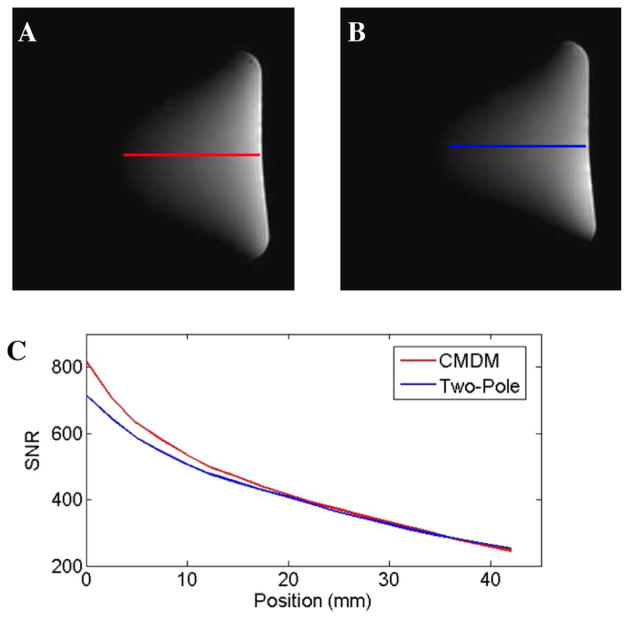
Fig. 6 shows MR imaging results of this comparison study. Proton images of a water phantom acquired using the two coils as well as their SNR measurements along the central line of each image illustrated that the proposed CMDM coil could provide an improved SNR over the conventional two-pole double-tuned coil. Quantitatively, the highest achievable SNR of the CMDM coil and the two-pole coil are 817 and 714, respectively, or a 13% improvement in this specific case. To compare the transmit efficiency of the two coils, the power was calibrated using a 7-mm-diameter water tube with 5-mm slice thickness to define the 90° pulse. The water tube was located 8 mm above the coil center. MR imaging experiments also demonstrated that the RF power required to achieve a nominal 90° flip angle using the proposed CMDM coil was approximately 20% less than that using the conventional two-pole coil, showing high transmit efficiency of the proposed CMDM design.

Fig. 6.

Results of the SNR comparison between the CMDM coil and the two-pole coil using a water phantom at 7T: (a) ¹H image of CMDM coil; (b) ¹H image of the two-pole coil; (c) SNR plot along the central line of the two images. The highest achievable SNR of the CMDM coil is 13% higher than that of the two-pole coil.

B. Microstrip CMDM Volume Coil Design

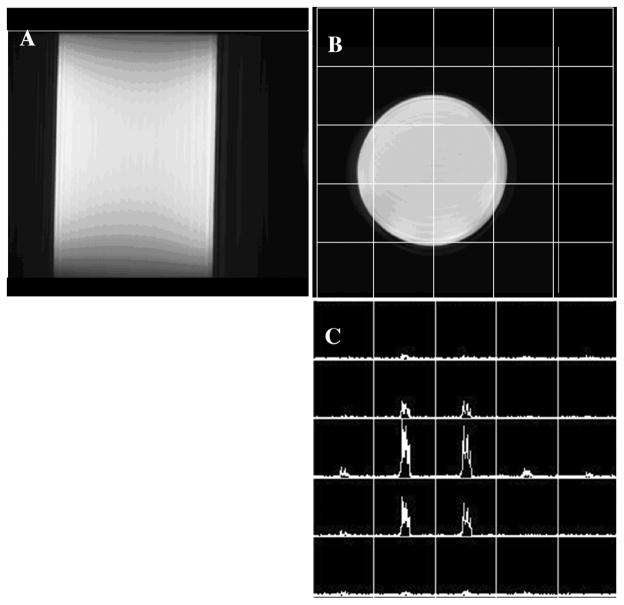
The ¹H and ¹³C channels of the microstrip CMDM volume coil were tuned to 298.1 MHz and 75 MHz on the two quadrature ports respectively. Each port of the ¹H channel was matched to system 50Ω via a series capacitor. Well defined five resonance peaks for both ¹H and ¹³C channels are clearly identified on the network analyzer showing a proper behavior of this 8-element volume coil in terms of resonance modes and the interaction between the two nuclear channels. On the bench test, the isolations between the quadrature driving ports of both ¹H and ¹³C channels were greater than −20 dB, indicating that the driving ports of each channel have been decoupled sufficiently, meeting the requirement of the 90° phase difference between the two quadrature ports. The S₂₁ -parameter between ¹H and ¹³C channels was better than −30 dB, showing excellent isolation between the two nuclear channels. This is essential to ensure the efficiency of the excitation and reception of the ¹H and ¹³C MR signals.

B₀ shimming was performed by using the common mode ¹H channel prior to the MR imaging experiments on the 7T system. Proton imaging and ¹³C spectroscopic imaging were acquired from the cylindrical corn oil phantom using the common mode channel and differential mode channel, respectively. Fig. 7 shows the ¹H FSE images in both sagittal and axial planes of the corn oil phantom, as well as a ¹³C FIDCSI image in the same axial plane. The ¹H images and ¹³C spectroscopic images of the oil phantom illustrated the homogeneous intrinsic B₁ distributions of this 7T double-tuned CMDM volume coil at both 298 MHz and 75 MHz.

Fig. 7.

MR experiment results of a corn oil phantom using the CMDM double-tuned volume coil at 7T: (a) ¹H spin echo sagittal image; (b) ¹H axial image and (c) ¹³C CSI spectroscopic image on axial plane acquired with natural abundance. The ¹H images demonstrate the fairly homogeneous axial B₁ distribution in the imaging area at the high frequency of ~300 MHz. In the ¹³C CSI result, given the partial volume effect, the ¹³C channel of this dual-tuned volume coil has a right behavior in terms of resonant mode and uniform field distributions at 75 MHz.

C. Evaluation of B₁ Field Behavior and Performance of the CMDM Volume Coils

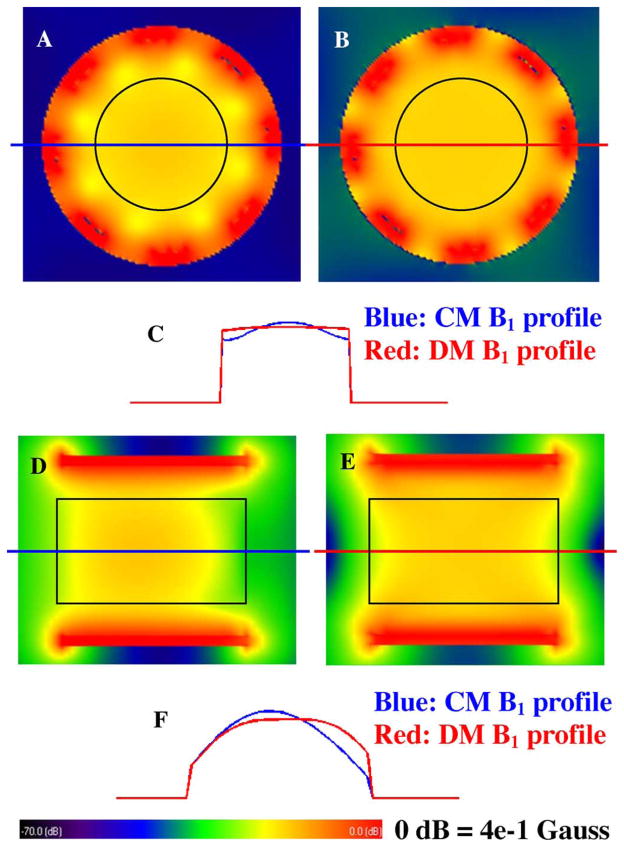
Fig. 8 shows the B₁ field distributions of both common mode and differential mode of the CMDM volume coil model after steady state has been achieved in FDTD simulation. The 2-D distributions of the B₁ fields in the axial plane for ¹H and ¹³C are illustrated in Fig. 8(a) and (b), respectively. The black circle on the B₁ maps denotes the position of the phantom. The standard deviation and mean of the ¹H channel are 4.7 × 10⁻³ Gauss and 5.3 × 10⁻² Gauss, respectively, while those for the ¹³C channel are 6.9 × 10⁻⁴ Gauss and 5.7 × 10⁻² Gauss. The ratio between the standard deviation and the mean are 9% and 1% for ¹H and ¹³C channel, respectively. The 1-D plots of the B₁ field distributions along the central line are also shown in Fig. 8(c). In this CMDM volume coil, the average B₁ intensity of the common mode is approximately 7% less than that of the differential mode, while the B₁ of the common mode in the center of the phantom is 3% higher than that of the differential mode. This difference results from the different B₁ distribution of the two resonance modes. The B₁ distribution and penetration of the common mode and differential mode change with geometry and dimension of CMDM units. Both quantitative calculation and the graphic illustrations demonstrate fairly homogeneous B₁ fields in axial plane can be achieved for ¹³C channel; while for ¹H channel (at a higher frequency of 298 MHz), the B₁ behaves properly although the “dielectric resonance” effect in the high permittivity biological samples at ultrahigh fields distorts B₁ the field distribution at certain level.

Fig. 8.

FDTD simulation results of the B₁ distribution of the double-tuned CMDM volume coil at 7T in the loaded case. The black circles in (a) and (b) and black rectangles in (d) and (e) denote the phantom position. (a) Axial plane B₁ distribution of the common mode channel for ¹H. (b) Axial plane B₁ distribution of the differential mode channel for ¹³C. (c) 1-D plot of the axial plane B₁ distribution, blue line and red line denote the ¹H and ¹³C, respectively. (d), (e) Sagittal plane B₁ distributions of the common mode channel for ¹H and the differential mode channel for ¹³C. (f) 1-D profile of the sagittal plane B₁ distribution, blue line and red line denote the ¹H and ¹³C respectively. It is shown that for ¹³C channel with the differential mode operating at 75 MHz, homogeneous B₁ field distribution was obtained in both axial and sagittal directions, while for ¹H channel with the common mode operating at 300 MHz, although “dielectric resonance” effects at ultrahigh fields distort the B₁ field, a fairly homogeneous B₁ distribution was still obtained in this case.

In Fig. 8(d)–(f), 2-D distributions and 1-D plots of B₁ fields for both ¹H and ¹³C channels in sagittal planes are illustrated. The black rectangle in the B₁ maps denotes the position of the phantom. For ¹H channel, the standard deviation and mean of the B₁ intensity are 1.34 × 10⁻² Gauss and 4.3 × 10⁻² Gauss, respectively, between which the ratio is 30%; while for ¹³C channel those are 1.0 × 10⁻² Gauss and 5.2 × 10⁻² Gauss respectively, between which the ratio is 20%. Based on this simulation, B₁ fields of ¹³C channel (at a relatively lower frequency of 75 MHz) have more uniform distribution along the volume coil axis than that of ¹H channel which operates at an approximately 4-times higher frequency of 298 MHz.

IV. Discussion and Conclusion

All the simulations, bench tests and MR imaging experiments have demonstrated that the proposed method based on the concepts of CMDM is a feasible and effective approach to design double-tuned coils at 7T. One important advantage of the CMDM design is that its common mode and differential mode are intrinsically decoupled because their magnetic fields are orthogonal to each other. This feature is critical for improving efficiency for both proton and heteronucleus MR signal excitation and reception in dual-tuned operations. The common mode and differential mode of CMDM resonator can be tuned independently. Compared with conventional approaches, the proposed CMDM method provides an easy and robust way to double-tuned RF coil designs. In this work, although the CMDM method is implemented by using microstrip technology in order to gain the performance at high and ultrahigh fields, the CMDM resonator can be also realized by using other type of circuits, such as lumped element designs. Moreover, if the CM and DM of a CMDM resonator are tuned to the same frequency, the CMDM coil becomes a quadrature coil due to the intrinsically orthogonal field distribution of the CM and DM. In the design of the proposed CMDM RF coils, it is important to keep circuit and structure symmetric in both electrical and mechanical aspects. Any circuit imbalance would contaminate the mode and sacrifice coil efficiency, particularly in quadrature CMDM case where the common mode and differential mode operate at the same frequency.

The FDTD simulation of the CMDM double-tuned single surface coil showed that its CM and DM possess a similar B₁ distribution. This indicates that the CM and DM coils have almost the same imaging coverage in the unloaded case. In the loaded case with a high permittivity biological sample at the ultrahigh field of 7T, the RF field penetration is increased due to the “dielectric resonance” effect. This guarantees the imaging coverage of proton channel to not be smaller than that in the unloaded case. In addition, this characteristic may help the B₀ shimming for heteronuclei, e.g., ¹³C, whose spin density is normally too low in human body to generate strong enough MR signals for shimming. Commonly, ¹H channel is used for B₀ shimming in double-tuned coils, which requires a similar magnetic field distribution for two frequency channels. The similar or same field distribution may help improving the shimming efficiency.

The concepts of CMDM RF coil design have been demonstrated in designing regular surface coils and volume coils. Potentially the proposed CMDM method can also be used to design double-tuned coil arrays or double-tuned transceiver arrays for parallel imaging or parallel excitation applications. The decoupling issue of the CMDM arrays can be addressed by employing the magnetic wall technique which is suitable for non-overlapped coil array designs and which also shows the unique advantage in double-tuned arrays [68], [69]. It is known that non-overlapped array can decrease the g-factor and increase the SNR, therefore it is desired in parallel imaging and parallel excitation applications.