Constant pH Molecular Dynamics Simulations of Nucleic Acids in Explicit Solvent

Abstract

The nucleosides of adenine and cytosine have pKa values of 3.50 and 4.08, respectively, and are assumed to be unprotonated under physiological conditions. However, evidence from recent NMR and X-Ray crystallography studies has revealed the prevalence of protonated adenine and cytosine in RNA macromolecules. Such nucleotides with elevated pKa values may play a role in stabilizing RNA structure and participate in the mechanism of ribozyme catalysis. With the work presented here, we establish the framework and demonstrate the first constant pH MD simulations (CPHMD) for nucleic acids in explicit solvent in which the protonation state is coupled to the dynamical evolution of the RNA system via λ-dynamics. We adopt the new functional form λ^Nexp for λ that was recently developed for Multi-Site λ-Dynamics (MSλD) and demonstrate good sampling characteristics in which rapid and frequent transitions between the protonated and unprotonated states at pH = pKa are achieved. Our calculated pKa values of simple nucleotides are in a good agreement with experimentally measured values, with a mean absolute error of 0.24 pKa units. This work demonstrates that CPHMD can be used as a powerful tool to investigate pH-dependent biological properties of RNA macromolecules.

1. INTRODUCTION

An increasing number of experimental studies in recent years have recognized the role of protonated nucleotides, particularly adenine and cytosine, in RNA structure and function. Experimental pKa values of the nucleosides have been measured to be 3.50 for adenosine and 4.08 for cytidine, which become protonated at the N1 and N3 atoms respectively (Figure 1).¹ These findings suggest that adenine and cytosine should typically be unprotonated at physiological pH and their contributions to RNA structure and function was initially assumed to be minimal. However, recent studies have revealed the prevalence of protonated adenine and cytosine in a wide variety of nucleic acid structures ranging from DNA triple helices to the anticodon stem loop of tRNA,^2-6 indicating that the pKa value of these residues may be shifted upwards to near physiological conditions of pH 7. Protonated bases have been reported to be responsible for a number of non-canonical base pair configurations, which suggests their ability to influence RNA structure.^7,8 A key example is the wobble A⁺•C base pair that has been implicated in stabilizing RNA loop structures^9,10 and in the pH-dependent conformational flexibility of the ribosomal peptidyl transferase center.¹¹ Wobble A⁺•C base pairs may also form in DNA under biologically relevant conditions,¹² where they can have mutagenic and carcinogenic effects.^13,14 Apart from these structural influences, it has been suggested that the elevated pKa of these nucleic acids may play a significant role in ribozyme catalysis, as these protonated residues may be involved in general acid-base catalysis, playing an analogous role to histidine residues in proteins.^15-19 Some examples of its role in catalysis include hepatitis delta virus ribozyme^20-24 and hairpin ribozyme,^25-30 where experimental studies have demonstrated that a loss-of-function mutation of key residues that have elevated pKa values led to a significant drop in catalytic activity.

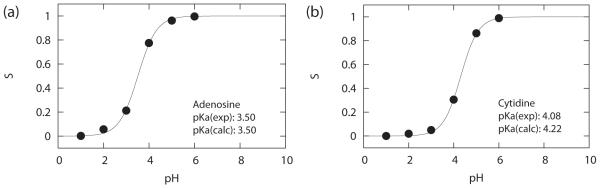
Figure 1.

Protonation site of (a) adenosine and (b) cytidine and their respective pKa values.

Despite the copious amount of biochemical and structural studies that are available for these RNA structures, there still remains some ambiguity as to the exact function of these protonated residues. For example, while experimental studies strongly suggest that adenine 38 (A₃₈) participates in the cleavage and ligation reaction that is catalyzed by the hairpin ribozyme, its specific role in the catalytic mechanism and the structural dynamics of the ribozyme remains disputed.^25-30 In such situations, in silico modeling of RNA structures may shed some light on the existing controversy. Walter and co-workers have demonstrated the usefulness of using molecular dynamics (MD) simulations to clarify the role of the protonated A₃₈ in the hairpin ribozyme by suggesting that it serves as a general acid in aligning reactive groups and stabilizing the negative charge.^31,32 However, such traditional MD simulations are limited in the sense that prior knowledge obtained from experiment about the identity of key catalytic residue(s) and its protonation state(s) is required. In terms of in silico prediction of pKa values, Honig and co-workers have recently demonstrated the ability to accurately calculate the pKa values of nucleotides using numerical solutions to the Poisson-Boltzmann equation from a series of representative static snapshots obtained from RNA NMR structures.³³ While these calculated pKa values may identify the correct protonation state to be used in a traditional MD simulation, the latter still lacks the ability to incorporate protonation state information on-the-fly. The ability to perform pH-coupled molecular dynamics is clearly desirable since it would model realistic pH-dependent responses to structural fluctuations and provide mechanistic insight to RNA catalyzed reactions.

In the development of MD simulations, there has been considerable success in calculating pKa values of protein residues. Warshel and co-workers first demonstrated the feasibility of using microscopic free energy calculations to determine the pKa values of protein residues.^34-37 Variations of this approach have been developed that couple the protonation state of a titratable residue with the protein conformation; in these strategies, the atomic coordinates and the protonation state itself evolve according to the dynamics of the system. Two distinct classes of implementation for this methodology exist, and differ in the manner in which the titration coordinates are treated – either discretely or continuously. The discrete titration variant is typically implemented by combining MD sampling of the atomic coordinates with Monte Carlo (MC) sampling of protonation states. At regular intervals during a typical MD simulation, a MC step is performed to determine the change of the protonation state. Implementation of discrete CPHMD in explicit solvent was first reported by Bürgi et. al.,³⁸ and Baptista and co-workers,³⁹ and a number of methodological improvements were made by Baptista and co-workers,^40-42 and Stern.⁴³ Discrete CPHMD has also been implemented with implicit solvent by Dlugosz and Antosiewicz,^44,45 and Mongan et. al.,⁴⁶ with improvements to achieve better sampling by Meng et. al. ⁴⁷ and Williams et. al.⁴⁸ More recently, Warshel and co-workers developed a more physically realistic form of pH-dependent MD⁴⁹ based on the time-dependent MC sampling of the proton transfer process,⁵⁰ which uses the empirical valence bond (EVB) framework to simulate a single proton transfer from the protein to a surrounding water molecule.⁵¹ In contrast, in the continuous titration variant of CPHMD, the titration coordinate is propagated continuously between the protonated and unprotonated states. Brooks and co-workers developed constant pH molecular dynamics (CPHMD) using implicit solvent^52-54 which utilized the λ dynamics approach^55-57 to treat the titration coordinates. Recent work by Shen and co-workers has improved the prediction accuracy of continuous CPHMD,^58-60 and it has been extended to explicit solvent by Grubmüller and co-workers.⁶¹ Yang and co-workers have also reported using orthogonal space random walk, an enhanced sampling technique based on λ-dynamics, that provided accurate pKa predictions for buried protein residues in explicit solvent simulations.⁶² CPHMD has been used by Brooks and co-workers to investigate numerous pH-dependent conformational changes in proteins,^63-65 and other investigators in the field have reported similar successes as well.^66-70 For a more comprehensive overview of CPHMD, we refer our readers to the following reviews.⁷¹

In this article, we will adopt the newer functional forms of λ developed by Knight and Brooks that have been implemented in Multi-Site λ-Dynamics (MSλD)^72,73 as the basis of a new MSλD-based constant pH molecular dynamics simulation framework (CPHMD^MSλD) and parameterize CPHMD^MSλD to investigate protonation events of nucleic acids in explicit solvent. We will demonstrate the quality of this new CPHMD^MSλD model by its ability to accurately reproduce experimental pKa values of simple mononucleotide systems to a mean absolute error of 0.24 pKa units. To the best of our knowledge, this is the first constant pH MD simulation for nucleic acids to be reported in literature.

2. THEORY

We briefly review the theory behind constant pH molecular dynamics (CPHMD) and highlight the relevant modification in our implementation of CPHMD^MSλD. In the original CPHMD model, the protonation/deprotonation process is simulated as a special case of λ-dynamics where the λ variables are used to define titration coordinates.^55-57 In λ-dynamics, the simulation is under the influence of a hybrid Hamiltonian and its potential energy is defined by:

$$U_{tot}(X,\left\{x\right\},\left\{\lambda \right\})=U_{env}\left(X\right)+\sum _{\alpha =1}^{N_{sites}}\left[{\lambda }_{\alpha =1}\left(U\left(X,x_{\alpha ,1}\right)\right)+{\lambda }_{\alpha ,2}\left(U\left(X,x_{\alpha ,2}\right)\right)\right]$$ (1)

where N_sites is the total number of titrating residues, X represents the coordinates of the environment atoms, and x_α,1 and x_α,2 represent the coordinates of atoms in residue α that are associated with the protonated and unprotonated states, respectively. The titrating proton and the other atoms whose charges vary according to the protonation state of the residue (usually atoms within 2-3 bonds from the titrating proton) are included in both x_α,1 and x_α,2 and are defined as a part of the “titrating fragment.” The scaling factor that is associated with the titrating residue α changes dynamically throughout the simulation and is described by a set of continuous coordinates that are governed by the following equations:

$${\lambda }_{\alpha ,1}={\sin }^2{\theta }_{\alpha }\mathrm{and}{\lambda }_{\alpha ,2}=1-{\sin }^2{\theta }_{\alpha }$$ (2)

The end points define the physically relevant protonated (λ_α,1 = 1, λ_α,2 = 0) and unprotonated (λ_α,1 = 0, λ_α,2 = 1) states. In recent work, Knight and Brooks developed the alternative λ^Nexp functional form of λ:

$${\lambda }_{\alpha ,i}^{N\exp }=\frac{e^{c\sin {\theta }_{\alpha ,i}}}{\sum _{j=1}^N{e}^{c\sin {\theta }_{\alpha },j}}$$ (3)

When applied to the two-state system representing the protonated and unprotonated forms this functional form becomes:

$${\lambda }_{\alpha ,1}=\frac{e^{c\sin {\theta }_{\alpha },1}}{e^{c\sin {\theta }_{\alpha ,1}}+e^{c\sin {\theta }_{\alpha ,2}}}\mathrm{and}{\lambda }_{\alpha ,2}=\frac{e^{c\sin {\theta }_{\alpha },2}}{e^{c\sin {\theta }_{\alpha ,1}}+e^{c\sin {\theta }_{\alpha ,2}}}$$ (4)

This new form implicitly satisfies the constraints as required by λ-dynamics:

$$0\le {\lambda }_i\le 1\mathrm{and}\sum _{i=1}^N{\lambda }_i=1$$ (5)

The use of the λ^Nexp functional form also expands the future functionality of our CPHMD^MSλD model to titrate between more than two states, such as the tautomeric forms of nucleic acids.

In CPHMD simulations, the overall free energy of deprotonation of a given residue, ΔG_exp(RNA), is obtained by calculating the difference between the free energy of deprotonation in the RNA environment, ΔG_sim(RNA), compared to that of a model compound in solvent, ΔG_sim(model). By equating this difference of free energies between the simulated system to that of the experimental system, we obtain:

$$\Delta G_{\exp }\left(\mathrm{RNA}\right)-\Delta G_{\exp }\left(\text{model}\right)=\Delta G_{sim}\left(\mathrm{RNA}\right)-\Delta G_{sim}\left(\text{model}\right)$$ (6)

which can be rearranged to estimate the experimental free energy of deprotonation of the RNA:

$$\Delta G_{\exp }\left(\mathrm{RNA}\right)=\Delta G_{sim}\left(\mathrm{RNA}\right)-\Delta G_{sim}\left(\text{model}\right)+\Delta G_{\exp }\left(\text{model}\right)$$ (7)

The free energy of deprotonation of the model compound may also be expressed as:

$$\Delta G_{sim}\left(\text{model}\right)=\ln \left(10\right)k_{B}T(\mathrm{pKa}-\mathrm{pH})$$ (8)

From this perspective, titratable groups in the RNA can be viewed as model compounds that are perturbed by the introduction of the RNA environment via non-bonded interactions and this is the fundamental expression that needs to be calibrated for each titratable residue in our model, in the present study, adenosine and cytidine. For the initial calibration, the free energy of deprotonation of each isolated model compound calculated using traditional λ-dynamics provided the ΔG_sim(model) value. When ΔG_sim(model) is applied to the simulation as a bias, it results in a zero free energy difference between the protonated and unprotonated states and this condition is equivalent to pH = pKa. To simulate the system under different pH environments, equation (8) is used to derive the equivalent ΔG_sim(model) value that should be applied to the simulation. The reference pKa used in equation (8) was obtained from experimental pKa values that were measured at zero ionic strength.¹

In our implementation of CPHMD^MSλD, two biases (F^fixed and F^var) are incorporated into the potential energy function and the resulting total potential energy function in our CPHMD simulation may be written as:

$$\begin{array}{cc}\hfill & U_{tot}(X,\left\{x\right\},\left\{\lambda \right\})=U_{env}\left(X\right)\hfill \\ \hfill & +\sum _{\alpha =1}^{N_{sites}}\left[{\lambda }_{\alpha ,1}\left(U\left(X,x_{\alpha ,1}\right)-F_{\alpha ,2}^{fixed}\right)+{\lambda }_{\alpha ,2}\left(U\left(X,x_{\alpha ,2}\right)-F_{\alpha ,2}^{fixed}\right)+F_{\alpha ,1}^{\mathrm{var}}\left({\lambda }_{\alpha ,1}\right)+F_{\alpha ,1}^{\mathrm{var}}\left({\lambda }_{\alpha ,2}\right)\right]\hfill \end{array}$$ (9)

In this formalism, the fixed biasing potential that is applied to the unprotonated state $\left({\mathrm{F}}_{\alpha ,2}^{\text{fixed}}\right)$ represents the calibrated ΔG_sim(model) value. The other fixed biasing potential applied to the protonated state $\left({\mathrm{F}}_{\alpha ,1}^{\text{fixed}}\right)$ is kept at zero. Using this setup, when the titration coordinates are allowed to propagate dynamically, the two end points that correspond to physical states may not be well-sampled. Thus, we included the variable biasing potential (F^var) which applies an additional bias to encourage sampling of physical states. Identical variable biases are applied to both protonation states.

$$F_{\alpha ,i}^{\text{variable}}=\{\begin{array}{cc}{k}_{bias}{\left({\lambda }_{\alpha ,i}-0.8\right)}^2;\hfill & if{\lambda }_i<0.8\hfill \\ 0;\hfill & otherwise\hfill \end{array}\phantom{\}}$$ (10)

The populations of unprotonated (N^unprot) and protonated (N^prot) states are extracted from the λ trajectory at each pH value, which are used to derive the unprotonated fraction (S^unprot):

$$S^{unprot}\left(\mathrm{pH}\right)=\frac{N^{unprot}\left(\mathrm{pH}\right)}{N^{unprot}\left(\mathrm{pH}\right)+N^{prot}\left(\mathrm{pH}\right)}$$ (11)

Overall pKa values can be calculated by running simulations at different pH values and fitting the series of S^unprot values to a more generalized version of the Hendenson-Hasselbach formula:

$$S^{unprot}\left(\mathrm{pH}\right)=\frac{1}{1+{10}^{-n(pH-pKa)}}$$ (12)

where n is the Hill coefficient. In this formalism, n has a theoretical value of one and deviations from this value indicate the degree of cooperativity (n > 1) or anti-cooperativity (n < 1) between strongly interacting titratable groups.^74,75

3. METHODS

3.1 Generating Input Structures

The input structures of the nucleic acids that were used for the simulations were generated from CHARMM topology files using the IC facility in CHARMM while hydrogen atoms were added using the HBUILD facility.⁷⁶ Model compounds, adenosine and cytidine, were solvated in a cubic box of explicit TIP3P water molecules⁷⁷ of length ~20 Å using the convpdb.pl tool from the MMTSB toolset.⁷⁸ The test compounds, adenosine monophosphate (AMP), cytidine monophosphate (CMP) and dinucleotide sequences of CYT-CYT, ADE-ADE and CYT-ADE were solvated in a cubic box of explicit water molecules of length ~50 Å using the convpdb.pl tool from the MMTSB toolset. The ionic strength was simulated by adding the appropriate number of Na⁺ and Cl⁻ ions to match experimentally reported salt concentrations using convpdb.pl. For the mononucleotides, two isomers in the form of 5′-phospate and 3′-phosphate were constructed using the patch keywords 5PHO and 3PHO respectively, in CHARMM. All other nucleic acid structures had hydroxyl groups patched to the terminal ends via patch keywords 5TER and 3TER. Additional patches were constructed to represent the protonated forms of adenine and cytosine and all of the associated bonds, angles and dihedrals were explicitly defined in the patch. Each titratable residue was simulated as a hybrid model that explicitly included atomic components of both the protonated and unprotonated forms. The titratable fragment included the nitrogen atom that is protonated, the protonated hydrogen and adjacent atoms whose partial charge differed according to the protonation state (see Table 1 and corresponding Tables S1-S3 in the supplementary material). The environment atoms were defined as all atoms that were not included in the titratable fragments.

Table 1.

Charges and atom types assigned to the protonated and unprotonated states of titratable nucleic acids.

Name	Atom	Unprotonated		Protonated
		Atom Type	Charge	Atom Type	Charge
ADE	H1	-	-	HN2	0.527
	N1	NN3A	−0.74	NN2G	−0.489
	C2	CN4	0.50	CN4	0.611
	C6	CN2	0.46	CN2	0.571
CYT	H3	-	-	HN2	0.52
	C5	CN3	−0.13	CN3	−0.174
	C2	CN1	0.52	CN1	0.75
	N3	NN3	−0.66	NN2C	−0.874
	C4	CN2	0.65	CN2	0.962
	N4	NN1	−0.75	NN1	−0.654
	H41	HN1	0.37	HN1	0.42
	H42	HN1	0.33	HN1	0.38

3.2 Molecular Dynamics (MD) Simulations

MD simulations were performed within the CHARMM macromolecular modeling program (version c36a6)⁷⁶ using the CHARMM36 all-atom force field for RNA and TIP3P water.⁷⁹ The simulation set up for λ dynamics is similar to that reported by Knight and Brooks.^72,73 The SHAKE algorithm⁸⁰ was used to constrain the hydrogen-heavy atom bond lengths. The Leapfrog Verlet integrator was used with an integration time step of 2 fs. A non-bonded cutoff of 15 Å was used with an electrostatic force shifting function and a VDW switching function between 10 Å and 12 Å. λ dynamics was performed within the BLOCK acility using the MSλD framework (MSLD) and selecting the λ^Nexp functional form for λ (FNEX). Linear scaling by λ was applied to all energy terms except bond, angle and dihedral terms, which were treated at full strength regardless of λ value to retain physically reasonable geometries. Each θ_α was assigned a fictitious mass of 12 amu•Å² and λ values were saved every 10 steps. The threshold value for assigning λ_α,i =1 was λ_α,i ≥ 0.8. Variable biases (F^var) were added to the hybrid potential energy function and the associated force constant (k_bias) was optimized to enhance transition rates between the two protonation states. Since identical k_bias values were applied to both protonated and unprotonated states, the PMF at the end-points were not altered and no reweighting scheme was required. The temperature was maintained at 298K by coupling to a Langevin heatbath using a frictional coefficient of 10ps⁻¹. Prior to the simulation, each system was minimized using 300 steps of steepest descents (SD), followed by 200 steps of adopted basis Newton-Raphson (ABNR). After an initial heating of 4 ps and equilibration of 4 ps, a production run of 1 ns was performed, unless otherwise stated.

3.3 Calculation of pKa value

In our protocol, a single S^unprot value was estimated by combining the populations of N^prot and N^unprot from 3 independent simulations that used different initial seed values. These combined S^unprot ratios that were computed at different pH values were then fitted to equation (12) to obtain a single pKa value. Unless otherwise specified, the reported pKa value and its error correspond to the mean and standard deviation calculated from 3 sets of pKa calculations.

4. RESULTS & DISCUSSION

4.1 New CHARMM Parameters for Protonated Adenine and Cytosine

We calculated the partial charges for the adenine and cytosine nucleobases in their neutral (unprotonated) and charged (protonated) states using the MMFF94 force field.⁸¹ The change in the partial charge was added to the existing partial charge parameters for neutral adenine and cytosine in CHARMM to assign the charge distribution for the protonated residues. A summary of the differences for charges and atom types between the protonated and unprotonated nucleic acids is reported in Table 1. Parameters for the bond, angle and dihedral energy terms for the protonated nucleic acid were adapted from existing nucleic acid structures in CHARMM (see Supporting Information). For the protonated adenine, the respective bonded parameters were obtained from guanine, specifically from the six-membered ring component that has atoms analogous to that of adenine (N1, H1, C2 and C6). For the protonated cytosine, the respective bonded parameters were obtained from a tautomeric form of neutral cytosine (obtained from patch CYT1).

4.2 Optimization of Model Potential Parameters

Our CPHMD^MSλD model was implemented using the recently developed λ^Nexp functional form for λ in Multi-Site λ-dynamics (MSλD): ⁷³

$${\lambda }_{\alpha ,i}^{N\exp }=\frac{e^{c\sin {\theta }_{\alpha ,i}}}{\sum _{j=1}^N{e}^{c\sin {\theta }_{\alpha },j}}$$

Knight and Brooks reported setting the coefficient to 5.5 for the optimal balance between enhancing transition rate and maintaining numerical stability of the integrator in different environments.⁷³ An identical setup was used successfully in our CPHMD^MSλD model. As with the previous implementation of CPHMD for protein residues,^52-54 we have used the calibrated free energy of deprotonation (G_bias) as the fixed biasing potential value in our simulation. The free energy of deprotonation was calibrated for each isolated model compound, i.e., adenosine and cytidine, embedded in explicit solvent using traditional λ-dynamics. In order to facilitate transitions between the two protonation states, we optimized the force constant (k_bias) on the variable biasing potential that was applied for each model compound.

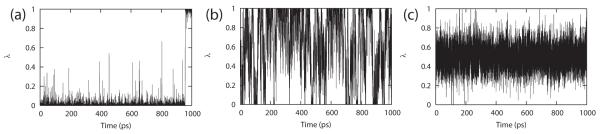
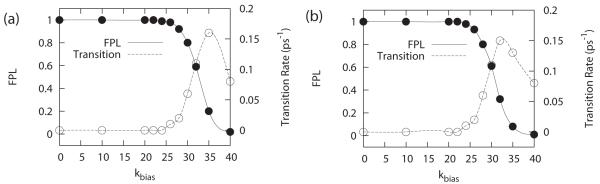
It is interesting to note that without the application of the variable bias, no transitions between the protonated and unprotonated states were observed at conditions pH = pKa, where one should expect equal population of both states and the maximum transition rate between the two states (see Figure 2). At values of k_bias < 20 kcal/mol, there were very few transitions in λ phase space between the two states for the entire duration of a 1 ns trajectory. At values k_bias > 40 kcal/mol, transitions were rapid but the end states were not adequately sampled. The optimal value of k_bias for each nucleoside was selected by considering the competing needs for a high number of transitions and adequate sampling of the end-points (i.e., maintaining a high fraction of physical ligands (FPL) that were sampled). As illustrated in Figure 3, these two properties were observed to be anticorrelated to each other and there is a distinct range of k_bias values (between 25 and 35 kcal/mol) that yielded good transition rates and where more than 80% of the simulation is spent at the physically-relevant end-points. The optimized parameters for the two model potentials are reported in Table 2.

Figure 2.

Transitions between the protonated and unprotonated state of adenosine in λ phase space at pH = pKa for a 1 ns trajectory with varying k_bias values of (a) 20, (b) 30 and (c) 40.

Figure 3.

Effect of increasing k_bias on the transition rate and fraction physical ligand (FPL) for (a) adenosine and (b) cytosine. Sampling characteristics were obtained from 5 independent MD runs of 1 ns each.

Table 2.

Parameters for the model potential. G_bias was assigned to be the free energy of deprotonation of adenosine or cytidine at zero ionic strength. k_bias was optimized to achieve a maximum transition rate while maintaining physical states for more than 80% of the entire trajectory.

Nucleotide	Gbias (kcal/mol)	kbias (kcal/mol)	Reference pKaa
Adenine	19.39	29.75	3.50
Cytosine	75.24	27.75	4.08

^aThe reference pKa is the experimental pKa values for the model compounds that were measured at zero ionic strength.¹

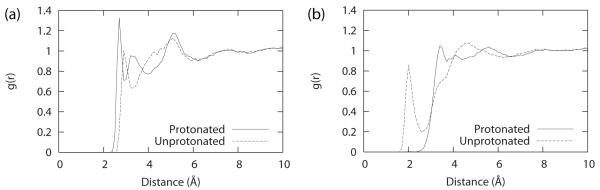
The variable bias with a relatively large force constant of 28 to 30 kcal/mol that is required to achieve a reasonable number of transitions in our simulation may be rationalized by noting that the appearance of a full charge unit when titrating between the two states is likely to significantly perturb the solvent environment around the nitrogen atom. We suggest that time is required for the solvent to reorganize and fully accommodate the new charge distribution as the system titrates from the unprotonated to the protonated state. Figure 4 provides a comparison of the radial distribution function (RDF) of water molecules surrounding the N1 atom of adenosine in its protonated and unprotonated state and indicates that considerable rearrangement of the first solvent shell upon ionization of the residue does occur. For the RDF that describes the distances between N1 and the TIP3P oxygen atoms, we observed that the charged protonated state had a first solvation shell (2.7 Å) that is slightly closer than the uncharged unprotonated state (2.9 Å). A more significant change, however, was observed for the RDF that describes the distances between N1 and the TIP3P hydrogen atoms in which the protonated state first solvation shell was pushed back (3.4 Å) compared to that of the unprotonated state (2.0 Å). These observations are consistent with the expectation that water molecules would orient their hydrogen atoms towards the partial negative charge of the nitrogen atom in the unprotonated state and subsequently would flip their hydrogen atoms “outwards” and orient their oxygen atoms closer towards the partial positive charge of the protonated hydrogen that is present in the protonated state. Similar trends were observed for the RDF of water molecules that surround the N3 atom of cytidine (data not shown). An analogous change in RDF of water molecules around the protonated N5 atom of the substrate of dihydrofolate reductase was also observed with MD simulations that sampled different protein conformation that altered the water accessibility of the ligand pocket.⁸²

Figure 4.

RDF of water molecules for (a) N1(ADE)-O(TIP3P) distances and (b) N1(ADE)-H(TIP3P) distances within a sphere of 10 Å from the N1 atom of adenosine in both protonated and unprotonated states.

4.3 Sampling Efficiency of Explicit Solvent CPHMD simulations

The sampling efficiency as measured by the transition rates between the two protonation states in our CPHMD^MSλD model is quite good with ~50 transitions per ns for our model compounds at pH = pKa. Given that the solvent reorganization upon the perturbation of a full charge unit was reported to be on a time scale of up to 3 ps in previous MD simulations³⁹ and that the mean duration of the physically-relevant protonation states in our simulations is 20 ps, the sampling characteristics of our system is sufficient to allow solvent reorganization to occur. However, the transition rate is markedly lower than what has been observed in CPHMD simulations that are performed using implicit solvent models.^52,53 It should be noted that our model potential parameters, specifically the k_bias values as implemented in CPHMD^MSλD have been selected conservatively. For example, the transition rate can be doubled at the expense of reducing the FPL to 0.6 (Figure 3) which, provided that simulations are long enough to sufficiently enumerate the relative end-state populations, may be a better option for simulating full RNA systems where observing transitions between protonation states may be more challenging.

The more limited sampling efficiency of explicit solvent CPHMD simulations was also recently reported by Grubmüller and co-workers where the titration of an imidazole model compound achieved ~100 transitions in a 20 ns trajectory,⁶¹ which is a rate of ~5 transitions per ns. Considering the computational expense of performing explicit solvent simulations, our rate of ~50 transitions per ns that is achieved with the optimization of our implementation of explicit solvent CPHMD is clearly advantageous. Finally, in Table 3, we present a comparison between the sampling characteristics of our simulation to that of previous work performed in the MSλD framework by Knight and Brooks for modeling series of inhibitors of HIV-1 reverse transcriptase.⁷² Using the same force constant for the variable bias (i.e., k_bias = 7) as what was previously reported, we observed a significant drop in sampling performance with virtually no transitions observed between the two protonation states at pH=pKa. Our optimization of k_bias assisted in improving the sampling characteristics, but the transition rate still remains about four fold less efficient than previous work. We note that earlier work performed by Knight and Brooks modeled hybrid ligands in which the substituents did not differ significantly in terms of their partial charge distributions. Thus, the introduction of a full charge unit when titrating between the two states in CPHMD^MSλD is likely to be the primary cause for the reduction sampling efficiency that we observe in the present simulations.

Table 3.

Sampling characteristics of simulations performed at pH = pKa

	Previous Worka	Adenosine (Default)b	Cytidine (Default)b	Adenosine (Optimized)c	Cytidine (Optimized)c
kbias	7.00	7.00	7.00	29.75	27.75
FPL	0.780	1.000	1.000	0.828	0.832
Transitions (ps−1)	0.190	0.001	0.001	0.050	0.051

^aSampling characteristics of a two-state hybrid ligand in explicit water investigated in previous work (obtained from Table 3, hybrid ligand F).⁷²

4.4 Convergence and Precision of Calculations

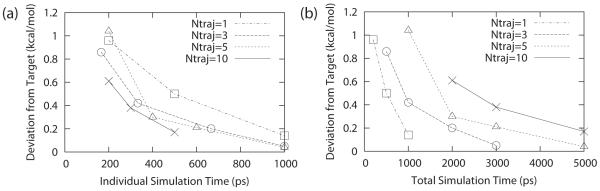
The challenges associated with sampling and convergence for CPHMD simulations has been reported on several occasions^48,54 and these are expected to be an even greater concern in explicit solvent CPHMD where sampling efficiency is reduced. To validate the robustness of our CPHMD^MSλD model in its ability to achieve adequate convergence, we performed a series of simulations at pH = pKa for our model compounds. The degree of convergence in our simulations was determined by calculating the unsigned deviation between the free energy of protonation, estimated from subsets of shortened trajectories, and the free energy of protonation that was estimated from ten 1ns trajectories. Different combinations of trajectory length and number of independent runs were systematically examined to determine the most cost effective tradeoff between computational expense and precision of the calculations. The results are summarized in Figure 5. It was observed that individual trajectories required at least 100 ps to reliably observe any transitions between protonation states. In fact, we observed that a minimum simulation time of ~ 500 ps per trajectory was required to obtain a precision of ~0.20 kcal/mol in our calculations (Figure 5a) and running multiple shorter independent runs would not produce converged results unless the 500 ps threshold was crossed. Our results indicate that good precision can be achieved by using a total simulation time of 3 ns in the form of 3 independent runs of 1 ns each, where the unsigned deviations for the free energy of deprotonation was 0.05 kcal/mol for adenosine (Figure 5b). It should be noted, however, that this level of precision was achieved in previous work three times more quickly for hybrid ligands whose charge distributions were similar. All subsequent calculations of pKa values in this paper were estimated using three independent runs of 1 ns each.

Figure 5.

Unsigned deviation for the free energy of deprotonation of adenosine as a function of (a) total simulation time from all N trajectories and (b) individual simulation time of each of the N trajectories.

The performance of the multi-site λ-dynamics (MSλD) approach, on which CPHMD^MSλD is based, has been evaluated in comparison to traditional FEP calculations by Knight and Brooks.⁷² For substituents with similar charge distributions, it has been established that relative hydration and relative binding free energies calculated from both MSλD and FEP are in good agreement with each other and MSλD was three times more efficient than regular FEP. Our current work involves substituents that have significantly different charge distributions from one another, i.e. the charges associated with the protonated and deprotonated states respectively, and consequently CPHMD^MSλD takes longer to converge. Analogously, we expect that FEP calculations will also take longer than what was reported in Knight and Brooks, but would still be less efficient in their convergence than MSλD calculations. In addition, traditional FEP calculations are not well-suited for simultaneously exploring multiple titrating sites or multiple tautomers, and so the MSλD-based approach of CPHMD^MSλD is more generalizable than FEP methods to model these more complex situations.

4.5 Calibration Curve of Model Systems: Adenosine and Cytidine

We calibrated our CPHMD^MSλD model at 298 K using zero salt concentration. The reference pKa that was used in the calibration was the experimental pKa that was measured under similar conditions (25°C at zero ionic strength).¹ The titration curve of the model nucleoside compounds, adenosine and cytidine, are shown in Figure 6. The best-fit Henderson-Hasselbalch curve has a near ideal Hill coefficient for adenosine (n = 0.94) and cytidine (n = 0.93). The calculated pKa value of 3.50 for adenosine was in excellent agreement with experimental values and the pKa of 4.22 for cytidine is only slightly higher than the reference value by 0.14 pKa units. The accuracy of the calculated pKa values is determined primarily by the sampling efficiency at pH = pKa and the quality of the calibration of the G_bias values that are used to simulate distinct pH conditions. Our results demonstrate that a series of 3 × 1 ns simulations is sufficient to provide reasonably accurate results, which is significantly less than the 20 ns trajectory employed by Grubmüller and co-workers in their explicit solvent CPHMD model.⁶¹

Figure 6.

Sample titration curves for model nucleoside compounds, (a) adenosine and (b) cytidine.

4.6 Quantitative pKa value calculations for simple nucleotides

First, we tested our CPHMD^MSλD model on single nucleotide test compounds, adenine monophosphate (AMP) and cytosine monophosphate (CMP), at zero ionic strength and the results are summarized in Table 4. The calculated pKa values for AMP-5 and β-AMP-3 were 4.08 and 4.20 respectively. Compared to adenosine, the pKa values of these nucleotide counterparts were slightly elevated by ~0.5 pKa units. Similarly, the nucleotide counterparts of cytidine with pKa values for CMP-5 and β-CMP-3 of 4.90 and 4.77, respectively, had slightly elevated pKa values by ~0.5 pKa units compared to cytidine. The calculated pKa values for both 5′-phosphate and 3′-phosphate isomers of adenosine and cytosine are not statistically different at the 95% confidence interval. The increase in the calculated pKa values from their nucleoside counterparts is expected, since the presence of the negative charge from the phosphate group may interact with the positively charged protonated base and weakly stabilize it, thus increasing the population of the protonated state and causing a corresponding increase in the calculated pKa value.

Table 4.

Calculated and experimental pKa values of test compounds.

Compound	[NaCl] (M)	Calculated	Experimental	Abs. Error
β-AMP-3	No salt	4.20 ± 0.06	-	-
β-AMP-3	0.15	3.79 ± 0.11	3.65	0.14
AMP-5	No salt	4.08 ± 0.03	-	-
AMP-5	0.15M	3.89 ± 0.16	3.74	0.15
β-CMP-3	No salt	4.77 ± 0.05	-	-
β-CMP-3	0.15M	4.56 ± 0.10	4.31	0.25
CMP-5	No salt	4.90 ± 0.07	-	-
CMP-5	0.10M	4.67 ± 0.08	4.24	0.43

In order to compare our calculated pKa values with experimental results, we performed simulations that mimicked the ionic strength of the environment (i.e., 100-150mM NaCl) in which the experiments were performed.^83,84 By explicitly incorporating the salt environment, the calculated pKa values are systematically lowered relative to those obtained from the zero ionic strength simulations. This shift in pKa values is to be expected since the presence of Na⁺ ions screens the electrostatic effects of the phosphate group. The results in Table 4 indicate that our pKa predictions had an average absolute error of 0.24 pKa units compared to experiment and we conclude that our CPHMD^MSλD model is capable of making accurate quantitative predictions of pKa values for simple nucleotides. These results also indicate that our model is capable of accounting for the differences between zero and non-zero ionic strength environments and highlights the importance of simulating the system at the appropriate ionic strength to mimic experimental conditions.

4.7 Modeling Interactions between Adjacent Titrating Residues

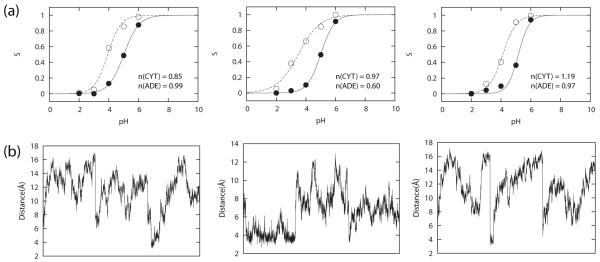
Finally, we tested our CPHMD^MSλD model on dinucleotide sequences ADE-ADE, CYT-CYT and CYT-ADE at zero ionic strength, where both nucleotides were titrated simultaneously in the same simulation. The pKa values were shifted upwards compared to the nucleoside model compounds for all sequences, ADE-ADE (4.08 ± 0.20 and 4.06 ± 0.16), CYT-CYT (4.93 ± 0.05 and 4.76 ± 0.09) and CYT-ADE (5.06 ± 0.07 and 3.85 ± 0.26), and were similar to the corresponding mononucleotide pKa values. For some of the sets of pKa calculations for the dinucleotide sequences, the Hill coefficient had more significant deviations from one compared to the monomeric compounds. Specifically, the value was lowered (n < 0.8) for 5 of the 9 sets of pKa calculations. When the Hill coefficient deviates from one, it suggests that adjacent residues are interacting with each other in either a cooperative (n > 1) or anti-cooperative (n < 1) fashion. Cross-correlation analysis of the protonation states (data not shown) however, indicates only weakly correlated behavior, which suggests that the interaction between adjacent residues is not strong. The second set of pKa calculations on CYT-ADE exhibited the lowest Hill coefficient (n = 0.60) indicating the strongest anti-cooperative behavior. Analysis of the individual titration curves as shown in Figure 7 indicate that the S^unprot ratio shows the greatest deviation between the second set and the other two sets at pH 3. We analyzed the mean distance between the nitrogen atom that is protonated in CPHMD (i.e., N3 CYT and N1 ADE) of adjacent residues at pH 3 and the results are shown in Figure 7. In one simulation of the second set, the mean distance sampled was about 4 to 6 Å, in comparison to the typical values of 8 to 16 Å for all other simulations. We suggest that this simulation contributed significantly to the higher S^unprot ratio for the second set that in turn gave rise to the lower Hill coefficient. The lack of strong interactions between adjacent titrating residues in the other two sets of pKa calculations of CYT-ADE is apparently due to the result of the lack of sampling of configuration space in which these two residues are close enough to influence each other’s protonation state. We suggest that stronger cooperative or anti-cooperative effects are likely to be observed when modeling RNA structures with stable conformations in which the nucleobases are held in close proximity to one another.

Figure 7.

(a) Titration curves for CYT-ADE and (b) time series of distance between N3 CYT and N1 ADE atoms at pH 3 for all 3 sets of pKa calculation.

4.7 Moving towards CPHMD of full RNA systems

The remarkable agreement of our calculated pKa values to experiment is encouraging; however, several challenges may be anticipated when applying our CPHMD^MSλD model to full RNA structures.

First, instead of isolated monomeric compounds, the titratable residues of interest in RNA macromolecules are nucleotides that are buried in the interior of the RNA which interact with multiple residues (e.g. via base-pairing interactions). Therefore, the increased perturbation of the titrating residue’s local environment and the increased complexity arising from non-bonded interactions with adjacent residues is likely to reduce sampling efficiency in full RNA structures. We illustrate this claim with a hypothetical example of a residue whose pKa value varies with RNA conformation. The formation of a Watson-Crick A-T base pair involves the N1 atom of adenine and this results in a depression of its pKa value relative to the isolated base since the nitrogen atom (that would be protonated in CPHMD) is now serving as a hydrogen bond acceptor. Conformational fluctuations, such as helical unwinding motions, may expose these buried nucleotides to the solvent and cause a corresponding increase in their respective pKa values. In order to reproduce experimentally measured pKa values from NMR studies in the above example, it may be necessary to sample these two conformational states that are observed at the timescale of which the measurements were taken. The use of advanced sampling methods such as replica exchange has been previously implemented in protein CPHMD by Brooks and co-workers to improve sampling performance,⁵⁴ and when used with CPHMD^MSλD may be expected to yield similar improvements in model performance. Similarly, accelerated molecular dynamics⁸⁵ has been implemented with CPHMD and it has yielded improvements in conformation sampling.⁴⁸ Other sampling methods developed to sample long timescale conformation changes such as self-guided langevin dynamics^86,87 may also achieve a similar effect.

Another challenge may arise from the sampling in λ phase space in the presence of many interacting titratable groups. Under the physiologically relevant pH range, protein residues typically have 4 titratable residues out of 20 amino acids. In contrast, half of the nucleic acid building blocks are titratable in our current CPHMD^MSλD model. While it may be common that titratable residues on a protein are seperated from one another in terms of spatial proximity, and thus the state of one titratable residue is unlikely to influence the others, this is not the case for RNA. In the absence of prior information about which residues will likely be in which protonation states, all adenosine and cytosine residues in the macromolecule could be modeled as titratable. However, in this case, the cooperative or anti-cooperative effect that these simultaneously titrating residues have on one another could be significant. Such a situation may lead to hidden barriers in adjacent λ phase spaces, in which the λ values of residue i are restricting the propogation of the λ values of residue j. Thus, the efficiency of sampling in λ phase space would need to be improved and a lower FPL without compromising the physical accuracy of the model may be necessary in order to maintain a reasonable minimum transition rate between the two protonation states. A recently developed enhanced sampling technique, orthorgonal space random walk (OSRW) has been developed to address such sampling challenges associated with strongly coupled hidden free energy barriers, and it has been successfully applied to predict the pKa values of buried protein residues that are typically not accurately reproduced in conventional CPHMD approaches. The implementation of OSRW with CPHMD^MSλD could potentially model strongly coupled titrating residues with better accuracy.^62,88

For MS-CPHMD to successfully investigate pH-dependent properties of RNA structures over a longer timescale (μs and beyond) or pH-dependent properties of large RNA structures such as a ribosomal subunit, a reduction of the computational expense that is associated with explicit solvent CPHMD is desirable. Greater computational efficiency may be achieved by using hybrid explicit/implicit solvation models, in which a few layers of explicit solvent water molecules are placed near the RNA surface with the rest of the environment described by an implicit solvation model.^89-91 Other models reduce the number of explicit waters in the simulation by using a thin shell of explicit water and hold these waters near the RNA surface with a restraining force,^92,93 The use of the surface constrained all atom solvent (SCAAS) model that requires fewer explicit water molecules than the periodic boundary conditions (PBC) implementation in MD simulations^94,95 has also been validated on a number of pKa calculations performed on protein residues.^37,96 Multiscale modeling approaches that use a coarse-grained model to provide the reference potential for the thermodynamic cycle that can be used to speed up the free energy calculations of protonation events to simulate pH-dependent dynamics have also been reported recently.^49,97 Alternatively, we have seen considerable advances in implicit solvent models in recent years⁹⁸ and they been been successfully implemented with protein CPHMD.^52-54 Established work in parameterizing implicit solvation models for RNA is encouraging,⁹⁹ but ongoing work in our lab (unpublished results) indicates that implicit solvent models do not accurately reproduce explicit solvent simulations results when simulating RNA. Therefore, the successful implementation of an implicit solvation model to CPHMD^MSλD would be an avenue for future development.

Finally, while the use of NaCl may serve to reproduce the ionic strength environment at which experimental studies are conducted, divalent ions such as Mg²⁺ play functional roles in many RNA structures and current parameters would need to be examined to ensure their ability experimental observables in RNA macromolecules. Our CPHMD^MSλD model may also be expanded to include titratable residues of guanine, uracil and thymine. Although the bulk of experimental studies have implicated adenine and cytosine as key protonated residues in RNA, there is some evidence that suggests that the presence of protonated guanine, such as the G8 residue in the active site of the hairpin ribozyme, may also play a mechanistic role.¹⁰⁰ The adoption of the λ^Nexp functional form for lambda in our CPHMD^MSλD model also allows us to expand the representation of the titratable fragments to include tautomeric forms of nucleotides in both the unprotonated and protonated states. Recent theoretical studies have also suggested that stable tautomers may exist under specific conditions.^101-103 Thus, the ability to titrate among four states (unprotonated, unprotonated tautomer, protonated and protonated tautomer) may assist in clarifying the structural or mechanistic roles that involve tautomeric forms in RNA.

5. CONCLUSION

In conclusion, we have parameterized a protonated adenine and protonated cytosine for use in the first reported constant pH molecular dynamics (CPHMD) for nucleic acids. We have adopted the new functional form λ^Nexp for λ that was recently developed for Multi-Site λ-Dynamics (MSλD) and demonstrate good sampling characteristics in which rapid and frequent transitions between the protonated and unprotonated states at pH = pKa are achieved, while sampling the physically-relevant protonation states for more than 80% of the trajectory. Compared to existing implementations of explicit solvent CPHMD, the sampling in our method sees a 10-fold improvement, while maintaining sufficient residency time of the physical protonation states to ensure proper solvent reorganization. A series of 3 independent runs of 1 ns each was determined to be sufficiently precise for calculating the pKa values for simple nucleotide systems. pKa values calculated for simple nucleotides are in a good agreement with experimentally measured values with a mean absolute error of 0.24 pKa units, affirming that our CPHMD^MSλD model has the ability to make accurate quantitative predictions for simple nucleotide systems. Our work paves the way for the deployment of CPHMD as a powerful tool to investigate pH-dependent biological properties of RNA macromolecules.