The Geometry of Visual Perception: Retinotopic and Non-retinotopic Representations in the Human Visual System

Abstract

Geometry is closely linked to visual perception; yet, very little is known about the geometry of visual processing beyond early retinotopic organization. We present a variety of perceptual phenomena showing that a retinotopic representation is neither sufficient nor necessary to support form perception. We discuss the popular “object files” concept as a candidate for non-retinotopic representations and, based on its shortcomings, suggest future directions for research using local manifold representations. We suggest that these manifolds are created by the emergence of dynamic reference-frames that result from motion segmentation. We also suggest that the metric of these manifolds is based on relative motion vectors.

I. Introduction

There exists a fundamental relationship between visual perception and geometry. Points, lines, angles, surfaces, shapes, and solids constitute elementary objects of both. They are both concerned with the measurement and characterization of these elements as well as their relationships. It seems reasonable therefore that geometry would be the appropriate branch of mathematics in understanding how information is represented and processed in the visual system. The geometry of early visual processing is relatively well understood. Three-dimensional stimuli are imaged on the retina through the optics of the eye following the laws of optics. This geometric transformation maps neighboring points in the environment to neighboring photoreceptors in the retina. The projections of neurons from retina to early visual cortical areas preserve these neighborhood relations, a property known as retinotopy. Thus, scenes create two-dimensional images like images created by a camera.

From the reverse-engineering perspective, computational theories of visual processing rely on these retinotopic neighborhood relationships. For example, in these theories, the processing of stimulus attributes such as orientation, contour, and shape is based on neighborhood relationships between points, lines, etc. Neural counterparts of these theories are based on processing carried out by neurons whose receptive fields reflect retinotopically-based computations that lead to edge detection, contour completion, etc. As an example, Fig. 1 shows schematically how local interactions between retinotopically organized neurons in the primary visual cortex can lead to the detection of oriented edges in the stimulus. Empirical studies also use extensively the knowledge of this retinotopic organization. For example, investigations, carried out at small-scale, probe the activities of a few neurons by single or small arrays of electrodes inserted into the cortex. By moving the stimulus in a small spatial neighborhood, one can probe interactions between the recorded cell and its neighbors and thereby map a “receptive field” for the cell which can be interpreted as local interactions between neurons in the retinotopic space. Large-scale investigations using the functional Magnetic Resonance Imaging (fMRI) technique routinely use retinotopic mapping approaches (Fig. 2) to determine the geometric correspondence between visual space and neural maps as well as to determine borders between different visual areas (e.g., V1, V2, V3, etc.) in the cortex.

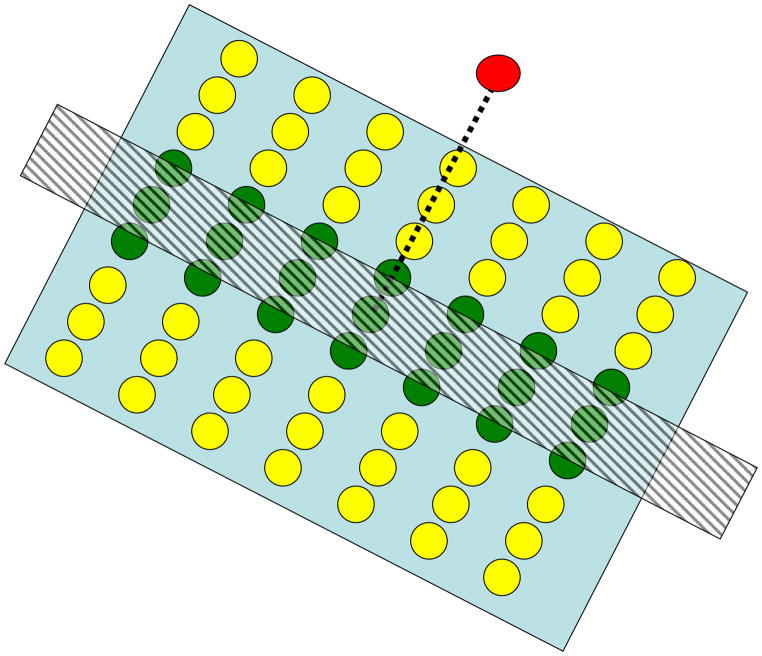
Fig. 1.

Depiction of oriented edges by retinotopically organized interactions. The red neuron receives excitatory and inhibitory connections from green and yellow neurons, respectively. Through retinotopic mapping, a spatially oriented stimulus (hatched rectangle) will activate a similarly oriented set of neurons in the retinotopic space. When the orientation of the stimulus matches the orientation of the excitatory region, the red cell becomes activated maximally. For other orientations, the activity of the red cell will be reduced due to the inhibitory signals generated by the surrounding yellow neurons.

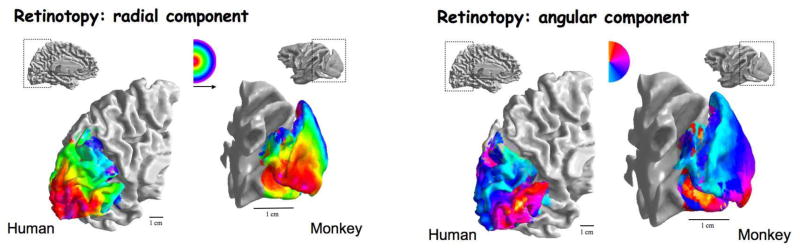
Fig. 2.

Example of retinotopic maps in polar coordinates in human and monkey cortex. The left and right panels show radial and angular components according to the color codes shown in the insets. Reproduced by permission from [31] with original data from [13], [23].

From the forward-engineering perspective, the knowledge of retinotopic representations is key in designing sophisticated retinal or cortical implants so as to match the geometry of implant electrodes to that of the nervous system.

While retinotopic representations in early visual areas are well established, very little is known about the organization of higher visual areas; although some recent studies revealed retinotopic maps driven by stimulus or attention beyond the early visual cortex [3], [72].

Regardless how far retinotopic representations persist in the visual cortex, based on psychophysical data, it has been known for more than a century that a retinotopic representation is neither sufficient nor necessary for the perception of spatially extended form. Therefore, a fundamental problem in neuroscience is to understand the geometrical properties of visual processing from the early retinotopic to the higher non-retinotopic levels. In the following, we will review evidence highlighting the shortcomings of retinotopic representations and point to future research directions that may be instrumental in revealing the geometry of visual representations beyond the basic retinotopic maps.

II. A Retinotopic Representation is not Sufficient for form perception

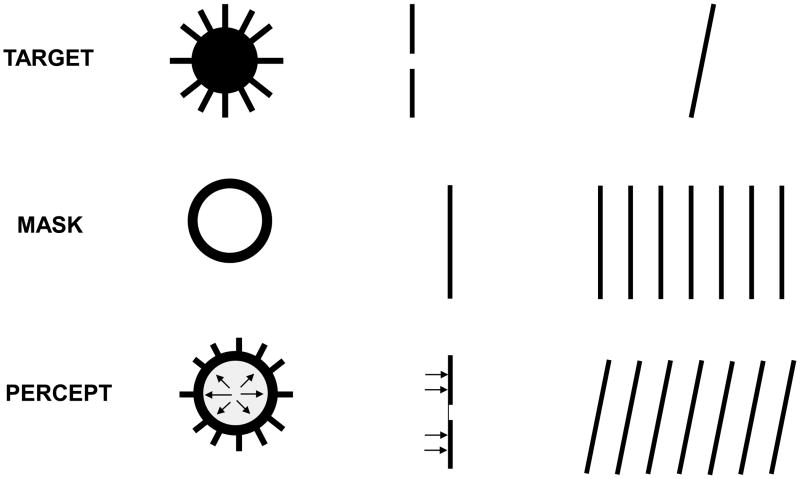
Metacontrast masking refers to the reduced visibility of one stimulus, called the target, due to the presence of a second, spatially non-overlapping, stimulus called the “mask” (Fig. 3) [7],[12]. The presentation of the mask is delayed with respect to the presentation of the target. Although the target is fully visible when presented without the mask, the spatially and thus retinotopically, non-overlapping mask can render it completely invisible. This empirical observation shows that the presence of a retinotopic image is not a sufficient condition for the perception of form. It also highlights the importance of the dynamic context in determining whether form perception takes place. In the following sub-sections, we discuss two dynamic aspects of natural viewing conditions that suggest why a retinotopic representation is insufficient in the computation of visual form.

Fig. 3.

A typical metacontrast stimulus. First, the disk (target) is presented briefly. After a temporal delay, the ring (the mask) is presented briefly. Observers are asked to judge a quality, e.g., brightness of the target.

A. Eye movements

Natural vision is highly dynamic in the sense that we continuously explore our environment by frequent gaze shifts. Our eyes undertake both voluntary and involuntary movements which can be conjunctive (the two eyes move in the same direction) or disjunctive (the two eyes move in opposite direction), smooth (for example, when we pursue a smoothly moving object) or non-smooth (for example when we make a “saccadic eye movement” by shifting our gaze rapidly from one fixation point to another). All these observations indicate that the retinotopic stimulus undergoes drastic and complex changes during normal vision, 3–4 times per second. Nevertheless, our perception of the world remains stable suggesting that the visual system transforms retinotopic representations to those that are invariant with respect to eye movements.

B. Movement of objects

A briefly presented stimulus remains visible after the stimulus offset, a phenomenon known as visible persistence. Under normal viewing conditions, visible persistence is approximately 120ms. Based on this value of visible persistence, one would expect moving objects to appear highly smeared, much like pictures of moving objects taken by a camera with a shutter speed of 1/120ms. Fig. 4 shows an illustrative picture where static objects appear clear while moving objects are highly blurred. Yet, under normal viewing conditions, moving objects appear relatively sharp and clear. This raises two questions: How is motion smear avoided and how is clarity of form achieved?

Fig. 4.

Picture illustrating the effect of visible persistence. Picture courtesy of Murat Kaptan.

With respect to the first question, as mentioned above, metacontrast masking operating in the retinotopic space can reduce the spatial extent of motion smear by suppressing activity underlying the motion smear [20],[64]. However, metacontrast mechanisms address only the first question stated above. If we consider Fig. 4, retinotopic metacontrast mechanisms would reduce the spatial extent of motion streaks thereby reducing the amount of blur in the picture. However, moving objects would lack clarity and thus would still suffer from having a “ghost-like” appearance. For example, in Fig. 4, stationary objects appear relatively clear with well-defined form. In contrast, moving objects are fuzzy and lack clarity of form. This is particularly true for objects that move fast in the image plane, or equivalently in retinotopic representations (e.g., the vehicle close to the observer crossing the street). This is because static objects remain long enough on a fixed region of the film to expose sufficiently the chemicals while moving objects expose each part of the film only briefly thus failing to provide sufficient exposure to any specific part of the film. A similar argument can be made for retinotopic representations. A moving object will stimulate each retinotopically localized neuron briefly resulting in an incompletely processed form information that is spread across the retinotopic space just like the ghostly appearances in Fig. 4. We call this fundamental problem of moving form computation “the problem of moving ghosts”. As we will discuss in the following sections, several lines of evidence suggest that the visual system overcomes this “problem of moving ghosts” by computing the form of moving objects in non-retinotopic representations.

III. A Retinotopic Representation is not necessary for form perception

The geometric transformation of the three-dimensional environment into a two-dimensional image implies that objects can partly or fully occlude each other in the retinotopic representations. As a result, retinotopic information about the occluded object will be incomplete; this can be partial or complete, steady (for static objects) or transient (for dynamic objects). In the presence of occlusions, we do not perceive a set of fragmented parts; rather, the occluded object appears as a whole, a phenomenon known as amodal completion [44]. For example, in Fig. 5, the three dark segments appear as parts of the same single object, an occluded triangle. While one can argue that amodal completion can be accomplished in retinotopic representations, a limiting case of dynamic occlusion where a moving object is viewed behind a narrow slit shows that a retinotopic image is not necessary for the perception of spatially extended form. This paradigm, called anorthoscopic perception, derives its name from the anorthoscope, a device invented by Plateau [63]. Since its invention, the anorthoscope has been used in several laboratories as a scientific equipment to study human perception (e.g., [32],[66],[70],[92]). Fig. 6 depicts the retinotopic representations generated in anorthoscopic viewing. Given the optics of the eye, all information about the moving object is mapped in a very narrow retinotopic region corresponding to the interior of the slit. In other words, there is no spatially extended retinotopic representation for the moving stimulus. Yet, observers perceive a spatially extended shape moving behind the slit rather than an incoherent pattern confined to the region of the slit. Can this be explained based on retinotopic representations? Helmholtz [32] put forward the “retinal painting” hypothesis to explain anorthoscopic perception. According to this hypothesis, if the eyes move smoothly during the presentation of the stimulus, then successive parts of the stimulus shown behind the slit will be imaged on adjacent retinotopic positions. Hence, a retinotopic picture of the figure will be “painted” as a consequence of eye movements. This explanation implies that retinotopic representations are sufficient to explain anorthoscopic perception. While it is true that retinal painting can give rise to the perception of form, several studies showed that anorthoscopic perception does occur without any contribution of eye movements (e.g. [27],[46]). Taken together, these results show that a retinotopic image is not necessary for the perception of spatially extended form and suggest that the visual system must be using non-retinotopic representations for spatially extended form. Thus understanding mechanisms of anorthoscopic perception can play a crucial role not only in revealing the characteristics of non-retinotopic representations used by the visual system but also the transformations that occur between early retinotopic representations and higher-level non-retinotopic representations.

Fig. 5.

Amodal completion. The three dark segments appear as parts of a single object, an occluded triangle.

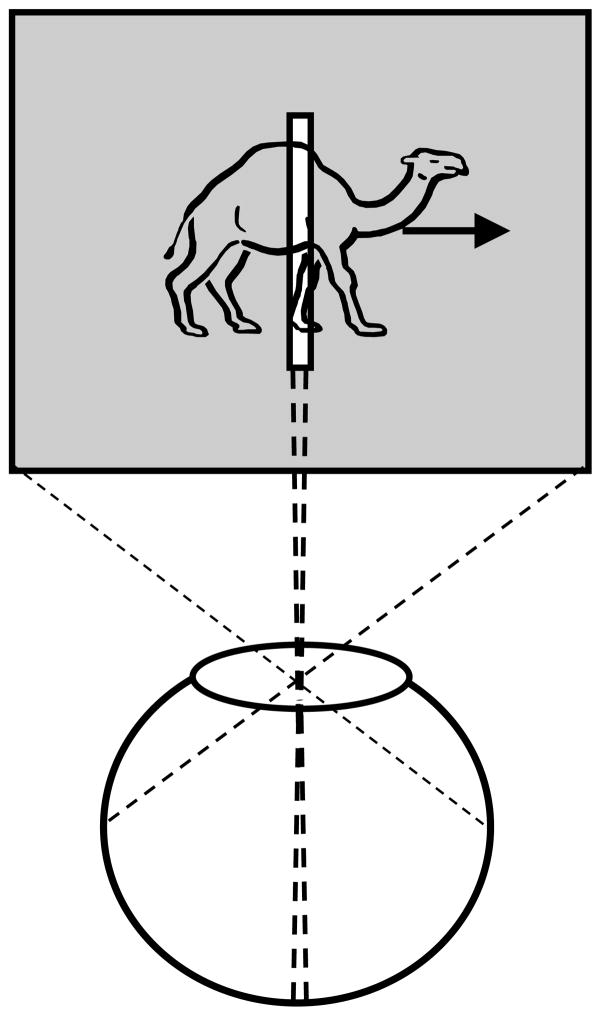
Fig. 6.

Retinotopic representation during anorthoscopic viewing. All information about the moving object falls into a very narrow retinotopic strip corresponding to the area of the slit. In other words, there is no spatially extended retinotopic representation for the moving stimulus.

Before we analyze anorthoscopic perception further, let us consider the geometrical aspects of an extensively studied function of the visual system, viz., the synthesis of invariant “object” representations and discrimination of different objects or patterns

IV. Insights on non-retinotopic representations from invariant pattern recognition and discrimination

From the mathematical point of view, natural visual stimuli reside in a very high-dimensional space and the probability of receiving the exact same stimulus more than once is quite low. For example, the proximal stimulus corresponding to a face can change over time due to changes in position, size, pose, expression, lighting, and occlusions to name just a few factors. Notwithstanding these variations, the visual system is capable of building more abstract representations that allow the integration of different instances of an “object” into a single category and, at the same time, segregation of instances of different objects into different categories. These dual problems of pattern recognition and discrimination attracted extensive interest from both biological and computer vision communities. Rosenblatt’s “Perceptron” is one of the earliest examples of biologically-inspired and mathematically-formulated pattern-recognition systems [70]. Interestingly, a geometrical analysis of elementary versions of Perceptron revealed that their scope is limited to linearly-separable problems [45]. The geometrical analysis also reveals that a cascade of such networks can solve arbitrarily complex pattern discrimination problems. They achieve this feat by transforming the geometrical representation of the inputs into linearly-separable internal representations [24]. Another key aspect of the geometrical transformations applied to inputs is the ability to reduce the dimensionality of the stimuli. Several methods for embedding high-dimensional inputs into low-dimensional manifolds have been proposed both as computer vision algorithms and as human vision models (e.g., [25],[41],[71],[73],[80]). In terms of neural substrates, object categorization in the ventral pathway of the primate visual system has been modeled by using the concept of linearly-separable manifolds (rev. [22]). While these remarks highlight the plausibility of manifolds as geometrical representations for complex inputs, much needs to be done to develop and test a comprehensive theory based on manifold representations.

In the following, we will analyze critical paradigms that shed light on the limitations of retinotopic representations and suggest a non-retinotopic manifold representation where motion information and reference frames play an essential role.

V. Insights on Non-Retinotopic Representations from Studies of anorthoscopic perception

A second theory of anorthoscopic perception, “time-of-arrival theory”, posits that a “post-retinal mechanism” stores in memory the information available through the slit and reconstructs a spatially extended version by converting the time-of-arrival into a spatial code [60]. However, this theory has also been refuted based on empirical data. Consider the stimulus shown in Fig. 7 [43],[75],[76]. The stimulus consists of dots depicting two triangular shapes that move in opposite directions. The tips of the triangles pass through the slit simultaneously, followed by the middle segments and finally the base segments. Denote by t₀, t₁, and t₂ with t₀<t₁<t₂ the time instants at which the tip, the middle, and the base of the triangles, respectively, become visible inside the slit. According to the time-of-arrival coding theory, the arrival times for the different parts of the figure t₀, t₁, and t₂ are converted to corresponding spatial positions s₀, s₁, and s₂ with s₀<s₁<s_2. As a result, the theory predicts that observers should perceive the two triangles pointing in the same direction [52]. However, observers perceive the orientation of the two triangles correctly, i.e., the upper triangle pointing to the left and the lower triangle to the right [43],[75],[76]. Thus, these experiments provide strong evidence against the time-of-arrival theory¹. A critical observation from these experiments is that, if one does not take into account the direction of motion, then the interpretation of the stimulus will be ambiguous in that mirror-symmetric images moving in opposite directions will generate identical patterns in the slit. Therefore, the direction of motion must be an essential component in building non-retinotopic representations associated with anorthoscopic perception [5],[6],[52],[57].

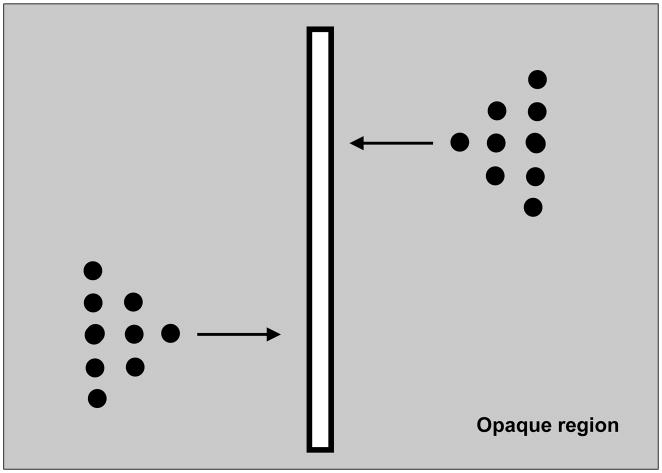
Fig. 7.

Stimulus used to test time-of-arrival and retinal painting theories. Note that in the actual stimulus, triangular stimuli are not visible to the observer when they reside behind the opaque region. They become visible part-by-part as they traverse the slit region.

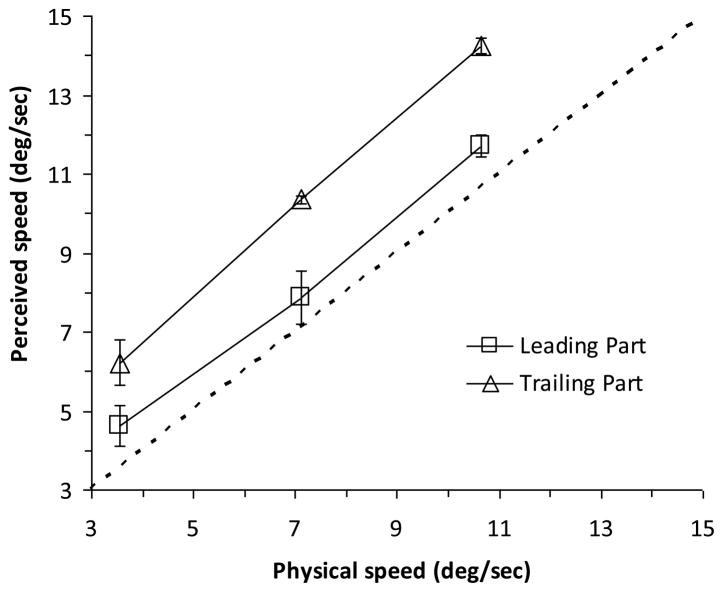
Based on these observations, we hypothesized that non-retinotopic representations are built using motion vectors and that the metric of non-retinotopic representations depends on the motion vectors. To test these hypotheses, we studied a well-known effect in anorthoscopic perception, viz., compression of perceived form along the direction of motion [1],[28],[32],[43],[46],[60],[66],[92]. A prediction of our hypotheses is that perceived shape should depend on perceived motion as the stimulus moves behind the slit and compression of form should occur when the trailing edge of the stimulus is perceived to move faster than its leading edge. We presented ellipses that moved behind a narrow slit and observers judged the perceived speed of the leading and trailing edges of the stimuli [5]. Fig. 8 shows the data averaged across observers. As predicted, the trailing edge of the ellipse appeared to move faster than the leading edge. In separate sessions, observers judged the compression of the ellipses and the data indicate that, perceptually, the ellipses appeared compressed. We attribute this compression to a velocity-dependent metric used in non-retinotopic representations. As we will discuss below, we suggest a general approach to non-retinotopic representations where an early segmentation of the scene based on motion vectors leads into the construction of local manifolds as the fundamental units of non-retinotopic representations.

Fig. 8.

Perceived speeds of leading and trailing parts of an ellipse moving behind a narrow slit. While both parts appear to move faster than their veridical speed, the trailing part appears even faster than the leading part in accordance with our hypothesis. Data, replotted from [6], represent the average and the standard error of the mean across the observers.

VI. Insights on Non-Retinotopic Representations from Studies of Non-retinotopic Feature Perception

Several researchers investigating the metacontrast phenomenon noticed and reported that, even though the mask can render the target invisible, some features of the target could still be seen. Remarkably, these features were not perceived at their retinotopic location but rather were perceptually displaced to appear as part of the mask [33],[34],[78],[79],[82],[87],[88]. This non-retinotopic perception of features was named “feature transposition” [88] or “feature inheritance” [33]. They were typically conceived as errors of the visual system along with other illusions of feature “mis-binding” attributed to lack of attention [83], masking [33],[87],[88], object substitution [26], crowding [59], pooling [8],[59], sampling [16], distributed micro-consciousness [91], and latency differences in stimulus transmission and processing [4],[9]. Yet, several lines of evidence suggest that not all retinotopic mislocalizations reflect errors of visual processing; rather, some follow strategies deployed by the visual system in order to cope with the dynamic constraints outlined in Section II.

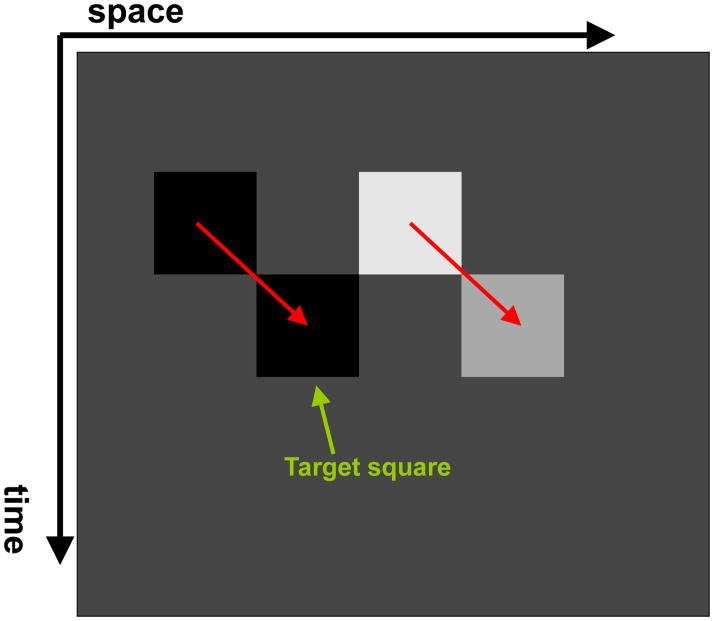
It has been shown that when an object is in motion, the information about its shape [53],[54],[55], luminance [74], color [51], and size [40] is integrated along its motion path. For example, Fig. 10 shows a stimulus configuration used by Shimozaki et al. [74]. The first frame contains two squares, one with low luminance and one with high luminance. In frame 2, these squares are shifted downward and randomly either to the right or left creating the percept of downward-right/left motion. In this example, the luminance of the square on the left remained low while the square on the right reduced its luminance to a medium level. Observers were asked to judge the perceived luminance of the target square (see Fig. 10) with respect to the other square in the second frame. Results indicate that luminance (more precisely relative contrast) is integrated along the motion pathway. It is well known that a rapid succession of red and green stimuli at the same retinotopic location leads to the integration of these colors into the percept of yellow [89]. In a recent study, however, it has been shown that the key in this color integration process is not retinotopy but rather the motion pathway of the stimulus (Fig. 11) [51] or selective attention tracking the motion pathway of the stimulus [17]. By using a repetitive version of metacontrast masking (called sequential metacontrast), we have shown that form information is integrated along the motion pathway even when the stimulus containing the form information is invisible (Fig. 12) [54].

Fig. 10.

Space–time diagram depicting the stimulus used by Shimozaki et al. [74] to study nonretinotopic integration of luminance along the motion path.

Fig. 11.

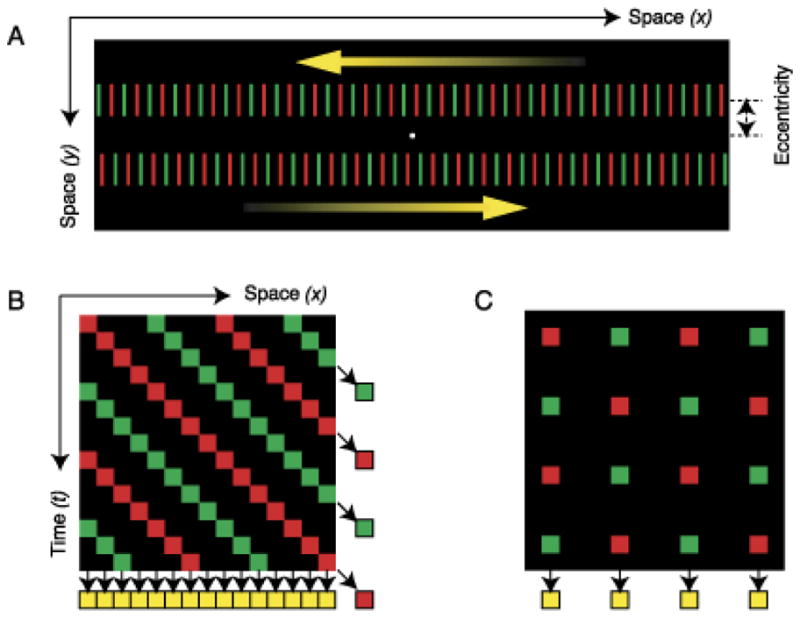
A. Depiction of a stimulus used to show that color is integrated non-retinotopically along the motion path. A series of line segments alternating in color are moved leftward (top) and rightward (bottom). B. Space-time plot of the stimulus where each line is depicted by a square. If the visual system integrates color inputs retinotopically, color combinations should be integrated along vertical direction and the observer should perceive yellow bars as indicated at the bottom of the plot. On the other hand, if the visual system integrates color inputs following the motion path, color combinations should be integrated along diagonal directions and the observer should perceive red and green bars, as indicated at the right of the figure along each diagonal motion path. C. Depiction of the control stimulus where the bars flickered at fixed locations instead of moving sideways. In this case, since the stimulus does not have motion, color integration is retinotopic yielding a percept of yellow. Reproduced by permission from [86] (copyright ARVO).

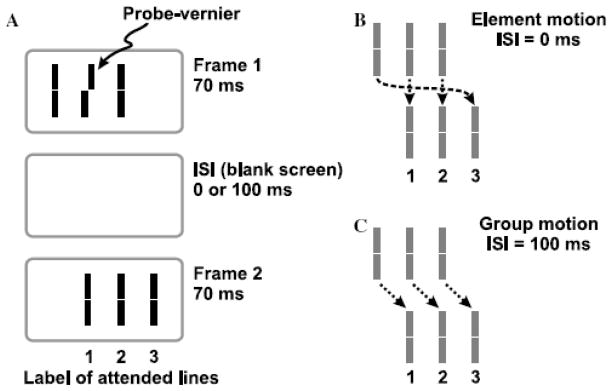
Fig. 12.

In the sequential metacontrast masking paradigm, the target (the central bar with a small offset called “Vernier offset”) is followed in time by a series of flanking bars. Observers perceive two streams of moving lines, one offset to the left and one to the right. The target itself is not visible in that observers cannot discriminate reliably trials where it is present from those where it is absent. The flanking bars do not contain any Vernier offset. The direction (left or right) of the Vernier offset is chosen randomly in each trial and the observers are asked to report the perceived direction of Vernier offset in the left or right stream. Performance of observers in Conditions A and C indicates that the Vernier offset of the invisible target is perceived in the flanking bars. Moreover, when adding a Vernier offset of opposite direction to the attended stream (B) this offset and the target offset cancel each other out. Reproduced by permission from [54] (copyright ARVO).

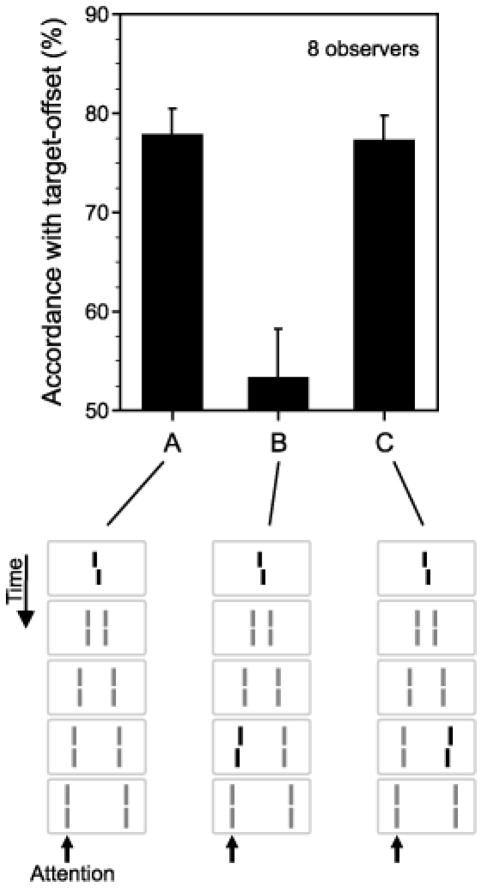
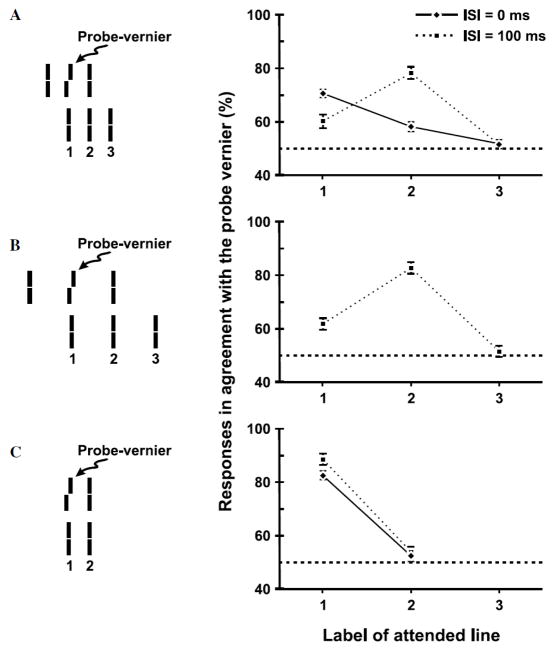
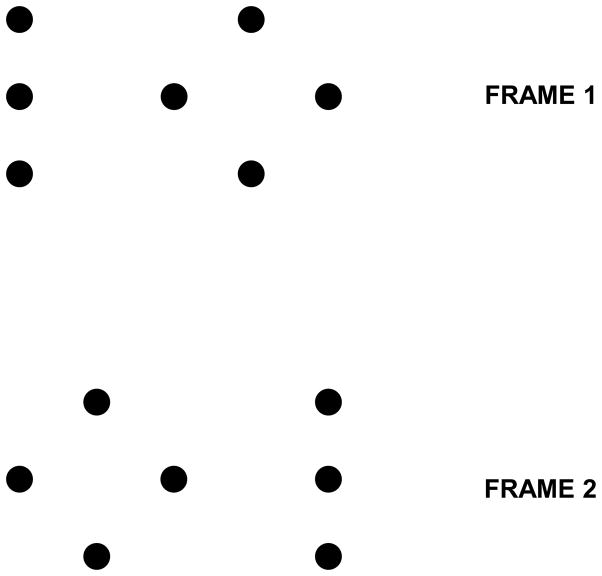
In order to pit directly retinotopic against non-retinotopic integration, we used a stimulus known as the “Ternus-Pikler” display [58],[61],[62],[81]. Fig. 13 shows the basic Ternus-Pikler stimulus. The first frame contains three bars that are shifted to the right by one inter-bar distance in the second frame. When the Inter-Stimulus Interval (ISI) between the two frames is brief, observers perceive the leftmost bar in the first frame to move to the rightmost bar in the second frame. The middle two bars appear stationary. This percept is called element motion. When ISI is long, a completely different percept emerges: Now the three bars appear to move together as a group rightwards, a percept called group motion. In order to investigate whether form is processed according to retinotopic or non-retinotopic geometry, we replaced the bars by line segments [53]. The central line segment contained a small offset, known as Vernier offset. Observers were asked to judge the Vernier offset (left of right) of one of the lines in the second frame. In the first experiment, physically none of the lines in the second frame contained an offset. If the geometry of feature integration were retinotopic, the Vernier offset in the middle segment of the first frame would be integrated with the leftmost element in the second frame because these two elements are retinotopically superimposed. As a result, the accordance of the observers’ response with the physical offset of the Vernier in the first frame should be high for the first element in the second frame and should be approximately at chance level for the other two elements. This prediction holds for all ISIs that fall within the temporal integration limit of the human visual system. On the other hand, if the geometry of feature integration is non-retinotopic and follows the rules of motion grouping, different predictions emerge as a function of ISI. As shown in Fig. 13, when ISI is brief, element motion is perceived and the central element of the first frame is perceptually mapped onto the leftmost element in the second frame. In this case, the prediction is identical to that of a retinotopic representation. On the other hand, when ISI is long, according to the group motion percept the central element of the first framed is perceptually mapped onto the central element in the second frame. Thus in this case retinotopic and non-retinotopic predictions are pitted against each other. According to the former, the accordance of the observers’ responses with the Vernier offset in the first frame should be highest for the leftmost element in the second frame. According to the latter, it should be highest for the central element in the second frame. Our data, shown in Fig. 14, are in agreement with the predictions of non-retinotopic motion-grouping based predictions. Several additional experiments further supported the conclusion that the form of moving stimuli is processed according to a non-retinotopic geometry [53].

Fig. 13.

A. The Ternus-Pikler stimulus. B. Top panel: When ISI=0ms, the leftmost bar in the first frame is perceived to move to the rightmost bar in the second frame while the other two bars appear stationary. This percept is called “element motion”. Bottom panel: When ISI=100ms, the three bars appear to move in tandem giving rise to the percept of “group motion”. Reproduced by permission from [53].

Fig. 14.

Experimental results for the Ternus-Pikler stimulus. Observers were asked to attend to one of the three bars in the second frame, labeled 1, 2, and 3, and report the perceived direction of Vernier offset for this attended bar. The prediction of the retinotopic hypothesis is that the agreement of the responses with the probe-Vernier should be high for element 1 and near chance for elements 2 and 3 for all conditions. The non-retinotopic hypothesis predicts the same for ISI=0 and in the case no motion is perceived (Panel C). On the other hand, the non-retinotopic hypothesis predicts the agreement of the responses with the probe Vernier will be highest for element 2 when group motion is perceived (ISI=100ms in Panel A, and Panel B). The results clearly support the non-retinotopic hypothesis. Reproduced by permission from [53].

Recently, we have shown that the Ternus-Pikler display can be used as a simple “litmus test” to investigate whether any given visual process occurs in retinotopic or non-retinotopic representations [10]. The three elements in the Ternus-Pikler display can assume any geometrical shape (e.g., disks) and inside these elements one can insert stimuli of interest. As an example, Fig. 15 shows a version of the Ternus-Pikler display where the stimulus of interest is a visual search display. The search stimuli in the display are defined on two feature dimensions (orientation: vertical/horizontal and color: red/green). The task of the observer is to report whether a target defined by a specific conjunction of two features (e.g., horizontal red bar) is present within the central disk. In conjunction search, performance, as measured by percent correct or reaction times, drops as the number of distractors is increased. According to current models of visual search and attention, each feature is represented in a retinotopic map and attention is required to look up at a given retinotopic location in each map and to bind features of the object at that retinotopic location. In sharp contrast to the predictions of these theories, we found that performance was close to 80% correct in the case of group motion and was near chance when the percept of motion was obliterated [10]. A consistent pattern was observed in reaction-time measures as well [10]. These findings indicate that conjunction search is carried out non-retinotopically. Therefore models of search and attention need to be modified to incorporate non-retinotopic geometries. All the findings reviewed in this and the previous section indicate that non-retinotopic information representation and processing depend critically on motion information. The Ternus-Pikler litmus test demonstrates that motion establishes a reference frame according to which non-retinotopic computations take place. In the next section, we discuss reference frames and the resulting relativity in processes associated with these reference frames.

Fig. 15.

Ternus-Pikler stimulus adapted to test whether conjunction search is based on retinotopic or non-retinotopic representations. A Ternus-Pikler stimulus consisting of two squares and a central disk is moved back on forth. Search stimuli consisted of horizontal/vertical red/green bars. The task of the observer was to indicate in each trial whether or not a pre-designated target (e.g., horizontal green bar ) was present within the central disk. According to current theories of search and attention, information is processed in retinotopic coordinates. A prediction of these theories is that different sets of search items will superimpose due to retinotopic integration (as shown by the purple dashed arrows and the depiction at the bottom of the figure) making it very difficult to detect the target. According to our non-retinotopic theory, integration should take place according to grouping relations (shown by the orange arrows). The consistent set of search items presented in the central disk from frame to frame should make the search relatively easy. Our data support the predictions of the non-retinotopic hypothesis. Adapted from [10].

VII. Relativity in perception and reference frames

The sensitivity of the visual system to relative physical quantities is well documented. For example, as shown by the Ebinghaus-Titchener illusion, a disk surrounded by large disks appears smaller compared to the same size disk surrounded by smaller disks (Fig. 16). An interpretation of this and a variety of other relativity effects is that some of the components in the stimulus serve as a reference frame against which the others are judged. There is evidence that the visual system may be using not a single but a variety of reference frames depending on the stimuli and the task. For example, as the eyes move, stationary stimuli move in retinotopic coordinates while they remain stationary in our perception. It has been therefore suggested that, at higher levels of the visual system, representations that make use of eye-movement command signals are in operation. The geometry of these representations may be spatiotopic in that the reference frames are in spatial rather than retinotopic coordinates.

Fig. 16.

Ebinghaus-Titchener illusion. A disk surrounded by large disks (left) appears smaller than a disk of equal size surrounded by small disks (right).

The importance of reference frames can be further appreciated by considering multi-sensory or sensory-motor coordination. The nervous system is confronted with establishing relations between different sensory-based representations so as to achieve multi-sensory coordination (e.g., audio-visual coordination so that sounds are perceived coherently with their visual sources). In addition, sensory representations need to be converted to motor representations to coordinate sensory-motor tasks (e.g., head or body centered reference frames may be used for motor systems). At the neural level, there is evidence of multiple reference frames including representations that reflect mixture of multiple reference frames [47].

At the input and output levels, the physics of the sensors and actuators, respectively, impose strong constraints that shape neural representations carrying out early encoding of stimuli and the control of actuators. As discussed earlier, the optics of the eye promotes early retinotopic representations. Similarly, the physics and physiology of the plants and the immediate controllers (such as the eye ball and eye muscles) promote pre-motor and motor representations. The major challenge is to understand intermediate representations and geometries that the visual system uses not only to achieve sensorimotor control but also to build a cognitive representation of the world. To study this problem of intermediate representations, we focus here on the representations in the perceptual system that succeed retinotopic representations but that are not necessarily linked to motor representations. A popular conceptual paradigm for such representations is the “object file” approach.

A. Objects as reference frames for visual perception

In his pioneering work, the Gestalt psychologist Joseph Ternus introduced the concept of phenomenal identity: “Experience consists far less in haphazard multiplicity than in the temporal sequence of self-identical objects. We see a moving object, and we say that “this object moves” even though our retinal images are changing at each instant of time and for each place which it occupies in space. Phenomenally the object retains its identity.” [81]. The notion of an object as a representational unit, or a reference frame, appeared in the literature various forms. Kahneman and colleagues introduced the metaphor “object file” [38]. According to this approach, for each object, a file is opened and accessed by the instantaneous location of the object. The visual system collects the sensory information received about the object at that location and inserts it in the object file. For example, Shimozaki et al. interpreted their results showing integration of luminance along the motion path (discussed in Section VI) as evidence for an object-file based (non-retinotopic) representation. Given that there is also evidence that neurons in the higher levels of the ventral pathway exhibit invariant representations that could be labeled as “objects”, the object file metaphor has been a popular approach to conceptualize non-retinotopic representations. While intuitively appealing, this approach has several challenges.

It is difficult to define a priori what an object is. Kahneman et al. acknowledge partly this problem when they discuss hierarchical organization of objects (e.g., the wheel of a car can be an object itself or can be part of the larger object “car” or can be part of the larger object “traffic on the highway”, etc.) and assumed that attention, “bottom-up constraints” and “grouping factors” would define the “preferred level” at which an object file is created. However, the details of these factors and how they determine the proper object level remain unsolved. Indeed, many of Ternus’ original experiments demonstrate the difficulty of deciding a priori which stimulus elements will constitute an object (see for example Fig. 17). As discussed in Section VI, the identities of “objects” can also vary depending on stimulus parameters such as ISI. When ISI is short, the middle two elements constitute one object while when ISI is long, the three elements constitute a single object.

Fig. 17.

An example of a stimulus from Ternus’ original experiments [81] showing that it is difficult to determine a priori what constitutes an “object”. A simple interpretation of the figure consists of two “objects”, one vertical bar and one diamond. The motion sequence would then predict that the bar should appear to move from left to right and the diamond from right to left. The percept is ambiguous. At short ISIs, the three horizontally-aligned central dots appear stationary while the outer dots appear to move rightwards. For longer ISIs, the percept appears to be that of a single object rotating 180 degrees in 3D.

Furthermore, the object-file approach is prone to be circular: to define an object and open a file, the visual system needs to distinguish the object from the background and from other objects in the image. However, this figure-ground segregation for the object necessitates that sufficient information about the object is already available to the visual system. But if the file is not open yet, how can this information be available for analysis? At the computational level, this circularity is a problem of bootstrapping. As we have argued in Section II, the read-out and processing of information for moving objects cannot be achieved in a satisfactory manner in retinotopic representations (“moving ghosts problem”) and therefore a non-retinotopic representation needs to be created before even an object file can be opened (if such a thing exists). In the next section, we discuss what this non-retinotopic representation can be.

B. Local manifolds induced by motion segregation

An alternative approach in building hierarchical representations relies on lower level motion analysis as opposed to high level object analysis. Johansson has been one of the pioneers in this area. From a perceptual geometrical perspective, he replaced Euclidian geometry by perspective geometry and devised several studies showing how motion can be analyzed in hierarchical frames of reference within perspective geometrical representations [35][36][37]. He introduced powerful demonstrations wherein complex biological motion, such as a walking human, is sampled by few visible points placed on joints, arms, legs, torso, etc. While the individual motion paths of these sampled points appear complex and unrelated, observers are able to organize them into a hierarchy of meaningful motion patterns that reveal the underlying biological motion. Johansson also proposed a vector analysis method to model his data [35]. Although the proposed vector analysis method has limitations [42], it serves as a good heuristic as a starting point.

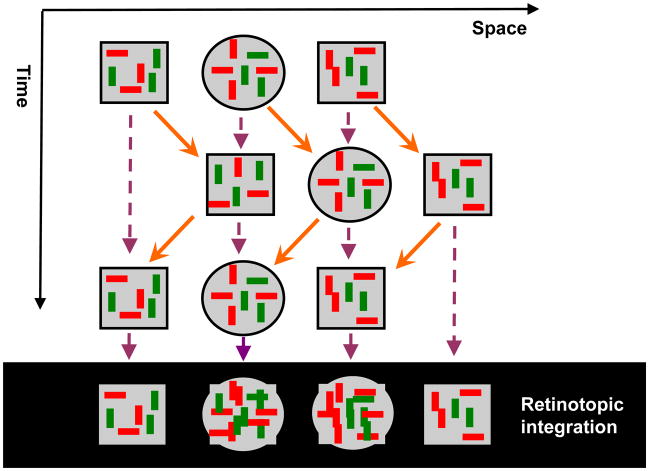
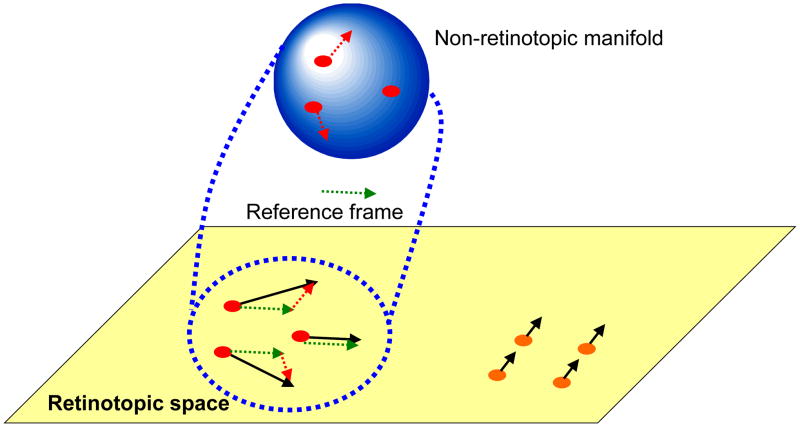
To gain insights into geometric representations underlying dynamic form perception, let us consider the “moving ghosts” problem. In order to integrate features of a moving object, the ideal approach would be to compensate for its motion so that it can be stabilized at a locus where integration occurs (e.g., [1],[56]). In normal viewing, pursuit eye movements partly accomplish this goal for a selected target. However, the environment contains multiple objects moving with different velocities and thus an eye movement or a single global motion-compensation scheme cannot “stabilize” all stimuli. We suggest that the visual system determines locally common motion vectors that can be used to minimize motion variations within a local neighborhood. The heuristic behind this local approach is that, due to their contiguous spatial extent, objects map into local neighborhoods in the retinotopic space. When an object moves, its various parts share a common motion vector, even though different parts of the object may have different velocities (e.g., the tail of a panther may be swinging in addition to the lateral motion of the animal). The “common motion vectors” in local retinotopic neighborhoods can be used to partially stabilize moving objects. The use of common motion in image grouping and segmentation (e.g., Gestalt law of “common faith”), common motion vector decomposition and the attendant relativity of motion have extensive empirical support [21],[35],[36],[39],[42],[65],[84],[85] and is related to the Johansson’s motion vector analysis. However, the exact rules of common vector determination and the nature of reference frames are poorly understood. Notwithstanding the details of how they are computed, one can view these common motion vectors as local reference frames to allow relative motion and form computations at non-retinotopic loci.

However, this local motion vector approach cannot be sufficient by itself to stabilize stimuli because (i) as mentioned above, objects can have multiple parts moving with different velocities, (ii) as an object moves in space and different parts of the same object become gradually exposed to the observer, the perspective projection of the object and therefore the underlying motion vectors can vary, (iii) velocities can vary for non-rigid objects/parts, (iv) at this early stage of processing, the visual system has not yet segregated an object from neighboring objects nor the background. The points (i)–(iii) imply that stabilization will not be perfect and the non-retinotopic representation should be able to accommodate residual motion vectors and be able to represent shape transformations that a moving object can undergo. In order to meet these constraints, we suggest that the non-retinotopic representations will have properties akin to manifolds of the mathematical field of topology. In other words, while the representation preserves local neighborhood relations, it is “stretchable” (cf. rubber-sheet geometry). The point (iv) implies that the units in non-retinotopic representations are not “objects”. Thus instead of concepts such as “object files” [38], we propose that non-retinotopic manifolds represent local geometries around reference frames in order to enable the visual system to accrue and process form information. The processed form information may belong to one or multiple objects. The notions of topology and non-Euclidian geometries have been previously used in visual perception [15],[18],[19],[29],[30],[48]. In our use, these geometric concepts represent the transformations from retinotopic to non-retinotopic representations for dynamic form computation. The proposed approach is depicted in Fig. 18. At the bottom of the figure, in the retinotopic space, a group of dots move rightwards (highlighted in red) while a group of dots move upwards (highlighted in orange). Based on differences in motion vectors, the two local neighborhoods are mapped into two different non-retinotopic representations; for clarity the figure shows only the non-retinotopic representation for rightward moving dots. A common vector for the neighborhood is determined (dashed green vector) and serves as the reference frame for the neighborhood. Accordingly, all motion vectors are decomposed into a sum of the reference motion and a residual motion vector. The stimulus in the local neighborhood is mapped on a manifold (in Fig. 18, for depiction purposes a sphere is used), i.e. a geometric structure that preserves local neighborhood relations. However, the surface can be stretched and deformed. The residual motion vectors, or relative motion components with respect to the reference frame, are then applied to the manifold so as to deform it to induce transformations that the shape undergoes during motion. Although these ideas need extensive empirical tests and refinements, the existing data discussed herein provide a good basis as a starting point. Ternus-Pikler displays indicate that a motion-based grouping is fundamental in non-retinotopic feature processing. Similarly, in a recent study we have shown that non-retinotopic processing observed in metacontrast is strongly correlated with perceived motion indicating that motion is the carrier for non-retinotopic feature processing [11]. As discussed in our review of anorthoscopic perception, which provides the strongest example of form perception in the absence of retinotopic representation, motion is essential in setting non-retinotopic representations. Furthermore, our studies on distortion effects support the view that motion vectors “stretch” non-retinotopic manifolds.

Fig. 18.

Schematic depiction of the proposed approach to conceptualize non-retinotopic representations. The retinotopic space is depicted at the bottom of the figure as a two-dimensional plane. In this example, a group of dots move rightwards (highlighted in red) while a second group of dots move upwards (highlighted in orange). Based on differences in motion vectors, the two local neighborhoods are mapped into two different non-retinotopic representations; for clarity the figure shows only the non-retinotopic representation for rightward moving dots. A common vector for the neighborhood (dashed green vector) serves as the reference frame for the neighborhood. All motion vectors in that neighborhood are decomposed into a sum of the reference motion and a residual motion vector. The stimulus in the local neighborhood is mapped on a manifold (for depiction purposes a sphere is used). The surface of this manifold is stretched and deformed by residual motion vectors without violating local neighborhood relations.

VIII. Conclusions

Understanding how information is represented and processed in the brain is key to reverse-engineering perceptual, cognitive, and motor functions carried out by the nervous system. Vision is the most predominant sense in humans and the visual system is the most extensively studied part of the cortex. While it is clear that geometry and visual perception are closely linked, very little is known about the geometry of the visual system beyond its early retinotopic organization. In this paper, we reviewed several lines of evidence that show the insufficiency of retinotopic representations in supporting real-time perception. The object-file concept, while intuitively appealing for non-retinotopic representations has several shortcomings. Based on our recent studies as well as findings published in the literature, we proposed an alternative approach where the units of non-retinotopic representations are not objects but rather local manifolds created by motion segmentation. We also proposed that the metric of these manifolds is based on relative motion vectors. While the proposed approach awaits further investigations, we believe that it will be a fruitful avenue combining the concepts of relativity and non-Euclidian geometries in deciphering the geometry of visual perception and the underlying neural representations.

Fig. 9.

Depiction of how target features are perceived as being part of the mask in metacontrast masking. Top and middle rows show three targets and masks. The bottom row depicts the percept for each combination. The arrows in the bottom row illustrate the sensation of motion.