Removal of malaria-infected red blood cells using magnetic cell separators: A computational study

Abstract

High gradient magnetic field separators have been widely used in a variety of biological applications. Recently, the use of magnetic separators to remove malaria-infected red blood cells (pRBCs) from blood circulation in patients with severe malaria has been proposed in a dialysis-like treatment. The capture efficiency of this process depends on many interrelated design variables and constraints such as magnetic pole array pitch, chamber height, and flow rate. In this paper, we model the malaria-infected RBCs (pRBCs) as paramagnetic particles suspended in a Newtonian fluid. Trajectories of the infected cells are numerically calculated inside a micro-channel exposed to a periodic magnetic field gradient. First-order stiff ordinary differential equations (ODEs) governing the trajectory of particles under periodic magnetic fields due to an array of wires are solved numerically using the 1^st –5^th order adaptive step Runge-Kutta solver. The numerical experiments show that in order to achieve a capture efficiency of 99% for the pRBCs it is required to have a longer length than 80 mm; this implies that in principle, using optimization techniques the length could be adjusted, i.e., shortened to achieve 99% capture efficiency of the pRBCs.

1. Introduction

Malaria is a parasitic disease transmitted by the bite of an infected mosquito, which afflicts 300 to 500 million people, consuming 40% of the health expenditures of over 100 countries. The malaria parasite lives by feeding off the hemoglobin. To avoid death from the toxic hemoglobin’s “heme”, the parasite converts it into an insoluble highly compacted crystal known as hemozoin. Since each heme contains one atom of iron, the hemozoin becomes paramagnetic [1–4]. Studies of Paul et al. [5] have shown that malaria infected red blood cells (pRBCs), which contain the parasite and the hemozoin, behave like paramagnetic particles in a magnetic field. This discovery has motivated investigation of magnetic cell separation to isolate in-vitro grown malaria-infected cells from the whole blood [5–10].

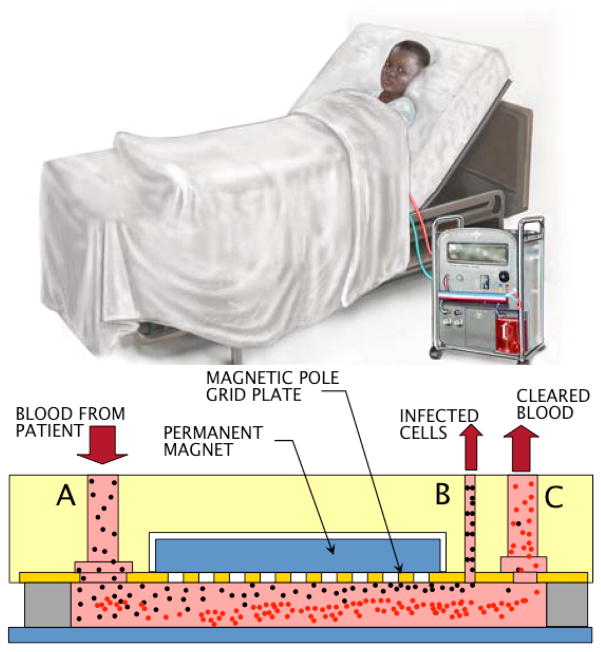
Recently, the magnetic separation of malaria-infected red blood cells (RBCs) from blood circulation in patients with severe malaria has been proposed in a dialysis-like treatment - known as the mPharesis^™ system (Fig. 1). In severe malaria, 5% or higher (up to 60% in worst cases) of the patient’s red blood cells (RBCs) may be infected [11]. Even when optimally treated, severe malaria results in mortality rates of 15%–22% [12, 13]. When available, blood exchange transfusion and erythropheresis have been effectively used to significantly accelerate the clearance of parasites - so that intravenous drug therapies may be more efficacious [14–19]. Unfortunately, current exchange transfuser (ET) and electrophoresis (EP) systems used in these treatments are not engineered to selectively separate the infected RBCs (pRBCs) from healthy RBCs, and consequently result in the consumption of donor blood up to 95% greater than necessary, increasing cost and the risks of transfusion trauma. The mPharesis^™ system (Figure 1) - a patent-pending technology [20] - developed by Tropical Health Systems, LLC and Carnegie Mellon University targets the pRBCs based on their unique magnetic properties. It represents the first medical device of its kind to employ magnetic separation technology [19, 21] to clear these toxic cells from circulation. This study was conducted to determine optimal parameters of such a device.

Figure 1.

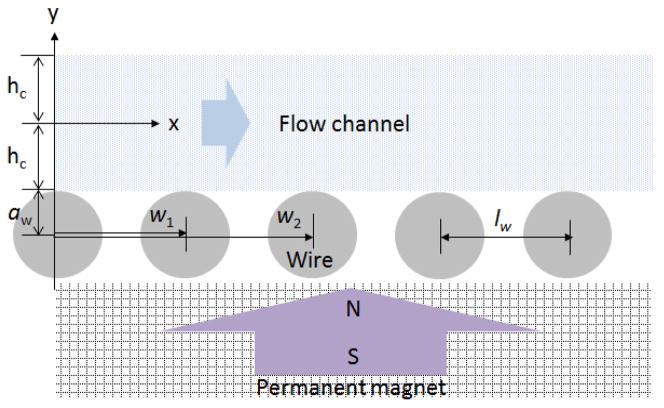
The direction of the flow and the magnetic field in the magnetic cell separator. The origin of the x-y plane is located at the center of the first wire with a diameter of a_w and each wire is displaced horizontally by the pitch (l_w). W_n−1 is the x-directional displacement for the n^th wire. The magnetic force is distributed about a circular wire under a uniform magnetic

Cell separation has been considered as a key element in the diagnosis and treatment of human disease; it is an initial step for further experimental analyses to disclose more information about the disease. However, manipulating of a cell still is a challenging task. The main needs are to achieve higher performance, lower cost of cell isolation systems, and a novel technique to manipulate some of the cells. Kumar and Lykke [22] reviewed various cell separation techniques using cell properties such as cell density (centrifugation), cell size (sedimentation and filtration), and cell charge (magnetism). For example, centrifugation can generate density gradients and is widely used for cell separation. Other separation techniques are based on surface properties (adherence and affinity) and functional properties (proliferation, phagoctosis, and antigen recognition). Among cell manipulation techniques, magnetic cell sorting has received more attention for cell separation. Melville et al. [23] showed erythrocytes can be isolated from other cells because of its different paramagnetic properties. Paul et al [5] used this principle to filtrate malaria-infected red blood cells from the whole blood. Magnetic forces are used to transport, position, isolate, and sort magnetic micro-/nano- particles as well as non-magnetic objects, i.e., diamagnetic particles in micro-fluidic systems.

In this paper, we report the use of numerical technique of the novel mPharesis^™ dialysis-like device for removal of malaria-infected, parasitized RBCs (pRBCs). These cells, known to exhibit a magnetic dipole moment, are modeled as paramagnetic particles suspended in a Newtonian fluid. Trajectories of the infected cells are numerically calculated inside a micro-channel exposed to a periodic magnetic gradient field. In Section 2, we briefly discuss the mechanics of a magnetic cell separator. In Section 3, we look at the mathematical formulation of forces acting on an idealized malaria infected RBC in a fluid, and in Section 4, we derive the equations of motion for a population of pRBCs flowing in a micro-channel subject to a magnetic field. Section 5 provides numerical simulations of particle trajectories for various cases. In addition, we have included the lift and Faxen forces in the particle equation; these terms are normally ignored. With the approach taken in this study, we can easily determine the dimensions of the microchannel, the size of the magnetic wire, the pitch, etc.

2. The mechanics of a magnetic cell separator

Inglis et al [24] discussed two methods of using high gradient magnetic (HGM) cell separation. One is to use the native susceptibility of cells and effectively separate the RBCs from the whole blood. Han et al. [25] showed the continuous separation of red and white blood cells (WBCs) in microdevices. They considered the three-stage cascade micro-separator on order to increase the efficiency of the separation of red and white blood cells, creating higher gradient magnetic fields [26]. Their experimental results showed that the three-stage cascade micro-separator achieved 93.5 % separation of red blood cells and 97.4 % of white blood cells while for the single-stage micro-separator, 91.1 % of red blood cells and 87.7 % of white blood cells were separated. A mathematical model indicated that deoxygenated RBCs can be separated from WBCs in plasma [27]. Zborowski et al. [28] considered deoxygenated and metHb-containing erythrocytes for cell separation. The other method is using magnetic beads where the specific cells which attach themselves to these magnetic beads are separated. Xia et al. [29] used HGMC-microfluidic separator to remove living E. coli bacteria (1×10⁷ cells/ml) bound to 130 nm magnetic nanoparticles from phosphate buffer solution (PBS) and saline containing a concentration of RBCs (2×10⁹ cells/ml). They introduced a triangular saw-tooth configuration to create high gradient magnetic fields. Shinha et al. [30] compared numerical prediction with measured data for magnetic particle trajectories and showed a very good agreement where they introduced a dimensionless ratio of the magnetic and the drag forces determining the capture efficiency of particles. Chen et al. [31] and Brandl et al. [32] have developed detoxification systems as a therapeutic tool for selective and rapid removal of biohazards using a magnetic separator. Convection-diffusion equations governing the concentration of magnetic beads have been integrated with numerical models for cell separation system (Mikkelsen and Bruus [33] and Li et al. [34]. Mohanty et al. [35]). Two good review papers on magnetic cell separation are Tonner and Irimia [36], and Pamme [37].

The mPharesis^™ (magnetic aphaeresis) system operates similar to a dialysis machine, where the patient’s peripheral blood is continuously withdrawn, purified, and returned to the circulation (Figure 1 top). The design of the mPharesis^™ filter features a series of cascaded laminar flow channels (Figure 1 bottom) through which the infected blood is transported and exposed to a high magnetic field gradient (> 1000 Tesla/m). The latter is created by an array of micro-sized ferromagnetic structures, placed in close proximity to the blood, that creates a localize force field, causing the infected cells to migrate or “marginate,” whereupon they are skimmed off by a side branch (bleed-slit, in Figure 1 bottom). A magnetic field is applied using a 0.3 Tesla permanent magnet adjacent to the array of micro-sized ferromagnetic structures. The purified blood is then returned to the patient from a return outlet, (C in Figure 1 bottom). This design allows continuous filtration, analogous to renal dialysis. The engineering challenge is to optimize the efficiency of this magnetic separator to maintain the overall size of the system within the desired envelope. The filtration efficiency of this device depends on many design variables and constraints such as magnetic pole array pitch, chamber height, and flow rate. In the next section we provide a brief review of the various forces acting on a particle flowing in a viscous fluid.

3. Mathematical formulation of forces acting on a particle in a fluid

Fluid dynamics of multiphase (or multi-component) problems employs two distinct approaches. In the first case, the amount of the dispersed component is so small that the motion of this component (usually referred to as the dispersed phase) does not greatly affect the motion of the continuous phase (the host fluid). This method is used extensively in applications such as atomization, sprays, and in flows where bubbles, droplets, and particles are treated as the dispersed phase. This approach is known as the Dilute Phase or the Lagrangian approach to particle studies. The second approach is employed when the two components interact to such an extent that each component directly influences the motion and the behavior of the other component. This is known as the Dense Phase approach, or the Eulerian (two-fluid) approach. This method is used extensively in fluidization, gas-solid flows, pneumatic conveying, and suspensions. For a review and discussion of the relevant issues, see the two recent articles by Massoudi [38, 39].

To describe the behavior of particles suspended or entrained in a fluid, most researchers resort to the equation of motion of a single (spherical) particle in a fluid. Tchen [40] synthesized the work of Basset, Boussinesq, Stokes, and Oseen on the motion of a sphere settling under the force of gravity in a fluid at rest. The resulting force balance, sometimes known as the Basset-Boussinesq-Oseen (BBO) equation, is given by:

$$\frac{4\pi a^3}{3}{\rho }_p{\stackrel{.}{\text{v}}}_p=-\frac{2\pi a^3}{3}{\rho }_{\text{f}}{\stackrel{.}{\text{v}}}_p-6\pi {\mu }_{\text{f}}a{\text{v}}_p-6\pi {\mu }_{\text{f}}a\frac{a}{\sqrt{\pi {\nu }_{\text{f}}}}{\int }_{-\infty }^t\frac{{\stackrel{.}{v}}_p(t_1)}{\sqrt{t-t_1}}{dt}_1-\frac{4\pi a^3}{3}\text{g}({\rho }_p-{\rho }_{\text{f}})$$ (1)

where v_p is the velocity of the particle, ρ_f and ρ_p are density of the fluid and particle, respectively, a is the particle radius, g is the acceleration of gravity, μ_f and ν_f are the dynamic viscosity and the kinematic viscosity of the fluid, respectively. The terms on the right-hand side of equation (1) reflect the presence of virtual mass, Stokes drag, Basset history effects, and buoyancy. Tchen (1947) modified equation (1) to describe the unsteady motion of a solid spherical particle in a fluid with a uniform flow field. His modifications include replacing the particle velocity by its relative velocity, and the addition of a term accounting for the pressure gradient in the fluid. The resulting expression is:

$$\frac{4\pi a^3}{3}{\rho }_p{\stackrel{.}{\text{v}}}_p=\frac{4\pi a^3}{3}{\rho }_{\text{f}}{\stackrel{.}{\text{v}}}_f-\frac{2\pi a^3}{3}{\rho }_{\text{f}}({\stackrel{.}{\text{v}}}_p-{\stackrel{.}{\text{v}}}_f)-6\pi {\mu }_{\text{f}}a({\text{v}}_p-{\text{v}}_f)-6\pi {\mu }_{\text{f}}a\frac{a}{\sqrt{\pi {\nu }_{\text{f}}}}{\int }_{-\infty }^t\frac{{\stackrel{.}{\text{v}}}_p(t_1)-{\stackrel{.}{\text{v}}}_f(t_1)}{\sqrt{t-t_1}}{dt}_1-\frac{4\pi a^3}{3}\text{g}({\rho }_p-{\rho }_{\text{f}})$$ (2)

where v_f is the velocity of the fluid in the neighborhood of the particle but far enough away to be unaffected by it.

It should be noted that equation (2) is a scalar component of a more general vector equation. Corrsin and Lumley [41] argued that, for a nonuniform flow field, the full Navier-Stokes equations should be used to determine the pressure gradient. Buevich [42] criticized both previous studies by pointing out that adding a term to the BBO equation is not necessary. Soo [43, 44] argued that the pressure gradient force is exactly balanced by the fluid inertia forces and should not appear in the force balance in any form. The importance of the force due to the fluid pressure gradient is still a subject of study and disagreement [see Table 1]. Maxey and Riley [45], based on an analysis similar to that of Buevich, proposed the following equation for the force on a sphere in a nonuniform flow:

$$\begin{array}{l}{m}_p\frac{{d\mathbf{v}}_p}{dt}=+m_f\frac{{D\mathbf{v}}_f}{Dt}|\mathbf{Y}(t)\\ -\frac{1}{2}{m}_f\frac{d}{dt}\left\{{\mathbf{v}}_p(t)-{\mathbf{v}}_f[\mathbf{Y}(t),t]-\frac{1}{10}{a}^2{\nabla }^2{\mathbf{v}}_f\mid \mathbf{Y}(t)\right\}\\ -6\pi a{\mu }_f\left\{{\mathbf{v}}_p(t)-{\mathbf{v}}_f[\mathbf{Y}(t),t]-\frac{1}{6}{a}^2{\nabla }^2{\mathbf{v}}_f\mid \mathbf{Y}(t)\right\}\\ +6\pi a^2{\mu }_f{\int }_0^{t}d\tau \frac{\left(\frac{d}{d\tau }\left\{{\mathbf{v}}_p(\tau )-{\mathbf{v}}_f[\mathbf{Y}(\tau ),\tau ]-\frac{1}{6}{a}^2{\nabla }^2{\mathbf{v}}_f\mid \mathbf{Y}(\tau )\right\}\right)}{\sqrt{\pi v_f(t-\tau )}}\\ +(m_p-m_f)\mathbf{g}\end{array}$$ (3)

Table 1.

Force due to pressure gradient [Massoudi and Rao 2001 [47])]

Author	Pressure Term
Tchen, 1947	$\frac{4\pi a^3}{3}{\rho }_{\text{f}}\left(\frac{\partial {\text{v}}_p}{\partial t}+{\text{v}}_p\frac{\partial {\text{v}}_p}{\partial \text{x}}\right)$
Corrsin and Lumley, 1956	$\frac{4\pi a^3}{3}{\rho }_{\text{f}}\left(\frac{\partial {\mathbf{v}}_p}{\partial t}+(\mathbf{grad}{\mathbf{v}}_p){\mathbf{v}}_p-\nu {\nabla }^2{\mathbf{v}}_p\right)$
Buevich, 1966	$\frac{4\pi a^3}{3}{\rho }_{\text{f}}\left(\frac{\partial {\mathbf{v}}_p}{\partial t}+(\mathbf{grad}{\mathbf{v}}_p){\mathbf{v}}_f\right)$
Soo, 1975, 1976	0
Maxey and Riley, 1983	${\frac{4\pi a^3}{3}{\rho }_{\text{f}}\left(\frac{\partial {\mathbf{v}}_p}{\partial t}+(\mathbf{grad}{\mathbf{v}}_p){\mathbf{v}}_p\right)|}_{\mathbf{x}=\mathbf{y}(\mathbf{t})}$

It is noted that the inclusion of velocity gradients in their analysis results in modifications to the virtual mass, Stokes drag, and Basset history terms in order to account for the effect of a nonuniform flow field. These velocity gradients correspond to the physical effect known as Faxen forces (Happel and Brenner [46]).

Though equation (3) appears to be complete for a single particle in Stokes flow, there are, in general, other forces that must be considered - even for a purely mechanical system. For example, in flows with high relative velocity between phases, or large velocity gradients in the fluid, lift may become an important effect (see McLaughlin [48], Ounis and Ahmadi [49]).

It is observed [50–52] that spheres in laminar Poiseuille flow through a pipe (at low Re) accumulate in an annulus some distance from the tube axis. Following the initial observations, a number of investigators verify this ‘tubular pinch’ effect and attempt to explain the lateral (or lift) force acting on the spheres. Though some authors attempt to explain the radial migrations in terms of particle spin (i.e., Magnus force), spheres prevented from spinning also reached equilibrium positions between wall and centerline. Saffman [53, 54] deduces that, since experimental results contradicted this conclusion, inertial effects must be involved. Saffman obtains the result for ‘slip-shear’ lift on a particle at low Reynolds number analogous to a result derived earlier for the ‘spin’ lift by Rubinow and Keller [55]. Saffman [53] includes particle spin in his analysis and shows that under circumstances where his results and Rubinow and Keller’s result strictly apply, the ‘shear’ lift dominates the ‘spin’ lift. The Saffman lift force is normal to the slip vector and the spin vector of the particle. If the particle lags the fluid, the lift will move the particle toward the faster adjacent fluid and vice versa if the particle leads the fluid. Ho and Leal [56] calculate another form of lift force on a single particle in a channel. This force is apparently a result of the wall effects. A detailed analysis, including experimental observation of lift forces in Couette systems is given by Halow and Wills [57, 58]. For an updated review of Saffman’s contribution to this field, we refer the reader to the recent article by Stone [59]. In majority of multiphase studies, lift forces are neglected. Massoudi [60] discusses the importance of these forces and through a simple order of magnitude analysis concludes that these forces, especially in the flows or in the regions of high velocity gradients (such as swirling flows), cannot be assumed to be negligible a priori. Massoudi [61] also provides a brief review of the interaction mechanisms. Ounis and Ahmadi [49] suggested the following equation:

$$\begin{array}{l}{m}_p\frac{{d\mathbf{v}}_p}{dt}=m_f\frac{{D\mathbf{v}}_f}{Dt}-\frac{1}{2}{m}_f\frac{d}{dt}\left({\mathbf{v}}_p-{\mathbf{v}}_f-\frac{d^2}{40}{\nabla }^2{\mathbf{v}}_f\right)\\ -3\pi {\mu }_{f}d\left({\mathbf{v}}_p-{\mathbf{v}}_f-\frac{d^2}{24}{\nabla }^2{\mathbf{v}}_f\right)-\frac{3}{2}\pi d^2{\mu }_f\underset{0}{\overset{t}{\int }}\frac{\frac{d}{d\tau }\left({\mathbf{v}}_p-{\mathbf{v}}_f-\frac{d^2}{24}{\nabla }^2{\mathbf{v}}_f\right)}{\sqrt{\pi {\nu }_f(t-\tau )}}d\tau \\ +\frac{K\pi d^2{\left({\rho }_f{\mu }_f\right)}^{1/2}{\mathbf{D}}_f}{3{\left({\mathbf{D}}_f:{\mathbf{D}}_f\right)}^{1/4}}\left({\mathbf{v}}_f-{\mathbf{v}}_p\right)+\left(m_p-m_f\right)\mathbf{g}\end{array}$$ (4)

where as before the subscripts f and p denote the fluid and the particle, respectively; v is the velocity vector, t is time, μ_f is the dynamic viscosity, υ_f is the kinematic viscosity, m is the mass ( $m=\frac{\pi }{6}{d_p}^3\rho$), ρ is the density, d is the particle diameter (=2a), K=2.594 is the constant coefficient of Saffman lift force, ${\mathbf{D}}_f=\frac{1}{2}\left[\nabla {\mathbf{v}}_f+{\left(\nabla {\mathbf{v}}_f\right)}^T\right]$, the time derivate for the moving particle is $\frac{{d\mathbf{v}}_p}{dt}=\frac{\partial {\mathbf{v}}_p}{\partial t}+{\mathbf{v}}_p\frac{\partial {\mathbf{v}}_p}{\partial \mathbf{x}}$, the fluid acceleration is defined as $\frac{{D\mathbf{v}}_f}{Dt}=\frac{\partial {\mathbf{v}}_f}{\partial t}+{\mathbf{v}}_f\frac{\partial {\mathbf{v}}_f}{\partial \mathbf{x}}$, and x_p = x_p e_x ⫑ y_pe_y. A generalized form of the Saffman shear lift force was proposed by Drew [62], Ahmadi [63], McTigue et al. [64]. Equation (4) is reduced to the lift force in a uniform shear field provided by Saffman [53, 54]. This form of the lift force is intended for Stokes flow regime and only valid for small particles. Also, spin of the particle is not taken into account in the above equations. In the next section, we look at a simplified case of magnetic particles flowing in a micro-channel subject to a magnetic field. The structure of this magnetic force is obtained from the work of Han et al. [65]. In reality, however, one must solve the Maxwell’s equations in conjunction with the equation of motion for the particles.

4. Flow of magnetic particles in a micro-channel

We consider a paramagnetic particle (representing the malaria-infected RBCs) in a steady fully-developed laminar flow between two plates (micro-channel). As the first approximation, we neglect the terms due to the pressure gradient, virtual mass, and Basset history force. However, we add a magnetic force on the right-hand side of equation 4. That is, only the Stokes drag, buoyancy, shear-lift and magnetic forces including the velocity gradients known Faxen force are considered. Thus equation (4) becomes:

$${\text{m}}_{\text{p}}\frac{\text{d}{\mathbf{v}}_{\text{p}}}{\text{dt}}=-3\pi {\mu }_{\text{f}}\text{d}\left({\mathbf{v}}_{\text{p}}-{\mathbf{v}}_{\text{f}}-\frac{{\text{d}}^2}{24}{\mathbf{\nabla }}^2{\mathbf{v}}_{\text{f}}\right)+\left({\text{m}}_{\text{p}}-{\text{m}}_{\text{f}}\right)\mathbf{g}+\frac{\text{K}\pi {\text{d}}^2{\left({\rho }_{\text{f}}{\mu }_{\text{f}}\right)}^{1/2}{\mathbf{D}}_{\text{f}}}{3{\left({\mathbf{D}}_{\mathbf{f}}:{\mathbf{D}}_{\mathbf{f}}\right)}^{1/4}}\left({\mathbf{v}}_{\mathbf{f}}-{\mathbf{v}}_{\mathbf{p}}\right)+{\mathbf{F}}_{\text{mag}}$$ (5)

We also adopt the magnetic force derived by Han et al. [65] for a ferromagnetic cylindrical wire placed under a uniform magnetic field H₀ applied normal to the axis of the wire. However, unlike Han, which prescribed the direction of flow parallel to the longitudinal axis of the wire, the flow is taken here across the wire. (See Figure 2) The corresponding components of magnetic force in the Cartesian coordinates are given as:

$$\begin{array}{l}{\mathbf{F}}_{\text{mag}}={\text{F}}_{\text{mag},\text{x}}(\text{x},\text{y}){\mathbf{e}}_{\text{x}}⫞{\text{F}}_{\text{mag},\text{y}}(\text{x},\text{y}){\mathbf{e}}_{\mathbf{y}}\\ {\text{F}}_{\text{mag},\text{x}}(\text{x},\text{y})=\frac{-2\text{k}{\mu }_0\left({\chi }_{\text{p}}-{\chi }_{\text{f}}\right){\text{V}}_{\text{p}}{{\text{a}}_{\text{w}}}^2{\text{H}}_0^2}{{\left({\text{x}}^2+{\text{y}}^2\right)}^3}\left[{\text{ka}}^2+3{\text{y}}^2-{\text{x}}^2\right]\text{x}\\ {\text{F}}_{\text{mag},\text{y}}(\text{x},\text{y})=\frac{-2\text{k}{\mu }_0\left({\chi }_{\text{p}}-{\chi }_{\text{f}}\right){\text{V}}_{\text{p}}{{\text{a}}_{\text{w}}}^2{\text{H}}_0^2}{{\left({\text{x}}^2+{\text{y}}^2\right)}^3}\left[{\text{ka}}^2-3{\text{x}}^2+{\text{y}}^2\right]\text{y}\end{array}$$ (6)

where $k=\frac{{\mu }_w-{\mu }_0}{{\mu }_w+{\mu }_0}$, μ_w and μ₀ are the magnetic permeability of the ferromagnetic wire and free space respectively, χ_f and χ_p are the magnetic susceptibilities of the fluid solution and the paramagnetic particle (or pRBC), V_p is the volume of the paramagnetic particle (or pRBC); and a_w is the radius of the wire.

Figure 2.

The direction of the flow and the magnetic field in the magnetic cell separator.

Let us consider an array of N_w wires located on the top of the permanent magnet shown in Figure 2. The center of the first wire is positioned at the origin of the x–y plane (x=w₀=0 and y=0), and all other wires are displayed side by side along the x-axis. The magnetic force distribution of the first wire (n=1) is given by Eq. 6. The center of the nth wire is located at x=w_n and its magnetic force distribution can be written in terms of Eq. 6 as:

$${\mathbf{F}}_{\mathit{mag}}^n(x,y)={\mathbf{F}}_{\mathit{mag}}^1(x-w_n,y)$$ (7)

where we can label each conductor using the index n=1,2,3,4,…, N_w. Therefore, we can define the total magnetic force distribution for the N_w array of wires by superposition:

$${\mathbf{F}}_{\mathit{mag}}^{\mathit{total}}(x,y)=\sum _{n=1}^{N_w}{\mathbf{F}}_{\mathit{mag}}^1(x-w_n,y)$$ (8)

To solve Eq. 5, we need an expression for the fluid velocity v_f in the micro-channel where flow is two-dimensional. It is known that the velocity profile for the flow between two plates is different from the flow through a channel (with side walls) with a square cross-section. In this problem, we assume a parabolic flow profile for a wide channel (width≫height), where L denotes the length of the channel, and h_c and w_c denote the half-height and the half-width of the cross section as shown in Figure 2. For the fully developed pressure-driven steady flow between two fixed plates, the velocity is given as [66],

$${\mathbf{v}}_{\text{f}}=-\frac{\text{dp}}{\text{dx}}\frac{{{\text{h}}_{\text{c}}}^2}{2{\mu }_{\text{f}}}\left[1-{\left(\frac{\text{y}-\left({\text{a}}_{\text{w}}+{\text{h}}_{\text{c}}\right)}{{\text{h}}_{\text{c}}}\right)}^2\right]{\mathbf{e}}_{\text{x}}$$ (9)

where $\frac{\text{dp}}{\text{dx}}$ is the pressure drop and μ_f is the viscosity of a fluid, a_w and h_c are defined and shown in Figure 3. The volumetric flow rate Q is defined as Q = A v̄_f where the cross sectional area of the channel is A=4h_cw_c. The average velocity v̄_f is determined by integrating the velocity over the cross section, i.e., v̄_f = 1/A∫v_f dA = 2/3 v_max. The maximum velocity v_max occurs at the centerline, y = a ⫞ h_c, i.e., v_max = −(dp/dx)(h_c²/2μ_f).

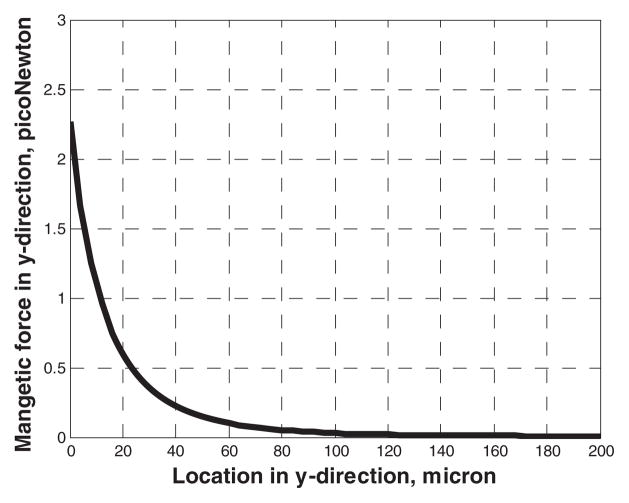
Figure 3.

The y component of the magnetic force along y direction from edge of the wire.

Thus, the velocity profile can be rewritten as,

$${\mathbf{v}}_{\text{f}}=\frac{3{\overline{\text{v}}}_{\text{f}}}{2}\left[1-{\left(\frac{\text{y}-\left({\text{a}}_{\text{w}}+{\text{h}}_{\text{c}}\right)}{{\text{h}}_{\text{c}}}\right)}^2\right]{\mathbf{e}}_{\text{x}}$$ (10)

Finally, by substituting Eq. (8) and Eq. (10) into Eq. (5) we obtain the expression for the components of the forces acting on the particle. Thus the equations for a paramagnetic particle/RBC moving through the cell separator can be rewritten as:

$$\begin{array}{l}{\text{m}}_{\text{p}}\frac{\text{d}{\text{v}}_{\text{p},\text{x}}}{\text{dt}}=-3\pi {\mu }_{\text{f}}\text{d}\left[{\text{v}}_{\text{p},\text{x}}-\frac{3{\overline{\text{v}}}_{\text{f}}}{2}\left[1-{\left(\frac{\text{y}-({\text{a}}_{\text{w}}+{\text{h}}_{\text{c}})}{{\text{h}}_{\text{c}}}\right)}^2\right]+\frac{{\text{d}}^2}{24}\frac{3{\overline{\text{v}}}_{\text{f}}}{{{\text{h}}_{\text{c}}}^2}\right]\\ +\frac{\text{K}\pi {\text{d}}^2{\left({\rho }_{\text{f}}{\mu }_{\text{f}}\right)}^{1/2}}{3{\left({\mathbf{D}}_{\mathbf{f}}:{\mathbf{D}}_{\mathbf{f}}\right)}^{1/4}}\left(\frac{3{\overline{\text{v}}}_{\text{f}}}{2{{\text{h}}_{\text{c}}}^2}[\text{y}-({\text{a}}_{\text{w}}+{\text{h}}_{\text{c}})]\right){\text{v}}_{\text{p},\text{y}}\\ +\sum _{\text{n}=1}^{{\text{N}}_{\text{w}}}{\text{F}}_{\text{mag},\text{x}}^1(\text{x}-{\text{w}}_{\text{n}},\text{y})\end{array}$$ (11)

and

$$\begin{array}{l}{\text{m}}_{\text{p}}\frac{\text{d}{\text{v}}_{\text{p},\text{y}}}{\text{dt}}=-3\pi {\mu }_{\text{f}}\text{d}{\text{v}}_{\text{p},\text{y}}-{\text{q}}_{\text{p}}\left({\rho }_{\text{p}}-{\rho }_{\text{f}}\right)\text{g}\\ +\frac{\text{K}\pi {\text{d}}^2{\left({\rho }_{\text{f}}{\mu }_{\text{f}}\right)}^{1/2}}{3{\left({\mathbf{D}}_{\mathbf{f}}:{\mathbf{D}}_{\mathbf{f}}\right)}^{1/4}}\left(\frac{3{\overline{\text{v}}}_{\text{f}}}{2{{\text{h}}_{\text{c}}}^2}[\text{y}-({\text{a}}_{\text{w}}+{\text{h}}_{\text{c}})]\right)\left({\text{v}}_{\text{p},\text{x}}-\frac{3{\overline{\text{v}}}_{\text{f}}}{2}\left[1-{\left(\frac{\text{y}-({\text{a}}_{\text{w}}+{\text{h}}_{\text{c}})}{{\text{h}}_{\text{c}}}\right)}^2\right]\right)\\ +\sum _{\text{n}=1}^{{\text{N}}_{\text{w}}}{\text{F}}_{\text{mag},\text{y}}^1(\text{x}-{\text{w}}_{\text{n}},\text{y})\end{array}$$ (12)

where ${\text{q}}_{\text{p}}\left(=\frac{4\pi a^3}{3}\right)$ is the volume of the particle and

$$\frac{{\text{dx}}_{\text{p}}}{\text{dt}}={\text{v}}_{\text{p},\text{x}}$$ (13)

$$\frac{{\text{dy}}_{\text{p}}}{\text{dt}}={\text{v}}_{\text{p},\text{y}}$$ (14)

and

$${\mathbf{D}}_{\mathbf{f}}:{\mathbf{D}}_{\text{f}}=\frac{9{{\overline{\text{v}}}_{\text{f}}}^2}{2{{\text{h}}_{\text{c}}}^4}{[\text{y}-({\text{a}}_{\text{w}}+{\text{h}}_{\text{c}})]}^2$$ (15)

Note that v_p = v_p,x e_x ⫞ v_p,y e_y at any position x_p = x_p e_x ⫞ y_pe_y. In these expressions, v_p,_x and v_p,y are the components of the particle velocity.

5. Numerical simulations and particle trajectories

Equations (11) – (14) represent a coupled system of first-order ordinary differential equations (ODEs) that are to be solved with appropriate initial conditions for the position x_p(0), y_p(0), and the velocity v_p,x(0)=v_f, and v_p,_y(0)=0 of the particle. These equations were solved numerically using the 1^st–5^th order adaptive step Runge-Kutta solver for stiff ODE systems (ode15s in MATLAB ODE solver). The relative and absolute error tolerances were set to 1e-5 and 1e-4 respectively. An alternative approach to simulate particle motion could be a discrete particle method when particle-fluid and particle-particle interactions are important.

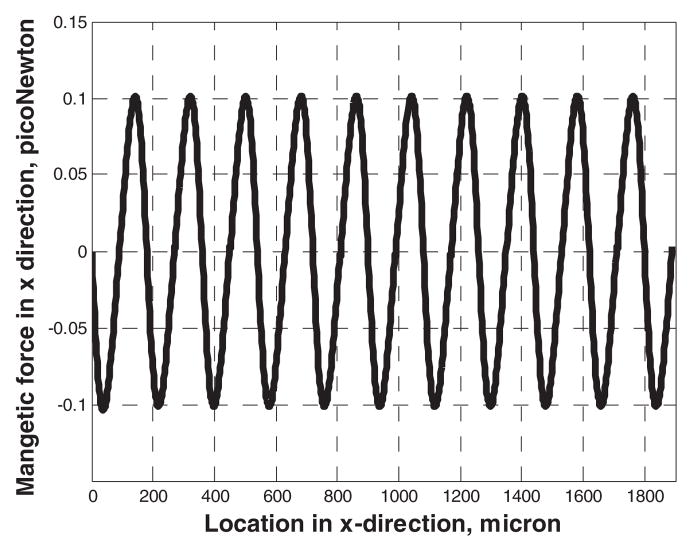
The magnetic force in the y-direction is illustrated in Figure 3. (The x-axis is shifted by 50 micron to reference the magnetic force field in the channel.) A cubic regression to these results show that the force scales as 1/x³. The x-component of the magnetic force plotted in Figure 4, at y=100 micron illustrates an approximately sinusoidal fluctuation along the x-direction.

Figure 4.

The x component of the magnetic force along x direction at y=100 micron.

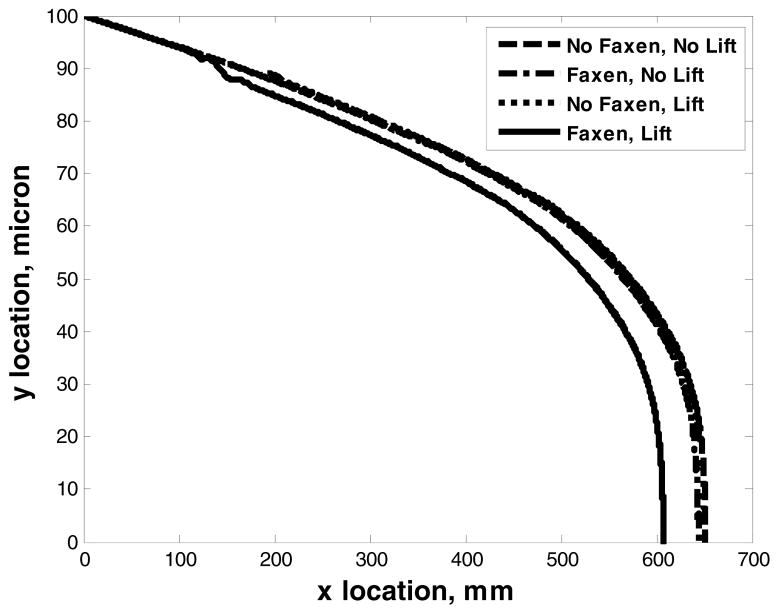
Figure 5 shows the trajectories of paramagnetic particles where Faxen and lift forces are included. It is observed that as the strength of the magnetic field decreases, the Faxen and the lift forces do not play a significant role on the motion of the particles. Therefore, the external magnetic flux was set to be 0.3 Tesla and we assumed that the Faxen and lift forces are negligible in the remainder of the numerical studies.

Figure 5.

Plot of ferromagnetic bead trajectories at 5 cc flow rate and 0.05 Tesla magnetic flux at the particle seeding point of x=0, y=100 micron. The wire pitch (l_w) is 200 micron and the diameter of the wire (a_w) is 100 micron. The height of the micro-channel is 200 micron.

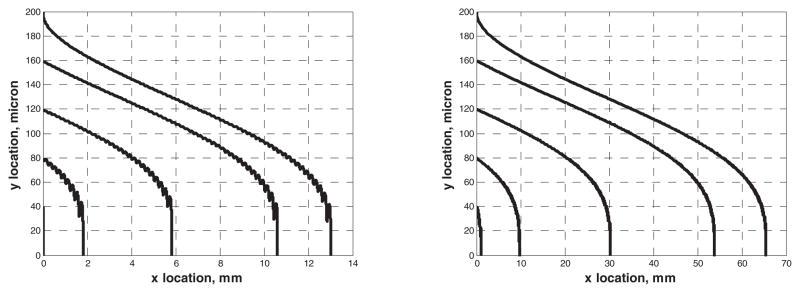
Figure 6 shows the trajectory of five ferromagnetic particles seeded at the entrance of the micro-channel, illustrating their deflection due to the magnetic force. The ferromagnetic particle has diameter of 0.3 micron and susceptibility of 0.26. The susceptibility of plasma is −7.7×10⁻⁶. The numerical results also show that most of the particles are captured at the bottom of the channel near the wires within 13mm (for 1 cc/min) and 65mm (for 5 cc/min), thus suggesting a minimum length of the channel could be achieved by optimizing the design parameters.

Figure 6.

Plot of ferromagnetic bead trajectories at 1 cc/min (left) and 5 cc/min (right) flow rate. The magnetic flux is 0.3 Tesla. The wire pitch (l_w) is 200 micron and the diameter of the wire (a_w) is 100 micron. The height of the micro-channel is 200 micron.

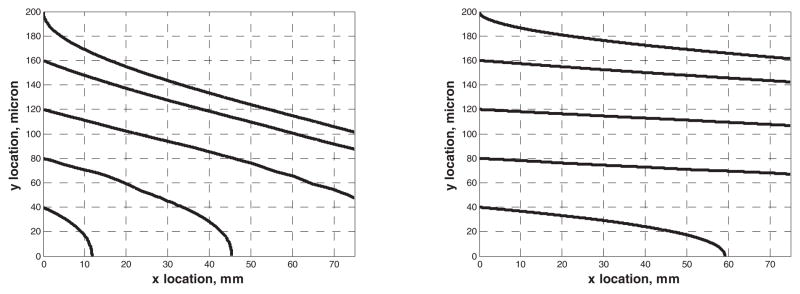
Next we considered the malaria-infected red blood cells (pRBCs) with diameter of 8 micron and susceptibility of −6.2×10⁻⁶ (See Figure 7). The susceptibility of plasma is −7.7×10⁻⁶. pRBC becomes paramagnetic due to its susceptibility with respect to plasma susceptibility. Some of the particles are not captured within the channel length of 75 mm for flow rates of 1 cc/min and 5 cc/min, since the infected RBCs are more paramagnetic than the ferromagnetic beads of the previous simulation. Paramagnetic particles are less deflected than the ferromagnetic particles by a permanent magnet. Paramagnetic substances have linear magnetization curves under normal circumstances and have no magnetism when the external magnetic field is removed, where the susceptibility is small and positive. Ferromagnetic magnetization curve is nonlinear. Its susceptibility is positive and large, which changes with H [67].

Figure 7.

Plot of pRBC trajectories at 1 cc/min (left) and 5 cc/min (right) flow rate. The magnetic flux is 0.3 Tesla. The wire pitch (l_w) is 200 micron and the diameter of the wire (a_w) is 100 micron. The height of the micro-channel is 200 micron.

6. Concluding remarks

The main assumptions in our simulations of particle trajectory are: (1) no particle-particle interaction (no collisions); and (2) the behavior or the response of the particle is affected by the fluid motion whereas the fluid motion is unaffected by the presence of the particle, (one-way interaction). For a system of dense particles, these assumptions would not be valid. In most studies the forces due to pressure gradient and lift force are neglected; however it is known that the lift forces could be important in a small scale geometry [53, 60, 62, 68].

In this study, we have used the Lagrangian approach to study the particle trajectory while estimating design dimensions of the cell separation device. For a complete three dimensional geometry, we can use a Lagrangian-Eulerian CFD approach. However, these methods do not consider particle-particle interactions that can affect the cell aggregation and deformability of the cells. To better predict the phase separation of the RBCs and the plasma, one should consider alternative approaches such as the mixture theory [47, 60, 61, 69–71] or the particulate dynamics [72–74]. In this paper, we modeled the malaria infected RBCs (pRBCs) as paramagnetic particles suspended in a Newtonian fluid. Trajectories of the infected cells are numerically calculated inside a micro-channel exposed to a periodic magnetic field gradient. First order stiff ordinary differential equations (ODEs) governing particle’s trajectory under periodic magnetic fields due to an array of wires were solved numerically using a the 1^st –5^th order adaptive step Runge-Kutta solver. The numerical experiments show that in order to achieve a capture efficiency of 99% for the pRBCs it is required to have a longer length than 80 mm; this implies that in principle, using optimization techniques the length could be adjusted, i.e., shortened to achieve 99% capture efficiency of the pRBCs.

For future study, we will consider more general cases using Eq. (4) for unsteady flow problems in complex geometries. We need to consider a 3-dimensional Lagrangian-Eulerian approach to investigate behavior of the pRBC in complex geometries where the magnetic field generated by a series of wires due to the external uniform field magnet also has to be considered using the Maxwell’s equations. We will also perform numerical optimization studies on the height of the chancel and the magnetic pitch.