Abstract
Purpose
Radioimmunotherapy (RIT) using 131I-3F8 injected into cerebrospinal fluid (CSF) was a safe modality for the treatment of leptomeningeal metastases (JCO, 25:5465, 2007). A single-compartment pharmacokinetic model described previously (JNM 50:1324, 2009) showed good fitting to the CSF radioactivity data obtained from patients. We now describe a two-compartment model to account for the ventricular reservoir of 131I-3F8 and to identify limiting factors that may impact therapeutic ratio.
Methods
Each parameter was examined for its effects on (1) the area under the radioactivity concentration curve of the bound antibody (AUC[CIAR]), (2) that of the unbound antibody AUC[CIA], and (3) their therapeutic ratio (AUC [CIAR]/AUC[CIA]).
Results
Data fitting showed that CSF kBq/ml data fitted well using the two-compartment model (R=0.95±0.03). Correlations were substantially better when compared to the one-compartment model (R=0.92±0.11 versus 0.77±0.21, p=0.005). In addition, we made the following new predictions: (1) Increasing immunoreactivity of 131I-3F8 from 10% to 90% increased both (AUC[CIAR]) and therapeutic ratio ([AUC[CIAR]/AUC[CIA]] by 7.4 fold, (2) When extrapolated to the clinical setting, the model predicted that if 131I-3F8 could be split into 4 doses of 1.4 mg each and given at ≥24 hours apart, an antibody affinity of KD of 4 × 10−9 at 50% immunoreactivity were adequate in order to deliver ≥100 Gy to tumor cells while keeping normal CSF exposure to <10 Gy.
Conclusions
This model predicted that immunoreactivity, affinity and optimal scheduling of antibody injections were crucial in improving therapeutic index.
Keywords: Pharmacokinetics, Radioimmunotherapy, Optimization, 3F8, Intra-Ommaya, Cerebrospinal fluid
Introduction
Leptomeningeal metastases cause serious neurological complications in the central nervous system (CNS) and contribute to life-threatening neurological disability [1–3]. It is diagnosed in 4% to 15% of patients with solid tumors and over 70% of patients with widely disseminated and progressive systemic cancer [3]. These figures probably underestimate the prevalence in the cancer population because leptomeningeal metastases are often microscopic and focal easily missed in autopsy studies [4, 5]. Furthermore, the incidence is expected to increase as cancer patients live longer and diagnostic tools are made more sensitive [1, 2]. With limited treatment options, the median survival for patients with leptomeningeal metastases is still unacceptable, ranging between 4 to 14 months [6–8].
Neuroblastoma (NB) is the most common extracranial solid tumor in children, and accounts for 6.7% of childhood cancer. The CNS serves as a sanctuary for NB tumor cells and can be the sole site of disease recurrence [6]. As expected with improved patient survival, the incidence of leptomeningeal and parenchymal metastases among NB patients has increased in the past decade. Radioimmunotherapy (RIT) through cerebral spinal fluid (CSF) has been applied successfully to cancer metastases to the brain and leptomeninges [9, 10]. Monoclonal antibodies (MoAbs) 3F8 and 8H9, targeting tumor-associated antigens (GD2 and B7H3, respectively), have been labeled with 131I and administered into CSF through Ommaya reservoirs in patients with CNS NB and other metastatic tumors [11]. Phase I/II clinical trials of RIT with intra-Ommaya (IO) 131I-3F8 and 131I-8H9 were well tolerated and have been successfully incorporated into a treatment plan with a favorable outcome among NB patients with CNS relapse [12]. Since the physiology of the CSF space and the physicochemical properties of MoAbs are well understood, pharmacokinetic modeling of the RIT applied to CSF could facilitate optimization this treatment modality to improve therapeutic efficacy.
Several pharmacokinetic models, mostly for intravenous antibodies, have been developed in humans and animals [13–15]. The CSF compartment differs substantially from the blood/plasma compartments in several aspects: (1) CSF does not re-circulate (unidirectional flow), (2) drug concentrations are higher when delivered into the small volume (140 ml of CSF in contrast to 5000 ml of blood), (3) in contrast to blood, CSF has few to none circulating cells, and protein levels (e.g. IgG) are nearly a thousand-fold lower, (4) because of the blood brain barrier, neutralizing antibodies cannot penetrate the CSF.
We recently described a simple one-compartment model to explore parameters that could improve RIT [16]. This model represented the entire CSF space as one compartment, where CSF was rapidly produced and unidirectionally drained out. Antibodies were assumed to be evenly distributed and exit with the CSF as the latter was reabsorbed. Of note was the discrepancy between actual patient CSF sampling data and model predictions of early post-injection time points. The high initial antibody concentration was likely a result of its confinement within the lateral ventricles immediately following injection into the Ommaya reservoir. Thus, the lateral ventricles serve as reservoirs causing an initial delay in its distribution to the subarachnoid space. Since the ventricles constitute only 21% of the total CSF volume, the radioactivity in the ventricles will be slightly higher initially than the radioactivity in the subarachnoid space [17, 18].
In addition to limitations of data fitting, several critical factors implicated in RIT efficacy (e.g. immunoreactivity, tumor distribution, and antibody specificity) were not initially explored [16]. For patients to be eligible for RIT delivered through the CSF, flow study has to be near normal without obstruction to CSF flow. When the initial one-compartment was built, it was assumed that tumor cells in this patient population were located primarily in the subarachnoid space and nearly absent in the ventricles. However, the impact of even a small percent of tumor cells in the ventricles was not formally tested. This could invalidate many of the derived predictions.
While in the brain ventricles, antibodies have low penetration into the brain and are impermeable to the blood-brain barrier [19, 20]. Hence, antibody elimination from the CNS is assumed to be primarily dependent on the rapid production and the net flow of CSF from the ventricles to the subarachnoid space. In the subarachnoid space, besides binding to tumor cells, antibodies are removed from the entire CSF system by the reabsorption of CSF into dural sinus [21]. In light of these considerations, we constructed a two-compartment pharmacokinetics model to study antibody clearance, accounting for the ventricular reservoir and tumor distribution. We verified this new model with an expanded cohort of data from 39 IO-RIT injections administered to 25 patients. We reexamined the two critical therapeutic end-points, namely the radioactivity concentration curve of the bound antibody (AUC[CIAR]) and the therapeutic ratio of bound versus free antibody (i.e., AUC[CIAR]/AUC[CIA]). We used the two-compartment model to examine additional treatment variables not considered in the model previously described [16].
Methods
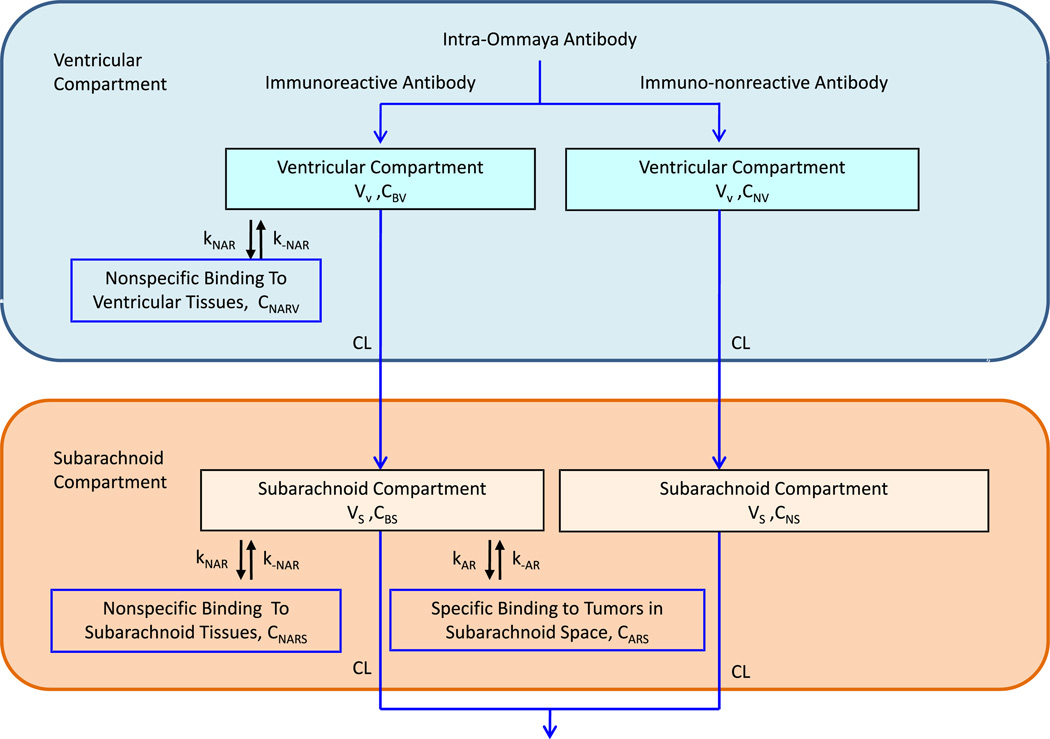
In this two-compartment model, antibodies are first introduced into the ventricular compartment, migrating from ventricles to subarachnoid space as part of CSF bulk flow, and exiting the ventricles into the subarachnoid space. Our model utilizes the antibody kinetics we previously proposed [16], which assumed that the antibodies bind to the receptors on tumor cells lining the surface of the compartment. Assuming even distribution of tumor in the CSF space, antibody binding was divided accordingly based on the CSF volume. Nonspecific binding was assumed to occur in both compartments. The total antibody concentration was divided into immunoreactive and immunononreactive parts. For 3F8 labeled with 131I, ~50% of the antibodies retained immunoreactivity after isotope labeling [22]. Therefore, 50% of the antibodies introduced into the system were modeled to have specific GD2 binding kinetics. A schematic of the model is shown in Fig. 1. For definition of parameters and a detailed description of model specifics, please refer to the Supplement online.
Fig. 1.
Flow chart of the two compartment model showing the movement of immunoreactive and immuno-nonreactive antibodies from the site of injection in the ventricular compartment into the subarachnoid compartment and clearing out of the cerebral spinal fluid
Model verification was done using an expanded cohort of CSF sampling data on 39 therapy cycles collected from 25 patients treated with IO-RIT with 131I-3F8 at Memorial Sloan-Kettering Cancer Center from two separate IO-RIT protocols (ClinicalTrials.gov, NCT00003022 and NCT00445965). Patients had a histologically confirmed diagnosis of a high risk or recurrent CNS/ leptomeningeal malignancy known to express GD2. Patients received 10 mCi 131-I-3F8 per injection (approximate volume 1 ml, 5 mCi/mg 3F8) via an Ommaya reservoir using sterile techniques. Serial CSF and blood were obtained for radioactivity levels at approximately time 0, 5, 15, and 30 minutes, 2–4 hours, 18–24, and 44–48 hours after injections. Data collection was in compliance with the institutional review board and hospital guidelines. A standard least-squared fit was used for data fitting. Only a subset of injections had complete data without outliers and enough data points for model fitting, i.e. 39 of the 74 therapy cycles (25 of the 41 patients). A subset of 32 injections was used for the comparison between the one-compartment model and the two-compartment model. For the one-compartment model, CSF clearance rate and CSF volume and tumor layer (n) were used as adjustable parameters as previously described [16]. For the two-compartment model, ventricular volume and CSF clearance rate were used as adjustable parameters, and tumor layer (n) was assumed to be one cell thick.
The same therapeutic endpoints were applied to both models [16]. Briefly, the time-dependent quantity of radioactivity of antibodies bound to receptors on the tumor cells (AUC[CIAR]) was used to represent the successfully targeted RIT. Maximizing AUC[CIAR] will maximize cytotoxic effect on tumor cells. The therapeutic ratio is the ratio of AUC[CIAR] to the AUC of free flowing (unbound) antibodies in the CSF space (i.e. AUC[CIA]). Maximizing therapeutic ratio will minimize normal tissue toxicity. We studied the impact on these two endpoints when variations were made in tumor antigen density, tumor distribution in the CSF space, antibody dosage, antibody affinity, percent immunoreactivity of MoAb, nonspecific binding, and isotope half-lives. Information on model specifics, parameter values, and calculation of radiation absorbed dose is found in Supplement. Certain parameters (e.g. ventricular volume, CSF volume, CSF flow rate) were kept constant during optimization calculations; average literature values for these parameters were used.
Results
Data fitting
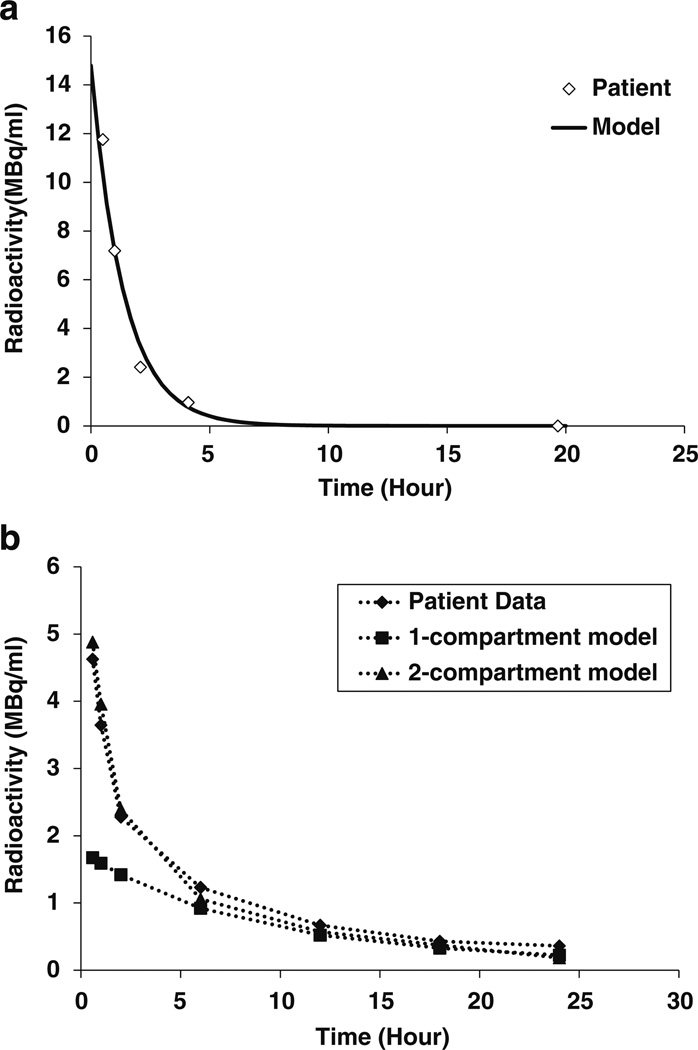
CSF sampling data from 39 therapy cycles administered to 25 patients were fitted using the two-compartment model. The model showed good correlation to the patient data (average correlation coefficient 0.95±0.03 (range from 0.88–0.995). The average computed value for ventricular volume and CSF clearance rate were 26.3±1.0 mL and 15.9±6.8 mL:/hour, respectively. These values were comparable to the published values of 30 mL for ventricular volume and 20 mL/hour for CSF clearance rate [17, 19]. Data fitting for a representative patient is shown in Fig. 2a. A comparison of fit between one-compartment model (average R = 0.77±0.21) and two-compartment model (R = 0.92±0.11) was performed using data from a subgroup of 32 injections from 24 patients (p=0.005). As shown in Fig. 2b, the two-compartment model consistently provided better correlation than the one-compartment model.
Fig. 2.
Comparison of model prediction to experimental data obtained from CSF sampling. a Comparison of model predictions to patient data. The patient received 2 mg dose at specific activity of 5 mCi/mg. The antigen density was fixed at 2.865 × 1014 antigens/ml. The ventricular volume and the clearance rate were fitted to be 25 ml and 18 ml/hour, respectively. b Comparison of data fitting between 1-compartment model and 2-compartment model. The dose administered was 3.54 mg at specific activity of 5 mCi/mg. The antigen density was 2.865 × 1014 antigens/ml. The ventricular volume was 40 ml and the clearance rate 20 ml/hour
Effects of isotope half-life, specific activity of antibody, and immunoreactivity on therapeutic ratio
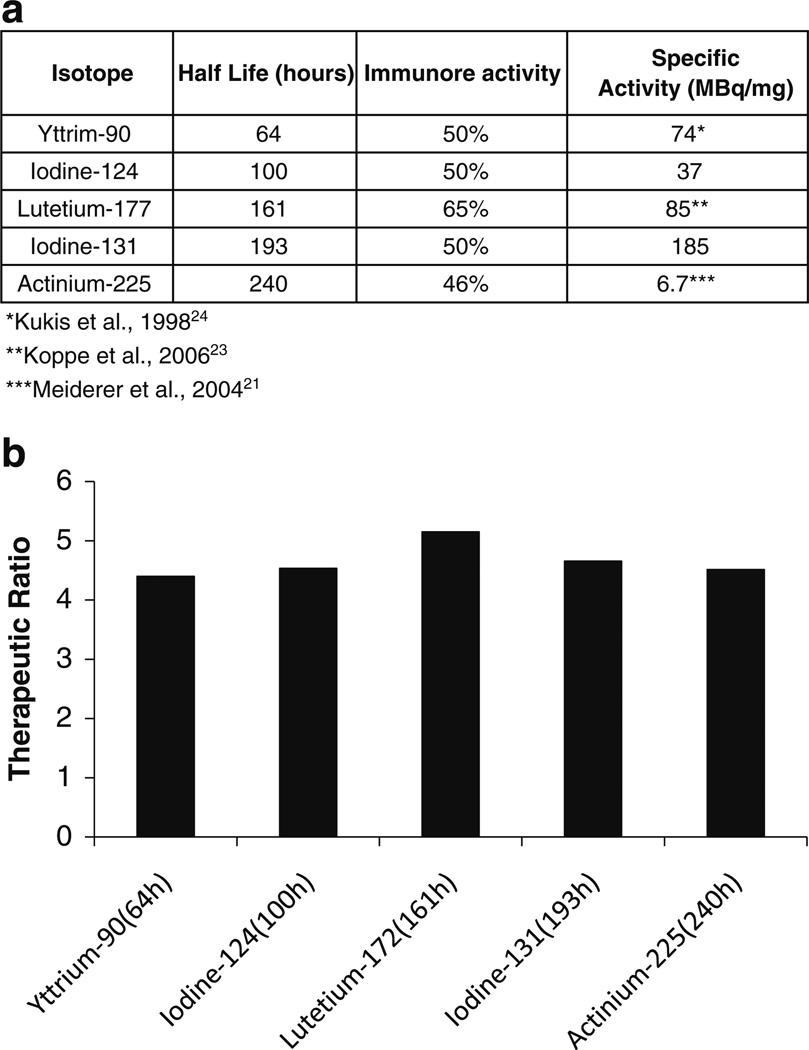
Different isotopes including yttrium-90, iodine-131, lutetium-177, and actinium-225 are being used for radioimmunotherapy (RIT) using MoAb. In addition to half-life, specific activity and immunoreactivity can vary when different isotopes are labeled onto the same antibody. Figure 3a summarizes the half-life, percent immunoreactivity, and specific activity for each of the radiolabeled 3F8 forms. Iodination modifies tyrosine while DOTA chelates affect lysine residues. In 3F8 there were 7 tyrosines and 1 lysine within the CDR regions of both heavy and light chains. Iodinated 3F8 generally yielded a 50% immunoreactivity. It is reasonable to expect that immunoreactivity of 3F8 after DOTA modification be superior over that of 3F8 following iodination. Hence, we assumed percent immunoreactivity of 50–65% for yttrium-90 and lutetium-177 labeled 3F8 based on published values for other antibodies [23, 24]. Figure 3b shows the therapeutic ratio predicted by the model when these isotopes were used. The therapeutic ratio was greatly influenced by an increase in immunoreactivity, while half life and specific activity had much less effect.
Fig. 3.
Therapeutic ratio corresponding to 3F8 labeled with different isotopes. Half life, percent immunoreactivity, and specific activity were varied as detailed in a. a Specific activity, immunoreactivity and half life for radiolabeled 3F8. b Therapeutic ratio corresponding to 3F8 labeled with different isotopes
Immunoreactivity had strong impact on both therapeutic endpoints: (1) AUC[CIAR] and (2) therapeutic ratio
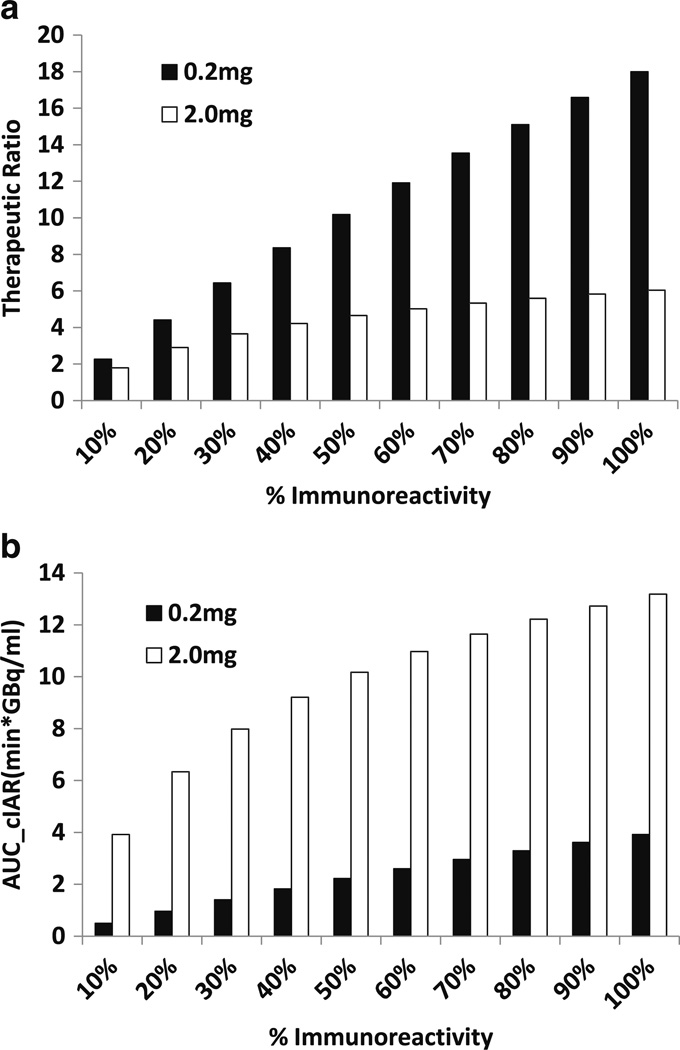
At low antibody dose (0.2 mg per injection), immunoreactivity alone had substantial impact on AUC[CIAR] (Fig. 4a) and therapeutic ratio (Fig. 4b). When immunoreactivity increased from 10% to 90%, both the AUC[CIAR] and therapeutic ratio increased by 7.9 fold. At higher antibody dose (e.g. 2 mg per injection), increasing immunoreactivity from 10% to 90% improved the therapeutic ratio and the AUC[CIAR] by only 3.4 fold. Here both the therapeutic ratio and AUC[CIAR] tended to plateau when immunoreactivity was >50%.
Fig. 4.
Increasing percent immunoreactivity can increase AUC[CIAR] and therapeutic ratio. Graphs of AUC[CIAR] (Fig. 3a) and therapeutic ratio (Fig. 3b) vs. percent immunoreactivity at 0.2 mg (low dose) and 2 mg (high dose)
Effect of antibody dose and antigen density on AUC[CIAR] and therapeutic ratio
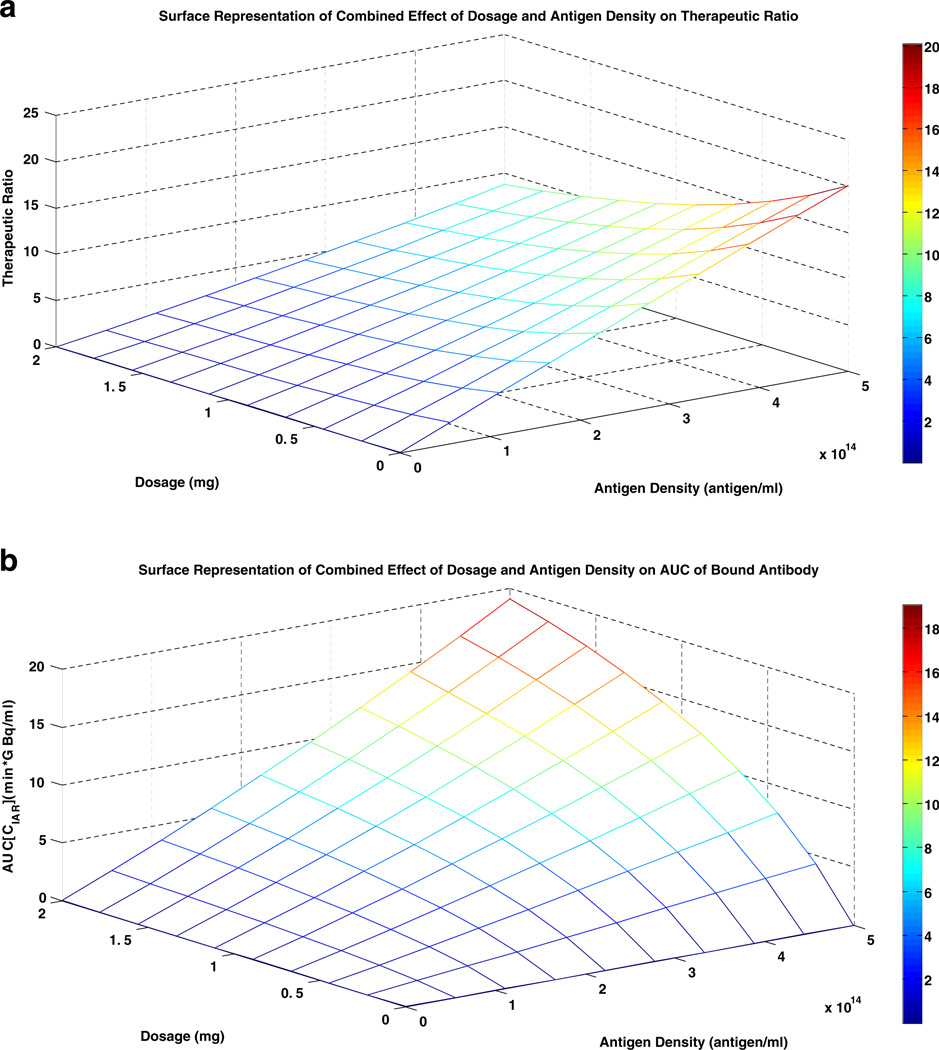
The effect of antibody dose on the therapeutic endpoints is dependent on the antigen density. As shown in Fig. 5a and b, at high antigen density (5.73 × 1014 antigens/mL), decreasing dosage could increase the therapeutic ratio up to 2.3 fold. However, the downside was a decrease in AUC [CIAR] by as much as a 1,000 fold. For example, decreasing dosage from 2 mg to 0.5 mg or from 2 mg to 0.1 mg increased therapeutic ratio by 1.76 and 2.17 fold, respectively. However, AUC[CIAR] decreased by 56% and 89%, respectively. At lower antigen density, decreasing antibody dosage did not significantly improve the therapeutic ratio, even though AUC[CIAR] still decreased substantially. At antigen density of 1010 antigens/ml, decreasing the dosage from 2 mg to 0.0001 mg increased the therapeutic ratio by merely 3 × 10−5, but decreased the AUC[CIAR] by 7,000 fold.
Fig. 5.
Surface representation of the effect of dosage and antigen density on AUC[CIAR] and Therapeutic ratio. a Surface Representation of Combined Effect of Dosage and Antigen Density on Therapeutic Ratio. b Surface Representation of Combined Effect of Dosage and Antigen Density on AUC of Bound Antibody
Antibody schedule and split dosing influenced therapeutic endpoints
Antibody dose of 2 mg can be given as a continuous infusion or as split doses. Increasing the antibody infusion time from 0 hour (a single bolus) to continuous infusion over 12 hours showed very little improvement in the therapeutic endpoints, with AUC[CIAR] increasing by 13% and therapeutic ratio by 15% (Supplementary Figure 1A). When infusion time was extended from 12 hours to 72 hours, AUC[CIAR] increased by 39%, and therapeutic ratio increased by 54%. Further lengthening the infusion time from 72 hours to 168 hours had little effect on AUC[CIAR] and therapeutic ratio. Changing infusion time from a single bolus to continual infusion over one week gave a maximum increase in therapeutic ratio of 2.1 fold, and AUC[CIAR] of 1.6 fold.
When the 2 mg antibody dose was split into 1 mg doses and given at increasing time intervals from 0 hour (single bolus) to 24 hours, both therapeutic ratio and AUC[CIAR] increased by 1.4 fold (Supplementary Figure 1B). Increasing the time interval further from 24 hours to 72 hours only increased therapeutic ratio and AUC[CIAR] by 3.6%. Similarly, when divided into four 0.5 mg doses, increasing the time interval from 0 hour to 24 hour increased both therapeutic ratio and AUC[CIAR] by 1.75 fold. Further lengthening the infusion from 24 hours to 72 hours only increased therapeutic ratio and AUC[CIAR] by 3.7% (Fig. 5b).
Effect of antibody affinity on therapeutic endpoints
Antibody affinity is a major contributing factor for successful delivery of RIT. However, improving the affinity of an antibody beyond 0.1 nM range can be technically challenging. We therefore use the model to derive treatment parameters in order to deliver a dose of ≥100 Gy to tumor cells while minimizing bystander radiation to CSF space to <10 Gy, i.e. achieving a therapeutic ratio >10.
In order to achieve this objective using one single intra-Ommaya antibody injection, the equilibrium constant (koff/kon) needs to be improved from 10−8 M to 2 × 10−10 M, a 50 fold improvement in KD. At such high antibody affinities, the antibody dose could be reduced from 2 to 0.4 mg, resulting in an increase of therapeutic ratio from 4.6 fold to 147.8. However, the same objective could be achieved even if KD could not be improved by ≥10 fold, as long as one split the antibody injection into two doses given ≥36 hours apart. Two injections of 0.8 mg each, at an antibody affinity of 1 × 10−9 M could achieve a therapeutic ratio of 34.1, while delivering over 100 Gy to tumor cells. Similarly, when the KD is 4 × 10−9 M, 4 injections of 1.4 mg each could achieve a therapeutic ratio of 10.1. The predicted values of tumor doses and therapeutic ratios corresponding to each dosage and affinity are tabulated in Table 1.
Table 1.
Values of optimization criteria at each dosage and affinity. Light grey represents AUC[CIAR] >10,000 rad and therapeutic ratio >10. Medium grey represents 10,000 rad >AUC[CIAR] >5,000 rad and therapeutic ratio >10. Black represents 5,000 rad >AUC[CIAR] >2,500 rad
| a. AUC[CIAR] in units of Gy at each doage and affinity | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Radiation of Bound Antibody (in unit of Gy) | |||||||||||
| Kd (× 10−8) | 1.00 | 0.80 | 0.60 | 0.40 | 0.20 | 0.10 | 0.08 | 0.06 | 0.04 | 0.02 | 0.01 |
| Dosage(mg) | |||||||||||
| 0.2 | 3.81 | 4.66 | 6.04 | 8.64 | 15.72 | 27.85 | 33.15 | 41.09 | 54.18 | 79.95 | 106.22 |
| 0.4 | 6.81 | 8.21 | 10.41 | 14.43 | 24.73 | 41.13 | 48.01 | 58.06 | 74.17 | 104.74 | 134.92 |
| 0.6 | 9.21 | 10.95 | 13.63 | 18.38 | 29.89 | 47.19 | 54.22 | 64.33 | 80.29 | 110.05 | 139.13 |
| 0.8 | 11.16 | 13.13 | 16.09 | 21.2 | 33.14 | 50.52 | 57.51 | 67.52 | 83.26 | 112.54 | 141.12 |
| 1 | 12.78 | 14.89 | 18.02 | 23.31 | 35.41 | 52.74 | 59.68 | 69.61 | 85.2 | 114.18 | 142.44 |
| 1.2 | 14.16 | 16.36 | 19.59 | 24.98 | 37.13 | 54.4 | 61.29 | 71.16 | 86.65 | 115.4 | 143.42 |
| 1.4 | 15.34 | 17.61 | 20.9 | 26.35 | 38.51 | 55.71 | 62.58 | 72.39 | 87.79 | 116.37 | 144.2 |
| 1.6 | 16.37 | 18.69 | 22.02 | 27.51 | 39.66 | 56.8 | 63.64 | 73.41 | 88.74 | 117.18 | 144.86 |
| 1.8 | 17.29 | 19.64 | 23 | 28.5 | 40.64 | 57.73 | 64.55 | 74.28 | 89.56 | 117.86 | 145.41 |
| 2 | 18.11 | 20.48 | 23.87 | 29.38 | 41.5 | 58.55 | 65.37 | 75.05 | 90.27 | 118.47 | 145.9 |
| 2.2 | 18.86 | 21.24 | 24.64 | 30.16 | 42.26 | 59.27 | 66.04 | 75.72 | 90.9 | 119 | 146.33 |
| 2.4 | 19.53 | 21.93 | 25.34 | 30.86 | 42.95 | 59.91 | 66.67 | 76.33 | 91.46 | 119.48 | 146.72 |
| 2.6 | 20.15 | 22.56 | 25.98 | 31.5 | 43.57 | 60.5 | 67.24 | 76.88 | 91.97 | 119.91 | 147.07 |
| 2.8 | 2.073 | 23.15 | 26.56 | 32.08 | 44.14 | 61.04 | 67.77 | 77.38 | 92.44 | 120.31 | 147.39 |
| 3 | 21.26 | 23.68 | 27.11 | 32.62 | 44.66 | 61.53 | 68.25 | 77.84 | 92.87 | 120.68 | 147.68 |
| 3.2 | 21.76 | 24.19 | 27.16 | 33.12 | 45.15 | 61.99 | 68.69 | 78.27 | 93.27 | 121.02 | 147.96 |
| 3.4 | 22.22 | 24.66 | 28.08 | 33.59 | 45.6 | 62.41 | 69.11 | 78.67 | 93.64 | 121.33 | 148.21 |
| 3.6 | 22.66 | 25.1 | 28.52 | 34.03 | 46.02 | 62.81 | 69.5 | 79.04 | 93.99 | 121.63 | 148.45 |
| 3.8 | 23.07 | 25.51 | 28.94 | 34.44 | 46.62 | 63.19 | 69.86 | 79.4 | 94.32 | 121.91 | 148.67 |
| 4 | 23.47 | 25.9 | 29.33 | 34.83 | 46.79 | 63.54 | 70.21 | 79.73 | 94.63 | 122.17 | 148.89 |
| b. Therapeutic ratio at each dosage and affinity | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Therapeutic Ratio | |||||||||||
| Kd (× 10−8) | 1.00 | 0.80 | 0.60 | 0.40 | 0.20 | 0.10 | 0.08 | 0.06 | 0.04 | 0.02 | 0.01 |
| Dosage(mg) | |||||||||||
| 0.2 | 10 | 13 | 16 | 23 | 43 | 91 | 114 | 153 | 233 | 322 | 91 |
| 0.4 | 9 | 11 | 14 | 19 | 33 | 66 | 80 | 103 | 148 | 195 | 66 |
| 0.6 | 8 | 10 | 12 | 16 | 27 | 49 | 58 | 73 | 102 | 131 | 49 |
| 0.8 | 7 | 9 | 11 | 14 | 22 | 39 | 46 | 57 | 77 | 98 | 39 |
| 1 | 7 | 8 | 10 | 13 | 19 | 32 | 38 | 46 | 62 | 79 | 32 |
| 1.2 | 6 | 7 | 9 | 11 | 17 | 28 | 32 | 39 | 52 | 66 | 28 |
| 1.4 | 6 | 7 | 8 | 10 | 15 | 24 | 28 | 34 | 45 | 56 | 24 |
| 1.6 | 5 | 6 | 7 | 9 | 13 | 21 | 25 | 30 | 40 | 49 | 21 |
| 1.8 | 5 | 6 | 7 | 8 | 12 | 19 | 22 | 27 | 35 | 44 | 19 |
| 2 | 5 | 5 | 6 | 8 | 11 | 18 | 20 | 24 | 32 | 40 | 18 |
| 2.2 | 5 | 5 | 6 | 7 | 10 | 16 | 19 | 22 | 29 | 36 | 16 |
| 2.4 | 4 | 5 | 6 | 7 | 10 | 15 | 17 | 21 | 27 | 33 | 15 |
| 2.6 | 4 | 5 | 5 | 6 | 9 | 14 | 16 | 19 | 25 | 31 | 14 |
| 2.8 | 4 | 4 | 5 | 6 | 8 | 13 | 15 | 18 | 23 | 38 | 13 |
| 3 | 4 | 4 | 5 | 6 | 8 | 12 | 14 | 17 | 22 | 27 | 12 |
| 3.2 | 4 | 4 | 5 | 6 | 8 | 12 | 13 | 16 | 20 | 25 | 12 |
| 3.4 | 3 | 4 | 4 | 5 | 7 | 11 | 12 | 15 | 19 | 24 | 11 |
| 3.6 | 3 | 4 | 4 | 5 | 7 | 10 | 12 | 14 | 18 | 22 | 10 |
| 3.8 | 3 | 4 | 4 | 5 | 7 | 10 | 11 | 13 | 17 | 21 | 10 |
| 4 | 3 | 3 | 4 | 5 | 6 | 9 | 11 | 13 | 16 | 20 | 9 |
Tumor distribution and nonspecific binding had little effect on therapeutic endpoints
The impact of tumor cells in the ventricles was tested in our model by assigning a percent of the total tumor load to the ventricles. It was reasonable to assume that too many tumor cells in the ventricles would cause obstruction to CSF and disqualify patients from enrollment onto these treatment protocols. Hence, the maximum percent of total tumor load assigned to the ventricles was assumed to be ≤5%. As tumor load was increased from 0% to 5%, both therapeutic endpoints decreased by only 4%. In addition to ventricular tumor load, the impact of nonspecific binding of antibodies to normal brain tissue was also tested. The percent of nonspecific binding relative to total binding was assumed to be ≤10%. A change in nonspecific binding from 0% to 10%did not impact either AUC[CIAR] or the therapeutic ratio.
Discussion
Once cancer metastasizes to the central nervous system, CSF is a natural conduit for further dissemination to the leptomeninges and other parts of the brain. Antibody-based therapy delivered through the CSF has potential for tumor control. GD2 is an adhesion molecule abundant on NB. It is also widely expressed among melanoma, small cell lung cancer, bone or soft tissue sarcoma, retinoblastoma and brain tumor [25], with limited expression in normal tissues, except neurons, skin cells and pain fibers. This antigen is genetically stable, rarely down-regulated, and not easily released from the cell membrane. Scintigraphy studies using radiolabeled MoAb confirms excellent tumor targeting [25]. At least two antibody families have been tested clinically, i.e. murine antibody 3F8 [26] and chimeric 14.18 [27]. Intra-Ommaya 131I-3F8 was successfully tested in delivering RIT through the CSF [11], and a single-compartment pharmacokinetic model was developed to study CSF RIT [16]. Ch14.18 consists of the variable region of murine MoAb 14.18 and the constant regions of human IgG1-K [28]. In a recent randomized phase III trial, the combination of intravenous ch14.18 with GM-CSF and IL-2 improved survival among high risk NB patients in remission undergoing stem cell transplant (ClinicalTrials.gov NCT00026312) [29].
In this report, the two-compartment model showed convincing fit to the actual CSF clearance data in a cohort of 25 patients receiving IO 131I-3F8. This was especially evident for the initial radioactivity values after each injection, with a much better data fitting than the corresponding values predicted by the one-compartment model. This discrepancy was due to the assumption in the one-compartment model that antibodies distributed evenly through the entire CSF space (ventricles and subarachnoid space) immediately after infusion. In contrast, the two-compartment model took into account the flow of antibodies would be delayed in the ventricular reservoir before entering into the subarachnoid space.
The one-compartment model predicted that the optimal half life of the isotope for RIT to be 64 hours, and half life beyond 64 hours did not significantly improve therapeutic ratio [16]. However, other parameters such as immunoreactivity and specific activity and antigen density must also be considered. Furthermore, the biological effect of radiation from different isotopes varies depending on the type of radioactive particles emitted and their respective energy levels (see footnote) [30]. Simulations of the combined effects of these isotope-dependent parameters suggest that only immunoreactivity has a significant effect on the therapeutic endpoints for isotopes with half-lives longer than 64 hours.
Analysis on the effect of immunoreactivity on the therapeutic ratio showed a linear relationship at low antibody dosage, with less obvious improvements when the dose was higher. This suggests that lower antibody dosage was necessary to achieve the benefit from higher immunoreactivity. This prediction is now being explored using 8H9, which has ≥90% immunoreactivity at a specific activity of 50 mCi/mg of 131I (ClinicalTrials.gov NCT00089245).
Antigen density should dictate the antibody dose required to optimize intrathecal RIT. When tumor (and antigen) density is low, a smaller antibody dose should be adequate to eliminate the tumor cells while minimizing the collateral damage to the bystander cells. Analysis using the two-compartment model showed that decreasing dosage only slightly improved the therapeutic ratio at high antigen density. Furthermore, this increase in therapeutic ratio was accompanied by a reduction in the AUC[CIAR]. When there was less antigen, lowering the antibody dose did not provide any significant benefit to therapeutic ratio, although AUC[CIAR] was greatly reduced. The implications are: (1) lowering antibody dose to adjust for the diminishing number of tumor cells is not beneficial, and (2) lowering the dosage alone has no overall benefit, since improvements in therapeutic ratio is negated by the reduction in AUC[CIAR].
An optimal schedule for IO RIT is emerging from these optimization studies. A continuous infusion of the 2 mg dose over a short period of time (<24 hours) only slightly improved the therapeutic endpoints over bolus injections. However, if the same dose was given over a slightly longer period of time from 24 hours up to 72 hours, both therapeutic endpoints could improve. Beyond 72 hours, the AUC[CIAR] did not improve further although therapeutic ratio continued to rise. Alternatively, splitting the 2 mg dose into smaller injections could yield similar results, e.g., two 1 mg doses or four 0.5 mg doses. Here, the optimal time interval between successive doses appeared to be 24 hours, regardless of the number of doses or the quantity of antibodies in each dose. These findings were consistent with the predictions using the one-compartment model [16].
Both the one-compartment model and the two-compartment model established antibody affinity as the major factor in maximizing therapeutic endpoints. Based on the two-compartment model, antibody affinities corresponding to KD values of 2 × 10−10 M or better, were necessary if a single bolus was used, irrespective of antibody dose between 0.2 mg and 2 mg. Compared to the KD of 4 × 10−9 M for 3F8, this required a 50 fold improvement in antibody affinity. Alternatively, if four 1.4 mg doses of antibodies with the current 3F8 affinity was given 24 hours apart, the same therapeutic goal could be achieved.
In conclusion, as antibodies gained increasing acceptance in cancer therapy, their well-known physicochemical properties, ease of genetic engineering and facile production will provide opportunities for RIT to a variety of human cancers metastatic to the LM and CNS, as long as there is no obstruction to CSF flow. As new novel radioisotopes and their microdosimetry become available, further improvement in the pharmacokinetic modeling of CNS RIT modality should refine this emerging therapy to fit the clinical context.
Supplementary Material
Acknowledgements
Supported in part by grants from the National Institutes of Health CA106450, Robert Steel Foundation, Hope Street Kids, Mr. William H. Goodwin and Mrs. Alice Goodwin and the Commonwealth Foundation for Cancer Research, Ludwig Center for Cancer Immunotherapy, and the Experimental Research Center of MSKCC. We want to thank Dr. Bingmei Fu of City College of the City University of New York for her critical review of the manuscript. Our thanks to Drs. Jorge Carasquillo and Neeta Pandit-Taskar of MSKCC for their administration of intraOmmaya 131I-3F8, and to Dr. Irene Cheung for critical review of the manuscript. N-K.V. Cheung was named as the inventor of antibody 3F8, which was assigned to Memorial-Sloan Kettering Cancer Center. 3F8 was licensed by Memorial-Sloan Kettering Cancer Center to United Therapeutics, Inc. United Therapeutics did not sponsor any of the laboratory or clinical research reported in these studies.
Footnotes
Electronic supplementary material The online version of this article (doi:10.1007/s00259-010-1633-8) contains supplementary material, which is available to authorized users.
The other authors disclosed no potential conflicts of interest.
Contributor Information
Ping He, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA.
Kim Kramer, Department of Pediatrics, Memorial Sloan-Kettering Cancer Center, 1275 York Avenue, New York, NY 10065, USA.
Peter Smith-Jones, Department of Radiology, Memorial Sloan-Kettering Cancer Center, New York, NY 10065, USA.
Pat Zanzonico, Department of Medical Physics, Memorial Sloan-Kettering Cancer Center, New York, NY 10065, USA.
John Humm, Department of Medical Physics, Memorial Sloan-Kettering Cancer Center, New York, NY 10065, USA.
Steven M. Larson, Department of Radiology, Memorial Sloan-Kettering Cancer Center, New York, NY 10065, USA
Nai-Kong V. Cheung, Email: cheungn@mskcc.org, Department of Pediatrics, Memorial Sloan-Kettering Cancer Center, 1275 York Avenue, New York, NY 10065, USA.
References
- 1.Gleissner B, Chamberlain MC. Neoplastic meningitis. Lancet Neurol. 2006;5:443–452. doi: 10.1016/S1474-4422(06)70443-4. [DOI] [PubMed] [Google Scholar]
- 2.Bruno MK, Raizer J. Leptomeningeal metastases from solid tumors (meningeal carcinomatosis) Cancer Treat Res. 2005;125:31–52. doi: 10.1007/0-387-24199-x_3. [DOI] [PubMed] [Google Scholar]
- 3.Grossman SA, Krabak MJ. Leptomeningeal carcinomatosis. Cancer Treat Rev. 1999;25:103–119. doi: 10.1053/ctrv.1999.0119. [DOI] [PubMed] [Google Scholar]
- 4.Smith DB, Howell A, Harris M. Carcinomatous meningitis associated with infiltrating lobular carcinoma of the breast. European Journal Surgical Oncology. 1985;11:33–36. [PubMed] [Google Scholar]
- 5.Posner JB. Neurologic Complications of Cancer, Comtemporary neurology series. Philadelphia: F.A. Davis Company; 1995. [Google Scholar]
- 6.Kramer K, Kushner B, Heller G, Cheung NK. Neuroblastoma metastatic to the central nervous system. The Memorial Sloan-kettering Cancer Center Experience and A Literature Review. Cancer. 2001;91:1510–1519. [PubMed] [Google Scholar]
- 7.Shaw PJ. Neuroblastoma with intracranial involvement: an ENSG study. Medical Pediatric Oncology. 1992;20:149–155. doi: 10.1002/mpo.2950200211. [DOI] [PubMed] [Google Scholar]
- 8.Kellie JJ, Hayes A, Bowman L, et al. Primary extracranial neuroblastoma with central nerbous system metastases: characterization by clinicopathologic findings and neuroimaging. Cancer. 1991;68:1999–2006. doi: 10.1002/1097-0142(19911101)68:9<1999::aid-cncr2820680926>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 9.Moseley RP, Davies AG, Richardson RB, et al. Intrathecal administration of I-131 radiolabelled monoclonal antibody as a treatment for neoplastic meningitis. Br J Cancer. 1990;62:637–642. doi: 10.1038/bjc.1990.345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bigner DD, Brown M, Coleman E, et al. Phase I studies of treatment of malignant gliomas and neoplastic meningitis with 131 I radiolabeled monoclonal antibodies anti-tenascin 81C6 and anti-chondroitin proteoglycan sulfate Mel-14 (ab')2 - a preliminary report. J Neuro-Oncol. 1995;24:109–122. doi: 10.1007/BF01052668. [DOI] [PubMed] [Google Scholar]
- 11.Kramer K, Humm JL, Souweidane MM, et al. Phase I study of targeted radioimmunotherapy for leptomeningeal cancers using intra-Ommaya 131-I-3F8. J Clin Oncol. 2007;25:5465–5470. doi: 10.1200/JCO.2007.11.1807. [DOI] [PubMed] [Google Scholar]
- 12.Kramer K, Kushner BH, Modak S, et al. Compartmental intrathecal radioimmunotherapy: results for treatment for metastatic CNS neuroblastoma. J Neurooncol. 2009 doi: 10.1007/s11060-009-0038-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Baxter LT, Jain RK. Transport of fluid and macromolecules in tumors. I. Role of interstitial pressure and convection. Microvascular research. 1989;37:77–104. doi: 10.1016/0026-2862(89)90074-5. [DOI] [PubMed] [Google Scholar]
- 14.Eger RR, Covell DG, Carrasquillo JA, et al. Kinetic model for the biodistribution of an 111In-labeled monoclonal antibody in humans. Cancer Res. 1987;47:3328–3336. [PubMed] [Google Scholar]
- 15.Thierens HM, Monsieurs MA, Brans B, Van Driessche T, Christiaens I, Dierckx RA. Dosimetry from organ to cellular dimensions. Comput Med Imaging Graph. 2001;25:187–193. doi: 10.1016/s0895-6111(00)00047-1. [DOI] [PubMed] [Google Scholar]
- 16.Lv Y, Cheung NK, Fu BM. A pharmacokinetic model for radio-immunotherapy delivered through cerebrospinal fluid for the treatment of leptomeningeal metastases. J Nucl Med. 2009;50:1324–1331. doi: 10.2967/jnumed.108.060798. [DOI] [PubMed] [Google Scholar]
- 17.Brassow F, Baumann K. Volume of brain ventricles inman determined by computer tomography. Neuroradiology. 1978;16:187–189. doi: 10.1007/BF00395246. [DOI] [PubMed] [Google Scholar]
- 18.Silverberg GD, Heit G, Huhn S, et al. The cerebrospinal fluid production rate is reduced in dementia of the Alzheimer's type. Neurology. 2001;57:1763–1766. doi: 10.1212/wnl.57.10.1763. [DOI] [PubMed] [Google Scholar]
- 19.Guyton A, Hall J. Textbook of medical physiology. Philadelphia: Saunders; 2000. [Google Scholar]
- 20.Blasberg RG, Patlak CS, Shapiro WR. Distribution of methotrexate in the cerebrospinal fluid and brain after intraventricular administration. Cancer treatment reports. 1977;61:633–641. [PubMed] [Google Scholar]
- 21.Davson H, Hollingsworth G, Segal MB. The mechanism of drainage of the cerebrospinal fluid. Brain. 1970;93:665–678. doi: 10.1093/brain/93.4.665. [DOI] [PubMed] [Google Scholar]
- 22.Yeh SD, Larson SM, Burch L, et al. Radioimmunodetection of neuroblastoma with iodine-131-3F8: Correlation with biopsy, iodine-131-metaiodobenzylguanidine (MIBG) and standard diagnostic modalities. J Nucl Med. 1991;32:769–776. [PubMed] [Google Scholar]
- 23.Koppe MJ, Hendriks T, Boerman OC, Oyen WJ, Bleichrodt RP. Radioimmunotherapy is an effective adjuvant treatment after cytoreductive surgery of experimental colonic peritoneal carcinomatosis. J Nucl Med. 2006;47:1867–1874. [PubMed] [Google Scholar]
- 24.Kukis DL, DeNardo SJ, DeNardo GL, O'Donnell RT, Meares CF. Optimized conditions for chelation of yttrium-90-DOTA immunoconjugates. J Nucl Med. 1998;39:2105–2110. [PubMed] [Google Scholar]
- 25.Modak S, Cheung NK. Disialoganglioside directed immunotherapy of neuroblastoma. Cancer Invest. 2007;25:67–77. doi: 10.1080/07357900601130763. [DOI] [PubMed] [Google Scholar]
- 26.Cheung NK, Saarinen UM, Neely JE, Landmeier B, Donovan D, Coccia PF. Monoclonal antibodies to a glycolipid antigen on human neuroblastoma cells. Cancer Res. 1985;45:2642–2649. [PubMed] [Google Scholar]
- 27.Mujoo K, Kipps TJ, Yang HM, et al. Functional properties and effect on growth suppression of human neuroblastoma tumors by isotype switch variants of monoclonal antiganglioside GD2 antibody 14.18. Cancer Res. 1989;49:2857–2861. [PubMed] [Google Scholar]
- 28.Gillies SD, Lo KM, Wesolowski J. High-level expression of chimeric antibodies using adapted cDNA variable region cassettes. J Immunol Methods. 1989;125:191–202. doi: 10.1016/0022-1759(89)90093-8. [DOI] [PubMed] [Google Scholar]
- 29.Gilman AL, Ozkaynak MF, Matthay KK, et al. Phase I study of ch14.18 with granulocyte-macrophage colony-stimulating factor and interleukin-2 in children with neuroblastoma after autologous bone marrow transplantation or stem-cell rescue: a report from the children's oncology group. J Clin Oncol. 2008 doi: 10.1200/JCO.2006.10.3564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.FDA US. Department of Health and Human Services. 2009. Radiation Quantities and Units. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.