Non-additive effects of pollen limitation and self-incompatibility reduce plant reproductive success and population viability

Abstract

Background and Aims

Mating system is a primary determinant of the ecological and evolutionary dynamics of wild plant populations. Pollen limitation and loss of self-incompatibility genotypes can both act independently to reduce seed set and these effects are commonly observed in fragmented landscapes. This study used a simulation modelling approach to assess the interacting effects of these two processes on plant reproductive performance and population viability for a range of pollination likelihood, self-incompatibility systems and S-allele richness conditions.

Methods

A spatially explicit, individual-based, genetic and demographic simulation model parameterized to represent a generic self-incompatible, short-lived perennial herb was used to conduct simulation experiments in which pollination probability, self-incompatibility type (gametophytic and sporophytic) and S-allele richness were systematically varied in combination to assess their independent and interacting effects on the demographic response variables of mate availability, seed set, population size and population persistence.

Key Results

Joint effects of reduced pollination probability and low S-allele richness were greater than independent effects for all demographic response variables except population persistence under high pollinator service (>50 %). At intermediate values of 15–25 % pollination probability, non-linear interactions with S-allele richness generated significant reductions in population performance beyond those expected by the simple additive effect of each independently. This was due to the impacts of reduced effective population size on the ability of populations to retain S alleles and maintain mate availability. Across a limited set of pollination and S-allele conditions (P = 0·15 and S = 20) populations with gametophytic SI showed reduced S-allele erosion relative to those with sporophytic SI, but this had limited effects on individual fecundity and translated into only modest increases in population persistence.

Conclusions

Interactions between pollen limitation and loss of S alleles have the potential to significantly reduce the viability of populations of a few hundred plants. Population decline may occur more rapidly than expected when pollination probabilities drop below 25 % and S alleles are fewer than 20 due to non-additive interactions. These are likely to be common conditions experienced by plants in small populations in fragmented landscapes and are also those under which differences in response between gameptophytic and sporophtyic systems are observed.

INTRODUCTION

Mating systems are primary determinants of the ecological and evolutionary dynamics of plant populations (Barrett and Harder, 1996; Charlesworth, 2006). Plant mating systems mediate reproductive, demographic and genetic responses to biotic and abiotic change at individual, population and species levels through their influence on processes such as pollination, fertilization, genetic recombination, gene flow and selection. Understanding the consequences of environmental change, and in particular habitat loss and fragmentation, for population viability and long term evolutionary trajectories of species has become a central focus of plant conservation genetics and ecology (Young and Clarke, 2000; Oostermeijer et al., 2003; Honnay and Jacquemyn, 2007). This trend reflects rapid increases in the number of species whose distributions have become more restricted as a result of landscape fragmentation. Quantifying the role that plant mating systems play in determining population and species persistence, and the implications of this knowledge for management, is now a primary conservation research question (Hobbs and Yates, 2003; Eckert et al., 2009). Indeed mating systems have recently been proposed as key predictors of the likely ecological responses of species to landscape-scale habitat change (Aguilar et al., 2006; Wagenius et al., 2007; Glemin et al., 2008; Eckert et al., 2009).

Most empirical evidence regarding the effect of mating system on the demographic performance of plant populations in fragmented habitats comes from the quantification of pollinator limitation and its consequences for reproductive success for species that are dependent on animals for pollen transfer. Many studies have identified reductions in abundance or changes in the behaviour or composition of pollinator communities associated with changes in landscape and population structure (Fabienne and Johnson, 2004) and such shifts are commonly correlated with reduced reproductive success (Ashman et al., 2004; Knight et al., 2005). These changes in pollinator service are commonly related directly to local plant population size, especially for plants with specialized pollinator relationships. As such these represent classic Allee effects as observed for both the Haleakala silversword (Forsyth, 2003) and Banksia goodii (Lamont et al., 1993).

A second recently observed impact of mating system on genetic and demographic responses of plants to changes in population size associated with landscape-scale habitat loss is mate limitation correlated with the loss of self-incompatibility genotypes in plants with genetically controlled self-incompatibility systems (Young et al., 2000; Willi et al., 2005; Wagenius et al., 2007). Here the impact on fecundity is mediated by the influence of low S-allele diversity on mate availability and fertilization success. In this case, significant reductions in individual fitness and population reproductive output can occur even when the level of pollinator service is still high (Young and Pickup, 2010). One important difference from the case of pollinator limitation is that with S allele-mediated mate limitation there is the potential for negative frequency-dependent selection to buffer, and at least partially restore, mate availability as rare genotypes are favoured and common ones selected against. In this respect, pollinator limitation represents an extrinsic problem associated with biotic interactions among species, while S-allele diversity is effectively an intrinsic problem resulting from changes in population genetic structure.

While the effects of both pollinator limitation and low S-allele diversity for self-incompatible plants have been quantified independently across a range of population sizes and landscape contexts for a variety of species, their joint effects on individual reproductive success and population viability have only rarely been assessed. In two cases, where this has been measured in wild populations of Brassica insularis (Glemin et al., 2008) and Rutidosis leptorrhynchoides (Young and Pickup, 2010) mate limitation and reduced reproductive output associated with low S-allele richness was identified, but little independent effect of pollinator service or interactions between genetic mate limitation and pollinator service were observed. In a third experimental study using artificial populations of the endangered herb Biscutletta neutriaca, Leducq et al. (2010) reported independent additive effects of both fertilization limitation due to reduced numbers of compatibility types and reduced pollination service on reproductive success, but again no evidence for any significant interaction.

This apparent lack of evidence for significant interacting effects of pollinator service and genetic mate limitation associated with low S-allele numbers is probably due at least in part to the difficulty in identifying wild populations, or being able to set up experiments, representing a sufficiently broad set of combinations of pollination service and S-allele richness to allow robust analysis of their independent and combined effects on plant demography. Moreover, disentangling these issues requires longitudinal studies that encompass multiple populations and generations which is empirically challenging. Nevertheless, as the potential negative effects of these two mating system issues on pollination dynamics and fertilization success are likely to be encountered at similar population sizes of a few hundred individuals and below, understanding their combined influence on plant fitness and population demography is important in determining the limitations they may place on population viability. Indeed the importance of understanding the interacting effects of pollen limitation and self-incompatibility on both population demography and mating system evolution has been highlighted recently by Busch and Schoen (2008).

Recently several modelling studies have used individual-based simulations to investigate interactions between genetic mate limitation due to self-incompatibility and demographic factors on plant reproductive performance and population demography. Hoebee et al. (2008) examined the joint and relative effects of low S-allele numbers and seedling recruitment rate in small populations of the bird-pollinated shrub Grevillea iaspicula which has gametophytic self-incompatibility. They showed that while low S-allele numbers could reduce population performance, recruitment failure was much more important in determining demographic outcomes over most biologically realistic sets of population conditions. Two simulation studies have explicitly looked at effects of self-incompatibility and pollination environment on population performance. Wagenius et al. (2007) demonstrated strong negative effects of reducing local plant density on genetic mate limitation while Levin et al. (2009) demonstrated that low S-allele numbers and constrained pollen dispersal could both reduce population performance.

Here we extend this general approach by using an individual-based simulation model to quantify and explore the independent and interacting effects of pollinator limitation and both gametophytic and sporophytic genetic self-incompatibility on individual reproductive fitness and long-term population viability. The simulation was used to explore a range of biologically realistic scenarios, using varied values for pollinator limitation as determined by pollination probability and self-incompatibility as defined by either gametophytic or sporophytic genetic control and different numbers of self-incompatibility alleles. Simulations were conducted assuming a model plant species generically parameterized to represent a short-lived, homomorphic self-incompatible, perennial herb with no seed bank.

Four specific questions were addressed. (1) What are the independent and joint effects of pollination probability, self-incompatibility system and S allelic richness on fecundity and population viability and over what parameter range are these important? (2) Are there significant non-additive interactions between pollinator limitation and self-incompatibility that either magnify or reduce these effects? (3) What are the genetic and demographic mechanisms that underlie any observed interactions? (4) What are the implications for conservation of plant populations?

MATERIALS AND METHODS

Model species

The model was parameterized to simulate a perennial herb with a maximum lifespan of approx. 10 years (reproductive cycles). Each plant could produce up to 100 flowers per year each containing a single ovule and there was no seed bank. All individuals were assumed to be hermaphrodites with diploid genetic inheritance. This generic life history was chosen as being broadly representative of many species that have been demonstrated empirically to exhibit significant effects of either pollinator limitation or self-incompatibility constraints on reproductive performance at population sizes of several hundred individuals, e.g. Amianthium muscaetoxicum (Travis, 1984); Lythrum salicaria (Ågren, 1996); Rutidosis leptorryhnchoides (Young et al., 2000); Ranunculus reptans (Willi et al., 2005).

Model structure and population simulation

The model used to conduct experimental simulations was an individual-based spatially explicit simulation of a closed population situated on a 100 × 100 two-dimensional grid with absorbing boundaries that has been previously described by Hoebee et al. (2008). A randomly allocated 30 % of the 10 000 possible locations were designated as suitable habitat. At the start of each simulation run, genotypes were randomly generated for each of 250 individuals for each of one self-incompatibility gene (numbers of S alleles available varied with simulations) and five unlinked neutral loci (set at five alleles per locus for all simulations) with the constraint that all SI genotypes were heterozygotes. For both the S locus and neutral loci, alleles were drawn at random from a distribution with even allele frequencies. Individuals in this initial cohort were then randomly assigned to spatial locations within suitable habitat.

At each yearly reproductive cycle, for each individual of at least 2 years of age (minimum reproductive age), per capita ovule production was calculated assuming a linear relationship with individual age (A), such that M = the age of first reproduction (in this case 2), L = the expected lifespan (1/d) where d = the death rate which was set at 0·1, and b₀ = maximum per capita ovule production which was 100. The number of ovules produced by an individual (Ov) is thus (b₀d)A when A is ≤ L, otherwise Ov = b₀ which is biologically reasonable for most plants, given that reproductive output does not increase indefinitely with size. Each ovule was then pollinated with a likelihood (P) that was set for the simulation and which varied from 0·01 to 1·0. This approach simulates pollination by multiple pollen donors at the maternal level, which has been shown to be important in generating biologically realistic fertilization probabilities under self-incompatibility (Vekemans et al., 1998).

Once an ovule was designated as having been pollinated, a pollen donor was chosen from all possible reproductive plants located within a pollen dispersal distance of 50 grid cells. Haploid pollen and ovule genotypes for the S locus and five neutral loci were then randomly generated from diploid parental genotypes. Pollen–ovule compatibility was assessed by comparing the diploid maternal genotype to the haploid pollen genotype for gametophytic self-incompatibility, or the diploid paternal genotype for sporophytic self-incompatibility. For the sporophytic system, this process assumed simple linear dominance relationships among S alleles on the paternal side such that S1 was dominant to S2 that was dominant to S3 and so on up to the maximum number of alleles in a population. In this, our model was similar to that of Cartwright's treatment of self-incompatibility in brassicas (Cartwright, 2009). Compatible pollinations resulted in successful fertilization that produced a seed with a diploid genotype that combined the two originally generated pollen and ovule haplotypes.

Seeds from successful fertilizations were dispersed randomly within a seed dispersal range of 25 grid cells of the maternal parent. Following seed dispersal, plant death occurred with a fixed probability of 0·1 and then in each empty cell, where one or more seeds had landed, a single seed was randomly chosen to germinate and other seeds were discarded. Plants remained non-reproductive for the first year and were then included into the pool of reproductive individuals in year 2.

Each generation, the location, genotype and reproductive status of every individual was tracked. These data were used to generate genetic and demographic summary statistics and associated variances including allelic richness, heterozygosity, inbreeding coefficient, reproductive effort (flower production), seed set and population size. The number of compatible mates was also calculated as the mean number of genetically compatible pollen donors within pollination range of each reproductive plant, based on comparison of S genotypes of plants as described previously. For sporophytic self-incompatibility, each potential pollen donor was counted a 0 if incompatible or 1 if compatible. For gametophytic self-incompatibility, pollen donors were counted as 0 if both possible pollen S haplotypes were incompatible, 0·5 if one was compatible and 1 if both were compatible with the observed maternal diploid genotype of the target reproductive plant.

Simulation experiments

To explore the demographic consequences of loss of pollinator service and reductions in S-allele numbers for populations of plants under both gametophytic and sporophytic self-incompatibility systems the following parameters were varied systematically in the simulation model: (1) the genetic mating system (self-compatible, and both gametophytic and sporophytic self-incompatible with simple linear dominance among S alleles); (2) the number of self-incompatibility alleles (S = 5, 10, 20, 30) and; (3) the probability of pollination P = 0·01,0·05, 0·10, 0·15, 0·20, 0·25, 0·50 and 1·0). Simulations were run for a maximum of 500 generations which was generally sufficient for population dynamics to either stabilize or, alternatively, for populations to go extinct. For each set of the parameter combinations outlined above 100 replicate runs were conducted.

Results were averaged across runs at each generation (year) for each set of starting conditions for four demographic variables that represent both individual plant fecundity and long-term population viability. These were: (1) the number of individuals with compatible genotypes within pollen dispersal distance of a reproductive plant (compatible mates); (2) the number of seeds produced per reproductive plant (seed set); (3) the total number of reproductive plants (population size); and (4) the number of generations that a population persisted (population persistence). Other data gathered at each generation were the number of alleles at the SI locus and the associated variance, as well as the mean fixation index (F_IS) based on the five neutral loci.

RESULTS

Independent effects of pollination likelihood and self-incompatibility

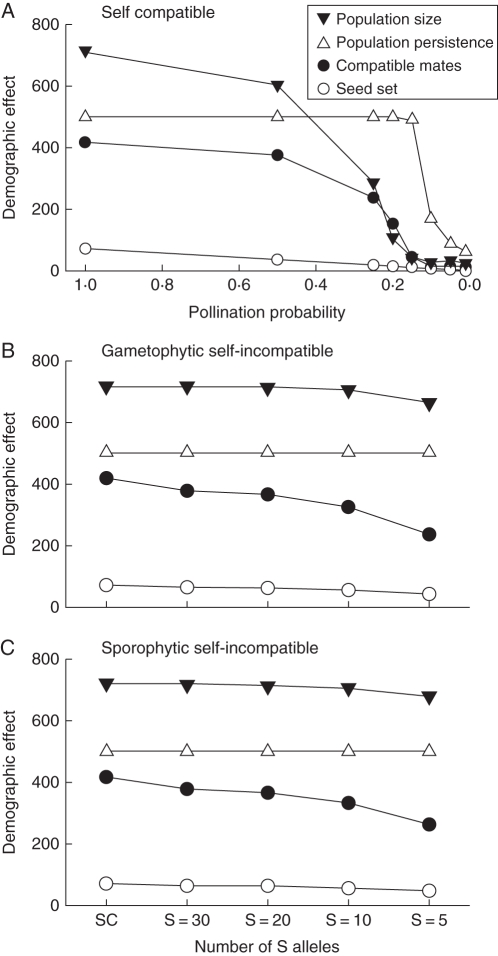
Results for baseline situations representing a self-compatible mating system and varied levels of pollinator service, or 100 % pollination service (P = 1·0) and varied S-allele numbers, are presented in Fig. 1. Results for populations of self-compatible plants showed that, even without any additional constraints imposed by self-incompatibility, reduced pollination probability had a strong, negative, non-linear effect on the mean number of compatible mates per plant within a population (Fig. 1A). This effect carried over to reduced seed set and lower mean population size; however, the pattern of reduction was not the same. For mate availability and population size, there was little additional loss of either individual or population performance below a pollination rate of P = 0·15. Individual seed set, however, continued to decline with reduced pollination probability from P = 0·15 down to P = 0·01.

Fig. 1.

Independent effects of pollination probability and S-allele number on availability of compatible mates, seed set, population size and population persistence: (A) shows the effects of pollination probability; (B) and C) show the effects of S-allele number for gametophytic and sporophytic self-incompatibility systems, respectively. All data represent mean observed parameter values based on 100 independent simulation runs. Compatible mates = number of individuals with compatible genotypes within pollen dispersal distance of a reproductive plant; seed set = number of seeds produced per reproductive plant; population size = total number of reproductive plants; and population persistence = number of generations that a population persisted.

At 100 % pollination probability, reducing the initial number of S alleles had a negative effect on the number of compatible mates and seed set for both gametophytic and sporophytic self-incompatiblity systems relative to the self-compatible case (Fig. 1B, C). For both mating systems these reductions were substantial, with the mean number of compatible mates or seed produced for a plant in a population with only five S alleles being 30 % less than that produced by an equivalent population of self-compatible plants. In contrast, while the effects of reducing S-allele number on population size were also negative under full pollination (P = 1·0) for either the gametophytic or sporophytic system, they were much less pronounced (Fig. 1B, C).

For a broad range of pollination rates from P = 1·0 to P = 0·15 there was almost no reduction in population persistence when plants were self-compatible. However, below P = 0·15, reductions in persistence with reduced pollination likelihood were dramatic, resulting in >60 % decreases in average population viability (Fig. 1A). In contrast, at 100 % pollinator service, S-allele richness had no effect on population persistence at all for either self-incompatibility system (Fig. 1B, C).

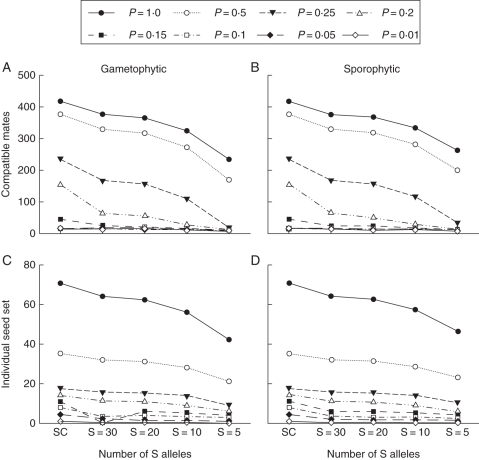
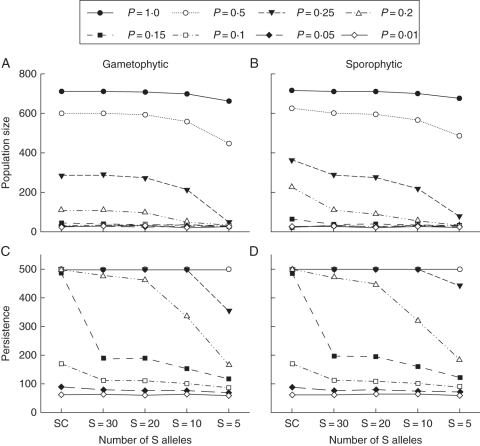
Combined effects of pollination likelihood and self-incompatibility

Simulations were conducted in which both pollination probability and S-allele number were systematically varied across all values of P = 0·01–1·0 and S = 5–30 (with the self-compatible situation included for comparison). The results demonstrate significant joint effects of these two types of mating limitation on all four individual- and population-level response variables (Figs 2 and 3) for both self-incompatibility types. These effects were not observed over the entire range of S and P values, however, with changes in either variable having little influence on individual (mate availability and seed set) or population level (population size and persistence) outcomes when pollinator service was lower than P = 0·15 for either gametophytic or sporophytic self-incompatibility. For population persistence, joint effects were only observed over a small range of simulations when P = 0·1–0·25 (Fig. 3C, D) with higher P values offsetting any apparent effect of reductions in S-allele numbers on population viability, though, when S-allele number was low under these conditions, surviving populations were smaller.

Fig. 2.

Joint effects of pollination probability and S-allele number on mate availability and seed set: (A, B) show results for mate availability for gametophytic and sporophytic self-incompatibility systems, and (C, D) show results for individual seed set. For all graphs, the lines represent different pollination probabilities, as indicated in the key. SC = self-compatible. All data represent mean observed parameter values based on 100 independent simulation runs.

Fig. 3.

Joint effects of pollination probability and S-allele number on population size and long-term persistence: (A, B) show results for population size for gametophytic and sporophytic self-incompatibility systems, and (C, D) show results for population persistence. For all graphs, the lines represent different pollination probabilities, as indicated in the key. SC = self-compatible. All data represent mean observed parameter values based on 100 independent simulation runs.

Interactions between pollination likelihood and self-incompatibility

Differences in the shape of responses of all four measured variables to S-allele richness across different pollination likelihoods (Figs 2 and 3) suggest non-additive interactions in their effects, particularly for population persistence (Fig. 3C, D). For example, reducing S-allele number from 30 to 5 under gametophytic self-incompatibility reduces persistence times by 130 generations on average when P = 0·25, but the same loss of S alleles at P = 0·2 results in a 330-generation reduction (Fig. 3C).

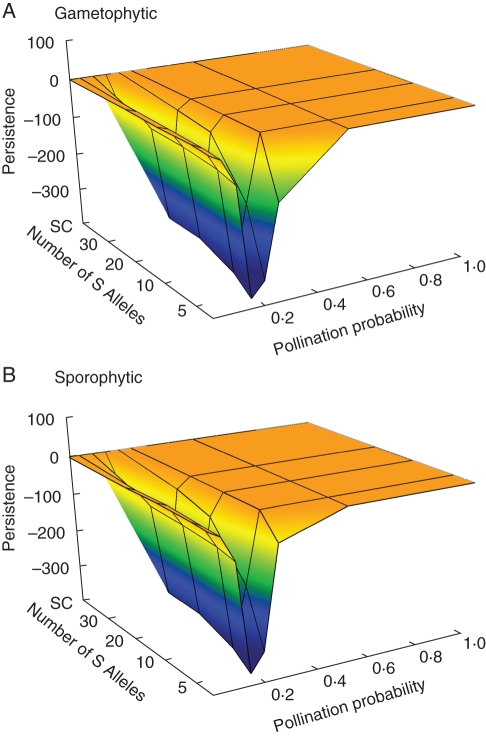
To explore further the range of combinations of S and P that generated non-additive impacts on the four demographic response variables, values generated by the simulation model for all combinations of S and P were compared with expected additive values. These baseline expected values were generated by adding the independent results for each variable presented in Fig. 1 for a given combination of S and P. Deviations of observed values from those predicted based on this assumption of simple additive action were examined for both gametophytic and sporophytic self-incompatibility against S-allele richness and pollination likelihood.

Results for mate availability, individual seed set and population size demonstrated that, for both self-incompatibility systems, over a significant range of pollination probabilities and S < 30, there were non-linear effects that could not be predicted by the additive effects of pollination and S-allele limitation acting independently (data not shown). This phenomenon was most pronounced for population persistence, which is the most obvious measure of population viability. In this case, strong non-additive interactions were restricted to a subset of P values between 0·1 and 0·25. This analysis is presented in Fig. 4 for both self-incompatibility types with zero values on the z-axis representing concordance with additive model predictions and deviations from zero representing non-additive interactions between P and S in determining demographic response. Thus, values <0 represent situations where the negative effect on these parameters was greater than the additive expectation, while values >0 represent outcomes where the negative impact was less than expected. Figure 4 illustrates that over this range of conditions, population persistence times were as much as 300–400 generations less than expected based on simple additive effects of reduced S-allele numbers and pollination probability.

Fig. 4.

Non-additive effects of pollination probability and S-allele number on population persistence for: (A) gametophytic and (B) sporophytic self-incompatibility systems. Deviations from zero represent effects that depart from a simple additive model of joint action. All data represent mean observed parameter values based on 100 independent simulation runs.

Mechanisms underlying non-additive interactions between pollination likelihood and self-incompatibility

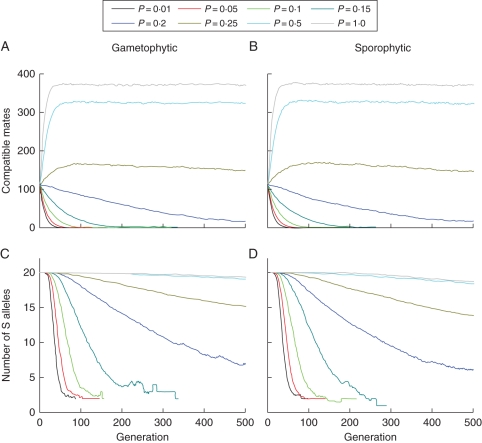
The dynamics of mate availability and S-allele number across generations are shown in Fig. 5 for population simulations initiated with 20 S alleles which represent part of the parameter space identified as exhibiting strong non-linear interaction effects of S and P on population persistence time. Figure 5 shows that for this starting value of S, populations with pollination rates of P > 0·25 maintain high mate availability (Fig. 5A, B) and S-allele numbers (Fig. 5C, D) for the full 500 simulated generations regardless of which self-incompatibility system is assumed. However, for P ≤ 0·25, negative impacts on mate availability become increasingly larger and non-linear and this is associated with a rapid increase in the rate of erosion of S alleles through generations. Generally the rate of loss of S alleles was similar for both mating systems, though for P = 0·1–0·15 loss of S-allele diversity took some 40 generations longer under gametophytic than sporophytic self-incompatability (Fig. 5C, D).

Fig. 5.

Temporal changes in mate availability and S-allele richness for populations initiated with 20 S alleles for a range of different pollination probabilities (P = 0·01 to P = 1·0): (A, B) show results for mate availability for gametophytic and sporophytic self-incompatibility systems, and (C, D) show results for S-allele richness. All data represent mean observed parameter values based on 100 independent simulation runs.

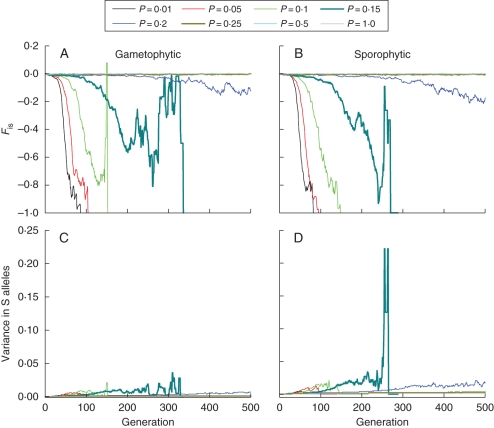
In Fig. 6A, B, the average inbreeding coefficient (F_IS) is plotted as a measure of mate limitation due to disassortative mating. Here values of P > 0·25 also correspond to F_IS values close to zero, indicating unrestricted random mating for both gametophytic and sporophytic self-incompatibility systems. When the pollination likelihood is reduced below P = 0·25, the number of S alleles present in populations begins to erode significantly over time, and below P = 0·2 S-allele numbers drop rapidly to below 3 (Fig. 5C, D) which reduces mate availability to zero (Fig. 5A, B). At the same time, population inbreeding coefficients for simulations with P < 0·20 become negative (Fig. 6A, B), eventually resulting in F_IS values of –1·0 when near to extinction, signalling very strong mate limitation due to a paucity of S alleles. Secondary spikes in inbreeding coefficients (where values increase sharply back towards F_IS = 0) for the gametophytic system for P = 0·1–0·15 (Fig. 6A) and for the sporophytic system for P = 0·15 (Fig. 6B), along with more modest spikes for lower pollination likelihood values, were clear features of the temporal dynamics of inbreeding. These indicate transient returns to more random mating in small populations prior to dramatic final declines to F_IS = –1·0 just before population extinction. Again, as with S-allele number (Fig. 5C, D), for P = 0·15 random mating is maintained some 40 generations longer for populations with gametophytic self-incompatibility than those with a sporophytic mating system. The differences in dynamics of S-allele loss between the two mating systems that underlie this difference in mating pattern can best be directly observed in the variance in S-allele numbers through time which is substantially larger in the sporophytic system than the gametophytic system (Fig. 6C, D).

Fig. 6.

Temporal changes in the inbreeding coefficient (F_IS) and variance in S-allele richness for populations initiated with 20 S alleles for a range of different pollination probabilities (P = 0·01 to P = 1·0): (A, B) show results for F_IS for gametophytic and sporophytic self-incompatibility systems, and (C, D) show results for variance in S-allele frequency. All data represent mean observed parameter values based on 100 independent simulation runs.

DISCUSSION

The results from the independent runs for self-incompatibility and pollination effects (Fig. 1) generally approximate empirical data reported from a range of plant species with similar life histories to that simulated here e.g. Amianthium muscaetoxium (Travis, 1984); Lythrum salicaria (Ågren, 1996); Eremophila glabra (Cunningham, 2000); Ranunculus reptans (Willi et al., 2005); Brassica insularis (Glemin et al., 2008); Grevillea iaspicula (Hoebee et al. (2008); Rutidosis leptorrhynchoides (Young and Pickup, 2010). For example, Young and Pickup (2010) observed reductions in percentage of compatible mates in small populations (<200 plants) of the grassland herb R. leptorrhynchoides from 65 % to 20 % as S-allele numbers are reduced from >10 to 4, which fits reasonably well with the simulation results we report here for sporophytic systems under full pollinator service (Fig. 1C). Similar results are also reported by Glemin et al. (2008) for Brassica insularis. This provides confidence in the simulation results presented here on the interacting effects of pollination failure and self-incompatibility on individual plant fitness and population viability, and their usefulness as a general tool for exploring the genetic and demographic dynamics that underpin these.

Analysis of simultaneous effects of pollination limitation and loss of S alleles showed that their joint impact has the potential to reduce both individual reproductive parameters and population viability beyond the individual impacts of either factor. This was primarily true for an intermediate range of pollination probability values from 0·15 to 0·25. In contrast, when the pollination rate became very limiting at <0·15, although self-incompatibility did compound the negative demographic effects over those seen for the self-compatible case, the initial level of S-allele diversity did not enhance this effect because S alleles were lost from populations very rapidly. At pollination rates above 0·25, self-incompatibility influenced individual reproductive performance as measured by mate availability and seed set but this did not translate into reduced population persistence, though persisting populations tended to be smaller.

Across a more restricted range of pollination rate and S-allele richness, parameter space non-additive interactive effects clearly result in dramatic reductions in population persistence below expectations based on independent effects of each (Fig. 4). These interaction effects appear to be a result of lower pollination probabilities reducing the genetic-effective population size which results in a stronger influence of genetic drift. Under these conditions, S alleles are lost from populations more rapidly than would otherwise be predicted, as negative frequency-dependent selection is less effective in maintaining equilibrium allele frequencies. This is illustrated in Fig. 6C, D which shows how the variance in S-allele frequencies changes over time for a population starting with 20 S alleles for both gametophytic and sporophytic systems.

Populations with high pollination probabilities exhibit very small variances in S-allele frequencies which are sustained over many generations. In contrast, for populations with pollination probabilities below P = 0·25, the variance in S-allele frequency increases rapidly until populations crash abruptly (Fig. 6C, D). This occurs because the weaker effect of frequency dependence in comparison to genetic drift in these populations means that S-allele frequencies diverge as some go to fixation and others are reduced in frequency. As this happens the increased inter-allele variance in frequency feeds back to limit mate availability and further reduces effective population size. This continues to increase the potential for genetic drift until there are fewer than three S alleles when mate availability becomes zero. Very similar effects on S-allele frequencies and N_e were reported by Neuhauser (1999) and Cartrwright (2009) under conditions of low pollen dispersal. Such processes are also the mechanism behind the ‘patch ageing’ effects on additional Allee effects described by Wagenius et al. (2007).

It is this interaction that explains the dramatic negative impact on population persistence of 300–400 generations beyond expectations based on the simple joint effects of either pollination limitation or self-incompatibility at pollination likelihoods of 0·15–0·25 illustrated in Fig. 4. This is primarily a one-way effect of pollination probability on the affect of self-compatibility as there is little potential for self-incompatibility system or S-allele number to influence pollination probability, except through their indirect influence on overall population size.

Interestingly, although S-allele richness does have an affect on population dynamics, and this is influenced by pollination probability, there is apparently little difference between the overall effects of either gametophytic or sporophytic control of self-incompatibility over a broad range of the simulated parameter space. This is counter to expectations based on differences in mechanisms of gene action which suggests that gametophytic self-incompatibility, which has haploid expression of the self-incompatibility gene in the pollen grain, should place fewer constraints on mate availability in comparison to the sporophytic system over most sets of population conditions. Closer investigations, as presented in Figs 5 and 6, do, however, show some potentially biologically important differences in the dynamics of S-allele erosion (Fig. 5C, D as well as Fig. 6C, D) and associated mate limitation (Fig. 5A, B) and mating behaviour (Fig. 6A, B) under a subset of population conditions (S = 20 and P = 0·15) that may not be uncommon in nature. Under these circumstances, populations exhibiting gametophytic self-incompatability lost S alleles due to drift more slowly and maintained mate availability longer than equivalent populations with sporophytic systems, and this translated into an increase in population persistence of approx. 40 generations. This result supports simulation analyses conducted by Levin et al. (2009) that showed populations with sporophytic self-incompatibility to be more extinction prone than those with gametophytic self-incompatibility, but suggests that this may only be true under a limited set of S-allele number and pollination probability conditions.

Taken together the simulation results presented here indicate that, in circumstances in which they co-occur, reductions in pollinator service and increases in S allele-based mate limitation can impose demographic constraints on populations of self-incompatible plants of a few hundred individuals (which are commonly observed in remnant habitat patches in fragmented landscapes) that are significantly greater than the effects that can be expected if either process is acting alone. Furthermore, for a smaller range of combinations of these two processes, significant non-linear interactions are generated by the effect of pollination likelihood on effective population size and the resulting reduced ability of negative frequency-dependent selection to buffer decreases in S-allele richness due to increased genetic drift. Ultimately, these interactions generate dramatic, negative, non-additive effects on population persistence. As a result, apparently ecologically unimportant changes in either variable may trigger unexpected loss of population viability depending on the state of the other variable in the population. Though the results presented here are for a generic model plant, the observed thresholds for pollinator service between 15 % and 25 % and for S-allelic richness of <20 alleles are representative of levels that are commonly reported for a range of self-incompatible species with restricted distributions (e.g. Fabienne and Johnson, 2004; Glemin et al., 2005; Young and Pickup, 2010).

These observations provide some guidance for conservation managers as to the circumstances under which rapid loss of population viability might be expected in populations in the field due to the interaction of these two mate-limiting processes. They also suggest targets for conservation of populations and habitat patches that are large and of sufficient ecological quality to maintain levels of pollinator service and S-allele richness higher than these thresholds. In this context, among-population spatial structure (i.e. connectivity) is also an important consideration for both gene-flow and potential impacts on pollinator dynamics (Cunningham, 2000; Kremen et al., 2007; Kolb, 2008). Kirchner et al. (2006) have recently demonstrated the importance of population structure in influencing the joint effects of genetic mate limitation and local negative density-dependent growth on the viability of re-established metapopulations of the narrow endemic Centaurea corymbosa.

In terms of rehabilitating populations our results also suggest that manipulating pollinator service may well be more effective than introducing new S alleles with regard to restoring reproductive success and population viability, although S-allele augmentation has been shown to increase seed set in mate-limited populations of some self-incompatible species (e.g. Willi and Fischer, 2005; Pickup and Young, 2009). This is because changes to pollination likelihood directly influence effective population size and through this determine the dynamics of S alleles in populations. In contrast, S-allele number has only limited second-order influence on pollination likelihood through its effect on population size. Interestingly, in this context, Levin et al. (2009), who used an individual-based model to explore the interacting effects of pollen dispersal distance and S-allele number, also found that when pollen was limiting (i.e. pollen dispersal distance was low and populations were small) increasing S-allele number had little positive effect on population persistence.

A direct measure of when a population is approaching thresholds of pollination service or S-allele richness that could induce rapid loss of viability would also be very useful in terms of managing populations. This is particularly the case because under some conditions collapsing populations can appear to be ecologically ‘healthy’ (Thrall et al., 1998). Unfortunately directly measuring pollinator service and S-allele status across multiple populations is not practical. However, analysis of the mechanisms underlying the non-additive interactions between pollination likelihood, effective population size, rate of erosion of S-allele richness and mating behaviour point to a parameter that can provide an indication of a population's threat status with regard to potential for population collapse. This parameter is the inbreeding coefficient (F_IS) which shows rapid and significant decline as the strength of disassortative mating increases in highly mate-limited situations that occur prior to population collapse. This parameter can easily be measured using codominant genetic markers such as allozymes or microsatellites. Indeed such negative inbreeding coefficient values have been observed empirically in small populations of the self-incompatible herb Rutidosis leptorrhynchoides (Young et al., 2000) which have been subsequently shown to be both mate limited and have poor reproductive output due to low S-allele numbers (Young and Pickup, 2010). Hoebee et al. (2008) also reported negative inbreeding coefficients for populations of the self-incompatible shrub Grevillea iaspicula consisting of <50 plants. Variance in S-allele richness is another such parameter but this is not easily measured empirically.

Demographic and genetic dynamics observed during simulations in which there was pollinator limitation alone did not reveal any such obvious signatures associated with reproductive failure. Therefore, occurrence of significant pollinator limitation is still best verified using within-population pollen augmentation experiments in which any increases in seed set from cross-pollinations over background levels from open-pollinated flowers may be taken as a signal of poor pollinator service. This general issue in conservation biology of both the need for reliable indicators of genetic and demographic problems, and the difficulty of identifying empirically tractable measures, has been highlighted previously (Thrall et al., 1998).

In summary, the results presented here suggest that when species are in an ecologically stable and ‘benign’ situation (e.g. large, well-connected populations), then reductions in either pollinator service or S-allele diversity can have some demographic consequences but more worrying non-linear interactions between these factors are not observed. At the other extreme (e.g. in small, isolated populations), when there are severe constraints associated with either factor, interactive demographic effects are also not observed because populations in this situation generally do not persist long enough, i.e. the system may be past the ‘point of no return’. Importantly, for many wild plant species, changes in both pollinator service and genetic diversity (including S alleles) are increasingly likely. To a large extent, such trends are a consequence of anthropogenic disturbance of various kinds that results in spatially fragmented ecosystems and natural communities. A key point is that, as a result of fragmentation, many plant species and communities are now being forced into exactly the sort of intermediate situations where our simulations suggest that non-additive consequences of population size decline, reduced pollinator service and erosion of S-allele richness are most likely to be observed. Finally, over and above the ecological and demographic consequences of these processes, the interactions that work to rapidly reduce mate availability also exacerbate conditions conducive to the breakdown of self-incompatibility. As such, these increasingly frequent situations are likely to prove important in shaping the future evolution of plant mating systems in the small populations that now commonly occur in fragmented landscapes. Data from several empirical studies suggest that just such evolutionary changes are already occurring (Reinartz and Les, 1994; Stone et al., 2006; Willi, 2009).