Pulse wave propagation in a model human arterial network: Assessment of 1-D visco-elastic simulations against in vitro measurements

Abstract

The accuracy of the nonlinear one-dimensional (1-D) equations of pressure and flow wave propagation in Voigt-type visco-elastic arteries was tested against measurements in a well-defined experimental 1:1 replica of the 37 largest conduit arteries in the human systemic circulation. The parameters required by the numerical algorithm were directly measured in the in vitro setup and no data fitting was involved. The inclusion of wall visco-elasticity in the numerical model reduced the underdamped high-frequency oscillations obtained using a purely elastic tube law, especially in peripheral vessels, which was previously reported in this paper [Matthys et al., 2007. Pulse wave propagation in a model human arterial network: Assessment of 1-D numerical simulations against in vitro measurements. J. Biomech. 40, 3476–3486]. In comparison to the purely elastic model, visco-elasticity significantly reduced the average relative root-mean-square errors between numerical and experimental waveforms over the 70 locations measured in the in vitro model: from 3.0% to 2.5% $(p<0.012)$ for pressure and from 15.7% to 10.8% $(p<0.002)$ for the flow rate. In the frequency domain, average relative errors between numerical and experimental amplitudes from the 5th to the 20th harmonic decreased from 0.7% to 0.5% $(p<0.107)$ for pressure and from 7.0% to 3.3% $(p<{10}^{-6})$ for the flow rate. These results provide additional support for the use of 1-D reduced modelling to accurately simulate clinically relevant problems at a reasonable computational cost.

Highlights

► We test the accuracy of the nonlinear 1-D equations of blood flow in large arteries. ► We compare wave measurements in a silicone tree with numerical predictions. ► 1-D modelling is able to capture the main features of pulse waveforms. ► Simulation of wall visco-elasticity significantly decreases relative errors. ► Energy losses at bifurcations have a secondary effect on pulse waveforms.

1. Introduction

Pressure and flow pulse waveforms carry information on the functionality of the cardiovascular system and the morphology of the arterial network, which can be valuable for the diagnosis and treatment of disease. Modelling allows us to study the effect on pulse waveforms of the physical properties of the system, such as arterial geometry and distensibility, cardiac output, heart rate and peripheral impedance to flow, and analyse the mechanisms underlying clinically relevant changes (Stergiopulos et al., 1992; Wang and Parker, 2004; Mynard and Nithiarasu, 2008; Liang et al., 2009). In particular, it allows us to test clinical diagnostic techniques that are based on pulse wave analysis and disentangle their underlying mechanisms (Karamanoglu et al., 1994; Trachet et al., 2010; Alastruey et al., 2006; Alastruey, 2011). These studies can be extremely challenging in vivo for technical and physiological reasons; e.g. some vessels are inaccessible, manipulation of the properties of interest can be dangerous or can elicit reflex compensation, and several parameters of interest are not directly measurable.

We have previously shown the ability of the nonlinear 1-D equations of pulse wave propagation in elastic vessels to capture the main features of pressure and flow waveforms measured in well-defined experimental 1:1 replicas of the larger conduit arteries in the human systemic circulation (Segers et al., 1998; Segers and Verdonck, 2000; Alastruey, 2006; Matthys et al., 2007). Matthys et al. (2007) reported average relative root-mean-square errors between numerical and experimental waveforms smaller than 3.5% for pressure and 19% for the flow rate at 70 locations in the tapered silicone network sketched in Fig. 1. Much of these errors arose from relatively high-frequency oscillations in the peripheral vessels predicted in the numerical model but not seen in the experimental measurements. Wall viscosity was suggested to play an important role in damping oscillations in the numerical pulse waveforms, but this hypothesis could not be tested since a purely elastic tube law was used in the 1-D model.

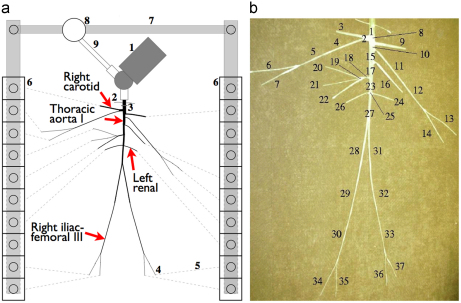
Fig. 1.

(left) Planview schematic of the 1:1 hydraulic model of the 37 larger conduit arteries in the human systemic circulation. Arteries were simulated using silicone tubes. 1: Pump (left heart); 2: catheter access; 3: aortic valve; 4: peripheral resistance tube; 5: stiff plastic tubing (veins); 6: venous overflow; 7: venous return conduit; 8: buffering reservoir; 9: pulmonary veins. The arrows indicate the location of the results shown in Figs. 3 to 5. (right) Topology and reference labels of the arteries simulated, whose properties are given in Table 1. (Modified from Matthys et al., 2007.)

Recent works have shown the benefits of modelling the arterial wall using a visco-elastic law. Bessems et al. (2008) tested a visco-elastic 1-D formulation against in vitro data measured in single tapered polyurethane vessels, showing that wall visco-elasticity is necessary to accurately predict the propagation and attenuation of pressure and flow waves. Reymond et al. (2009) compared the predictions of a visco-elastic 1-D distributed model of the human arterial tree with average pressure and flow waveforms measured at several arterial locations in a group of young subjects. Qualitative comparison of these waveforms and quantitative comparison of systolic, diastolic and mean pressure and flow indicated that the visco-elastic effects may be significant, especially in peripheral branches. They argued that energy losses and damping effects due to wall visco-elasticity are of the same order of magnitude as wall friction in large and medium size vessels. However, the parameters of their model were not specific to each subject.

Several works (Armentano et al., 1995a,b; Craiem et al., 2005; Čanić et al., 2006) have used Voigt-type visco-elastic models to simulate the visco-elastic behaviour of human and animal arteries, and improve the agreement between measured and simulated pulse waveforms. These models feature hysteresis (different stress–strain relationship for loading and unloading) and creep (continuous extension at constant load).

The aim of this work is to study the role of visco-elasticity in explaining the discrepancies of the results presented in Matthys et al. (2007). We will use a nonlinear, time-domain 1-D formulation that simulates the arterial wall as a Voigt-type visco-elastic material. Except for the shape of the velocity profile, the parameters required by the numerical algorithm will be directly measured in the in vitro setup and no data fitting will be involved. We will, therefore, provide an assessment of nonlinear visco-elastic 1-D modelling by comparison against in vitro measurements in a well-defined arterial network with tapered vessels. The notation and SI units of the quantities used in this paper are given in Table 1.

Table 1.

Notation and SI units.

A (m${}^2$)	Luminal cross-sectional area
A0 (m2)	Initial luminal cross-sectional area
c0$(\mathrm{m}{\mathrm{s}}^{-1})$	Initial pulse wave speed
E (Pa)	Young's modulus of silicone
${\mathcal{E}}_P$ (%)	Relative pressure error over one cardiac cycle
${\mathcal{E}}_{\overline{P}}$ (%)	Relative mean pressure error
${\mathcal{E}}_{\widehat{P}}$ (%)	Relative error of the amplitude of the pressure harmonics over one cardiac cycle
${\mathcal{E}}_Q$ (%)	Relative flow rate error over one cardiac cycle
${\mathcal{E}}_{\overline{Q}}$ (%)	Relative mean flow rate error
${\mathcal{E}}_{\widehat{Q}}$ (%)	Relative error of the amplitude of the flow harmonics over one cardiac cycle
F (N)	Load in the uniaxial extension test
Fmax (N)	Maximum load in the uniaxial extension test
f$(\mathrm{N}{\mathrm{m}}^{-1})$	Friction force per unit length of vessel
freq (Hz)	Wave frequency
h (m)	Vessel wall thickness
Je (m)	Jacobian of the elemental mapping from ${\Omega }_{\mathit{st}}$
Lp	Legendre polynomial of order p used for the expansion of the numerical solution
N	Total number of samples in one cardiac cycle
Nel	Number of elemental regions ${\Omega }_e$ in the numerical mesh of an arterial segment
P (Pa)	Average internal pressure over the luminal cross-section
Pe (Pa)	Elastic component of pressure
Pext (Pa)	External (or extramural) pressure
$\widehat{P}$ (Pa)	Amplitude of the pressure harmonic
$\mathcal{P}$	Order of the polynomial space of the expansion bases used for the numerical solution
Q$({\mathrm{m}}^3{\mathrm{s}}^{-1})$	Volume flow rate
$\widehat{Q}({\mathrm{m}}^3{\mathrm{s}}^{-1})$	Amplitude of the flow harmonic
$\mathcal{Q}$	Order of the Gauss-Lobatto-Legendre quadrature used in the numerical solution
Rp$(\mathrm{Pa}\mathrm{s}{\mathrm{m}}^{-3})$	Peripheral resistance of a terminal vessel
r (m)	Luminal radius
r0 (m)	Initial luminal radius
t (s)	Time
tini (s)	Initial time in a load–unload cycle of the uniaxial extension test
tend (s)	Final time in a load–unload cycle of the uniaxial extension test
U$(\mathrm{m}{\mathrm{s}}^{-1})$	Average axial velocity over the luminal cross-section
x (m)	Axial coordinate along the vessel
xel (m)	Axial coordinate of the lower point of the elemental region ${\Omega }_e$
xeu (m)	Axial coordinate of the upper point of the elemental region ${\Omega }_e$
$\beta$ (Pa m)	Parameter related to the elastic tone of silicone
$\Gamma$ (Pa s m)	Parameter related to the viscosity of silicone
$\mathrm{\Delta }t$ (s)	Time step of the numerical simulation
$ϵ$	Tensile strain of silicone
${ϵ}_{\mathit{ini}}$	Initial tensile strain in a load–unload cycle of the uniaxial extension test
${ϵ}_{\mathit{end}}$	Final tensile strain in a load–unload cycle of the uniaxial extension test
$\eta$ (m)	Change of radius of the vessel wall
$\mu$ (Pa s)	Viscosity of the water–glycerol mixture
$\xi$	Non-dimensional coordinate of the domain ${\Omega }_{\mathit{st}}$
$\rho$$(\mathrm{kg}{\mathrm{m}}^{-3})$	Density of the water–glycerol mixture
$\sigma$	Poisson's ratio of silicone
$\tau$ (Pa)	Tensile stress of silicone
$\phi$ (Pa s)	Viscosity of silicone
$\psi$ (m)	Extension in the uniaxial extension test
${\psi }_{\mathit{max}}$ (m)	Maximum extension in the uniaxial extension test
$\Omega$	Arterial domain of the spatial discretisation
${\Omega }_e$	Elemental region in $\Omega$
${\Omega }_{\mathit{st}}$	Reference (or standard) domain of the spatial discretisation

2. Methods

2.1. Visco-elastic 1-D formulation

Conservation of mass and momentum applied to a 1-D impermeable and deformable tubular control volume of incompressible and Newtonian fluid flowing with a constant axisymmetric velocity profile yields (Sherwin et al., 2003)

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial A}{\partial t}}+{\displaystyle \frac{\partial (\mathit{AU})}{\partial x}}=0,\hfill \\ {\displaystyle \frac{\partial U}{\partial t}}+U{\displaystyle \frac{\partial U}{\partial x}}+{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial P}{\partial x}}={\displaystyle \frac{f}{\rho A}},\hfill \end{array}\right)$$ (1)

where x is the axial coordinate along the vessel, t the time, $A(x,t)$ the cross-sectional area of the lumen, $U(x,t)$ the average axial velocity, $P(x,t)$ the average internal pressure over the cross-section, and $f=-22\mu \pi U$ (Alastruey, 2006) the friction force per unit length. The constant density and viscosity of the 65–35% water–glycerol mixture used to mimic blood were $\rho =1050\mathrm{kg}{\mathrm{m}}^{-3}$ and $\mu =2.5\mathrm{mPa}\mathrm{s}$, respectively.

We have modelled the silicone used to make the experimental arteries as a Voigt-type material; i.e. its tensile stresses $\tau$ and strains $ϵ$ are related through (Fung, 1993)

$$\tau =Eϵ+\phi \frac{\mathrm{d}ϵ}{\mathrm{d}t}\text{,}$$ (2)

where E is the Young's modulus and $\phi$ the viscosity of silicone. Assuming the in vitro arterial walls to be thin, isotropic, homogeneous and incompressible, and to deform axisymmetrically, each circular cross-section independently of the others, $\tau$ can be related to the internal pressure P and $ϵ$ to the change of radius of the vessel wall $\eta =r-r_0$ using Laplace's law (Olufsen et al., 2000)

$$\tau =\frac{r(P-P_{\mathit{ext}})}{h},ϵ=\frac{1}{1-{\sigma }^2}\frac{\eta }{r_0}\text{,}$$ (3)

where $r=\sqrt{A/\pi }$, h(x) is the wall thickness, $\sigma =0.5$ the Poisson's ratio and $r_0(x)$ the luminal radius at $P=P_{\mathit{ext}}$; P_ext being the constant external pressure (Matthys et al., 2007). Combining Eqs. (2) and (3) and assuming that $1/r$ can be approximated by $1/r_0$ yields

$$P=P_{\mathit{ext}}+\frac{4\mathit{Eh}}{3{(r_0)}^2}\eta +\frac{4\phi h}{3{(r_0)}^2}\frac{\partial \eta }{\partial t}\text{.}$$ (4)

Expressing $\eta$ as a function of $A=\pi r^2$ and $A_0=\pi {(r_0)}^2$, yields the visco-elastic tube law

$$P=P_{\mathit{ext}}+\frac{\beta }{A_0}(\sqrt{A}-\sqrt{A_0})+\frac{\Gamma }{A_0\sqrt{A}}\frac{\partial A}{\partial t}\text{,}$$ (5)

$$\beta =\frac{4}{3}\sqrt{\pi }\mathit{Eh},\Gamma =\frac{2}{3}\sqrt{\pi }\phi h\text{.}$$

The parameters $\beta (x)$ and $\Gamma (x)$ are related to the elastic and visco-elastic properties of the arterial wall, respectively. It is important to remark that Eq. (5) can also be derived from a generalised string model (Quarteroni et al., 2000; Formaggia et al., 2003).

2.2. Numerical solution

Eqs. (1) and (5) were solved in the 37 arterial segments of the hydraulic model in Fig. 1 using a discontinuous Galerkin scheme with a spectral/hp spatial discretisation. This is a convenient scheme for high-order discretisation of convection-dominated flows (Cockburn and Shu, 1998), such as arterial flows. It allows us to propagate waves of different frequencies without suffering from excessive dispersion and diffusion errors.

Eqs. (1) and (5) can be written in the following conservative form:

$$\frac{\partial \mathbf{U}}{\partial t}+\frac{\partial \mathbf{F}}{\partial x}={\mathbf{S}}_U\text{,}$$

with

$$\mathbf{U}=\left[\begin{array}{c}\hfill A\hfill \\ \hfill U\hfill \end{array}\right],{\mathbf{S}}_U=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill {\displaystyle \frac{f}{\rho A}}\hfill \end{array}\right]\text{,}$$

$$\mathbf{F}={\mathbf{F}}_e+{\mathbf{F}}_v=\left[\begin{array}{c}\hfill \mathit{AU}\hfill \\ \hfill \frac{U^2}{2}+\frac{P_{\mathit{ext}}+P_e}{\rho }\hfill \end{array}\right]+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill -\frac{\Gamma }{\rho A_0\sqrt{A}}\frac{\partial (\mathit{AU})}{\partial x}\hfill \end{array}\right]\text{,}$$

and $P_e=(\beta /A_0)(\sqrt{A}-\sqrt{A_0})$ being the elastic component of pressure. The flux $\mathbf{F}$ was separated into an elastic $({\mathbf{F}}_e)$ and a viscous $({\mathbf{F}}_v)$ term, and the mass conservation $\partial A/\partial t=-\partial (\mathit{AU})/\partial x$ was applied to change the time derivative to a spatial derivative in the viscous term of Eq. (5).

The discrete form of this conservative law in a domain $\Omega$ discretised into a mesh of N_el elemental non-overlapping regions ${\Omega }_e=[x_e^l,x_e^u]$, such that $x_e^u=x_{e+1}^l$ for $e=1,\dots ,N_{\mathit{el}}-1$, and ${\bigcup }_{e=1}^{N_{\mathit{el}}}{\Omega }_e=\Omega$ is given by (Karniadakis and Sherwin, 2005; Alastruey, 2006)

$$\sum _{e=1}^{N_{\mathit{el}}}\left[{\left(\frac{\partial {\mathbf{U}}^{\delta }}{\partial t},{\mathit{\psi }}^{\delta }\right)}_{{\Omega }_e}+{\left(\frac{\partial \mathbf{F}({\mathbf{U}}^{\delta })}{\partial x},{\mathit{\psi }}^{\delta }\right)}_{{\Omega }_e}+{[{\mathit{\psi }}^{\delta }·\{{\mathbf{F}}^u-\mathbf{F}({\mathbf{U}}^{\delta })\}]}_{x_e^l}^{x_e^u}\right]=\sum _{e=1}^{N_{\mathit{el}}}{({\mathbf{S}}_U^{\delta },{\mathit{\psi }}^{\delta })}_{{\Omega }_e}\text{,}$$ (6)

for all ${\mathit{\psi }}^{\delta }$ in ${\mathbf{V}}^{\delta }$, where ${(\mathbf{u},\mathbf{v})}_{\Omega }={\int }_{\Omega }\mathbf{uv}\mathrm{d}x$ is the standard ${\mathbf{L}}^2(\Omega )$ inner product, ${\mathbf{U}}^{\delta }$ and ${\mathit{\psi }}^{\delta }$ denote the approximation of $\mathbf{U}$ and test functions $\mathit{\psi }$, respectively, in the finite space ${\mathbf{V}}^{\delta }$ of piecewise polynomial vector functions (they may be discontinuous across inter-element boundaries), and ${\mathbf{F}}^u={\mathbf{F}}_e^u+{\mathbf{F}}_v^u$ is the approximation of the flux at the interface.

The term ${\mathbf{F}}_e^u$ was treated through the solution of a Riemann problem as described by Alastruey (2006). The term ${\mathbf{F}}_v^u$ requires a different treatment. Various ways of dealing with this term were analysed by Zienkiewicz et al. (2003) and the references therein. Here, ${\mathbf{F}}_v^u$ at the inter-element boundaries was approximated as

$${\mathbf{F}}_v^u{|}_{x_e^u}={\mathbf{F}}_v^u{|}_{x_{e+1}^l}=\frac{1}{2}({\mathbf{F}}_v{|}_{x_e^u}+{\mathbf{F}}_v{|}_{x_{e+1}^l}),e=1,\dots ,N_{\mathit{el}}-1\text{,}$$

with ${\mathbf{F}}_v^u{|}_{x_1^l}={\mathbf{F}}_v{|}_{x_1^l}$ at the inlet of the domain and ${\mathbf{F}}_v^u{|}_{x_{N_{\mathit{el}}}^u}={\mathbf{F}}_v{|}_{x_{N_{\mathit{el}}}^u}$ at the outlet, so that ${\mathbf{F}}_v^u-{\mathbf{F}}_v({\mathbf{U}}^{\delta })=0$ at both boundaries.

The expansion bases were selected to be a polynomial space of order $\mathcal{P}$ and the solution was expanded on each region ${\Omega }_e$ in terms of Legendre polynomials $L_p(\xi )$; i.e.

$${\mathbf{U}}^{\delta }{|}_{{\Omega }_e}(x_e(\xi ),t)=\sum _{p=0}^{\mathcal{P}}{L}_p(\xi ){\widehat{\mathbf{U}}}_e^p\text{,}$$ (7)

where ${\widehat{\mathbf{U}}}_e^p(t)$ are the expansion coefficients. Legendre polynomials are particularly convenient because the basis is orthogonal with respect to the ${\mathrm{L}}^2({\Omega }_e)$ inner product. Following standard finite element techniques, the following elemental affine mapping was introduced:

$$x_e(\xi )=x_e^l\frac{(1-\xi )}{2}+x_e^u\frac{(1+\xi )}{2}\text{,}$$

with $\xi$ in the reference element ${\Omega }_{\mathit{st}}=\{-1\le \xi \le 1\}$.

The choice of discontinuous discrete solution and test functions allows us to decouple the problem on each element, the only link coming through the boundary fluxes. Substitution of (7) into (6) and letting ${\mathit{\psi }}^{\delta }{|}_{{\Omega }_e}={\mathbf{U}}^{\delta }{|}_{{\Omega }_e}$, yields $2\mathcal{P}$ equations to be solved for each ${\Omega }_e$, $e=1,\dots ,N_{\mathit{el}}$,

$$\frac{\mathrm{d}{\widehat{U}}_{i,e}^p}{\mathrm{d}t}=\mathcal{F}({\mathbf{U}}^{\delta }{|}_{{\Omega }_e}),p=0,\dots ,\mathcal{P},i=1,2\text{,}$$ (8)

where ${\widehat{U}}_{i,e}^p,i=1,2$ are the two components of ${\widehat{\mathbf{U}}}_e^p$,

$$\mathcal{F}({\mathbf{U}}^{\delta }{|}_{{\Omega }_e})=-{\left(\frac{\partial F_i}{\partial x},L_p\right)}_{{\Omega }_e}-\frac{1}{J_e}{[L_p[F_i^u-F_i({\mathbf{U}}^{\delta }{|}_{{\Omega }_e})]]}_{x_e^l}^{x_e^u}+{(S_i({\mathbf{U}}_e^{\delta }),L_p)}_{{\Omega }_e}\text{,}$$

and $J_e=\frac{1}{2}(x_e^u-x_e^l)$ is the Jacobian of the elemental mapping from ${\Omega }_{\mathit{st}}$. For every ${\Omega }_e$, ${\mathbf{U}}^{\delta }{|}_{{\Omega }_e}$ was evaluated at Gauss–Lobatto–Legendre quadrature points of order $\mathcal{Q}$ to evaluate the integrals ${(\partial F_i/\partial x,L_p)}_{{\Omega }_e}$ and ${(S_i,L_p)}_{{\Omega }_e}$. All spatial derivatives were calculated using collocation differentiation at the quadrature points (Karniadakis and Sherwin, 2005).

Arterial segments were divided into non-overlapping elements with a 2 cm length, when possible, and a polynomial and quadrature order of 3. Elements or segments shorter than 1.5 cm were given a polynomial and quadrature order of 2. Zero pressures and velocities were considered as initial conditions.

The discretisation in time was performed by a second-order Adams–Bashforth scheme. The time step was $\mathrm{\Delta }t=100\mathrm{\mu }\mathrm{s}$ for the elastic case and $\mathrm{\Delta }t=20\mathrm{\mu }\mathrm{s}$ for the visco-elastic case, since the convection $\mathrm{\Delta }t$ scales like the square of the polynomial order $\mathcal{P}$, whereas the diffusion $\mathrm{\Delta }t$ scales like twice the square of $\mathcal{P}$ (Karniadakis and Sherwin, 2005). Although $\mathrm{\Delta }t$ had to be reduced in the visco-elastic model, it is still practical to use an explicit scheme because of the small $\mathcal{P}$ used and the fact that wave speeds are much larger than flow velocities.

Visco-elasticity was neglected at the boundary conditions of the network and the junctions, which were implemented as described in Matthys et al. (2007, Section 2.2.3) for both the purely elastic and visco-elastic models.

2.3. Numerical parameters from in vitro data

Table 2 shows the geometry, elasticity and boundary conditions required by the elastic and visco-elastic formulations, which were measured in the silicone network without any parameter fitting, as we detailed in Matthys et al. (2007). Most of the arterial segments were linearly tapered and their wall thickness decreased toward distal locations. Their Young's modulus was approximately constant (1.2 MPa), since they were made of the same silicone material. We assumed $P_{\mathit{ext}}=0$ since the experimental setup was not submerged in water.

Table 2.

Data of the 37 silicone vessels in the in vitro model (Fig. 1). $r_0^{\mathit{in}}\to r_0^{\mathit{out}}$: initial luminal radii at the inlet and the outlet; h: average wall thickness; $c_0^{\mathit{in}}\to c_0^{\mathit{out}}$: initial wave speed at the inlet and the outlet; $\Gamma$: wall viscosity parameter; R_p: peripheral resistance calculated from mean pressure and flow rate measurements close to the outlet of each terminal branch. Single numbers indicate vessels with a constant cross-section. The interval of confidence of the geometrical measurements is indicated in the heading.

Arterial segment	Length (mm) ±2.0%	$r_0^{\mathit{in}}\to r_0^{\mathit{out}}$ (mm) ±3.5%	h (mm) ±2.5%	$c_0^{\mathit{in}}\to c_0^{\mathit{out}}$ ($\mathrm{m}{\mathrm{s}}^{-1}$)	$\Gamma$ (Pa s m)	Rp$(\mathrm{GPa}\mathrm{s}{\mathrm{m}}^{-3}$)
1. Ascending aorta	36	$14.40\to 13.00$	0.51	$5.21\to 5.49$	1.82	–
2. Innominate	28	$11.00\to 7.29$	0.35	$4.89\to 6.01$	1.23	–
3. R. carotid	145	$5.37\to 3.86$	0.28	$6.35\to 7.49$	1.01	2.67
4. R. subclavian I	218	$4.36\to 3.34$	0.27	$6.87\to 7.84$	0.96	–
5. R. subclavian II	165	$3.34\to 2.78$	0.16	$6.00\to 6.58$	0.56	–
6. R. radial	235	2.07	0.15	7.43	0.53	3.92
7. R. ulnar	177	2.10	0.21	8.81	0.76	3.24
8. Aortic arch I	21	$13.00\to 12.50$	0.50	$5.41\to 5.52$	1.77	–
9. L. carotid	178	$5.58\to 3.73$	0.31	$6.55\to 8.00$	1.11	3.11
10. Aortic arch II	29	$12.50\to 11.80$	0.41	$4.98\to 5.12$	1.44	–
11. L. subclavian I	227	$4.42\to 3.39$	0.22	$6.21\to 7.10$	0.79	–
12. L. subclavian II	175	$3.39\to 2.84$	0.17	$6.26\to 6.84$	0.62	–
13. L. radial	245	2.07	0.21	8.84	0.75	3.74
14. L. ulnar	191	2.07	0.16	7.77	0.58	3.77
15. Thoracic aorta I	56	$11.80\to 11.00$	0.43	$5.29\to 5.48$	1.53	–
16. Intercostals	195	$4.12\to 3.22$	0.27	$7.07\to 7.99$	0.96	2.59
17. Thoracic aorta II	72	$11.00\to 9.26$	0.34	$4.84\to 5.26$	1.19	–
18. Celiac I	38	3.97	0.20	6.20	0.71	–
19. Celiac II	13	4.31	1.25	14.90	4.43	–
20. Splenic	191	1.83	0.13	7.24	0.45	3.54
21. Gastric	198	1.92	0.11	6.73	0.40	4.24
22. Hepatic	186	$3.31\to 2.89$	0.21	$6.95\to 7.44$	0.74	3.75
23. Abdominal aorta I	62	$9.26\to 8.01$	0.33	$5.19\to 5.59$	1.16	–
24. L. renal	120	2.59	0.19	7.39	0.66	3.46
25. Abdominal aorta II	7	7.90	0.35	5.83	1.25	–
26. R. renal	118	2.55	0.16	6.95	0.57	3.45
27. Abdominal aorta III	104	$7.80\to 5.88$	0.30	$5.41\to 6.24$	1.06	–
28. R. iliac-femoral I	205	$3.9\to 3.38$	0.21	$6.47\to 6.94$	0.76	–
29. R. iliac-femoral II	216	$3.38\to 2.31$	0.15	$5.89\to 7.13$	0.55	–
30. R. iliac-femoral III	206	$2.31\to 2.10$	0.20	$8.04\to 8.44$	0.69	–
31. L. iliac-femoral I	201	$4.02\to 3.34$	0.20	$6.19\to 6.79$	0.72	–
32. L. iliac-femoral II	195	$3.34\to 2.26$	0.16	$6.11\to 7.44$	0.58	–
33. L. iliac-femoral III	207	$2.26\to 2.12$	0.13	$6.67\to 6.89$	0.47	–
34. R. anterior tibial	163	1.55	0.15	8.47	0.52	5.16
35. R. posterior tibial	151	1.53	0.12	7.73	0.43	5.65
36. L. posterior tibial	149	1.58	0.11	7.23	0.38	4.59
37. L. anterior tibial	126	1.55	0.10	7.01	0.35	3.16

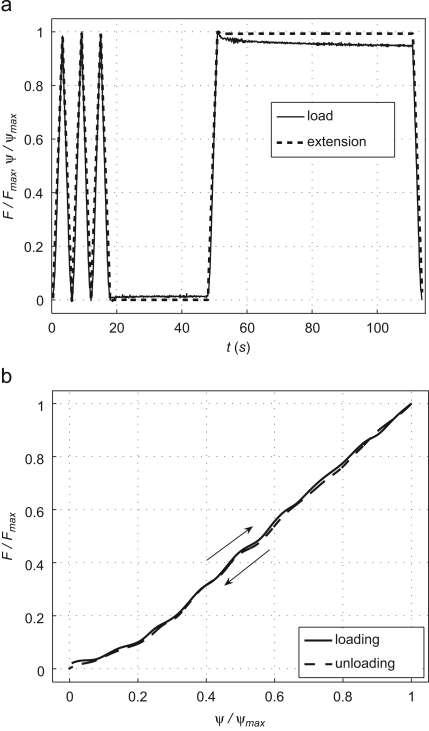
Here we estimated $\phi$ (which was not measured in Matthys et al., 2007) from an uniaxial extension test in a sample of the same silicone material used in the experimental setup. Fig. 2 (top) shows the extension $\psi$ and measured load F used in the test, which were normalised by their corresponding maximum values F_max and ${\psi }_{\mathit{max}}$. The test was carried out using a tensometer and 1 kN load cell (Instron 5542, High Wycombe, UK), loading and unloading at a rate of 20 mm ${\min }^{-1}$ to a maximum extension of 1 mm. Three consecutive loading and unloading cycles were followed by 30 s at zero extension, loading to maximum extension which was held for 60 s before the final unloading to zero extension.

Fig. 2.

(top) Experimental uniaxial load and extension with time for a sample of the silicone used in the experimental arterial network. (bottom) Load-extension loop for the first load–unload cycle, whose direction is indicated by the arrows. A cubic spline was fitted to the loading and unloading points measured in the extension test. Loads and extensions are shown normalised by their corresponding maximum values.

A cubic spline was fitted to F(t) and $\psi (t)$, separating loading and unloading. Stresses $\tau (t)$ were calculated as the ratio of F and the cross-sectional area of the sample, and strains $ϵ(t)$ as the ratio of $\psi (t)$ and the initial sample length. Fig. 2 (bottom) shows the $F\psi \text{-loop}$ for the first loading–unloading cycle (only the first cycle is shown for clarity; the following cycles were similar with no evidence of conditioning). We calculated $\phi$ as

$$\phi =\frac{{\int }_{{ϵ}_{\mathit{ini}}}^{{ϵ}_{\mathit{end}}}\tau \mathrm{d}ϵ}{{\int }_{t_{\mathit{ini}}}^{t_{\mathit{end}}}{\left({\displaystyle \frac{\mathrm{d}ϵ}{\mathrm{d}t}}\right)}^2\mathrm{d}t}\text{,}$$ (9)

which follows from integrating both sides of Eq. (2) over one load–unload cycle and using ${\int }_{{ϵ}_{\mathit{ini}}}^{{ϵ}_{\mathit{end}}}Eϵ\mathrm{d}ϵ=0$. The limits of the integrals are the initial (t_ini, ${ϵ}_{\mathit{ini}}$) and final (t_end, ${ϵ}_{\mathit{end}}$) time and strain in a load–unload cycle, with ${ϵ}_{\mathit{ini}}={ϵ}_{\mathit{end}}$. We obtained $\phi =3.0\pm 0.3\mathrm{kPa}\mathrm{s}$.

2.4. Error calculations

To assess the accuracy of the numerical predictions of pressure P and volume flow rate Q=AU, the following relative errors were calculated at each measuring site,

$${\mathcal{E}}_P=\frac{1}{N}\sum _{i=1}^N\sqrt{{\left({\displaystyle \frac{P_i^{\mathit{exp}}-P_i}{P_i^{\mathit{exp}}}}\right)}^2},{\mathcal{E}}_Q=\frac{1}{N}\sum _{i=1}^N\frac{\sqrt{{(Q_i^{\mathit{exp}}-Q_i)}^2}}{\max (Q^{\mathit{exp}})}\text{,}$$

$${\mathcal{E}}_{\overline{P}}=\frac{\sqrt{{(\mathrm{mean}(P^{\mathit{exp}})-\mathrm{mean}(P))}^2}}{\mathrm{mean}(P^{\mathit{exp}})},{\mathcal{E}}_{\overline{Q}}=\frac{\sqrt{{(\mathrm{mean}(Q^{\mathit{exp}})-\mathrm{mean}(Q))}^2}}{\mathrm{mean}(Q^{\mathit{exp}})}\text{,}$$ (10)

where N is the total number of samples in one cardiac cycle, the subscript i indicates the sampling point (the sampling rate was 1 kHz), the superscript exp indicates experimental data, the operator $\max (·)$ calculates the maximum value within $i=1,\dots ,N$, and $\mathrm{mean}(·)$ calculates the mean value within $i=1,\dots ,N$. In the frequency domain, we calculated

$${\mathcal{E}}_{\widehat{P}}=\frac{1}{M}\sum _{j=1}^M\frac{\sqrt{{({\widehat{P}}_j^{\mathit{exp}}-{\widehat{P}}_j)}^2}}{{\widehat{P}}_1^{\mathit{exp}}},{\mathcal{E}}_{\widehat{Q}}=\frac{1}{M}\sum _{j=1}^M\frac{\sqrt{{({\widehat{Q}}_j^{\mathit{exp}}-{\widehat{Q}}_j)}^2}}{{\widehat{Q}}_1^{\mathit{exp}}}\text{,}$$ (11)

where M is the total number of harmonics and ${\widehat{P}}_j$ and ${\widehat{Q}}_j$ are the amplitudes of the pressure and flow jth harmonic, respectively.

3. Results

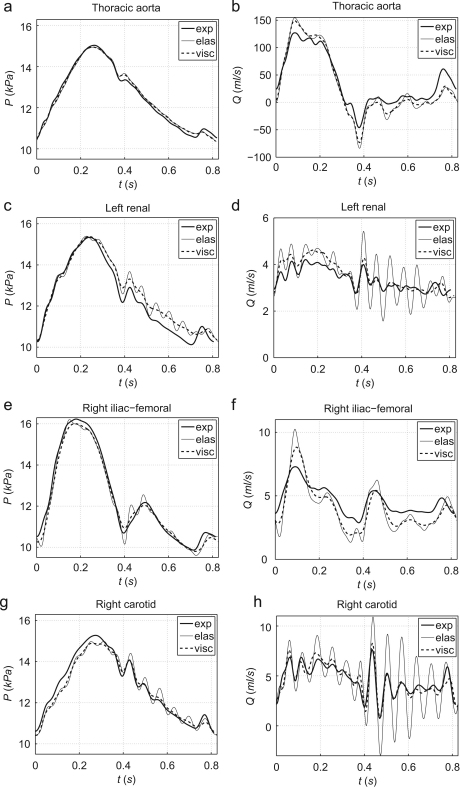
Fig. 3 compares the ensemble averaged experimental waveforms at four locations with the numerical predictions obtained using both the elastic and the visco-elastic 1-D formulations. As in the purely elastic study, we matched the onset of the experimental and numerical systolic ejections. These comparisons are representative of the results obtained at other measurement sites and show the ability of visco-elasticity to reduce the high-frequency oscillations produced by the elastic formulation, especially in peripheral vessels.

Fig. 3.

Experimental (exp) and simulated elastic (elas) and visco-elastic (visc) pressure (left) and flow (right) waveforms in the midpoint of the thoracic aorta I, left renal artery, right iliac-femoral III artery and right carotid artery in the hydraulic model in Fig. 1. Note the different scales of flow rates.

Wall visco-elasticity reduces relative errors for pressure and the flow rate in the time domain for all the 70 measurement sites. Table 3 shows these errors for both the (original) purely elastic and the (new) visco-elastic formulations in the midpoint of the arterial segments, and Table 4 shows average relative errors over all 70 measuring sites, and over all the sites in the aorta and the vessels of the first, second and third generation of bifurcations.

Table 3.

Relative errors (in %) of the numerical pulse waveforms calculated using Eqs. (10) and (11) in the midpoint of the arterial segments in Fig. 1. Errors in the frequency domain (Eq. (11)) were calculated for the first five pressure (${\mathcal{E}}_{\widehat{P}}$ I) and flow (${\mathcal{E}}_{\widehat{Q}}$ I) harmonics $(j=1,\dots ,5)$, and from the 5th to the 20th pressure (${\mathcal{E}}_{\widehat{P}}$ II) and flow (${\mathcal{E}}_{\widehat{Q}}$ II) harmonics $(j=5,\dots ,20)$. They are expressed relative to the amplitude of the first experimental pressure or flow harmonic. All errors are given as a pair of numbers: the first corresponds to the purely elastic formulation (elas) and the second to the visco-elastic formulation (visc).

Arterial segmenta	${\mathcal{E}}_P$ (%)		${\mathcal{E}}_Q$ (%)		${\mathcal{E}}_{\overline{P}}$ (%)		${\mathcal{E}}_{\overline{Q}}$ (%)		${\mathcal{E}}_{\widehat{P}}$ I (%) 1–5 harm.		${\mathcal{E}}_{\widehat{Q}}$ I (%) 1–5 harm.		${\mathcal{E}}_{\widehat{P}}$ II (%) 5–20 harm.		${\mathcal{E}}_{\widehat{Q}}$ II (%) 5–20 harm.
	elas	visc	elas	visc	elas	visc	elas	visc	elas	visc	elas	visc	elas	visc	elas	visc
1. Ascending aorta	1.0	0.7	0.0	0.0	0.6	0.5	0.0	0.0	0.5	0.4	0.0	0.0	0.2	0.1	0.0	0.0
2. Innominate	2.7	2.5	10.7	9.0	2.7	2.7	12.6	12.5	0.9	0.9	6.4	6.3	0.2	0.2	5.8	2.9
3. R. carotid	1.9	1.7	19.9	5.5	0.7	0.8	0.5	0.0	0.8	0.8	5.1	5.1	0.5	0.2	15.7	3.1
4. R. subclavian I	2.9	2.6	27.3	22.5	2.9	2.9	14.9	14.5	1.7	1.6	30.2	29.6	0.4	0.3	4.3	2.7
5. R. subclavian II	2.5	2.3	14.0	10.8	3.2	3.2	11.8	11.7	0.8	0.8	21.9	21.1	0.3	0.3	9.2	5.8
6. R. radial	2.2	1.4	11.0	7.2	1.5	1.4	7.1	7.0	1.6	1.5	7.6	7.2	0.2	0.1	4.1	2.6
7. R. ulnar	2.3	1.2	8.2	4.7	1.3	1.2	4.5	4.3	1.3	1.2	3.8	3.3	0.5	0.3	2.3	1.6
8. Aortic arch I	2.0	1.7	7.0	6.1	0.1	0.1	2.5	2.4	0.8	0.7	8.4	8.3	0.2	0.1	1.9	1.2
9. L. carotid	2.6	2.5	12.2	5.9	2.5	2.4	3.0	3.0	0.8	0.8	6.9	6.3	0.4	0.3	13.8	4.5
10. Aortic arch II	1.5	1.2	10.6	9.5	0.3	0.2	8.8	8.4	0.5	0.4	15.0	14.7	0.1	0.1	3.3	2.9
11. L. subclavian I	2.9	2.7	7.8	6.6	3.5	3.5	5.5	5.4	0.8	0.8	21.5	19.5	0.3	0.2	6.4	3.8
12. L. subclavian II	2.6	2.4	12.5	11.7	3.8	3.8	7.4	7.4	1.4	1.4	12.8	12.3	0.5	0.4	5.4	3.8
13. L. radial	2.7	2.4	9.1	7.8	2.9	2.9	6.2	6.2	1.7	1.7	2.8	2.7	0.3	0.3	3.9	2.4
14. L. ulnar	2.7	2.4	11.1	10.3	3.1	3.1	11.4	11.4	1.6	1.6	3.9	3.8	0.3	0.3	3.5	2.8
15. Thoracic aorta I	1.1	0.9	11.3	10.9	0.1	0.1	19.2	19.2	0.7	0.6	15.7	15.3	0.1	0.1	4.8	3.0
16. Intercostals	2.1	1.9	15.1	7.3	2.9	2.9	4.3	4.2	0.9	0.9	3.8	3.4	0.5	0.3	9.0	4.3
17. Thoracic aorta II	1.9	1.6	19.4	18.8	1.9	1.9	1.0	1.0	0.5	0.4	39.3	38.7	0.2	0.1	8.1	5.7
18. Celiac I	3.8	3.3	13.7	8.1	2.7	2.6	2.2	2.1	1.1	1.0	7.0	6.2	0.3	0.2	10.6	6.5
20. Splenic	3.1	1.9	7.8	5.2	1.9	1.9	8.6	8.5	1.8	1.6	3.7	3.6	0.6	0.3	3.1	1.4
21. Gastric	2.8	1.7	15.2	10.0	1.7	1.7	6.3	6.2	1.4	1.1	4.6	4.5	0.7	0.2	8.8	2.2
22. Hepatic	2.3	1.6	12.9	6.8	2.6	2.5	0.7	0.5	0.7	0.7	4.5	4.5	0.3	0.2	10.0	5.2
23. Abdominal aorta I	2.0	1.6	18.7	16.4	1.9	1.9	9.7	9.7	0.8	0.7	29.6	28.7	0.3	0.2	7.9	4.8
24. L. renal	3.0	2.9	11.9	5.6	2.4	2.3	5.1	4.9	1.0	1.0	4.2	4.1	0.6	0.3	6.6	2.7
26. R. renal	2.9	2.7	12.0	5.5	2.8	2.8	3.5	3.4	0.8	0.8	4.3	3.9	0.3	0.2	6.4	2.5
27. Abdominal aorta III	2.7	2.4	20.8	18.2	2.7	2.6	3.0	3.0	1.2	1.1	35.7	34.4	0.3	0.2	6.1	3.4
28. R. iliac-femoral I	3.0	2.7	35.3	30.5	3.2	3.1	10.6	10.7	0.8	0.8	19.1	18.6	0.5	0.4	17.4	7.7
29. R. iliac-femoral II	1.9	1.6	20.6	16.3	1.5	1.4	11.9	11.8	5.4	5.4	36.9	33.7	4.2	4.0	12.0	7.5
30. R. iliac-femoral III	2.0	1.7	13.9	11.3	1.1	1.1	12.5	12.5	1.5	1.5	13.4	10.0	0.6	0.4	7.6	3.2
31. L. iliac-femoral I	5.5	4.1	26.3	23.2	3.5	3.5	35.4	34.1	2.2	2.2	30.5	27.7	0.9	0.7	11.1	7.6
32. L. iliac-femoral II	5.5	5.1	21.5	21.4	2.9	2.8	12.4	12.4	5.2	5.2	28.4	26.3	1.2	0.9	8.0	4.9
33. L. iliac-femoral III	4.7	4.0	11.2	9.1	3.5	3.4	7.8	7.8	1.2	1.2	9.5	7.7	0.8	0.6	7.0	2.9
34. R. anterior tibial	5.6	4.7	11.9	9.1	2.4	2.3	8.3	8.3	4.8	4.5	4.6	3.7	1.6	1.1	5.2	3.7
35. R. posterior tibial	3.0	2.3	8.2	6.7	3.1	3.0	7.7	7.7	1.8	1.7	5.5	5.3	1.4	1.1	3.7	2.3
36. L. posterior tibial	5.9	4.6	11.4	10.3	2.0	2.0	8.0	8.0	5.4	5.4	6.2	6.0	1.5	1.3	4.3	2.4

^aWe did not take in vitro measurements at the celiac II (Segment 19), abdominal aorta II (Segment 25) and left anterior tibial (Segment 37).

Table 4.

Average relative errors (in %) of the numerical pulse waveforms over all 70 measuring sites, and over all the sites in the aorta and the vessels of the first, second and third generation of bifurcations. Single errors were calculated as described in Table 2. The standard deviation is given for each error. The probability p of the two-sample t-test is given for the average errors over all 70 measuring sites assuming equal variances.

Arterial segments	${\mathcal{E}}_P$ (%)		${\mathcal{E}}_Q$ (%)		${\mathcal{E}}_{\overline{P}}$ (%)		${\mathcal{E}}_{\overline{Q}}$ (%)		${\mathcal{E}}_{\widehat{P}}$ I (%) 1–5 harm.		${\mathcal{E}}_{\widehat{Q}}$ I (%) 1–5 harm.		${\mathcal{E}}_{\widehat{P}}$ II (%) 5–20 harm.		${\mathcal{E}}_{\widehat{Q}}$ II (%) 5–20 harm.
	elas	visc	elas	visc	elas	visc	elas	visc	elas	visc	elas	visc	elas	visc	elas	visc
All	3.0	2.5	15.7	10.8	2.8	2.8	7.1	7.0	1.6	1.5	13.4	12.4	0.7	0.5	7.0	3.3
	$\pm 1.0$	$\pm 1.0$	$\pm 5.6$	$\pm 5.5$	$\pm 0.8$	$\pm 0.8$	$\pm 6.0$	$\pm 5.9$	$\pm 1.3$	$\pm 1.2$	$\pm 11.5$	$\pm 10.1$	$\pm 0.6$	$\pm 0.5$	$\pm 3.6$	$\pm 1.7$
	$p<0.012$		$p<0.002$		$p<0.414$		$p<0.458$		$p<0.339$		$p<0.231$		$p<0.107$		$p<{10}^{-6}$
Aorta	1.7	1.5	13.6	11.4	1.3	1.3	4.9	4.9	0.7	0.6	20.5	20.0	0.3	0.2	4.5	3.0
	$\pm 0.5$	$\pm 0.5$	$\pm 6.9$	$\pm 6.5$	$\pm 0.8$	$\pm 0.8$	$\pm 6.0$	$\pm 5.8$	$\pm 0.2$	$\pm 0.2$	$\pm 13.5$	$\pm 12.1$	$\pm 0.1$	$\pm 0.0$	$\pm 2.6$	$\pm 1.3$
1st generation	3.5	3.2	18.8	13.1	3.0	3.0	9.7	9.7	1.7	1.7	14.4	13.1	0.9	0.7	9.3	4.7
	$\pm 1.2$	$\pm 1.0$	$\pm 7.6$	$\pm 6.9$	$\pm 0.6$	$\pm 0.6$	$\pm 7.5$	$\pm 7.2$	$\pm 1.2$	$\pm 1.2$	$\pm 11.1$	$\pm 9.3$	$\pm 0.9$	$\pm 0.8$	$\pm 3.1$	$\pm 1.8$
2nd generation	3.5	3.0	15.8	11.0	3.0	3.0	6.9	6.9	2.1	2.0	9.7	8.6	0.8	0.6	6.6	3.2
	$\pm 1.4$	$\pm 1.2$	$\pm 5.8$	$\pm 4.9$	$\pm 0.7$	$\pm 0.7$	$\pm 4.6$	$\pm 4.6$	$\pm 1.4$	$\pm 1.4$	$\pm 9.2$	$\pm 7.2$	$\pm 0.5$	$\pm 0.4$	$\pm 3.8$	$\pm 1.1$
3rd generation	2.3	1.1	11.3	6.6	1.6	1.5	6.8	6.7	1.5	1.2	5.1	4.5	0.5	0.2	4.6	1.9
	$\pm 0.5$	$\pm 0.5$	$\pm 3.1$	$\pm 2.2$	$\pm 0.3$	$\pm 0.3$	$\pm 1.6$	$\pm 1.6$	$\pm 0.2$	$\pm 0.2$	$\pm 1.7$	$\pm 1.6$	$\pm 0.2$	$\pm 0.1$	$\pm 2.7$	$\pm 0.4$

For both formulations, relative errors are larger for the flow rate than for pressure. If visco-elasticity is modelled, the averaged pressure ${\mathcal{E}}_P$ and flow ${\mathcal{E}}_Q$ errors over all measuring sites are significantly decreased (from 3.0% to 2.5% and from 15.7% to 10.8%, respectively). Variations in $\phi$ of $\pm 0.3\mathrm{kPa}\mathrm{s}$ (the standard deviation of the measured $\phi$) leads to non-significant changes in the previous errors of less than 0.05% for pressure and 0.2% for the flow rate. Changes in the errors for mean pressures ${\mathcal{E}}_{\overline{P}}$ and flow rates ${\mathcal{E}}_{\overline{Q}}$ are not significant if visco-elasticity is modelled (Table 4).

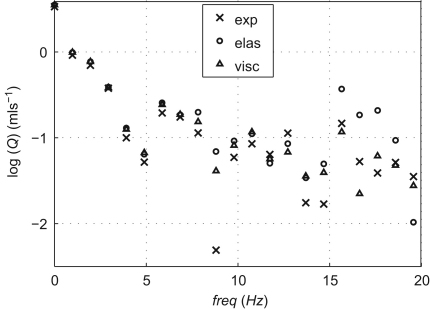
In the frequency domain, the visco-elastic formulation produces greater decreases in the relative errors of the amplitudes from the 5th to the 20th pressure ${\mathcal{E}}_{\widehat{P}}$ and flow ${\mathcal{E}}_{\widehat{Q}}$ harmonics than for the first five harmonics (Tables 3 and 4). Fig. 4 compares the amplitudes of the first 20 experimental flow harmonics in the midpoint of a vessel of the first generation of bifurcations, with the numerical predictions obtained using the elastic and the visco-elastic formulations. The latter captures these amplitudes better, especially with the increasing frequency. Similar results were obtained at the other locations studied.

Fig. 4.

Spectrum of the flow harmonics $\widehat{Q}$ on a semi-logarithm scale in the midpoint of the left renal artery (Fig. 1) of the experimental (crosses) and simulated elastic (circles) and visco-elastic (triangles) models.

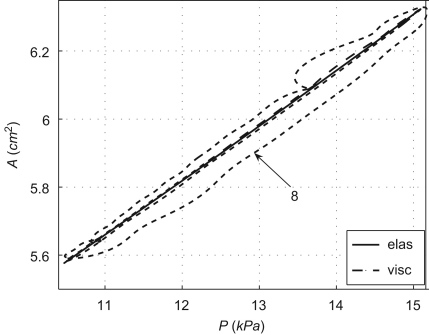
The A–P curves obtained using the visco-elastic model present an area of hysteresis that is much smaller than the area obtained from in vivo measurements (Armentano et al., 1995a,b; Valdez-Jasso et al., in press), as Fig. 5 shows in an aortic location. The numerical formulation predicts an increase in this area with the increasing wall viscosity $\phi$ (Fig. 5).

Fig. 5.

Area–pressure curve in the midpoint of the thoracic aorta I (Fig. 1) simulated using the elastic (elas) and visco-elastic (visc) numerical models. We also show the curve obtained using the visco-elastic model with eight times the measured viscosity of silicone $(8\phi )$.

4. Discussion

We have shown that simulation of wall visco-elasticity decreases the relative root-mean-square errors of numerical pressure and flow predictions in the aorta and all the generations of bifurcations of the silicone model, in both the frequency and time domains.

According to our frequency–domain analysis, the damping effect due to visco-elasticity is more significant from the 5th flow harmonic (Table 4). This leads to a decrease in the high-frequency oscillations of the purely elastic model and supports the hypothesis suggested in Matthys et al. (2007) that visco-elasticity has a more significant effect on damping oscillations predicted by the purely elastic formulation (with higher amplitudes than those observed in vivo) than energy losses at junctions and peripheral compliances in the overflow reservoirs. The damping effect in the visco-elastic model is greater in distal vessels, which is in agreement with the increase in the viscous term of the tube law (5) with the decreasing cross-sectional area toward distal locations. The minor reductions in the relative errors of mean pressure and flow rate when visco-elasticity was modelled suggest that the effect of visco-elasticity on mean pressures and flow rates is secondary.

The relative errors of flow rate predictions were larger than corresponding pressure predictions, which is consistent with the larger uncertainty of the experimental flow measurements compared with the experimental pressure measurements discussed in Matthys et al. (2007). Additional uncertainties were introduced by changes in the boundary conditions of the experimental setup every time the pressure and flow transducers were repositioned. Indeed, significantly different errors were obtained between measured and predicted mean flow rates ${\mathcal{E}}_{\overline{Q}}$ at several locations within the same vessel (e.g. Segments 31–33 in Table 3). The uncertainties in the measurement of the visco-elastic modulus were relatively small and did not introduce large errors in the numerical results. However, the uniaxial extension tests were carried out at a slower speed (about 6 s for a load–unload cycle) than the experimental inflow imposed by the pump (70 beats per minute). This difference may be responsible for some of the errors observed in the visco-elastic pressure and flow predictions.

Another limitation of this study is the use of a linear model to describe the dynamics of the vessel walls (Eq. (2)) that does not account for the stress relaxation observed in the uniaxial tests (Fig. 2, top). Models accounting for stress relaxation (Bessems et al., 2008; Devault et al., 2008; Valdez-Jasso et al., 2009), and the nonlinear behaviour of the wall (Reymond et al., 2009; Valdez-Jasso et al., in press) have been proposed, but their applicability to patient-specific 1-D modelling is more challenging, since more parameters must be estimated than in the Voigt model. We believe that a linear constitutive model is a reasonable approach, since wall deformations are small under normal physiological conditions. According to the 1-D visco-elastic results, changes in the diameter of the ascending aorta over the cardiac cycle are less than 6.5% of its mean diameter. These changes decrease toward distal locations.

Although the areas of hysteresis produced by the visco-elastic formulation (Fig. 5) are smaller than those observed in vivo, they are in agreement with the corresponding areas measured experimentally (Fig. 2, bottom). We could not assess the accuracy of the diameter waveforms predicted by the 1-D model, since we did not measure them experimentally. However, the area of hysteresis increases if a greater wall visco-elasticity $\phi =24\mathrm{kPa}\mathrm{s}$ is used. This is a more physiological value according to data in Armentano et al. (1995b) and Gariepy et al. (1993) for the carotid and femoral arteries of normotensive men.

Using an anatomically realistic model of the arterial network, we have shown that wall viscosities about an order of magnitude smaller than those measured in the human play a significant role in shaping the high-frequency components of the pressure and flow waveforms, especially in the periphery. This result supports the qualitative observations by Reymond et al. (2009) in the human and our previous conclusion that energy losses at bifurcations have a secondary effect on the blood flow in large arteries compared to visco-elasticity (Matthys et al., 2007).

We have provided further evidence to support the conclusions given in the previous works (Segers et al., 1998; Segers and Verdonck, 2000; Olufsen et al., 2000; Alastruey, 2006; Matthys et al., 2007; Steele et al., 2007; Bessems et al., 2008; Reymond et al., 2009) about the ability of the 1-D formulation to capture the main features of pressure and flow wave propagation in large arteries (and hence the use of this mathematical model to simulate clinically relevant problems), if accurate measurements of the parameters of the model are provided. The 1-D formulation is computationally inexpensive (it takes the order of minutes to solve one cardiac cycle for a whole body model) and, hence, offers a good balance between accuracy and computational cost when a global assessment of pressure wave propagation in the cardiovascular system is required.

Conflict of interest statement

There are no conflicts of interest between the authors of this paper and other external researchers or organisations that could have inappropriately influenced this work.