Considerations for Reporting Finite Element Analysis Studies in Biomechanics

Abstract

Simulation-based medicine and the development of complex computer models of biological structures is becoming ubiquitous for advancing biomedical engineering and clinical research. Finite element analysis (FEA) has been widely used in the last few decades to understand and predict biomechanical phenomena. Modeling and simulation approaches in biomechanics are highly interdisciplinary, involving novice and skilled developers in all areas of biomedical engineering and biology. While recent advances in model development and simulation platforms offer a wide range of tools to investigators, the decision making process during modeling and simulation has become more opaque. Hence, reliability of such models used for medical decision making and for driving multiscale analysis comes into question. Establishing guidelines for model development and dissemination is a daunting task, particularly with the complex and convoluted models used in FEA. Nonetheless, if better reporting can be established, researchers will have a better understanding of a model’s value and the potential for reusability through sharing will be bolstered. Thus, the goal of this document is to identify resources and considerate reporting parameters for FEA studies in biomechanics. These entail various levels of reporting parameters for model identification, model structure, simulation structure, verification, validation, and availability. While we recognize that it may not be possible to provide and detail all of the reporting considerations presented, it is possible to establish a level of confidence with selective use of these parameters. More detailed reporting, however, can establish an explicit outline of the decision-making process in simulation-based analysis for enhanced reproducibility, reusability, and sharing.

Introduction

Advances in computer model development and simulation software facilitate physics-based explorations relying on the principles of mechanics. Due to the increased capabilities of solvers to accommodate robust and speedy simulations, the availability of algorithms to represent various physiological phenomena, and the development of user interfaces that bring model development to the masses, numerous contributions have been made through the broad use of modeling and simulation in medicine and clinical translational research by a diverse group of investigators. The downside, however, is that the modeler’s decision-making process and the solution approach have become less transparent. Moreover, modelers are sometimes uninformed about the limitations of their model and the simulation software, causing the readers, users, and reviewers of such models to be uninformed. Standards for model and data sharing (ISO, 2000; ISO, 2006; CGNS, v2.0.20) and a variety of guides and standards for verification and validation (ASME, 2006; ASME, 2009) try to establish confidence in modeling and simulation results for the readers, users, and reviewers. However, while these existing standards are helpful, they do not explicitly address the issue of reporting and communication, particularly regarding finite element analysis (FEA) in the field of medicine and biomechanics, where complex models of nonlinear mechanics of biological structures are developed.

FEA was developed over 70 years ago to solve complex elasticity and structural analysis problems in civil and aeronautical engineering (Zienkiewicz, 2004). Applications of FEA were expanded to simulations in biomechanics, as portrayed by investigations utilizing this computational tool for more than three decades, dating back to late 1970s (Miller, 1979). For example, the potential of FEA to address problems in orthopedic biomechanics (Huiskes and Chao, 1983) and ventricular systems (Yin, 1985) has been demonstrated. Currently, studies incorporating FEA to support basic and clinical translational research in medicine exceed ten thousand (as of July 7, 2010, the cumulative total number of citations for the search string “finite element” is 11,300; searched in PubMed, http://www.pubmed.org). Of these, more than 250 are review articles and more than 50 articles focus on multiscale analysis. In addition, the number of studies using FEA appears to be increasing geometrically (Figure 1).

Figure 1.

Published studies utilizing finite element analysis as a research tool (from 1980 to 2009). Search conducted on Pubmed (http://www.pubmed.org) with the search string “finite element”. As of July 7, 2010, 839 articles published in year 2010 included this keyword (not shown in figure). Total number of citations before 1980 is 22. Image courtesy of Ahmet Erdemir, Department of Biomedical Engineering, Cleveland Clinic.

With the increasing number of FEA studies, FEA practice in biomechanics continues to pose a challenge for model development, sharing and reporting. In FEA, model definitions and development procedures are tightly coupled to the simulation method and the solver capabilities. FEA software (commercial or otherwise) commonly relies on embedded mathematical models of physical phenomena, e.g., solid mechanics. Some packages are specifically designed for the analysis of biological structures, e.g., Continuity 6 for cardiac mechanics (http://www.continuity.ucsd.edu/Continuity) and FEBio for biomechanical applications (http://mrl.sci.utah.edu/software/febio), but many are presented as general analysis tools.

In many cases, decisions made during model development depend on the specific solver capabilities. Furthermore, while many simulation software packages exist, a universally accepted unified model definition language, i.e., mark-up language, does not exist. Current model related data exchange standards (ISO, 2006) may not readily be applicable to complex biomechanical FEA models. Therefore, a practical solution is needed to enhance current model development and dissemination efforts. One possible solution is to establish reporting parameters of FEA models and simulation studies. Although it may not be practical to immediately realize the long term goal of adopting standards for model exchangeability, immediately augmenting model reporting across disciplines could facilitate transition to higher level modeling standards. Because most FEA share common features during model development and simulation process, it is possible to compile parameters for reporting items that may be important for model reproducibility and may help the scientific community to assess the overall quality, scientific rigor, and utility of the model. Thus, the purpose of this document is not to present “how-to-run FEA studies” or “best practices in FEA” but to present easy to follow, adaptive, and expandable reporting parameters for modeling and simulation studies in biomechanics with an emphasis on FEA. The document is targeted for scientists and engineers (in academia, industry, government, etc.) for the purpose of disseminating biomechanical models, publishing, and evaluating others’ simulation research; for journal editors and reviewers judging manuscript quality; for agencies and grant reviewers during crucial decision making; and for professionals (in biomedical and clinical translational research) to promote good modeling and simulation practice. This lengthy document is not a substitute for author or reviewer expertise. However, it can highlight the important aspects of the modeling and simulation process, particularly in multi-disciplinary research where the necessary expertise may not be readily available.

Throughout this document, the term “model” refers to the computational representation of the biological structure and its components, e.g., cartilage between knee joints or vessel wall with stent, for FEA, including discretized geometric representation, constitutive relationships of substructures, interactions between substructures, and loading and boundary conditions representative of the biomechanical environment. The term “simulation” refers to the solution process of the finite element representation of the biological structure and its components through the use of finite element analysis techniques. Finally, the term “multiscale” conveys the interactions between higher spatial scales of the Physiome, between joint/organ biomechanics and tissue mechanics, and between tissue mechanics and cell biomechanics (Tawhai et al., 2009).

Reporting Parameters

Initiatives and guidelines for reporting research methods and findings have been listed by the National Library of Medicine, National Institutes of Health (http://www.nlm.nih.gov/services/research_report_guide.html). This list includes many standards that address a wide range of applications. These standards are undoubtedly valuable for the reporting process and result in valid (consistent, reproducible and accountable) studies to their respective fields. For example, the Consolidated Standards of Reporting Trials (CONSORT) provides a well established 25-item checklist for reporting of randomized clinical trials (Moher et al., 2010; Schulz et al., 2010). Within that list, computational studies addressing biological processes have generally adopted the Minimum Information of Biological and Biomedical Investigations (MIBBI) (Taylor et al., 2008). Within MIBBI, the Minimum Information About a Simulation Experiment (MIASE) specifically addresses the minimum necessary information to recreate general computational simulations. While the general guidelines provided by MIASE may be applicable to FEA studies, specific and detailed recommendations are missing for adequate reporting of this complex analysis tool in biomechanical investigations.

For reporting on FEA, a few general guidelines have been recommended. Clinical Biomechanics specifies that simulations need to comply with the requirements listed in a useful editorial by Viceconti et al. (2005). However, it stops short of developing reporting parameters for the scientific community that should be included or addressed in a manuscript for complete understanding and potential reproducibility of the model. Generalizations such as “Model Selection” and “Proper Parameter Identification” are discussed without specifically highlighting relevant model features. The Annals of Biomedical Engineering requests that authors indicate that models conform to standard modeling practice and that the studies include important parameters and assess associated variability and model sensitivities (http://www.springerlink.com/content/q072n75584247042/fulltext.pdf). Examples in other disciplines also exist. The Engineering Fracture Mechanics prepared a general guide to educate researchers on proper scientific and publishing practices (http://www.elsevier.com/wps/find/journaldescription.cws_home/322/preface2). It includes a section on computational work stating that basic features such as boundary conditions, element types, and input parameters should be provided for publication. Along the same lines, ASTM International has published F2514-08 (ASTM, 2008), where section ten discusses reporting considerations for FEA studies of uniform radial loading of stents. The above examples all attempt to define a minimum level of publication criteria while reporting on finite element analysis studies but lack the specific details and definitions necessary to completely and accurately assess these models. Therefore, the intention of the paper is to provide a compilation of reporting parameters for broad distribution and use.

Ideally, a published FEA study would provide substantial details for reproducibility and of appropriate verification and validation procedures. Condensing all this information in a usable form may be difficult, but might be necessary for the future of model and data sharing and exchangeability. Due to space constraints and possible oversight by the developers, many valuable steps and decisions made during the modeling process might be omitted in the publication. Based upon our compilation of reporting parameters for different aspects of the modeling and simulation process (construction, processing, post-processing, etc.) for reproducibility, reusability, and accountability, which we present in the following sections, we examined the details of one FEA study from the literature (Yao et al. 2006) to illustrate the reporting elements that could be independently gleaned from this manuscript (Appendix A). This example also reveals the decision-making process involved in complex model development, where details were not provided as a parameter list, per se, but could be described in the text of a manuscript, on a need basis. Finally, it is important to note that not all of the reporting parameters presented below need to be detailed in a document. As the authors of these reporting parameters, we feel that the some parameters are important for establishing confidence in the model, and thus are presented in underlined text. This does not preclude other parameters from being reported, depending on the purpose of the model, and particularly when the target reader population may be seeking for facilitated reproducibility, reusability, and sharing.

Model Identification

The model identification description should provide an overall explanation of the model to enable proper categorization and elucidate the overall capabilities and limitations. These items identified below collectively assist the audience in establishing the intended purpose of the model (particularly through the parameter primary utility) and the relevance of the model for others’ needs.

• Model name. Offer a specific and concise descriptor which distinguishes it from other similar models.

• Model keywords. Identify the biological phenomena under investigation (body/organ/tissue/cell of interest) and the modeling and simulation approaches, which enable indexing of the model for repositories and establishing ontologies.

• Version. Identify the version of the published model, as it is possible that a model may be revised or adapted multiple times through the development and publication cycle, and during its evolution through the scientific process.

• Physiological domain. Describe the biological model, i.e., motion of segments, deformation and/or loading of the biological structure(s).

• Mechanical domain. Describe the mathematical formulation used to simulate the model, i.e., linear/nonlinear elasticity, static/dynamic equations of equilibrium, biphasic simulations.

• Structure of interest. Identify the anatomical structure under investigation, i.e. specific body, organ, tissue or cell.

• Demographics. Explain the population of which the model belongs, i.e., human, animal, artificial, male, female, age, etc.

• State of represented organism. Describe the state of the organism as “in vivo”, “in vitro”, or “in situ”, if appropriate.

• Disease state. Describe any pathology, if appropriate.

• Spatial scale. Identify the spatial scale (with units) of the model, which may also be defined by the structure of interest, macroscopic aspects, or microstructural architecture of a given biological segment.

• Time scale. Describe the temporal scale (with units) and identify whether a transient or steady state response is sought.

• Primary utility. Explain the motivation for model creation and its main purpose and function. Outline the scope, as not every model is developed for predictive “what if” type of simulations but sometimes for descriptive analysis to provide mechanical insight into a physiologic process, e.g., deformation at the level of a single cell. A clear delineation of the model’s primary goal will likely to imply the expectations from its reporting.

• Secondary utility. Discuss additional uses of the model.

• Primary highlight. Identify the most innovative component or the expected key finding that can be deduced from model’s predictions.

• Secondary highlight. Identify any additional features that may promote the value of the model.

• Primary limitation. Identify the most significant limitation that hinders the primary utility of the model and interpretation of the model’s prediction.

• Secondary limitation. Identify the additional limitations that can cause uncertainty in model performance.

• Reference to publication(s). If exists, list relevant publications about the model, e.g., peer-reviewed articles, conference proceedings, etc., particularly when disseminating the model.

• Pointer to publication. Direct the audience to a peer-reviewed publication, if it exists, i.e., using a Digital Object Identifier (http://www.doi.org/)

• Related models. Describe the different versions (competing and/or complementing models) of the same model, if they exist.

Model Structure

Model structure should provide adequate information for reproducing the model, including all its subcomponents and input-output relationships. This information is pertinent for those who want to evaluate the results of the model in detail, potentially reuse the model to conduct simulations with same or different inputs, and also to customize the model for their research needs. Note that if the model files are not shared, detailed reporting is important for portability.

• Loading and boundary conditions. Describe the constraints and loads (magnitudes, time history, etc.) that are externally imposed on the model structure to represent the effect of the surrounding environment.

  • Type. Identify whether the condition is kinematic (displacement/velocity or constraint) or kinetic (load), followed by the relevant specific type(s), e.g. prescribed motion (displacement/velocity), point force or pressure (load).

  • Region. Describe which region of the model the condition is applied, e.g., gravitational force to the whole model.

  • Magnitude and direction. Describe the magnitude and direction of the condition and how it relates to the physiological meaning of the model and simulation.

  • Time history. Describe the time history of the boundary conditions and their physical meaning. If it is a nonlinear static analysis, the time history is abstract and can be used to represent a simulation scenario.

• Primary output variables. Describe the primary variable the model predicts, e.g., shear stress, which is relevant to the primary utility and is important for determining the appropriate verification and validation procedures.

• Secondary output variables. Report secondary outputs that may enhance the utility of the model for other purposes.

• Source of anatomy. Describe the main source of anatomical representation for the model and its subcomponents, e.g., imaging modality. Discuss the imaging resolution. For individual subcomponents, provide descriptions in more detail as described below.

  • Modality. Report the basic protocol settings of the imaging modality used to acquire the anatomy, e.g., CT, MRI, OCT, etc. Discern between macroscopic and microscopic imaging techniques.

  • Resolution. Report the resolution of the imaging technique.

• Reference configuration. The coordinate system of the model should be described. In addition, the zero load state should be specified. Typically, the state, at which the biological structure is imaged, is assumed to be the zero load state. If this is not the case, describe the procedures to modify the reference state and the coordinate system.

• Subcomponents (subsidiary models). Many models used in biomechanical simulations incorporate multiple components, e.g., bone and cartilage, stent and vessel wall. These components are subsidiary models of the artificial or sub-biological structures and they require detailed reporting, e.g., geometric representation and material properties.

  • Name. Provide a descriptor for the substructure for adequate cross-referencing to the component.

  • Geometric representation. Geometric representation for subcomponents of the model may or may not rely on the main source of anatomy (as described above). If not, the source of geometry for individual biological and non-biological subcomponents, e.g., medical devices, should be reported along with errors associated with geometric reconstruction.

    • Source. Describe the source of the geometry if different than the modality of the main source of anatomy (as described above). This can be based on other imaging modalities or design drawings. Provide a citation if it is available from a previous work.

    • Resolution. If geometry is reconstructed from imaging different than the main source of anatomy, report the resolution of the source of geometry.

    • Segmentation procedure. If geometry is reconstructed from medical imaging, describe the segmentation approaches, and report associated segmentation errors.

    • Representative geometry. When imaging is not used to generate the geometry, provide details on the construction of the simplified biological and artificial structures. In case of approximations, describe the assumptions made regarding the geometry, e.g., artery modeled as a uniform tube with constant thickness.

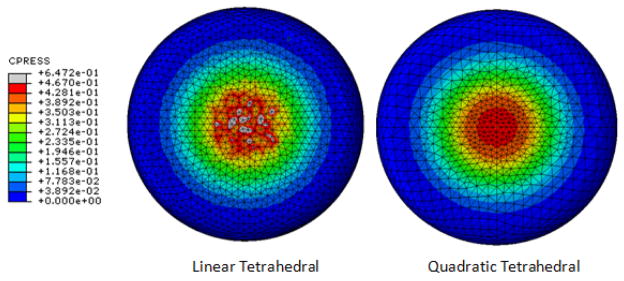
  • Mesh. The performance of the simulation likely relies on the quality and characteristics of the mesh (Figure 2); summarize the specific details for adequate mesh reproducibility.

    • Element name. Provide the name as used in the finite element analysis package, e.g., C3D8H.

    • Element shape. Because the geometry of the element may influence the performance and accuracy of simulation, describe the element shape and include any acceptance criteria, e.g., max aspect ratio.

    • Element formulation. Describe the formulations used to interpolate the field variable within an element. Provide additional information necessary for the integration to satisfy equations of equilibrium and other constraints, e.g., mixed formulation to handle material incompressibility, reduced integration.

    • Mesh density. Report the total number of nodes, elements, and average element edge length to indicate an adequate mesh for geometric complexity.

  • Constitutive representation. Provide the relationship between field variables, e.g., stress and strain, specific to the underlying material.

    • Formulation. Provide a clear description of the chosen material behavior, as many FEA codes provide built-in material models, which may also differ between solvers.

    • Coefficients. Provide values for all coefficients required to describe the constitutive relationship.

    • Source. Outline the data fitting procedure used to obtain coefficients, and describe the data collection procedures. Applicability of these parameters to the model may be demonstrated by the experimental procedures and loading modes used to determine the material coefficients. Provide the reference if the coefficients are available or can be derived from previously reported data.

  • Reference configuration. Discuss whether or not the reference configuration (coordinate system and zero load state) of the subcomponent is updated separately from the main model component. Also provide (relative) placement of the subcomponent, including its pose and orientation.

  • Other properties. Report other properties, e.g., density, that are necessary to conduct the simulation.

• Interactions. In multi-component models, complex interactions between substructures may need to be resolved, e.g., contact. Provide a complete list of interactions (interacting components and type of interaction), and summarize the formulation and relevant properties. Provide references when relevant.

  • Interacting components. List each component and individual interaction.

  • Interaction type. Describe the interaction between components, e.g., contact, kinematic constraint.

  • Interaction formulation. Describe the interaction formulation, and provide a reference for previously determined formulations as many exist.

  • Interaction properties. Describe the interaction properties as these will dictate how the physical interaction is represented. For example, if contact with friction is utilized, the coefficient of friction should be provided with appropriate citations.

Figure 2.

An incomplete description of mesh details may hinder reproducibility of the study. For the same element shape, e.g. tetrahedral in this example, different element formulations exist to interpolate the field variables, as well as to solve for them. One tetrahedral element formulation may result in significantly different distributions for the field variable of interest, in this case contact pressures predicted for the compression of a heel pad analog. Image courtesy of Srinivas Tadepalli, Department of Orthopaedics, University of Washington.

Simulation Structure

The simulation process in FEA commonly encapsulates the mathematical model that represents the mechanics. The development of the computational model, in this case the finite element representation of the biological structure, is tightly coupled to the simulation software capabilities. The information provided in this section identifies the underlying simulation architecture necessary to reproduce the results of the model. It is advised to refer to the relevant sections of simulation software manuals.

• Name of simulation software. State the software platform and its analysis components.

• Version of simulation software. State the version of the FEA software used because aspects of the FEA software can be different between versions. Some models are not compatible between versions.

• Solution strategy. Identify the solution strategy, e.g., implicit static, implicit dynamic, explicit, and its relevant settings, e.g., incrementation.

• Numerical algorithms. Summarize the algorithms used. Many FEA solvers adopt a variety of numerical algorithms which may affect the solution and/or convergence. For example, in a nonlinear implicit static analysis, the equations can be solved through full Newton or quasi-Newton iterations. State if default procedures of the simulation software are used.

• Convergence criteria. Provide the convergence tolerances used to determine the completion of a simulation. State if default convergence criteria of the simulation software are used.

• Post-processing. Provide the post-processing approach if the primary and secondary outputs are calculated from raw simulation results.

Verification

For a given problem, verification is asking “are you solving the equations right”, whereas validation is asking “are you solving the right equations”. Therefore, verification of the simulation software is to determine if the underlying mathematical formulation and numerical procedures utilized to solve the model are appropriate, repeatable, and correct. In biomechanics, the procedures to conduct verification and validation studies and current practice of verification and validation have been described in detail by Anderson et al. (2007) and Henninger et al. (2010). Despite the fact that many model developers will conduct their own verification or rely on tools and documentation provided by the simulation software developers, it may be useful to consider reporting the verification procedures. Please note that current complex models in FEA require interaction of various mathematical models and numerical algorithms. Although verified individually, when combined, these algorithms may behave in an unstable fashion.

• Methods of verification. Summarize verification analysis conducted in addition to the verification procedures provided by the simulation software and/or performed by others available in the literature.

• Correctness of formulation. If the functionality of the simulation software was extended to accommodate the additional processes for the model, e.g., new constitutive formulations through user subroutines, report the techniques used to confirm correct implementation.

• Comparisons with known solutions. Summarize any simplified analysis (analytical or numerical with previously verified known solutions) that represent the mechanical domain and subsidiary models.

• Sensitivity to simulation settings. Report the influence of different solution strategies, numerical algorithms, and convergence criteria on the model’s prediction (if tested) as this information helps users balance computational cost and numerical accuracy.

• Mesh convergence. State the output variables used to confirm that the simulation results are independent from further increases in mesh density. Also, identify if the variables represent overall model response or regional solutions, as these assumptions will influence convergence (Figure 3). If the primary output of the model is not used in mesh convergence, report the relationship between the variable used and the primary output.

• Assessment of repeatability. Report the outcomes, if any, of simulating the model on different platforms. Independence of the model and simulation process from the hardware platform and operating system results in a more robust and adaptable model for other users.

Figure 3.

The outputs of the finite element analysis may depend on mesh density. During reporting, it is necessary to establish confidence in the adequacy of the mesh to reproduce the variable of interest without dependency on the mesh. If primary output of the model is not used for the mesh convergence analysis, document the relationship between the variable used and the primary output of the model. For example, in a finite element representation of a ligament (pulled in one end under displacement control), prediction of ligament force requires a lower mesh density when compared to calculation of peak regional von Misses stress. Image courtesy of Ahmet Erdemir, Department of Biomedical Engineering, Cleveland Clinic.

Validation

As stated above, validating the model determines if you are solving the right equations to represent the biomechanics of the problem at hand. Establishing and reporting details on validation procedures and results provides the foundation for the utility of the model, which is a part of good reporting practices. Investigators can consult work by Anderson et al. (2007) and Henninger et al. (2010) to establish procedures for conducting validation studies. Validation, in general, should match the purpose of the model. Some models are developed solely for exploratory purposes and may not need rigorous validation. The items provided below are considerations to aid in the reporting of validation studies, whereas technical details on validation can also be found in guides and standards from professional societies (ASME, 2006; ASME, 2009).

• Validation procedure. Outline the procedure, or lack there of, for model validation. The procedure may include direct validation (experimentation done by model developer where an output from the experiment directly matches the predicted output from the model), and indirect validation (based on data from literature) (Henninger et al., 2010). Alternatively, describe how the model development approach is valid, portrayed by modeling and experimentation of a simpler, yet physiologically and mechanically representative problem.

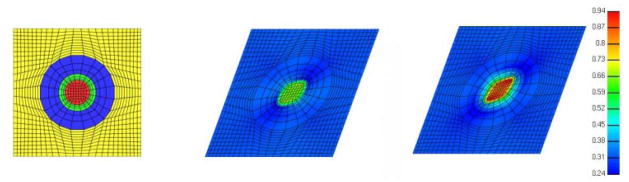
• Validated output. State the output used for validation. Discuss if the validation output is the primary output of the model or a secondary output, or if it is an overall response of the whole model or a regional one, and how the output variable is relevant to demonstrating the primary utility of the model. Also note that a model that is validated for a single output variable, e.g., deformation, and may not necessarily be valid for another (Figure 4).

• Overall modeling assumptions. List the main assumptions relevant to the simplification of the biological structure and its physiological response during the process of its physical representation. These may include geometric assumptions for anatomical representation and mechanical simplifications, such as neglecting viscoelasticity.

• Physiological relevance of loading and boundary conditions. Report the source of loading and boundary conditions and describe how the loading and boundary conditions were derived so that the user can understand the physiological relevance of the model.

• Justification of parameters. Provide adequate justification to support the selection of parameters for model simulation to further support utility of the model.

• Data used for model development. Describe the source and type of data for the model development. For example, state whether the data are specimen and/or sample specific, are based on average of population results, and/or compiled from a variety of literature sources.

• Data used for model comparison. Describe the source and type of data for the model comparison to establish validity. Note that data used for this purpose may be obtained from a different set of experiments (compared to the source of data for model development) conducted on the same sample or different samples. State whether the data are specimen and/or sample specific, are based on average of population results, and/or compiled from a variety of literature sources.

• Sensitivity analysis. Discuss any uncertainties in model inputs and parameters that can diminish the reliability of the model, i.e., estimated material properties may affect predicted deformations (Figure 5). Furthermore, discuss how the uncertainties may affect the interpretation of the results. If a sensitivity analysis is performed, report the list of parameters, the range of perturbations, and the justification. Additionally, for complex models, discuss any elaborate sensitivity analysis that utilize systematic procedures, such as the Monte Carlo technique.

• Predictive capacity. Describe the predictive capacity and limitations of the model based on the validation. Additionally, if appropriate, discuss the features that enhance or limit the predictive capacity.

Figure 4.

Explicit reporting of the utilization of primary or secondary variables as a measure of model validity can facilitate reader’s judgment to evaluate confidence in simulation results. For example, a model validated for the same averaged quantities or structural level variables, e.g. joint reaction force, contact area, may not necessarily provide similar results for material level field variables, e.g. von Mises stress or contact pressure. Image courtesy of Craig Bennetts, Ahmet Erdemir and Jason Halloran, Department of Biomedical Engineering, Cleveland Clinic.

Figure 5.

Uncertainties in subsidiary models, used for the representation of loading and boundary conditions or description of the constitutive response, may establish confidence in the study and a better interpretation of the results. For example, in multiscale analysis, microstructural models are subsidiary models that are driven by macroscopic tissue strains. Microstructural models with same geometric representations but different chondrocyte properties (as obtained from two separate works; from left to right: undeformed mesh, Michalek and Iatridis, 2007 and Guilak and Mow, 2000) may result in disparate predictions of cell deformations under the same macroscopic tissue strains. Effective strain distributions across the microstructural models are pictured, as predicted by finite element analysis. If possible, reporting or citing sensitivity studies to illustrate that the conclusions are not significantly affected by such uncertainties, increases the strength and confidence of the research. For complex models, referrals to elaborate sensitivity analysis utilizing systematic procedures such as the Monte Carlo technique, are helpful. Image courtesy of Scott Sibole and Jason Halloran, Department of Biomedical Engineering, Cleveland Clinic.

Availability

By making the model available for public access (with the appropriate conditions of distribution), developers can establish confidence in the simulation results by enabling the user to run the model, evaluate, manipulate and expand the capabilities of the model. Infrastructure to support model development and dissemination exists, i.e. by Simbios, National Institutes of Health Center for Biomedical Computation at Stanford (https://www.simtk.org). If sharing is part of your research paradigm, then the following items could aid in the reporting of dissemination mechanism.

• Contact. Investigator(s) that can accept inquiries for the model should be listed in model related documentation, including publications. Include physical and online contact information. If possible, provide alternates in case of project abandonment by the principal investigator. If a development website is provided, contact information should be updated to reflect changes in the development team.

• Licensing. If the model is distributed, report the licensing terms in a clear fashion to aid the prospective user in understanding the legality of model use and redistribution. Many licensing schemes exist to refer directly, e.g. http://www.opensource.org/, if they deem to be suitable for the distribution. Attempts to resolve issues relevant to licensing of scientific research, e.g. http://sciencecommons.org/, may help the developers accommodate the needs of themselves, their institutes, sponsors, and the scientific community.

• Website for downloads. Provide an online resource for the source code or a binary file representative of the described model. This may enable customization of the model to match the user’s simulation needs, if licensing permits.

• Website for development. Provide an online resource to track development of the model by its originators to aid the audience in understanding the evolution of the model, access information on potential updates, and potentially contribute to the model’s further development. Enable users, if possible, to add their updated models and uses.

• Website for public commentary, responses, and rating. The reporting of the model may not conclude its assessment. Provide a website for feedback and increased visibility to expand the population of the reviewers to further enhance the model and its applications. While this can be accomplished by forums at development related websites, certain journals also provide mechanisms for rating, i.e. those from Public Library of Science (http://www.plos.org/) to accommodate wide-spread feedback.

Case Study

We analyzed one FEA study (Yao et al.; 2006) in view of the parameters provided above to illustrate and highlight the utility and limitations with taking a given model and having a different user try to summarize it for potential reproduction. This article was selected because of the authors’ comprehensive reporting of the modeling and simulation steps. The details can be found in Appendix A.

Issues in Multiscale Analysis

The reporting parameters presented in this document are geared towards reporting of computer models of a single spatial scale due to their current and past frequent use and anticipated utility in decision making, surgical simulation, intervention design, and clinical practice. Models of the single spatial scale will likely be reused in multiscale simulations and potentially dictate response at higher spatial scales (Tawhai, 2009). For example, finite element representations of joints can provide the kinematic-kinetic response of the whole joint defined by the underlying tissue organization. Such models may be used in higher level musculoskeletal models for more realistic representation of joints with the possibility to simultaneously predict regional tissue stresses along with body level movements (Figure 6). Tissue level mechanical response in joint level finite element representations can be defined using analytical constitutive relationships or can be a function of a microstructural model, which may incorporate cells or even lower spatial scales, e.g., fibers within the extracellular matrix (Figure 6). In all these cases, FEA may be conducted at the higher or lower (or both) scales of the Physiome. Because these reporting considerations have the potential to establish confidence in single scale studies, similar reporting consideration could be paid to the following when reporting multiscale analysis incorporating the finite element method.

Figure 6.

Finite element representations of biological structures can be used as a subsidiary model in different modeling modalities, e.g. musculoskeletal movement simulations coupled with finite element analysis of joints. In addition, finite element analysis can be conducted at the macro level or at the micro level to understand mechanical interactions at varying spatial scales. Image courtesy of Ahmet Erdemir, Department of Biomedical Engineering, Cleveland Clinic.

• Scale coupling. Multiscale analysis can be conducted in a post-processing sense, i.e., using the results of a macro model to drive a micro model, through an on-the-fly hierarchical coupling incorporating data transfer in between scales during simulation iterations, e.g., computational homogenization, or through strong coupling, i.e., simultaneous solution of models of multiple scales all at the same time. Regardless, explicitly report the selected approach and its suitability, based on the simulation process and physical phenomena.

• Scale separation. In multiscale analysis, one may need to rely on the assumption of the relative size of macroscopic scale and the microscopic scale, particularly in the post-processing approach and during computational homogenization. When possible, report on the acceptability of scale separation and provide relevant justification.

• Representative volume element convergence. In many cases, multiscale finite element analysis requires the utilization of a representative volume element (RVE), which is a model representing the lower spatial scale. Report the capacity of the RVE geometry to adequately represent the local microstructural geometry. Also, note the influence of RVE size on the constitutive response. Discuss whether changing RVE size affects the average mechanical response of the RVE, or the microstructural variable of interest.

• Mechanical consistency. When a post-processing approach is used, mechanical consistency of the individual representations of the same organ/joint/tissue at different length scales need to established. State if the average stress-strain response of a microstructural tissue model is the same as the constitutive relationship used in a macro model for the same tissue. Furthermore, discuss if the finite element representation of joint level model, e.g. of the knee, results in the same kinematics-kinetics relationship of a simplified joint representation that can be used in the musculoskeletal model.

Conclusions

This article presented reporting considerations of FEA studies of biological structures with a focus on solid mechanics of biomechanical systems. In the short-term, we hope this compilation will encourage collaborative evolution and adoption of these parameters by investigators, journals, funding agencies, and societies and more thoughtful documentation and review of modeling studies. In return, the uncertainty in the review process of FEA models might be diminished due to utilization of a systematized approach to understand the content of a modeling-based investigation. In the scientific community, this will likely establish confidence through model reproducibility, reusability, and accountability.

We are certainly aware that these parameters are only considerations and are not complete. Our hope is they will evolve along side the evolution of scientific research in computer modeling of biological structures. We further hope that these parameters will be utilized as the basis for customization in other disciplines, for different types of modeling modalities, and also for multidomain, multiphysics, and multiscale analysis. In biomechanics for example, musculoskeletal models commonly used in movement simulations (Erdemir et al., 2007) and fluid-solid coupling utilized in multiphysics investigations of the cardiovascular system (Humphrey and Taylor, 2008) may utilize these parameters for their specific discipline. An online version for prospective editing, adapting, and feedback is available in http://www.imagwiki.nibib.nih.gov/mediawiki/index.php?title=Reporting_in_FEA.

As we gain experience in systematically describing and reporting on models of complex systems, it is possible to form a collaborative evolutionary pathway to move from reporting standards to model exchange and sharing standards. Clarification of model exchange parameters to translate between open mark-up languages (Christie et al., 2009; Tsafnat, 2008; Chang et al., 2009;) and commercial ones used by proprietary software may be realized. These reporting considerations may also enable identification of metadata to be stored with models, as well as with simulation results (Chang et al., 2009); using open, portable, extensible and high performance data formats, i.e. Hierarchical Data Format (http://www.hdfgroup.org/), which can help automated reporting processes. Additionally, we may be able to establish detailed criteria for implementation in mark-up languages and for incorporation of complex models in multiscale simulation frameworks.

One should note that it may not be feasible to discuss or present all of these reporting parameters in a manuscript. However, many journals provide repositories for supplemental information; details (and perhaps the model and the data) might be provided there. The extent of model reporting may depend on its development stage. Early in the process, the models are usually exploratory and it may not be possible to provide elaborate reporting with complete details. Additionally, the detail of reporting will also depend on the utility of the model and simulation process. However, for some models, such as one utilized for simulation-based evaluation of a medical device, our perspective is that adequate review might rely on considerable reporting. Explicit identification of lacking components can also provide new directions for prospective developments. If a researcher decides to outline the reporting parameters, then the scientific community will surely benefit from the transparency of a model developer’s decision-making regarding computer modeling and simulation of biomechanical and biological structures, advancing the state of the bioeconomy.

Appendix A - Case Study

See supplementary material appendix_A-case_study.doc